Adaptive Compensation Tracking Control for Time-Varying Delay Nonlinear Systems with Unknown Actuator Dead Zone
Abstract
1. Introduction
2. Preliminaries
3. Main Results
4. Simulation Analysis
4.1. Nonlinear System with an Unknown Actuator Dead Zone in Known Time-Varying Delay Form
4.2. Nonlinear System with an Unknown Actuator Dead-Zone in Unknown Time-Varying Delay Form
4.3. Industrial Application Case of a Chemical Cycle
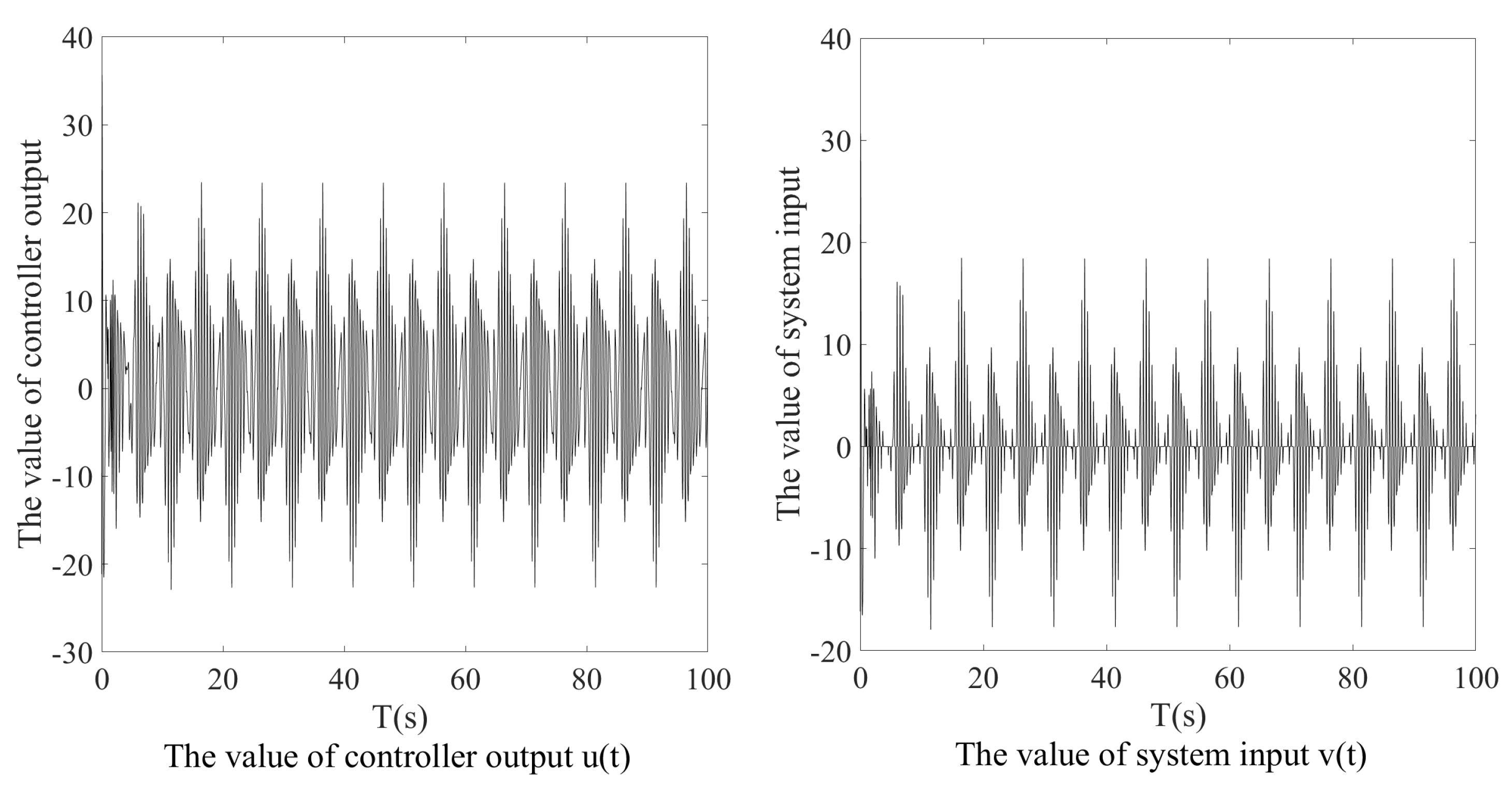
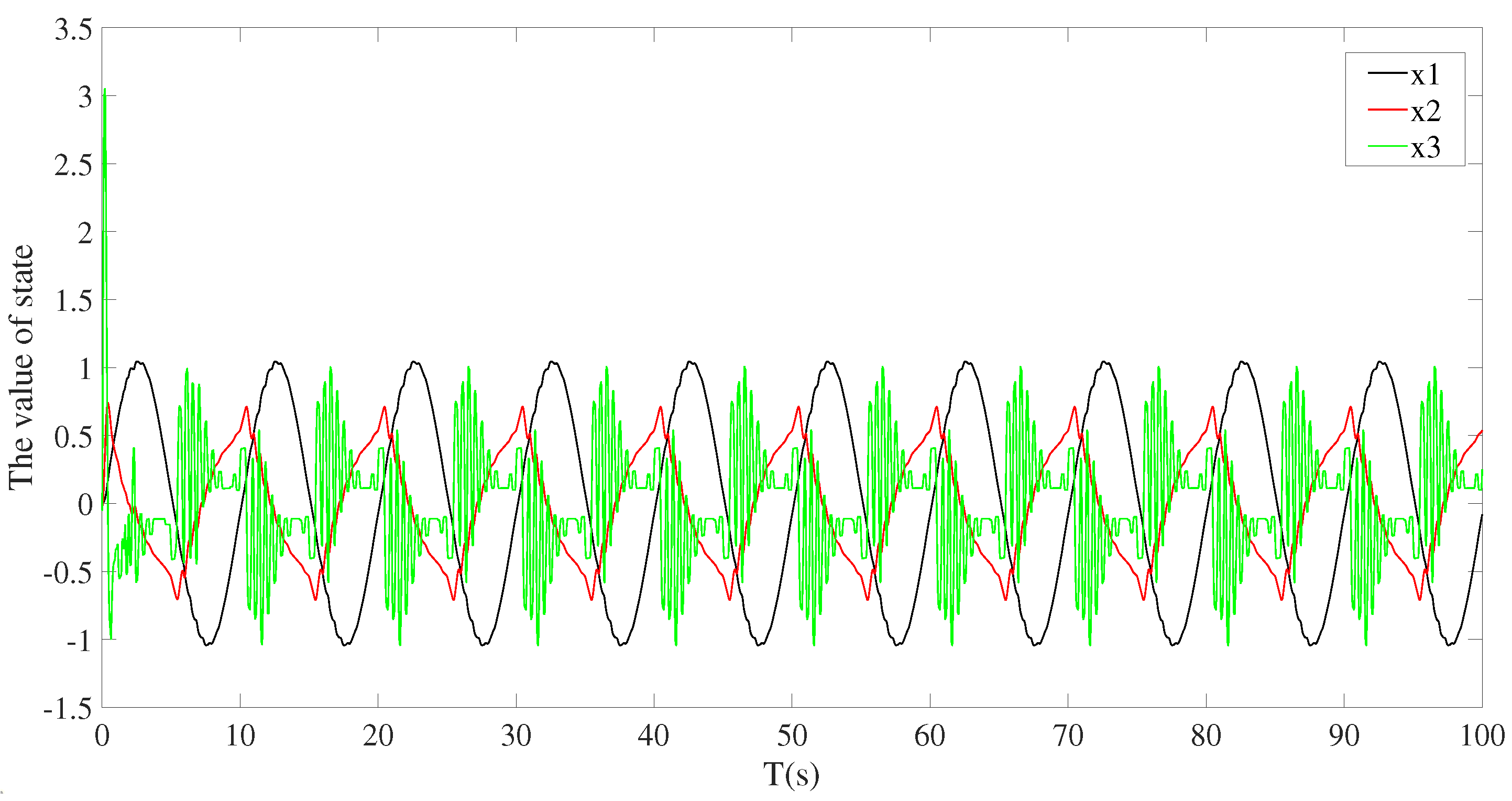
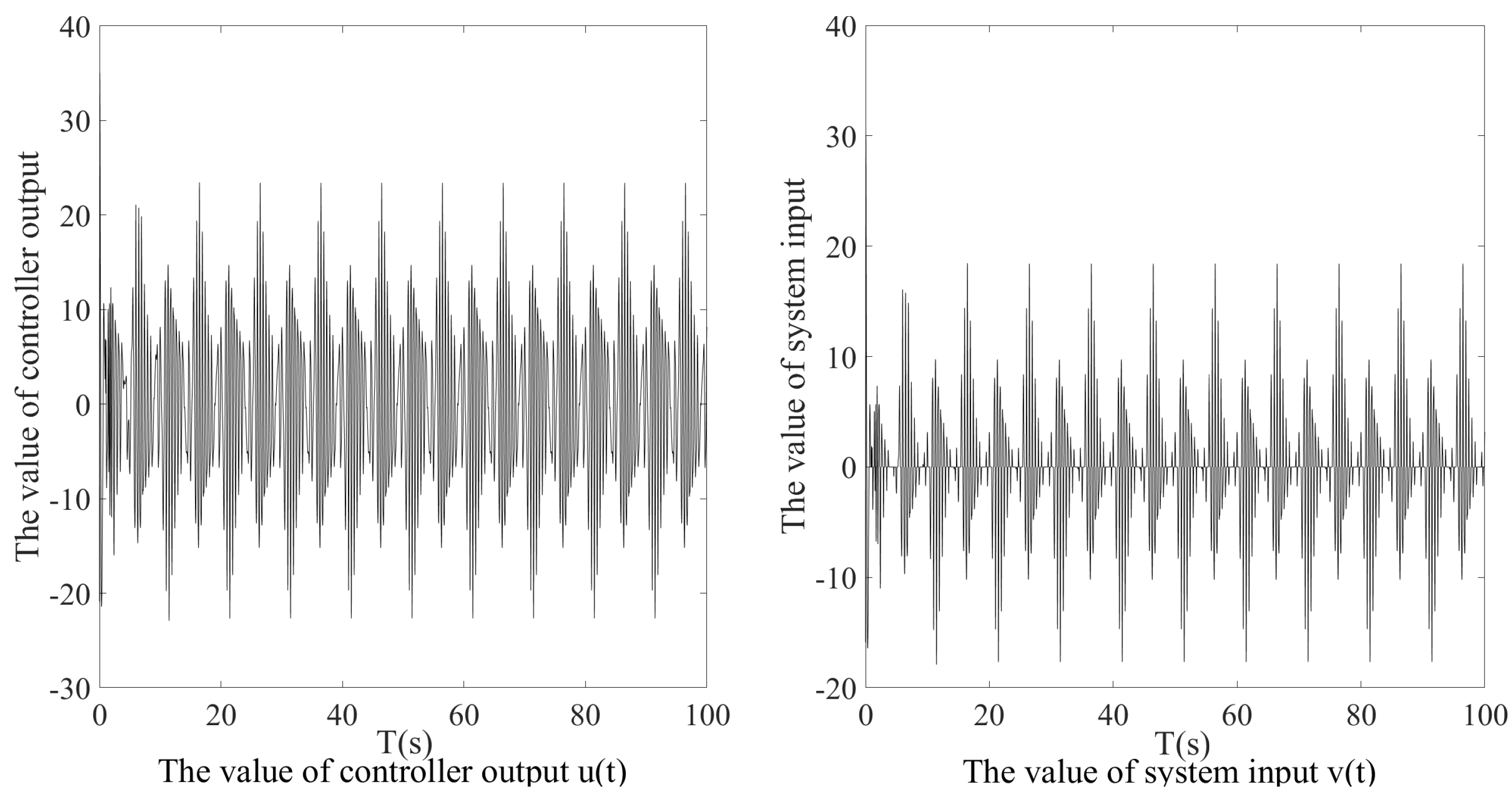
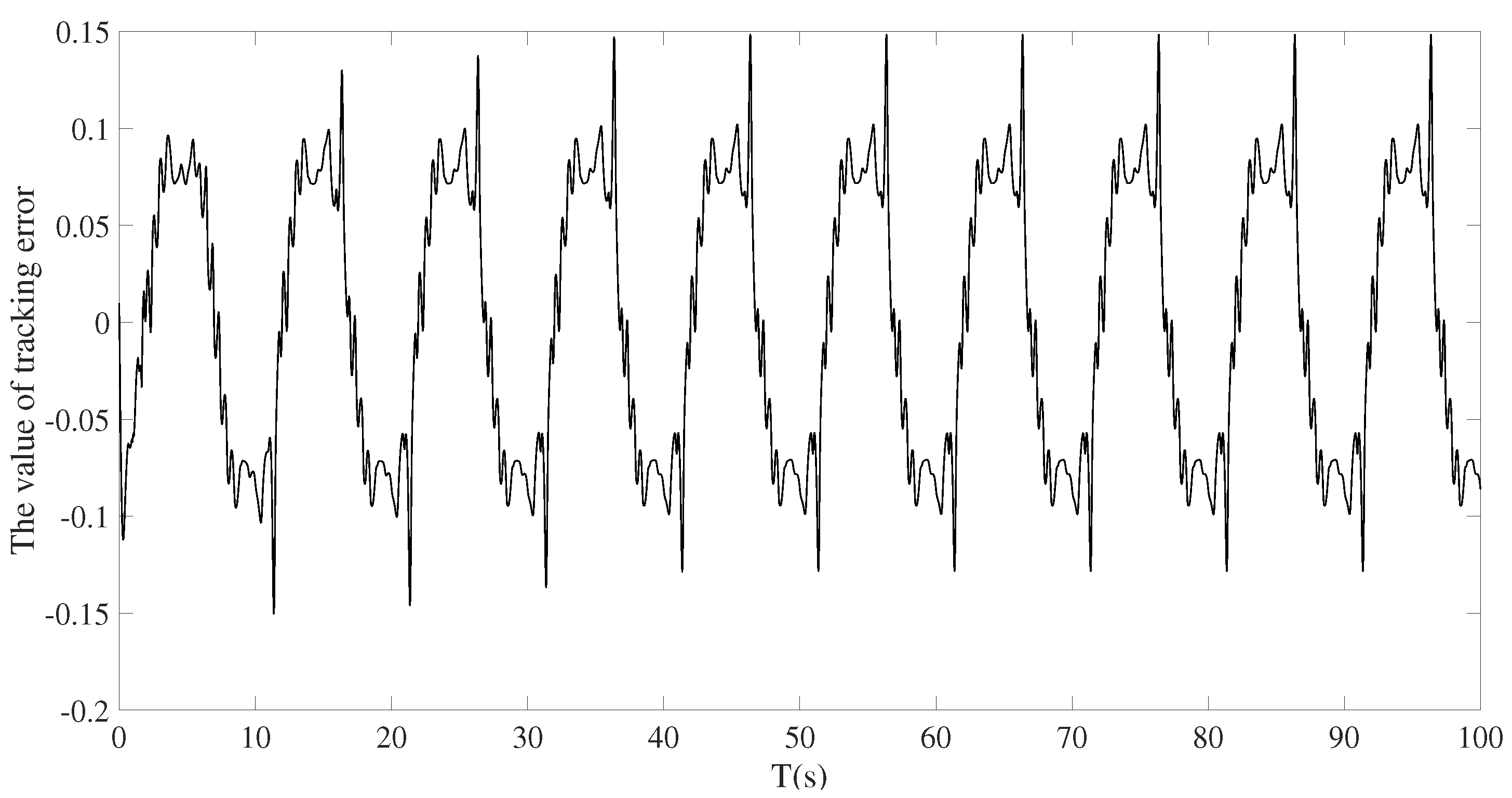
4.4. Description of Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Lemma 2
Appendix B. Proof of Theorem 1
References
- Liu, Q.; Liao, X.; Liu, Y.; Zhou, S.; Guo, S. Dynamics of an inertial two-neuron system with time delay. Nonlinear Dyn. 2009, 58, 573–609. [Google Scholar] [CrossRef]
- Fridman, E.; Shaked, U. A descriptor system approach to H ∞ control of linear time-delay systems. IEEE Trans. Autom. Control 2002, 47, 253–270. [Google Scholar] [CrossRef]
- Kim, J.H.; Hong, B.P. H ∞ state feedback control for generalized continuous/discrete time-delay system. Automatica 1999, 35, 1443–1451. [Google Scholar] [CrossRef]
- He, Y.; Wu, M.; Liu, G.-P.; She, J.-H. Output Feedback Stabilization for a Discrete-Time System With a Time-Varying Delay. IEEE Trans. Autom. Control 2008, 53, 2372–2377. [Google Scholar] [CrossRef]
- Sun, J. Global synchronization criteria with channel time-delay for chaotic time-delay system. Chaos Solitons Fractals 2004, 21, 967–975. [Google Scholar] [CrossRef]
- Wang, X.F.; Chen, G.; Yu, X. Anticontrol of chaos in continuous-time systems via time-delay feedback. Chaos: Interdiscip. J. Nonlinear Sci. 2000, 10, 771. [Google Scholar] [CrossRef]
- Yu, Y.B.; Bao, J.F.; Zhang, H.B.; Zhong, Q.-S.; Liao, X.-F.; Yu, J.-B. Impulsive control of nonlinear systems with time-varying delays. Chin. Phys. B 2008, 17, 2377–2387. [Google Scholar]
- Xu, Z.; Li, X.; Duan, P. Synchronization of complex networks with time-varying delay of unknown bound via delayed impulsive control. Neural Netw. 2020, 125, 224–232. [Google Scholar] [CrossRef]
- Tong, S.; Li, Y. Observer-based fuzzy adaptive robust control of nonlinear systems with time delays and unmodeled dynamics. Neurocomputing 2010, 74, 369–378. [Google Scholar] [CrossRef]
- Ghadiri, H.; Khodadadi, H.; Mobayen, S.; Asad, J.H.; Rojsiraphisal, T.; Chang, A. Observer-Based Robust Control Method for Switched Neutral Systems in the Presence of Interval Time-Varying Delays. Mathematics 2022, 9, 2473. [Google Scholar] [CrossRef]
- Xue, X.J.; Qiu, D.M. Robust H-infinity-compensator design for time-delay systems with norm-bounded time-varying uncertainties. IEEE Trans. Autom. Control 2000, 45, 1363–1369. [Google Scholar]
- Baskar, P.; Padmanabhan, S.; Ali, M.S. Finite-time H-infinity control for a class of markovian jumping neural networks with distributed time varying delays LMI approach. ACTA Math. Sci. 2018, 38, 561–579. [Google Scholar] [CrossRef]
- Abdollahi, A.; Chowdhary, G. Adaptive-optimal control under time-varying stochastic uncertainty using past learning. Int. J. Adapt. Control. Signal Process. 2019, 33, 1803–1824. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, F. Adaptive neural control of non-strict feedback system with actuator failures and time-varying delays. Appl. Math. Comput. 2019, 362, 124512. [Google Scholar] [CrossRef]
- Mazenc, F.; Bowong, S. Backstepping with bounded feedbacks for time-varying systems. SIAM J. Control Optim. 2004, 43, 856–871. [Google Scholar] [CrossRef]
- Liu, L.J.; Zhou, J.; Wen, C.; Zhao, X. Robust adaptive tracking control of uncertain systems with time-varying input delays. Int. J. Syst. Sci. 2017, 48, 3440–3449. [Google Scholar] [CrossRef]
- Wang, T.; Li, W. State-Feedback Stabilization of Stochastic Nonlinear Systems with Time-Varying Delay and Different Orders. Asian J. Control 2016, 18, 1159–1164. [Google Scholar] [CrossRef]
- Chol, J.Y.; Krstic, M. Compensation of time-varying input delay for discrete-time nonlinear systems. Int. J. Robust Nonlinear Control 2016, 26, 1755–1776. [Google Scholar]
- Hashemi, M. Adaptive neural dynamic surface control of MIMO nonlinear time delay systems with time-varying actuator failures. Int. J. Adapt. Control Signal Process. 2017, 31, 275–296. [Google Scholar] [CrossRef]
- Chen, W.; Jiao, L.; Li, J.; Li, R. Adaptive NN Backstepping Output-Feedback Control for Stochastic Nonlinear Strict-Feedback Systems With Time-Varying Delays. IEEE Trans. Syst. Man, Cybern. Part B (Cybernetics) 2010, 40, 939–950. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Cui, W.-Y.; Alsaadi, F.E. Adaptive Backstepping Control Design for Uncertain Non-smooth Strictfeedback Nonlinear Systems with Time-varying Delays. Int. J. Control. Autom. Syst. 2019, 17, 2220–2233. [Google Scholar] [CrossRef]
- Cui, G.; Jiao, T.; Wei, Y.; Song, G.; Chu, Y. Adaptive neural control of stochastic nonlinear systems with multiple time-varying delays and input saturation. Neural Comput. Appl. 2014, 25, 779–791. [Google Scholar] [CrossRef]
- Yu, Z.; Li, S.; Du, H. Razumikhin-Nussbaum-lemma-based adaptive neural control for uncertain stochastic pure-feedback nonlinear systems with time-varying delays. Int. J. Robust Nonlinear Control 2013, 23, 1214–1239. [Google Scholar] [CrossRef]
- Chang, R.; Fang, Y.-M.; Liu, L.; Kang, K.-S. Prescribed performance adaptive neural tracking control for strict-feedback Markovian jump nonlinear systems with time-varying delay. Int. J. Control. Autom. Syst. 2017, 15, 1020–1031. [Google Scholar] [CrossRef]
- Liu, Y.-J.; Ma, L.; Liu, L.; Tong, S.; Chen, C.L.P. Adaptive Neural Network Learning Controller Design for a Class of Nonlinear Systems With Time-Varying State Constraints. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 66–75. [Google Scholar] [CrossRef] [PubMed]
- Senjyu, T.; Kashiwagi, T.; Uezato, K. Position control of ultrasonic motors using MRAC and dead-zone compensation with fuzzy inference. IEEE Trans. Power Electron. 2002, 17, 265–272. [Google Scholar] [CrossRef]
- Prodic, A.; Maksimovic, D.; Erickson, R. Dead-zone digital controllers for improved dynamic response of low harmonic rectifiers. IEEE Trans. Power Electron. 2006, 21, 173–181. [Google Scholar] [CrossRef]
- Lee, J.-Y. Single-Stage AC/DC Converter With Input-Current Dead-Zone Control for Wide Input Voltage Ranges. IEEE Trans. Ind. Electron. 2007, 54, 724–732. [Google Scholar] [CrossRef]
- Liu, Y.-J.; Tong, S. Adaptive NN Tracking Control of Uncertain Nonlinear Discrete-Time Systems With Nonaffine Dead-Zone Input. IEEE Trans. Cybern. 2017, 45, 497–505. [Google Scholar] [CrossRef]
- Jing, Y.-H.; Yang, G.-H. Fuzzy Adaptive Fault-Tolerant Control for Uncertain Nonlinear Systems With Unknown Dead-Zone and Unmodeled Dynamics. IEEE Trans. Fuzzy Syst. 2019, 27, 2265–2278. [Google Scholar] [CrossRef]
- Liu, Z.; Xue, L.; Sun, W.; Sun, Z. Robust output feedback tracking control for a class of high-order time-delay nonlinear systems with input dead-zone and disturbances. Nonlinear Dyn. 2019, 97, 921–935. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Zhou, B. Stability analysis of non-linear time-varying systems by Lyapunov functions with indefinite derivatives. IET Control Theory Appl. 2017, 11, 1434–1442. [Google Scholar] [CrossRef]
- Zou, W.; Ahn, C.K.; Xiang, Z. Analysis on existence of compact set in neural network control for nonlinear systems. Automatica 2020, 120, 109155. [Google Scholar] [CrossRef]












Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, L.; Wang, M. Adaptive Compensation Tracking Control for Time-Varying Delay Nonlinear Systems with Unknown Actuator Dead Zone. Machines 2022, 10, 943. https://doi.org/10.3390/machines10100943
Ma L, Wang M. Adaptive Compensation Tracking Control for Time-Varying Delay Nonlinear Systems with Unknown Actuator Dead Zone. Machines. 2022; 10(10):943. https://doi.org/10.3390/machines10100943
Chicago/Turabian StyleMa, Libin, and Mao Wang. 2022. "Adaptive Compensation Tracking Control for Time-Varying Delay Nonlinear Systems with Unknown Actuator Dead Zone" Machines 10, no. 10: 943. https://doi.org/10.3390/machines10100943
APA StyleMa, L., & Wang, M. (2022). Adaptive Compensation Tracking Control for Time-Varying Delay Nonlinear Systems with Unknown Actuator Dead Zone. Machines, 10(10), 943. https://doi.org/10.3390/machines10100943






