A Two-Stage Method for Weak Feature Extraction of Rolling Bearing Combining Cyclic Wiener Filter with Improved Enhanced Envelope Spectrum
Abstract
:1. Introduction
2. Cyclic Wiener Filter
3. Improved Enhanced Envelope Spectrum
4. Simulation
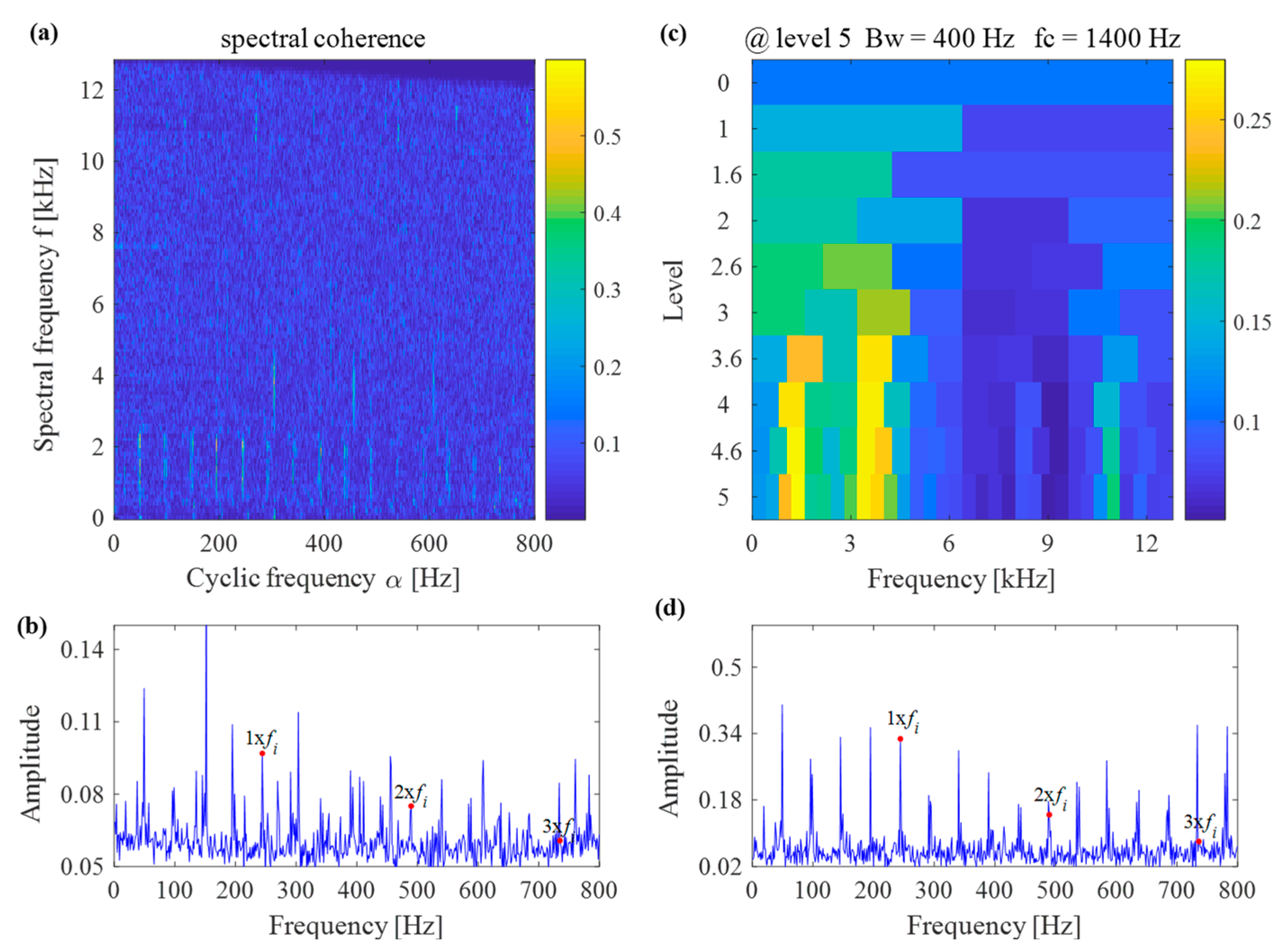
5. Experiment Verification
6. Engineering Verification
7. Conclusions
- (1)
- The periodic weak impact component of faulty bearing buried in strong background noise could be enhanced effectively by the cyclic Wiener filter using the prior knowledge such as fault characteristic frequencies, rotating frequency and so on. However, the enhancement effect is not enough to achieve satisfactory feature extraction result under strong background noise, especially in the early weak fault stage of rolling bearing, and requires further processing.
- (2)
- The proposed IEES could excavate the fault information hidden in SCoh adaptively and could select the fault information sensitive frequency band for further envelope analysis. Though the traditional EES has the similar extraction effect with the proposed IEES, the latter has the advantage of a much better effect.
- (3)
- Satisfactory extraction results could be achieved by using the combination of the cyclic Wiener filter with IEES in feature extraction the bearing’s early weak fault through the verification of simulation, experiment and engineering.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| IEES | Improved enhanced envelope spectrum |
| SCoh | Spectral coherence |
| BD | Blind deconvolution |
| MED | Minimum entropy deconvolution |
| SK | Spectral kurtosis |
| SC | Spectral correlation |
| EES | Enhanced envelope spectrum |
| SES | Square envelope spectrum |
References
- Azeez, A.A.; Alkhedher, M.; Gadala, M.S. Thermal imaging fault detection for rolling element bearings. In Proceedings of the Advances in Science and Engineering Technology International Conferences (ASET), Dubai, United Arab Emirates, 4 February–9 April 2020; pp. 1–5. [Google Scholar]
- Harlisca, C.; Szabó, L.; Frosini, L.; Albini, A. Diagnosis of rolling bearings faults in electric machines through stray magnetic flux monitoring. In Proceedings of the 8th international symposium on advanced topics in electrical engineering (atee), Bucharest, Romania, 23–25 May 2013; pp. 1–6. [Google Scholar]
- Kanemaru, M.; Tsukima, M.; Miyauchi, T.; Hayashi, K. Bearing fault detection in induction machine based on stator current spectrum monitoring. IEEJ J. Ind. Appl. 2018, 7, 282–288. [Google Scholar] [CrossRef]
- Qin, Y.; Mao, Y.F.; Tang, B.P.; Wang, Y.; Chen, H.Z. M-band flexible wavelet transform and its application to the fault diagnosis of planetary gear transmission systems. Mech. Syst. Signal Process. 2019, 134, 106298. [Google Scholar] [CrossRef]
- Yu, H.; Li, H.R.; Li, Y.L. Vibration signal fusion using improved empirical wavelet transform and variance contribution rate for weak fault detection of hydraulic pumps. ISA Trans. 2020, 107, 385–401. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Xu, C.; Zhao, Q.; Jiang, H.M.; Weng, Y.H. High-fidelity noise-reconstructed empirical mode decomposition for mechanical multiple and weak fault extractions. ISA Trans. 2022. online. [Google Scholar] [CrossRef]
- Gao, Z.H.; Liu, Y.; Wang, Q.J.; Wang, J.L.; Luo, Y.G. Ensemble empirical mode decomposition energy moment entropy and enhanced long short-term memory for early fault prediction of bearing. Measurement 2022, 188, 110417. [Google Scholar] [CrossRef]
- Deng, F.Y.; Qiang, Y.W.; Yang, S.P.; Hao, R.J.; Liu, Y.Q. Sparse representation of parametric dictionary based on fault impact matching for wheelset bearing fault diagnosis. ISA Trans. 2021, 110, 368–378. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.G.; Song, Z.S.; Zhang, C.; Wang, J.; Shi, J.J.; Jiang, X.X.; Zhu, Z.K. Multi-source fidelity sparse representation via convex optimization for gearbox compound fault diagnosis. J. Sound Vib. 2021, 496, 115879. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Z.W.; Wang, L.; Zhang, J.T.; Han, W. Bearing fault diagnosis based on sparse representations using an improved OMP with adaptive Gabor sub-dictionaries. ISA Trans. 2020, 106, 355–366. [Google Scholar] [CrossRef]
- Ding, J.M.; Zhao, W.T.; Miao, B.R. Adaptive sparse representation based on circular-structure dictionary learning and its application in wheelset-bearing fault detection. Mech. Syst. Signal Process. 2018, 111, 399–422. [Google Scholar] [CrossRef]
- Li, Q.C.; Ding, X.X.; Huang, W.B.; He, Q.B.; Shao, Y.M. Transient feature self-enhancement via shift-invariant manifold sparse learning for rolling bearing health diagnosis. Measurement 2019, 148, 106957. [Google Scholar] [CrossRef]
- Meng, Z.; Shi, Y.; Pan, Z.Z.; Chen, Z.J. Fault diagnosis of rolling bearing based on adaptive block forward and backward stagewise orthogonal matching pursuit algorithm. J. Mech. Eng. 2020, 56, 91–101. [Google Scholar]
- Li, G.; Zhao, Q. Minimum entropy deconvolution optimized sinusoidal synthesis and its application to vibration based fault detection. J. Sound Vib. 2017, 390, 218–231. [Google Scholar] [CrossRef]
- Mcdonald, G.L.; Zhao, Q.; Zuo, M.J. Maximum correlated Kurtosis deconvolution and application on gear tooth chip fault detection. Mech. Syst. Signal Process. 2012, 33, 237–255. [Google Scholar] [CrossRef]
- Mcdonald, G.L.; Zhao, Q. Multipoint optimal minimum entropy deconvolution and convolution fix: Application to vibration fault detection. Mech. Syst. Signal Process. 2016, 82, 461–477. [Google Scholar] [CrossRef]
- Buzzoni, M.; Antoni, J.; D’Elia, G. Blind deconvolution based on cyclostationarity maximization and its application to fault identification. J. Sound Vib. 2018, 432, 569–601. [Google Scholar] [CrossRef]
- Antoni, J.; Randall, R.B. The spectral kurtosis: Application to the vibratory surveillance and diagnostics of rotating machines. Mech. Syst. Signal Process. 2006, 20, 308–331. [Google Scholar] [CrossRef]
- Antoni, J. The spectral kurtosis: A useful tool for characterising non-stationary signals. Mech. Syst. Signal Process. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Antoni, J. Fast computation of the kurtogram for the detection of transient faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- Barszcz, T.; Jabło´nski, A. A novel method for the optimal band selection for vibration signal demodulation and comparison with the Kurtogram. Mech. Syst. Signal Process. 2011, 25, 431–451. [Google Scholar] [CrossRef]
- Tse, P.W.; Wang, D. The design of a new sparsogram for fast bearing fault diagnosis: Part 1 of the two related manuscripts that have a joint title as two automatic vibration-based fault diagnostic methods using the novel sparsity measurement–Parts 1 and 2. Mech. Syst. Signal Process. 2013, 40, 499–519. [Google Scholar] [CrossRef]
- Antoni, J. The infogram: Entropic evidence of the signature of repetitive transients. Mech. Syst. Signal Process. 2016, 74, 73–94. [Google Scholar] [CrossRef]
- Moshrefzadeh, A.; Fasana, A. The Autogram: An effective approach for selecting the optimal demodulation band in rolling element bearings diagnosis. Mech. Syst. Signal Process. 2018, 105, 294–318. [Google Scholar] [CrossRef]
- Wang, D.; Tse, P.W.; Tsui, K.L. An enhanced kurtogram method for fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2013, 35, 176–199. [Google Scholar] [CrossRef]
- Smith, W.A.; Fan, Z.Q.; Peng, Z.X.; Li, H.Z.; Randall, R.B. Optimised spectral kurtosis for bearing diagnostics under electromagnetic interference. Mech. Syst. Signal Process. 2015, 75, 371–394. [Google Scholar] [CrossRef]
- Wang, D. An extension of the infograms to novel Bayesian inference for bearing fault feature identification. Mech. Syst. Signal Process. 2016, 80, 19–30. [Google Scholar] [CrossRef]
- Antoni, J. Cyclostationarity by examples. Mech. Syst. Signal Process. 2017, 23, 987–1036. [Google Scholar] [CrossRef]
- Antoni, J.; Xin, G.; Hamzaoui, N. Fast computation of the spectral correlation. Mech. Syst. Signal Process. 2017, 92, 248–277. [Google Scholar] [CrossRef]
- Wang, D.; Zhao, X.J.; Kou, L.L.; Qin, Y.; Zhao, Y.; Tsui, K.L. A simple and fast guideline for generating enhanced/squared envelope spectra from spectral coherence for bearing fault diagnosis. Mech. Syst. Signal Process. 2019, 122, 754–768. [Google Scholar] [CrossRef]
- Schmidt, S.; Mauricio, A.; Heyns, P.S.; Gryllias, K.C. A methodology for identifying information rich frequency bands for diagnostics of mechanical components-of-interest under time-varying operating conditions. Mech. Syst. Signal Process. 2020, 142, 106739. [Google Scholar] [CrossRef]
- Chen, B.Y.; Cheng, Y.; Zhang, W.H.; Gu, F.S.; Mei, G.M. Optimal frequency band selection using blind and targeted features for spectral coherence-based bearing diagnostics: A comparative study. ISA Trans. 2021, in press. [Google Scholar] [CrossRef]
- Zhang, B.Y.; Miao, Y.H.; Lin, J.; Li, H. Wghted envelope spectrum based on the spectral coherence for bearing diagnosis. ISA Trans. 2022, 123, 398–412. [Google Scholar] [CrossRef] [PubMed]
- McFadden, P.D.; Smith, J.D. Model for the vibration produced by a single point defecting in a rolling element bearing. J. Sound Vib. 1984, 96, 69–82. [Google Scholar] [CrossRef]
- McFadden, P.D.; Smith, J.D. The vibration produced by multiple point defects in a rolling element bearing. J. Sound Vib. 1985, 98, 263–273. [Google Scholar] [CrossRef]


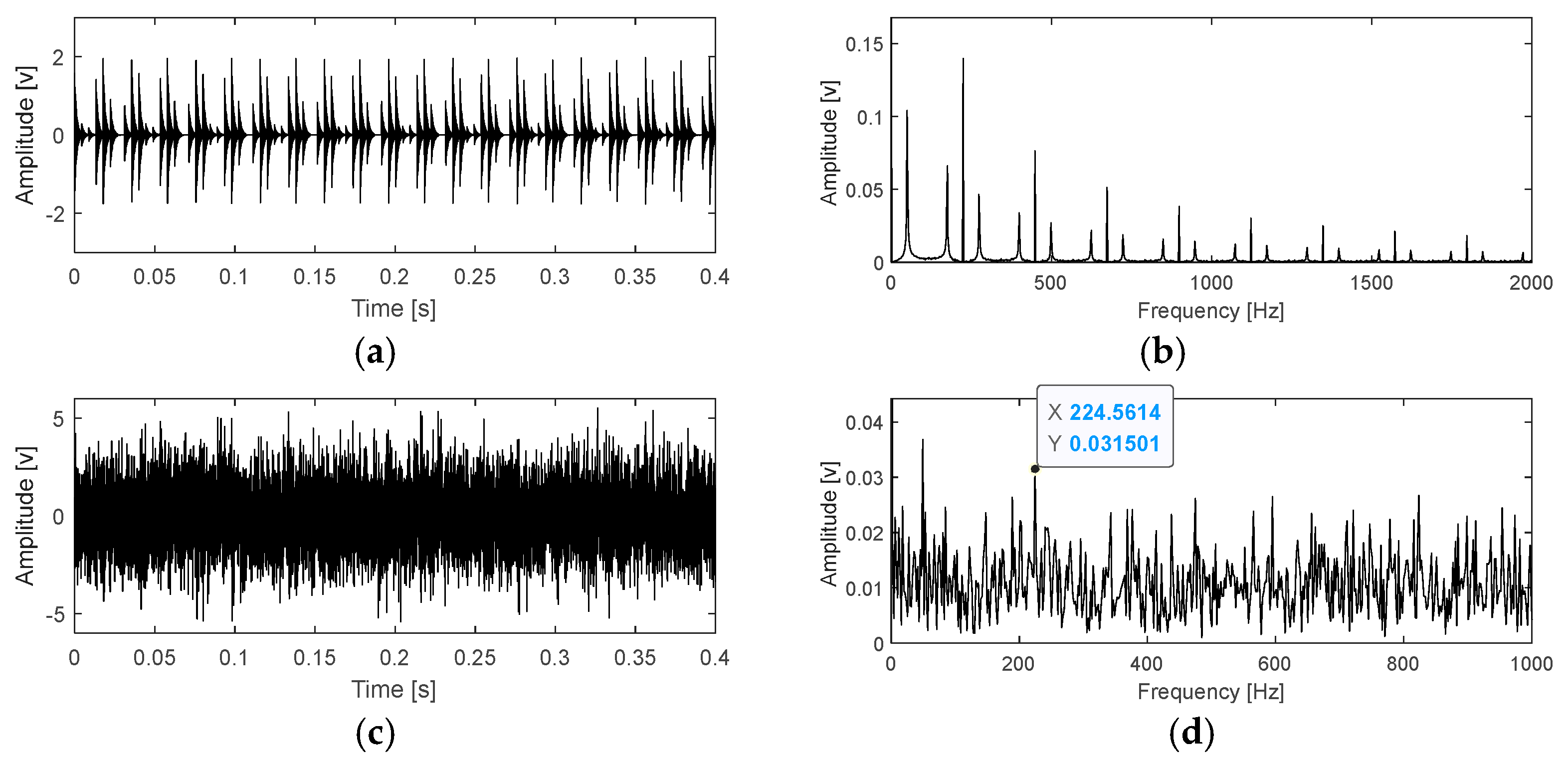

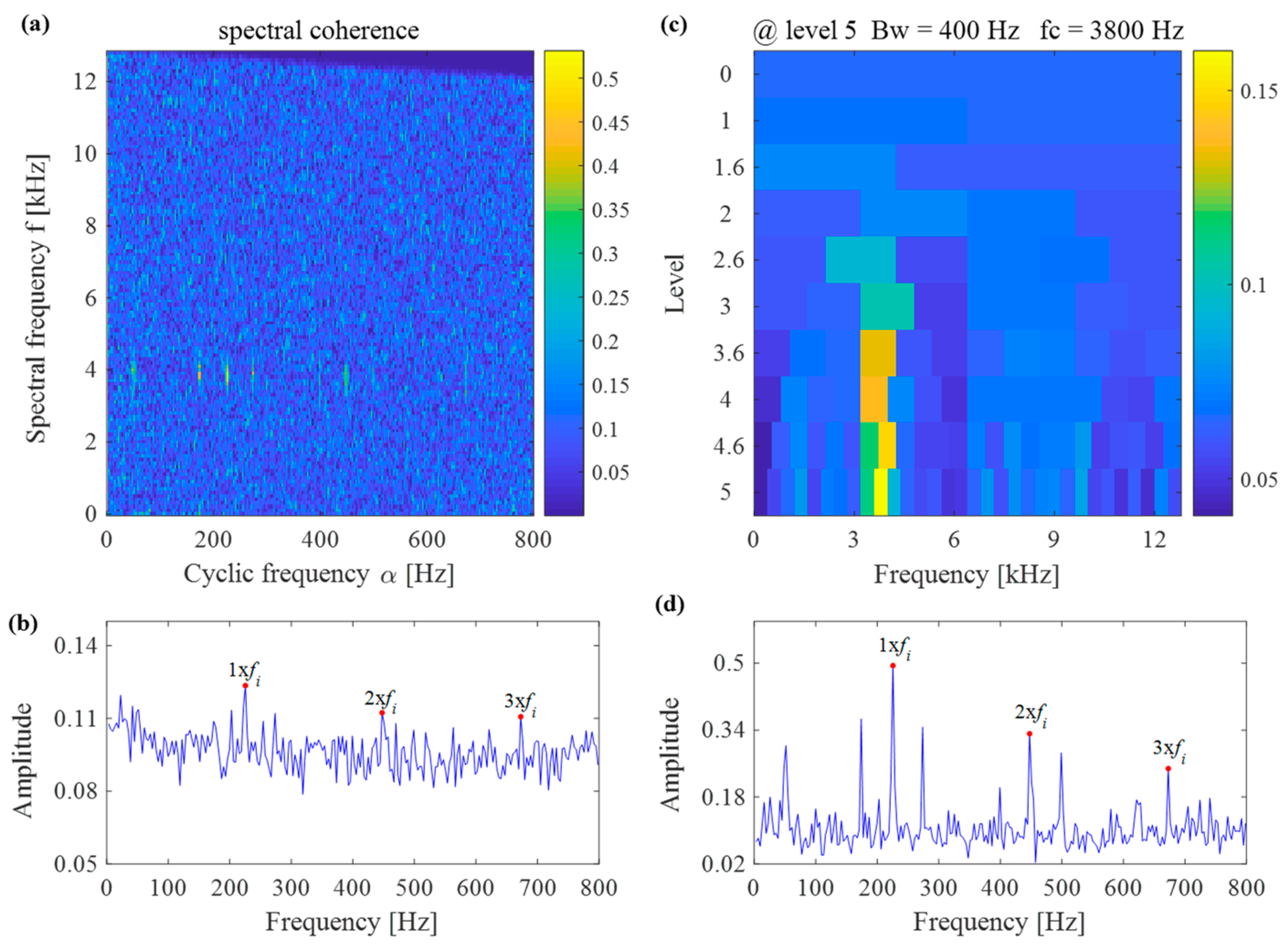
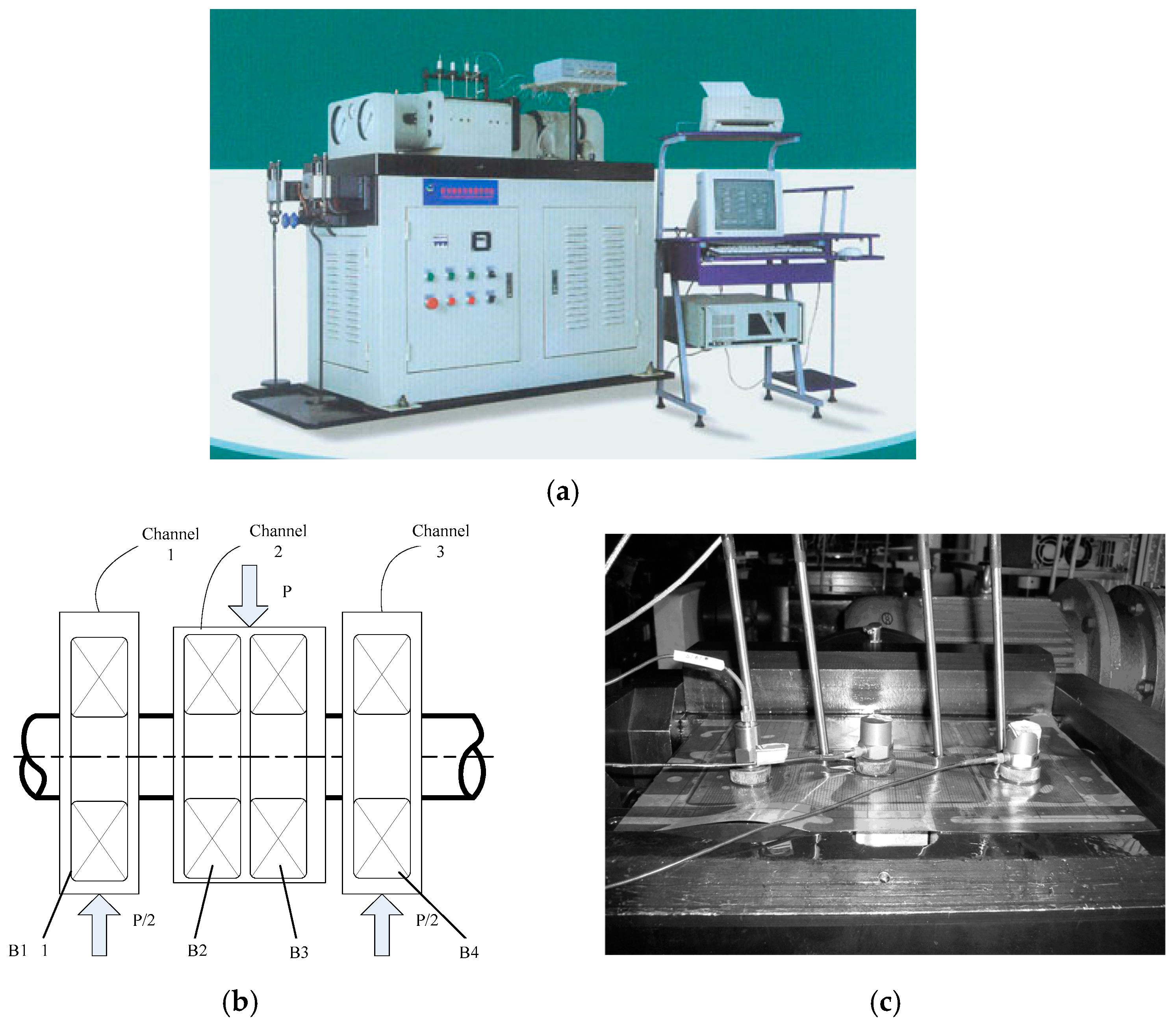

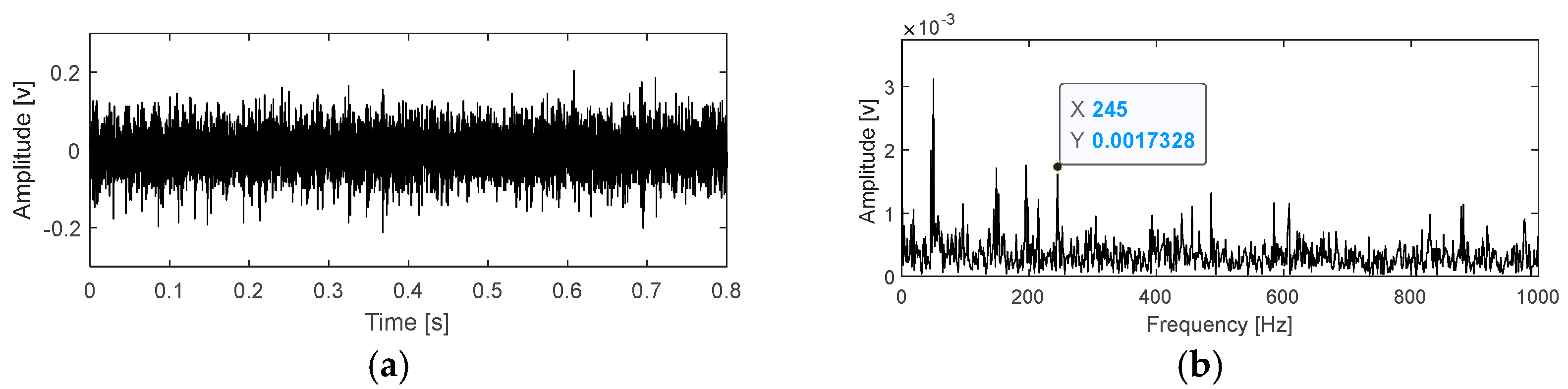





| Measuring Points | Measuring Directions | Vibration Amplitudes of January 20.2 pm (mm/s2) | Vibration Amplitudes of January 21.2 pm (mm/s2) |
|---|---|---|---|
| 1 | Horizontal | 5.72 | 6.17 |
| 2 | Horizontal | 9.68 | 9.01 |
| 3 | Vertical | 1.49 | 1.91 |
| 4 | Vertical | 4.02 | 10.37 |
| Bearing Type | ||||
|---|---|---|---|---|
| 230/560 CA/W33 | 121 | 100.5 | 3.6 | 42.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, L.; Jiang, L.; Wen, Y. A Two-Stage Method for Weak Feature Extraction of Rolling Bearing Combining Cyclic Wiener Filter with Improved Enhanced Envelope Spectrum. Machines 2022, 10, 863. https://doi.org/10.3390/machines10100863
Jia L, Jiang L, Wen Y. A Two-Stage Method for Weak Feature Extraction of Rolling Bearing Combining Cyclic Wiener Filter with Improved Enhanced Envelope Spectrum. Machines. 2022; 10(10):863. https://doi.org/10.3390/machines10100863
Chicago/Turabian StyleJia, Lianhui, Lijie Jiang, and Yongliang Wen. 2022. "A Two-Stage Method for Weak Feature Extraction of Rolling Bearing Combining Cyclic Wiener Filter with Improved Enhanced Envelope Spectrum" Machines 10, no. 10: 863. https://doi.org/10.3390/machines10100863
APA StyleJia, L., Jiang, L., & Wen, Y. (2022). A Two-Stage Method for Weak Feature Extraction of Rolling Bearing Combining Cyclic Wiener Filter with Improved Enhanced Envelope Spectrum. Machines, 10(10), 863. https://doi.org/10.3390/machines10100863





