The Effect of Inflow Distortion on the Rotordynamic Characteristics of a 1400-MW Reactor Coolant Pump Annular Seal
Abstract
:1. Introduction
2. Numerical Analysis
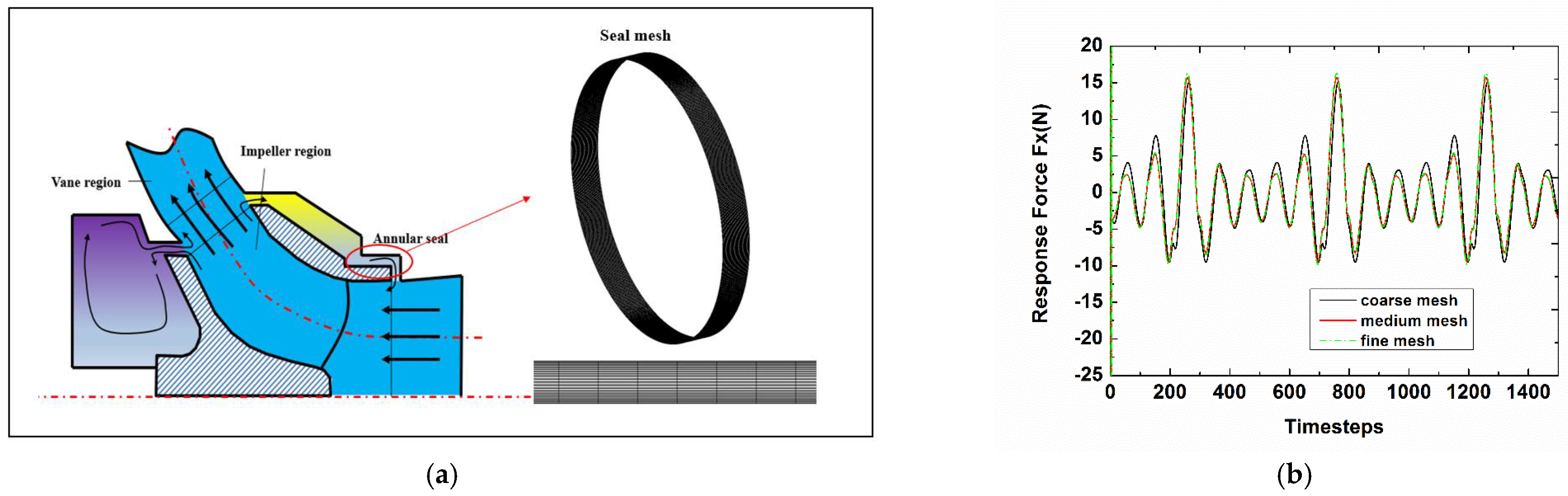
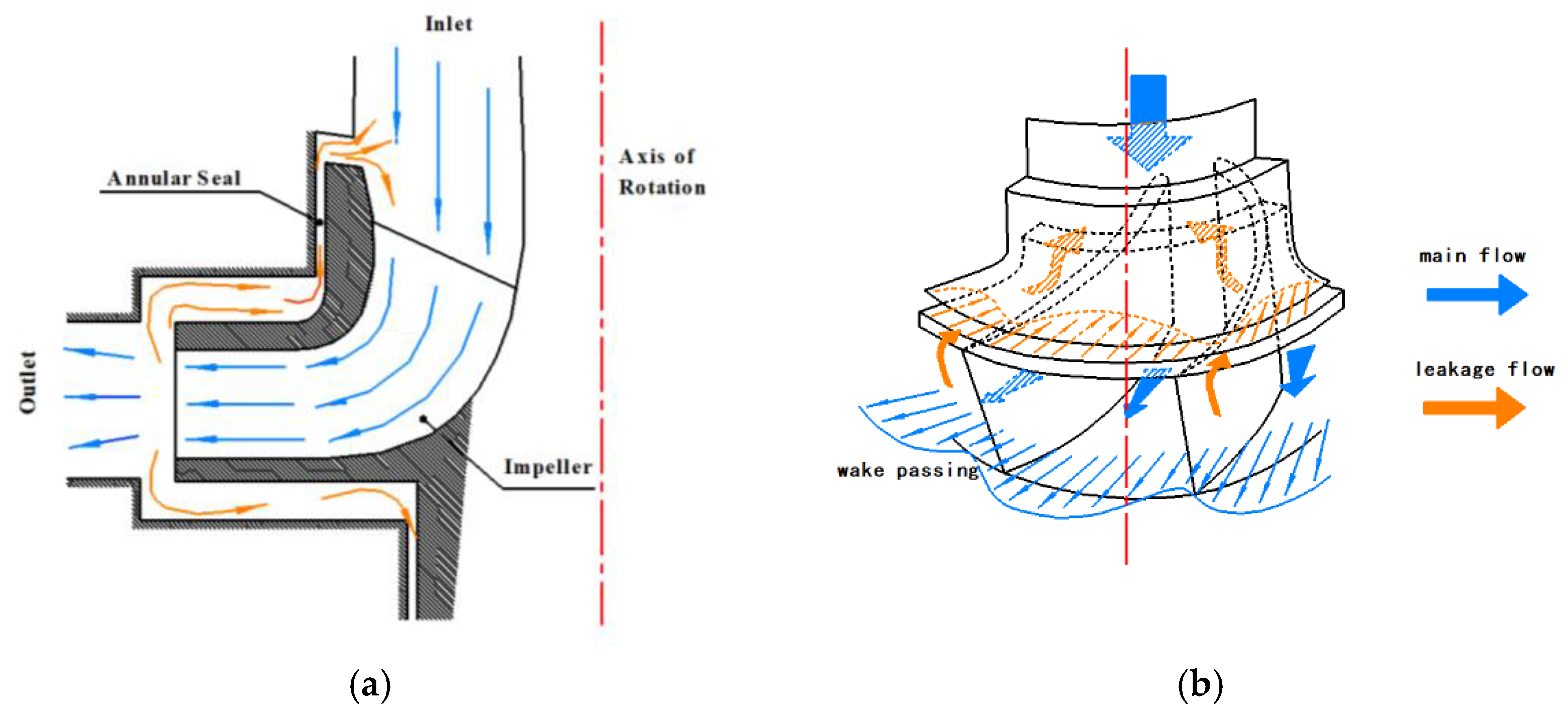
2.1. Seal Geometry and Computational Model
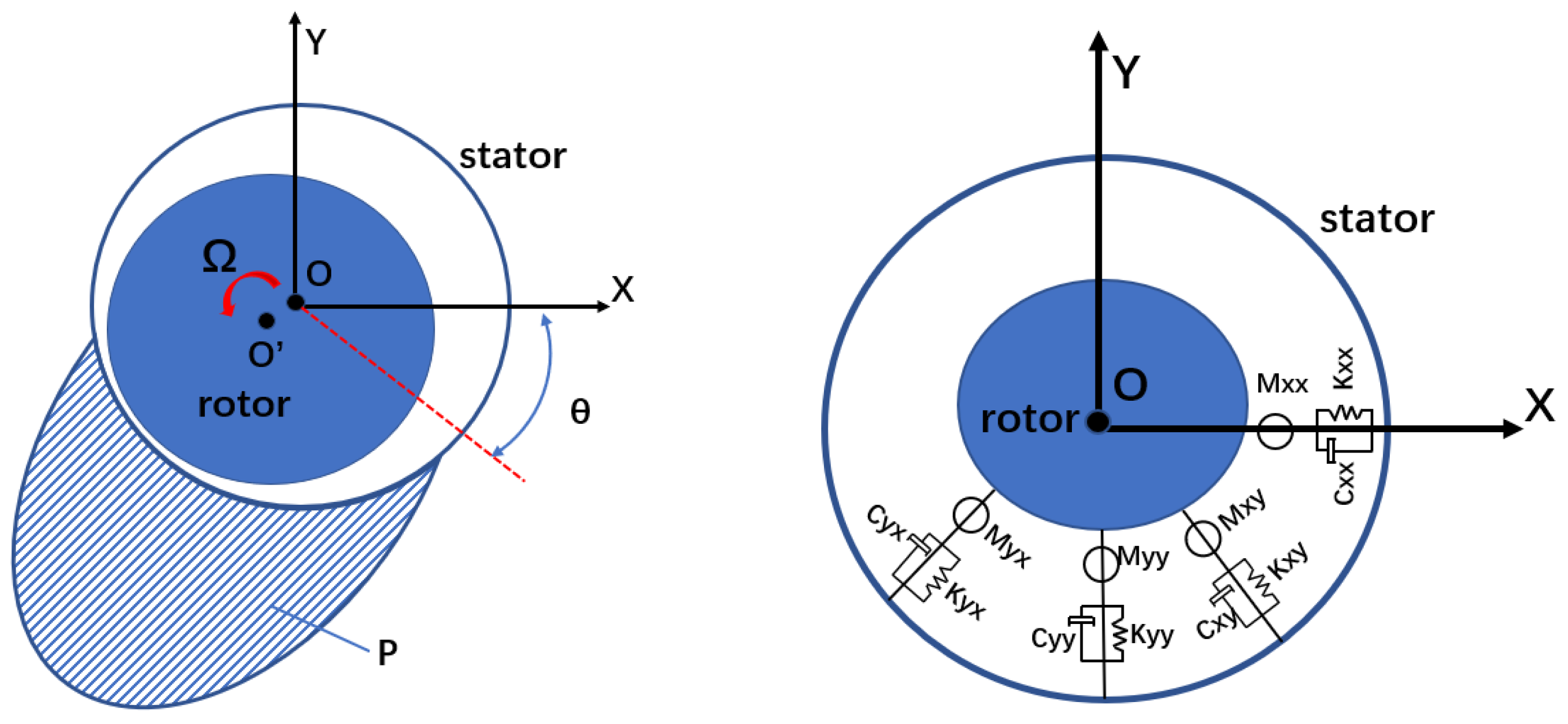
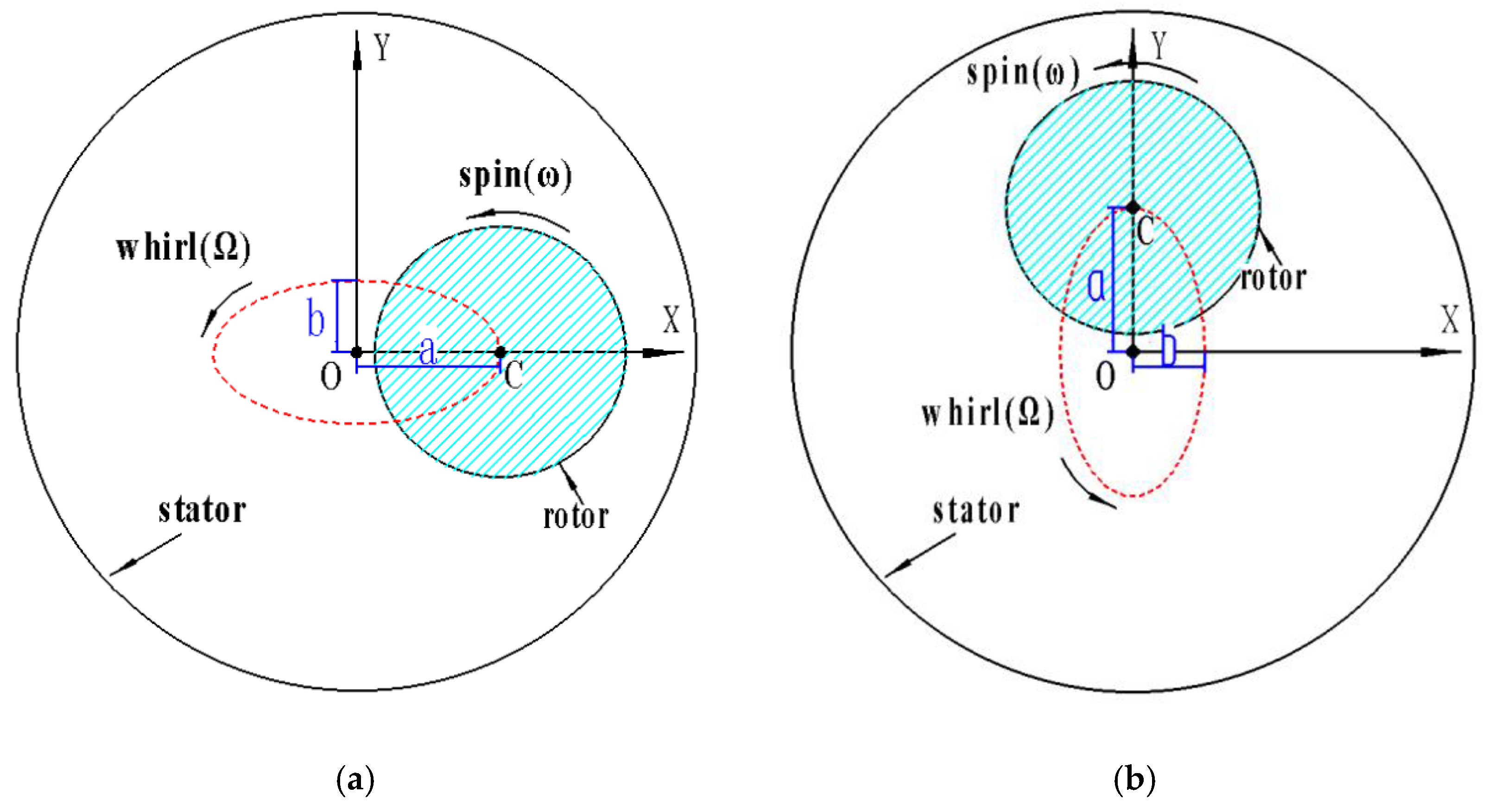
2.2. Rotor Motion
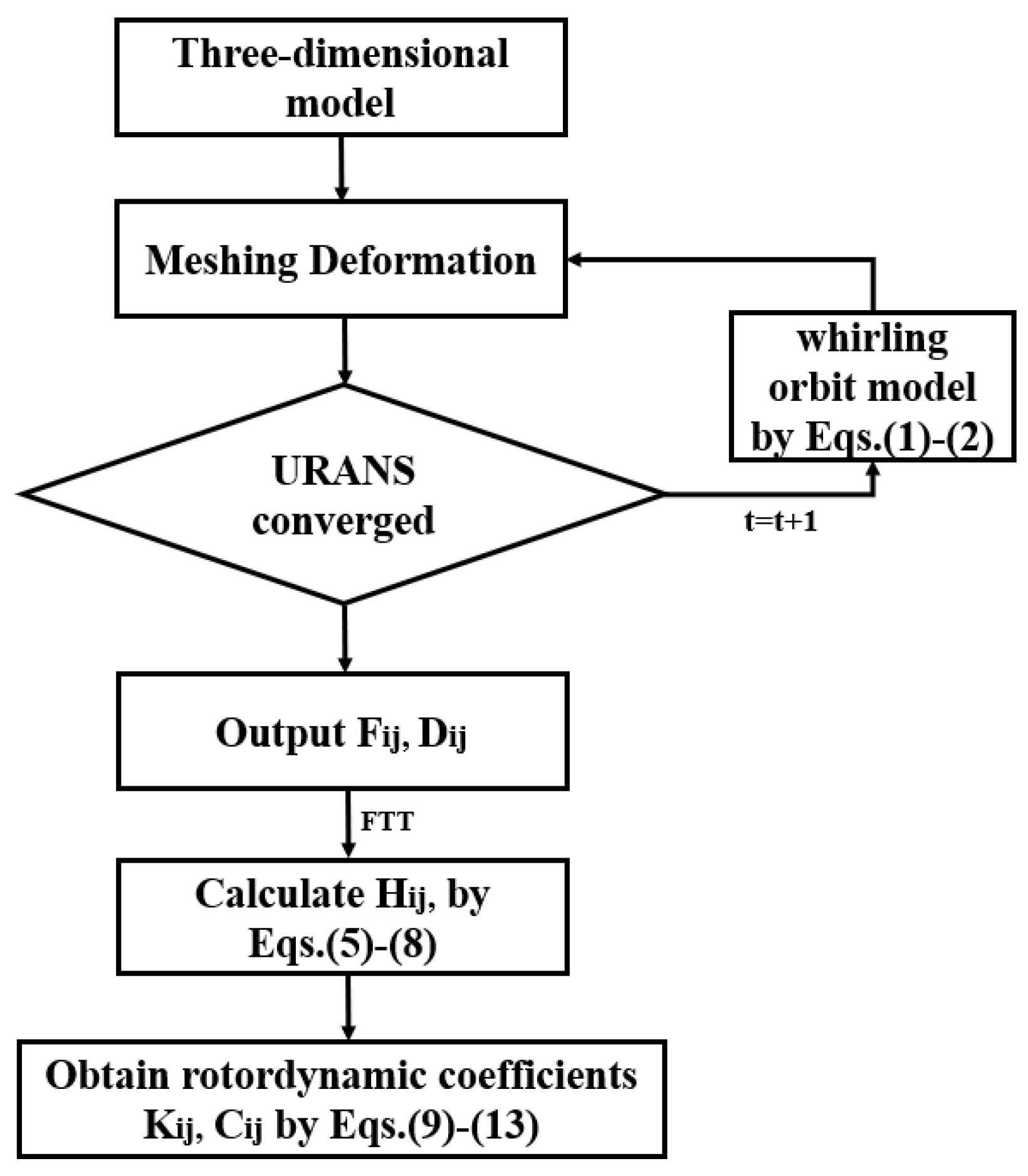
2.3. Rotordynamic Coefficients Solution Method
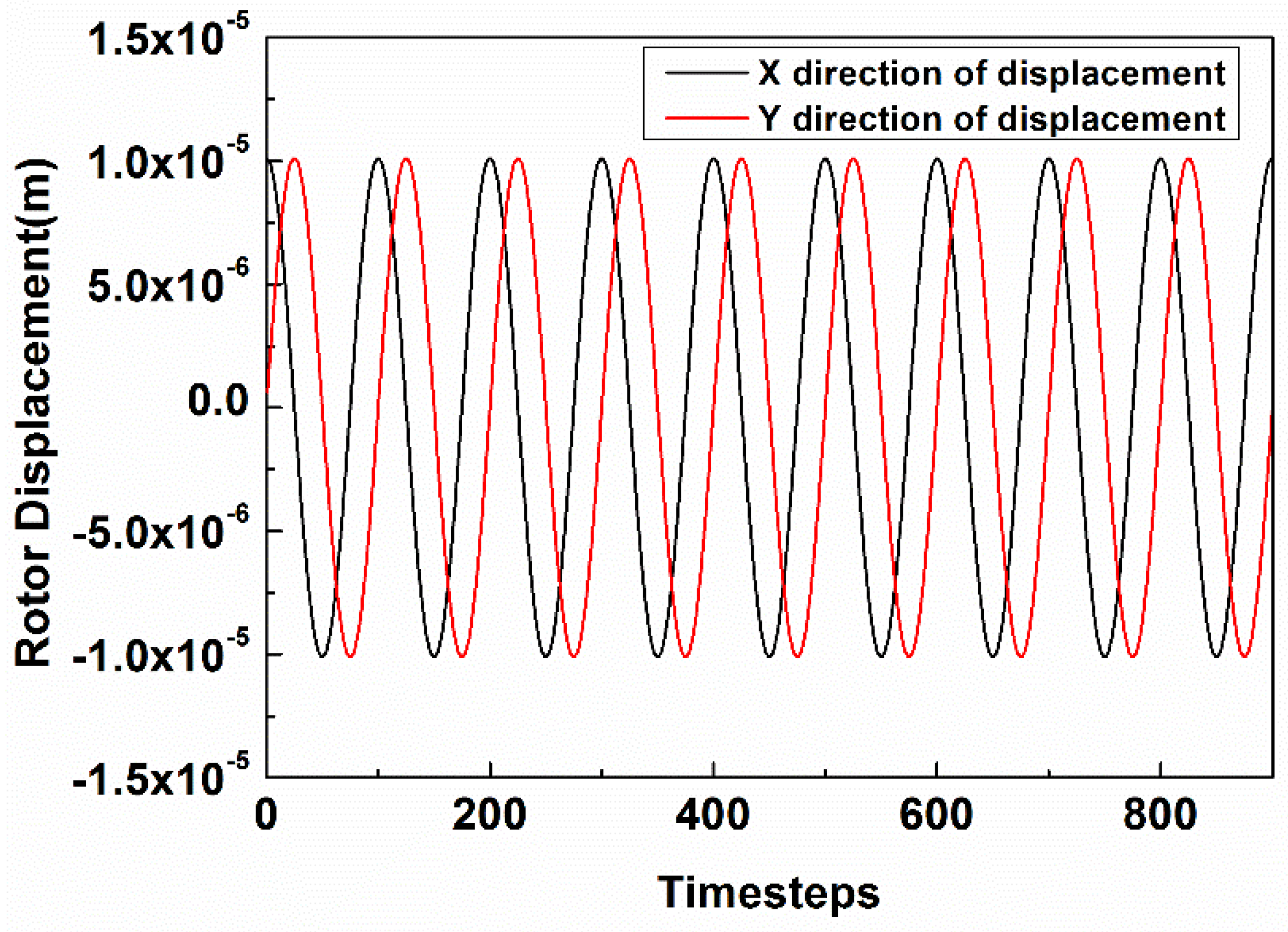
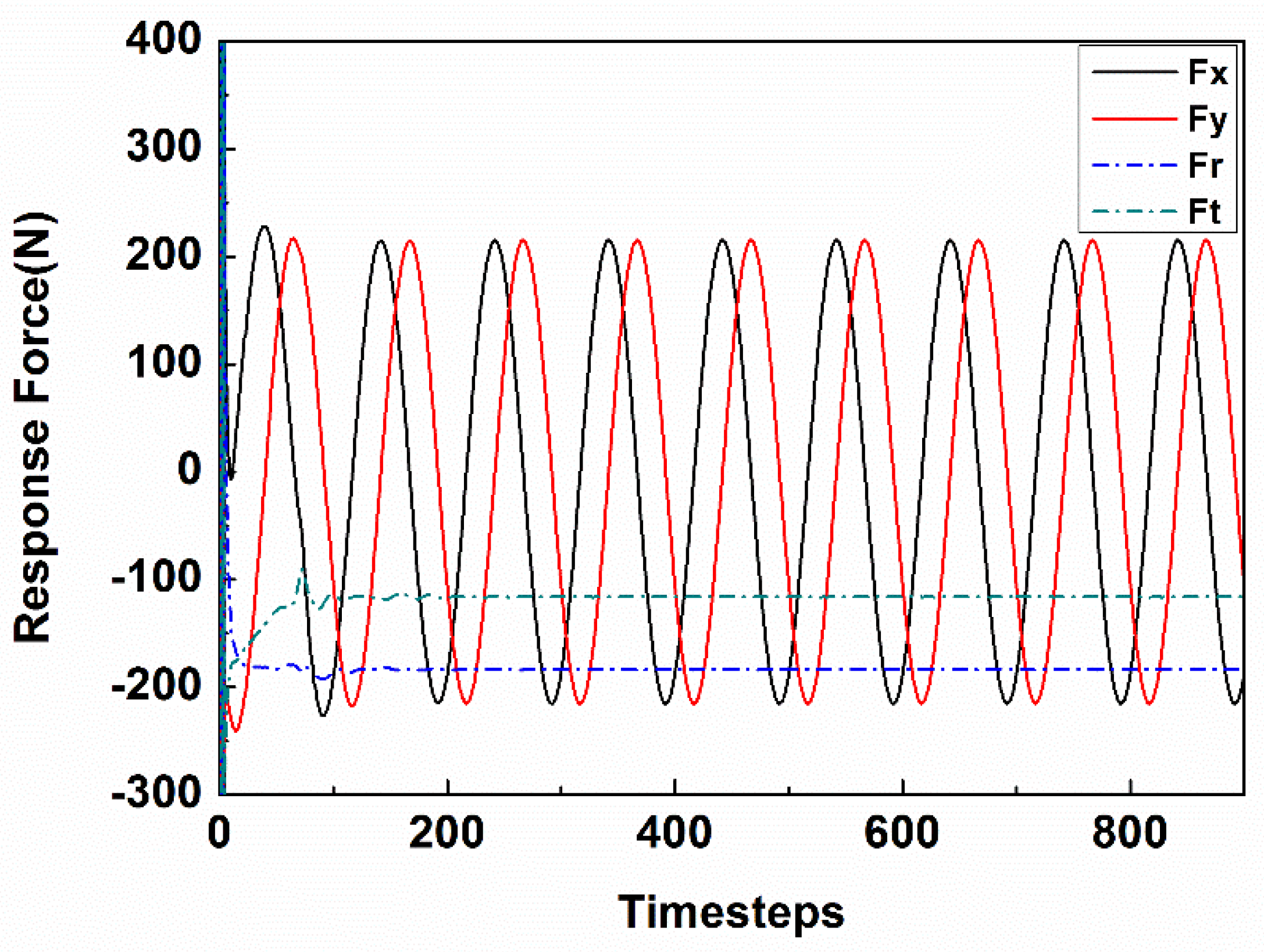
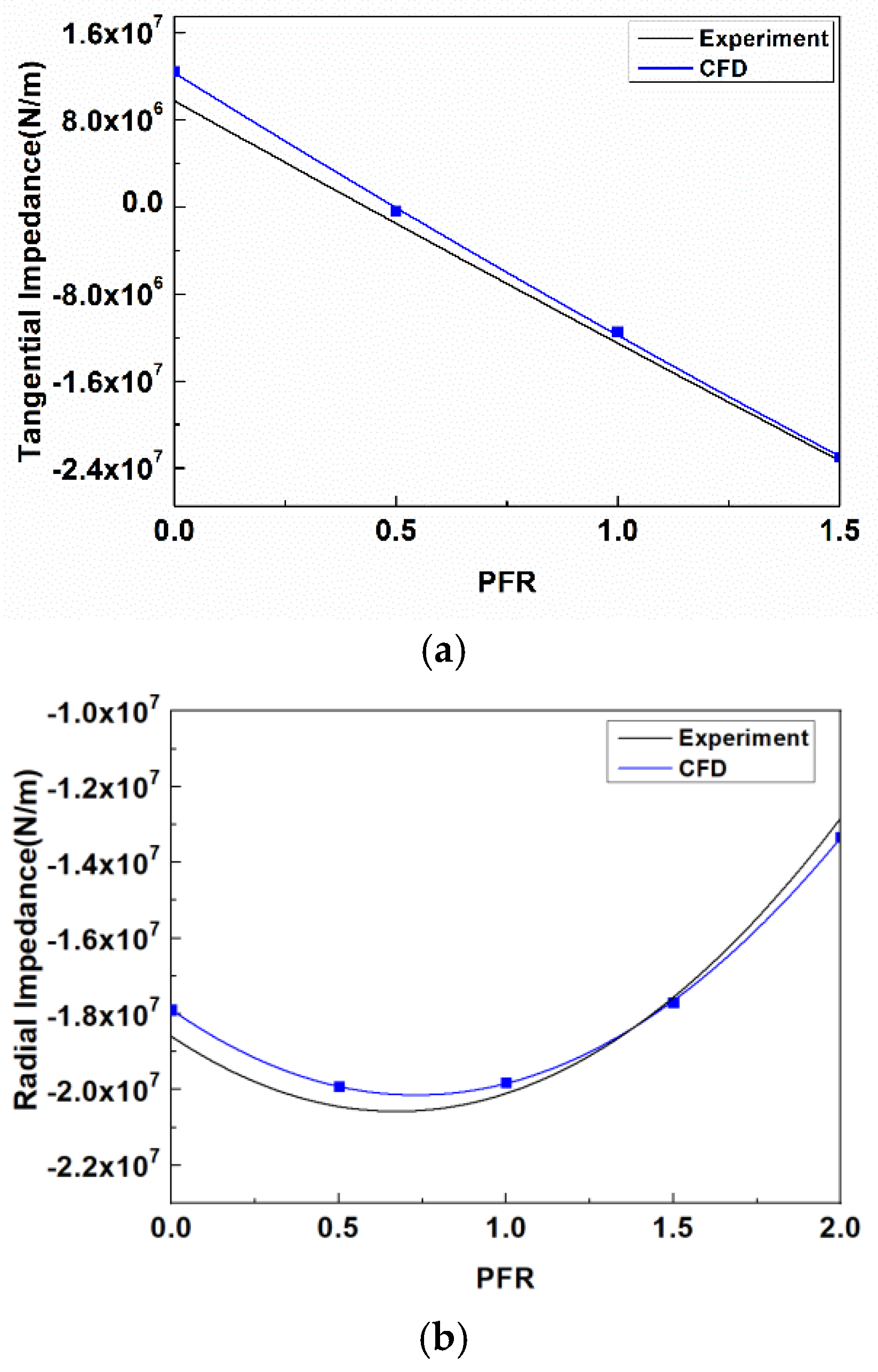
2.4. Numerical Method Validations
2.5. Inflow Distortion
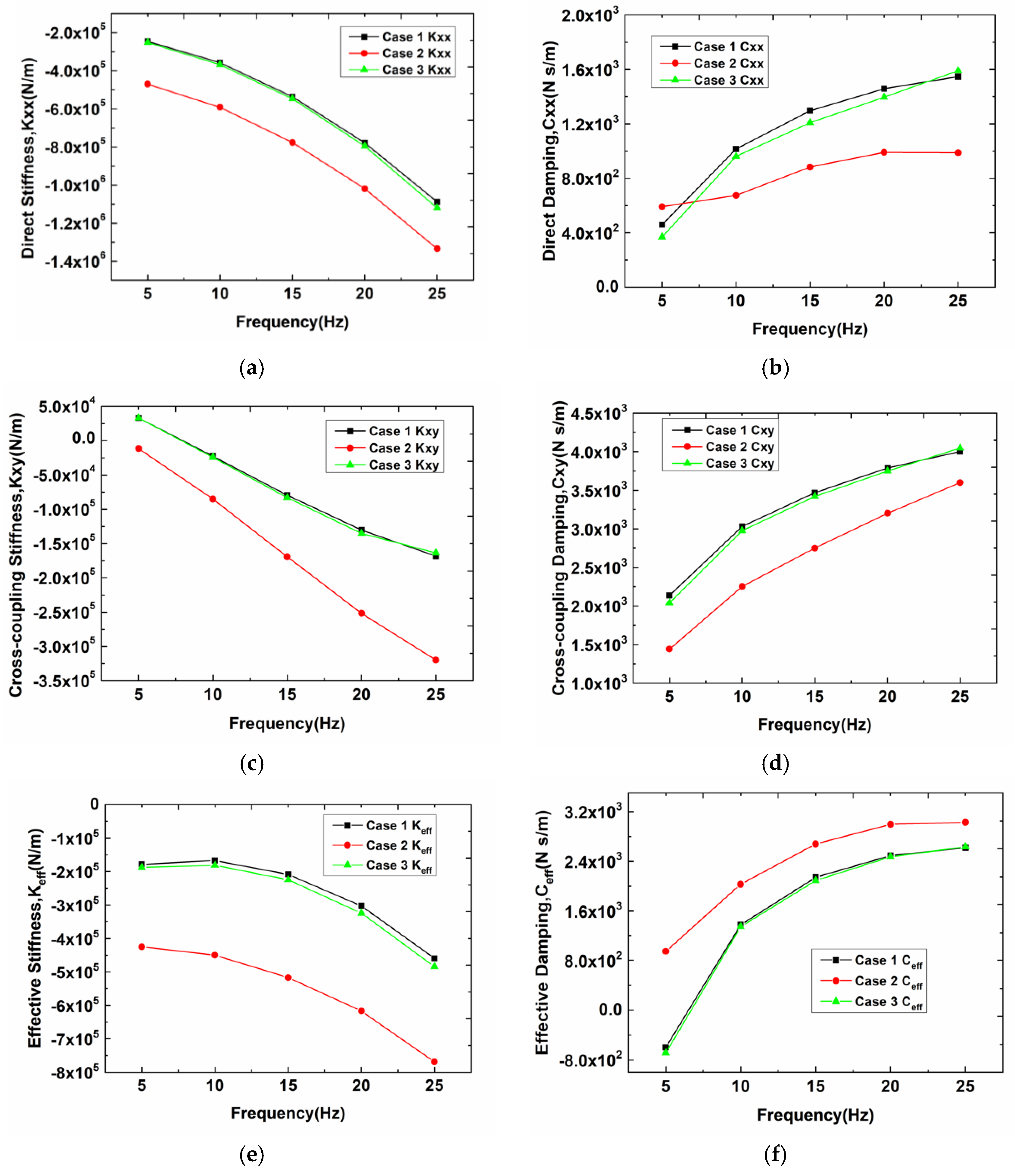
3. Results and Discussions
3.1. Rotordynamic Coefficients Results for Different Cases
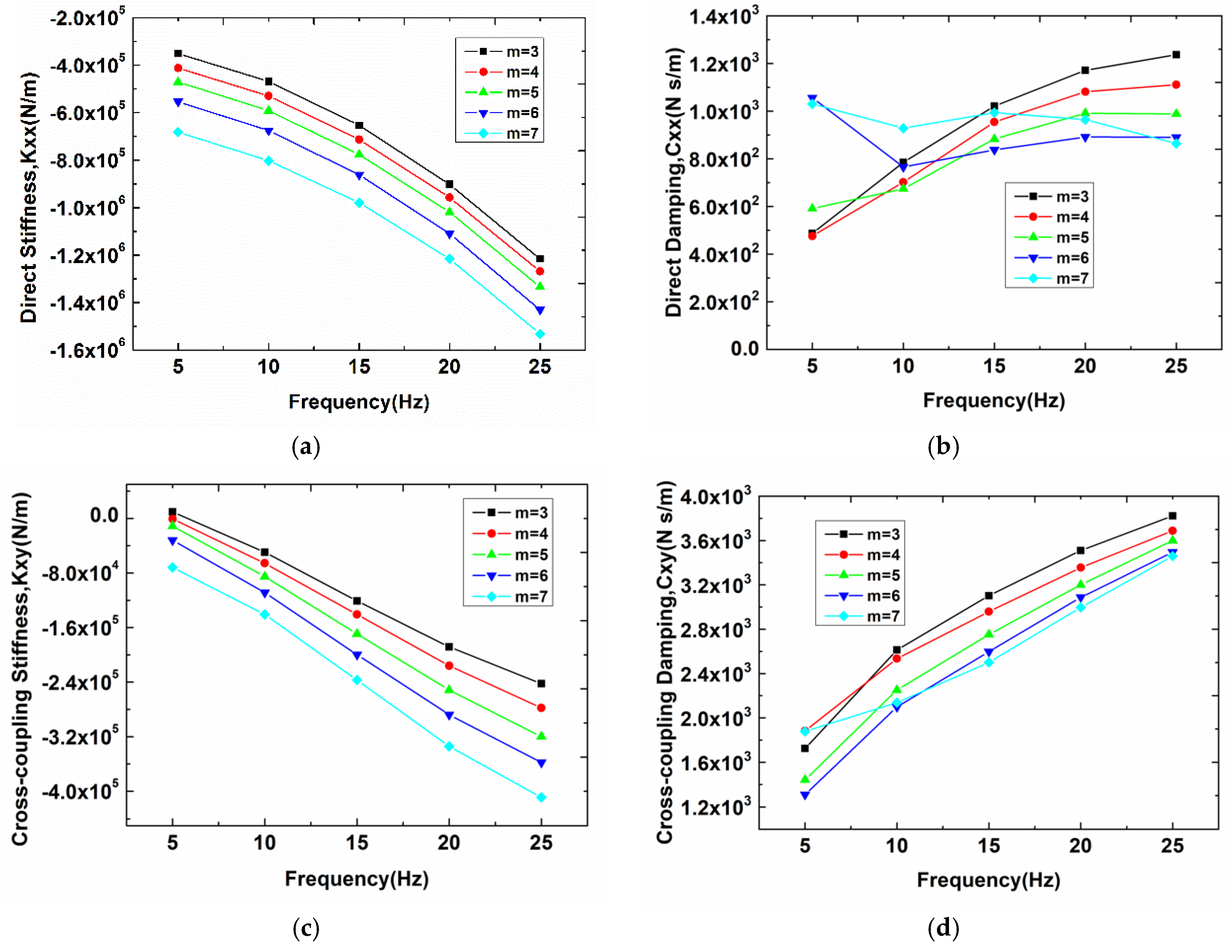
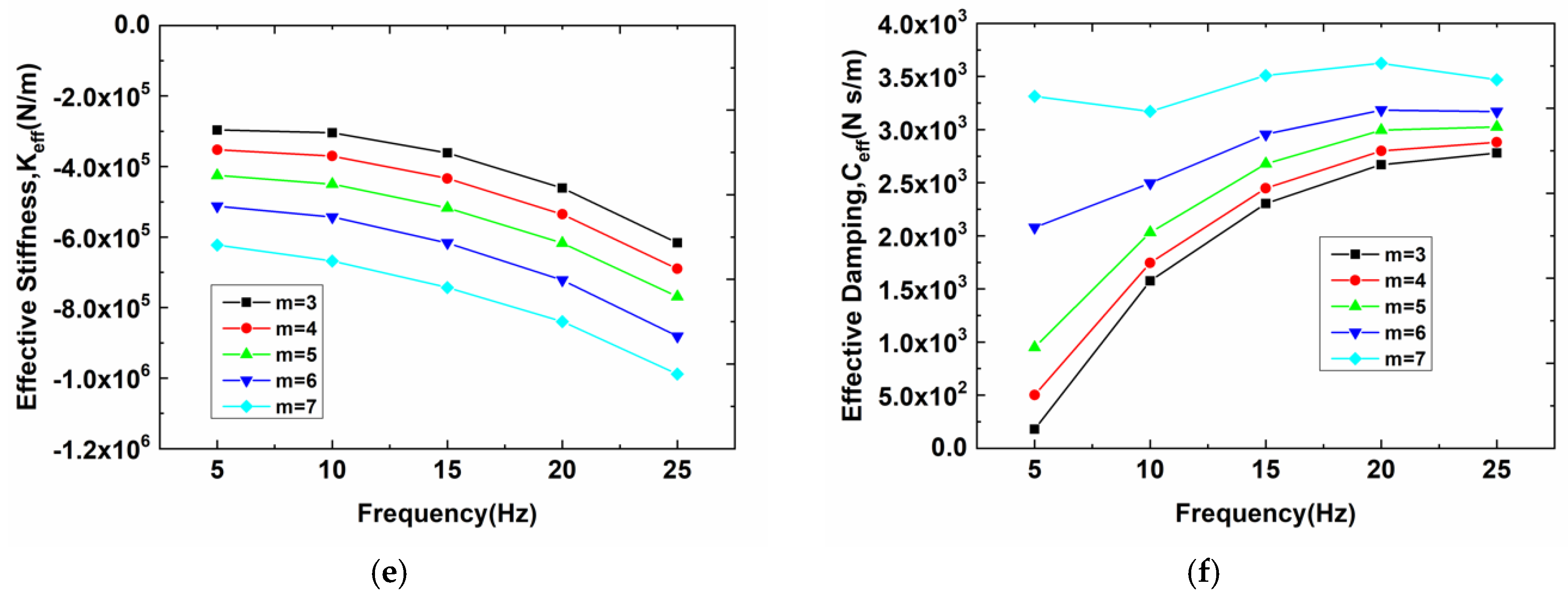
3.2. Effects of Impeller Blades Number
3.3. Effects of Pressure Fluctuation
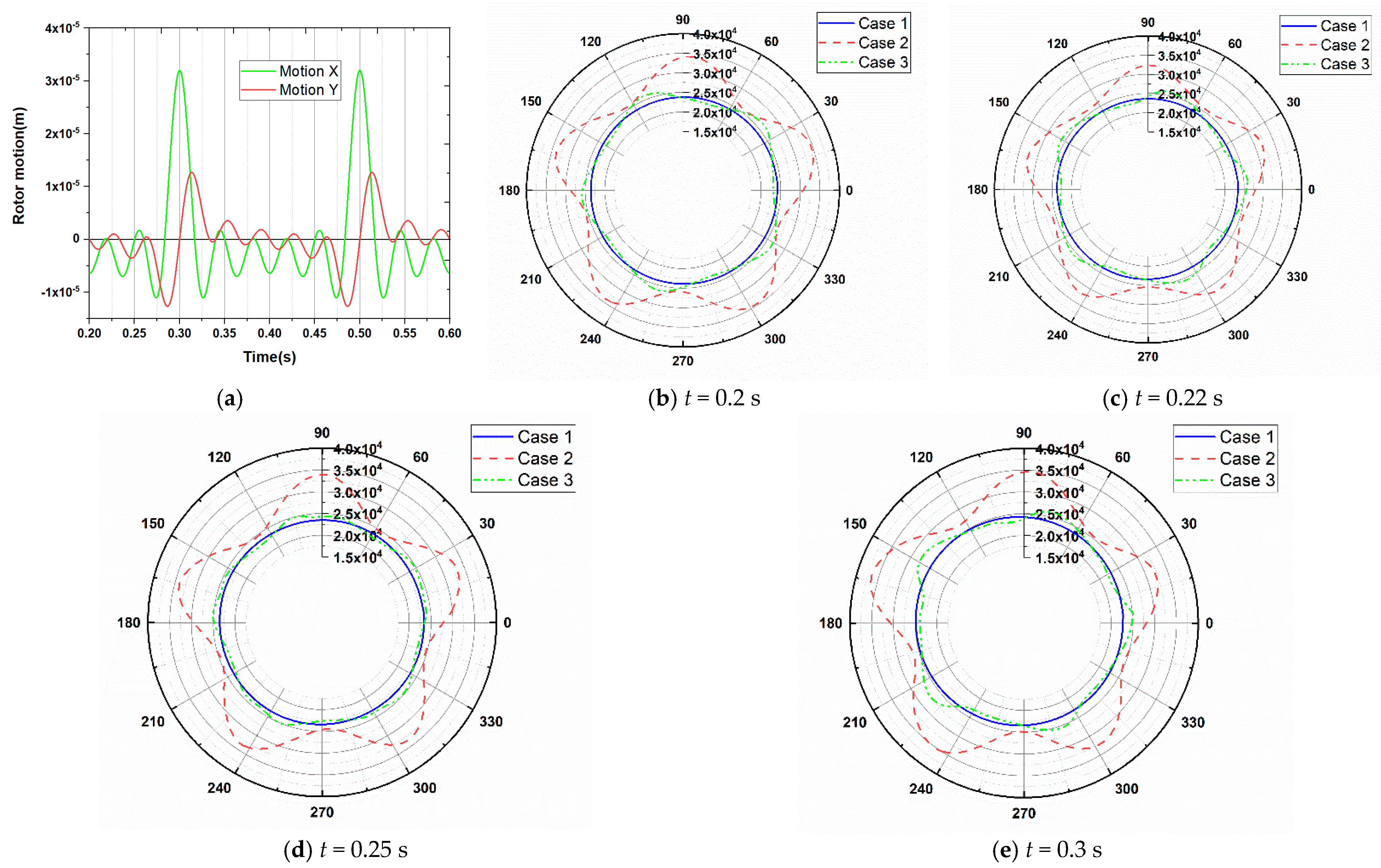
3.4. Details of Inner Flow Field
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclatures
| a | Major axis of the elliptical orbit (m) |
| b | Minor axis of the elliptical orbit (m) |
| c | Cross-coupling damping (N-s/m2) |
| C | Direct damping (N-s/m2) |
| Cxx | Direct damping in x-direction (N-s/m2) |
| Cxy | Cross-coupling damping in x-direction (N-s/m2) |
| Cyy | Direct damping in y-direction (N-s/m2) |
| Cyx | Cross-coupling damping in y-direction (N-s/m2) |
| Ceff | Effective damping (N-s/m2) |
| Dxx | Rotor orbit motion in x-direction for x-direction excitation (m) |
| Dxy | Rotor orbit motion in y-direction for x-direction excitation (m) |
| Dyy | Rotor orbit motion in y-direction for y-direction excitation (m) |
| Dyx | Rotor orbit motion in x-direction for y-direction excitation (m) |
| Fxx | Rotor reaction force in x-direction for x-direction excitation (N) |
| Fxy | Rotor reaction force in y-direction for x-direction excitation (N) |
| Fyy | Rotor reaction force in y-direction for y-direction excitation (N) |
| Fyx | Rotor reaction force in y-direction for x-direction excitation (N) |
| Fr | Rotor reaction force in radial direction (N) |
| Ft | Rotor reaction force in tangential direction (N) |
| Hxx | Direct force impedance in x-direction (N/m) |
| Hxy | Cross-coupling force impedance in x-direction (N/m) |
| Hyy | Direct force impedance in y-direction (N/m) |
| Hyx | Cross-coupling force impedance in y-direction (N/m) |
| k | Cross-coupling stiffness (N/m) |
| K | Direct stiffness (N/m) |
| Kxx | Direct stiffness in x-direction (N/m) |
| Kxy | Cross-coupling stiffness in x-direction (N/m) |
| Kyy | Direct stiffness in y-direction (N/m) |
| Kyx | Cross-coupling stiffness in y-direction (N/m) |
| Keff | Effective direct stiffness (N-s/m2) |
| m | Impeller blade number |
| Rotational speed (rpm) | |
| Inlet pressure (Pa) | |
| Pressure fluctuation (Pa) | |
| PFR | Precessional frequency ratio |
| R | Seal radius (mm) |
| e | Rotor eccentricity(m) |
| s | Sealing clearance (m) |
| f | Rotor whirling frequency (Hz) |
| Rotor spinning speed (rad/s) | |
| Rotor whirling speed (rad/s) | |
| Pressure fluctuation ratio (%) |
References
- Vance, J.M.; Zeidan, F.Y.; Murphy, B.G. Machinery Vibration and Rotordynamics, 1st ed.; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Jiang, Q.; Zhai, L.; Wang, L.; Wu, Z. Fluid-Structure Interaction Analysis on Turbulent Annular Seals of Centrifugal Pumps during Transient Process. Math. Probl. Eng. 2011, 2011, 929574. [Google Scholar] [CrossRef]
- Armstrong, J.; Perricone, F. Turbine Instability Solution-Honeycomb Seals. 1996. Available online: https://oaktrust.library.tamu.edu/bitstream/handle/1969.1/163441/T2547-56.pdf?sequence=1&isAllowed=y (accessed on 17 December 2021).
- Thomas, H.J. Instable Eigenschwingungen von Turbine-Nlaufern, Angefaucht Durch die Spaltstromungen Stopfbuschsen un Beschaufelungen. 1958. Available online: https://ci.nii.ac.jp/naid/20001276617/#cit (accessed on 17 December 2021).
- Black, H.F. Effects of Hydraulic Forces in Annular Pressure Seals on the Vibrations of Centrifugal Pump Rotors. J. Mech. Eng. Sci. 1969, 11, 206–213. [Google Scholar] [CrossRef]
- Childs, D.W. Finite-Length Solutions for Rotordynamic Coefficients of Turbulent Annular Seals. J. Lubr. Technol. 1983, 105, 437–444. [Google Scholar] [CrossRef]
- Antunes, J.; Axisa, F.; Grunenwald, T. Dynamics of Rotors Immersed in Eccentric Annular Flow. Part 1: Theory. J. Fluids Struct. 1996, 10, 893–918. [Google Scholar] [CrossRef]
- Hirs, G.G. Fundamentals of a Bulk-Flow Theory for Turbulent Lubricant Films. Ph.D. Thesis, Delft University of Technology, Delft, Holland, July 1970. [Google Scholar]
- Nelson, C.C. Rotordynamic coefficients for compressible flow in tapered annular seals. J. Tribol. 1985, 107, 318–325. [Google Scholar] [CrossRef]
- Zhai, L.; Chi, Z.; Guo, J.; Zhang, Z.; Zhu, Z. Theoretical Solutions for Dynamic Characteristics of Liquid Annular Seals with Herringbone Grooves on the Stator Based on Bulk-Flow Theory. Sci. Technol. Nucl. Install. 2018, 2018, 9412154. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Liu, Y.; Jiang, P.; Chen, H. Numerical analysis of leakage flow through two labyrinth seals. J. Hydrodyn. Ser. B. 2007, 19, 107–112. [Google Scholar] [CrossRef]
- Zhang, J.; Yuan, S.; Fu, Y.; Fang, Y. A numerical simulation of 3-D inner flow in up-stream pumping mechanical seal. J. Hydrodyn. 2006, 18, 572–577. [Google Scholar] [CrossRef]
- Mortazavi, F. CFD-Based Impeller and Seal Rotordynamic Forces. Ph.D. Thesis, Texas A & M University, College Station, TX, USA, December 2018. [Google Scholar]
- Moor, J.J. Three-dimensional CFD rotordynamic analysis of gas labyrinth seals. J. Vib. Acoust. 2003, 125, 427–433. [Google Scholar] [CrossRef]
- Chochua, G.; Soulas, T.A. Numerical modeling of rotordynamic coefficients for deliberately roughened stator gas annular seals. J. Tribol. 2007, 129, 424–429. [Google Scholar] [CrossRef]
- Li, J.; Li, Z.; Feng, Z. Investigations on the Rotordynamic Coefficients of Pocket Damper Seals Using the Multifrequency, One-Dimensional, Whirling Orbit Model and RANS Solutions. In Proceedings of the Journal of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012. [Google Scholar]
- Cao, L.; Wang, J.; Li, P.; Li, Y. Numerical analysis on steam exciting force caused by rotor eccentricity. Shock. Vib. 2017, 2017, 8602965. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Li, J.; Feng, Z. Labyrinth seal rotordynamic characteristics part I: Operational conditions effects. J. Propuls. Power 2016, 32, 1199–1211. [Google Scholar] [CrossRef]
- Li, Z.; Li, J.; Feng, Z. Labyrinth seal rotordynamic characteristics part II: Geometrical parameter effects. J. Propuls. Power 2016, 32, 1281–1291. [Google Scholar] [CrossRef]
- Subramanian, S.; Sekhar, A.S.; Prasad, B.V.S.S.S. Rotordynamic characteristics of rotating labyrinth gas turbine seal with centrifugal growth. Tribol. Int. 2016, 97, 349–359. [Google Scholar] [CrossRef]
- Childs, D.W.; Mclean, J.E.; Zhang, M.; Arthur, S.P. Rotordynamic performance of a negative-swirl brake for a tooth-on-stator labyrinth seal. J. Eng. Gas Turbines Power 2016, 138, 062505. [Google Scholar] [CrossRef]
- Zhang, M.; Childs, D.W.; Tran, D.L.; Shrestha, H. Clearance Effects on Rotordynamic Performance of a Long Smooth Seal with Two-Phase, Mainly-Air Mixtures. J. Eng. Gas Turbines Power 2019, 141, 012502. [Google Scholar] [CrossRef]
- Tran, D.L.; Childs, D.W.; Shrestha, H.; Zhang, M. Preswirl and Mixed-Flow (Mainly Liquid) Effects on Rotordynamic Performance of a Long (L/D = 0.75) Smooth Seal. J. Eng. Gas Turbines Power 2020, 142, 031012. [Google Scholar] [CrossRef]
- Lee, K.H.; Ha, T.W. Analysis of hybrid brush seal rotordynamic coefficients according to position of brush and clearance using 3D CFD. Int. J. Fluid Mach. Syst. 2020, 13, 90–102. [Google Scholar] [CrossRef]
- Tsukuda, T.; Hirano, T.; Watson, C.; Morgtan, N.R.; Weaver, B.K.; Wood, H.G. A numerical investigation of the effect of inlet preswirl ratio on rotordynamic characteristics of labyrinth seal. J. Eng. Gas Turbines Power 2018, 140, 082506. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, P.; Ruan, X.; Xu, Z.; Fu, X. Analysis of pressure pulsation induced by rotor-stator interaction in nuclear reactor coolant pump. Shock. Vib. 2017, 2017, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Zhou, F.; Wang, X. Effects of staggered blades on the hydraulic characteristics of a 1400-MW canned nuclear coolant pump. Adv. Mech. Eng. 2016, 8. [Google Scholar] [CrossRef] [Green Version]
- Childs, D.W. Turbomachinery Rotordynamics: Phenomena, Modeling, and Analysis, 1st ed.; Wiley-Interscience: Hoboken, NJ, USA, 1993. [Google Scholar]
- Marquette, O. Experimental versus Theoretical Comparison of the Static and Dynamic Characteristics of One Smooth and Two Grooved Liquid Annulas Seals with l/d of 0.457; Technical Report No. TL-SEAL-5-95; Turbomachinery Laboratory, Texas A&M University System: College Station, TX, USA, 1995. [Google Scholar]


| Parameter | Nomenclature | Value |
|---|---|---|
| Seal clearance (mm) | s | 0.32 |
| Seal radius (mm) | R | 140 |
| Ratio of seal length to diameter | φ | 0.107 |
| Rotational speed (rpm) | n | 1485 |
| Type of Mesh | Coarse Mesh | Medium Mesh | Fine Mesh |
|---|---|---|---|
| Inlet mass flow (kg/s) | 1.205 | 1.194 | 1.193 |
| Outlet total pressure (Pa) | 57,594 | 56,958 | 56,911 |
| Solution Type | Transient |
|---|---|
| Fluid | Water |
| Computational method | Time marching method |
| Turbulence model | model with scalable log wall function |
| Discretization scheme | High resolution |
| Mesh motion | Mesh deformation |
| Yplus | ≤19 |
| Frequency (Hz) | 5, 10, 15, 20, 25 |
| Wall properties | Smooth surface |
| Eccentric ratio | 10% |
| Timesteps (s) | 0.0004 s |
| K(MN/m) | k(MN/m) | C(MNs/m) | c(MNs/m) | |
|---|---|---|---|---|
| Experiment | 18.7 | 9.62 | 20.5 | 5.37 |
| CFD | 17.9 | 12.3 | 25.4 | 6.17 |
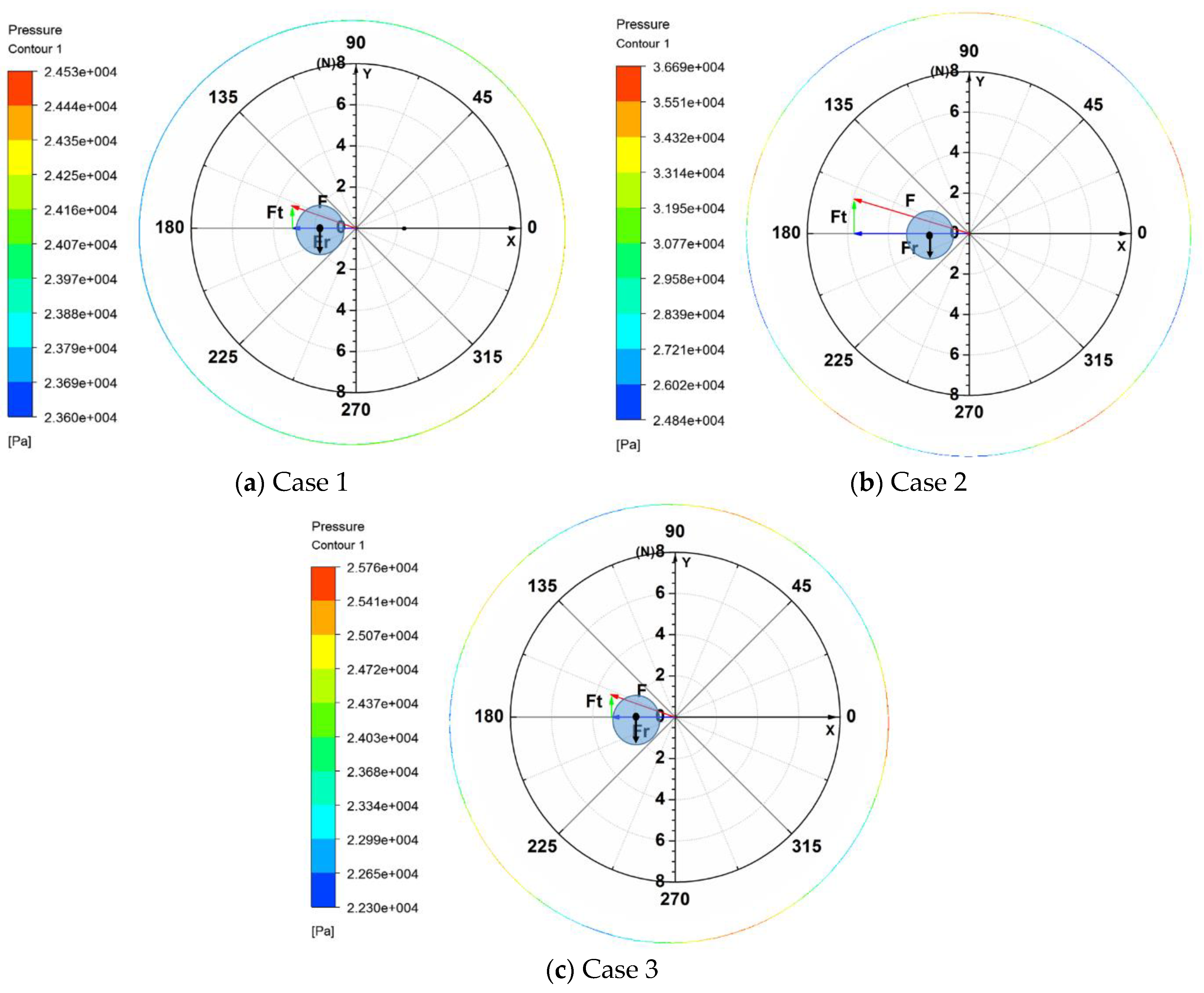
| Design Cases | Case 1 | Case 2 | Case 3 |
|---|---|---|---|
| Inlet pressure conditions | |||
| Schematic diagram of the pressure cloud |  |  |  |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L.; Wang, X.; Liu, H.; Xin, J. The Effect of Inflow Distortion on the Rotordynamic Characteristics of a 1400-MW Reactor Coolant Pump Annular Seal. Machines 2022, 10, 65. https://doi.org/10.3390/machines10010065
Zhou L, Wang X, Liu H, Xin J. The Effect of Inflow Distortion on the Rotordynamic Characteristics of a 1400-MW Reactor Coolant Pump Annular Seal. Machines. 2022; 10(1):65. https://doi.org/10.3390/machines10010065
Chicago/Turabian StyleZhou, Lusheng, Xiaofang Wang, Haitao Liu, and Jianchi Xin. 2022. "The Effect of Inflow Distortion on the Rotordynamic Characteristics of a 1400-MW Reactor Coolant Pump Annular Seal" Machines 10, no. 1: 65. https://doi.org/10.3390/machines10010065
APA StyleZhou, L., Wang, X., Liu, H., & Xin, J. (2022). The Effect of Inflow Distortion on the Rotordynamic Characteristics of a 1400-MW Reactor Coolant Pump Annular Seal. Machines, 10(1), 65. https://doi.org/10.3390/machines10010065





