In-Process Chatter Detection Using Signal Analysis in Frequency and Time-Frequency Domain
Abstract
:1. Introduction
2. In-Process Chatter-Identification Strategies
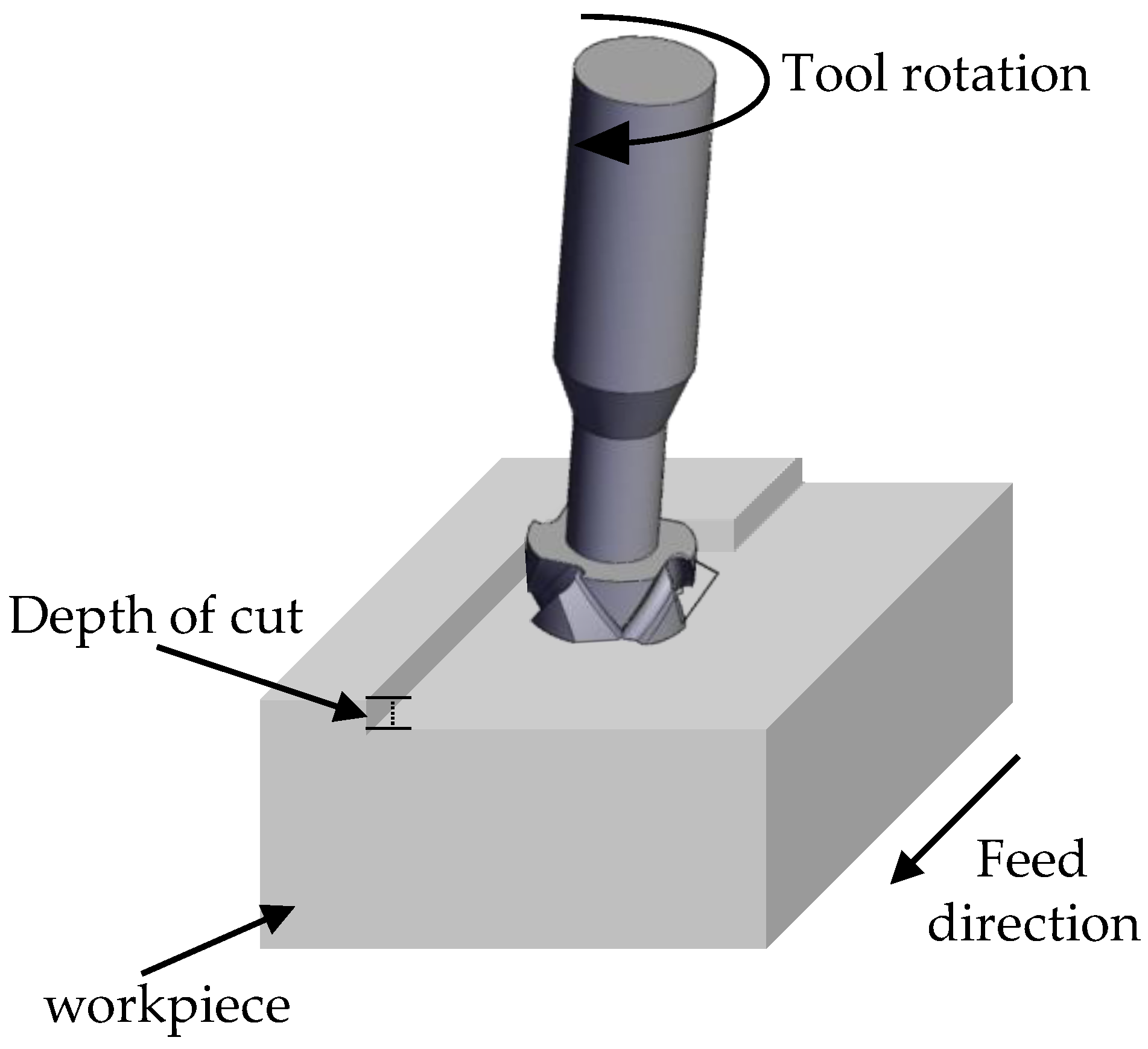
2.1. Basic Principles of Chatter Dynamics
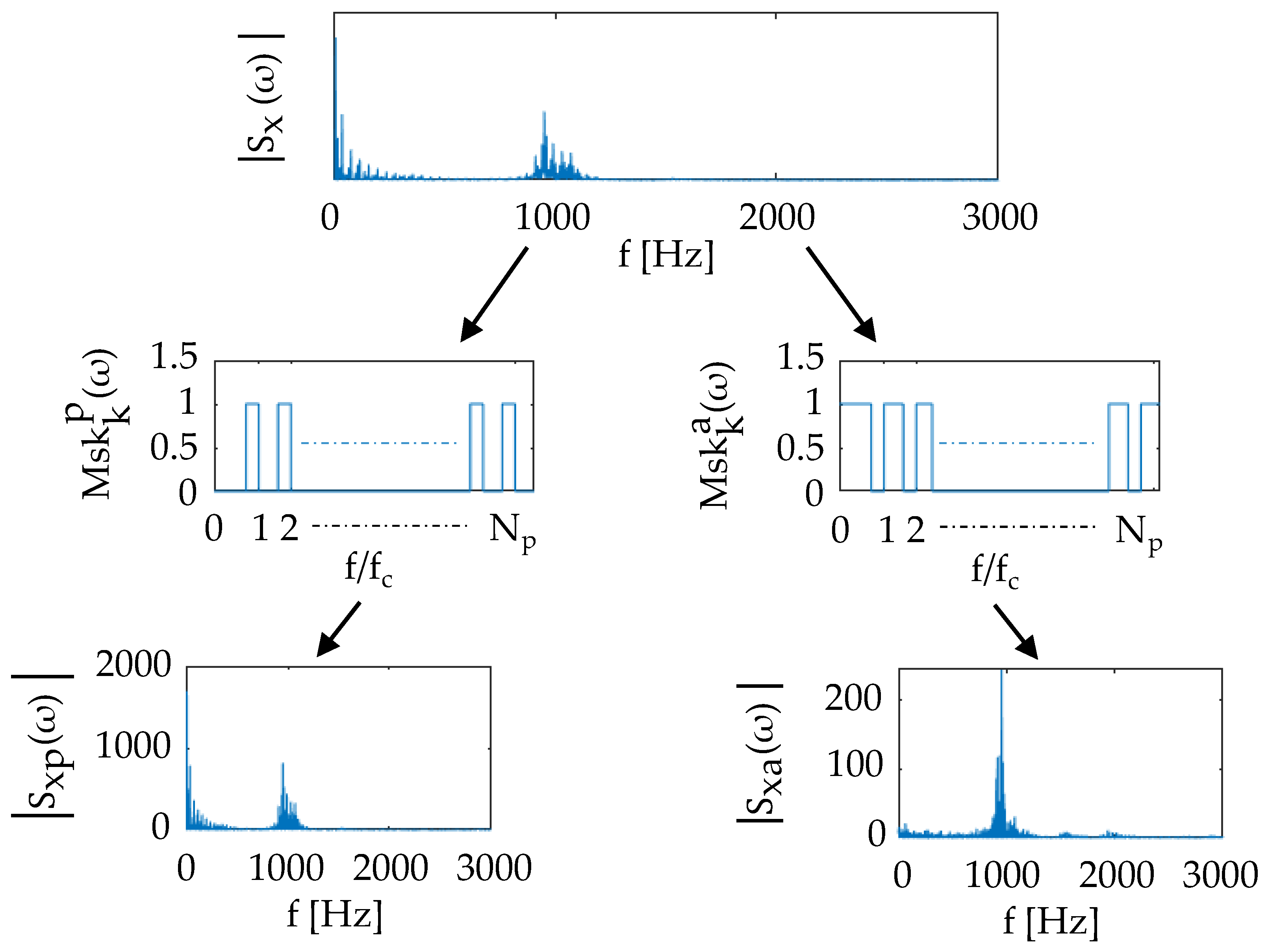
2.2. Power-Spectral-Density-Based In-Process Chatter Index: PSD-iP-CI
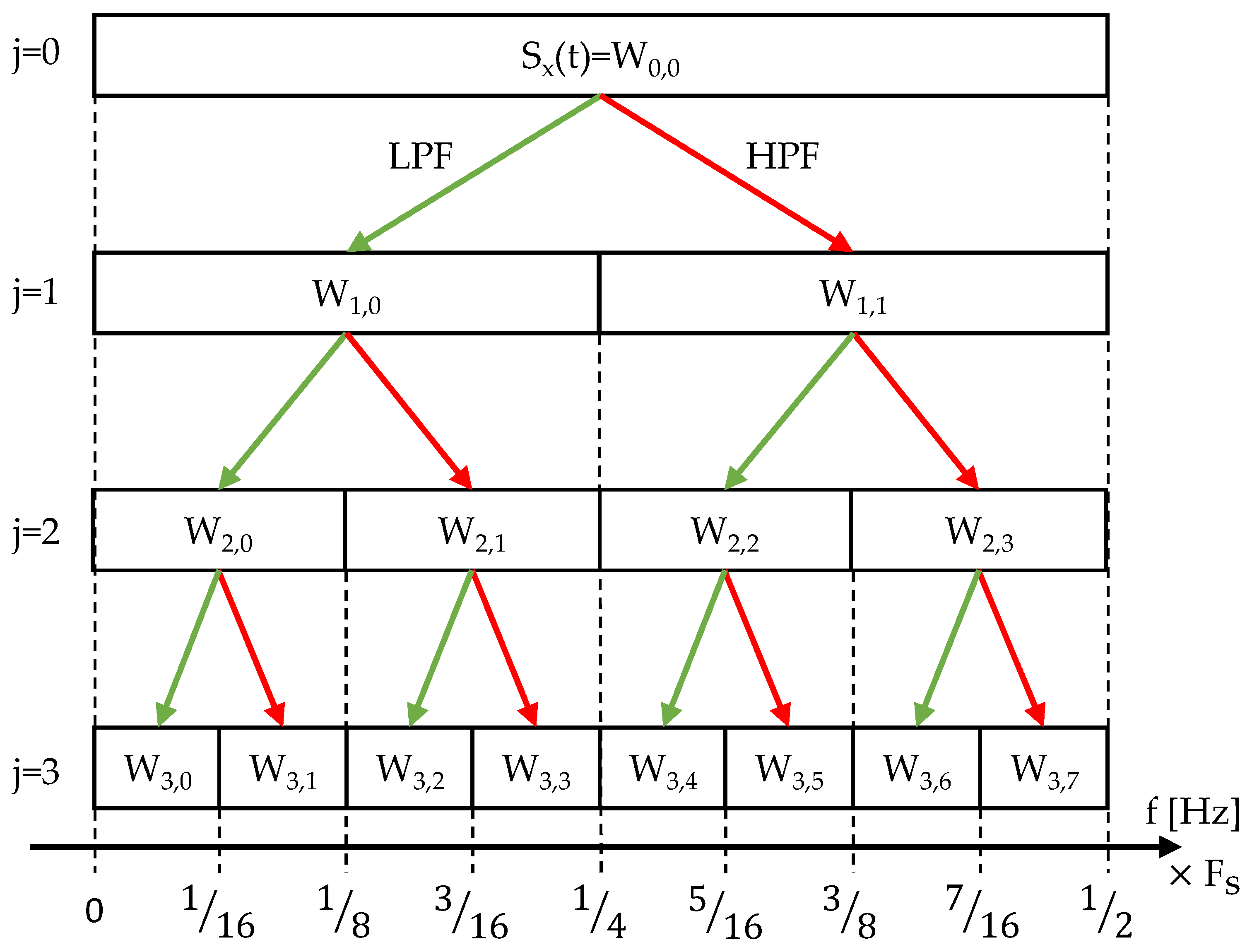
2.3. Wavelet-Packet-Decomposition-Based In-Process Chatter Index: WPD-iP-CI
3. Experimental Validations
3.1. Experimental Setup
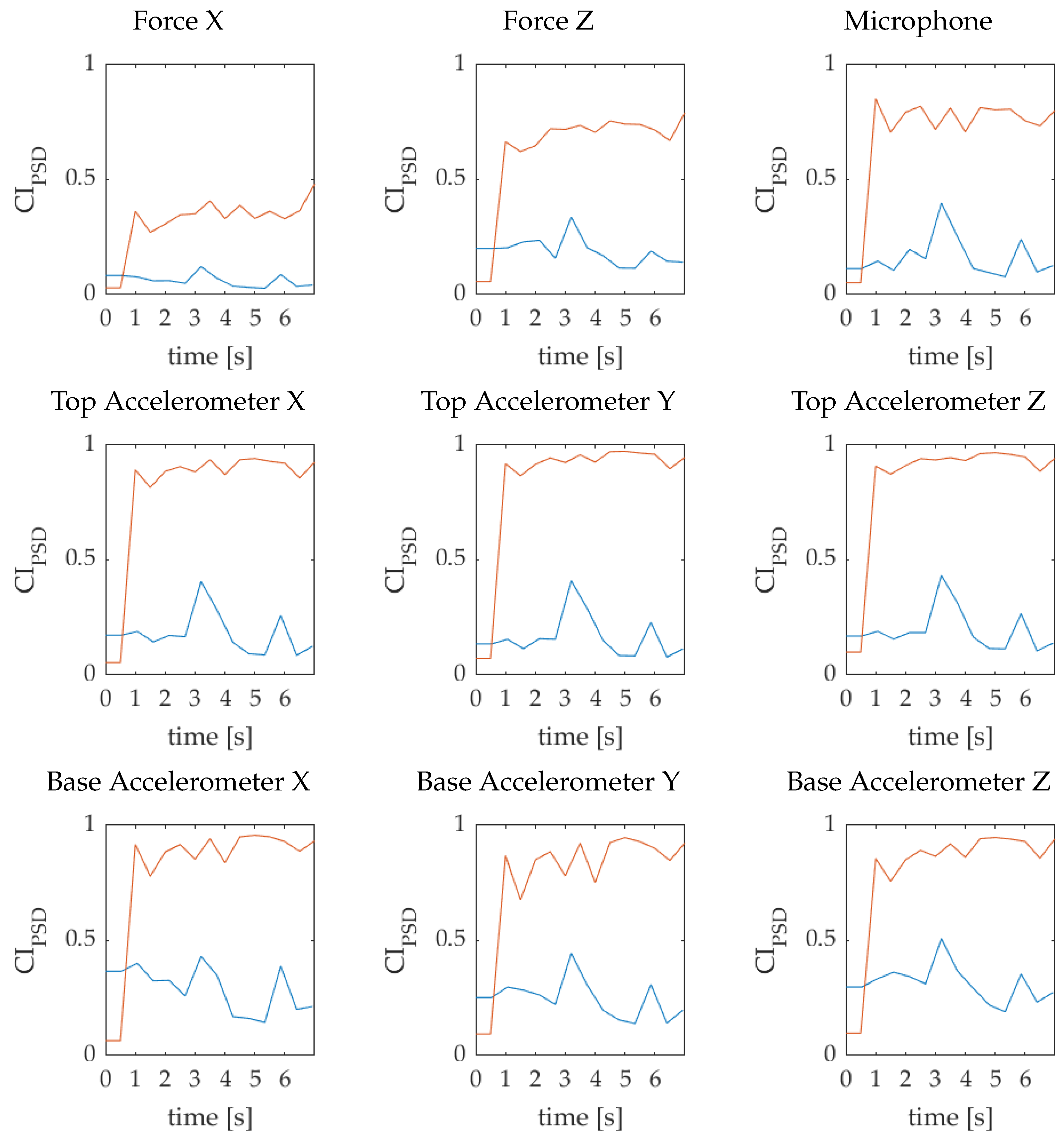
3.2. Case 1. A Multi-Sensor Comparative Benchmark in Chatter-Free and in Chatter Conditions
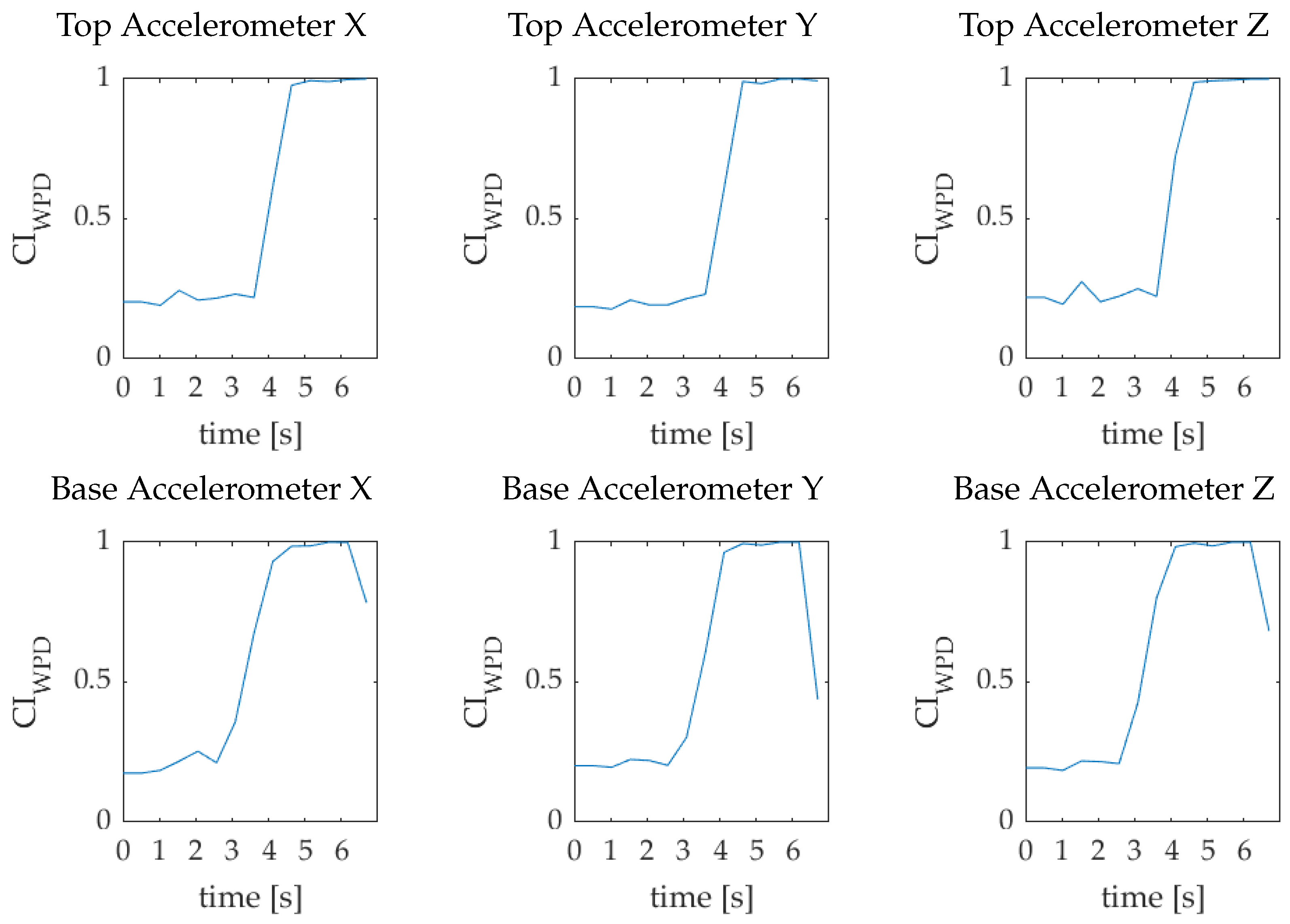
3.3. Case 2. CI Calculation in Transition Scenario from Chatter-Free to Chatter
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Galloro, A.; Capalbo, C.; Cosco, F.; Ambrogio, G.; Filice, L.; Mundo, D. On the influence of the tool holder on chatter predictions in CNC milling processes. In Proceedings of the International Conference on Machine Design MD2021, Porto, Portugal, 7–8 September 2021. [Google Scholar]
- Siddhpura, M.; Paurobally, R. Experimental Investigation of Chatter Vibrations in Facing and Turning Processes. Int. J. Mech. Mechatronics Eng. 2013, 7, 968–973. [Google Scholar]
- Budak, E.; Altintaş, Y. Analytical prediction of chatter stability in milling—Part I: General formulation. J. Dyn. Syst. Meas. Control. Trans. ASME 1998, 120, 22–30. [Google Scholar] [CrossRef]
- Altintas, Y.; Stépán, G.; Budak, E.; Schmitz, T.L.; Kilic, Z.M. Chatter Stability of Machining Operations. J. Manuf. Sci.-Eng.-Trans. Asme 2020, 142, 110801. [Google Scholar] [CrossRef]
- Altintas, Y. Analytical Prediction of Three Dimensional Chatter Stability in Milling. JSME Int. J. Ser. Mech. Syst. Mach. Elem. Manuf. 2001, 44, 717–723. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.J.; Uhlmann, E.; Oberschmidt, D.; Sung, C.F.; Perfilov, I. Critical depth of cut and asymptotic spindle speed for chatter in micro milling with process damping. CIRP Ann. 2016, 65, 113–116. [Google Scholar] [CrossRef]
- Yamato, S.; Nakanishi, K.; Suzuki, N.; Kakinuma, Y. Development of Automatic Chatter Suppression System in Parallel Milling by Real-Time Spindle Speed Control with Observer-Based Chatter Monitoring. Int. J. Precis. Eng. Manuf. 2021, 22, 227–240. [Google Scholar] [CrossRef]
- Altintaş, Y.; Budak, E. Analytical Prediction of Stability Lobes in Milling. CIRP Ann. 1995, 44, 357–362. [Google Scholar] [CrossRef]
- Grossi, N.; Sallese, L.; Scippa, A.; Campatelli, G. ScienceDirect Chatter stability prediction in milling using speed-varying cutting force coefficients review under responsibility of the International Scientific Committee of the 6th CIRP International Conference on High Performance Cutting. Procedia CIRP 2014, 14, 170–175. [Google Scholar] [CrossRef] [Green Version]
- Quintana, G.; Ciurana, J. Chatter in machining processes: A review. Int. J. Mach. Tools Manuf. 2011, 51, 363–376. [Google Scholar] [CrossRef]
- Siddhpura, M.; Paurobally, R. A review of chatter vibration research in turning. Int. J. Mach. Tools Manuf. 2012, 61, 27–47. [Google Scholar] [CrossRef]
- Munoa, J.; Beudaert, X.; Erkorkmaz, K.; Iglesias, A.; Barrios, A.; Zatarain, M. Active suppression of structural chatter vibrations using machine drives and accelerometers. CIRP Ann. 2015, 64, 385–388. [Google Scholar] [CrossRef]
- Tangjitsitcharoen, S.; Pongsathornwiwat, N. Development of chatter detection in milling processes. Int. J. Adv. Manuf. Technol. 2013, 65, 919–927. [Google Scholar] [CrossRef]
- Schmitz, T.L.; Davies, M.A.; Medicus, K.; Snyder, J. Improving High-Speed Machining Material Removal Rates by Rapid Dynamic Analysis. CIRP Ann. 2001, 50, 263–268. [Google Scholar] [CrossRef]
- Huda, F.; Darman, D.; Rusli, M. Chatter detection in turning process using sound signal and simple microphone. IOP Conf. Ser. Mater. Sci. Eng. 2020, 830, 042027. [Google Scholar] [CrossRef]
- Delio, T.; Tlusty, J.; Smith, S. Use of audio signals for chatter detection and control. J. Manuf. Sci. Eng. Trans. ASME 1992, 114, 146–157. [Google Scholar] [CrossRef]
- Kuljanic, E.; Sortino, M.; Totis, G. Multisensor approaches for chatter detection in milling. J. Sound Vib. 2008, 312, 672–693. [Google Scholar] [CrossRef]
- Faassen, R.; Doppenberg, E.; van de Wouw, N.; Oosterling, J.; Nijmeijer, H. Online detection of the onset and occurrence of machine tool chatter in the milling process. In Proceedings of the CIRP 2nd International Conference on High Performance Cutting, Vancouver, BC, Canada, 12–13 June 2006. [Google Scholar]
- Vashisht, R.K.; Peng, Q. Online Chatter Detection for Milling Operations Using LSTM Neural Networks Assisted by Motor Current Signals of Ball Screw Drives. J. Manuf. Sci. Eng. 2020, 143, 011008. [Google Scholar] [CrossRef]
- Dong, X.; Tu, G.; Wang, X.; Chen, S. Real-time chatter detection via iterative Vold-Kalman filter and energy entropy. Int. J. Adv. Manuf. Technol. 2021. [Google Scholar] [CrossRef]
- Obinna, N.N.; Ugochukwu, O.C.; Christian, O.E.; Imhade, O.P. Evaluation of chatter vibration frequency in cnc turning of 4340 alloy steel material. Int. J. Sci. Eng. Res. 2017, 8, 487–495. [Google Scholar]
- Wang, A.; Jin, W.; Chen, W.; Feng, R.; Xu, C. Bifurcation and chaotic vibration of frictional chatter in turning process. Adv. Mech. Eng. 2018, 10, 1687814018771262. [Google Scholar] [CrossRef]
- Rusinek, R.; Wiercigroch, M.; Wahi, P. Modelling of frictional chatter in metal cutting. Int. J. Mech. Sci. 2014, 89, 167–176. [Google Scholar] [CrossRef]
- Hajmohammadi, M.S.; Movahhedy, M.R. Investigation of thermal effects on machining chatter using FEM simulation of chip formation. Procedia CIRP 2012, 1, 50–55. [Google Scholar] [CrossRef]
- Yuan, L.; Pan, Z.; Ding, D.; Sun, S.; Li, W. A Review on Chatter in Robotic Machining Process Regarding Both Regenerative and Mode Coupling Mechanism. IEEE/ASME Trans. Mechatron. 2018, 23, 2240–2251. [Google Scholar] [CrossRef]
- Gasparetto, A. Eigenvalue Analysis of Mode-Coupling Chatter for Machine-Tool Stabilization. J. Vib. Control. 2001, 7, 181–197. [Google Scholar] [CrossRef]
- Yue, C.; Gao, H.; Liu, X.; Liang, S.Y.; Wang, L. A review of chatter vibration research in milling. Chin. J. Aeronaut. 2019, 32, 215–242. [Google Scholar] [CrossRef]
- Li, K.; He, S.; Li, B.; Liu, H.; Mao, X.; Shi, C. A novel online chatter detection method in milling process based on multiscale entropy and gradient tree boosting. Mech. Syst. Signal Process. 2020, 135, 106385. [Google Scholar] [CrossRef]
- Kim, J.D.; Chin, D.H.; Kim, K.H.; Yoon, M.C. Monitoring of Tooth Passing and Chatter Properties in End-Milling. In Proceedings of the International Conference on Advanced Engineering Theory and Applications, Ho Chi Minh, Vietnam, 7–9 December 2017; pp. 509–519. [Google Scholar] [CrossRef]
- Wirsing, K. Time Frequency Analysis of Wavelet and Fourier Transform. In Wavelet Theory; IntechOpen: London, UK, 2020. [Google Scholar] [CrossRef]
- Tiwari, V.K.; Sandhibigraha, H.B.; Umarikar, A.C.; Jain, T. Undecimated Wavelet Packet Transform Based Visualization of Time-Varying Power Quality Disturbance. In Proceedings of the 2018 20th National Power Systems Conference, NPSC 2018, Tiruchirappalli, India, 14–16 December 2018. [Google Scholar] [CrossRef]
- Yesilli, M.C.; Khasawneh, F.A.; Otto, A. On transfer learning for chatter detection in turning using wavelet packet transform and ensemble empirical mode decomposition. CIRP J. Manuf. Sci. Technol. 2020, 28, 118–135. [Google Scholar] [CrossRef]








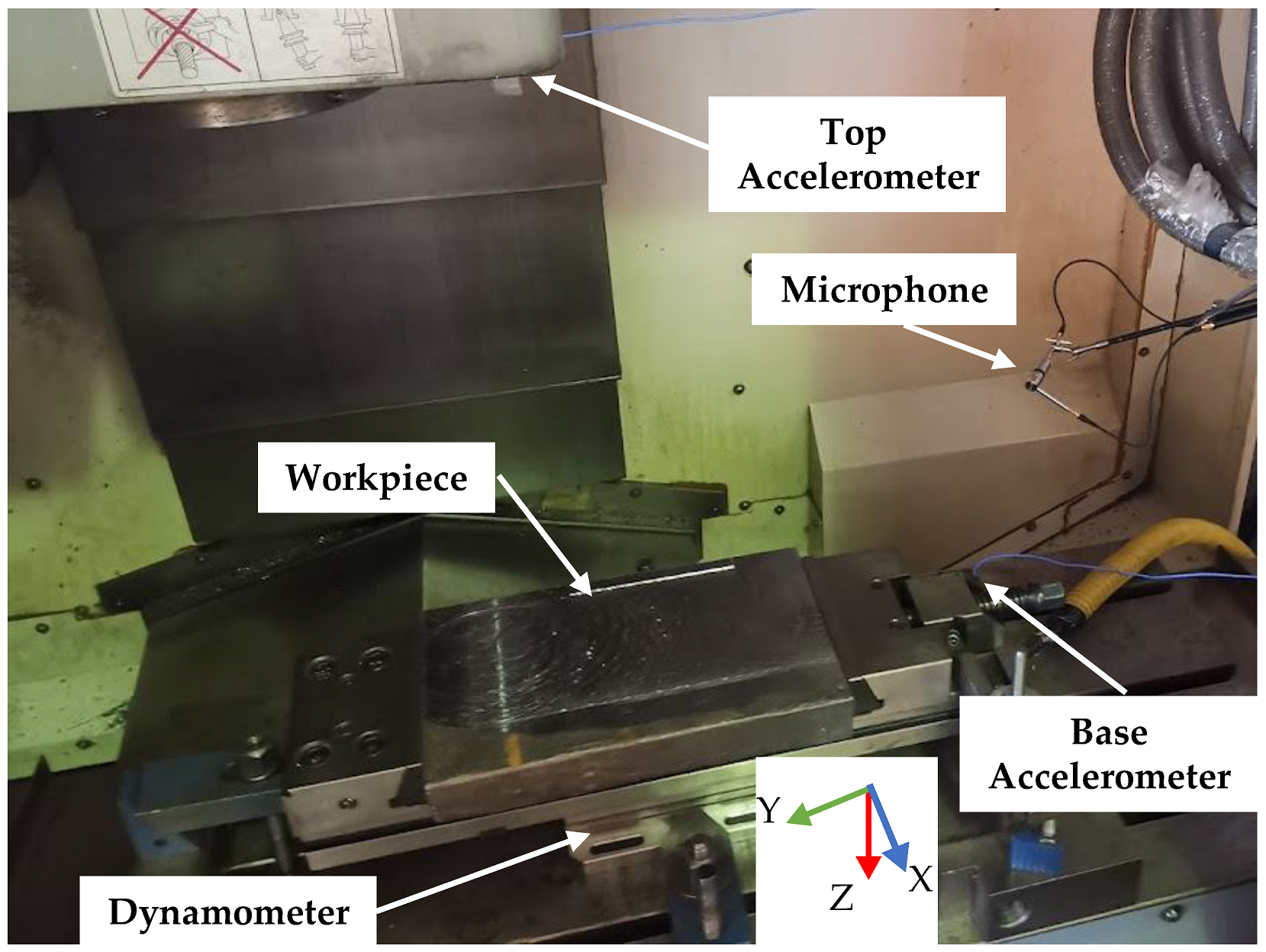
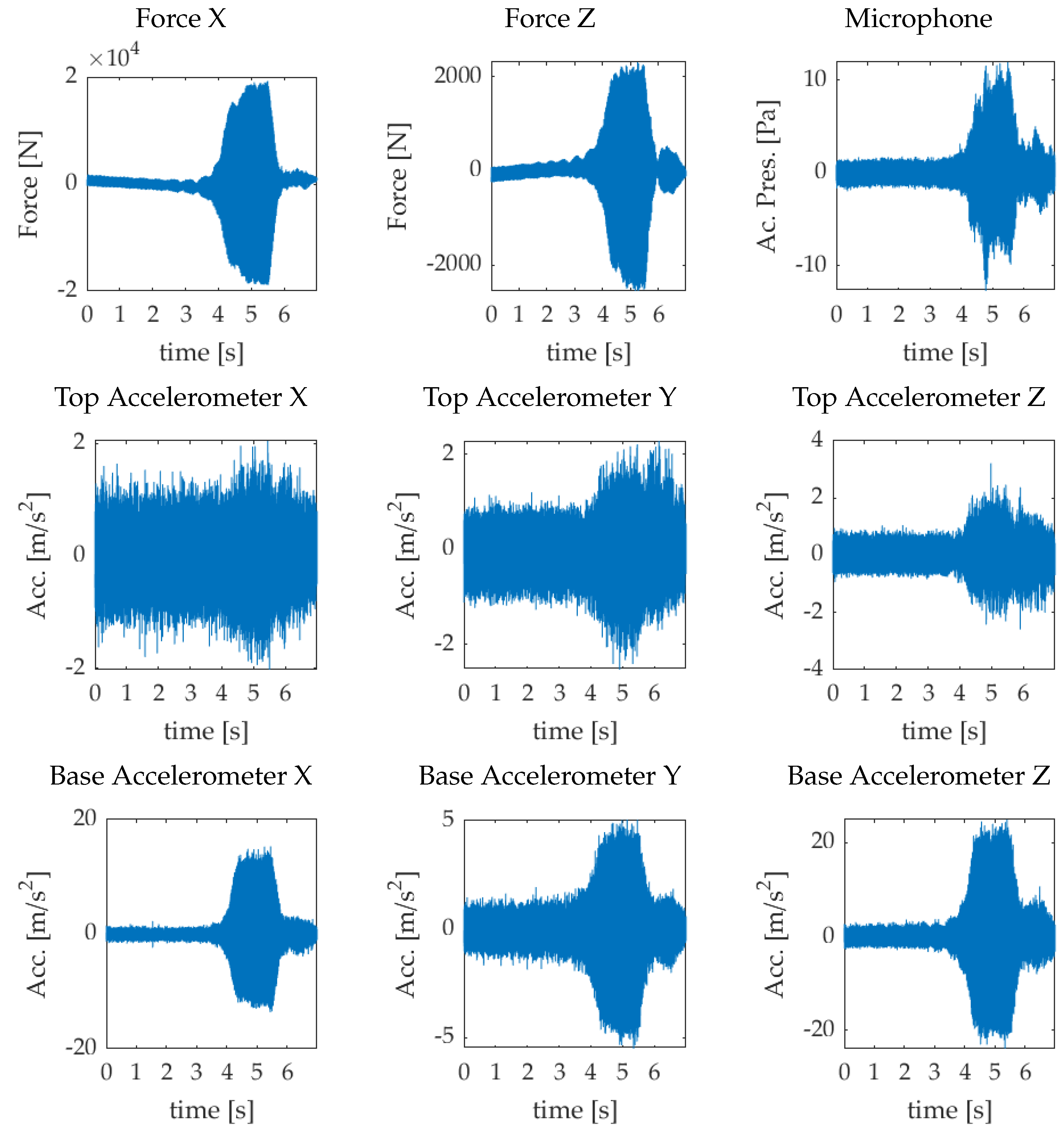
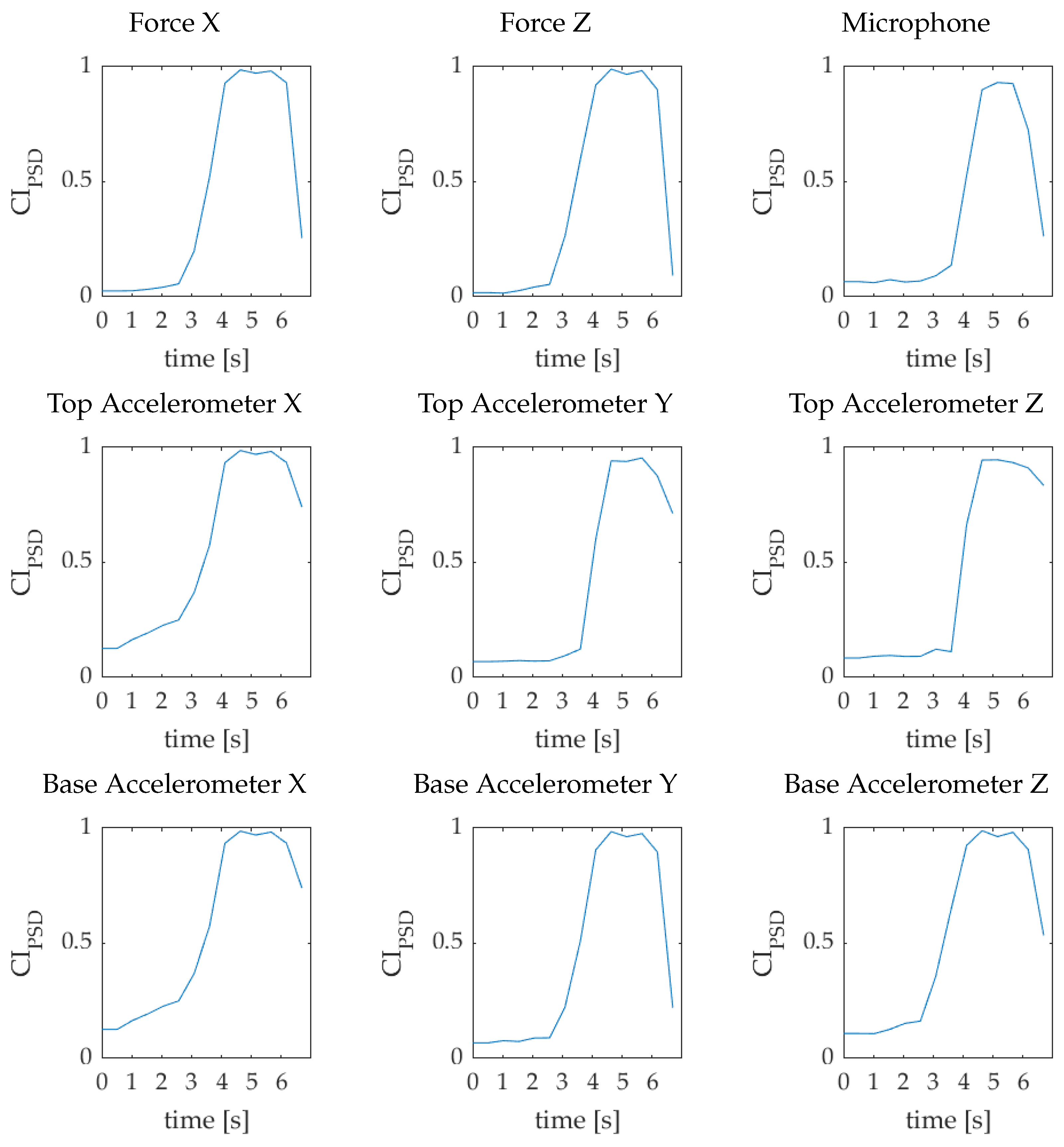
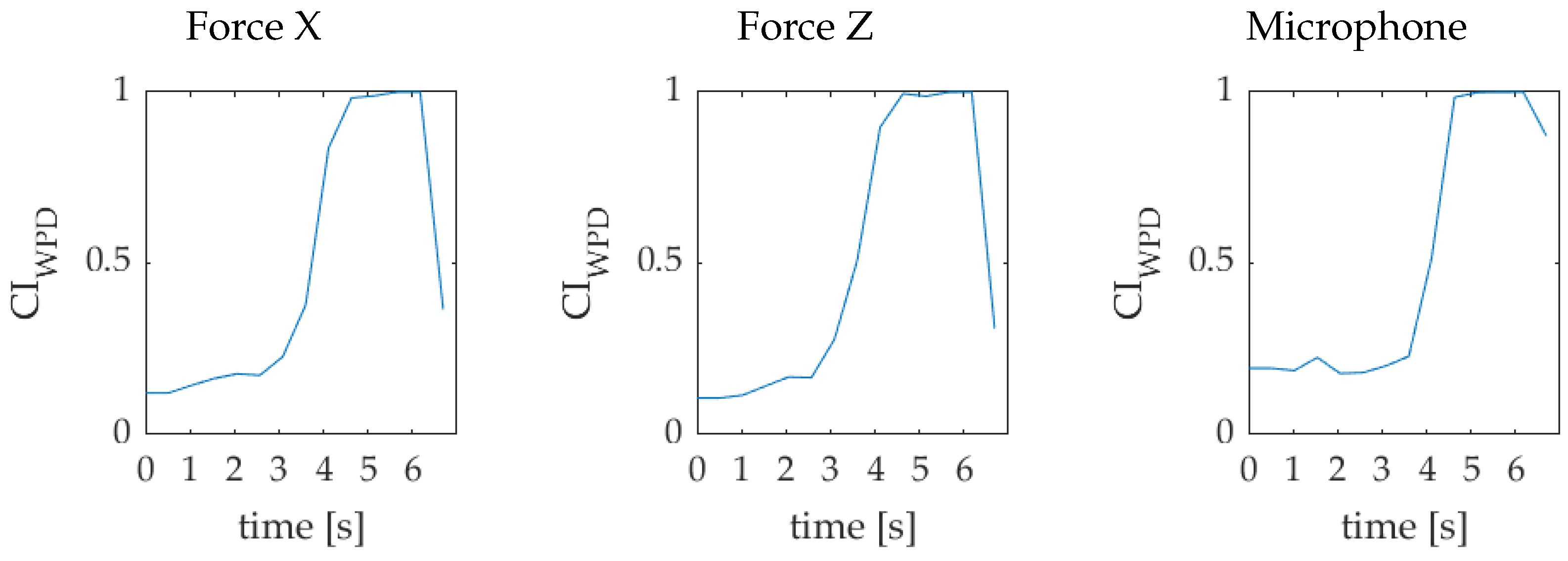
| Sensor Name | Sensor Model | Details |
|---|---|---|
| Multicomponent Dynamometer | Kistler model 9257B | Three-axial force sensors Fx, Fy, Fz measuring range kN Clamping area 100 × 170 mm |
| Top and Base Accelerometer | PCB Piezotronics model 356A32 | Tri-axial ICP sensor Sensitivity 100 mV/g Measuring range ± 50 g |
| Microphone | GRAS microphone model 40GI | Free-field microphone Sensitivity 12.5 mV/Pa Frequency range 30 to 10 kHz |
| Experiment ID | Spindle Speed (rpm) | Depth pf Cut (mm) | Feed (mm/m) |
|---|---|---|---|
| Chatter-free | 900 | 4.5 | 500 |
| Chatter | 600 | 4.5 | 500 |
| Experiment ID | Spindle Speed (rpm) | Depth pf Cut (mm) | Feed (mm/m) |
|---|---|---|---|
| Stable-to-chatter transition | 1750 | 2 | 1000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perrelli, M.; Cosco, F.; Gagliardi, F.; Mundo, D. In-Process Chatter Detection Using Signal Analysis in Frequency and Time-Frequency Domain. Machines 2022, 10, 24. https://doi.org/10.3390/machines10010024
Perrelli M, Cosco F, Gagliardi F, Mundo D. In-Process Chatter Detection Using Signal Analysis in Frequency and Time-Frequency Domain. Machines. 2022; 10(1):24. https://doi.org/10.3390/machines10010024
Chicago/Turabian StylePerrelli, Michele, Francesco Cosco, Francesco Gagliardi, and Domenico Mundo. 2022. "In-Process Chatter Detection Using Signal Analysis in Frequency and Time-Frequency Domain" Machines 10, no. 1: 24. https://doi.org/10.3390/machines10010024
APA StylePerrelli, M., Cosco, F., Gagliardi, F., & Mundo, D. (2022). In-Process Chatter Detection Using Signal Analysis in Frequency and Time-Frequency Domain. Machines, 10(1), 24. https://doi.org/10.3390/machines10010024









