Application of Bernoulli Polynomials for Solving Variable-Order Fractional Optimal Control-Affine Problems
Abstract
1. Introduction
2. Preliminaries
2.1. The Variable-Order Fractional Calculus
2.2. Bernoulli Polynomials
3. Operational Matrix of Variable-Order Fractional Integration
4. Methods of Solution
4.1. Approach I
4.2. Approach II
5. Error Bounds
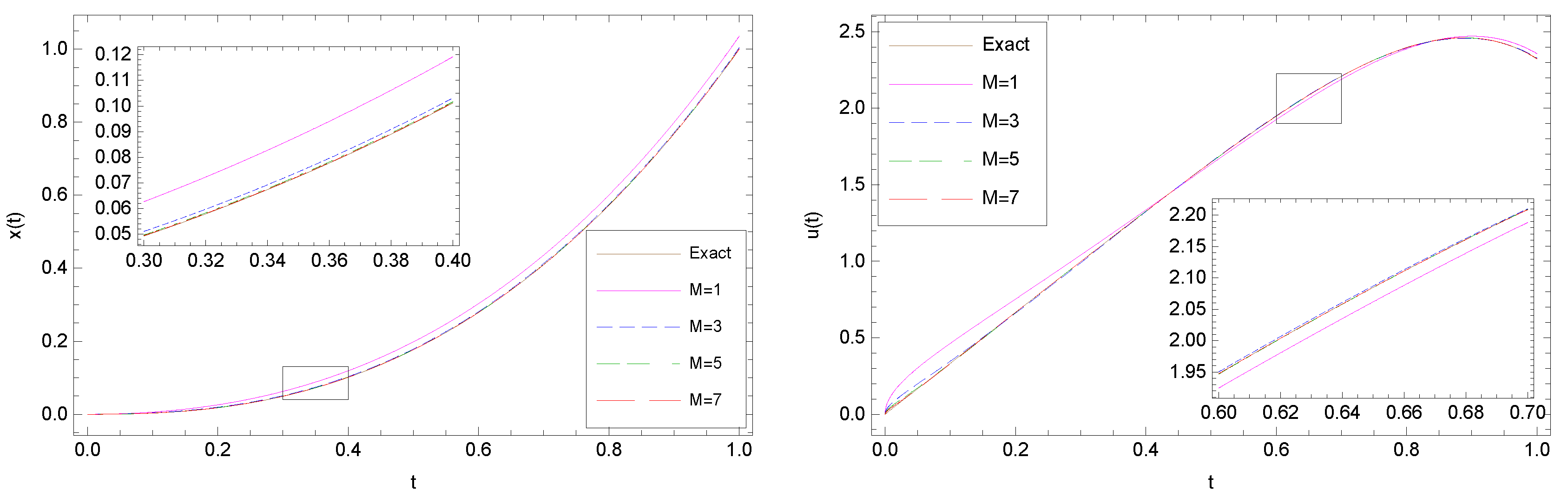
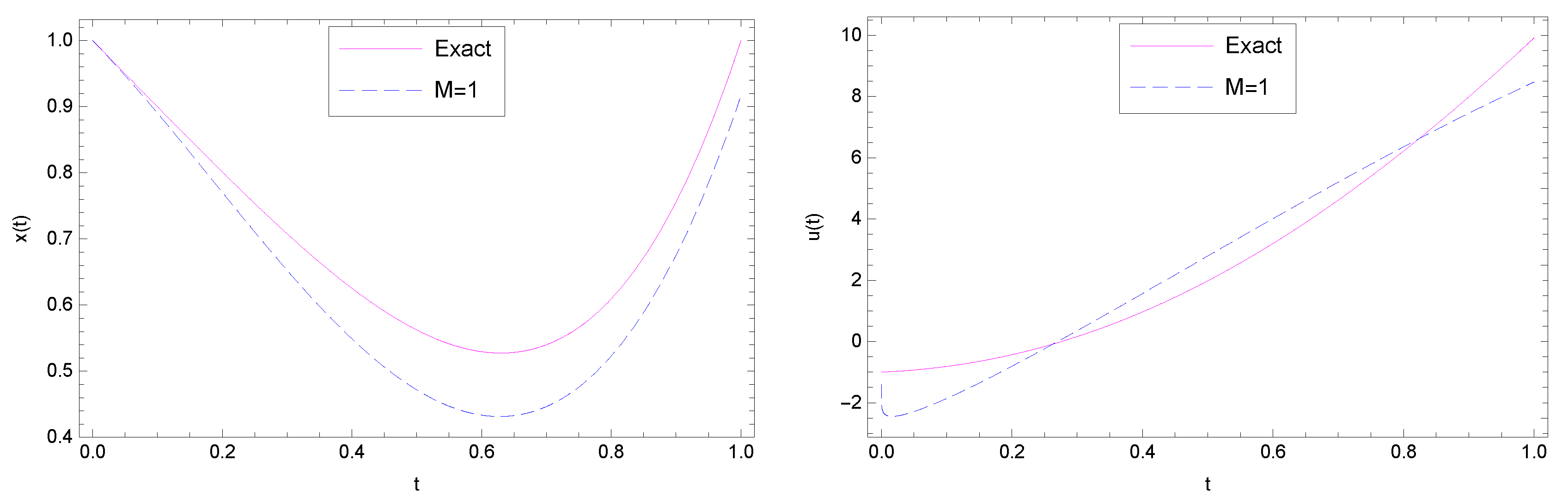
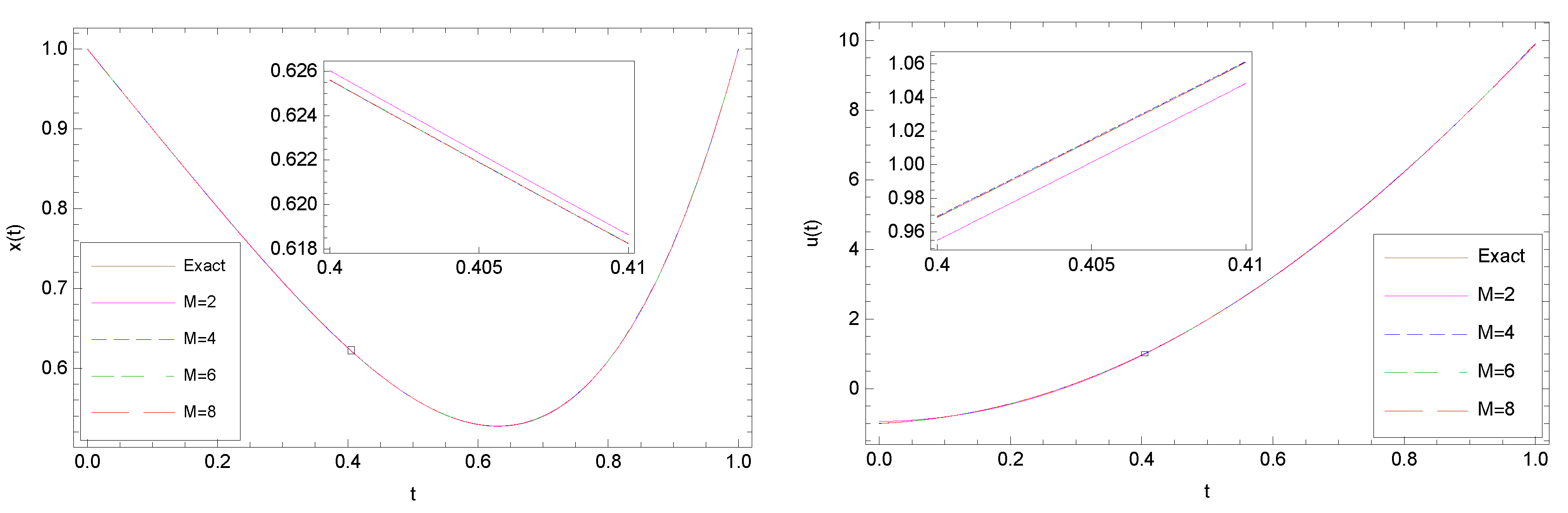
6. Test Problems
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Machado, J.T.; Kiryakova, V.; Mainardi, F. Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1140–1153. [Google Scholar] [CrossRef]
- Keshavarz, E.; Ordokhani, Y.; Razzaghi, M. A numerical solution for fractional optimal control problems via Bernoulli polynomials. J. Vib. Control 2016, 22, 3889–3903. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Tohidi, E.; Soleymani, F. A new Bernoulli matrix method for solving high-order linear and nonlinear Fredholm integro-differential equations with piecewise intervals. Appl. Math. Comput. 2012, 219, 482–497. [Google Scholar] [CrossRef]
- Tohidi, E.; Bhrawy, A.H.; Erfani, K. A collocation method based on Bernoulli operational matrix for numerical solution of generalized pantograph equation. Appl. Math. Model. 2013, 37, 4283–4294. [Google Scholar] [CrossRef]
- Toutounian, F.; Tohidi, E. A new Bernoulli matrix method for solving second order linear partial differential equations with the convergence analysis. Appl. Math. Comput. 2013, 223, 298–310. [Google Scholar] [CrossRef]
- Bazm, S. Bernoulli polynomials for the numerical solution of some classes of linear and nonlinear integral equations. J. Comput. Appl. Math. 2015, 275, 44–60. [Google Scholar] [CrossRef]
- Sahu, P.K.; Mallick, B. Approximate solution of fractional order Lane-Emden type differential equation by orthonormal Bernoulli’s polynomials. Int. J. Appl. Comput. Math. 2019, 5, 89. [Google Scholar] [CrossRef]
- Loh, J.R.; Phang, C. Numerical solution of Fredholm fractional integro-differential equation with right-sided Caputo’s derivative using Bernoulli polynomials operational matrix of fractional derivative. Mediterr. J. Math. 2019, 16, 28. [Google Scholar] [CrossRef]
- Rosa, S.; Torres, D.F.M. Optimal control of a fractional order epidemic model with application to human respiratory syncytial virus infection. Chaos Solitons Fractals 2018, 117, 142–149. [Google Scholar] [CrossRef]
- Malinowska, A.B.; Torres, D.F.M. Introduction to the Fractional Calculus of Variations; Imperial College Press: London, UK, 2012. [Google Scholar] [CrossRef]
- Malinowska, A.B.; Odzijewicz, T.; Torres, D.F.M. Advanced methods in the fractional calculus of variations. In Springer Briefs in Applied Sciences and Technology; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Almeida, R.; Pooseh, S.; Torres, D.F.M. Computational Methods in the Fractional Calculus of Variations; Imperial College Press: London, UK, 2015. [Google Scholar] [CrossRef]
- Ali, M.S.; Shamsi, M.; Khosravian-Arab, H.; Torres, D.F.M.; Bozorgnia, F. A space-time pseudospectral discretization method for solving diffusion optimal control problems with two-sided fractional derivatives. J. Vib. Control 2019, 25, 1080–1095. [Google Scholar] [CrossRef]
- Nemati, S.; Lima, P.M.; Torres, D.F.M. A numerical approach for solving fractional optimal control problems using modified hat functions. Commun. Nonlinear Sci. Numer. Simul. 2019, 78, 104849. [Google Scholar] [CrossRef]
- Salati, A.B.; Shamsi, M.; Torres, D.F.M. Direct transcription methods based on fractional integral approximation formulas for solving nonlinear fractional optimal control problems. Commun. Nonlinear Sci. Numer. Simul. 2019, 67, 334–350. [Google Scholar] [CrossRef]
- Rabiei, K.; Ordokhani, Y.; Babolian, E. Numerical solution of 1D and 2D fractional optimal control of system via Bernoulli polynomials. Int. J. Appl. Comput. Math. 2018, 4, 7. [Google Scholar] [CrossRef]
- Behroozifar, M.; Habibi, N. A numerical approach for solving a class of fractional optimal control problems via operational matrix Bernoulli polynomials. J. Vib. Control 2018, 24, 2494–2511. [Google Scholar] [CrossRef]
- Rahimkhani, P.; Ordokhani, Y. Generalized fractional-order Bernoulli-Legendre functions: An effective tool for solving two-dimensional fractional optimal control problems. IMA J. Math. Control Inf. 2019, 36, 185–212. [Google Scholar] [CrossRef]
- Samko, S.G.; Ross, B. Integration and differentiation to a variable fractional order. Integral Transform. Spec. Funct. 1993, 1, 277–300. [Google Scholar] [CrossRef]
- Lorenzo, C.F.; Hartley, T.T. Variable order and distributed order fractional operators. Nonlinear Dyn. 2002, 29, 57–98. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Mert, R.; Torres, D.F.M. Variable order Mittag-Leffler fractional operators on isolated time scales and application to the calculus of variations. In Fractional Derivatives with Mittag-Leffler Kernel; Springer: Cham, Switzerland, 2019; Volume 194, pp. 35–47. [Google Scholar]
- Hassani, H.; Naraghirad, E. A new computational method based on optimization scheme for solving variable-order time fractional Burgers’ equation. Math. Comput. Simul. 2019, 162, 1–17. [Google Scholar] [CrossRef]
- Odzijewicz, T.; Malinowska, A.B.; Torres, D.F.M. Fractional variational calculus of variable order. In Advances in Harmonic Analysis and Operator Theory; Birkhäuser/Springer Basel AG: Basel, Switzerland, 2013; Volume 229, pp. 291–301. [Google Scholar] [CrossRef]
- Yan, R.; Han, M.; Ma, Q.; Ding, X. A spectral collocation method for nonlinear fractional initial value problems with a variable-order fractional derivative. Comput. Appl. Math. 2019, 38, 66. [Google Scholar] [CrossRef]
- Almeida, R.; Tavares, D.; Torres, D.F.M. The variable-order fractional calculus of variations. In Springer Briefs in Applied Sciences and Technology; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Heydari, M.H.; Avazzadeh, Z. A new wavelet method for variable-order fractional optimal control problems. Asian J. Control 2018, 20, 1804–1817. [Google Scholar] [CrossRef]
- Mohammadi, F.; Hassani, H. Numerical solution of two-dimensional variable-order fractional optimal control problem by generalized polynomial basis. J. Optim. Theory Appl. 2019, 180, 536–555. [Google Scholar] [CrossRef]
- Costabile, F.; Dell’Accio, F.; Gualtieri, M.I. A new approach to Bernoulli polynomials. Rend. Mat. Appl. 2006, 26, 1–12. [Google Scholar]
- Arfken, G. Mathematical Methods for Physicists; Academic Press: New York, NY, USA; London, UK, 1966. [Google Scholar]
- Shen, J.; Tang, T.; Wang, L.L. Spectral Methods; Springer Series in Computational Mathematics; Springer: Heidelberg, Germany, 2011; Volume 41. [Google Scholar] [CrossRef]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods. In Scientific Computation; Springer: Berlin, Germany, 2006. [Google Scholar]
- Lotfi, A.; Yousefi, S.A.; Dehghan, M. Numerical solution of a class of fractional optimal control problems via the Legendre orthonormal basis combined with the operational matrix and the Gauss quadrature rule. J. Comput. Appl. Math. 2013, 250, 143–160. [Google Scholar] [CrossRef]
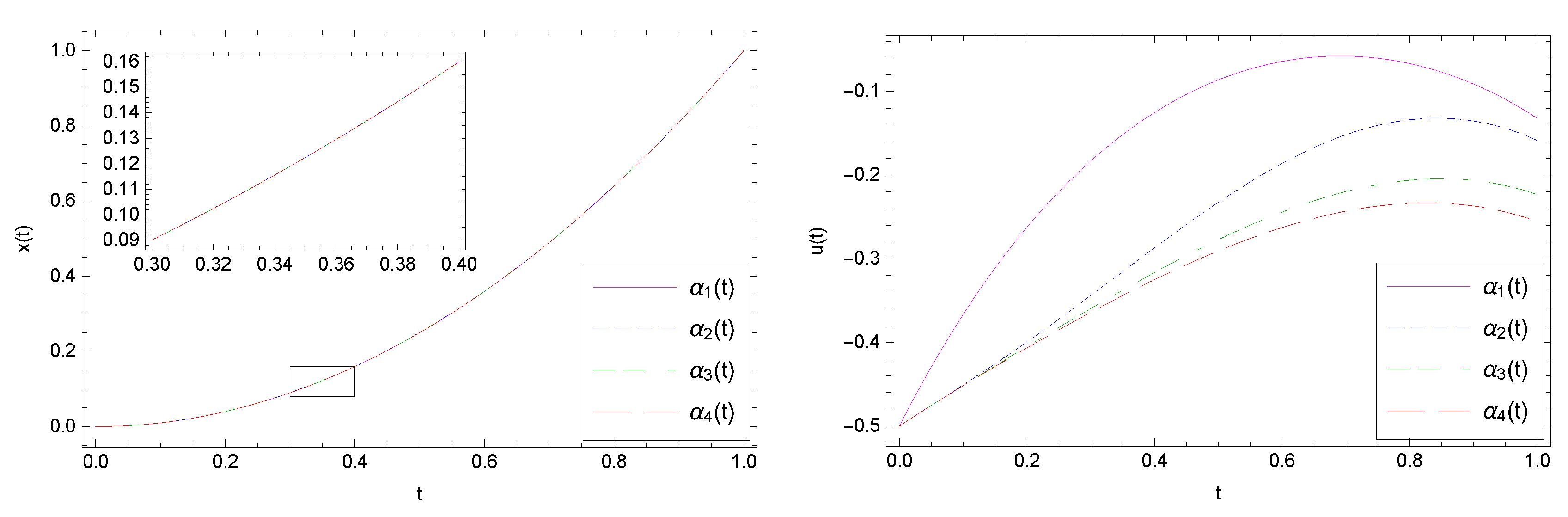
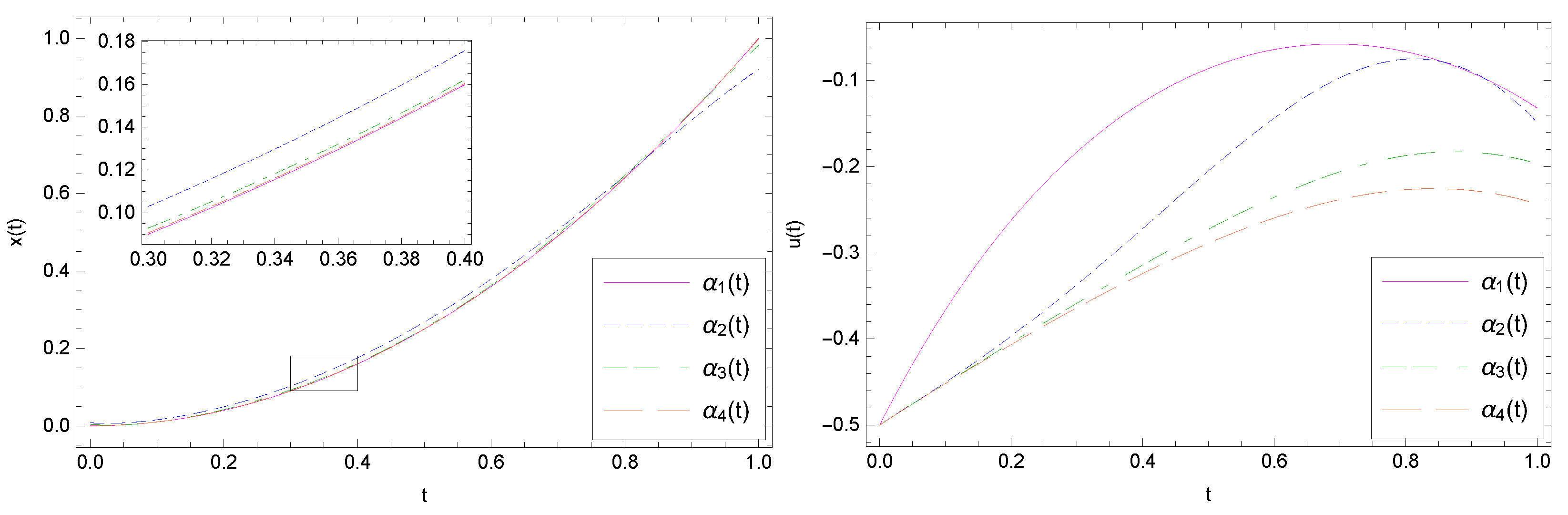
| M | 1 | 2 | 3 | 2 | 5 |
|---|---|---|---|---|---|
| J |
| Method | ||||
|---|---|---|---|---|
| Approach I | ||||
| Approach II |
| M | 1 | 3 | 5 | 7 |
|---|---|---|---|---|
| J |
| M | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| J |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nemati, S.; Torres, D.F.M. Application of Bernoulli Polynomials for Solving Variable-Order Fractional Optimal Control-Affine Problems. Axioms 2020, 9, 114. https://doi.org/10.3390/axioms9040114
Nemati S, Torres DFM. Application of Bernoulli Polynomials for Solving Variable-Order Fractional Optimal Control-Affine Problems. Axioms. 2020; 9(4):114. https://doi.org/10.3390/axioms9040114
Chicago/Turabian StyleNemati, Somayeh, and Delfim F. M. Torres. 2020. "Application of Bernoulli Polynomials for Solving Variable-Order Fractional Optimal Control-Affine Problems" Axioms 9, no. 4: 114. https://doi.org/10.3390/axioms9040114
APA StyleNemati, S., & Torres, D. F. M. (2020). Application of Bernoulli Polynomials for Solving Variable-Order Fractional Optimal Control-Affine Problems. Axioms, 9(4), 114. https://doi.org/10.3390/axioms9040114






