A Non-Intrusive Stochastic Isogeometric Analysis of Functionally Graded Plates with Material Uncertainty
Abstract
1. Introduction
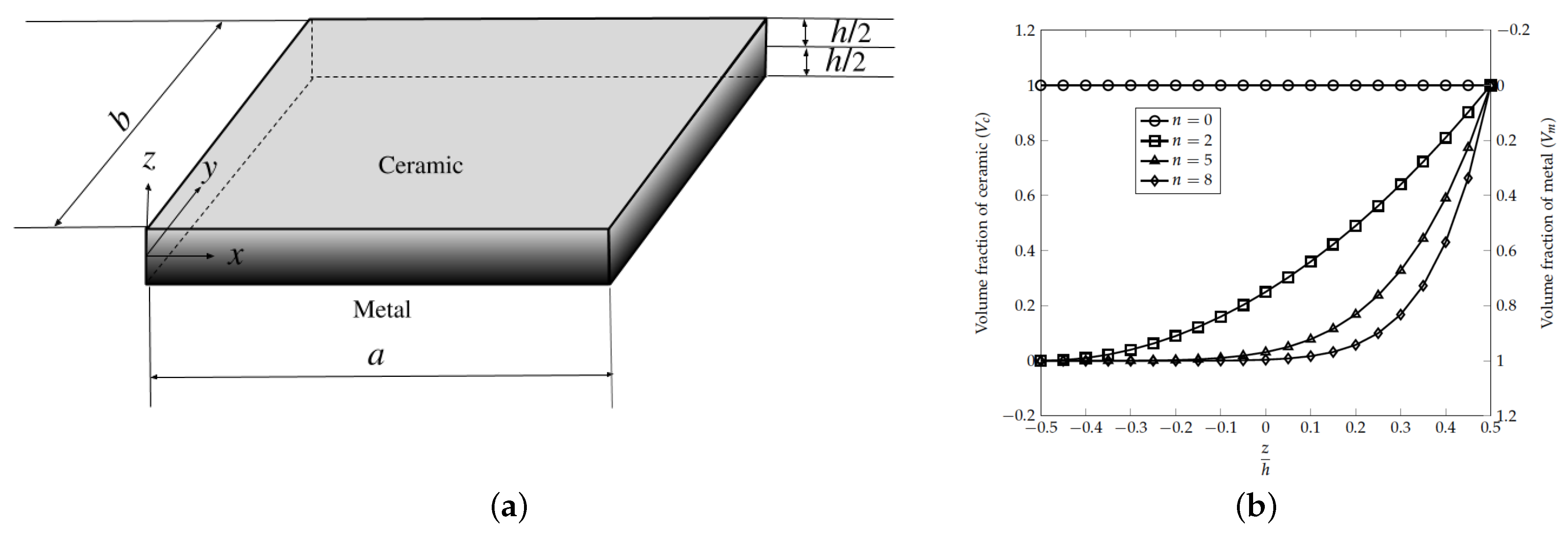
2. Analysis of Functionally Graded Panels
2.1. Effective Modulus and Poisson’s Ratio
2.2. First Order Shear Deformation Theory
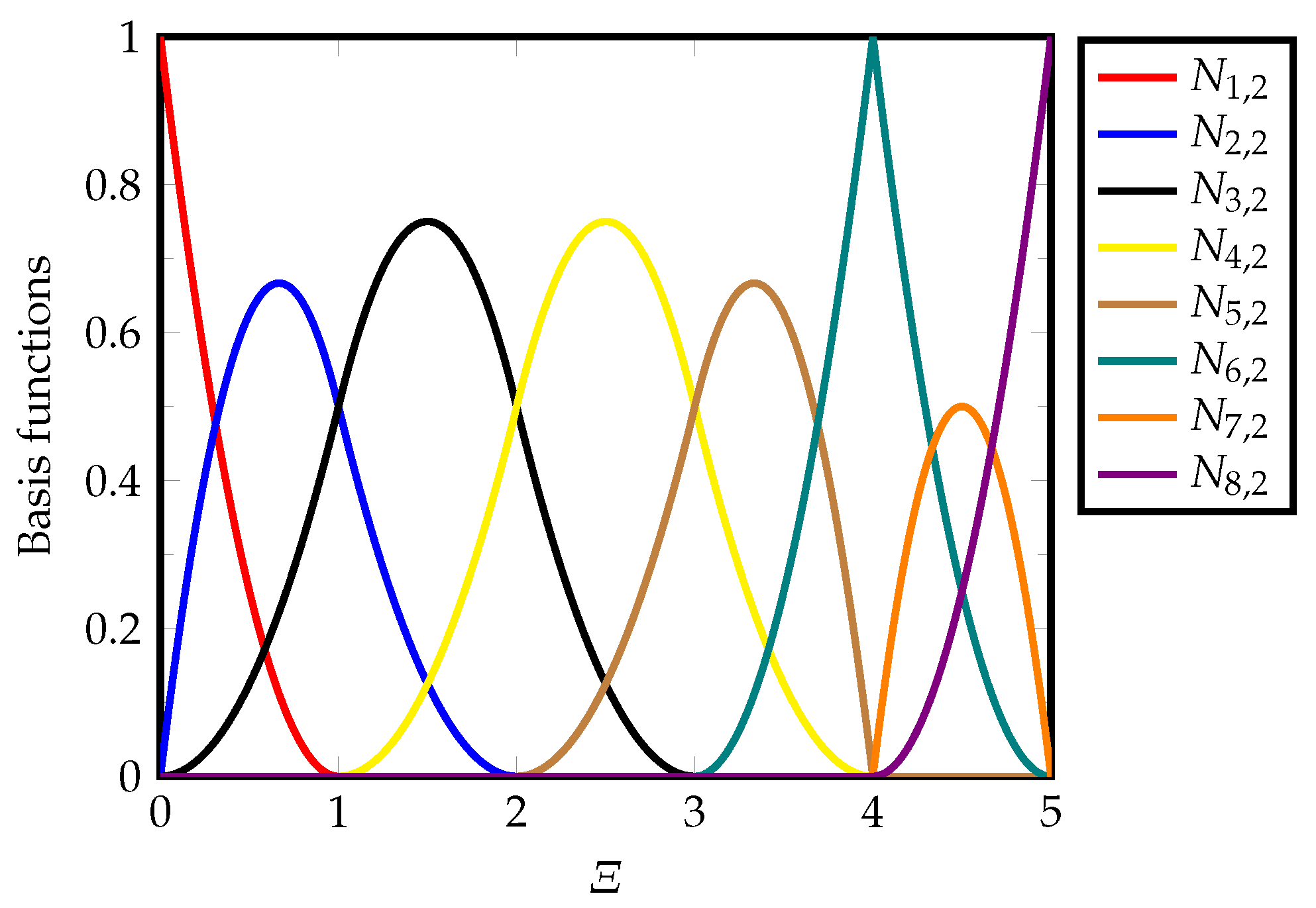
3. Overview of Isogeometric Analysis
4. Non-Intrusive Spectral Projection
5. Numerical Examples
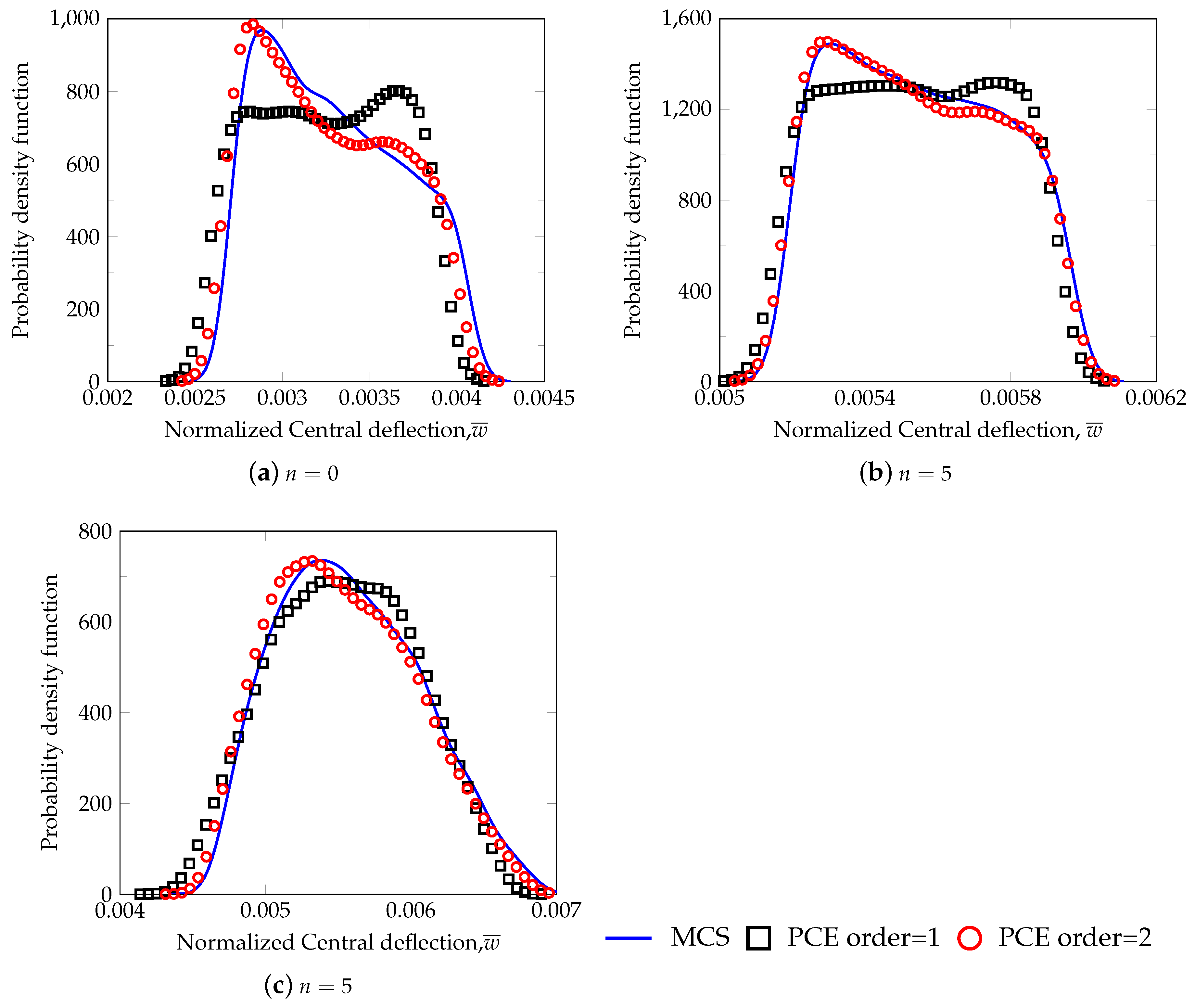
5.1. Validation
5.2. Static Bending
- Case A: is random,
- Case B: and is random.
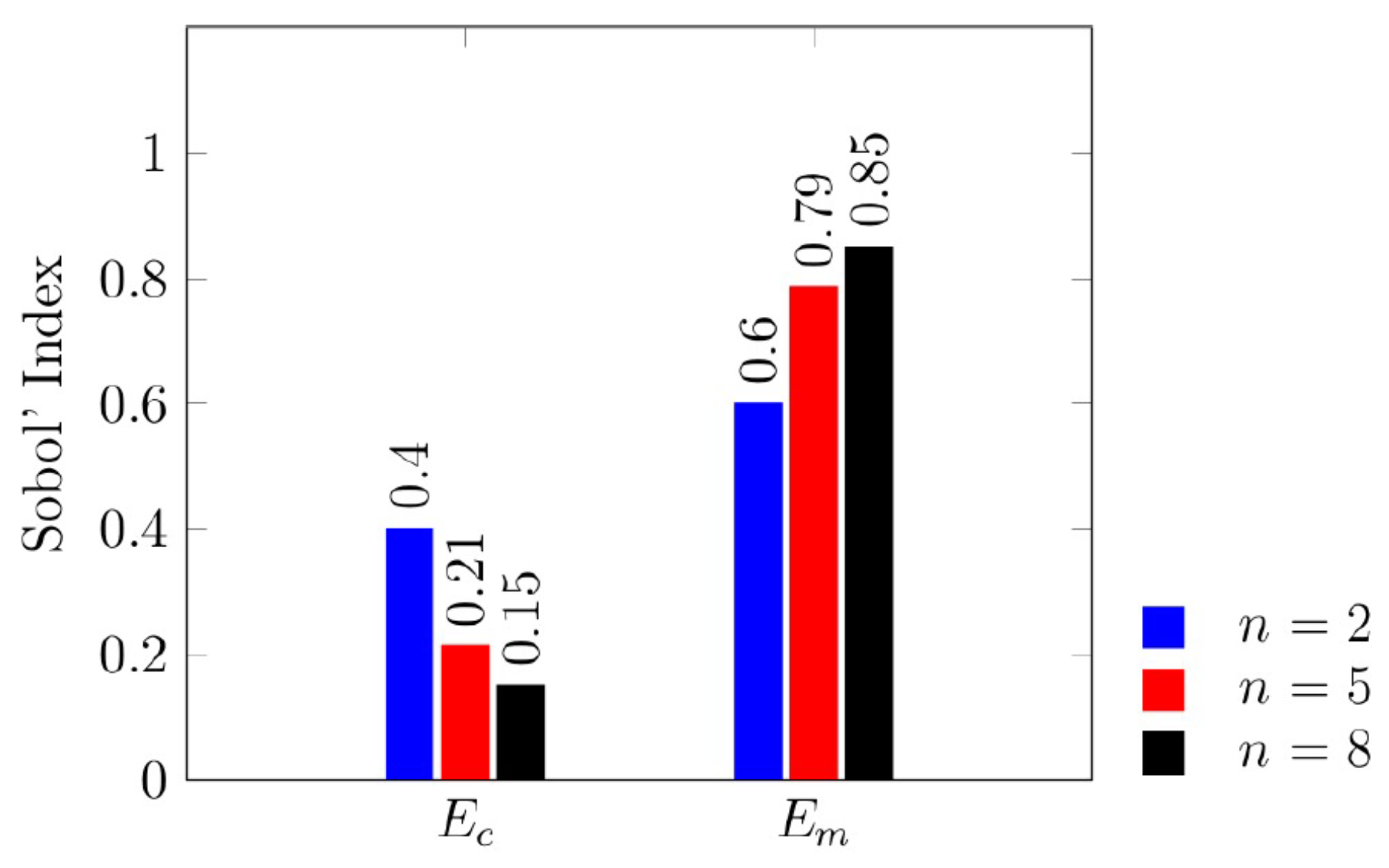
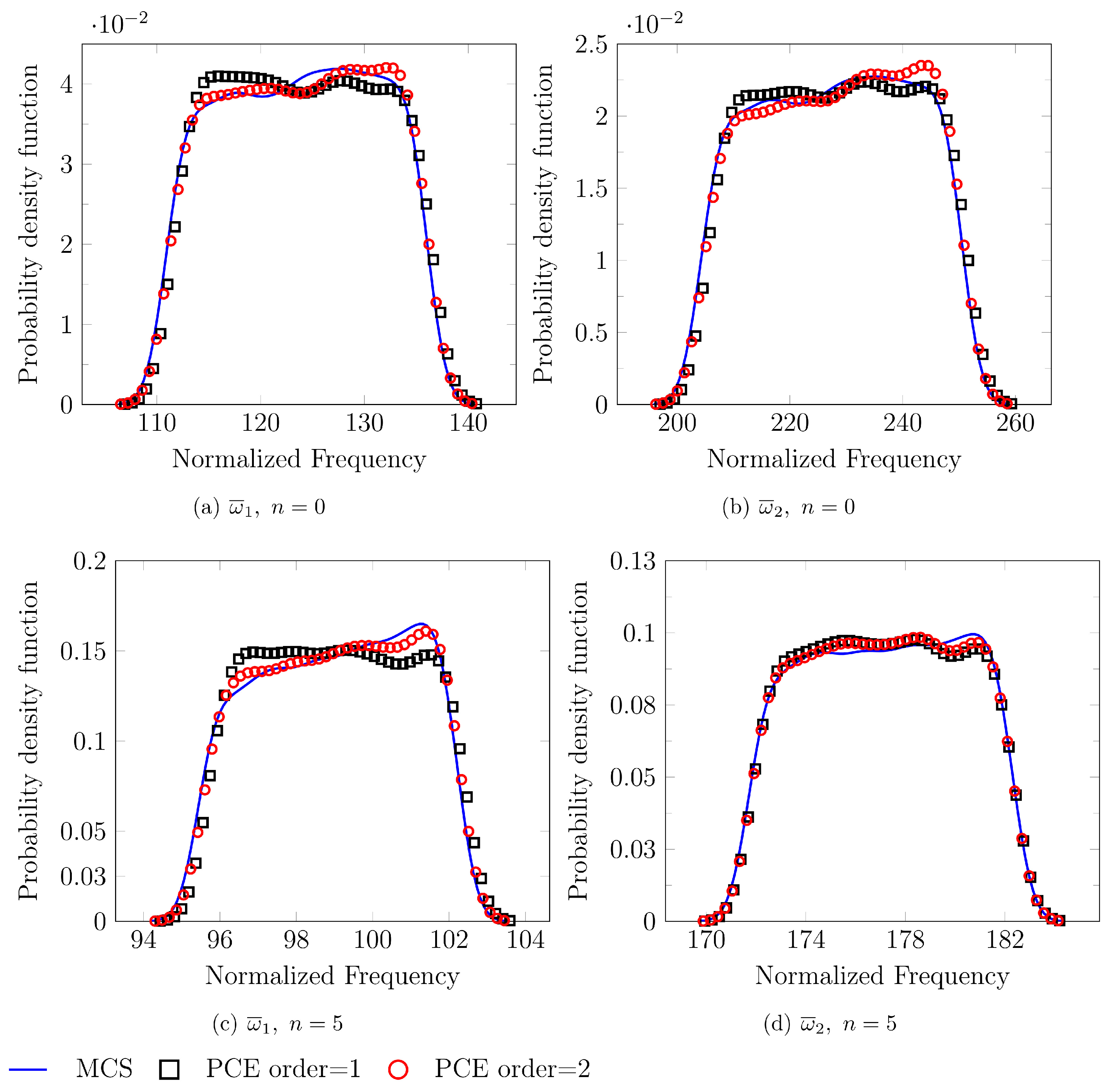
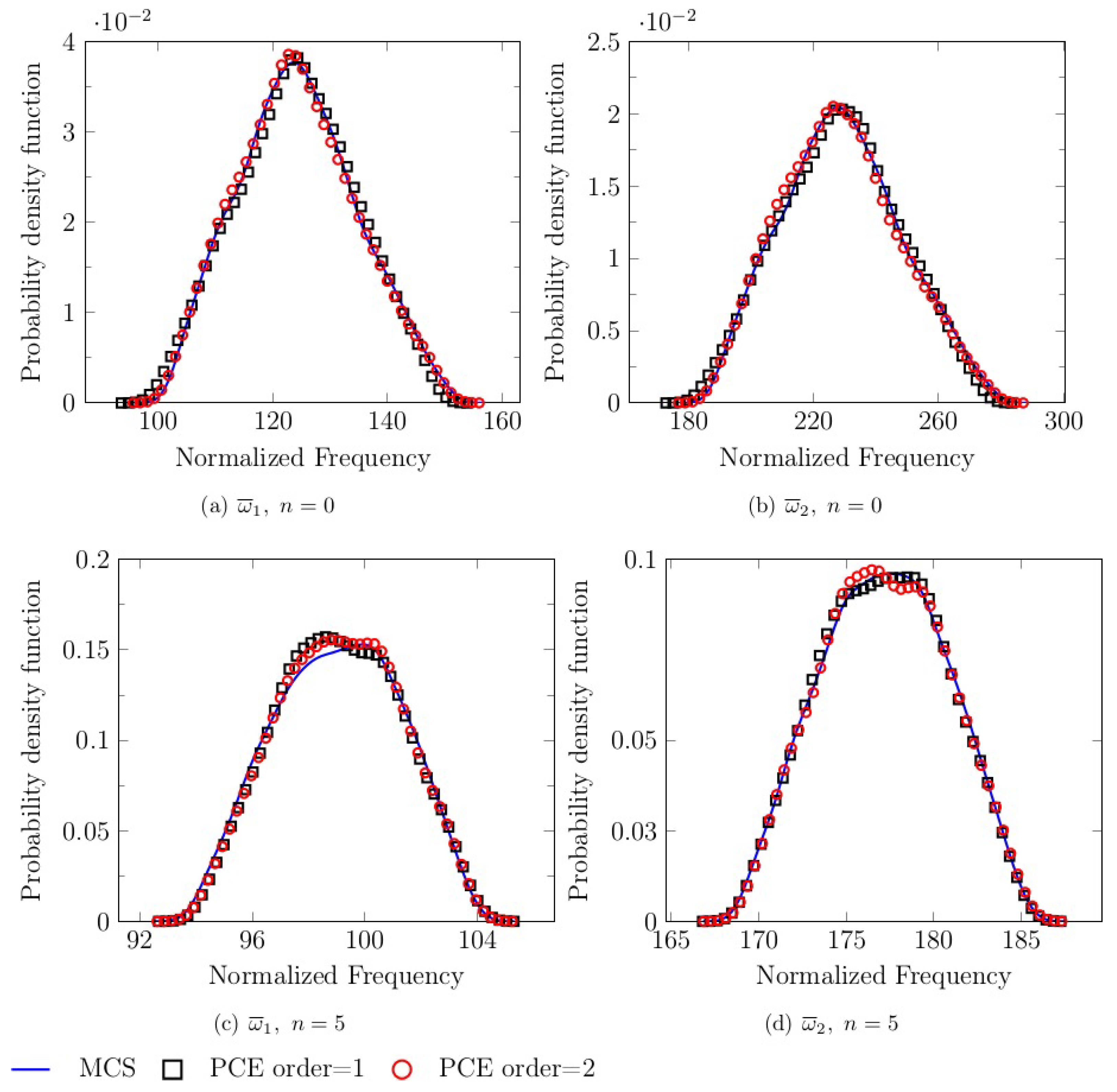
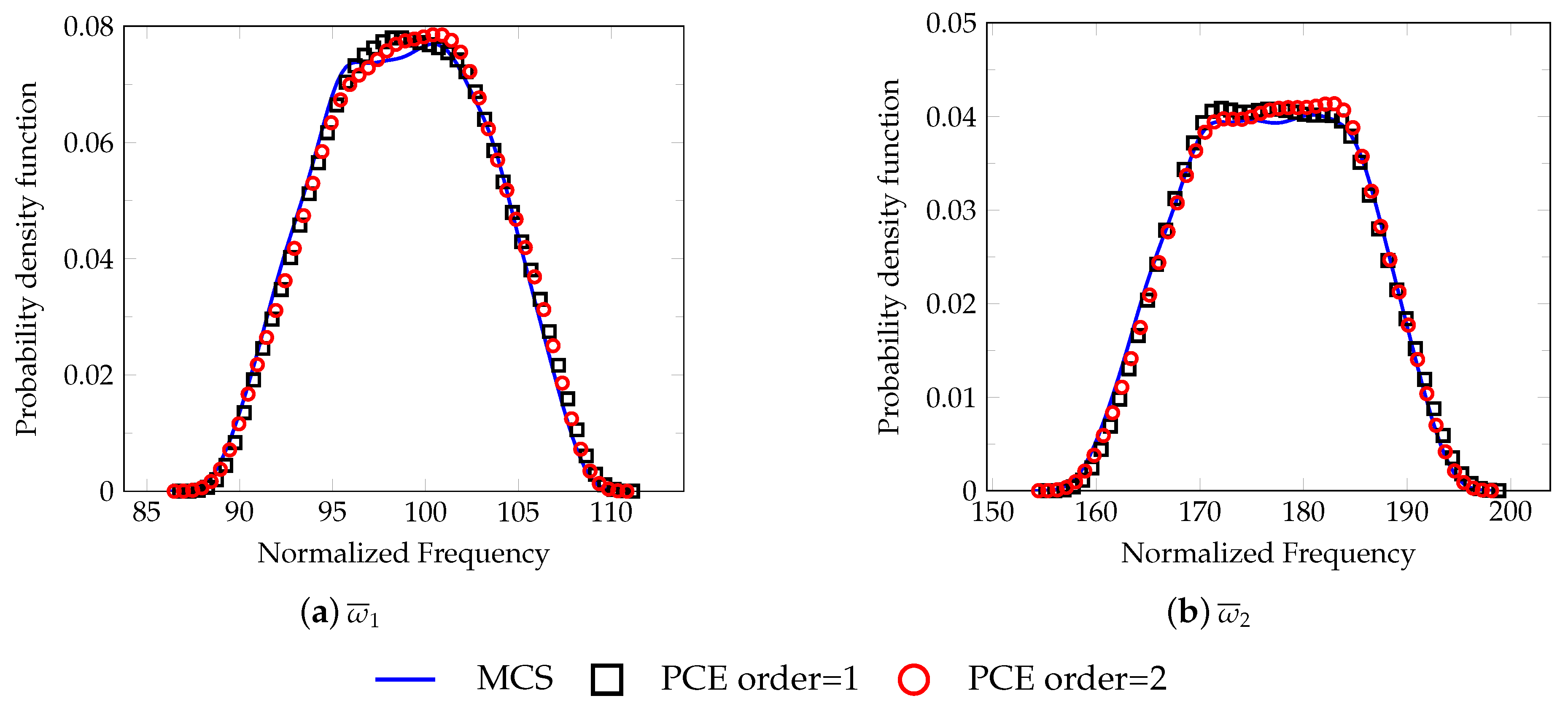
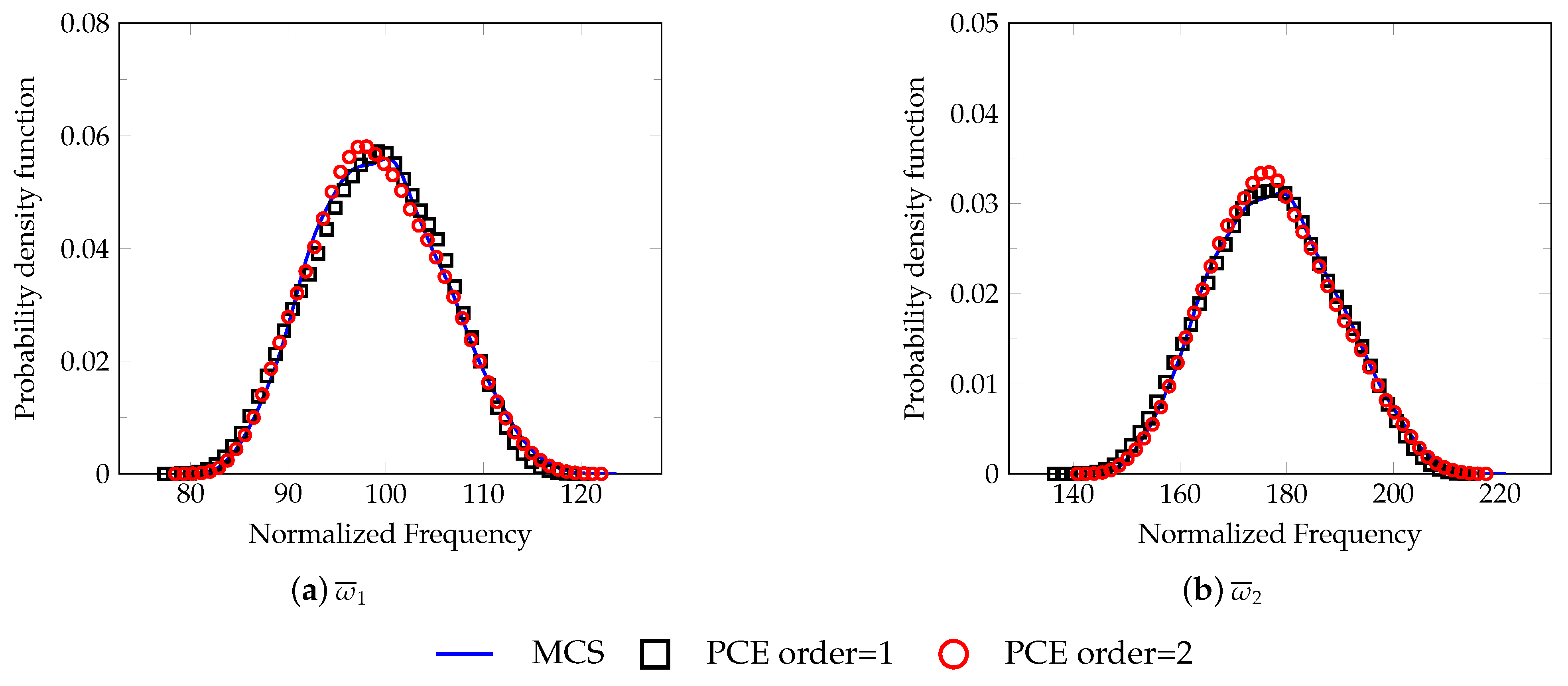
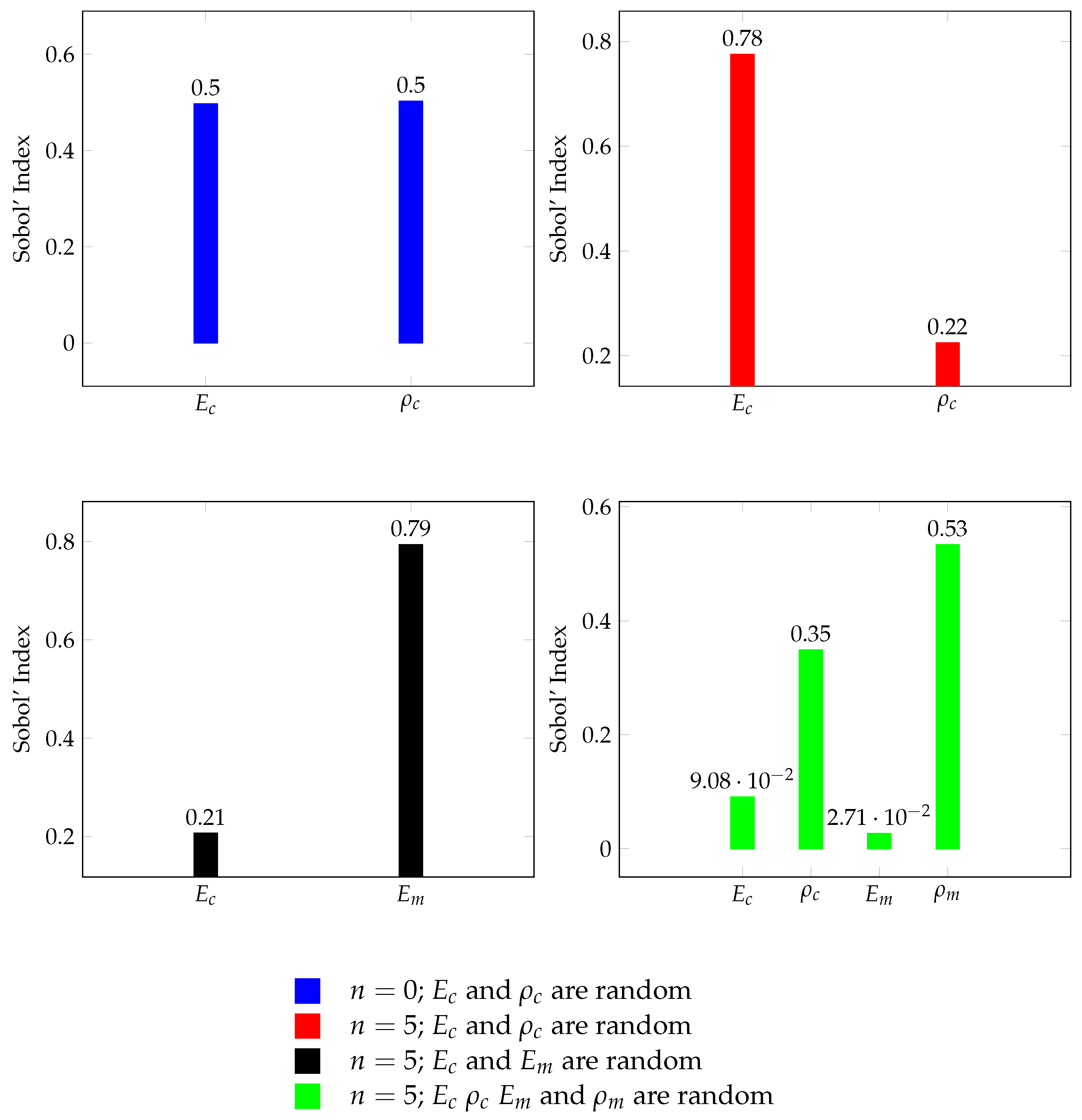
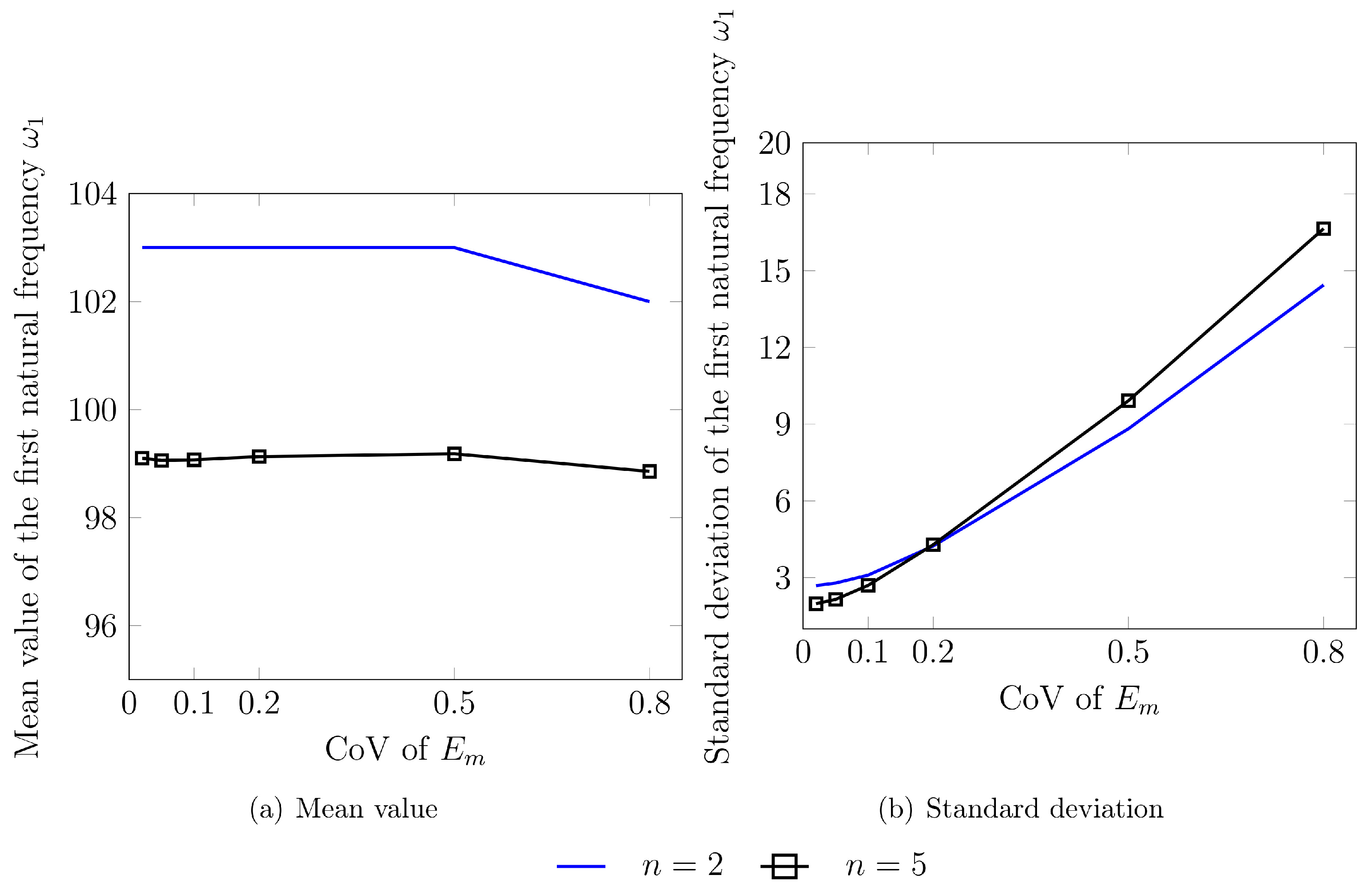
5.3. Free Vibration Analysis
- Case A: is random.
- Case B: and is random.
- Case C: and is random.
- Case D: and is random.
6. Conclusions
- It can handle a wider range of CoV, unlike the perturbation based methods.
- Does not require to modify the existing code like the intrusive based approaches.
Author Contributions
Funding
Conflicts of Interest
References
- Balaganesan, G.; Khan, V.C. Energy absorption of repaired composite laminates subjected to impact loading. Compos. Part B Eng. 2016, 98, 39–48. [Google Scholar] [CrossRef]
- Budarapu, P.; Kumar, S.; Prusty, B.G.; Paggi, M. Stress transfer through the interphase in curved-fiber pullout tests of nanocomposites. Compos. Part B Eng. 2019, 165, 417–434. [Google Scholar] [CrossRef]
- Budarapu, P.; Thakur, S.; Kumar, S.; Paggi, M. Micromechanics of engineered interphases in nacre-like composite structures. Mech. Adv. Mater. Struct. 2020, 1–16. [Google Scholar] [CrossRef]
- Jagtap, K.; Lal, A.; Singh, B. Stochastic nonlinear free vibration analysis of elastically supported functionally graded materials plate with system randomness in thermal environment. Compos. Struct. 2011, 93, 3185–3199. [Google Scholar] [CrossRef]
- Kitipornchai, S.; Yang, J.; Liew, K. Random vibration of the functionally graded laminates in thermal environments. Comput. Methods Appl. Mech. Eng. 2006, 195, 1075–1095. [Google Scholar] [CrossRef]
- Liu, W.K.; Belytschko, T.; Mani, A. Random field finite elements. Int. J. Num. Methods Eng. 1986, 23, 1831–1845. [Google Scholar] [CrossRef]
- Takada, T. Weighted integral method in stochastic finite element analysis. Probab. Eng. Mech. 1990, 5, 146–156. [Google Scholar] [CrossRef]
- Ghanem, R.G.; Spanos, P.D. Spectral Stochastic Finite Element Formulation for Reliability Analysis. J. Eng. Mech. 1991, 117, 2351–2372. [Google Scholar] [CrossRef]
- Kleiber, M.; Hien, T.D. The Stochastic Finite Element Method: Basic Perturbation Technique and Computer Implementation; Applied Stochastic Models and Data Analysis; Wiley: Chichester, UK, 1992; p. 297. [Google Scholar]
- Sudret, B.; Kiureghian, A.D. Stochastic Finite Element Methods and Reliability: A State-of-the-art Report; Report No. UCB/SEMM-2000/08; Department of Civil and Environmental Engineering, University of California: Berkeley, CA, USA, 2000. [Google Scholar]
- Chiba, R.; Sugano, Y. Stochastic analysis of a thermoelastic problem in functionally graded plates with uncertain material properties. Arch. Appl. Mech. 2007, 78, 749. [Google Scholar] [CrossRef]
- Shaker, A.; Abdelrahman, W.; Tawfik, M.; Sadek, E. Stochastic Finite element analysis of the free vibration of functionally graded material plates. Comput. Mech. 2008, 41, 707–714. [Google Scholar] [CrossRef]
- Li, K.; Wu, D.; Gao, W. Spectral stochastic isogeometric analysis for static response of FGM plate with material uncertainty. Thin-Walled Struct. 2018, 132, 504–521. [Google Scholar] [CrossRef]
- Kumar, R.; Mukhopadhyay, T.; Pandey, K.; Dey, S. Stochastic buckling analysis of sandwich plates: The importance of higher order modes. Int. J. Mech. Sci. 2019, 152, 630–643. [Google Scholar] [CrossRef]
- Thanh, C.L.; Tran, L.V.; Bui, T.Q.; Nguyen, H.X.; Abdel-Wahab, M. Isogeometric analysis for size-dependent nonlinear thermal stability of porous FG microplates. Compos. Struct. 2019, 221, 110838. [Google Scholar] [CrossRef]
- Wu, F.; Gao, Q.; Xu, X.M.; Zhong, W.X. A Modified Computational Scheme for the Stochastic Perturbation Finite Element Method. Latin Am. J. Solids Struct. 2015, 12, 2480–2505. [Google Scholar] [CrossRef]
- Kumaraian, M.L.; Rebbagondla, J.; Mathew, T.V.; Natarajan, S. Stochastic vibration analysis of functionally graded material paltes with material randomness using cell based smoothed discrete shear gap method. Int. J. Struct. Stabil. Dyn. 2019, 19, 1950037-1–1950037-20. [Google Scholar] [CrossRef]
- Minh, P.P.; Duc, N.D. The effect of cracks on the stability of the functionally graded plates with variable-thickness using HSDT and phase-field theory. Compos. Part B Eng. 2019, 175, 107086. [Google Scholar] [CrossRef]
- Sepahvand, K.; Marburg, S.; Hardtke, H.J. Stochastic free vibration of orthotropic plates using generalized polynomial chaos expansion. J. Sound Vibr. 2012, 331, 167–179. [Google Scholar] [CrossRef]
- Karsh, P.; Mukhopadhyay, T.; Chakraborty, S.; Naskar, S.; Dey, S. A hybrid stochastic sensitivity analysis for low-frequency vibration and low-velocity impact of functionally graded plates. Compos. Part B Eng. 2019, 176, 107221. [Google Scholar] [CrossRef]
- Tran, L.V.; Phung-Van, P.; Lee, J.; Wahab, M.A.; Nguyen-Xuan, H. Isogeometric analysis for nonlinear thermomechanical stability of functionally graded plates. Compos. Struct. 2016, 140, 655–667. [Google Scholar] [CrossRef]
- Lieu, Q.X.; Lee, J. Modeling and optimization of functionally graded plates under thermo-mechanical load using isogeometric analysis and adaptive hybrid evolutionary firefly algorithm. Compos. Struct. 2017, 179, 89–106. [Google Scholar] [CrossRef]
- Sundararajan, N.; Prakash, T.; Ganapathi, M. Nonlinear free flexural vibrations of functionally graded rectangular and skew plates under thermal environments. Finite Elem. Anal. Des. 2005, 42, 152–168. [Google Scholar] [CrossRef]
- Rajasekaran, S.; Murray, D. Incremental finite element matrices. ASCE J. Struct. Div. 1973, 99, 2423–2438. [Google Scholar]
- Cottrell, J.A.; Hughes, T.J.; Bazilevs, Y. Isogeometric Analysis: Toward Integration of CAD and FEA; John Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Nguyen, V.P.; Simpson, R.N.; Bordas, S.; Rabczuk, T. An introduction to Isogeometric Analysis with Matlab implementation: FEM and XFEM formulations. arXiv 2012, arXiv:1205.2129. [Google Scholar]
- Kikuchi, F.; Ishii, K. An improved 4-node quadrilateral plate bending element of the Reissne-Mindlin type. Comput. Mech. 1999, 23, 240–249. [Google Scholar] [CrossRef]
- Valizadeh, N.; Natarajan, S.; Gonzalez-Estrada, O.A.; Rabczuk, T.; Bui, T.Q.; Bordas, S.P. NURBS-based finite element analysis of functionally graded plates: Static bending, vibration, buckling and flutter. Compos. Struct. 2013, 99, 309–326. [Google Scholar] [CrossRef]
- Wiener, N. The homogeneous chaos. Am. J. Math. 1938, 60, 897–936. [Google Scholar] [CrossRef]
- Nguyen-Xuan, H.; Tran, L.V.; Thai, H.; Nguyen-Thoi, T. Analysis of functionally graded plates by an efficient finite element method with node-based strain smoothing. Thin Walled Struct. 2012, 54, 1–18. [Google Scholar] [CrossRef]
- Matsunaga, H. Free vibration and stability of functionally graded plates according to a 2D higher-order deformation theory. Compos. Struct. 2008, 82, 499–512. [Google Scholar] [CrossRef]
- Lee, Y.; Zhao, X.; Liew, K. Thermo-elastic analysis of functionally graded plates using the element free kp−Ritz method. Smart Mater. Struct. 2009, 18, 035007. [Google Scholar] [CrossRef]
- Zhao, X.; Lee, Y.; Liew, K. Free vibration analysis of functionally graded plates using the element free kp−Ritz method. J. Sound Vibr. 2009, 319, 918–939. [Google Scholar] [CrossRef]
- Nguyen-Xuan, H.; Tran, L.V.; Nguyen-Thoi, T.; Vu-Do, H. Analysis of functionally graded plates using an edge-based smoothed finite element method. Compos. Struct. 2011, 93, 3019–3039. [Google Scholar] [CrossRef]
| Distribution Types | Polynomials | Support | |
|---|---|---|---|
| Continuous | Beta | Jacobi | |
| Exponential | Laguerre | ||
| Gamma | General Laguerre | ||
| Normal | Hermite | ||
| Uniform | Legendre | ||
| Discrete | Poisson | Charlier | |
| Binomial | Krawtchouk | ||
| Negative Binomial | Meixner | ||
| Hypergeometric | Hahn |
| Random Input Variable | Symbol | Mean Value | CoV | |
|---|---|---|---|---|
| ZrO | Young’s modulus | 151 GPa | 0.2 | |
| Density | 3000 kg/m | 0.2 | ||
| Al | Young’s modulus | 70 GPa | 0.2 | |
| Density | 2770 kg/m | 0.2 |
| Method | Number of | Gradient Index, n | |||
|---|---|---|---|---|---|
| Control Points | 0 | 0.5 | 1 | 2 | |
| Quadratic | 4 | 0.162098 | 0.218914 | 0.256018 | 0.293806 |
| 8 | 0.171617 | 0.232392 | 0.271879 | 0.311459 | |
| 16 | 0.171649 | 0.232439 | 0.271935 | 0.311520 | |
| 24 | 0.171651 | 0.232441 | 0.271938 | 0.311523 | |
| ES-DSG3 [30] | 0.1700 | 0.2296 | 0.2680 | 0.3066 | |
| MITC4 [30] | 0.1715 | 0.2317 | 0.2704 | 0.3093 | |
| Ritz [32] | 0.1722 | 0.2403 | 0.2811 | 0.3221 | |
| Method | Control Points | Gradient Index, n | ||||
|---|---|---|---|---|---|---|
| 0 | 0.5 | 1 | 4 | 10 | ||
| IGA-Quadratic | 8 | 0.21128 | 0.18051 | 0.16309 | 0.13962 | 0.13231 |
| 16 | 0.21121 | 0.18045 | 0.16303 | 0.13957 | 0.13227 | |
| 24 | 0.21121 | 0.18044 | 0.16303 | 0.13957 | 0.13227 | |
| MITC4 (16×16) [34] | 0.21182 | 0.18082 | 0.16323 | 0.13968 | 0.13251 | |
| HSDT [31] | 0.21210 | 0.18190 | 0.16400 | 0.13830 | 0.13060 | |
| Ritz [33] | 0.20550 | 0.17570 | 0.15870 | 0.13560 | 0.12840 | |
| Central | Gradient | Random | Mean | Standard Deviation | ||
|---|---|---|---|---|---|---|
| Deflection | Index, n | Variables | MCS | PCE | MCS | PCE |
| 0 | ||||||
| 5 | ||||||
| Frequency | Gradient | Random | Mean | Standard Deviation | ||
|---|---|---|---|---|---|---|
| Index, n | Variables | MCS | PCE | MCS | PCE | |
| 0 | 123.72 | 123.97 | 7.20 | 7.19 | ||
| 124.42 | 124.02 | 1.95 | 1.95 | |||
| 5 | 99.03 | 99.02 | 2.22 | 2.20 | ||
| 99.03 | 99.02 | 2.22 | 2.20 | |||
| 98.80 | 99.03 | 4.28 | 4.24 | |||
| 99.27 | 99.05 | 6.53 | 6.44 | |||
| 0 | 227.89 | 228.59 | 13.27 | 13.34 | ||
| 229.17 | 228.39 | 18.93 | 18.80 | |||
| 5 | 177.15 | 177.14 | 3.05 | 3.02 | ||
| 177.16 | 177.14 | 3.56 | 3.53 | |||
| 176.85 | 177.25 | 7.85 | 7.86 | |||
| 177.69 | 177.04 | 11.84 | 11.80 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dsouza, S.M.; Varghese, T.M.; Budarapu, P.R.; Natarajan, S. A Non-Intrusive Stochastic Isogeometric Analysis of Functionally Graded Plates with Material Uncertainty. Axioms 2020, 9, 92. https://doi.org/10.3390/axioms9030092
Dsouza SM, Varghese TM, Budarapu PR, Natarajan S. A Non-Intrusive Stochastic Isogeometric Analysis of Functionally Graded Plates with Material Uncertainty. Axioms. 2020; 9(3):92. https://doi.org/10.3390/axioms9030092
Chicago/Turabian StyleDsouza, Shaima M., Tittu Mathew Varghese, P. R. Budarapu, and S. Natarajan. 2020. "A Non-Intrusive Stochastic Isogeometric Analysis of Functionally Graded Plates with Material Uncertainty" Axioms 9, no. 3: 92. https://doi.org/10.3390/axioms9030092
APA StyleDsouza, S. M., Varghese, T. M., Budarapu, P. R., & Natarajan, S. (2020). A Non-Intrusive Stochastic Isogeometric Analysis of Functionally Graded Plates with Material Uncertainty. Axioms, 9(3), 92. https://doi.org/10.3390/axioms9030092






