The Modified Helmholtz Equation on a Regular Hexagon—The Symmetric Dirichlet Problem
Abstract
1. Introduction
- (1)
- a global relation, which is an algebraic equation that involves certain transforms of all (known and unknown) boundary values.
- (2)
- an integral representation of the solution, which involves transforms of all boundary values.
- Given a PDE, define its formal adjoint and construct a one parameter family of solutions of this equation.
- By employing the given PDE and its adjoint, obtain a one parameter family of equations in conservation form. This family, together with Green’s theorem, yield the global relation.
- The above family also gives rise to a certain closed differential form. The spectral analysis of this form gives rise to a scalar Riemann–Hilbert problem, which consequently yields an integral representation of the solution. This representation involves integral transforms of all the boundary values, and since some of them are not prescribed as boundary conditions, this form of solution is not yet effective.
- The explicit solution of the problem is derived by determining the contribution of the unknown boundary values to the integral representation. This can be achieved by using the global relation, as well as equations obtained from the global relation through certain invariant transformations.
Organisation of the Paper
2. The Basic Elements
2.1. The Global Relation and the Integral Representation of the Solution in the Interior of a Convex Polygon
2.2. The Dirichlet Problem on a Regular Hexagon
2.3. The Symmetric Dirichlet Problem
- The modified Helmholtz operator is invariant under the transformation , namely under rotation of . Since the Dirichlet data are invariant under this rotation, then the (unique) solution of the Helmholtz equation is also invariant under this rotation.
- If q is invariant under this transformation, then the differential form is also invariant under the transformation :
- Evaluating the above differential form on each side we obtainwhere the second equality is a direct consequence of the fact that the Dirichlet data are invariant under this rotation.
- (i)
- the odd case, ;
- (ii)
- the even case .
- (i)
- in the odd case, , which yields ;
- (ii)
- in the even case, , which yields for all .
3. Derivation of the Solution for the Symmetric Odd Case
- The zeros of occur when , thus .
- The function is bounded and analytic for .Indeed, if , then . Thus, if , it follows that . Hence, .Therefore, the exponentials and are bounded.
- The function is bounded and analytic for , namely in the region where .Indeed, this expression involves the exponentials and , which are bounded in this region, since .
- The functionis bounded and analytic for .Indeed, since k is at the lower half plane, thenwhich is bounded if .If , then , which yields .
- The function is bounded and analytic for .
- The function is bounded and analytic for , namely in the region where .
- In the lower half planeThus, it is bounded and analytic for .
- 1.
- the fraction remains invariant;
- 2.
- the rays become ;
- 3.
- the exponent becomes ;
- 4.
- the remaining integrands are equal to the corresponding integrands in and .
4. The Symmetric Even Case
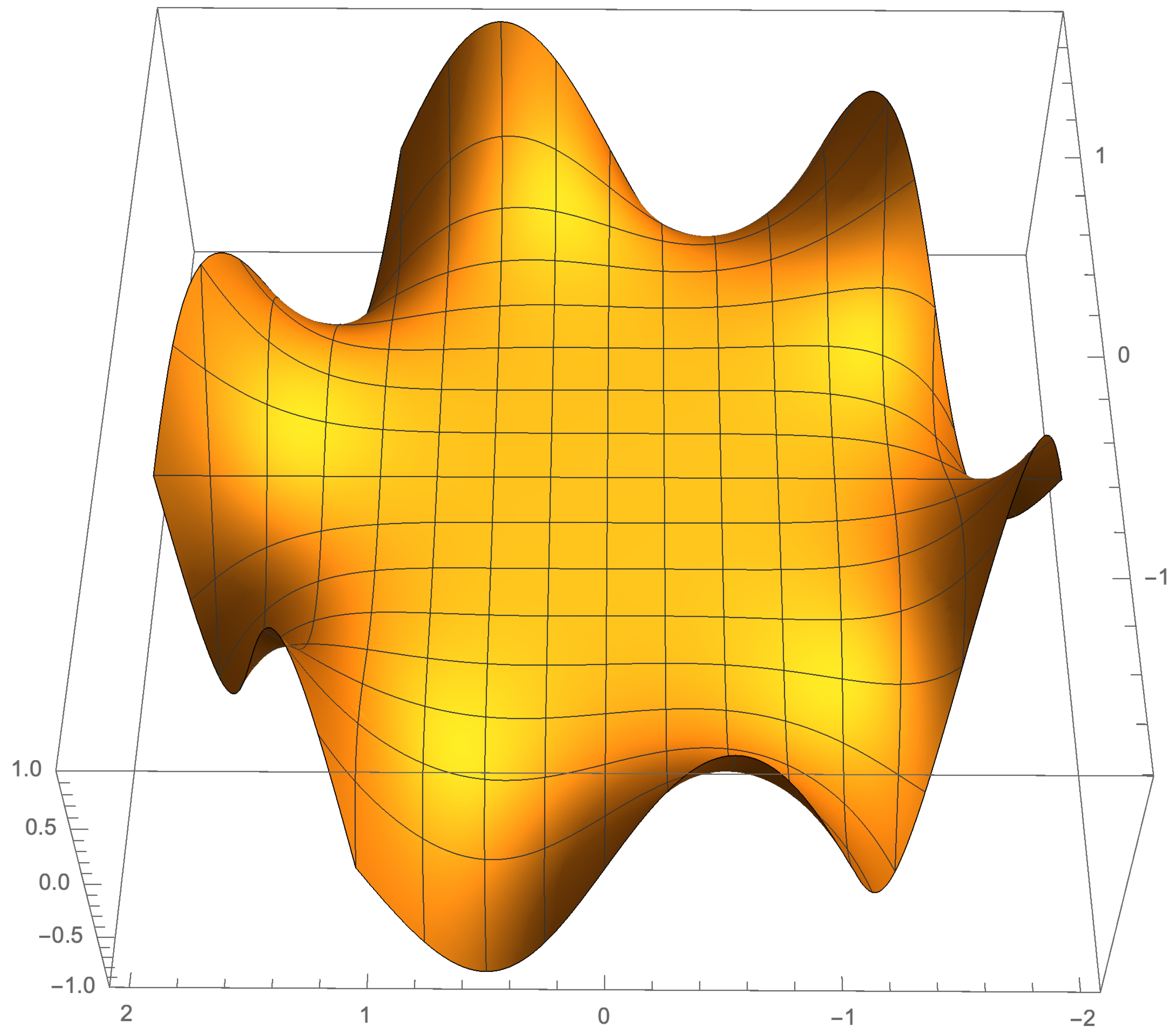
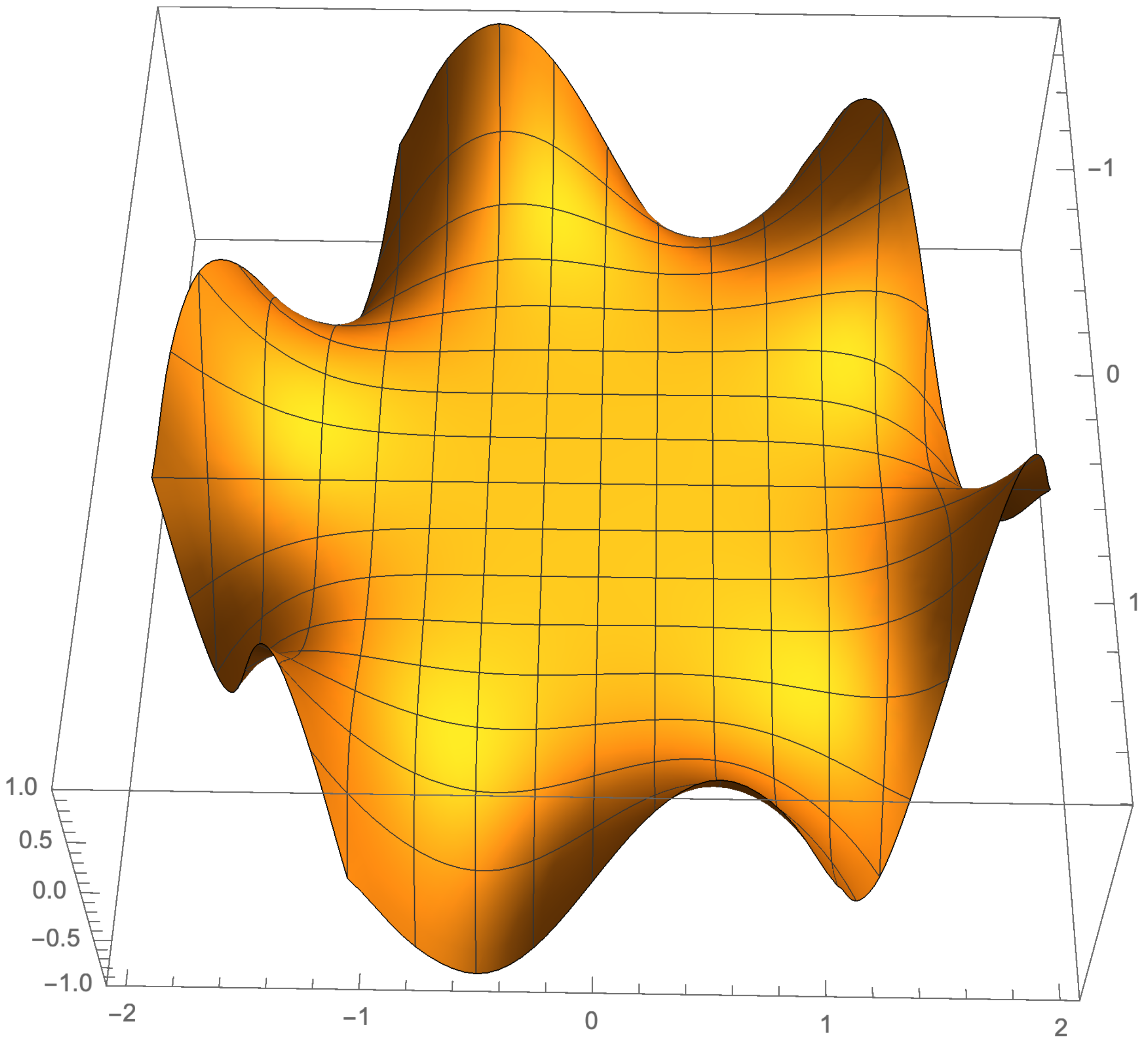
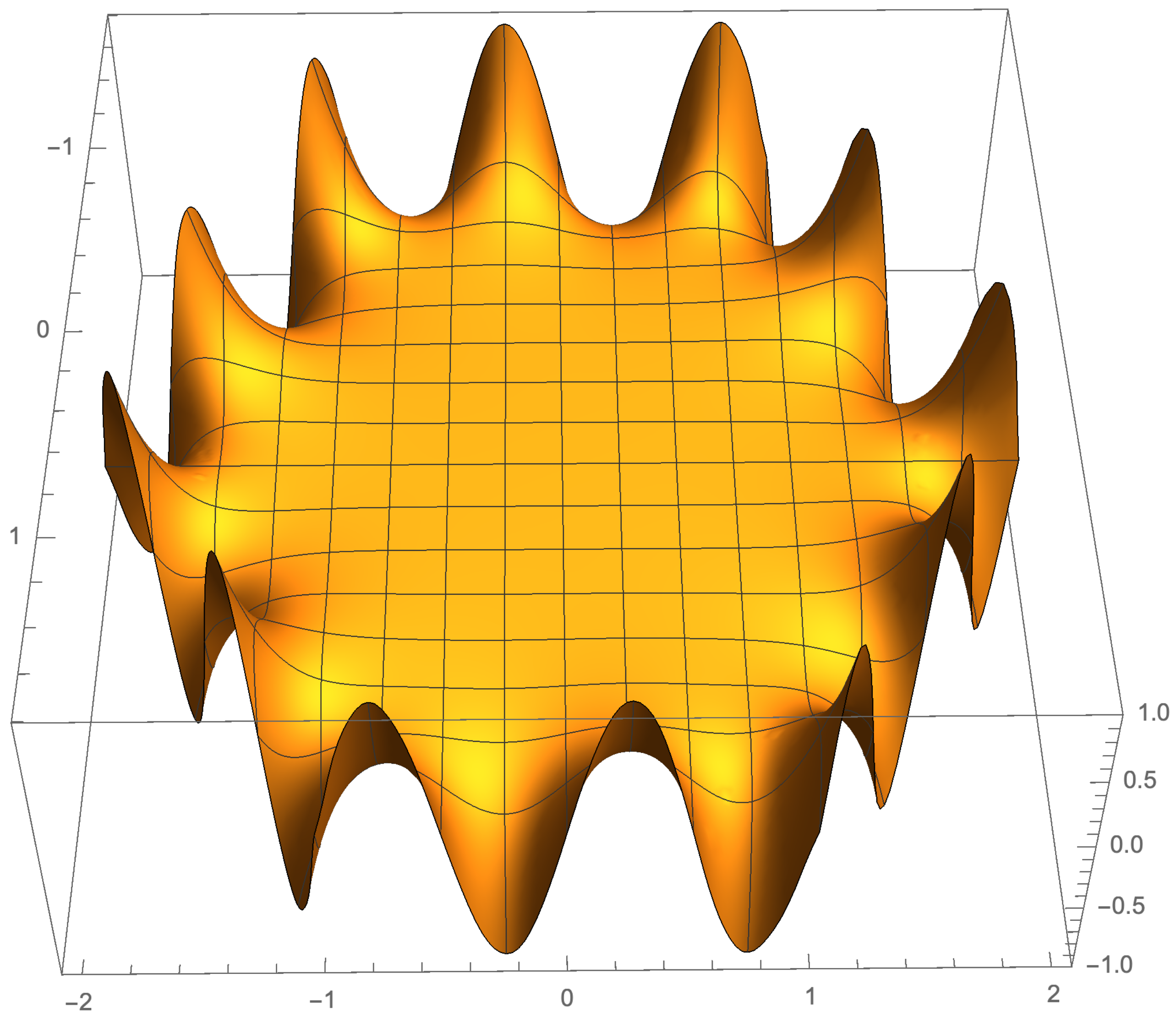
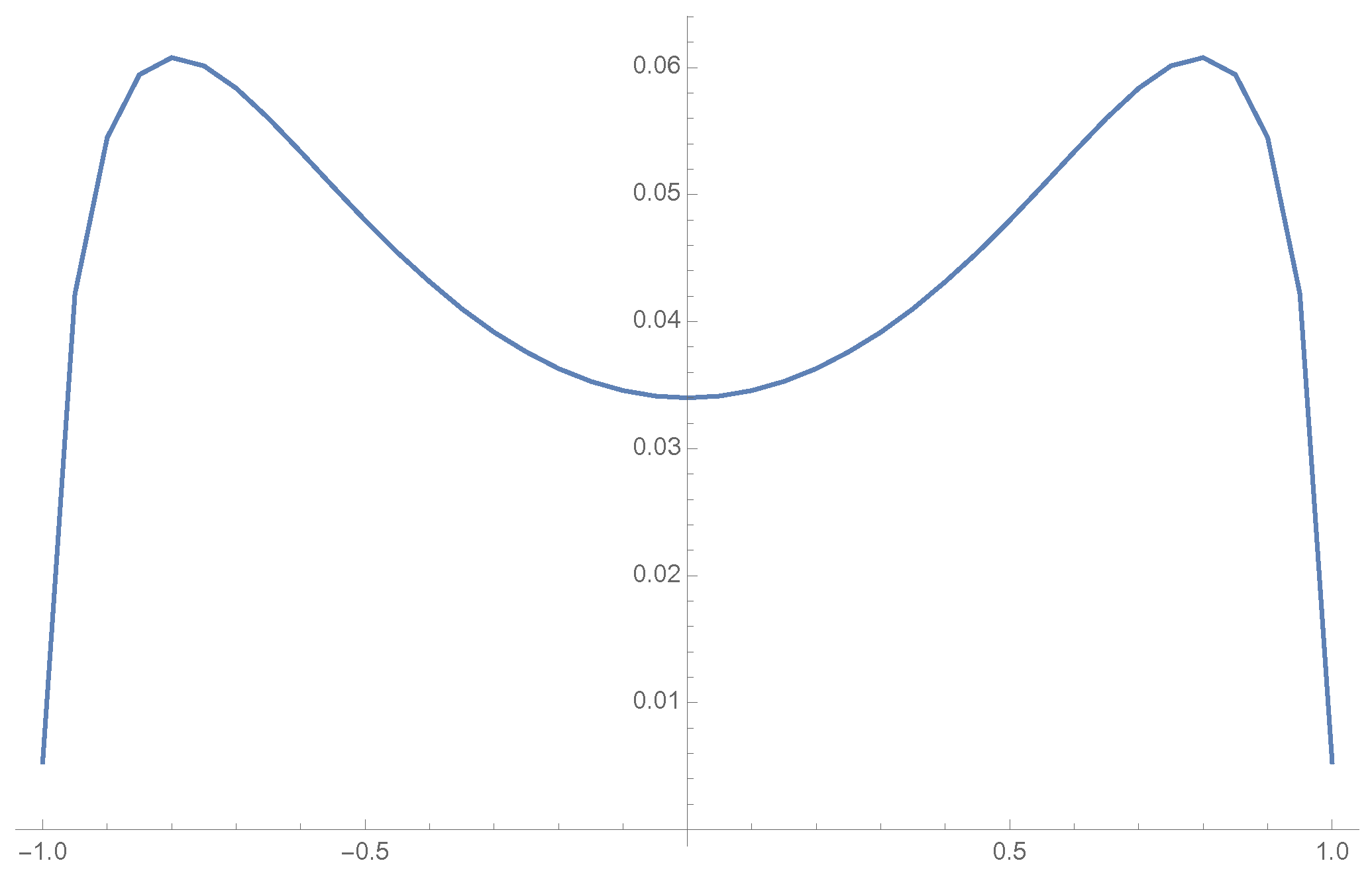
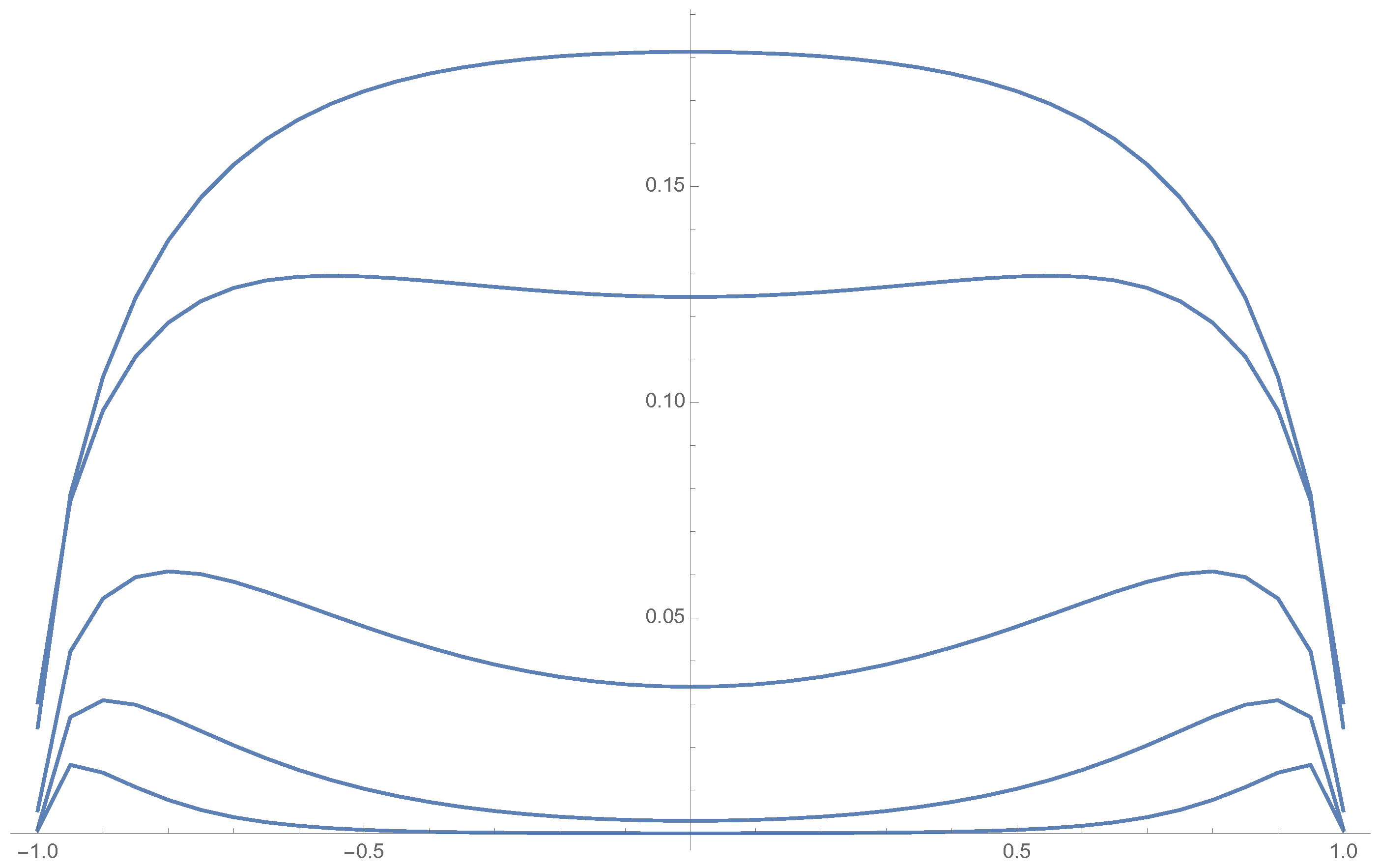
5. Illustration of the Results
5.1. Odd Case
5.2. Even Case
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fokas, A.S. A unified transform method for solving linear and certain nonlinear PDEs. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1997, 453, 1411–1443. [Google Scholar] [CrossRef]
- Fokas, A.S. On the integrability of linear and nonlinear partial differential equations. J. Math. Phys. 2000, 41, 4188–4237. [Google Scholar] [CrossRef]
- Fokas, A.S. A new transform method for evolution partial differential equations. IMA J. Appl. Math. 2002, 67, 559–590. [Google Scholar] [CrossRef]
- Biondini, G.; Wang, D. Initial-boundary-value problems for discrete linear evolution equations. IMA J. Appl. Math. 2010, 75, 968–997. [Google Scholar] [CrossRef]
- Deconinck, B.; Trogdon, T.; Vasan, V. The method of Fokas for solving linear partial differential equations. SIAM Rev. 2014, 56, 159–186. [Google Scholar] [CrossRef]
- Fokas, A.S. A Unified Approach to Boundary Value Problems; SIAM: Garden Grove, CA, USA, 2008. [Google Scholar]
- Pelloni, B. The spectral representation of two-point boundary-value problems for third-order linear evolution partial differential equations. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2005, 461, 2965–2984. [Google Scholar] [CrossRef]
- Pelloni, B.; Smith, D.A. Spectral theory of some non-selfadjoint linear differential operators. Proc. R. Soc. A Math. Phys. Eng. Sci. 2013, 469, 20130019. [Google Scholar] [CrossRef]
- Pelloni, B.; Smith, D.A. Evolution PDEs and augmented eigenfunctions. Half-line. J. Spectr. Theory 2016, 6, 185–213. [Google Scholar] [CrossRef]
- Smith, D.A. Well-posed two-point initial-boundary value problems with arbitrary boundary conditions. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 2012; Volume 152, pp. 473–496. [Google Scholar]
- Fokas, A.S. Two-dimensional linear partial differential equations in a convex polygon. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2001, 457, 371–393. [Google Scholar] [CrossRef]
- Kalimeris, K. INITIAL and Boundary Value Problems in Two and Three Dimensions. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2010. [Google Scholar]
- Spence, E.A. Boundary Value Problems for Linear Elliptic PDEs. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2011. [Google Scholar]
- Batal, A.; Fokas, A.S.; Özsari, T. Uniform transform method for boundary value problems involving mixed derivatives. arXiv 2020, arXiv:2002.01057. [Google Scholar]
- Fokas, A.S.; Himonas, A.A.; Mantzavinos, D. The nonlinear Schrödinger equation on the half-line. Trans. Am. Math. Soc. 2017, 369, 681–709. [Google Scholar] [CrossRef]
- Himonas, A.A.; Mantzavinos, D. On the Initial-Boundary Value Problem for the Linearized Boussinesq Equation. Stud. Appl. Math. 2015, 134, 62–100. [Google Scholar] [CrossRef]
- Himonas, A.A.; Mantzavinos, D.; Yan, F. Initial-boundary value problems for a reaction-diffusion equation. J. Math. Phys. 2019, 60, 081509. [Google Scholar] [CrossRef]
- Özsari, T.; Yolcu, N. The initial-boundary value problem for the biharmonic Schrödinger equation on the half-line. Commun. Pure Appl. Anal. 2019, 18, 3285–3316. [Google Scholar] [CrossRef]
- Kalimeris, K.; Özsarı, T. An elementary proof of the lack of null controllability for the heat equation on the half line. Appl. Math. Lett. 2020, 104, 106241. [Google Scholar] [CrossRef]
- Crowdy, D.G.; Davis, A.M. Stokes flow singularities in a two-dimensional channel: A novel transform approach with application to microswimming. Proc. R. Soc. A 2013, 469, 20130198. [Google Scholar]
- Deconinck, B.; Oliveras, K. The instability of periodic surface gravity waves. J. Fluid Mech. 2011, 675, 141–167. [Google Scholar] [CrossRef]
- Fokas, A.S.; Kalimeris, K. Water waves with moving boundaries. J. Fluid Mech. 2017, 832, 641–665. [Google Scholar] [CrossRef]
- Oliveras, K. Stability of Periodic Surface Gravity Water Waves. Ph.D. Thesis, University of Washington, Seattle, WA, USA, 2009. [Google Scholar]
- Plümacher, D.; Oberlack, M.; Wang, Y.; Smuda, M. On a non-linear droplet oscillation theory via the unified method. Phys. Fluids 2020, 32, 067104. [Google Scholar] [CrossRef]
- Vasan, V.; Deconinck, B. The inverse water wave problem of bathymetry detection. J. Fluid Mech. 2013, 714, 562–590. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Fokas, A.S.; Musslimani, Z.H. On a new non-local formulation of water waves. J. Fluid Mech. 2006, 562, 313–343. [Google Scholar] [CrossRef]
- Nicholls, D. A high-order perturbation of surfaces (HOPS) approach to Fokas integral equations: Three-dimensional layered-media scattering. Q. Appl. Math. 2016, 74, 61–87. [Google Scholar] [CrossRef]
- Ashton, A.C.L. Laplace’s equation on convex polyhedra via the unified method. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20140884. [Google Scholar] [CrossRef]
- Crowdy, D. A transform method for Laplace’s equation in multiply connected circular domains. IMA J. Appl. Math. 2015, 80, 1902–1931. [Google Scholar] [CrossRef]
- Dassios, G.; Fokas, A.S. The basic elliptic equations in an equilateral triangle. Proc. R. Soc. A Math. Phys. Eng. Sci. 2005, 461, 2721–2748. [Google Scholar] [CrossRef]
- Fokas, A.S.; Kapaev, A.A. A Riemann-Hilbert approach to the Laplace equation. J. Math. Anal. Appl. 2000, 251, 770–804. [Google Scholar] [CrossRef]
- Fokas, A.S.; Kapaev, A.A. On a transform method for the Laplace equation in a polygon. IMA J. Appl. Math. 2003, 68, 355–408. [Google Scholar] [CrossRef]
- Luca, E.; Crowdy, D.G. A transform method for the biharmonic equation in multiply connected circular domains. IMA J. Appl. Math. 2018, 83, 942–976. [Google Scholar] [CrossRef]
- Antipov, Y.A.; Fokas, A.S. The modified Helmholtz equation in a semi-strip. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 2005; Volume 138, pp. 339–365. [Google Scholar]
- Ashton, A.C.L. On the rigorous foundations of the Fokas method for linear elliptic partial differential equations. Proc. R. Soc. A Math. Phys. Eng. Sci. 2012, 468, 1325–1331. [Google Scholar] [CrossRef]
- Ashton, A.C.L. The Spectral Dirichlet–Neumann Map for Laplace’s Equation in a Convex Polygon. SIAM J. Math. Anal. 2013, 45, 3575–3591. [Google Scholar] [CrossRef]
- Colbrook, M.J. Extending the unified transform: Curvilinear polygons and variable coefficient PDEs. IMA J. Numer. Anal. 2020, 40, 976–1004. [Google Scholar] [CrossRef]
- Colbrook, M.J.; Flyer, N.; Fornberg, B. On the Fokas method for the solution of elliptic problems in both convex and non-convex polygonal domains. J. Comput. Phys. 2018, 374, 996–1016. [Google Scholar] [CrossRef]
- Colbrook, M.J.; Fokas, A.S. Computing eigenvalues and eigenfunctions of the Laplacian for convex polygons. Appl. Numer. Math. 2018, 126, 1–17. [Google Scholar] [CrossRef]
- Colbrook, M.J.; Fokas, A.S.; Hashemzadeh, P. A Hybrid Analytical-Numerical Technique for Elliptic PDEs. SIAM J. Sci. Comput. 2019, 41, A1066–A1090. [Google Scholar] [CrossRef]
- de Barros, F.P.J.; Colbrook, M.J.; Fokas, A.S. A hybrid analytical-numerical method for solving advection-dispersion problems on a half-line. Int. J. Heat Mass Transf. 2019, 139, 482–491. [Google Scholar] [CrossRef]
- Davis, C.I.R.; Fornberg, B. A spectrally accurate numerical implementation of the Fokas transform method for Helmholtz-type PDEs. Complex Var. Elliptic Equ. 2014, 59, 564–577. [Google Scholar] [CrossRef]
- Fokas, A.S.; Nachbin, A. Water waves over a variable bottom: A non-local formulation and conformal mappings. J. Fluid Mech. 2012, 695, 288–309. [Google Scholar] [CrossRef]
- Fornberg, B.; Flyer, N. A numerical implementation of Fokas boundary integral approach: Laplace’s equation on a polygonal domain. Proc. R. Soc. A Math. Phys. Eng. Sci. 2011, 467, 2983–3003. [Google Scholar] [CrossRef]
- Grylonakis, E.N.G.; Filelis-Papadopoulos, C.K.; Gravvanis, G.A. A class of unified transform techniques for solving linear elliptic PDEs in convex polygons. Appl. Numer. Math. 2018, 129, 159–180. [Google Scholar] [CrossRef]
- Hashemzadeh, P.; Fokas, A.S.; Smitheman, S.A. A numerical technique for linear elliptic partial differential equations in polygonal domains. Proc. Math. Phys. Eng. Sci. 2015, 471, 20140747. [Google Scholar] [CrossRef]
- Trogdon, T.; Biondini, G. Evolution partial differential equations with discontinuous data. Q. Appl. Math. 2019, 77, 689–726. [Google Scholar] [CrossRef]
- Lamé, G. Mémoire sur la propagation de la chaleur dans les polyèdres, et principalement dans le prisme triangulaire régulier. J. I’Ecole Poly Tech. 1833, 22, 194–251. [Google Scholar]
- Fokas, A.S.; Kalimeris, K. Eigenvalues for the Laplace operator in the interior of an equilateral triangle. Comput. Methods Funct. Theory 2014, 14, 1–33. [Google Scholar] [CrossRef]
- Pinsky, M.A. The eigenvalues of an equilateral triangle. SIAM J. Math. Anal. 1980, 11, 819–827. [Google Scholar] [CrossRef]
- Pinsky, M.A. Completeness of the eigenfunctions of the equilateral triangle. SIAM J. Math. Anal. 1985, 16, 848–851. [Google Scholar] [CrossRef]
- Práger, M. Eigenvalues and eigenfunctions of the Laplace operator on an equilateral triangle. Appl. Math. 1998, 43, 311–320. [Google Scholar] [CrossRef]
- Terras, R.; Swanson, R. Image methods for constructing Green’s functions and eigenfunctions for domains with plane boundaries. J. Math. Phys. 1980, 21, 2140–2153. [Google Scholar] [CrossRef]
- McCartin, B.J. Eigenstructure of the equilateral triangle, Part I: The Dirichlet problem. Siam Rev. 2003, 45, 267–287. [Google Scholar] [CrossRef]
- McCartin, B.J. Eigenstructure of the equilateral triangle, Part II: The Neumann problem. Math. Probl. Eng. 2002, 8. [Google Scholar] [CrossRef]
- McCartin, B.J. Laplacian Eigenstructure of the Equilateral Triangle; Hikari Limited: Rousse, Bulgaria, 2011. [Google Scholar]
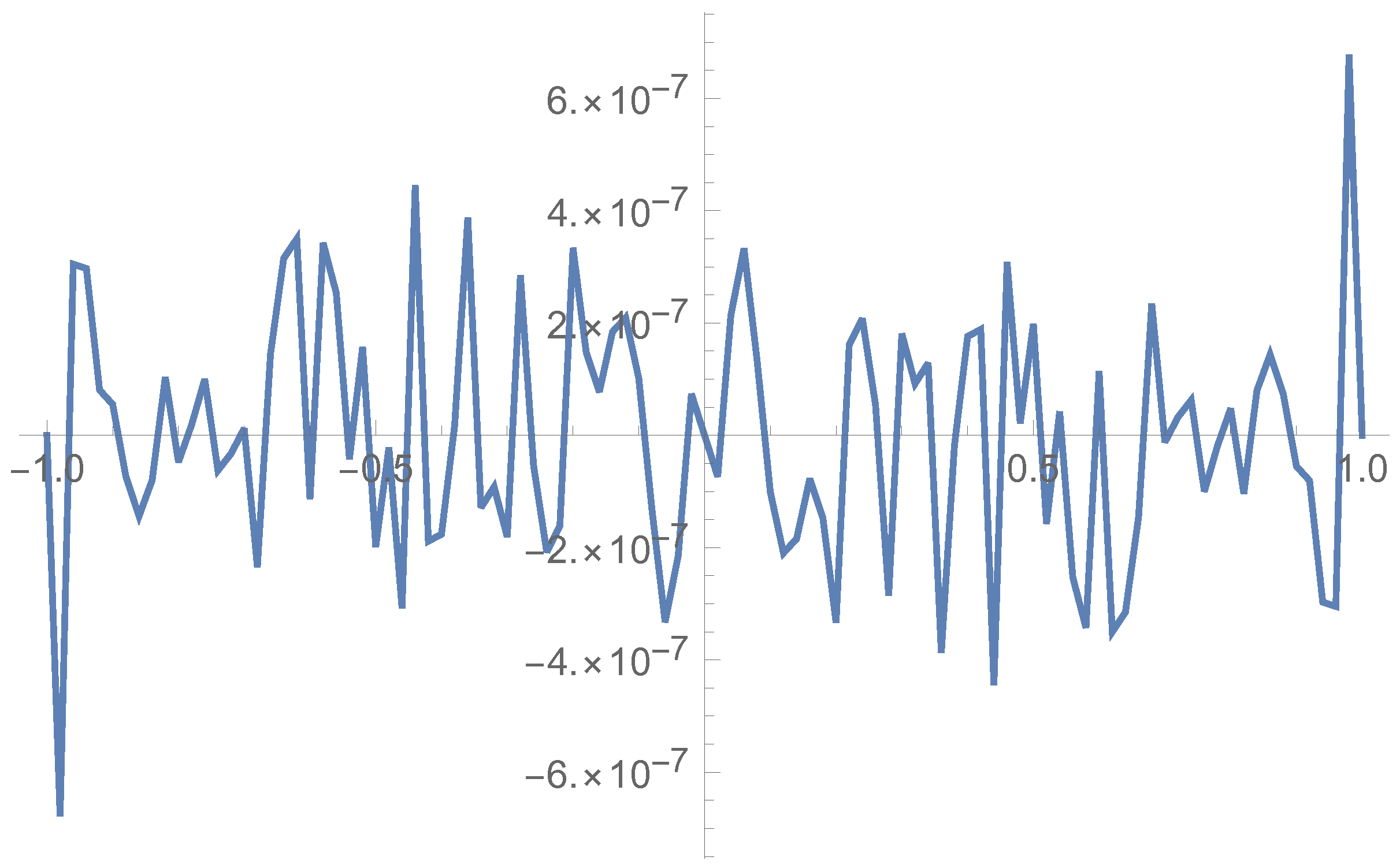


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalimeris, K.; Fokas, A.S. The Modified Helmholtz Equation on a Regular Hexagon—The Symmetric Dirichlet Problem. Axioms 2020, 9, 89. https://doi.org/10.3390/axioms9030089
Kalimeris K, Fokas AS. The Modified Helmholtz Equation on a Regular Hexagon—The Symmetric Dirichlet Problem. Axioms. 2020; 9(3):89. https://doi.org/10.3390/axioms9030089
Chicago/Turabian StyleKalimeris, Konstantinos, and Athanassios S. Fokas. 2020. "The Modified Helmholtz Equation on a Regular Hexagon—The Symmetric Dirichlet Problem" Axioms 9, no. 3: 89. https://doi.org/10.3390/axioms9030089
APA StyleKalimeris, K., & Fokas, A. S. (2020). The Modified Helmholtz Equation on a Regular Hexagon—The Symmetric Dirichlet Problem. Axioms, 9(3), 89. https://doi.org/10.3390/axioms9030089



