1. Introduction and Main Results
Magnetic curves represent, in physics, the trajectories of charged particles moving on a Riemannian manifold under the action of magnetic fields. A magnetic field
F on a Riemannian manifold
is a closed
—form
F and the Lorentz force associated to
F is an endomorphism field
, such that
for all
.
The magnetic trajectories of
F are curves
in
M that satisfy the Lorentz equation (called also the Newton equation)
which generalizes the equation of geodesics under arc length parametrization, namely
Here ▽ denotes the Levi–Civita connection associated to the metric
Usually, the investigation is restricted to a single energy level and only unit speed magnetic curves are considered together with a strength
Therefore, the study focuses on normal magnetic curves satisfying the Lorentz equation
where by dot we denote the derivative with respect to the arc-length parameter
s.
In some settings, magnetic fields arise in a natural way. For instance, in contact (resp. paracontact) metric geometry, there is a naturally given closed two-form, which can be considered as a magnetic field, that we call the contact (resp. paracontact) magnetic field. In [
1], the authors considered contact magnetic fields that are associated to the family of
g-natural contact metric structures on the unit tangent bundle of a Riemannian manifold (cf. [
2]) and studied the corresponding contact magnetic trajectories (we also refer to [
3,
4] for the Sasaki metric case).
In this paper, we consider the paracontact setting on unit tangent bundles. More precisely, we consider the unit tangent bundle
of a Riemannian manifold
endowed with an arbitrary pseudo-Riemannian
g-natural metric, i.e., a metric determined by four fixed constants
a,
b,
c d,
,
,
, as follows
for all
,
and
, where
and
(resp.
and
) are the horizontal (resp. vertical) lifts to
of
X and
Y (resp.
Z and
W). When
, then
is said to be a Kaluza–Klein metric, and when
it is said to be a Kaluza–Klein type metric. G. Calvaruso and V. Martin-Molina proved that paracontact metric structures on the unit tangent bundle associated to pseudo-Riemannian
g-natural metrics constitute a three-parameter family, and they called such structures
g-natural paracontact metric structures (cf. [
5]).
Given a
g-natural paracontact metric structure
on the unit tangent bundle
of
M, the two-form
associated to
is clearly closed, giving rise to a magnetic field. We call its associated magnetic trajectories
natural paracontact magnetic trajectories, which are characterized by the Lorentz equation
where
q is a real constant and
is the Levi–Civita connection of
. In this paper, we shall investigate natural paracontact magnetic trajectories.
At first, we give a characterization of natural paracontact magnetic trajectories as solutions of a system of differential equations, which turns out to be a highly nontrivial relationship that involves the curvature tensor, and whose solution in the full generality is very difficult to find. For the particular case of the velocity vector field of a unit-speed curve c of M (which is a curve of ), we prove that is not a natural paracontact magnetic trajectory unless c is a Riemannian circle and the metric on is of Kaluza–Klein type (Theorem 5).
In the sequel, we restrict to manifolds M of constant sectional curvature k and to pseudo-Riemannian g-natural metrics of Kaluza–Klein type on , and we characterize natural paracontact magnetic trajectories, which are slant, i.e., of constant contact angle. Recall that the contact angle of a curve in an almost paracontact metric manifold is defined as the angle between its tangent vector field and the Reeb vector field in the corresponding point. We shall prove the following.
Theorem 1. Let be a Riemannian manifold of constant sectional curvature k, be a Kaluza–Klein type metric on given by (3) (with ) and be a g-natural paracontact metric structure over . - 1
If , then every paracontact normal magnetic curve in is slant.
- 2
If , then a paracontact normal magnetic curve is slant if and only if both and are constant.
Note that the condition in the theorem above is necessary (cf. Remark 2).
Using the preceding theorem, we will give a complete classification of slant magnetic curves on , when is a two-dimensional Riemannian manifold of constant Gaussian curvature k. In particular, for , we will prove the following
Theorem 2. Let be a Riemannian surface of constant Gaussian curvature k, be a Kaluza–Klein type metric on given by (3) (with ), such that , and be a g-natural paracontact metric structure over . Then a slant paracontact normal magnetic curve of is either a parallel vector field along a geodesic in or the velocity vector field along a non-geodesic Riemannian circle in . Conversely, we will give explicitly sufficient conditions for the existence of such slant paracontact normal magnetic curves (Proposition 5).
For , we find a third type of slant paracontact normal magnetic curves on , i.e., those along curves that are not necessarily Riemannian circles. More precisely, we have
Theorem 3. Let be a Riemannian surface of constant Gaussian curvature , be a Kaluza–Klein type metric on given by (3) (), with , (i.e., ) and , and be a g-natural paracontact metric structure over . Subsequently, a curve is a paracontact normal magnetic trajectory with strength q and a contact angle θ in if and only if one of the following cases occurs: - 1
, x is a geodesic on and V is parallel along x;
- 2
, θ is constant, x is a Riemannian circle in with constant speed and (which is constant) is non zero;
- 3
, θ is constant; and,where are constants satisfying and .
Note that, as before, the condition is necessary in the theorem above, and that, by Theorem 1, is constant.
In [
1], the authors gave the classification of geodesics on unit tangent bundles of constant Gaussian curvature surfaces endowed with pseudo-Riemannian Kaluza-Klein type metrics, except in the case when the Gaussian curvature is negative equal to
. As a consequence of Theorem 3, we have the following corollaries that extend the classification of geodesics to the case
:
Corollary 1. Let be a Riemannian surface of constant Gaussian curvature , be a Kaluza–Klein type metric on given by (3) (), with , (i.e., ) and , and be a g-natural paracontact metric structure over . Subsequently, a curve is a geodesic in if and only if one of one of the following cases occurs: - 1
x is a geodesic on and V is parallel along x;
- 2
x is a Riemannian circle in of constant speed making a constant angle with V and (which is constant) is non zero.
Corollary 2. Let be a Riemannian surface of constant Gaussian curvature , be a Kaluza–Klein type metric on given by (3) (), with , , and , and be a g-natural paracontact metric structure over . Subsequently, a curve is a geodesic in if and only if one of one of the following cases occurs: - 1
x is a geodesic or a Riemannian circle of constant speed in , and V is orthogonal to x;
- 2
the system (4) holds, where , , are constants satisfying and .
Finally, to give a geometric insight to the second type of paracontact normal magnetic trajectories in Theorem 3, we will draw some pictures of slant magnetic curves along Riemannian circles on the unit tangent bundle of the hyperbolic plane of constant Gaussian curvature endowed with a pseudo-Riemannian Kaluza–Klein type metric.
2. -Natural Metrics on Tangent and Unit Tangent Bundles
Let be an n-dimensional Riemannian manifold and ▽ the Levi–Civita connection of g. We shall denote by the tangent space of M at a point and by the bundle projection. For and , there exists a unique vector , such that , where is the natural projection. We call the horizontal lift of X to the point . The vertical lift of a vector to is a vector such that , for all functions f on M. Here, we consider 1-forms on M as functions on (i.e., ).
Observe that the map
is an isomorphism between the vector spaces
and
. Similarly, the map
is an isomorphism between the vector spaces
and
. Obviously, each tangent vector
can be written in the form
, where
are uniquely determined vectors. Hence, the tangent space of
at any point
splits into the horizontal and vertical subspaces with respect to ▽:
Horizontal and vertical lifts of vector fields on M are defined in a corresponding way.
Now, starting from a Riemannian manifold
, a natural construction leads to introduce a wide class of metrics, called
g-natural, on the tangent bundle
([
6,
7]). Such metrics are characterized by the following (cf. [
8]):
Proposition 1. Given an arbitrary g-natural metric G on the tangent bundle of a Riemannian manifold , there exist six smooth functions , , , such thatfor every u, X, , where . Putting
,
and
, for all
, it is known (cf. [
9]) that
G is
non-degenerate if and only if
Riemannian if and only if
The wide class of g-natural metrics includes several well known metrics (Riemannian and not) on . In particular:
The set
of unit tangent vectors to
M is a hypersurface of
called the unit tangent bundle of
M. The tangent space of
at a point
is given by
By definition,
g-natural metrics on the unit tangent bundle
are the metrics induced by
g-natural metrics on
. As proved in [
12] for the Riemannian case, and extended to pseudo-Riemannian settings in [
5], they are completely determined by the values of the four real constants
giving the explicite expression (
3).
By a simple calculation, using the Schmidt’s orthonormalization process, it is easy to check that the vector field on
defined by
for all
is normal to
and unitary at any point of
. We define the “tangential lift”
with respect to the metric
G on
of a vector
to
as the tangential projection of the vertical lift of
X to
with respect to
N, which is
If is orthogonal to u, then The tangent space of at is spanned by vectors of the form and where
Using tangential lifts and (
3), it is easy to see that
g-natural metrics on
admit the following explicit description (cf. [
12]):
Proposition 2. Let be a Riemannian manifold. For every pseudo-Riemannian metric on induced from a g-natural G on , there exist four constants a, b, c and d, satisfying the inequalities(in particular, they are Riemannian if and only if ), such thatfor all , and where . In particular, the Sasaki metric on corresponds to the case where and ; Kaluza–Klein metrics are obtained when ; metrics of Kaluza–Klein type are given by the case .
3. Natural Paracontact Metric Structures on Unit Tangent Bundles
The study of paracontact geometry was initiated by Kaneyuki and Williams [
13]. A systematic study of paracontact metric manifolds and their subclasses was started out by Zamkovay [
14]. Since then, several geometers studied paracontact metric manifolds and obtained various important properties of them.
A contact manifold is an odd-dimensional manifold
equipped with a global 1-form
such that
everywhere. Given such a form
, there exists a unique vector field
, called the characteristic vector field or the Reeb vector field of
, satisfying
and
, for any vector field
X on
. A pseudo-Riemannian metric
g is said to be an associated metric if there exists a tensor field
of type
, such that
for all vector fields
on
. In this case, the structure
on
is called a paracontact metric structure and the manifold
equipped with such a structure is said to be a paracontact metric manifold. It can be easily seen that, in a paracontact metric manifold, the following relations hold:
for any vector fields
on
.
We now give necessary and sufficient conditions for a pseudo-Riemannian
g-natural metric on
to be associated to the very natural contact structure given by
where
r is a positive constant. Let
be an arbitrary pseudo-Riemannian
g-natural metric over
. Subsequently, it is easy to see that, by
,
is completely determined by the relation
We deduce that
so that
if and only if
and
. But since
, then
. It follows, on one hand, that
and, on the other hand, that the relation
is always satisfied. We deduce then the following (cf. [
5])
Proposition 3. is a paracontact metric structures over if and only if the following holds The set of , described by Proposition 3, is a three-parameter family of paracontact metric structures on , that we call natural paracontact metric structures.
Remark 1. The condition confirms the fact that is not Riemannian. It is of signature .
4. Natural Paracontact Magnetic Curves in Unit Tangent Bundles
Let
be a Riemannian manifold, ▽ its Levi–Civita connection and
R its Riemannian curvature. Given a natural paracontact metric structure
on the unit tangent bundle
of
M, the two-form
associated to
is clearly closed, giving rise to a magnetic field. We call its associated magnetic trajectories natural paracontact magnetic trajectories, which are characterized by the Lorentz equation
where
q is a real constant and
is the Levi–Civita connection of
. We start this section by giving equations characterizing natural paracontact magnetic trajectories on
.
Let
be a curve in
Subsequently,
is a unit vector field along the base curve
in
The velocity vector field
is given by
In [
1], we have proved that the tension vector field
is given by
On the other hand, using (
11) and (
14), we get
In terms of horizontal and vertical lifts, the previous relation becomes:
Taking into account (
15) and (
16), Lorentz Equation (
13) gives the following characterization of natural paracontact magnetic curves on the unit tangent bundle:
Theorem 4. A curve in is a paracontact magnetic trajectory with strength q if and only if In the special case of velocity vector fields, we have
Corollary 3. Let be a unit speed curve in Subsequently, its velocity vector field is a paracontact magnetic trajectory with strength q in if and only if As a consequence of system (
18), we find
We distinguish two situations:
- •
If
x is a geodesic, then Equation (
18) is automatically satisfied.
- •
If
x is not a geodesic, then let
be the (first) normal, that is
, where
. Then we have
While using (
20) in (
19), we obtain
Hence, one gets , i.e., is a Kaluza-Klein type metric on .
We conclude with the following result:
Theorem 5. Let be a non-geodesic unit speed curve in Subsequently, its velocity vector field is a paracontact magnetic trajectory with strength q in if and only if
- 1
is a Kaluza-Klein type metric on ,
- 2
,
- 3
x is a Riemannian circle.
Corollary 4. Let be a Riemannian manifold of constant curvature k and be a non-geodesic unit speed curve in Then its velocity vector field is a paracontact magnetic trajectory with strength q in if and only if
- 1
is a Kaluza-Klein type metric on ,
- 2
x is a Riemannian circle,
- 3
.
5. Contact Angle
Recall that the contact angle of a curve
in an almost paracontact metric manifold is defined as the angle between its tangent vector field and the Reeb vector field in the corresponding point. For a unit speed curve
in
, we have
and so the contact angle
of
is given by
Hence, a unit speed curve is slant, which is the contact angle is constant, if and only if is constant.
We now investigate natural paracontact magnetic curves that are slant in the unit tangent bundle of a space form with is a metric of Kaluza–Klein type. We first reformulate the equation of natural paracontact magnetic curves in a space form, in terms of the contact angle.
Proposition 4. Let be a space form of curvature k. Subsequently, any paracontact magnetic curve on , where is a metric of Kaluza–Klein type satisfies the following differential equations system: We are now in position to prove Theorem 1, which gives a characterization of slant paracontact magnetic curves in .
Proof of Theorem 1 By normality of
, we have
and, by the first equation of (
23), we obtain
On the other hand, deriving (
22) with respect to
s and using the first equation of (
23), we obtain the following:
So, we have two possibilities:
- 1
. In this case, we have by (
26)
, and hence
is slant.
- 2
. Suppose that
is slant. Subsequently,
is constant and, then, by (
26), we have
since
. Hence, (
25) gives
, i.e.,
is constant. Because, in (
24)
and
are constant, then
is constant.
Conversely, if we suppose that both and are constant, then we can distinguish two cases:
. In this case, from (
24),
is constant, i.e.,
is slant.
and
. In this case, we have by virtue of (
25),
. Hence (
26) implies that
is constant, i.e.,
is slant.
☐
Remark 2. The condition in Theorem 1 is mandatory. Indeed, since then we obtain , i.e, .
6. Slant Magnetic Curves on the Unit Tangent Bundle of
We are now interested in what happens when , i.e., when M is a Riemannian surface of constant Gaussian curvature k and we shall restrict ourselves to the Kaluza–Klein type metrics on the unit tangent bundle . The investigation yields to Theorems 2 () and 3 (), whose proofs are given below.
Proof of Theorem 2 Suppose that
is a slant paracontact normal magnetic curve. Subsequently, by Theorem 1, (
24) and (
26), we have
where
is a positive real constant.
Let us distinguish two situations:
Moreover, from the first Equation (
23), we obtain that
, namely
x is a geodesic on
On the other hand, from the second equation of (
23), we get
- Subcase A1
If we choose , we get . As V is unitary and , we obtain . We deduce that . Accordingly, we obtain the magnetic curve , with strength , where x is geodesic on .
- Subcase A2
If , then we can distinguish two possibilities:
Case B:, then the vector fields
and
V are linearly independent. Hence, at every point
, the vector
is a linear combination of
V and
. Using
, we find
and
. Because
, we have
, i.e.,
. As
does not vanish, we have
From the first equation in (
23), it follows that
. If we put
, then
is a non-zero constant and, hence,
x is a non-geodesic circle in
. It is then easy to see that the second equation of (
23) is equivalent to
Thus, the magnetic curve is obtained as , where x is a non-geodesic circle in . ☐
In the preceding proof, we have proven that, to have slant paracontact normal magnetic curves, some restrictions should be imposed on the g-natural metrics and the strengths of the curves. This gives the following classification result:
Proposition 5. Let be a Riemannian surface of constant Gaussian curvature k, be a Kaluza–Klein type metric on given by (3) (with ), such that , be a g-natural paracontact metric structure over and . Then a curve of is a slant paracontact normal magnetic curve of strength q and contact angle if and only if one of the following assertions holds: - 1
x is a geodesic in of speed σ, V is parallel and one of the following holds:
- (i)
, and ;
- (ii)
, , and σ satisfies the inequality (29).
- 2
x is a non-geodesic Riemannian circle in of constant speed σ, , and .
Remark 3. - 1
In the subcase (i) of the case 1. of the previous proposition, the contact angle .
- 2
Using the identity , it is easy to see that condition (29) is equivalent to: , if ;
, if ;
, if .
Proof of Theorem 3. Suppose that
is a paracontact normal magnetic trajectory with strength
q and a contact angle
in
. Subsequently,
is constant, by Theorem 1. For
, let
be the unit vector normal to
. Subsequently, we have
for certain
-functions
A and
B. It follows that
Using (
23),
is a magnetic curve if and only if
where
. Hence,
If , which is , it follows that and , where A and B are real constants. Moreover, we obtain .
If , then x is a geodesic on and .
If , we obtain and . In this case, , and , i.e., , and are constants. In particular, x is a Riemannian circle in .
Notice that and V are collinear vectors if and only if the constant A is zero.
If
, then system (
30) leads to
Because
, the general solution of (
32) is
where
, and
are constants. We also obtain
The arc-length condition (
24) for
yields
Conversely, we shall prove that if we have one of the conditions (1), (2), or (3), then (
30) is satisfied.
In the case (1) of the theorem,
implies that
. Because
and
V are parallel, then
is constant, i.e.,
is constant. On the other hand, since
, then
, and since
is a geodesic, then its speed is constant, i.e.,
is constant, and hence
A is constant. We deduce that (
30) is satisfied.
In the case (2) of the theorem, we also have
. Because
is constant, then
B is constant. On the other hand,
x is a Riemannian circle, i.e.,
is constant. We deduce that
is constant. Becasue
and
B are constant, then
A is constant, and, consequently, (
30) is satisfied.
In the case (3) of the theorem, it is easy to check that
A and
B given by (
33) and (
34), respectively, satisfy (
30).
☐
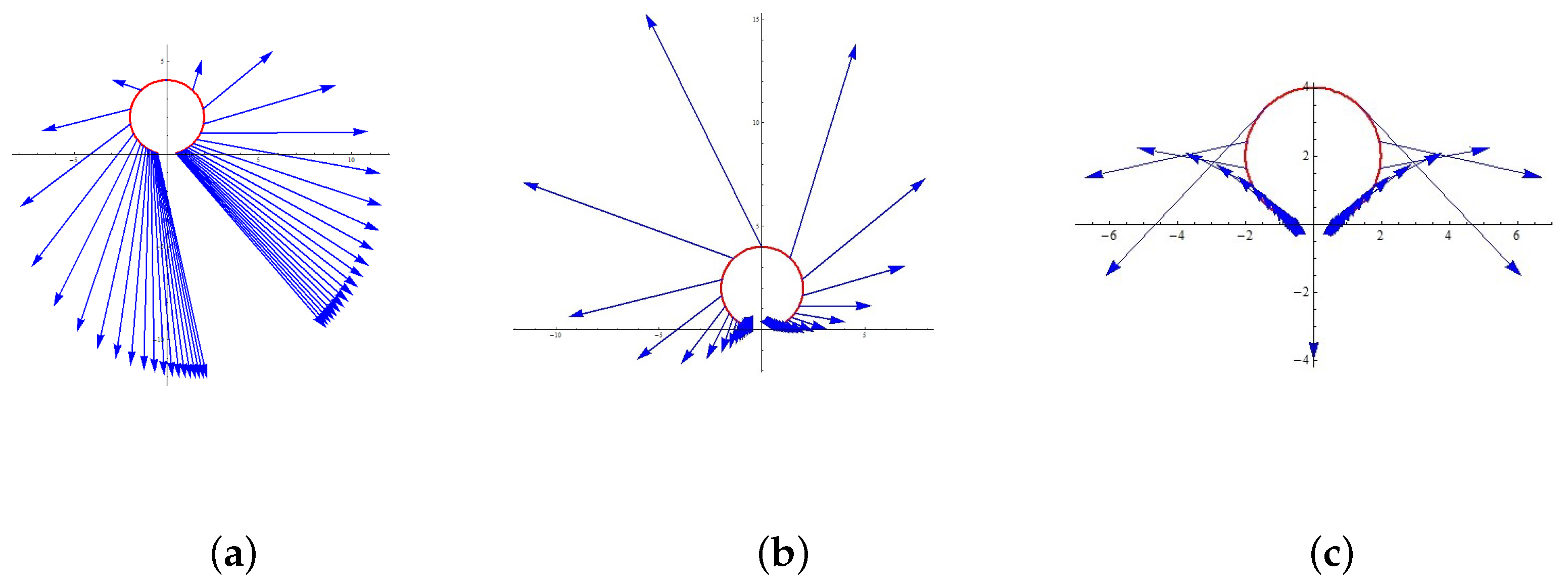
Examples in
We conclude this section drawing some pictures of magnetic curves along Riemannian circles that correspond to different values for the constants that appeared so far. The base manifold is , equipped with the metric , and the constant from the proof of the Theorem 3 is taken as equal to zero.
In [
15], the authors give a complete description of Riemannian circles on
. Using their results, we consider the normal Riemannian circle on
given by the parametrization
where
. It is easy to see that
, so that
We deduce that .
Here,
. Thus, we obtain
that is
where
,
,
,
,
,
and
.
To visualize graphically some slant natural paracontact magnetic trajectories on the unit tangent bundle of
along Riemannian circles,
Figure 1 below presents the base curve
x on
, together with the vector field
V along it, in the three following situations that correspond to different values for the constants that appeared so far:
- (a)
,
,
,
,
,
,
and
(
Figure 1a);
- (b)
,
,
,
,
,
and
(
Figure 1b);
- (c)
,
,
,
,
,
,
and
(
Figure 1c).