An Extended MABAC Method Based on Triangular Fuzzy Neutrosophic Numbers for Multiple-Criteria Group Decision Making Problems

Abstract

In this manuscript, we extend the traditional multi-attributive border approximation area comparison (MABAC) method for the multiple-criteria group decision-making (MCGDM) with triangular fuzzy neutrosophic numbers (TFNNs) to propose the TFNNs-MABAC method. In the proposed method, we utilize the TFNNs to express the values of criteria for each alternative in MCGDM problems. First, we briefly acquaint the basic concept of TFNNs and describe its corresponding some operation laws, the functions of score and accuracy, and the normalized hamming distance. We then review two aggregation operators of TFNNs. Afterward, we combine the traditional MABAC method with the triangular fuzzy neutrosophic evaluation and provide a sequence of calculation procedures of the TFNNs-MABAC method. After comparing it with some TFNNs aggregation operators and another method, the results showed that our extended MABAC method can not only effectively handle the conflicting attributes, but also practically deal with incomplete and indeterminate information in the MCGDM problem. Therefore, the extended MABAC method is more effective, conformable, and reasonable. Finally, an investment selection problem is demonstrated as a practice to verify the reasonability of our MABAC method.

1. Introduction

The MABAC (multi-attributive border approximation area comparison) approach has been widely utilized to investigate multiple-criteria group decision-making (MCGDM) problems and has been extensively applied in various case studies by many fabulous researchers. In many existing prestigious pieces of literature, many original MCGDM approaches have been continually discussed, such as the TODIM model [1,2,3], the PROMETHEE model [4,5,6], the TOPSIS model [7,8,9], SAW model [10,11], the ELECTRE model [12,13], the VIKOR model [14], and the EDAS model [15].

In reality, many real-life MCGDM problems cannot easily interpret the criteria and linguistic values with appropriate values as a consequence of the complexity and fuzziness of the alternatives. These values should be described in the form of fuzzy to be more useful, rational, and feasible. The theory of the fuzzy set (FS), initially apprised by Zadeh in [16], has been frequently utilized as a worthy instrument for MCGDM [17,18] problems. This theory can capture objects into members of the set through a degree of membership that can be presented by arbitrary values within the real-number interval from 0 to 1. Atanassov [19] then introduced the intuitionistic fuzzy set (IFS) that characterizes each element of an object not only in the form of a membership degree but also in the term of non-membership. Thus, it can describe the fuzzy information more definitively and specifically than the FS. However, it can only manage uncertainty and incomplete information but not the inconsistent and indeterminacy information that occurs usually in practice. Therefore, Smarandache [20] initiated the neutrosophic, a branch of philosophy, to propose the theory of neutrosophic sets (NSs). To be more helpful for applying the NSs in real-case studies, Wang et al. [21] defined a sub-class of NSs, the single-valued neutrosophic sets (SVNSs), in which each element of an object is depicted by the degrees of truth-membership, indeterminacy-membership, and falsity-membership spreading over in the real-number interval. Ye [22] introduced the simplified neutrosophic sets (SNSs) to solve a multicriteria decision-making (MCDM) problem. Afterward, Ye [23] offered the idea of a single-valued neutrosophic linguistic set (SVNLS) combined with the TOPSIS method. Ye also explored two aggregation operators of SVNLS to an environment of SVNLS. Deli and Braumi [24] exposed the neutrosophic soft matrix (NSM) and investigated their operators to store NSs in computer memory. Deli et al. [25] first developed the concept of NSs by introducing bipolar NSs for MCDM problems. Based on the bipolar NSs, the functions of a score of accuracy can evaluate the values of alternatives and select the best one. Stanujkic et al. [26] proposed a novel MCDM approach based on bipolar NSs and the Hamming distance for assessing the quality of the websites. Stanujkic et al. [27] utilized SVNSs to extend the MULTIMOORA method for handling complex problems through prediction and judgment. Biswas et al. [28] innovated the idea of a triangular fuzzy neutrosophic number (TFNN) by combining the concepts of NS and triangular fuzzy number (TFN). Deli and Şubaş [29] integrated the TFN and triangular intuitionistic fuzzy numbers (TIFN) for reviewing several MCDM problems. Aal et al. [30] explored two ranking means through information system quality under the TFN information. Liu [31] studied the operators of SVNs weighted averaging and SVNs weighted geometric to implement a decision-making problem.

Additionally, many recent MCGDM problems have actively involved a group of decision-makers (DMs) in the process of decision-making to minimize the subjectivity of the DMs’ judgment. They tend to have their own different opinions to assess alternatives and criteria and usually give their evaluation opinions using the linguistic variables term. To deal with this, there are some studies of hesitant fuzzy linguistic term sets (HFLTSs) [32] in MCGDM. Zhang et al. [33] introduced three novel algorithms for solving MCGDM problems with multi granular unbalanced hesitant fuzzy linguistic information. The first algorithm was utilized to express a linguistic distribution assessment (LDA) using a hesitant linguistic distribution (HLD). Two others were used to modify an unbalanced HFLTS into a balanced LDA and to modify a balanced LDA into an unbalanced LDA. Yu et al. [34] proposed a novel consensus reaching model in MCGDM with multi-granular HFLTSs. This optimization model was established to minimize the overall adjustment amount of DMs’ preference and to be very simpler than the use of HFLTSs.

Many researchers have extensively developed applications of SVNs in MCGDM problem. However, in uncertain and complex situations, the degrees of truth-membership, indeterminacy-membership, and falsity-membership of SVNs cannot be used to delineate an element with precise real-numbers. Meanwhile, TFN can effectively manage fuzzy information rather than the real-number interval. Therefore, the combination of TFN with SVNs, or TFNNs, will be a suitable tool to handle incomplete, indeterminacy, and uncertain information occurring in MCGDM problems.

The MABAC approach was first conveyed by Pamučar and Ćirović [35] in solving a selection problem of transportation and resource distribution at a logistic center. The basic concept of this approach is to look at many ideal attributes respond to criteria located at the border approximation area (BAA). It can consider the conflicting attributes. Consequently, the MABAC takes the advantages of BAA in concerning the inconsistency of decision maker and uncertainty conditions, whereas other traditional decision-making approaches cannot conduct it. Additionally, this approach has an uncomplicated computation procedure and can reveal the decision theory in logical and systematic ways. Later on, Pamučar et al. [36] improved the MABAC by utilizing interval-valued fuzzy-rough numbers (IVFRNs). Pamučar et al. [37] integrated AHP (Analytical Hierarchy Process) and MABAC in developing a software to assess some official university websites. Jia et al. [38] have utilized analytically the concept of FS to develop a new MABAC model for MCGDM based on rough numbers (RNs). Alluding the advantages of interval type-2 fuzzy set (IT2FS), Dorfeshan and Mousavi in [39] developed a novel MABAC to determine the attribute path of beneficial projects under MCGDM process in a case study of aircraft maintenance industries. Yu et al. [40] proposed a MABAC based on an improvement of type-1 fuzzy sets (T1FSs), interval type-2 fuzzy sets (IT2FSs) to handle intrinsic and extrinsic uncertainties. Zhang et al. [41] extended MABAC for MCGDM cases with picture 2-tuple linguistic in evaluating the project of renewable energy power. Mishra et al. [42] utilized interval valued intuitionistic fuzzy sets (IVIFSs) to develop an extension of MABAC method for a programming language assessment.

In recent years, there are several MCGDM methods which can enhance the methods’ adaptability. As far as we know, there have been no studies regarding the MABAC approach under TFNNs environment for MCGDM problems. Therefore, we emphasize our attention to enlarging the MABAC method to support the TFNN environment and implement it for evaluating an investment selection problem. Later on, we summarize some contributions and motivations of this study as follows:

• There are at least two motivations for using TFNNs. Firstly, TFNNs which are adopted by TFN with NSs can effectively support uncertain information. In real practical cases, the same judgment in the form of the linguistic variable may express different meanings for various people. TFNNs provide DMs freedom decisions in defining the membership function and it can better explain and handle inaccurate information. Secondly, TFNNs are a proper instrument to deal with incomplete and indeterminacy information in MCGDM problems.
• Because the computational complexity of TFNN, especially the loop performance in using some aggregation operators of TFNNs, is relatively a bit slow, we require a simple and uncomplicated method to determine decisions. Compared with some other methods, the MABAC has not only abilities to effectively handle the conflicting attributes, but also logically reveal the decision-making theory with uncomplicated and systematic computation procedures.

The remaining of our paper is managed systematically as follows: Section 2 discusses things related to TFNNs, such as the definition of TFNNs, some operation laws, the functions of score and accuracy, and the normalized hamming distance between two TFNNs. Later on, in Section 2, we also depict the operators of triangular fuzzy neutrosophic number weighted averaging (TFNNWA) and triangular fuzzy neutrosophic number weighted geometric (TFNNWG). Section 3 modifies the original MABAC method to triangular fuzzy neutrosophic environment and shows a sequence of calculation procedures of TFNN-MABAC model. Section 4 demonstrates an illustrative-example to select a possible invested technology enterprise to investigate the proposed MABAC method and performs a comparative analysis between our proposed MABAC and some other aggregation operators. Section 5 recapitulates our paper conclusions and discuses all possible future studies and researches.

2. Preliminaries

In this section, we re-discuss the definition of TFNNs, operation laws of TFNNs, the functions of score and accuracy of TFNNs, and the normalized hamming distance between two arbitrary TFNNs. We also recall the definition of TFNNWA and TFNNWG operators.

2.1. Triangular Fuzzy Number Neutrosophic Sets

Based on the concepts of single-valued neutrosophic sets and triangular fuzzy number intuitionistic fuzzy sets (TFNIFSs), Biswas et al. [28] first developed the triangular fuzzy number neutrosophic (TFNNSs) by presenting the truth-membership degree (TMD), the indeterminacy-membership degree (IMD), and the falsity-membership degree (FMD) in the form of triangular-fuzzy numbers.

Definition 1 ([28]).

Let X be the universal set, the TFNNSs $\mu$ can be represented as: $\mu = \left\{\left(x,{\alpha }_{\mu }\left(x\right),{\beta }_{\mu }\left(x\right),{\gamma }_{\mu }\left(x\right)|x\in X\right)\right\}$ where ${\alpha }_{\mu }\left(x\right),{\beta }_{\mu }\left(x\right),{\gamma }_{\mu }\left(x\right)\in \left[0,1\right]$ describe the truth-membership degree, the indeterminacy-membership degree, and the falsity-membership degree respectively that can be formulated by TFNs as follows.

$${\alpha }_{\mu }\left(x\right)=\left({\alpha }_{\mu }^L\left(x\right),{\alpha }_{\mu }^M\left(x\right),{\alpha }_{\mu }^U\left(x\right)\right), 0\le {\alpha }_{\mu }^L\left(x\right)\le {\alpha }_{\mu }^M\left(x\right)\le {\alpha }_{\mu }^U\left(x\right)\le 1$$

(1)

$${\beta }_{\mu }\left(x\right)=\left({\beta }_{\mu }^L\left(x\right),{\beta }_{\mu }^M\left(x\right),{\beta }_{\mu }^U\left(x\right)\right), 0\le {\beta }_{\mu }^L\left(x\right)\le {\beta }_{\mu }^M\left(x\right)\le {\beta }_{\mu }^U\left(x\right)\le 1$$

(2)

$${\gamma }_{\mu }\left(x\right)=\left({\gamma }_{\mu }^L\left(x\right),{\gamma }_{\mu }^M\left(x\right),{\gamma }_{\mu }^U\left(x\right)\right), 0\le {\gamma }_{\mu }^L\left(x\right)\le {\gamma }_{\mu }^M\left(x\right)\le {\gamma }_{\mu }^U\left(x\right)\le 1$$

(3)

For notational convenience, we assume that $\mu = \left(\left({\alpha }_{\mu }^L\left(x\right),{\alpha }_{\mu }^M\left(x\right),{\alpha }_{\mu }^U\left(x\right)\right),\left({\beta }_{\mu }^L\left(x\right),{\beta }_{\mu }^M\left(x\right),{\beta }_{\mu }^U\left(x\right)\right),\left({\gamma }_{\mu }^L\left(x\right),{\gamma }_{\mu }^M\left(x\right),{\gamma }_{\mu }^U\left(x\right)\right)\right)$ is a TFNN, it has to satisfy the condition $0\le {\alpha }_{\mu }^U\left(x\right)+{\beta }_{\mu }^U\left(x\right)+{\gamma }_{\mu }^U\left(x\right)\le 3$.

Definition 2 ([28]).

Let ${\mu }_1= \left(\left({\alpha }_{{\mu }_1}^L\left(x\right),{\alpha }_{{\mu }_1}^M\left(x\right),{\alpha }_{{\mu }_1}^U\left(x\right)\right),\left({\beta }_{{\mu }_1}^L\left(x\right),{\beta }_{{\mu }_1}^M\left(x\right),{\beta }_{{\mu }_1}^U\left(x\right)\right),\left({\gamma }_{{\mu }_1}^L\left(x\right),{\gamma }_{{\mu }_1}^M\left(x\right),{\gamma }_{{\mu }_1}^U\left(x\right)\right)\right)$, ${\mu }_2= \left(\left({\alpha }_{{\mu }_2}^L\left(x\right),{\alpha }_{{\mu }_2}^M\left(x\right),{\alpha }_{{\mu }_2}^U\left(x\right)\right),\left({\beta }_{{\mu }_2}^L\left(x\right),{\beta }_{{\mu }_2}^M\left(x\right),{\beta }_{{\mu }_2}^U\left(x\right)\right),\left({\gamma }_{{\mu }_2}^L\left(x\right),{\gamma }_{{\mu }_2}^M\left(x\right),{\gamma }_{{\mu }_2}^U\left(x\right)\right)\right)$, and ${\mu }_3= \left(\left({\alpha }_{{\mu }_3}^L\left(x\right),{\alpha }_{{\mu }_3}^M\left(x\right),{\alpha }_{{\mu }_3}^U\left(x\right)\right),\left({\beta }_{{\mu }_3}^L\left(x\right),{\beta }_{{\mu }_3}^M\left(x\right),{\beta }_{{\mu }_3}^U\left(x\right)\right),\left({\gamma }_{{\mu }_3}^L\left(x\right),{\gamma }_{{\mu }_3}^M\left(x\right),{\gamma }_{{\mu }_3}^U\left(x\right)\right)\right)$ be three TFNNs, the following mathematical operation laws are satisfied as:

$${\mu }_1\oplus {\mu }_2=\left(\begin{array}{c}\left({\alpha }_{{\mu }_1}^L\left(x\right)+{\alpha }_{{\mu }_2}^L\left(x\right)-{\alpha }_{{\mu }_1}^L\left(x\right){\alpha }_{{\mu }_2}^L\left(x\right),{\alpha }_{{\mu }_1}^M\left(x\right)+{\alpha }_{{\mu }_2}^M\left(x\right)-{\alpha }_{{\mu }_1}^M\left(x\right){\alpha }_{{\mu }_2}^M\left(x\right),{\alpha }_{{\mu }_1}^U\left(x\right)+{\alpha }_{{\mu }_2}^U\left(x\right)-{\alpha }_{{\mu }_1}^U\left(x\right){\alpha }_{{\mu }_2}^U\left(x\right)\right),\\ \left({\beta }_{{\mu }_1}^L\left(x\right){\beta }_{{\mu }_2}^L\left(x\right), {\beta }_{{\mu }_1}^M\left(x\right){\beta }_{{\mu }_2}^M\left(x\right), {\beta }_{{\mu }_1}^U\left(x\right){\beta }_{{\mu }_2}^U\left(x\right)\right),\\ \left({\gamma }_{{\mu }_1}^L\left(x\right){\gamma }_{{\mu }_2}^L\left(x\right), {\gamma }_{{\mu }_1}^M\left(x\right){\gamma }_{{\mu }_2}^M\left(x\right), {\gamma }_{{\mu }_1}^U\left(x\right){\gamma }_{{\mu }_2}^U\left(x\right)\right)\end{array}\right)$$

(4)

$${\mu }_1\otimes {\mu }_2=\left(\begin{array}{c}\left({\alpha }_{{\mu }_1}^L\left(x\right){\alpha }_{{\mu }_2}^L\left(x\right), {\alpha }_{{\mu }_1}^M\left(x\right){\alpha }_{{\mu }_2}^M\left(x\right), {\alpha }_{{\mu }_1}^U\left(x\right){\alpha }_{{\mu }_2}^U\left(x\right)\right),\\ \left({\beta }_{{\mu }_1}^L\left(x\right)+{\beta }_{{\mu }_2}^L\left(x\right)-{\beta }_{{\mu }_1}^L\left(x\right){\beta }_{{\mu }_2}^L\left(x\right),{\beta }_{{\mu }_1}^M\left(x\right)+{\beta }_{{\mu }_2}^M\left(x\right)-{\beta }_{{\mu }_1}^M\left(x\right){\beta }_{{\mu }_2}^M\left(x\right),{\beta }_{{\mu }_1}^U\left(x\right)+{\beta }_{{\mu }_2}^U\left(x\right)-{\beta }_{{\mu }_1}^U\left(x\right){\beta }_{{\mu }_2}^U\left(x\right)\right),\\ \left({\gamma }_{{\mu }_1}^L\left(x\right)+{\gamma }_{{\mu }_2}^L\left(x\right)-{\gamma }_{{\mu }_1}^L\left(x\right){\gamma }_{{\mu }_2}^L\left(x\right),{\gamma }_{{\mu }_1}^M\left(x\right)+{\gamma }_{{\mu }_2}^M\left(x\right)-{\gamma }_{{\mu }_1}^M\left(x\right){\gamma }_{{\mu }_2}^M\left(x\right),{\gamma }_{{\mu }_1}^U\left(x\right)+{\gamma }_{{\mu }_2}^U\left(x\right)-{\gamma }_{{\mu }_1}^U\left(x\right){\gamma }_{{\mu }_2}^U\left(x\right)\right)\end{array}\right)$$

(5)

$$\lambda {\mu }_3=\left(\begin{array}{c}\left(1-{\left(1-{\alpha }_{{\mu }_3}^L\left(x\right)\right)}^{\lambda }, 1-{\left(1-{\alpha }_{{\mu }_3}^M\left(x\right)\right)}^{\lambda },1-{\left(1-{\alpha }_{{\mu }_3}^U\left(x\right)\right)}^{\lambda }\right),\\ \left( {\left({\beta }_{{\mu }_3}^L\left(x\right)\right)}^{\lambda }, {\left({\beta }_{{\mu }_3}^M\left(x\right)\right)}^{\lambda }, {\left({\beta }_{{\mu }_3}^U\left(x\right)\right)}^{\lambda }\right),\\ \left( {\left({\gamma }_{{\mu }_3}^L\left(x\right)\right)}^{\lambda }, {\left({\gamma }_{{\mu }_3}^M\left(x\right)\right)}^{\lambda }, {\left({\gamma }_{{\mu }_3}^U\left(x\right)\right)}^{\lambda }\right)\end{array}\right), \mathrm{for}\lambda >0$$

(6)

$${\mu }_3{}^{\lambda }=\left(\begin{array}{c}\left( {\left({\alpha }_{{\mu }_3}^L\left(x\right)\right)}^{\lambda }, {\left({\alpha }_{{\mu }_3}^M\left(x\right)\right)}^{\lambda }, {\left({\alpha }_{{\mu }_3}^U\left(x\right)\right)}^{\lambda }\right),\\ \left(1-{\left(1-{\beta }_{{\mu }_3}^L\left(x\right)\right)}^{\lambda }, 1-{\left(1-{\beta }_{{\mu }_3}^M\left(x\right)\right)}^{\lambda },1-{\left(1-{\beta }_{{\mu }_3}^U\left(x\right)\right)}^{\lambda }\right),\\ \left(1-{\left(1-{\gamma }_{{\mu }_3}^L\left(x\right)\right)}^{\lambda }, 1-{\left(1-{\gamma }_{{\mu }_3}^M\left(x\right)\right)}^{\lambda },1-{\left(1-{\gamma }_{{\mu }_3}^U\left(x\right)\right)}^{\lambda }\right)\end{array}\right), \mathrm{for}\lambda >0$$

(7)

According to the properties of the real-number system, the operators mentioned in Definition 2 has satisfied clearly as all TFNN properties follows.

$${\mu }_1\oplus {\mu }_2= {\mu }_2\oplus {\mu }_1, {\mu }_1\otimes {\mu }_2={\mu }_2\otimes {\mu }_1;$$

(8)

$$\lambda \left({\mu }_1\oplus {\mu }_2\right)= \lambda {\mu }_2\oplus \lambda {\mu }_1, {\left({\mu }_1\otimes {\mu }_2\right)}^{\lambda } ={\left({\mu }_1\right)}^{\lambda }\otimes {\left({\mu }_2\right)}^{\lambda }, for \lambda >0$$

(9)

$${\lambda }_1{\mu }_1\oplus {\lambda }_2{\mu }_1=\left({\lambda }_1+{\lambda }_2\right){\mu }_1, {\mu }_1{}^{{\lambda }_1}\oplus {\mu }_1{}^{{\lambda }_2}={\mu }_1{}^{({\lambda }_1+{\lambda }_2)}, for {\lambda }_1,{\lambda }_2>0.$$

(10)

Definition 3 ([28]).

Let ${\mu }_1= \left(\left({\alpha }_{{\mu }_1}^L\left(x\right),{\alpha }_{{\mu }_1}^M\left(x\right),{\alpha }_{{\mu }_1}^U\left(x\right)\right),\left({\beta }_{{\mu }_1}^L\left(x\right),{\beta }_{{\mu }_1}^M\left(x\right),{\beta }_{{\mu }_1}^U\left(x\right)\right),\left({\gamma }_{{\mu }_1}^L\left(x\right),{\gamma }_{{\mu }_1}^M\left(x\right),{\gamma }_{{\mu }_1}^U\left(x\right)\right)\right)$ be a TFNN, the functions of score $S({\mu }_1)$ and accuracy $A\left({\mu }_1\right)$ can be respectively calculated by:

$$\begin{gathered} S({\mu }_1)=\frac{1}{12}\left[8+\left({\alpha }_{{\mu }_1}^L\left(x\right)+2{\alpha }_{{\mu }_1}^M\left(x\right)+{\alpha }_{{\mu }_1}^U\left(x\right)\right)-\left({\beta }_{{\mu }_1}^L\left(x\right)+2{\beta }_{{\mu }_1}^M\left(x\right)+{\beta }_{{\mu }_1}^U\left(x\right)\right) \\ -\left({\gamma }_{{\mu }_1}^L\left(x\right)+2{\gamma }_{{\mu }_1}^M\left(x\right)+{\gamma }_{{\mu }_1}^U\left(x\right)\right)\right], for S({\mu }_1)\in \left[0,1\right] \end{gathered}$$

(11)

$$A({\mu }_1)=\frac{1}{4}\left[\left({\alpha }_{{\mu }_1}^L\left(x\right)+2{\alpha }_{{\mu }_1}^M\left(x\right)+{\alpha }_{{\mu }_1}^U\left(x\right)\right)-\left({\gamma }_{{\mu }_1}^L\left(x\right)+2{\gamma }_{{\mu }_1}^M\left(x\right)+{\gamma }_{{\mu }_1}^U\left(x\right)\right)\right], for A({\mu }_1)\in \left[-1,1\right]$$

(12)

Consider two TFNNs in the real-number set: ${\mu }^{-}= \left(\left(0,0,0\right),\left(1,1,1\right),\left(1,1,1\right)\right)$ and ${\mu }^{+}= \left(\left(1,1,1\right),\left(0,0,0\right),\left(0,0,0\right)\right)$, then the values of score function ${\mu }^{-}$ and ${\mu }^{+}$ are $S({\mu }^{-})=0$ and $S({\mu }^{+})=1$, respectively. Moreover, the values of accuracy function $A({\mu }^{-})$ is −1 for the TFNN ${\mu }^{-}$ and $A({\mu }^{+})$ is 1 for the TFNN ${\mu }^{+}$. The accuracy function $A({\mu }_1)\in \left[-1,1\right]$ states the discrepancy between truth and falsity [28]. Larger the discrepancy indicates the most affirmative of the TFNNs.

Assume that there are two TFNNs ${\mu }_1$ and ${\mu }_1$, then, according to Definition 3, the following conditions reach a true value.

$$\begin{array}{c}if S({\mu }_1)<S({\mu }_2), then {\mu }_1<{\mu }_2;\\ if S({\mu }_1)>S({\mu }_2), then {\mu }_1>{\mu }_2;\\ if S({\mu }_1)=S({\mu }_2) and A({\mu }_1)<A({\mu }_2), then {\mu }_1<{\mu }_2;\\ if S({\mu }_1)=S({\mu }_2) and A({\mu }_1)>A({\mu }_2), then {\mu }_1>{\mu }_2;\\ if S({\mu }_1)=S({\mu }_2) and A({\mu }_1)=A({\mu }_2), then {\mu }_1={\mu }_2;\end{array}$$

(13)

Definition 4 ([28]).

Let ${\mu }_j= \left(\left({\alpha }_{{\mu }_j}^L\left(x\right),{\alpha }_{{\mu }_j}^M\left(x\right),{\alpha }_{{\mu }_j}^U\left(x\right)\right),\left({\beta }_{{\mu }_j}^L\left(x\right),{\beta }_{{\mu }_j}^M\left(x\right),{\beta }_{{\mu }_j}^U\left(x\right)\right),\left({\gamma }_{{\mu }_j}^L\left(x\right),{\gamma }_{{\mu }_j}^M\left(x\right),{\gamma }_{{\mu }_j}^U\left(x\right)\right)\right)$ be a TFNNs group and $W=\left\{w_j\right\}$ be a set of the weighted criteria for $j=1,2,3,\dots ,n$ in the group of real-numbers respectively, the operator of TFNNWA notated by $TFNNWA\left({\mu }_1,{\mu }_2,{\mu }_3,\dots ,{\mu }_n\right)$ is determined by:

$$TFNNWA\left({\mu }_1,{\mu }_2,{\mu }_3,\dots ,{\mu }_n\right)=w_1{\mu }_1\oplus w_2{\mu }_2\oplus w_3{\mu }_3\oplus \dots \oplus w_n{\mu }_n=\begin{array}{c}n\\ \oplus \\ j=1\end{array}{w}_j{\mu }_j$$

(14)

Theorem 1 ([28]).

Let ${\mu }_j= \left(\left({\alpha }_{{\mu }_j}^L\left(x\right),{\alpha }_{{\mu }_j}^M\left(x\right),{\alpha }_{{\mu }_j}^U\left(x\right)\right),\left({\beta }_{{\mu }_j}^L\left(x\right),{\beta }_{{\mu }_j}^M\left(x\right),{\beta }_{{\mu }_j}^U\left(x\right)\right),\left({\gamma }_{{\mu }_j}^L\left(x\right),{\gamma }_{{\mu }_j}^M\left(x\right),{\gamma }_{{\mu }_j}^U\left(x\right)\right)\right)$ be a TFNNs group in the real-numbers set, the aggregated value of TFNNWA operator is also a TFNN as the form as follows.

$$TFNNWA\left({\mu }_1,{\mu }_2,{\mu }_3,\dots ,{\mu }_n\right)=\begin{array}{c}n\\ \oplus \\ j=1\end{array}{w}_j{\mu }_j=\left(\begin{array}{c}\left(1-\prod _{j=1}^n\left(1-{\left({\alpha }_j^L\right)}^{w_j}\right), 1-\prod _{j=1}^n\left(1-{\left({\alpha }_j^M\right)}^{w_j}\right), 1-\prod _{j=1}^n\left(1-{\left({\alpha }_j^U\right)}^{w_j}\right) \right),\\ \left(\prod _{j=1}^n\left({\left({\beta }_j^L\right)}^{w_j}\right), \prod _{j=1}^n\left({\left({\beta }_j^M\right)}^{w_j}\right), \prod _{j=1}^n\left({\left({\beta }_j^U\right)}^{w_j}\right) \right),\\ \left(\prod _{j=1}^n\left({\left({\gamma }_j^L\right)}^{w_j}\right), \prod _{j=1}^n\left({\left({\gamma }_j^M\right)}^{w_j}\right), \prod _{j=1}^n\left({\left({\gamma }_j^U\right)}^{w_j}\right) \right)\end{array}\right)$$

(15)

Definition 5 ([28]).

Let ${\mu }_j= \left(\left({\alpha }_{{\mu }_j}^L\left(x\right),{\alpha }_{{\mu }_j}^M\left(x\right),{\alpha }_{{\mu }_j}^U\left(x\right)\right),\left({\beta }_{{\mu }_j}^L\left(x\right),{\beta }_{{\mu }_j}^M\left(x\right),{\beta }_{{\mu }_j}^U\left(x\right)\right),\left({\gamma }_{{\mu }_j}^L\left(x\right),{\gamma }_{{\mu }_j}^M\left(x\right),{\gamma }_{{\mu }_j}^U\left(x\right)\right)\right)$ be a TFNNs group and $W=\left\{w_j\right\}$ be a set of the weighted criteria for $j=1,2,3,\dots ,n$ in the group of real-numbers respectively, the operator of TFNNWG notated by $TFNNWG\left({\mu }_1,{\mu }_2,{\mu }_3,\dots ,{\mu }_n\right)$ is presented by:

$$TFNNWG\left({\mu }_1,{\mu }_2,{\mu }_3,\dots ,{\mu }_n\right)={\mu }_1{}^{w_1}\otimes {\mu }_2{}^{w_2}\otimes {\mu }_3{}^{w_3}\otimes \dots \otimes {\mu }_n{}^{w_n}=\begin{array}{c}n\\ \otimes \\ j=1\end{array}{\mu }_j{}^{w_j}$$

(16)

Theorem 2 ([28]).

Let ${\mu }_j= \left(\left({\alpha }_{{\mu }_j}^L\left(x\right),{\alpha }_{{\mu }_j}^M\left(x\right),{\alpha }_{{\mu }_j}^U\left(x\right)\right),\left({\beta }_{{\mu }_j}^L\left(x\right),{\beta }_{{\mu }_j}^M\left(x\right),{\beta }_{{\mu }_j}^U\left(x\right)\right),\left({\gamma }_{{\mu }_j}^L\left(x\right),{\gamma }_{{\mu }_j}^M\left(x\right),{\gamma }_{{\mu }_j}^U\left(x\right)\right)\right)$ be a TFNNs group in the real-numbers set, the aggregated value of TFNNWG operator is also a TFNN as the form as follows:

$$TFNNWG\left({\mu }_1,{\mu }_2,{\mu }_3,\dots ,{\mu }_n\right)=\begin{array}{c}n\\ \otimes \\ j=1\end{array}{\mu }_j{}^{w_j}=\left(\begin{array}{c}\left(\prod _{j=1}^n\left({\left({\alpha }_j^L\right)}^{w_j}\right), \prod _{j=1}^n\left({\left({\alpha }_j^M\right)}^{w_j}\right), \prod _{j=1}^n\left({\left({\alpha }_j^U\right)}^{w_j}\right) \right),\\ \left(1-\prod _{j=1}^n\left(1-{\left({\beta }_j^L\right)}^{w_j}\right), 1- \prod _{j=1}^n\left(1-{\left({\beta }_j^M\right)}^{w_j}\right), 1-\prod _{j=1}^n\left(1-{\left({\beta }_j^U\right)}^{w_j}\right) \right),\\ \left(1-\prod _{j=1}^n\left(1-{\left({\gamma }_j^L\right)}^{w_j}\right), 1-\prod _{j=1}^n\left(1-{\left({\gamma }_j^M\right)}^{w_j}\right), 1-\prod _{j=1}^n\left(1-{\left({\gamma }_j^U\right)}^{w_j}\right) \right)\end{array}\right)$$

(17)

2.2. The Distance of Normalized Hamming between Any Two TFNNs

In many practical and theoretical issues, once we have two fuzzy sets in the same finite universe of discourse, the way to measure a difference between them can be reflected by a distance. In this paper, we reconsider the normalized Hamming distance for the fuzzy sets in an TFN circumstance for MCGDM problem. The normalized Hamming distance of two TFNNs was initially identified by Wang et al. [43] by adopting the basic concept of Hamming distance for triangular intuitionistic fuzzy numbers (TIFN) [44].

Definition 6 ([43]).

Assume that there are two TFNNs: ${\mu }_1=\left(\left({\alpha }_{{\mu }_1}^L\left(x\right),{\alpha }_{{\mu }_1}^M\left(x\right),{\alpha }_{{\mu }_1}^U\left(x\right)\right),\left({\beta }_{{\mu }_1}^L\left(x\right),{\beta }_{{\mu }_1}^M\left(x\right),{\beta }_{{\mu }_1}^U\left(x\right)\right),\left({\gamma }_{{\mu }_1}^L\left(x\right),{\gamma }_{{\mu }_1}^M\left(x\right),{\gamma }_{{\mu }_1}^U\left(x\right)\right)\right)$ and ${\mu }_2= \left(\left({\alpha }_{{\mu }_2}^L\left(x\right),{\alpha }_{{\mu }_2}^M\left(x\right),{\alpha }_{{\mu }_2}^U\left(x\right)\right),\left({\beta }_{{\mu }_2}^L\left(x\right),{\beta }_{{\mu }_2}^M\left(x\right),{\beta }_{{\mu }_2}^U\left(x\right)\right),\left({\gamma }_{{\mu }_2}^L\left(x\right),{\gamma }_{{\mu }_2}^M\left(x\right),{\gamma }_{{\mu }_2}^U\left(x\right)\right)\right)$; the normalized Hamming distance $H({\mu }_1,{\mu }_2)$ between these two TFNNs can be depicted precisely by:

$$\begin{array}{ll}H({\mu }_1,{\mu }_2)=& \frac{1}{9}[\left|{\alpha }_{{\mu }_1}^L\left(x\right)-{\alpha }_{{\mu }_2}^L\left(x\right)\right|+\left|{\alpha }_{{\mu }_1}^M\left(x\right)-{\alpha }_{{\mu }_2}^M\left(x\right)\right|+\left|{\alpha }_{{\mu }_1}^U\left(x\right)-{\alpha }_{{\mu }_2}^U\left(x\right)\right|+\left|{\beta }_{{\mu }_1}^L\left(x\right)-{\beta }_{{\mu }_2}^L\left(x\right)\right|+\left|{\beta }_{{\mu }_1}^M\left(x\right)-{\beta }_{{\mu }_2}^M\left(x\right)\right|\\ & +\left|{\beta }_{{\mu }_1}^U\left(x\right)-{\beta }_{{\mu }_2}^U\left(x\right)\right|+\left|{\gamma }_{{\mu }_1}^L\left(x\right)-{\gamma }_{{\mu }_2}^L\left(x\right)\right|+\left|{\gamma }_{{\mu }_1}^M\left(x\right)-{\gamma }_{{\mu }_2}^M\left(x\right)\right|+\left|{\gamma }_{{\mu }_1}^U\left(x\right)-{\gamma }_{{\mu }_2}^U\left(x\right)\right|\\ & +\left|{\gamma }_{{\mu }_1}^U\left(x\right)-{\gamma }_{{\mu }_2}^U\left(x\right)\right|]\end{array}$$

(18)

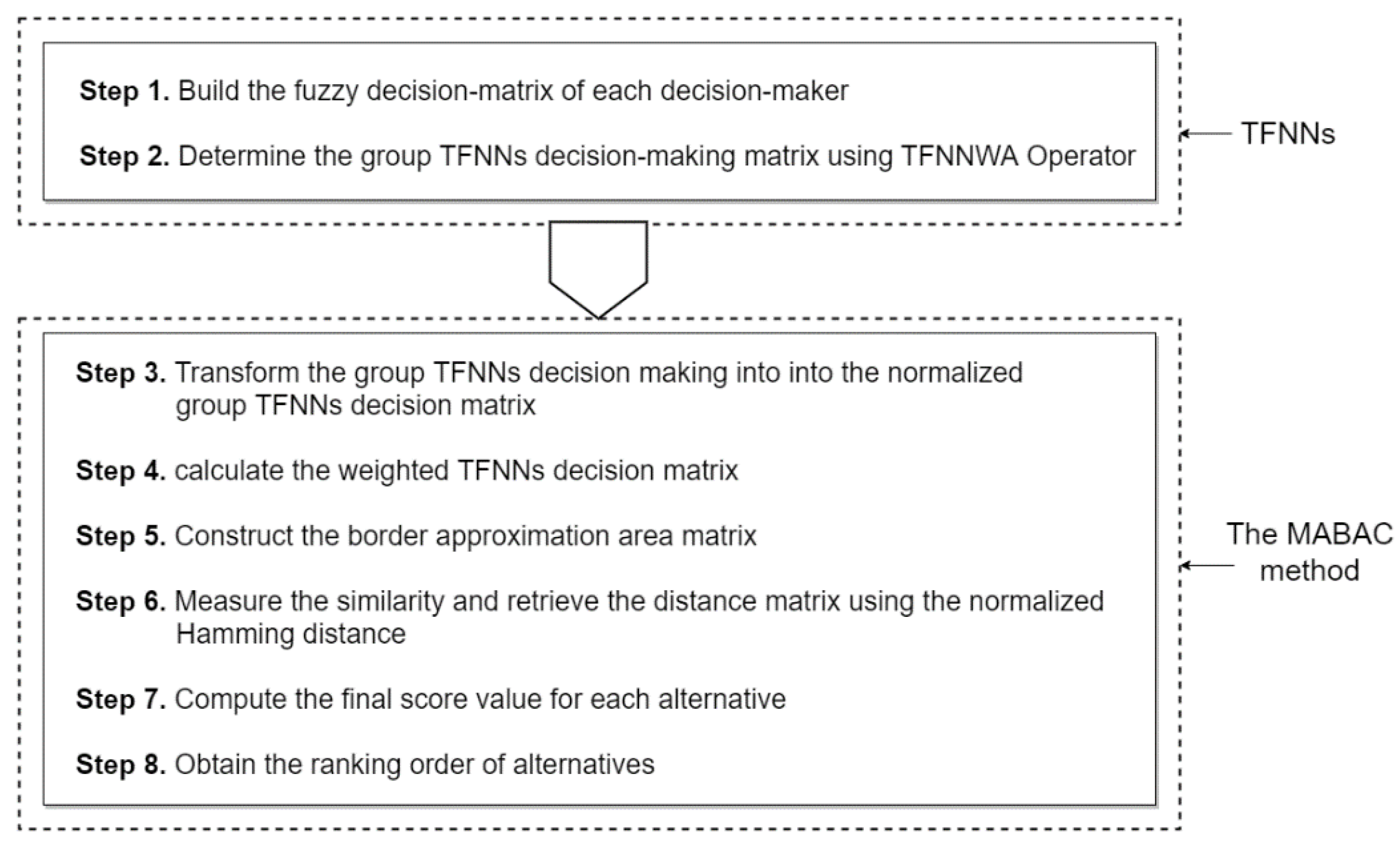
3. The Proposed MABAC Method for MCGDM Problems under TFNNs Environment

In recent MCGDM problems, the MABAC model has become one of the prospective decision-making approaches, due to its ability to consider conflicting attributes. It makes many scholars frequently innovate in venturing to utilize it in many fuzzy set circumstances. We also attempt to blend the MABAC model with the TFNNs environment by revealing the assessment values in the term of TFNNs. To be more specific, we provide the calculation procedures for our proposed MABAC method as follows and also show it in Figure 1.

Let $\left\{{{\rm E}}_1, {{\rm E}}_2, \dots , {{\rm E}}_m\right\}$ be a number of alternatives, $\left\{d_1, d_2, \dots , d_s\right\}$ be a group of decision makers with weighting-vector for each decision maker being $\left\{v_1, v_2, \dots , v_s\right\}$, and $\left\{c_1, c_2, \dots , c_n\right\}$ be a number of criteria with weighting-vector for each criterion being $\left\{w_1, w_2, \dots , w_n\right\}$, which thus satisfies $w_i\in \left[0,1\right]$, $v_k\in \left[0,1\right]$, ${\displaystyle \sum }_{j=1}^n{w}_j=1$, and ${\displaystyle \sum }_{k=1}^s{v}_k=1$.

 Step 1.

Build the fuzzy decision-matrix ${\mu }^{\left(k\right)}={\left[{\mu }_{ij}^k\right]}_{m x n}$ of each decision-maker, in which ${\mu }_{ij}^k=\left(\left({\left({\alpha }_{ij}^L\right)}^k,{\left({\alpha }_{ij}^M\right)}^k,{\left({\alpha }_{ij}^U\right)}^k \right), \left({\left({\beta }_{ij}^L\right)}^k,{\left({\beta }_{ij}^M\right)}^k,{\left({\beta }_{ij}^U\right)}^k \right), \left({\left({\gamma }_{ij}^L\right)}^k,{\left({\gamma }_{ij}^M\right)}^k,{\left({\gamma }_{ij}^U\right)}^k \right) \right)$, and assume that $\left({\left({\alpha }_{ij}^L\right)}^k,{\left({\alpha }_{ij}^M\right)}^k,{\left({\alpha }_{ij}^U\right)}^k \right)\in \left[0,1\right]$ is the TMD, $\left({\left({\beta }_{ij}^L\right)}^k,{\left({\beta }_{ij}^M\right)}^k,{\left({\beta }_{ij}^U\right)}^k \right)\in \left[0,1\right]$ is the IMD, $\left({\left({\gamma }_{ij}^L\right)}^k,{\left({\gamma }_{ij}^M\right)}^k,{\left({\gamma }_{ij}^U\right)}^k \right)\in \left[0,1\right]$ is the FMD, and $0 \le {\left({\alpha }_{ij}^U\right)}^k+{\left({\beta }_{ij}^U\right)}^k+{\left({\gamma }_{ij}^U\right)}^k \le 3$ where $i=1, 2, 3, \dots , m$, $j=1, 2, 3, \dots ,n$, and $k=1, 2, 3, \dots , s$.

 Step 2.

Determine the group TFNNs decision-making matrix $F= {\left[\left(\left({\alpha }_{f_{ij}}^L,{\alpha }_{f_{ij}}^M,{\alpha }_{f_{ij}}^U\right),\left({\beta }_{f_{ij}}^L,{\beta }_{f_{ij}}^M,{\beta }_{f_{ij}}^U\right),\left({\gamma }_{f_{ij}}^L,{\gamma }_{f_{ij}}^M,{\gamma }_{f_{ij}}^U\right)\right)\right]}_{ m x n}$ in which $F= {\left[f_{ij}\right]}_{m x n}$ where for TFNNWA Operator

$$f_{ij}=\left(\begin{array}{c}\left(1-\prod _{k=1}^s{\left(1-{\left({\alpha }_{ij}^L\right)}^k\right)}^{v_k}, 1-\prod _{k=1}^s{\left(1-{\left({\alpha }_{ij}^M\right)}^k\right)}^{v_k}, 1-\prod _{k=1}^s{\left(1-{\left({\alpha }_{ij}^U\right)}^k\right)}^{v_k} \right),\\ \left(\prod _{k=1}^s{\left({\left({\beta }_{ij}^L\right)}^k\right)}^{v_k}, \prod _{k=1}^s{\left({\left({\beta }_{ij}^M\right)}^k\right)}^{v_k}, \prod _{k=1}^s{\left({\left({\beta }_{ij}^U\right)}^k\right)}^{v_k} \right),\\ \left(\prod _{k=1}^s{\left({\left({\gamma }_{ij}^L\right)}^k\right)}^{v_k}, \prod _{k=1}^s{\left({\left({\gamma }_{ij}^M\right)}^k\right)}^{v_k}, \prod _{k=1}^s{\left({\left({\gamma }_{ij}^U\right)}^k\right)}^{v_k} \right)\end{array}\right)$$

(19)

or for TFNNWG Operator

$$f_{ij}=\left(\begin{array}{c}\left(\prod _{k=1}^s{\left({\left({\alpha }_{ij}^L\right)}^k\right)}^{v_k}, \prod _{k=1}^s{\left({\left({\alpha }_{ij}^M\right)}^k\right)}^{v_k}, \prod _{k=1}^s{\left({\left({\alpha }_{ij}^U\right)}^k\right)}^{v_k} \right),\\ \left(1-\prod _{k=1}^s{\left(1-{\left({\beta }_{ij}^L\right)}^k\right)}^{v_k}, 1- \prod _{k=1}^s{\left(1-{\left({\beta }_{ij}^M\right)}^k\right)}^{v_k}, 1-\prod _{k=1}^s{\left(1-{\left({\beta }_{ij}^U\right)}^k\right)}^{v_k} \right),\\ \left(1-\prod _{k=1}^s{\left(1-{\left({\gamma }_{ij}^L\right)}^k\right)}^{v_k}, 1-\prod _{k=1}^s{\left(1-{\left({\gamma }_{ij}^M\right)}^k\right)}^{v_k}, 1-\prod _{k=1}^s{\left(1-{\left({\gamma }_{ij}^U\right)}^k\right)}^{v_k} \right)\end{array}\right)$$

(20)

 Step 3.

Transform the group TFNNs decision making $F= {\left[f_{ij}\right]}_{m x n}$ into the normalized group TFNNs decision matrix $N= {\left[\left(\left({\alpha }_{n_{ij}}^L,{\alpha }_{n_{ij}}^M,{\alpha }_{n_{ij}}^U\right),\left({\beta }_{n_{ij}}^L,{\beta }_{n_{ij}}^M,{\beta }_{n_{ij}}^U\right),\left({\gamma }_{n_{ij}}^L,{\gamma }_{n_{ij}}^M,{\gamma }_{n_{ij}}^U\right)\right)\right]}_{ m x n}$ in which $N= {\left[n_{ij}\right]}_{m x n}$ where n_ij can be reached by using Equation (22) or (23). We then calculate the minimum and the maximum values of TFNNs for each criterion $C_j \left(j=1,2,3, \dots , n\right)$.

$$\begin{gathered} {\alpha }_{f_{ij}}^{L-}=\underset{1 \le i \le m}{\min }\left\{{\alpha }_{f_{ij}}^L\right\},{\beta }_{f_{ij}}^{L-}=\underset{1 \le i \le m}{\min }\left\{{\beta }_{f_{ij}}^L\right\}, {\gamma }_{f_{ij}}^{L-}=\underset{1 \le i \le m}{\min }\left\{{\gamma }_{f_{ij}}^L\right\}, {\alpha }_{f_{ij}}^{U+}=\underset{1 \le i \le m}{\max }\left\{{\alpha }_{f_{ij}}^U\right\}, \\ {\beta }_{f_{ij}}^{U+}=\underset{1 \le i \le m}{\max }\left\{{\beta }_{f_{ij}}^U\right\},\mathrm{and} {\gamma }_{f_{ij}}^{U+}=\underset{1 \le i \le m}{\max }\left\{{\gamma }_{f_{ij}}^U\right\}. \end{gathered}$$

(21)

If $C_j$ is a benefit criterion, each element of the matrix $F$ can be normalized as follows.

$$n_{ij}=\left(\begin{array}{c}\left(\frac{{\alpha }_{f_{ij}}^L- {\alpha }_{f_{ij}}^{L-}}{{\alpha }_{f_{ij}}^{U+}- {\alpha }_{f_{ij}}^{L-}}, \frac{{\alpha }_{f_{ij}}^M- {\alpha }_{f_{ij}}^{L-}}{{\alpha }_{f_{ij}}^{U+}- {\alpha }_{f_{ij}}^{L-}}, \frac{{\alpha }_{f_{ij}}^U- {\alpha }_{f_{ij}}^{L-}}{{\alpha }_{f_{ij}}^{U+}- {\alpha }_{f_{ij}}^{L-}}\right)\left(\frac{{\beta }_{f_{ij}}^{U+}- {\beta }_{f_{ij}}^U}{{\beta }_{f_{ij}}^{U+}- {\beta }_{f_{ij}}^{L-}}, \frac{{\beta }_{f_{ij}}^{U+}- {\beta }_{f_{ij}}^M}{{\beta }_{f_{ij}}^{U+}- {\beta }_{f_{ij}}^{L-}}, \frac{{\beta }_{f_{ij}}^{U+}- {\beta }_{f_{ij}}^L}{{\beta }_{f_{ij}}^{U+}- {\beta }_{f_{ij}}^{L-}} \right),\\ \left(\frac{{\gamma }_{f_{ij}}^L- {\gamma }_{f_{ij}}^{L-}}{{\gamma }_{f_{ij}}^{U+}- {\gamma }_{f_{ij}}^{L-}}, \frac{{\gamma }_{f_{ij}}^M- {\gamma }_{f_{ij}}^{L-}}{{\gamma }_{f_{ij}}^{U+}- {\gamma }_{f_{ij}}^{L-}}, \frac{{\gamma }_{f_{ij}}^U- {\gamma }_{f_{ij}}^{L-}}{{\gamma }_{f_{ij}}^{U+}- {\gamma }_{f_{ij}}^{L-}}\right)\end{array}\right)$$

(22)

If $C_j$ is a cost criterion, each element of the matrix $F$ can be normalized as follows.

$$n_{ij}=\left(\begin{array}{c}\left(\frac{{\alpha }_{f_{ij}}^{U+}- {\alpha }_{f_{ij}}^U}{{\alpha }_{f_{ij}}^{U+}- {\alpha }_{f_{ij}}^{L-}}, \frac{{\alpha }_{f_{ij}}^{U+}- {\alpha }_{f_{ij}}^M}{{\alpha }_{f_{ij}}^{U+}- {\alpha }_{f_{ij}}^{L-}}, \frac{{\alpha }_{f_{ij}}^{U+}- {\alpha }_{f_{ij}}^L}{{\alpha }_{f_{ij}}^{U+}- {\alpha }_{f_{ij}}^{L-}}\right), \left(\frac{{\beta }_{f_{ij}}^{U+}- {\beta }_{f_{ij}}^U}{{\beta }_{f_{ij}}^{U+}- {\beta }_{f_{ij}}^{L-}}, \frac{{\beta }_{f_{ij}}^{U+}- {\beta }_{f_{ij}}^M}{{\beta }_{f_{ij}}^{U+}- {\beta }_{f_{ij}}^{L-}}, \frac{{\beta }_{f_{ij}}^{U+}- {\beta }_{f_{ij}}^L}{{\beta }_{f_{ij}}^{U+}- {\beta }_{f_{ij}}^{L-}} \right),\\ \left(\frac{{\gamma }_{f_{ij}}^{U+}- {\gamma }_{f_{ij}}^U}{{\gamma }_{f_{ij}}^{U+}- {\gamma }_{f_{ij}}^{L-}}, \frac{{\gamma }_{f_{ij}}^{U+}- {\gamma }_{f_{ij}}^M}{{\gamma }_{f_{ij}}^{U+}- {\gamma }_{f_{ij}}^{L-}}, \frac{{\gamma }_{f_{ij}}^{U+}- {\gamma }_{f_{ij}}^L}{{\gamma }_{f_{ij}}^{U+}- {\gamma }_{f_{ij}}^{L-}}\right)\end{array}\right)$$

(23)

 Step 4.

Utilize Equation (24) to calculate the weighted matrix $P= {\left[\left(\left({\alpha }_{p_{ij}}^L,{\alpha }_{p_{ij}}^M,{\alpha }_{p_{ij}}^U\right),\left({\beta }_{p_{ij}}^L,{\beta }_{p_{ij}}^M,{\beta }_{p_{ij}}^U\right),\left({\gamma }_{p_{ij}}^L,{\gamma }_{p_{ij}}^M,{\gamma }_{p_{ij}}^U\right)\right)\right]}_{ m x n}$ in which $P= {\left[p_{ij}\right]}_{m x n}$ and ${\displaystyle \sum }_{j=1}^n{w}_j=1$.

$$p_{ij}=w_j\ast n_{ij}=\left(\begin{array}{c}\left(1-{\left(1-{\alpha }_{n_{ij}}^L\right)}^{w_j}, 1-{\left(1-{\alpha }_{n_{ij}}^M\right)}^{w_j}, 1-{\left(1-{\alpha }_{n_{ij}}^U\right)}^{w_j} \right),\\ \left({\left({\beta }_{n_{ij}}^L\right)}^{w_j}, {\left({\beta }_{n_{ij}}^M\right)}^{w_j}, {\left({\beta }_{n_{ij}}^U\right)}^{w_j} \right),\\ \left({\left({\gamma }_{n_{ij}}^L\right)}^{w_j}, {\left({\gamma }_{n_{ij}}^M\right)}^{w_j}, {\left({\gamma }_{n_{ij}}^U\right)}^{w_j} \right)\end{array}\right)$$

(24)

 Step 5.

Based on Equation (25), the border-approximation-area (BAA) matrix $Q= {\left[\left(\left({\alpha }_{q_j}^L,{\alpha }_{q_j}^M,{\alpha }_{q_j}^U\right),\left({\beta }_{q_j}^L,{\beta }_{q_{ij}}^M,{\beta }_{q_{ij}}^U\right),\left({\gamma }_{q_j}^L,{\gamma }_{q_j}^M,{\gamma }_{q_j}^U\right)\right)\right]}_{ 1 x n}$ in which $Q= {\left[q_j\right]}_{1 x n}$ can be constructed and $q_j$ stands for the BAA for criterion $j$.

$$q_j=\left(\begin{array}{c}\left(\prod _{i=1}^m\left({\left({\alpha }_{p_{ij}}^L\right)}^{1/m}\right), \prod _{i=1}^m\left({\left({\alpha }_{p_{ij}}^M\right)}^{1/m}\right), \prod _{i=1}^m\left({\left({\alpha }_{p_{ij}}^U\right)}^{1/m}\right) \right),\\ \left(1-\prod _{i=1}^m\left(1-{\left({\beta }_{p_{ij}}^L\right)}^{1/m}\right), 1- \prod _{i=1}^m\left(1-{\left({\beta }_{p_{ij}}^M\right)}^{1/m}\right), 1-\prod _{i=1}^m\left(1-{\left({\beta }_{p_{ij}}^U\right)}^{1/m}\right)\right),\\ \left(1-\prod _{i=1}^m\left(1-{\left({\gamma }_{p_{ij}}^L\right)}^{1/m}\right), 1- \prod _{i=1}^m\left(1-{\left({\gamma }_{p_{ij}}^M\right)}^{1/m}\right), 1-\prod _{i=1}^m\left(1-{\left({\gamma }_{p_{ij}}^U\right)}^{1/m}\right)\right)\end{array}\right)$$

(25)

 Step 6.

Based on Equation (13) and Definition 6, calculate the distance matrix $D= {\left[d_{ij}\right]}_{m x n}$. The element $d_{ij}$ is called the alternatives’ distance from BAA and is depicted by using Equation (26).

$$d_{ij}=\{\begin{array}{cc}\hfill H\left(p_{ij}, q_j\right),& if p_{ij}>q_j\hfill \\ \hfill 0,& \hfill if p_{ij}=q_j\\ -H\left(p_{ij}, q_j\right),& \hfill if p_{ij}<q_j\end{array}$$

(26)

where $H\left(p_{ij}, q_j\right)$ is the normalized Hamming distance between the alternative $p_{ij}$ and the BAA $q_j$.

According to the traditional MABAC’s principle, we can see that if $d_{ij}=0$, the alternative ${{\rm E}}_i$ will be a part of the border approximation area $\left(G\right)$; if $d_{ij}>0$ ($d_{ij}$ has a positive value), the alternative ${{\rm E}}_i$ will be a part of the upper approximation area $\left(G^{+}\right)$; and if $d_{ij}<0$ ($d_{ij}$ has a negative value), the alternative ${{\rm E}}_i$ will be a part of the lower approximation area (G⁻).

Since the ideal alternative ${{\rm E}}_i^{+}$ and the non-ideal alternative ${{\rm E}}_i^{-}$ are spread across the upper approximation border $\left(G^{+}\right)$ and the lower approximation border $\left(G^{-}\right)$, respectively, in order to decide the best alternative, we should have as many the criterion of the alternative as possible located on the upper approximation border $\left(G^{+}\right)$.

 Step 7.

Compute the final score value $V\left({{\rm E}}_i\right)$ by using Equation (27).

$$V\left({{\rm E}}_i\right)= \begin{array}{cc}{\displaystyle {\displaystyle \sum }_{j=1}^n}{d}_{ij},& \left(i=1,2,3,\dots ,m\right)\end{array}.$$

(27)

 Step 8.

Based on the value of $V\left({{\rm E}}_i\right)$, rank all the alternatives in descending order. In MCGDM problems for a selection case study, the alternative ${{\rm E}}_i$ will be the best alterative when the final score value $V\left({{\rm E}}_i\right)$ has the highest value.

4. Numerical Example and Discussion

This section separated into two subsections. Firstly, we present calculating steps of the proposed TFNNs-MABAC model for MCGDM, in this case, we illustrate an invest selection problem. Secondly, we compare our proposed TFNNs-MABAC method with TFNNWA Operator, TFNNWG Operator, and VIKOR method.

4.1. Calculating Steps of the Proposed TFNNs-MABAC Method for MCGDM Problems

This sub-section demonstrates an illustrative example for evaluating an invest selection problem under the TFNNs environment to show the proposed MABAC method. Suppose that a growth investor wants to provide a sum of money to invest in one of the five technology enterprise candidates ${{\rm E}}_i\left(i=1,2,\dots ,5\right)$. The investor has assigned three decision-makers $d_k\left(k=1,2,3\right)$ to evaluate these five technology enterprises. Each technology enterprise will be assessed based on four prerequisite criteria $C_j\left(j=1,2,3,4\right)$, which are the market-growth analysis ($C_1$), the market-risk analysis ($C_2$), the employee’s analysis ($C_3$), and the environmental impact analysis ($C_4$), where $C_1$, $C_2$, and $C_3$ are benefit criteria, and $C_4$ is a cost criterion. The weighting-vector for each criterion $w_j=\left\{w_1,w_2,w_3,w_4\right\}$ has been given as $w=\left\{0.41, 0.14, 0.25, 0.20\right\}$ and the weighting-vector for each decision-maker $v_k=\left\{v_1,v_2,v_3\right\}$ has been determined as $v=\left\{0.35, 0.40, 0.25\right\}$. Based on the decision-makers’ experience and knowledge, the evaluation process will be conducted in the form of TFNNs.

In order to determine the best technology enterprise, we present the proposed calculation procedure step by step as follows.

 Step 1.

Build the fuzzy decision-matrix ${\mu }^{\left(k\right)}={\left[{\mu }_{ij}^k\right]}_{m x n}$ based on the evaluation of the decision makers $d_k$ for each alternative ${{\rm E}}_i$ into each criterion $C_j$ that can be illustrated in

Table 1. TFNNs judgement matrix by the decision maker $d_1$.

	C1	C2	C3	C4
Ε1	$\left(\begin{array}{c}\left(0.5, 0.7, 0.9\right),\\ \left(0.1, 0.2, 0.4\right),\\ \left(0.1, 0.2, 0.3\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.2, 0.4, 0.6\right),\\ \left(0.3, 0.4, 0.5\right),\\ \left(0.1, 0.3, 0.4\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.4, 0.5, 0.6\right),\\ \left(0.1, 0.2, 0.3\right),\\ \left(0.1, 0.2, 0.3\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.3, 0.6, 0.9\right),\\ \left(0.4, 0.5, 0.7\right),\\ \left(0.1, 0.3, 0.5\right)\end{array}\right)$
Ε2	$\left(\begin{array}{c}\left(0.4, 0.5, 0.6\right),\\ \left(0.3, 0.4, 0.5\right),\\ \left(0.2, 0.3, 0.4\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.1, 0.3, 0.5\right),\\ \left(0.2, 0.4, 0.6\right),\\ \left(0.1, 0.2, 0.4\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.4, 0.5, 0.9\right),\\ \left(0.5, 0.6, 0.7\right),\\ \left(0.4, 0.5, 0.6\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.3, 0.4, 0.6\right),\\ \left(0.2, 0.3, 0.5\right),\\ \left(0.4, 0.5, 0.7\right)\end{array}\right)$
Ε3	$\left(\begin{array}{c}\left(0.2, 0.4, 0.5\right),\\ \left(0.1, 0.3, 0.4\right),\\ \left(0.4, 0.5, 0.7\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.1, 0.2, 0.3\right),\\ \left(0.3, 0.4, 0.5\right),\\ \left(0.5, 0.6, 0.7\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.6, 0.7, 0.9\right),\\ \left(0.2, 0.4, 0.5\right),\\ \left(0.1, 0.3, 0.4\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.3, 0.4, 0.7\right),\\ \left(0.4, 0.6, 0.9\right),\\ \left(0.1, 0.2, 0.3\right)\end{array}\right)$
Ε4	$\left(\begin{array}{c}\left(0.1, 0.4, 0.6\right),\\ \left(0.2, 0.5, 0.7\right),\\ \left(0.1, 0.2, 0.3\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.4, 0.6, 0.7\right),\\ \left(0.2, 0.3, 0.4\right),\\ \left(0.1, 0.4, 0.6\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.3, 0.5, 0.7\right),\\ \left(0.2, 0.3, 0.4\right),\\ \left(0.1, 0.2, 0.5\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.4, 0.6, 0.9\right),\\ \left(0.3, 0.5, 0.7\right),\\ \left(0.1, 0.2, 0.4\right)\end{array}\right)$
Ε 5	$\left(\begin{array}{c}\left(0.6, 0.7, 0.9\right),\\ \left(0.1, 0.2, 0.3\right),\\ \left(0.1, 0.2, 0.3\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.4, 0.6, 0.7\right),\\ \left(0.3, 0.4, 0.7\right),\\ \left(0.1, 0.3, 0.4\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.4, 0.5, 0.6\right),\\ \left(0.1, 0.3, 0.4\right),\\ \left(0.1, 0.3, 0.5\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.2, 0.3, 0.9\right),\\ \left(0.1, 0.3, 0.4\right),\\ \left(0.1, 0.4, 0.5\right)\end{array}\right)$

,

Table 2. TFNNs judgement matrix by the decision maker $d_2$.

	C1	C2	C3	C4
Ε1	$\left(\begin{array}{c}\left(0.4, 0.6, 0.7\right),\\ \left(0.1, 0.2, 0.3\right),\\ \left(0.1, 0.2, 0.3\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.1, 0.3, 0.5\right),\\ \left(0.2, 0.3, 0.4\right),\\ \left(0.1, 0.2, 0.3\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.3, 0.4, 0.5\right),\\ \left(0.1, 0.3, 0.4\right),\\ \left(0.2, 0.4, 0.6\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.2, 0.4, 0.7\right),\\ \left(0.3, 0.4, 0.6\right),\\ \left(0.2, 0.3, 0.4\right)\end{array}\right)$
Ε2	$\left(\begin{array}{c}\left(0.3, 0.4, 0.6\right),\\ \left(0.2, 0.5, 0.7\right),\\ \left(0.3, 0.5, 0.6\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.2, 0.3, 0.4\right),\\ \left(0.1, 0.3, 0.5\right),\\ \left(0.2, 0.3, 0.4\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.3, 0.4, 0.6\right),\\ \left(0.4, 0.5, 0.9\right),\\ \left(0.2, 0.3, 0.5\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.1, 0.3, 0.5\right),\\ \left(0.1, 0.2, 0.3\right),\\ \left(0.1, 0.2, 0.4\right)\end{array}\right)$
Ε3	$\left(\begin{array}{c}\left(0.3, 0.6, 0.9\right),\\ \left(0.2, 0.4, 0.7\right),\\ \left(0.5, 0.7, 0.9\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.1, 0.2, 0.4\right),\\ \left(0.1, 0.3, 0.6\right),\\ \left(0.4, 0.7, 0.9\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.1, 0.3, 0.4\right),\\ \left(0.2, 0.4, 0.6\right),\\ \left(0.1, 0.3, 0.5\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.3, 0.4, 0.6\right),\\ \left(0.4, 0.7, 0.9\right),\\ \left(0.1, 0.2, 0.5\right)\end{array}\right)$
Ε4	$\left(\begin{array}{c}\left(0.2, 0.3, 0.6\right),\\ \left(0.2, 0.6, 0.9\right),\\ \left(0.1, 0.3, 0.4\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.1, 0.7, 0.9\right),\\ \left(0.3, 0.4, 0.5\right),\\ \left(0.3, 0.4, 0.6\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.4, 0.6, 0.9\right),\\ \left(0.2, 0.3, 0.4\right),\\ \left(0.1, 0.2, 0.3\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.3, 0.4, 0.5\right),\\ \left(0.1, 0.2, 0.3\right),\\ \left(0.1, 0.2, 0.3\right)\end{array}\right)$
Ε5	$\left(\begin{array}{c}\left(0.4, 0.5, 0.6\right),\\ \left(0.1, 0.3, 0.4\right),\\ \left(0.1, 0.2, 0.5\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.5, 0.6, 0.9\right),\\ \left(0.3, 0.4, 0.6\right),\\ \left(0.2, 0.3, 0.4\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.4, 0.5, 0.7\right),\\ \left(0.2, 0.3, 0.4\right),\\ \left(0.3, 0.4, 0.5\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.2, 0.3, 0.6\right),\\ \left(0.1, 0.3, 0.4\right),\\ \left(0.1, 0.2, 0.5\right)\end{array}\right)$

and

Table 3. TFNNs judgement matrix by the decision maker $d_3$.

	C1	C2	C3	C4
Ε1	$\left(\begin{array}{c}\left(0.4, 0.5, 0.7\right),\\ \left(0.1, 0.2, 0.5\right),\\ \left(0.1, 0.2, 0.3\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.2, 0.3, 0.5\right),\\ \left(0.3, 0.4, 0.6\right),\\ \left(0.1, 0.2, 0.3\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.3, 0.4, 0.7\right),\\ \left(0.2, 0.3, 0.4\right),\\ \left(0.2, 0.5, 0.7\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.3, 0.5, 0.7\right),\\ \left(0.3, 0.5, 0.6\right),\\ \left(0.2, 0.3, 0.4\right)\end{array}\right)$
Ε2	$\left(\begin{array}{c}\left(0.3, 0.4, 0.5\right),\\ \left(0.4, 0.5, 0.6\right),\\ \left(0.4, 0.5, 0.6\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.2, 0.3, 0.5\right),\\ \left(0.1, 0.3, 0.4\right),\\ \left(0.2, 0.3, 0.4\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.2, 0.4, 0.6\right),\\ \left(0.1, 0.5, 0.9\right),\\ \left(0.2, 0.3, 0.6\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.2, 0.3, 0.5\right),\\ \left(0.1, 0.2, 0.4\right),\\ \left(0.1, 0.2, 0.4\right)\end{array}\right)$
Ε3	$\left(\begin{array}{c}\left(0.4, 0.6, 0.7\right),\\ \left(0.3, 0.4, 0.6\right),\\ \left(0.6, 0.7, 0.9\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.1, 0.2, 0.4\right),\\ \left(0.1, 0.3, 0.4\right),\\ \left(0.4, 0.6, 0.9\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.2, 0.3, 0.4\right),\\ \left(0.2, 0.3, 0.5\right),\\ \left(0.1, 0.3, 0.4\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.2, 0.4, 0.6\right),\\ \left(0.4, 0.6, 0.9\right),\\ \left(0.1, 0.2, 0.3\right)\end{array}\right)$
Ε4	$\left(\begin{array}{c}\left(0.2, 0.3, 0.4\right),\\ \left(0.2, 0.7, 0.9\right),\\ \left(0.1, 0.3, 0.4\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.1, 0.4, 0.7\right),\\ \left(0.3, 0.4, 0.9\right),\\ \left(0.3, 0.5, 0.6\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.4, 0.5, 0.9\right),\\ \left(0.2, 0.3, 0.5\right),\\ \left(0.1, 0.2, 0.4\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.2, 0.4, 0.6\right),\\ \left(0.1, 0.2, 0.4\right),\\ \left(0.1, 0.2, 0.3\right)\end{array}\right)$
Ε5	$\left(\begin{array}{c}\left(0.4, 0.5, 0.7\right),\\ \left(0.1, 0.3, 0.5\right),\\ \left(0.1, 0.2, 0.4\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.5, 0.6, 0.7\right),\\ \left(0.3, 0.4, 0.5\right),\\ \left(0.2, 0.3, 0.4\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.4, 0.5, 0.6\right),\\ \left(0.2, 0.3, 0.5\right),\\ \left(0.3, 0.4, 0.6\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.2, 0.3, 0.4\right),\\ \left(0.1, 0.3, 0.4\right),\\ \left(0.1, 0.2, 0.3\right)\end{array}\right)$

.

 Step 2.

Utilize Equation (19) to determine the group TFNNs decision-making matrix $F= {\left[f_{ij}\right]}_{m x n}$ using TFNNWA Operator and the results are presented in

Table 4. The group TFNNs decision matrix $F$ by TFNNWA Operator.

	C1	C2	C3	C4
Ε1	$\left(\begin{array}{c}\left(0.437, 0.6175, 0.7957\right),\\ \left(0.1, 0.2, 0.3769\right),\\ \left(0.1, 0.2, 0.3\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.161, 0.3367, 0.5375\right),\\ \left(0.255, 0.3565, 0.4786\right),\\ \left(0.1, 0.2304, 0.3317\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.3367, 0.437, 0.593\right),\\ \left(0.1189, 0.260, 0.3616\right),\\ \left(0.1569, 0.3318, 0.4892\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.262, 0.5025, 0.7957\right),\\ \left(0.3317, 0.4573, 0.633\right),\\ \left(0.1569, 0.3, 0.4324\right)\end{array}\right)$
Ε2	$\left(\begin{array}{c}\left(0.3367, 0.437, 0.577\right),\\ \left(0.274, 0.4624, 0.5987\right),\\ \left(0.2797, 0.4181, 0.5206\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.1663, 0.3, 0.4621\right),\\ \left(0.1274, 0.3317, 0.504\right),\\ \left(0.1569, 0.2603, 0.4\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.3142, 0.437, 0.7537\right),\\ \left(0.3058, 0.5329, 0.824\right),\\ \left(0.2549, 0.3587, 0.5578\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.1996, 0.337, 0.5375\right),\\ \left(0.1274, 0.230, 0.3854\right),\\ \left(0.162, 0.2756, 0.4865\right)\end{array}\right)$
Ε3	$\left(\begin{array}{c}\left(0.2942, 0.539, 0.7688\right),\\ \left(0.1736, 0.362, 0.5537\right),\\ \left(0.484, 0.6222, 0.8242\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.1, 0.2, 0.3667\right),\\ \left(0.1468, 0.3317, 0.509\right),\\ \left(0.4324, 0.6381, 0.8242\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.342, 0.4796, 0.6795\right),\\ \left(0.2, 0.3722, 0.5378\right),\\ \left(0.1, 0.3, 0.4373\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.2762, 0.4, 0.6383\right),\\ \left(0.4, 0.6381, 0.9\right),\\ \left(0.1, 0.2, 0.368\right)\end{array}\right)$
Ε4	$\left(\begin{array}{c}\left(0.166, 0.3367, 0.5573\right),\\ \left(0.2, 0.585, 0.8242\right),\\ \left(0.1, 0.2603, 0.3616\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.219, 0.6054, 0.8066\right),\\ \left(0.260, 0.3616, 0.5356\right),\\ \left(0.2042, 0.4229, 0.6\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.3667, 0.5426, 0.8531\right),\\ \left(0.2, 0.3, 0.4229\right),\\ \left(0.1, 0.2, 0.3854\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.314, 0.4793, 0.7307\right),\\ \left(0.1468, 0.276, 0.4336\right),\\ \left(0.1, 0.2, 0.3317\right)\end{array}\right)$
Ε5	$\left(\begin{array}{c}\left(0.479, 0.5818, 0.7708\right),\\ \left(0.1, 0.2603, 0.3824\right),\\ \left(0.1, 0.2, 0.3954\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.467, 0.6, 0.8066\right),\\ \left(0.3, 0.4, 0.605\right),\\ \left(0.1569, 0.3, 0.4\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.4, 0.5, 0.6434\right),\\ \left(0.1569, 0.3, 0.4229\right),\\ \left(0.2042, 0.3616, 0.5233\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.2, 0.3, 0.7275\right),\\ \left(0.1, 0.3, 0.4\right),\\ \left(0.1, 0.2549, 0.44\right)\end{array}\right)$

.

 Step 3.

Use Equation (22) or (23) to transform the group TFNNs decision making $F= {\left[f_{ij}\right]}_{m x n}$ into the normalized group TFNNs decision matrix $N={\left[n_{ij}\right]}_{ m x n}$ and the results are shown in

Table 5. The normalized TFNNs decision matrix $N$.

	C1	C2	C3	C4
Ε1	$\left(\begin{array}{c}\left(0.4301, 0.7168, 1\right),\\ \left(0, 0.138, 0.3824\right),\\ \left(0, 0.138, 0.2761\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.0868, 0.335, 0.6191\right),\\ \left(0.267, 0.4796, 0.7353\right),\\ \left(0, 0.1801, 0.32\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.0417, 0.2279, 0.517\right),\\ \left(0, 0.2004, 0.3442\right),\\ \left(0.1243, 0.5064, 0.8502\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0, 0.4918, 0.8961\right),\\ \left(0.3334, 0.5533, 0.710\right),\\ \left(0.1398, 0.4825, 0.8527\right)\end{array}\right)$
Ε2	$\left(\begin{array}{c}\left(0.2707, 0.430, 0.6525\right),\\ \left(0.240, 0.5004, 0.6886\right),\\ \left(0.2481, 0.4392, 0.5807\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.0938, 0.283, 0.5124\right),\\ \left(0, 0.4278, 0.7884\right),\\ \left(0.0785, 0.2213, 0.4142\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0, 0.2779, 0.8156\right),\\ \left(0.2649, 0.587, 1\right),\\ \left(0.3393, 0.5651, 1\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.4331, 0.77, 1\right),\\ \left(0.643, 0.8368, 0.9656\right),\\ \left(0, 0.5456, 0.8384\right)\end{array}\right)$
Ε3	$\left(\begin{array}{c}\left(0.2032, 0.592, 0.9572\right),\\ \left(0.1017, 0.361, 0.6265\right),\\ \left(0.5302, 0.721, 1\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0, 0.1415, 0.3774\right),\\ \left(0.0406, 0.4278, 0.798\right),\\ \left(0.5491, 0.743, 1\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.052, 0.3069, 0.6778\right),\\ \left(0.1149, 0.359, 0.5939\right),\\ \left(0, 0.4368, 0.7368\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.264, 0.6639, 0.8715\right),\\ \left(0, 0.3272, 0.625\right),\\ \left(0.3066, 0.7412, 1\right)\end{array}\right)$
Ε4	$\left(\begin{array}{c}\left(0, 0.2707, 0.6211\right),\\ \left(0.138, 0.6697, 1\right),\\ \left(0, 0.2213, 0.3613\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.1684, 0.7152, 1\right),\\ \left(0.278, 0.4904, 0.8546\right),\\ \left(0.1439, 0.4459, 0.6904\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.974, 0.4239, 1\right),\\ \left(0.1149, 0.2567, 0.431\right),\\ \left(0, 0.2184, 0.6235\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.109, 0.531, 0.8078\right),\\ \left(0.5829, 0.7804, 0.941\right),\\ \left(0.4003, 0.7412, 1\right)\end{array}\right)$
Ε5	$\left(\begin{array}{c}\left(0.497, 0.6601, 0.9604\right),\\ \left(0, 0.2213, 0.3899\right),\\ \left(0, 0.138, 0.4079\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.5194, 0.7075, 1\right),\\ \left(0.3612, 0.5706, 1\right),\\ \left(0.0785, 0.2761, 0.4142\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.159, 0.3447, 0.6109\right),\\ \left(0.0538, 0.2567, 0.431\right),\\ \left(0.2276, 0.5716, 0.9246\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.1145, 0.832, 0.9994\right),\\ \left(0.625, 0.75, 13\right),\\ \left(0.1202, 0.5992, 1\right)\end{array}\right)$

.

 Step 4.

Utilize Equation (24) to calculate the weighted TFNNs matrix $P={\left[p_{ij}\right]}_{m x n}$. The elements of matrix $P$ can be listed sequentially in

Table 6. The weighted normalized TFNNs decision matrix $P$.

	C1	C2	C3	C4
Ε1	$\left(\begin{array}{c}\left(0.2059, 0.4039, 1\right),\\ \left(0, 0.444, 0.6743\right),\\ \left(0, 0.444, 0.59\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.0126, 0.0555, 0.126\right),\\ \left(0.831, 0.9022, 0.9578\right),\\ \left(0, 0.7866, 0.8525\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.0106, 0.063, 0.1664\right),\\ \left(0, 0.6691, 0.7659\right),\\ \left(0.5938, 0.844, 0.9602\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0, 0.1266, 0.3642\right),\\ \left(0.803, 0.8883, 0.9338\right),\\ \left(0.6747, 0.8644, 0.9686\right)\end{array}\right)$
Ε2	$\left(\begin{array}{c}\left(0.1214, 0.2059, 0.3516\right),\\ \left(0.5574, 0.7529, 0.8581\right),\\ \left(0.5647, 0.7137, 0.8002\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.014, 0.0455, 0.0956\right),\\ \left(0, 0.8879, 0.9672\right),\\ \left(0.7004, 0.8096, 0.8839\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0, 0.0626, 0.3447\right),\\ \left(0.7174, 0.8753, 1\right),\\ \left(0.7626, 0.867, 1\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.1073, 0.2547, 1\right),\\ \left(0.9155, 0.965, 0.993\right),\\ \left(0, 0.8859, 0.9653\right)\end{array}\right)$
Ε3	$\left(\begin{array}{c}\left(0.0889, 0.3076, 0.7253\right),\\ \left(0.3917, 0.6587, 0.8255\right),\\ \left(0.7709, 0.8745, 1\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0, 0.0211, 0.0641\right),\\ \left(0.639, 0.8879, 0.9689\right),\\ \left(0.8967, 0.9592, 1\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.013, 0.0875, 0.2466\right),\\ \left(0.582, 0.7741, 0.8778\right),\\ \left(0, 0.8129, 0.9265\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.0595, 0.1959, 0.337\right),\\ \left(0, 0.7998, 0.9102\right),\\ \left(0.7894, 0.9418, 1\right)\end{array}\right)$
Ε4	$\left(\begin{array}{c}\left(0, 0.1214, 0.3283\right),\\ \left(0.444, 0.8484, 1\right),\\ \left(0, 0.5388, 0.6587\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.0255, 0.1612, 1\right),\\ \left(0.8359, 0.905, 0.9782\right),\\ \left(0.7623, 0.893, 0.9494\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.0252, 0.1288, 1\right),\\ \left(0.582, 0.7118, 0.8102\right),\\ \left(0, 0.6836, 0.8886\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.023, 0.1404, 0.2809\right),\\ \left(0.8976, 0.952, 0.9879\right),\\ \left(0.8327, 0.9418, 1\right)\end{array}\right)$
Ε5	$\left(\begin{array}{c}\left(0.2457, 0.3575, 0.7339\right),\\ \left(0, 0.5388, 0.6797\right),\\ \left(0, 0.444, 0.6923\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.0974, 0.1581, 1\right),\\ \left(0.8671, 0.9244, 1\right),\\ \left(0.7004, 0.8351, 0.8839\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.042, 0.1002, 0.2102\right),\\ \left(0.4817, 0.7118, 0.81\right),\\ \left(0.6907, 0.8695, 0.9806\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.024, 0.2998, 0.7807\right),\\ \left(0.9102, 0.944, 1\right),\\ \left(0.6546, 0.9026, 1\right)\end{array}\right)$

.

 Step 5.

Construct the BAA matrix $Q={\left[q_j\right]}_{1 x n}$ by using Equation (25) as seen in

Table 7. The TFNNs-BAA matrix $Q{\left[q_j\right]}_{1 x 4}$.

	C1	C2	C3	C4
qj	$\left(\begin{array}{c}\left(0, 0.2565, 0.5724\right),\\ \left(0.316, 0.6815, 1\right),\\ \left(0.3694, 0.6517, 1\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0, 0.0671, 0.2388\right),\\ \left(0.7341, 0.9025, 1\right),\\ \left(0.7058, 0.8761, 1\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0, 0.085, 0.3124\right),\\ \left(0.5197, 0.7613, 1\right),\\ \left(0.5047, 0.8257, 1\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0, 0.1927, 0.4852\right),\\ \left(0.8274, 0.9267, 1\right),\\ \left(0.6692, 0.9126, 1\right)\end{array}\right)$

.

 Step 6.

Determine the distance matrix $D= {\left[d_{ij}\right]}_{m x n}$ by using Equation (26) and the elements of matrix $D$ can be seen in

Table 8. The distance between the matrix $N$ and the matrix Q.

	C1	C2	C3	C4
Ε1	0.294133218	0.135433717	0.13017763	0.044585725
Ε2	−0.14492263	0.127541677	−0.073960167	0.17199896
Ε3	−0.132228984	−0.070633077	0.096657248	0.156082795
Ε4	−0.166411125	0.125660975	0.201853503	−0.064361377
Ε5	0.241339491	0.140794649	0.076253482	0.061268628

.

 Step 7.

Calculate $V\left({{\rm E}}_i\right)$ by using Equation (27) as listed in

Table 9. The final score values of alternatives.

	${{\rm E}}_1$	${{\rm E}}_2$	${{\rm E}}_3$	${{\rm E}}_4$	${{\rm E}}_5$
$V\left({{\rm E}}_i\right)$	0.60433029	0.08065784	0.049877982	0.096741976	0.51965625

.

 Step 8.

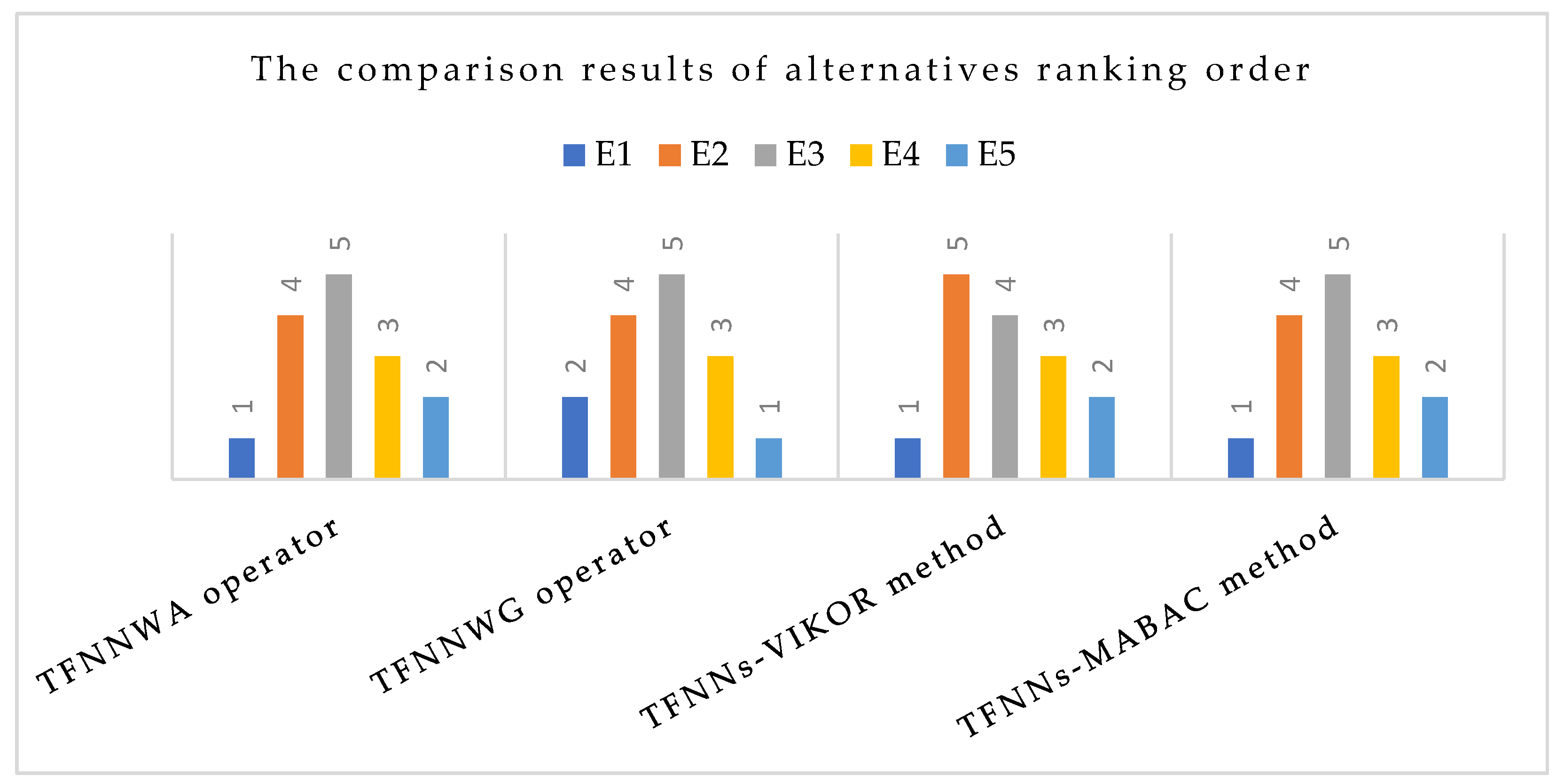
Based on the results of $V\left({{\rm E}}_i\right)$, all alternatives can be sorted in descending order. The alternative ${{\rm E}}_i$ that has maximum value is the most possible selected alternative. Obviously, the result in term of the ranking order of those alternatives is ${{\rm E}}_1>{{\rm E}}_5>{{\rm E}}_4>{{\rm E}}_2>{{\rm E}}_3$. Thus, the selected technology enterprise in which the investment company invest to is the alternative ${{\rm E}}_1$.

4.2. Compare the TFNNs-MABAC Method with Some TFNNs Aggregation Operators and VIKOR Method

This sub-section demonstrates the comparison between our proposed TFNNs-MABAC with TFNNWA operator and TFNNWG operator to examine the effectiveness of our proposed MABAC method in the TFNN environment. Based on the obtained results of Table 4 and weighting-vector for each criterion $w_j=\left\{0.41, 0.14, 0.25, 0.20\right\}$, the operators of TFNNWA and TFNNWG can be used to calculate overall $f_{ij}$ to $f_i$ (See

Table 10. The overall alternative values by using some TFNNs aggregation operators.

	$f_1$	$f_2$	$f_3$	$f_4$	$f_5$
TFNNWA	$\left(\begin{array}{c}\left(0.34, 0.52, 0.72\right),\\ \left(0.15, 0.27, 0.42\right),\\ \left(0.12, 0.25, 0.36\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.28, 0.4, 0.61\right),\\ \left(0.21, 0.39, 0.57\right),\\ \left(0.22, 0.34, 0.5\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.27, 0.45, 0.68\right),\\ \left(0.2, 0.4, 0.59\right),\\ \left(0.23, 0.41, 0.59\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.25, 0.46, 0.72\right),\\ \left(0.19, 0.39, 0.57\right),\\ \left(0.11, 0.24, 0.38\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.41, 0.51, 0.74\right),\\ \left(0.13, 0.29, 0.42\right),\\ \left(0.12, 0.25, 0.43\right)\end{array}\right)$
TFNNWG	$\left(\begin{array}{c}\left(0.32, 0.49, 0.69\right),\\ \left(0.17, 0.29, 0.45\right),\\ \left(0.12, 0.25, 0.38\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.27, 0.39, 0.58\right),\\ \left(0.23, 0.42, 0.63\right),\\ \left(0.23, 0.35, 0.5\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.25, 0.42, 0.64\right),\\ \left(0.22, 0.42, 0.66\right),\\ \left(0.32, 0.49, 0.69\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.23, 0.44, 0.68\right),\\ \left(0.19, 0.43, 0.65\right),\\ \left(0.11, 0.25, 0.4\right)\end{array}\right)$	$\left(\begin{array}{c}\left(0.38, 0.49, 0.73\right),\\ \left(0.14, 0.29, 0.43\right),\\ \left(0.13, 0.26, 0.43\right)\end{array}\right)$

). The use of these two operators aims to fuse overall the weighted input data that are expressed as TFNNs into a single TFNN (see Theorem 1 and 2). In other words, the aggregation result of both TFNNWA or TFNNWG operators is still in terms of fuzzy information. Moreover, to look at an exact number or a crips value representing the aggregation result for each alternative, we will easily find them through the score function value of TFNNs. After calculating the values of the TFNNs score function $S\left(f_i\right)$, we can generate the results of alternatives score as presented in

Table 11. The score function value of alternatives $S\left(f_i\right)$.

	$S\left(f_1\right)$	$S\left(f_2\right)$	$S\left(f_3\right)$	$S\left(f_4\right)$	$S\left(f_5\right)$
TFNNWA	0.6661	0.5566	0.5505	0.6129	0.6641
TFNNWG	0.6476	0.5393	0.5010	0.5868	0.6511

. Afterward, the alternatives’ ranking order by these two TFNNs aggregation operators can be seen in Table 13 and Figure 2.

Analyzing the results of our proposed TFNNs-MABAC method with TFNNWA and TFNNWG operators, we confirm that the results of our proposed MABAC method are the same as the results generated by the TFNNWA operator but insignificantly changed with the TFNNWG operator. The proposed TFNNs-MABAC method showed that the alternatives ${{\rm E}}_1$ and ${{\rm E}}_5$, respectively, placed in the first position and the second position, whereas the TFNNWG advised vice versa. Since the results in terms of ranking order provided by both aggregation operators are different, we then investigated further the discrepancy between truth and falsity of the TFNNWA and TFNNWG results for each alternative through the accuracy function of TFNNs. After calculating the accuracy function values of the TFNNs $A\left(f_i\right)$ for each aggregation operator, as seen in

Table 12. The accuracy function value of alternatives $S\left(f_i\right)$.

	$A(f_1)$	$A(f_2)$	$A(f_3)$	$A(f_4)$	$A(f_5)$
TFNNWA	0.2799	0.0680	0.0546	0.2309	0.2779
TFNNWG	0.2479	0.0480	−0.0603	0.1937	0.2476

, we obtain the accuracy function values for all alternatives determined by TFNNWA have a bit larger than TFNNWG. It indicates that the ranking order suggested by TFNNWA is more affirmative in this aggregate comparison.

Nevertheless, in terms of the computational complexity, those two aggregation operators need relatively shorter computations to obtain decision-making by evaluating overall alternatives with their operators. Considering the abovementioned TFNNWA’s advantage and from its result, as shown in Table 4, we then continued to perform the procedures of our proposed TFNNs-MABAC method for selecting the best alternative. The TFNNs-MABAC method evaluates ideal and non-ideal alternatives by spreading as many the criterion of the alternative as possible located on the upper approximation border. Although the TFNNs-MABAC takes a bit more time in returning the decision, it considers the conflicting attribute to avoid the inconsistency and uncertainty of DMs. Therefore, our proposed TFNNs-MABAC can be more scientific and reasonable in real-life MCGDM applications.

Furthermore, comparing our TFNNs-MABAC method with the TFNNs-VIKOR [43] method, as displayed in

Table 13. The results of ranking order of alternatives.

	Ranking order
TFNNWA	${{\rm E}}_1>{{\rm E}}_5>{{\rm E}}_4>{{\rm E}}_2>{{\rm E}}_3$
TFNNWG	${{\rm E}}_5>{{\rm E}}_1>{{\rm E}}_4>{{\rm E}}_2>{{\rm E}}_3$
TFNNs-VIKOR method [43]	${{\rm E}}_1>{{\rm E}}_5>{{\rm E}}_4>{{\rm E}}_3>{{\rm E}}_2$
TFNNs-MABAC method	${{\rm E}}_1>{{\rm E}}_5>{{\rm E}}_4>{{\rm E}}_2>{{\rm E}}_3$

and Figure 2, the best alternative selected by the VIKOR method is similar; however, the result of ranking order is slightly different to our proposed method. The VIKOR method advised the alternative ${{\rm E}}_3$ and the alternative ${{\rm E}}_2$, respectively, placed in the fourth position and the fifth position, whereas the proposed method suggested vice versa. Additionally, the alternatives’ evaluation process in the VIKOR method is based on distance measures from the positive and negative ideal solutions in terms of each criterion like set-pair Analysis and TOPSIS. In contrast to other decision-making methods, the VIKOR method chooses an alternative with the lowest final score as the best alternative.

5. Conclusions

In this article, we proposed the TFNNs-MABAC method based on some fundamental theories in TFNNs and the traditional MABAC model for MCGDM. Firstly, we reviewed the concepts, some essential operators, and operation laws of TFNNs, and then encapsulated the score and accuracy functions of TFNNs. Afterward, we discussed two aggregation operators regarding TFNNs and reviewed the definition of normalized Hamming distance among two TFNNs. Secondly, we developed the TFNNs-MABAC method by integrating the traditional MABAC with TFNNs. We demonstrated the steps of calculating the procedure of our proposed TFNNs-MABAC in detail through a numerical-example for an invest selection problem. Eventually, we performed a comparative-analysis to underline the benefits of the proposed TFNNs-MABAC. The proposed method verified conformity, effectiveness, and reasonableness for implemented to MCGDM problems.

In practice decision-making real-life time, the TFNNs are an effective instrument to solve the impreciseness and incompleteness of DMs. However, there is a limitation of the proposed method. Due to the number of functions for each membership degree of TFNNs, increasingly, the computational complexity in particular to calculate the overall value of some aggregation TFNN operators for a large of TFNNs group will be a bit slower and more complex. Therefore, it needs a high-performance computing technology or a database indexing technique to retrieve the overall aggregated value fast in the decision-making process.

Future works can utilize our proposed TFNNs-MABAC method to risk assessment for MCGDM cases, such as [45,46,47,48,49,50], many other uncertain and fuzzy circumstances [51,52,53,54,55,56,57,58,59,60]. The neutrosophic sets, such as [61,62,63,64,65,66,67,68,69], can be many possible chances to improve our proposed MABAC method for further studies. Other interesting future studies are to develop a novel decision-making model based on the TFNNs in social network group decision making [70] or apply the model to two-sided matching decision-making problems [71].