Cantor Waves for Signorini Hyperelastic Materials with Cylindrical Symmetry
Abstract
:1. Introduction
2. Cantor Metric Tensor
3. Local Fractional Calculus
3.1. Yang Local Fractional Derivative
3.2. Local Fractional Covariant Derivatives in Cantor Cylindrical Coordinates
4. Local Fractional Covariant Equations in Cylindrical Coordinates for Signorini Hyperelastic Materials
4.1. Signorini Hyperelastic Materials
4.2. Fractional Covariant Equations
4.3. Fractional Differential Equations for Longitudinal Waves
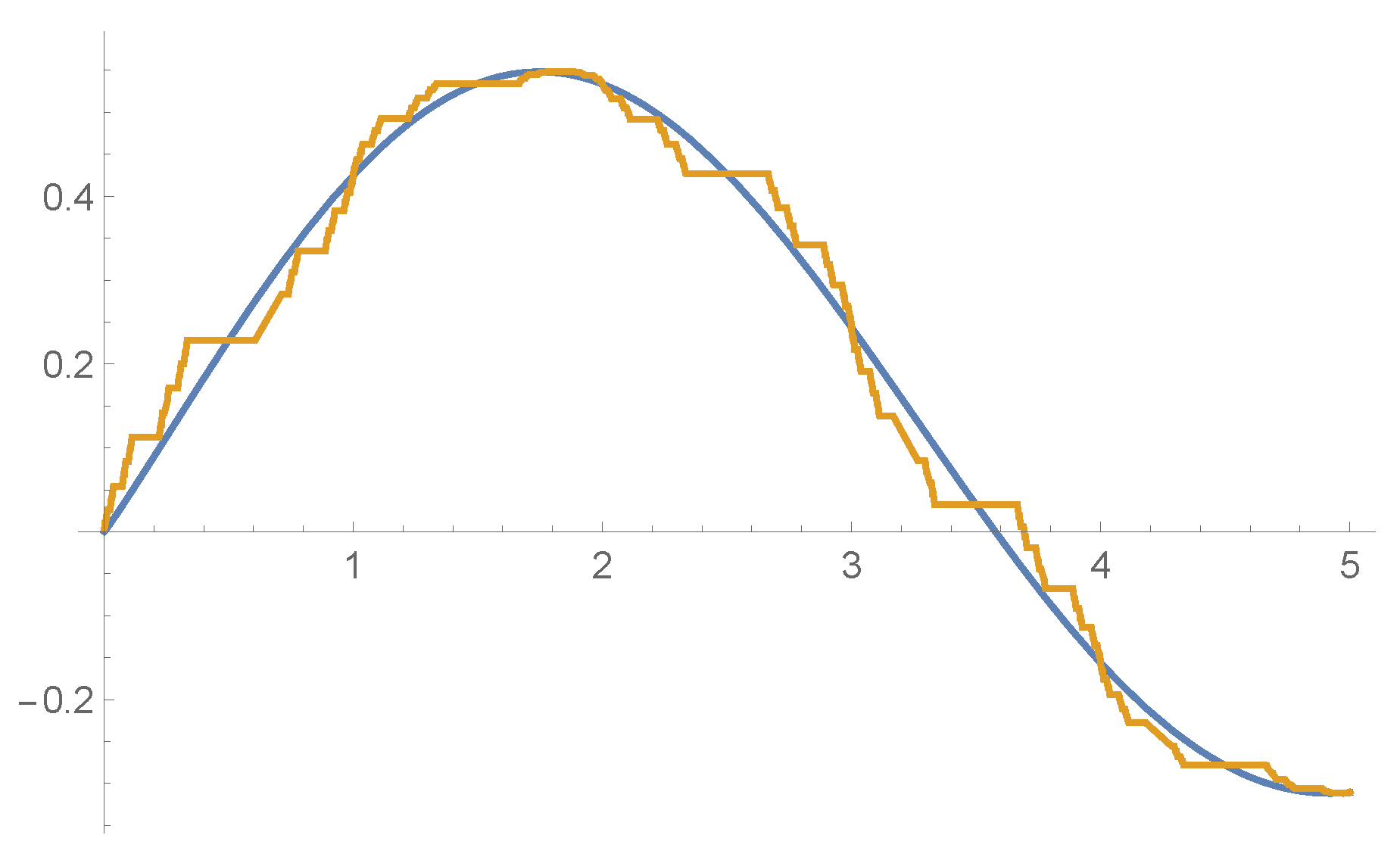
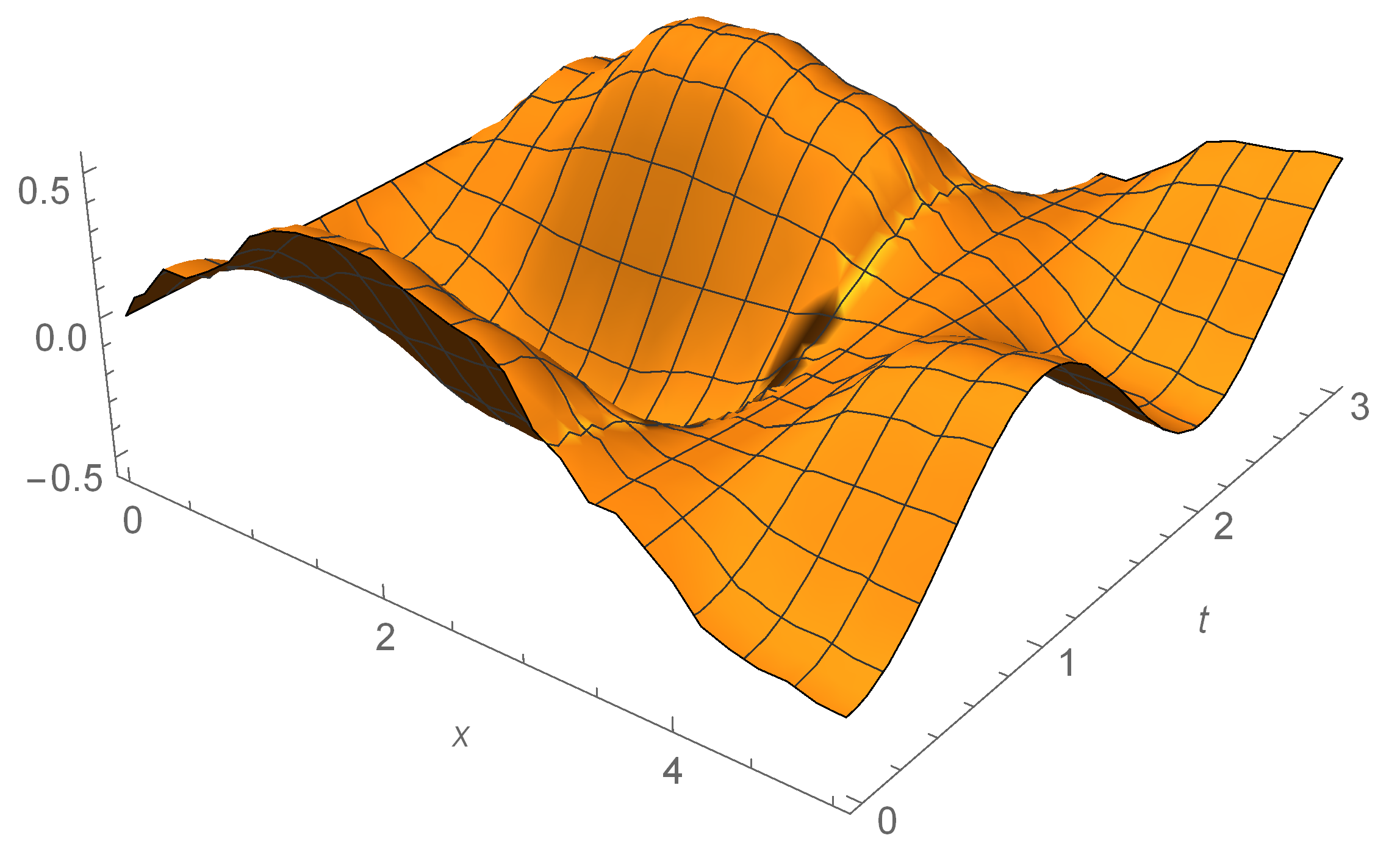
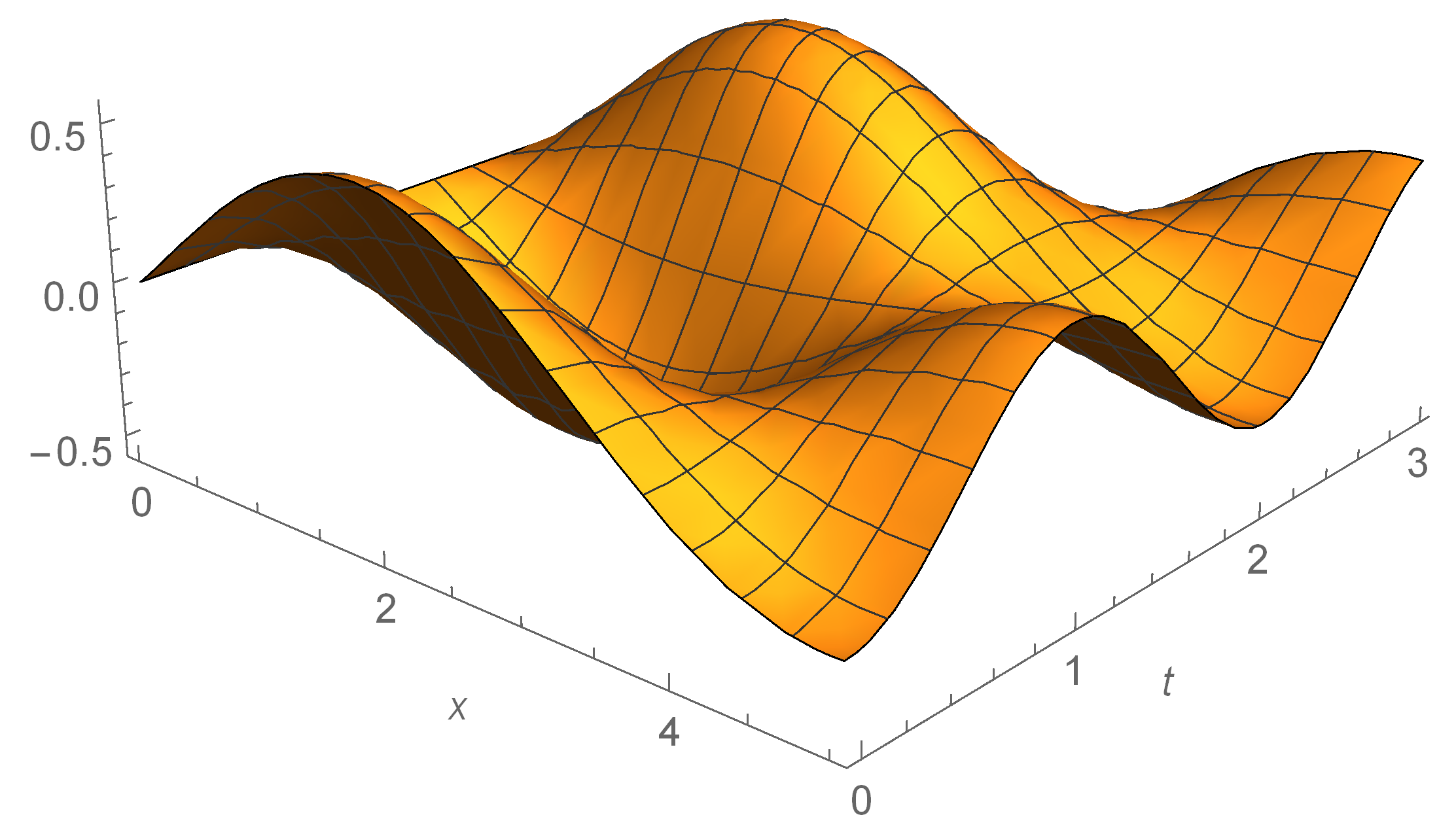
5. Local Fractional Longitudinal Waves on Cantor Coordinates
Linear Equation
6. Conclusions
Funding
Conflicts of Interest
References
- Achenbach, J.D. Wave Propagation in Solids; North-Holland: Amsterdam, The Netherlands, 1973. [Google Scholar]
- Cattani, C.; Rushchitsky, J.J. Wavelet and Wave Analysis as Applied to Materials with Micro or Nanostructure; Series on Advances in Mathematics for Applied Sciences; World Scientific: Singapore, 2007; p. 74. [Google Scholar]
- Ogden, R.W. Non-Linear Elastic Deformations; Dover: Kentm, UK, 1974. [Google Scholar]
- Bower, A. Applied Mechanics of Solids; CRC Press: New York, NY, USA, 2009. [Google Scholar]
- Signorini, A. Trasformazioni termoelastiche finite. Ann. Mater. Pura Appl. 1943, 22, 33–143. [Google Scholar] [CrossRef]
- Cattani, C.; Rushchitsky, J.J. Similarities and differences between the Murnaghan and Signorini descriptions of the evolution of quadratically nonlinear hyperelastic plane waves. Int. Appl. Mech. 2006, 42, 997–1010. [Google Scholar] [CrossRef]
- Cattani, C.; Rushchitsky, J.J. Nonlinear plane waves in Signorini hyperelastic materials. Int. Appl. Mech. 2006, 42, 895–903. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, Y.; Liu, Y.; Wang, Y.; Cao, F.; Yang, Q.; Tian, F. Explanation of the cell orientation in a nanofiber membrane by the geometric potential theory. Results Phys. 2019, 15, 102537. [Google Scholar] [CrossRef]
- Cattani, C. Signorini Cylindrical Waves and Shannon Wavelets. Adv. Numer. Anal. 2012, 2012, 24. [Google Scholar] [CrossRef]
- Cattani, C.; Nosova, E. Transversal Waves in Nonlinear Signorini Model; Lecture Notes in Computer Science, LNCS 5072, Part I; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1181–1190. [Google Scholar]
- Cattani, C.; Rushchitsky, J.J. Nonlinear cylindrical waves in Signorini hyperelastic materials. Int. Appl. Mech. 2006, 42, 765–774. [Google Scholar] [CrossRef]
- Zwillinger, D. Handbook of Differential Equations, 3rd ed.; Academic Press: Boston, MA, USA, 1997. [Google Scholar]
- Yang, X.J. Advanced Local Fractional Calculus and Its Applications; World Science: New York, NY, USA, 2012. [Google Scholar]
- Pobludny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Ortigueira, M.D. Fractional Calculus for Scientists and Engineers; Springer: Berlin, Germany, 2011. [Google Scholar]
- Herrmann, R. Fractional Calculus, 2nd ed.; World Scientific: Singapore, 2014. [Google Scholar]
- Cattani, C.; Srivastava, H.M.; Yang, X.-J. Fractional Dynamics; Walter de Gruyter GmbH & Co KG: Berlin, Germany, 2015. [Google Scholar]
- Yang, X.J.; Baleanu, D.; Srivastava, H.M. Local Fractional Integral Transforms and Their Applications; Academic Press: New York, NY, USA, 2016. [Google Scholar]
- Yang, X.J.; Srivastava, H.M.; He, J.H.; Baleanu, D. Cantor-type Cylindrical-coordinate Method for Differential Equations with Local Fractional Derivatives. Phys. Lett. A 2013, 377, 1696–1700. [Google Scholar] [CrossRef]
- Wang, K.L.; He, C.H. A remark on Wang’s fractal variational principle. Fractals 2019. [Google Scholar] [CrossRef]
- He, C.H.; Shen, Y.; Ji, F.Y.; He, J.H. Taylor series solution for fractal Bratu-type equation arising in electrospinning process. Fractals 2019. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cattani, C. Cantor Waves for Signorini Hyperelastic Materials with Cylindrical Symmetry. Axioms 2020, 9, 22. https://doi.org/10.3390/axioms9010022
Cattani C. Cantor Waves for Signorini Hyperelastic Materials with Cylindrical Symmetry. Axioms. 2020; 9(1):22. https://doi.org/10.3390/axioms9010022
Chicago/Turabian StyleCattani, Carlo. 2020. "Cantor Waves for Signorini Hyperelastic Materials with Cylindrical Symmetry" Axioms 9, no. 1: 22. https://doi.org/10.3390/axioms9010022
APA StyleCattani, C. (2020). Cantor Waves for Signorini Hyperelastic Materials with Cylindrical Symmetry. Axioms, 9(1), 22. https://doi.org/10.3390/axioms9010022




