Global Analysis and the Periodic Character of a Class of Difference Equations
Abstract
1. Introduction
2. Periodic Solutions with Period
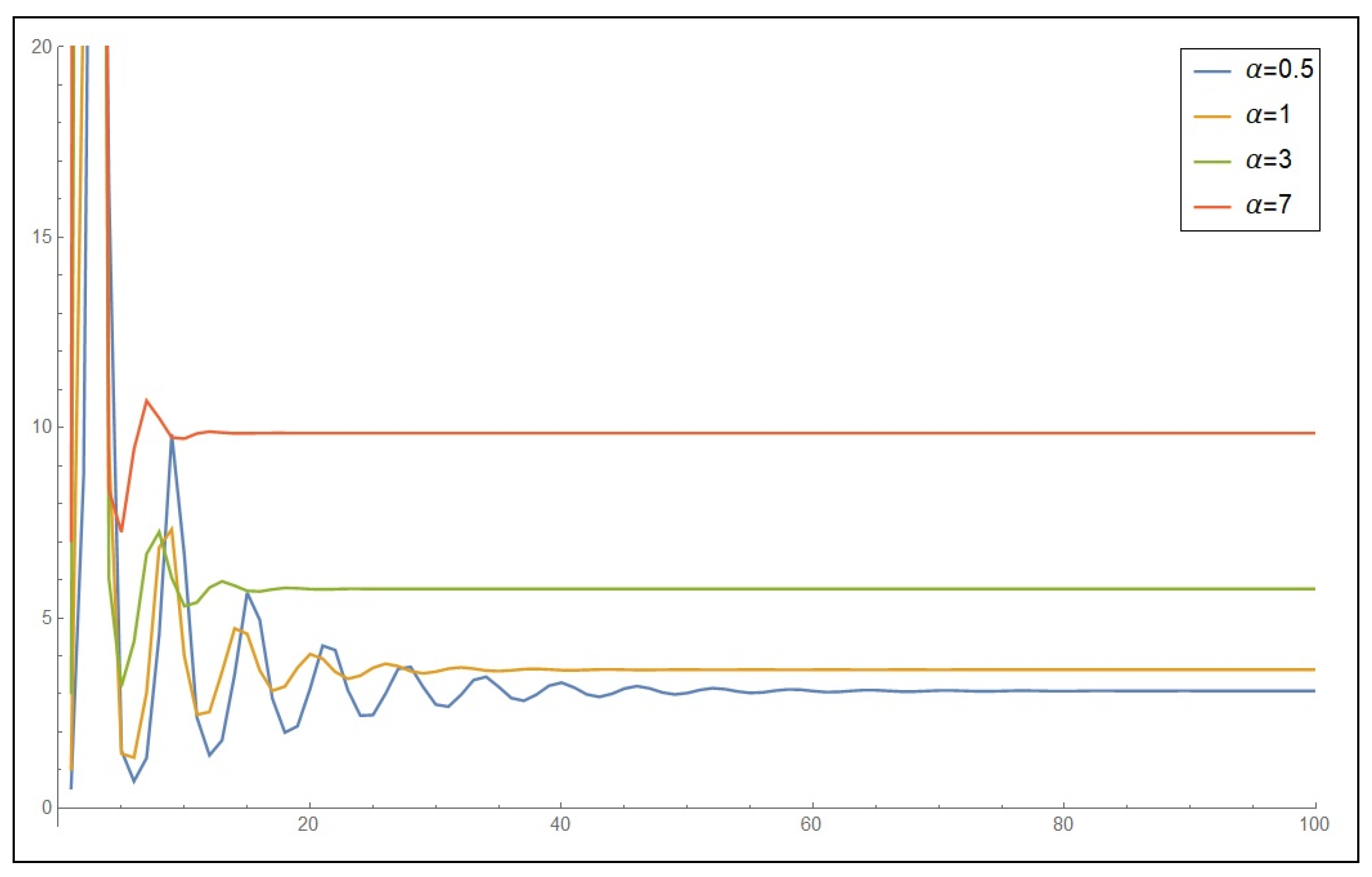
3. Stability and Boundedness
4. Application and Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Abdelrahman, M.A.E.; Chatzarakis, G.E.; Li, T.; Moaaz, O. On the difference equation Jn+1 = aJn−l + bJn−k + f(Jn−l, Jn−k). Adv. Differ. Equ. 2018, 431, 2018. [Google Scholar]
- Agarwal, R.P.; Elsayed, E.M. Periodicity and stability of solutions of higher order rational difference equation. Adv. Stud. Contemp. Math. 2008, 17, 181–201. [Google Scholar]
- Ahlbrandt, C.D.; Peterson, A.C. Discrete Hamiltonian Systems: Difference Equations, Continued Fractions, and Riccati Equations; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1996. [Google Scholar]
- Ahmad, S. On the nonautonomous Volterra-Lotka competition equations. Proc. Am. Math. Soc. 1993, 117, 199–204. [Google Scholar] [CrossRef]
- Allman, E.S.; Rhodes, J.A. Mathematical Models in Biology: An Introduction; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Andres, J.; Pennequin, D. Note on Limit-Periodic Solutions of the Difference Equation xt+1 − [h(xt) + λ]x = rt,λ > 1. Axioms 2019, 8, 19. [Google Scholar] [CrossRef]
- Din, Q.; Elsayed, E.M. Stability analysis of a discrete ecological model. Comput. Ecol. Soft. 2014, 4, 89–103. [Google Scholar]
- Grove, E.A.; Ladas, G. Periodicities in Nonlinear Difference Equations; Chapman & Hall/CRC: Boca Raton, FL, USA, 2005; Volume 4. [Google Scholar]
- Elabbasy, E.M.; El-Metwally, H.; Elsayed, E.M. On the difference equation Jn+1 = (aJn−l + bJn−k)/(cJn−l + dJn−k). Acta Math. Vietnam. 2008, 33, 85–94. [Google Scholar]
- Elabbasy, E.M.; Elsayed, E.M. Dynamics of a rational difference equation. Chin. Ann. Math. Ser. B 2009, 30, 187–198. [Google Scholar] [CrossRef]
- El-Dessoky, M.M. On the difference equation Jn+1 = aJn−l + bJn−k + cJn−s/(dJn−s − e). Math. Methods Appl. Sci. 2016, 1, 082579. [Google Scholar]
- Elettreby, M.F.; El-Metwally, H. On a system of difference equations of an economic model. Discret. Dyn. Nat. Soc. 2013, 2013, 405628. [Google Scholar] [CrossRef][Green Version]
- Elsayed, E.M. Dynamics and behavior of a higher order rational difference equation. J. Nonlinear Sci. Appl. 2015, 9, 1463–1474. [Google Scholar] [CrossRef]
- Elsayed, E.M. New method to obtain periodic solutions of period two and three of a rational difference equation. Nonlinear Dyn. 2015, 79, 241–250. [Google Scholar] [CrossRef]
- Elsayed, E.M.; Iricanin, B.D. On a max-type and a min-type difference equation. Appl. Math. Comput. 2009, 215, 608–614. [Google Scholar] [CrossRef]
- Elsayed, E.M.; El-Dessoky, M.M. Dynamics and behavior of a higher order rational recursive sequence. Adv. Differ. Equ. 2012, 69, 2012. [Google Scholar] [CrossRef]
- Foupouagnigni, M.; Mboutngam, S. On the Polynomial Solution of Divided-Difference Equations of the Hypergeometric Type on Nonuniform Lattices. Axioms 2019, 8, 47. [Google Scholar] [CrossRef]
- Foupouagnigni, M.; Koepf, W.; Kenfack-Nangho, M.; Mboutngam, S. On Solutions of Holonomic Divided-Difference Equations on Nonuniform Lattices. Axioms 2013, 2, 404–434. [Google Scholar] [CrossRef]
- Gil, M. Solution Estimates for the Discrete Lyapunov Equation in a Hilbert Space and Applications to Difference Equations. Axioms 2019, 8, 20. [Google Scholar] [CrossRef]
- Haghighi, A.M.; Mishev, D.P. Difference and Differential Equations with Applications in Queueing Theory; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Kalabusic, S.; Kulenovic, M.R.S. On the recursive sequnence Jn+1 = (αJn−1 + βJn−2)/(γJn−1 + δJn−2). J. Differ. Equ. Appl. 2003, 9, 701–720. [Google Scholar]
- Kelley, W.G.; Peterson, A.C. Difference Equations: An Introduction with Applications, 2nd ed.; Harcour Academic: New York, NY, USA, 2001. [Google Scholar]
- Kocic, V.L.; Ladas, G. Global Behavior of Nonlinear Difference Equations of Higher Order with Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Kulenovic, M.R.S.; Ladas, G. Dynamics of Second Order Rational Difference Equations with Open Problems and Conjectures; Chapman & Hall/CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Liu, X. A note on the existence of periodic solutions in discrete predator-prey models. Appl. Math. Model. 2010, 34, 2477–2483. [Google Scholar] [CrossRef]
- Ma, W.-X. Global behavior of a new rational nonlinear higher-order difference equation. Complexity 2019, 2019, 2048941. [Google Scholar] [CrossRef]
- Migda, M.; Migda, J. Nonoscillatory Solutions to Second-Order Neutral Difference Equations. Symmetry 2018, 10, 207. [Google Scholar] [CrossRef]
- Moaaz, O. Comment on new method to obtain periodic solutions of period two and three of a rational difference equation [Nonlinear Dyn 79: 241–250]. Nonlinear Dyn. 2017, 88, 1043–1049. [Google Scholar] [CrossRef]
- Moaaz, O. Dynamics of difference equation Jn+1 = f(Jn−l, Jn−k). Adv. Differ. Equ. 2018, 447, 2018. [Google Scholar]
- Moaaz, O.; Chalishajar, D.; Bazighifan, O. Some Qualitative Behavior of Solutions of General Class of Difference Equations. Mathematics 2019, 7, 585. [Google Scholar] [CrossRef]
- Pogrebkov, A. Hirota Difference Equation and Darboux System: Mutual Symmetry. Symmetry 2019, 11, 436. [Google Scholar] [CrossRef]
- Stevic, S. On the recursive sequance xn+1 = α + /. J. Appl. Math. Comput. 2005, 18, 229–234. [Google Scholar]
- Stevic, S.; Kent, C.; Berenaut, S. A note on positive nonoscillatory solutions of the differential equation xn+1 = α + /. J. Diff. Eqs. Appl. 2006, 12, 495–499. [Google Scholar]
- Stevic, S. On the recursive sequence xn+1 = αn + xn−1/xn. Dynam. Contin. Discret. Impuls. Syst. Ser. A Math. Anal. 2003, 10, 911–917. [Google Scholar]
- Stevic, S. A note on periodic character of a difference equation. J. Differ. Equ. Appl. 2004, 10, 929–932. [Google Scholar] [CrossRef]
- Stevic, S. A short proof of the Cushing–Henson conjecture. Discret. Dyn. Nat. Soc. 2006, 4, 37264. [Google Scholar] [CrossRef]
- Stevic, S. Global stability and asymptotics of some classes of rational difference equations. J. Math. Anal. Appl. 2006, 316, 60–68. [Google Scholar] [CrossRef]
- Stevic, S. Asymptotics of some classes of higher order difference equations. Discret. Dyn. Nat. Soc. 2007, 2007, 56813. [Google Scholar] [CrossRef]
- Stevic, S. Asymptotic periodicity of a higher order difference equation. Discret. Dyn. Nat. Soc. 2007, 2007, 13737. [Google Scholar] [CrossRef][Green Version]
- Stevic, S. Existence of nontrivial solutions of a rational difference equation. Appl. Math. Lett. 2007, 20, 28–31. [Google Scholar] [CrossRef]
- Taousser, F.Z.; Defoort, M.; Djemai, M.; Djouadi, S.M.; Tomsovic, K. Stability analysis of a class of switched nonlinear systems using the time scale theory. Nonlinear Anal. Hybrid Syst. 2019, 33, 195–210. [Google Scholar] [CrossRef]
- Wang, C.; Agarwal, R.P. Almost periodic solution for a new type of neutral impulsive stochastic Lasota–Wazewska timescale model. Appl. Math. Lett. 2017, 70, 58–65. [Google Scholar] [CrossRef]
- Yang, C. Positive Solutions for a Three-Point Boundary Value Problem of Fractional Q-Difference Equations. Symmetry 2018, 10, 358. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatzarakis, G.E.; Elabbasy, E.M.; Moaaz, O.; Mahjoub, H. Global Analysis and the Periodic Character of a Class of Difference Equations. Axioms 2019, 8, 131. https://doi.org/10.3390/axioms8040131
Chatzarakis GE, Elabbasy EM, Moaaz O, Mahjoub H. Global Analysis and the Periodic Character of a Class of Difference Equations. Axioms. 2019; 8(4):131. https://doi.org/10.3390/axioms8040131
Chicago/Turabian StyleChatzarakis, George E., Elmetwally M. Elabbasy, Osama Moaaz, and Hamida Mahjoub. 2019. "Global Analysis and the Periodic Character of a Class of Difference Equations" Axioms 8, no. 4: 131. https://doi.org/10.3390/axioms8040131
APA StyleChatzarakis, G. E., Elabbasy, E. M., Moaaz, O., & Mahjoub, H. (2019). Global Analysis and the Periodic Character of a Class of Difference Equations. Axioms, 8(4), 131. https://doi.org/10.3390/axioms8040131






