Fractional Whitham–Broer–Kaup Equations within Modified Analytical Approaches
Abstract
1. Introduction
2. Preliminaries Concepts
3. The Procedure of NDM
4. Fundamental Idea of q-Homotopy Analysis Transform Method
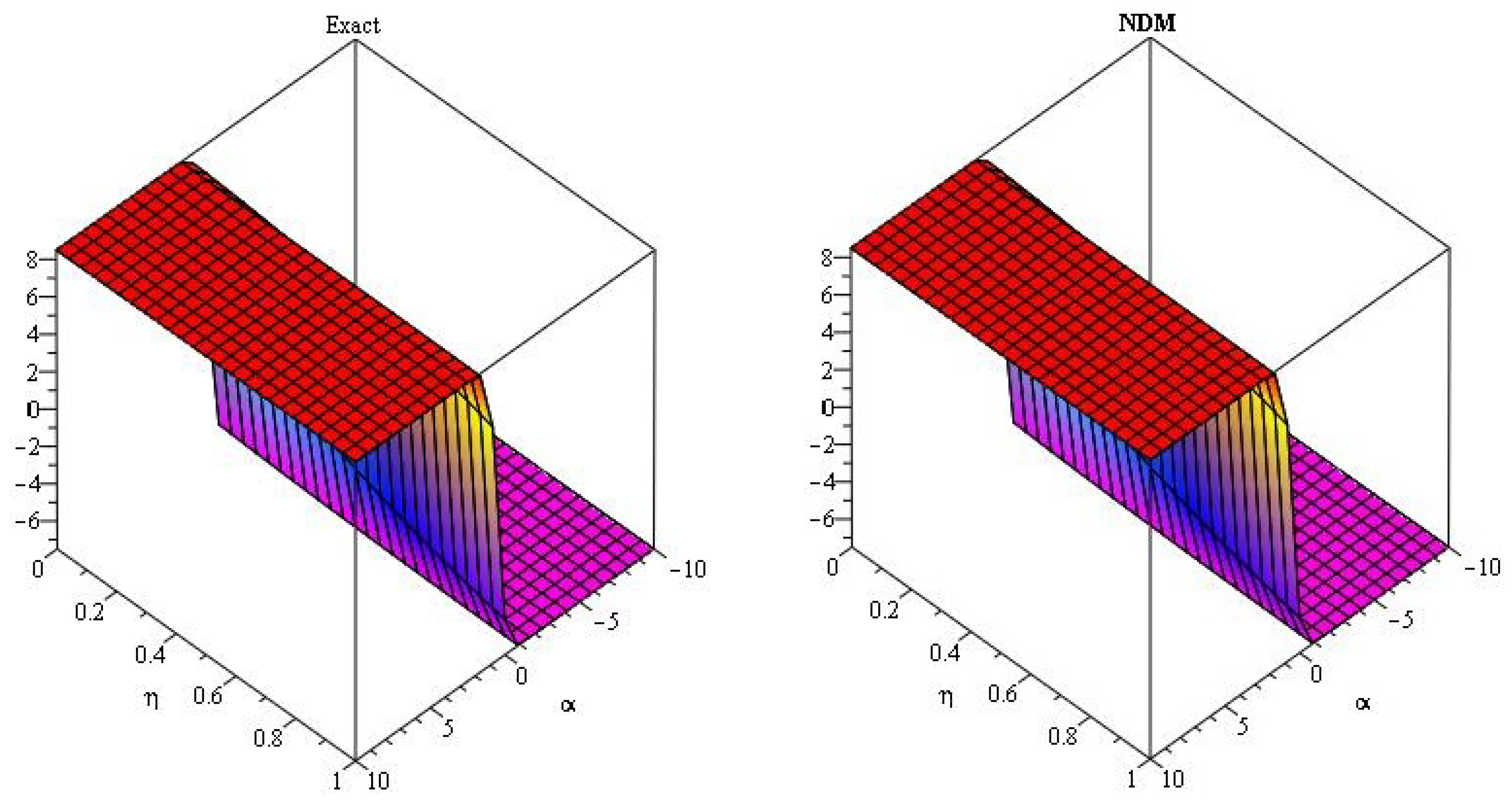
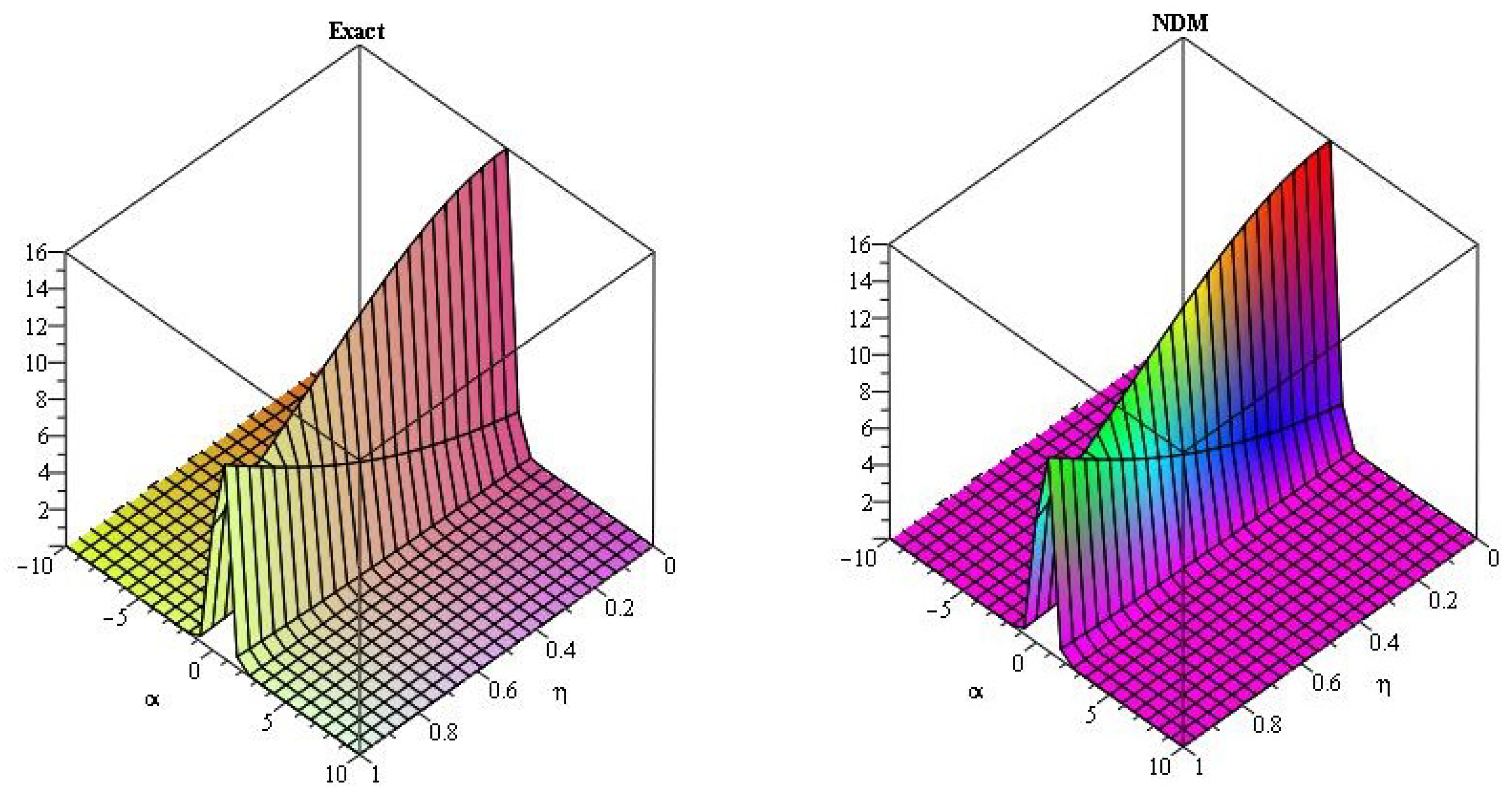
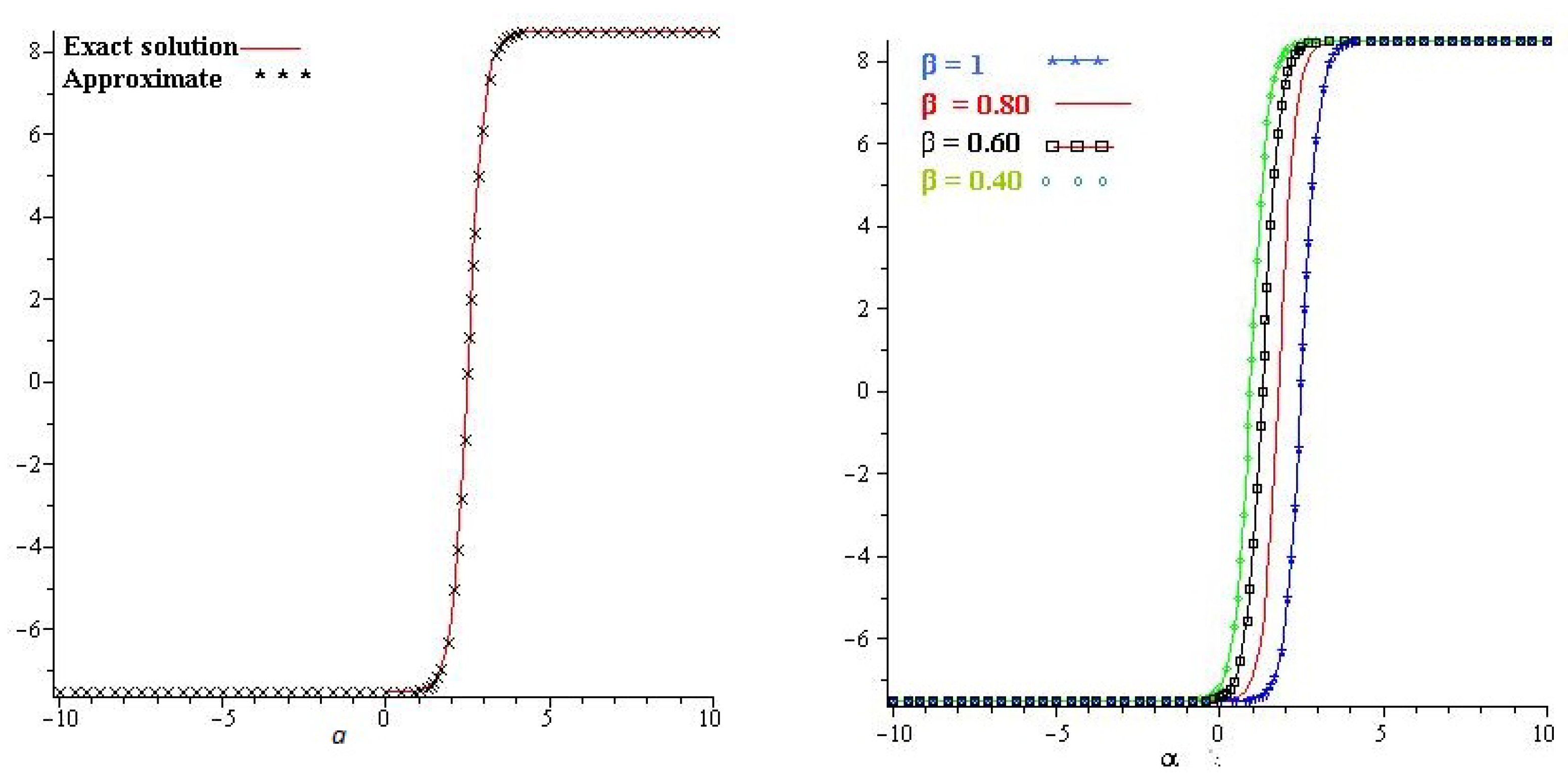
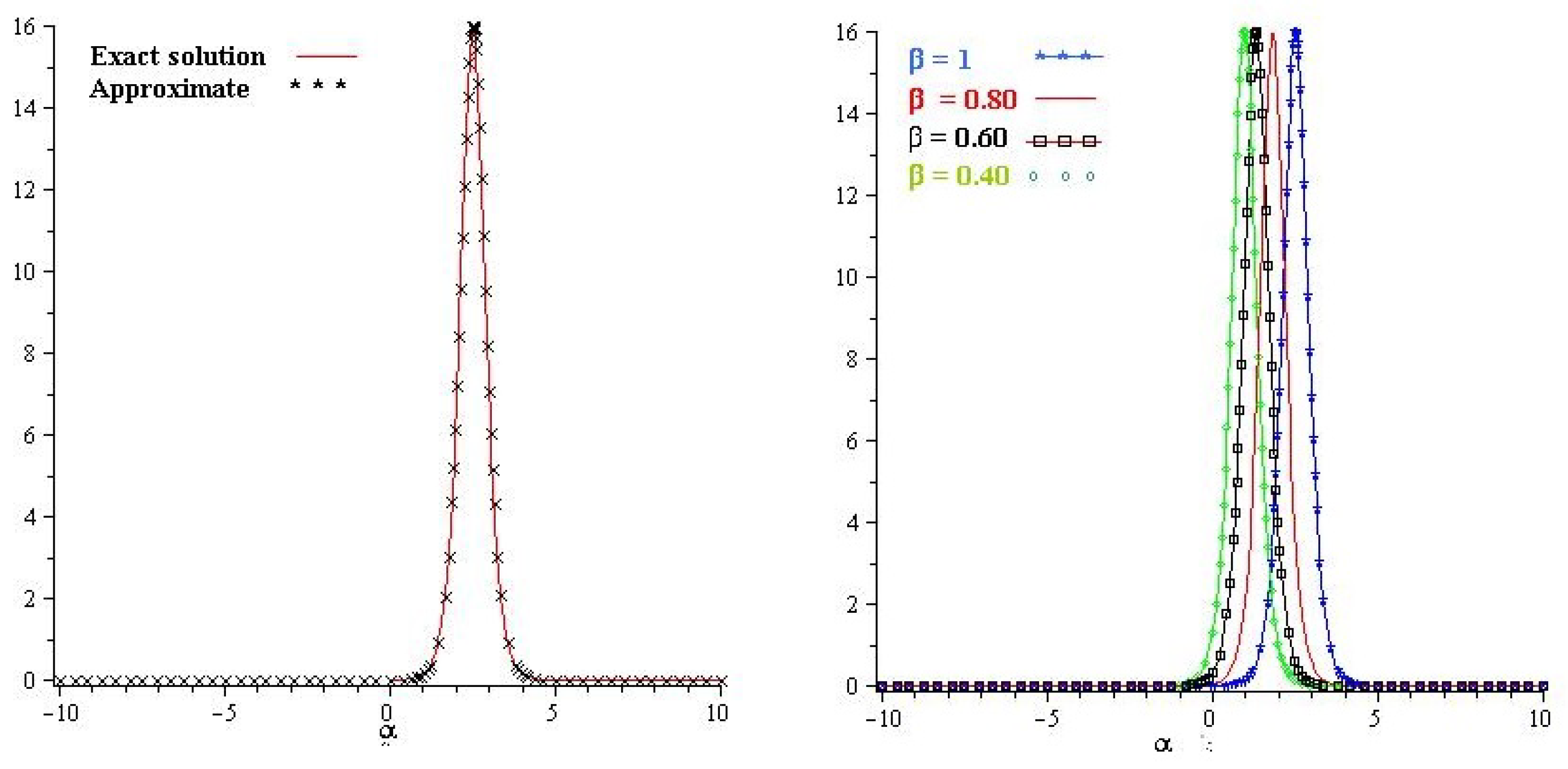
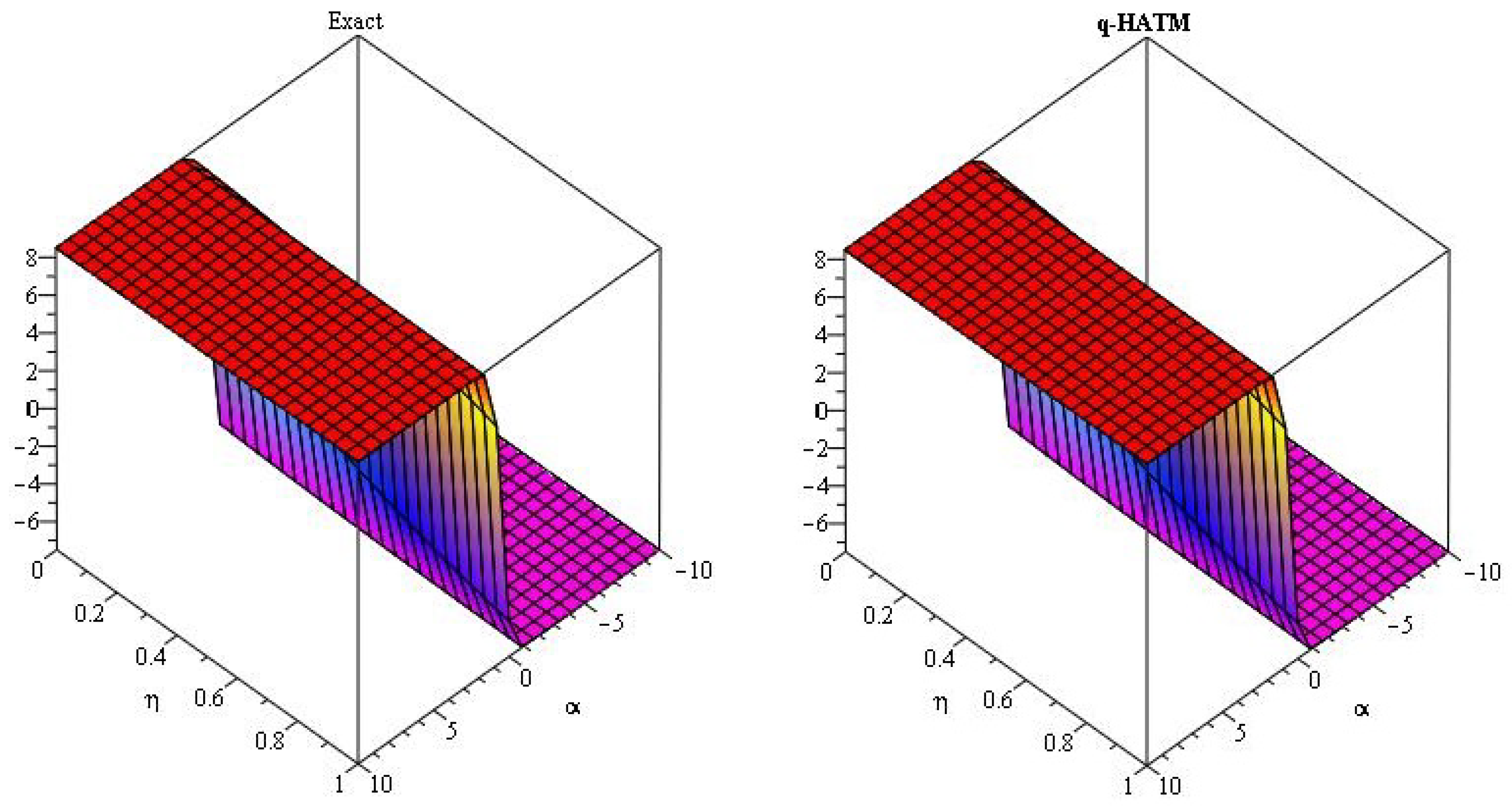
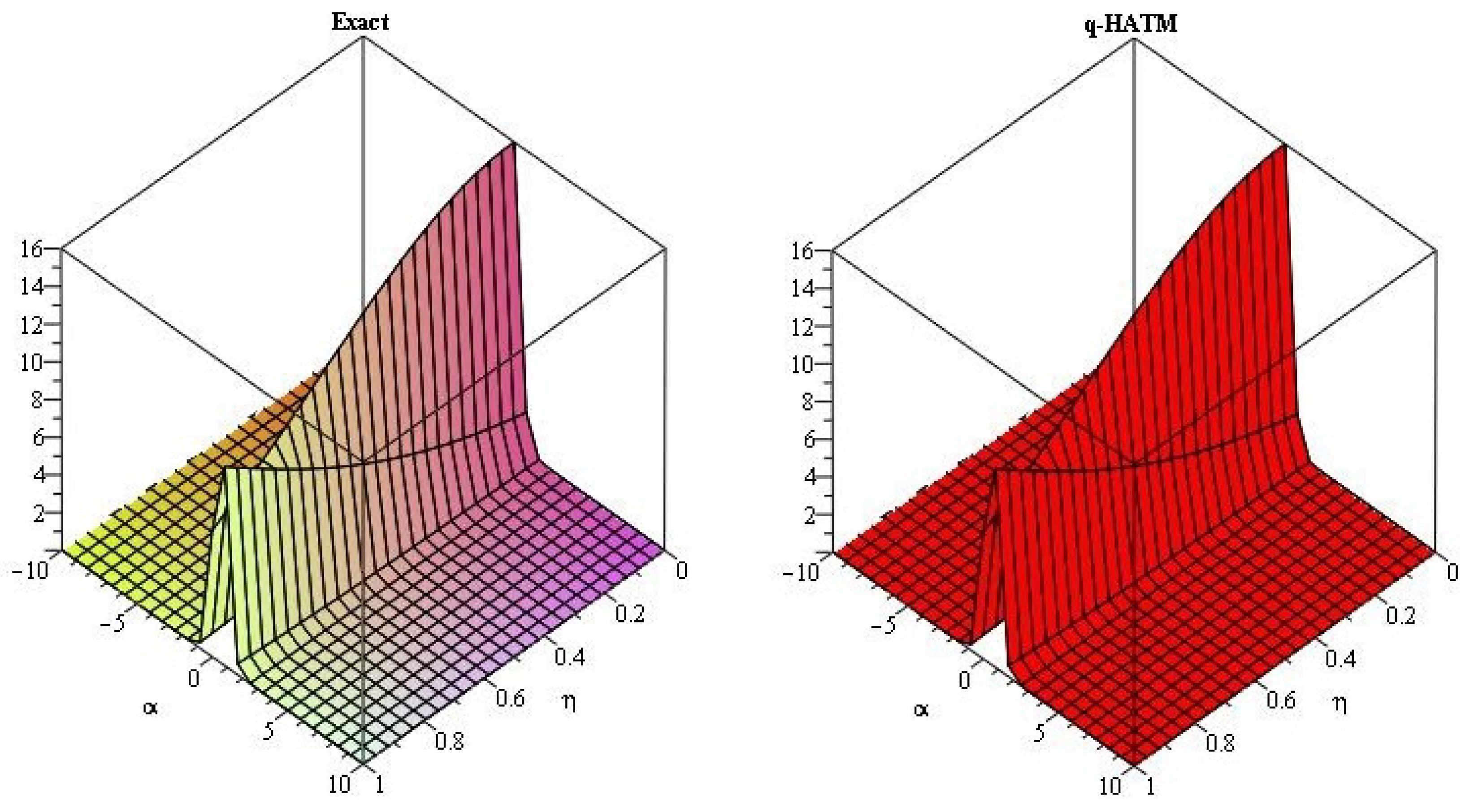
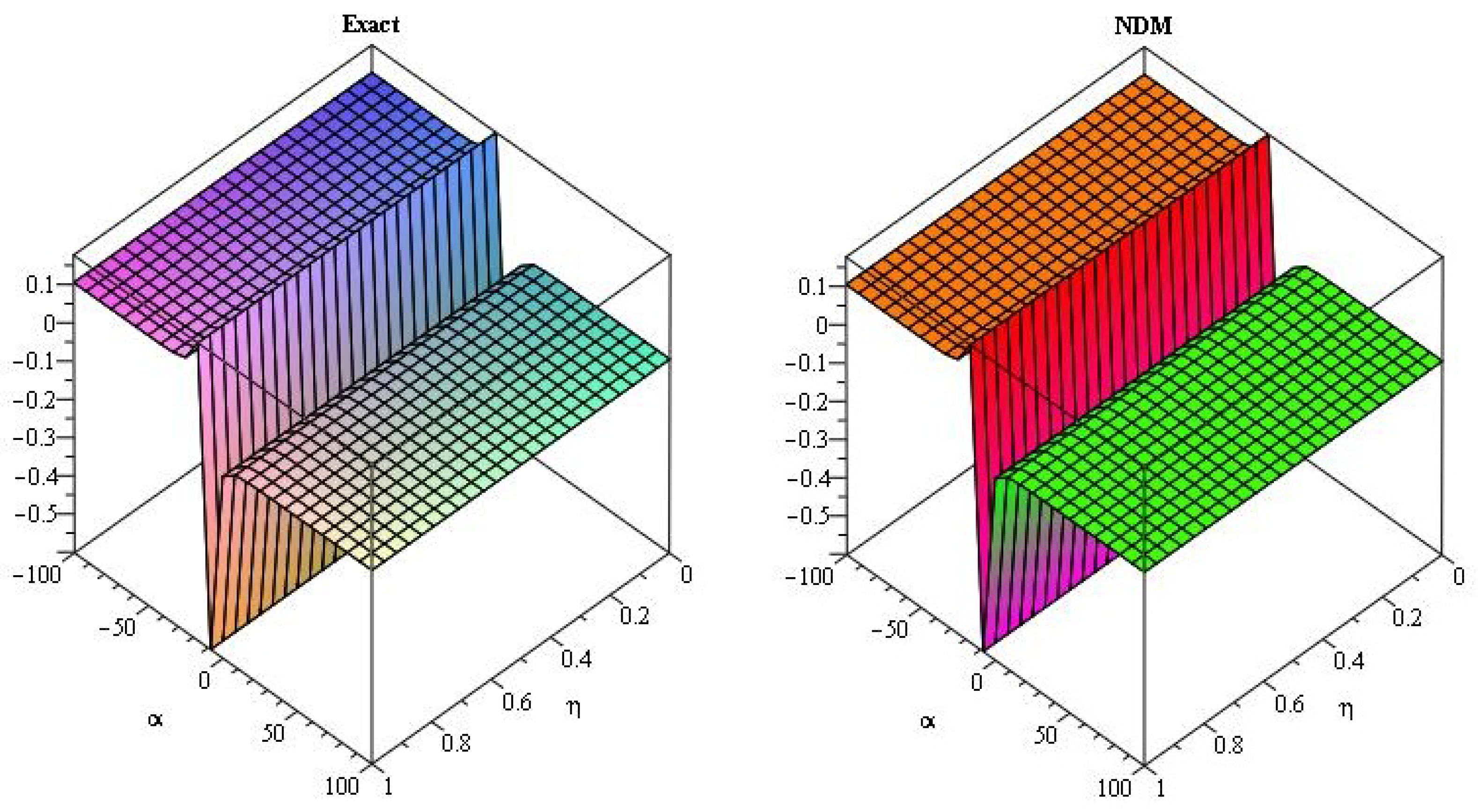
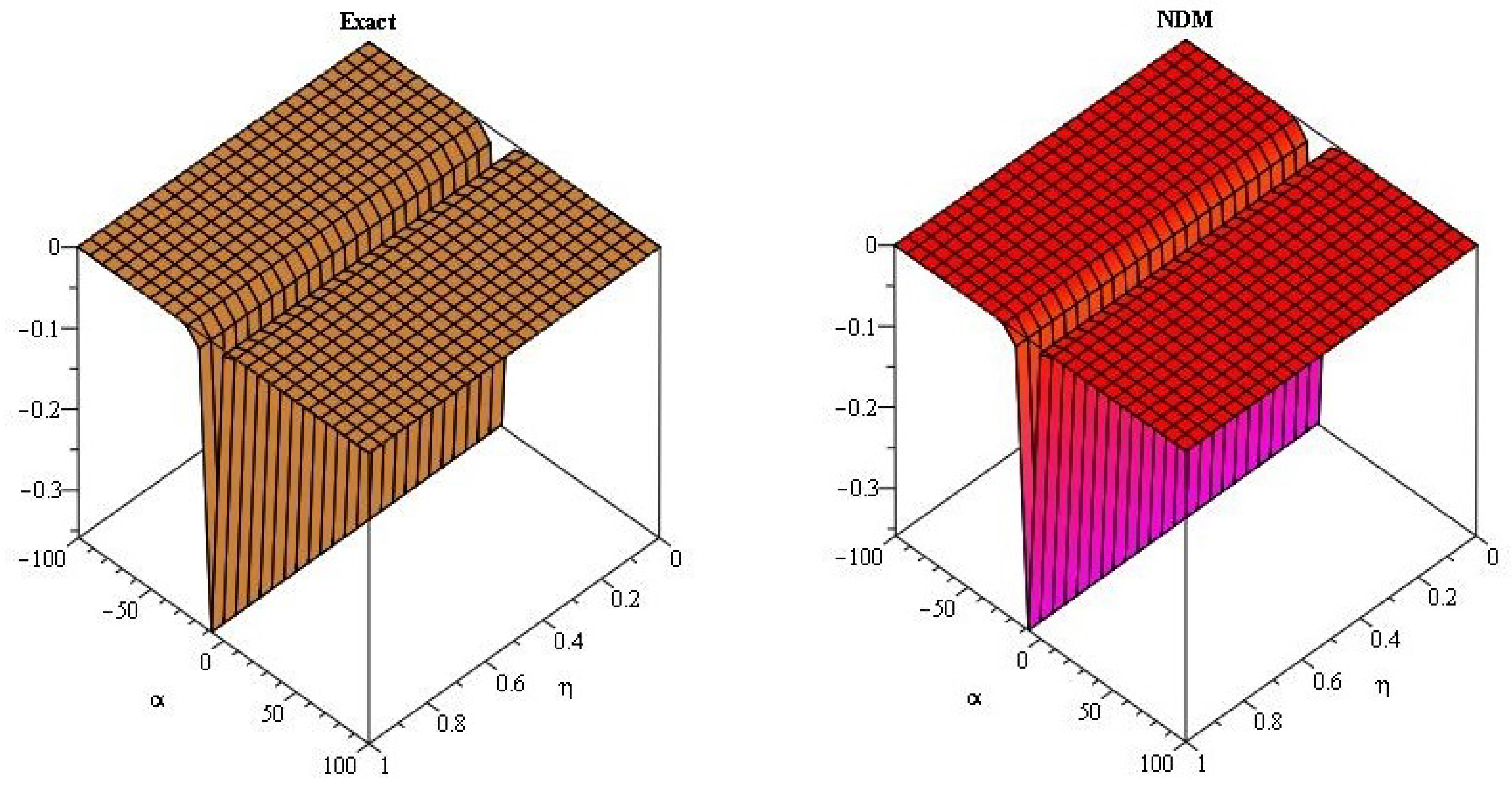
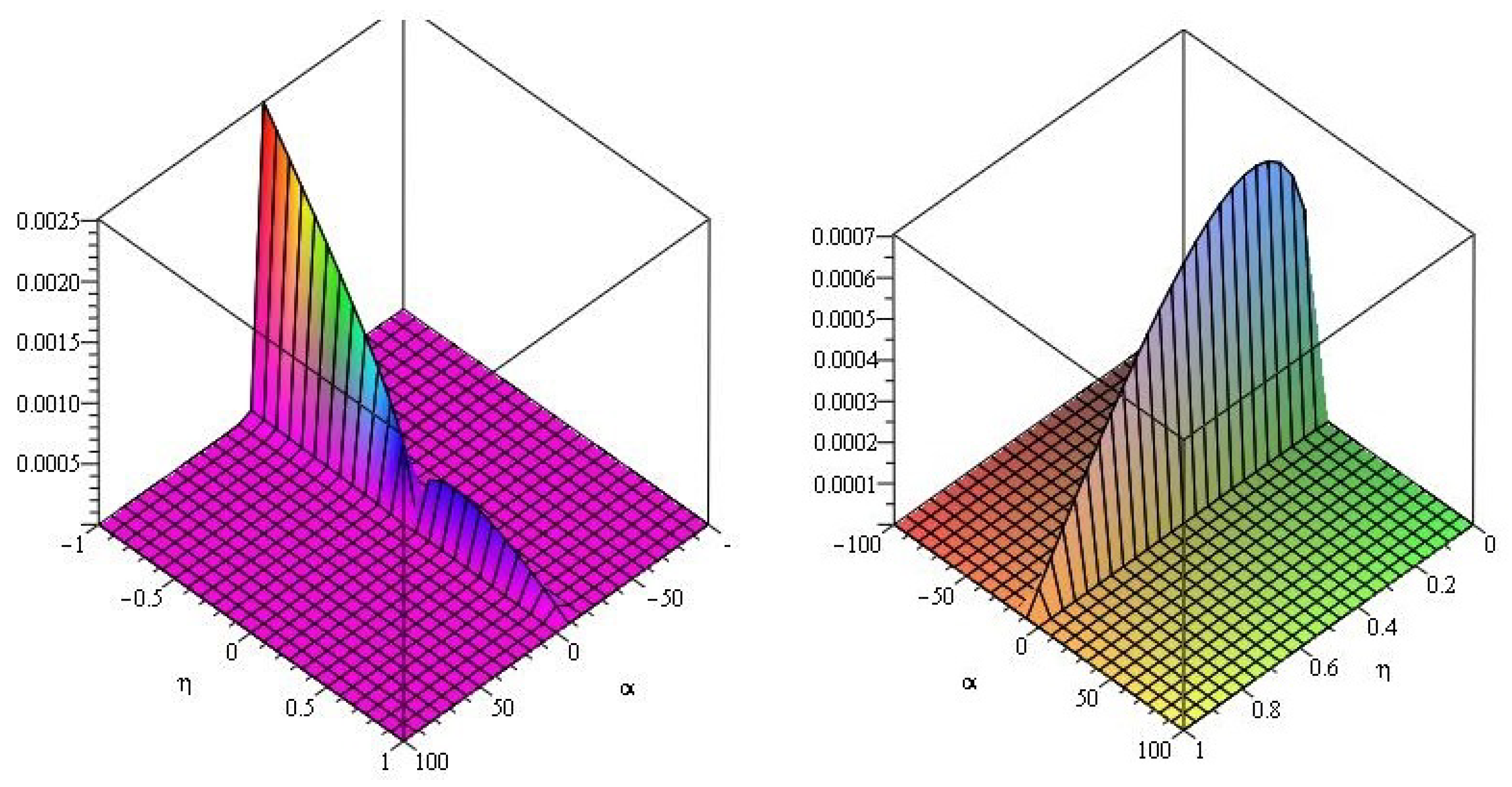
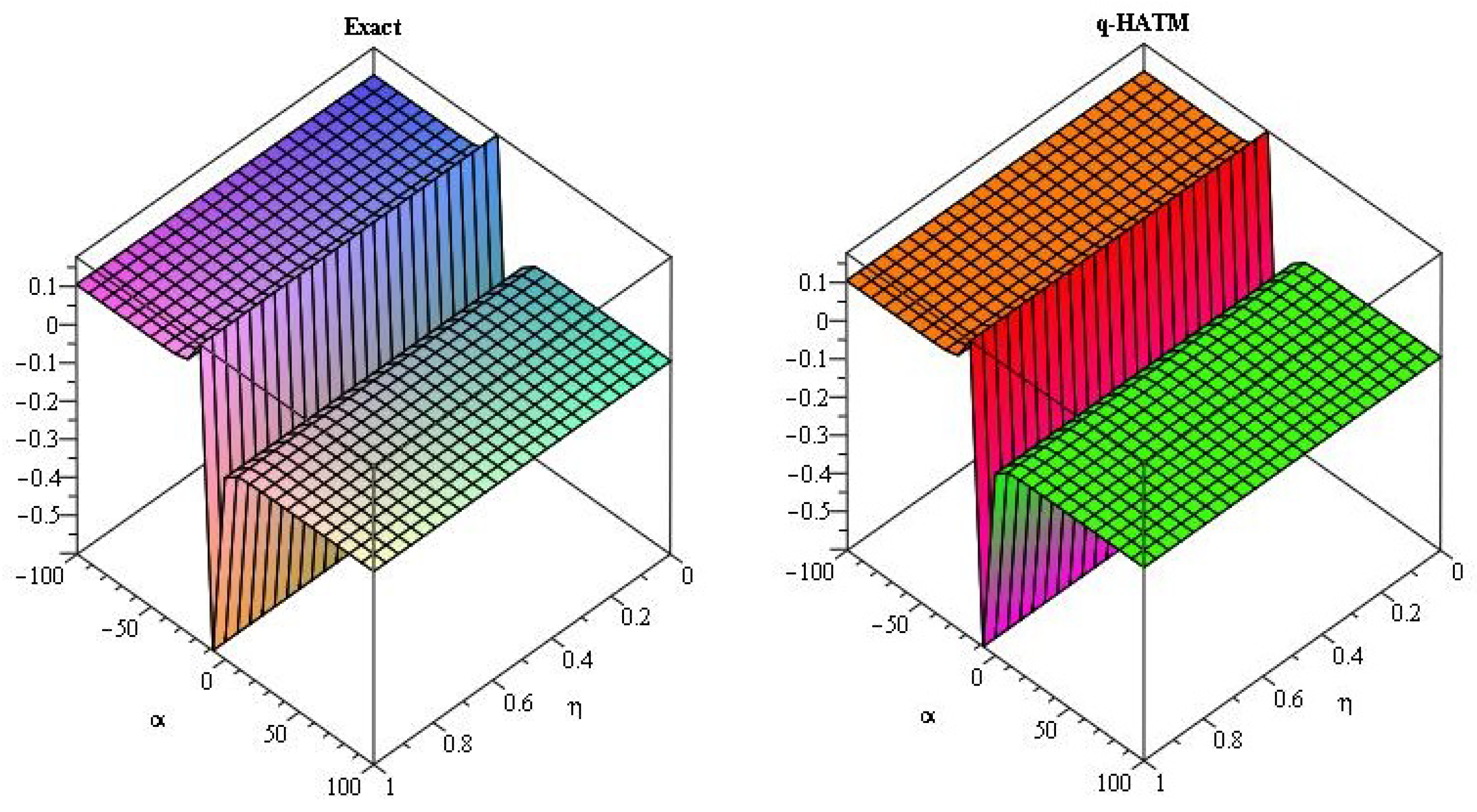
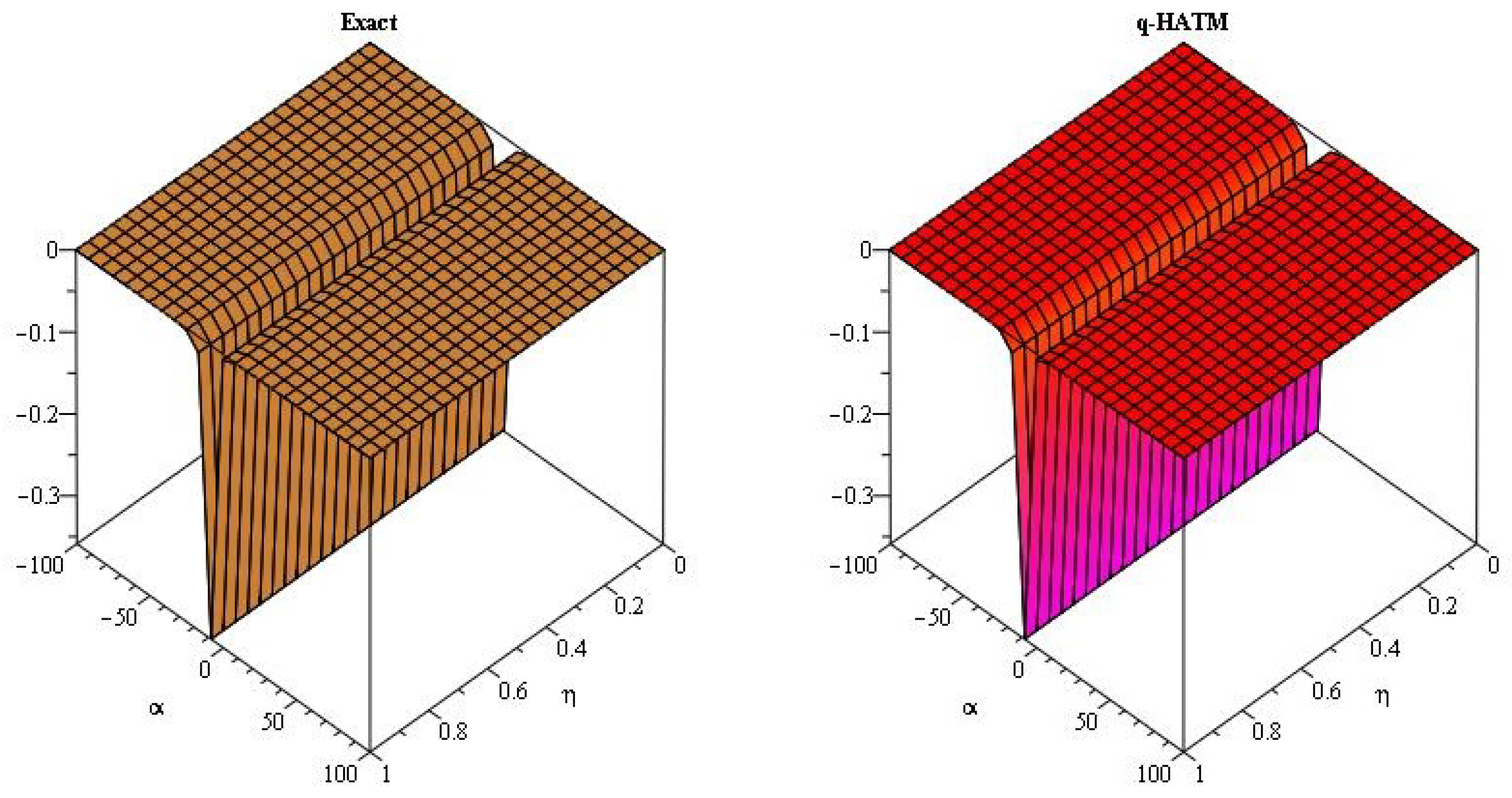
5. Numerical Examples
5.1. q-Homotopy Analysis Transform Method
5.2. q-Homotopy Analysis Transform Method
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Rudolf, H. (Ed.) Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Katugampola, U.N. A new approach to generalized fractional derivatives. Bull. Math. Anal. Appl. 2014, 6, 1–15. [Google Scholar]
- Srivastava, H.M.; Baleanu, D.; Li, C. Preface: Recent Advances in Fractional Dynamics; AIP Publishing LLC: College Park, MD, USA, 2016. [Google Scholar]
- Ahmad, J.; Mushtaq, M.; Sajjad, N. Exact Solution of Whitham Broer-Kaup Shallow Water Wave Equations. J. Sci. Arts 2015, 15, 5. [Google Scholar]
- Kupershmidt, B.A. Mathematics of dispersive water waves. Commun. Math. Phys. 1985, 99, 51–73. [Google Scholar] [CrossRef]
- Whitham, G.B. Variational methods and applications to water waves. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1967, 299, 6–25. [Google Scholar]
- Broer, L.J.F. Approximate equations for long water waves. Appl. Sci. Res. 1975, 31, 377–395. [Google Scholar] [CrossRef]
- Kaup, D.J. A higher-order water-wave equation and the method for solving it. Prog. Theor. Phys. 1975, 54, 396–408. [Google Scholar] [CrossRef]
- Ali, A.; Shah, K.; Khan, R.A. Numerical treatment for traveling wave solutions of fractional Whitham–Broer–Kaup equations. Alex. Eng. J. 2018, 57, 1991–1998. [Google Scholar] [CrossRef]
- Biazar, J.; Aminikhah, H. Study of convergence of homotopy perturbation method for systems of partial differential equations. Comput. Math. Appl. 2009, 58, 2221–2230. [Google Scholar] [CrossRef]
- Mohyud-Din, S.T.; Noor, M.A. Homotopy perturbation method for solving partial differential equations. Z. Naturforschung 2009, 64, 157–170. [Google Scholar] [CrossRef]
- Xie, F.; Yan, Z.; Zhang, H. Explicit and exact traveling wave solutions of Whitham–Broer–Kaup shallow water equations. Phys. Lett. A 2001, 285, 76–80. [Google Scholar] [CrossRef]
- Wang, L.; Chen, X. Approximate analytical solutions of time fractional Whitham–Broer–Kaup equations by a residual power series method. Entropy 2015, 17, 6519–6533. [Google Scholar] [CrossRef]
- El-Sayed, S.M.; Kaya, D. Exact and numerical traveling wave solutions of Whitham–Broer–Kaup equations. Appl. Math. Comput. 2005, 167, 1339–1349. [Google Scholar] [CrossRef]
- Saha Ray, S. A novel method for travelling wave solutions of fractional Whitham–Broer–Kaup, fractional modified Boussinesq and fractional approximate long wave equations in shallow water. Math. Methods Appl. Sci. 2015, 38, 1352–1368. [Google Scholar] [CrossRef]
- Mohyud-Din, S.T.; Yıldırım, A.; Demirli, G. Traveling wave solutions of Whitham–Broer–Kaup equations by homotopy perturbation method. J. King Saud-Univ.-Sci. 2010, 22, 173–176. [Google Scholar] [CrossRef]
- Kadem, A.; Baleanu, D. On Fractional Coupled Whitham–Broer–Kaup Equations; Publishing House of the Romanian Academy: Wellington, New Zealand, 2011. [Google Scholar]
- Iqbal, M. A fractional Whitham–Broer–Kaup equation and its possible application to Tsunami prevention. Therm. Sci. 2017, 21, 1847–1855. [Google Scholar]
- Ghehsareh, H.R.; Majlesi, A.; Zaghian, A. Lie Symmetry analysis and Conservation Laws for time fractional coupled Whitham–Broer–Kaup equations. UPB Sci. Bull. Ser. A Appl. Math. Phys. 2018, 80, 153–168. [Google Scholar]
- Zhang, Z.; Yong, X.; Chen, Y. Symmetry analysis for whitham-Broer-Kaup equations. J. Nonlinear Math. Phys. 2008, 15, 383–397. [Google Scholar] [CrossRef]
- Arshed, S.; Sadia, M. G′/G2-Expansion method: New traveling wave solutions for some nonlinear fractional partial differential equations. Opt. Quantum Electron. 2018, 50, 123. [Google Scholar] [CrossRef]
- Rani, A.; Ul-Hassan, Q.M.; Ashraf, M.; Ayub, K.; Khan, M.Y. A novel technique for solving nonlinear WBK equations of fractionl-order. J. Sci. Arts 2018, 18, 301–316. [Google Scholar]
- Singh, J.; Kumar, D.; Swroop, R. Numerical solution of time-and space-fractional coupled Burgers’ equations via homotopy algorithm. Alex. Eng. J. 2016, 55, 1753–1763. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G. Solution for fractional Zakharov–Kuznetsov equations by using two reliable techniques. Chin. J. Phys. 2019, 60, 313–330. [Google Scholar] [CrossRef]
- Singh, J.; Secer, A.; Swroop, R.; Kumar, D. A reliable analytical approach for a fractional model of advection-dispersion equation. Nonlinear Eng. 2019, 8, 107–116. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Kumar, D.; Singh, J. An efficient analytical technique for fractional model of vibration equation. Appl. Math. Model. 2017, 45, 192–204. [Google Scholar] [CrossRef]
- Rawashdeh, M.; Maitama, S. Finding exact solutions of nonlinear PDEs using the natural decomposition method. Math. Methods Appl. Sci. 2017, 40, 223–236. [Google Scholar] [CrossRef]
- Rawashdeh, M.S. The fractional natural decomposition method: Theories and applications. Math. Methods Appl. Sci. 2017, 40, 2362–2376. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Mustafa, S.; Kumam, P.; Arif, M. Analytical Solutions of Fractional-Order Diffusion Equations by Natural Transform Decomposition Method. Entropy 2019, 21, 557. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Kumam, P.; Arif, M.; Baleanu, D. Natural Transform Decomposition Method for Solving Fractional-Order Partial Differential Equations with Proportional Delay. Mathematics 2019, 7, 532. [Google Scholar] [CrossRef]
- Rawashdeh, M.S.; Maitama, S. Solving nonlinear ordinary differential equations using the NDM. J. Appl. Anal. Comput. 2015, 5, 77–88. [Google Scholar]
- Shah, R.; Khan, H.; Farooq, U.; Baleanu, D.; Kumam, P.; Arif, M. A New Analytical Technique to Solve System of Fractional-Order Partial Differential Equations. IEEE Access 2019, 7, 150037–150050. [Google Scholar] [CrossRef]
- Cherif, M.H.; Ziane, D.; Belghaba, K. Fractional natural decomposition method for solving fractional system of nonlinear equations of unsteady flow of a polytropic gas. Nonlinear Stud. 2018, 25, 753–764. [Google Scholar]
- Abdel-Rady, A.S.; Rida, S.Z.; Arafa, A.A.M.; Abedl-Rahim, H.R. Natural transform for solving fractional models. J. Appl. Math. Phys. 2015, 3, 1633. [Google Scholar] [CrossRef]
- Khan, H.; Shah, R.; Kumam, P.; Arif, M. Analytical Solutions of Fractional-Order Heat and Wave Equations by the Natural Transform Decomposition Method. Entropy 2019, 21, 597. [Google Scholar] [CrossRef]
- Eltayeb, H.; Abdalla, Y.T.; Bachar, I.; Khabir, M.H. Fractional Telegraph Equation and Its Solution by Natural Transform Decomposition Method. Symmetry 2019, 11, 334. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, R.; Khan, H.; Baleanu, D. Fractional Whitham–Broer–Kaup Equations within Modified Analytical Approaches. Axioms 2019, 8, 125. https://doi.org/10.3390/axioms8040125
Shah R, Khan H, Baleanu D. Fractional Whitham–Broer–Kaup Equations within Modified Analytical Approaches. Axioms. 2019; 8(4):125. https://doi.org/10.3390/axioms8040125
Chicago/Turabian StyleShah, Rasool, Hassan Khan, and Dumitru Baleanu. 2019. "Fractional Whitham–Broer–Kaup Equations within Modified Analytical Approaches" Axioms 8, no. 4: 125. https://doi.org/10.3390/axioms8040125
APA StyleShah, R., Khan, H., & Baleanu, D. (2019). Fractional Whitham–Broer–Kaup Equations within Modified Analytical Approaches. Axioms, 8(4), 125. https://doi.org/10.3390/axioms8040125





