Hereditary Coreflective Subcategories in Certain Categories of Abelian Semitopological Groups

Abstract

Let $\mathbf{A}$ be an epireflective subcategory of the category of all semitopological groups that consists only of abelian groups. We describe maximal hereditary coreflective subcategories of $\mathbf{A}$ that are not bicoreflective in $\mathbf{A}$ in the case that the $\mathbf{A}$-reflection of the discrete group of integers is a finite cyclic group, the group of integers with a topology that is not $T_0$, or the group of integers with the topology generated by its subgroups of the form $⟨p^n⟩$, where $n\in \mathbb{N}$, $p\in P$ and P is a given set of prime numbers.

1. Introduction

By $\mathbf{STopGr}$ we denote the category of all semitopological groups and continuous homomorphisms. All subcategories of $\mathbf{STopGr}$ are assumed to be full and isomorphism-closed. All homomorphisms are assumed to be continuous. It is well-known that a subcategory $\mathbf{A}$ of $\mathbf{STopGr}$ is epireflective in $\mathbf{STopGr}$ if and only if it is closed under the formation of subgroups and products. A coreflective subcategory $\mathbf{B}$ of $\mathbf{A}$ is called monocoreflective (bicoreflective) if every $\mathbf{B}$-coreflection is a monomorphimsm (a bimorphism, i.e., simultaneously a monomorphism and an epimorphism). A subcategory $\mathbf{B}$ of $\mathbf{A}$ is monocoreflective in $\mathbf{A}$ if and only if it is closed under the formation of coproducts and extremal quotient objects. It is interesting to investigate coreflective subcategories of $\mathbf{A}$ closed under additional constructions, namely products or subgroups. Productive (closed under the formation of arbitrary products) coreflective subcategories were studied in [1,2,3]. In [4] the author investigated hereditary (closed under the formation of subgroups) coreflective subcategories of $\mathbf{A}$. It is shown that in the categories $\mathbf{STopGr}$ and $\mathbf{QTopGr}$ (the category of all quasitopological groups), every hereditary coreflective subcategory that contains a group with a non-indiscrete topology is bicoreflective. Maximal hereditary coreflective subcategories of $\mathbf{A}$ that are not bicoreflective in $\mathbf{A}$ are described in the case that $\mathbf{A}$ is extremal epireflective (closed under the formation of products, subgroups and semitopological groups with finer topologies) in $\mathbf{STopGr}$, it contains only abelian groups and the $\mathbf{A}$-reflection $r\left(\mathbb{Z}\right)$ of the discrete groups of integers is a finite discrete cyclic group ${\mathbb{Z}}_n$. In this paper we describe the maximal hereditary coreflective, not bicoreflective subcategories in other epireflective subcategories of $\mathbf{STopGr}$.

2. Preliminaries and Notation

Recall that a semitopological group is a group with such topology that the group operation is separately continuous. A quasitopological group is a semitopological group with a continuous inverse. A paratopological group is a group with such topology that the group operation is continuous. The category of all paratopological groups will be denoted by $\mathbf{PTopGr}$. The category of all topological groups will be denoted by $\mathbf{TopGr}$. The subcategory of all abelian semitopological (paratopological) groups will be denoted by $\mathbf{STopAb}$ ($\mathbf{PTopAb}$).

Let $\mathbf{A}$ be an epireflective subcategory of $\mathbf{STopGr}$. Note that every hereditary coreflective subcategory of $\mathbf{A}$ is monocoreflective in $\mathbf{A}$ (see [4]). Hence a subcategory of $\mathbf{A}$ is hereditary and coreflective in $\mathbf{A}$ if and only if it is closed under the formation of coproducts, extremal quotients and subgroups.

Let $\mathbf{A}$ be an epireflective subcategory of $\mathbf{STopGr}$ consisting only of abelian groups and ${\left\{G_i\right\}}_{i\in I}$ be a family of groups from $\mathbf{A}$. By ${⨁}_{i\in I}^{*}{G}_i$ we denote the direct sum with the cross topology (see [5] (Example 1.2.6)). Let $i_0\in I$, $H_{i_0}=G_{i_0}$ and $H_i=\left\{g_i\right\}$, where $g_i\in G_i$, for $i\ne i_0$. A subset U is open in ${⨁}_{i\in I}^{*}{G}_i$ if and only if $U\cap {⨁}_{i\in I}^{*}{H}_i$ is open in ${⨁}_{i\in I}^{*}{H}_i$ for every choice of $i_0$ and $g_i$. The groups ${⨁}_{i\in I}^{*}{G}_i$ and ${\coprod }_{i\in I}^{\mathbf{A}}{G}_i$ (the coproduct of the family ${\left\{G_i\right\}}_{i\in I}$ in $\mathbf{A}$) have the same underlying set and the identity considered as a map ${⨁}_{i\in I}^{*}{G}_i\to {\coprod }_{i\in I}^{\mathbf{A}}{G}_i$ is continuous.

Note that monomorphisms in $\mathbf{A}$ are precisely the injective homomorphisms. However, epimorphisms do not need to be surjective.

3. Results

Let $\mathbf{A}$ be an epireflective subcategory of $\mathbf{STopGr}$ that contains only abelian groups. Our goal is to describe maximal hereditary coreflective subcategories of $\mathbf{A}$ that are not bicoreflective in $\mathbf{A}$. It is well known that if a coreflective subcategory $\mathbf{B}$ of $\mathbf{A}$ contains the $\mathbf{A}$-reflection $r\left(\mathbb{Z}\right)$ of the discrete group of integers, then it is bicoreflective in $\mathbf{A}$ (see [6] (Proposition 16.4)). It is easy to see that also the converse holds if $r\left(\mathbb{Z}\right)$ is a discrete group (see [4]). Now we show that it holds also in other cases. The case of discrete groups is included for the sake of completeness.

Lemma 1.

Let $\mathbf{A}$ be an epireflective subcategory of $\mathbf{STopGr}$ such that the $\mathbf{A}$-reflection of the discrete group of integers is one of the following:

1. 

a finite cyclic group,

2. 

the discrete group of integers,

3. 

the indiscrete group of integers,

4. 

the group of integers with the topology generated by its subgroups of the form $⟨p^n⟩$, where $n\in \mathbb{N}$, $p\in P$ and P is a given set of prime numbers.

Then a coreflective subcategory $\mathbf{B}$ of $\mathbf{A}$ is bicoreflective in $\mathbf{A}$ if and only if it contains the group $r\left(\mathbb{Z}\right)$.

Proof. 

Let $\mathbf{B}$ be a bicoreflective subcategory of $\mathbf{A}$. We show that the $\mathbf{B}$-coreflection of the group $r\left(\mathbb{Z}\right)$ is homeomorphic to $r\left(\mathbb{Z}\right)$. Let $r\left(\mathbb{Z}\right)$ be the group $Z_n$ for some $n\in \mathbb{N}$ and $c:cr\left(\mathbb{Z}\right)\to r\left(\mathbb{Z}\right)$ be the $\mathbf{B}$-coreflection of $r\left(\mathbb{Z}\right)$. Assume it is not surjective. Then $c\left(1\right)=k$ for some $k\in \mathbb{N}$, $k>1$, $k|n$. Let $⟨\frac{n}{k}⟩$ be the subgroup of $r\left(\mathbb{Z}\right)$ generated by $\frac{n}{k}$. There exists a continuous homomorphism $f:r\left(\mathbb{Z}\right)\to ⟨\frac{n}{k}⟩$ such that $f\left(1\right)=\frac{n}{k}$. Let $g:r\left(\mathbb{Z}\right)\to ⟨\frac{n}{k}⟩$ be the trivial homomorphism. Then $f\ne g$ but $f\circ c=g\circ c$. Hence c is not an epimorphism, a contradiction. It follows that c is bijective. The identity considered as a map $r\left(\mathbb{Z}\right)\to cr\left(\mathbb{Z}\right)$ is continuous, hence $r\left(\mathbb{Z}\right)\cong cr\left(\mathbb{Z}\right)$.

Now let $r\left(\mathbb{Z}\right)$ be the group of integers with one of the topologies specified in the lemma. Consider the $\mathbf{B}$-coreflection $c:cr\left(\mathbb{Z}\right)\to r\left(\mathbb{Z}\right)$. The image of $cr\left(\mathbb{Z}\right)$ under c is a non-trivial subgroup of $r\left(\mathbb{Z}\right)$ (otherwise c would not be an epimorphism). Note that the topologies on $r\left(\mathbb{Z}\right)$ specified in the lemma (part 2–4) have the property that all the non-trivial subgroups of $r\left(\mathbb{Z}\right)$ are homeomorphic to $r\left(\mathbb{Z}\right)$. Hence the image of $cr\left(\mathbb{Z}\right)$ is homeomorphic to $r\left(\mathbb{Z}\right)$. It follows from the definition of reflection that the topology on $r\left(\mathbb{Z}\right)$ is the finest topology on the group of integers in the subcategory $\mathbf{A}$, therefore also $cr\left(\mathbb{Z}\right)$ is homeomorphic to $r\left(\mathbb{Z}\right)$. □

Corollary 1.

Let $\mathbf{A}$ be an epireflective subcategory of $\mathbf{STopGr}$ such that $\mathbf{A}\subseteq \mathbf{STopAb}$ and $r\left(\mathbb{Z}\right)$ is the group of integers with the indiscrete topology. Let $\mathbf{B}$ be the subcategory of $\mathbf{A}$ consisting of all torsion groups from $\mathbf{A}$. Then $\mathbf{B}$ is the largest hereditary coreflective subcategory of $\mathbf{A}$ that is not bicoreflective in $\mathbf{A}$.

We will need also the following lemma:

Lemma 2.

Let $\mathbf{A}$ be an epireflective subcategory of $\mathbf{STopGr}$ and $\mathbf{B}$ be a monocoreflective subcategory of $\mathbf{A}$. Then $\mathbf{B}$ is bicoreflective in $\mathbf{A}$ if and only if the $\mathbf{B}$-coreflection of $r\left(\mathbb{Z}\right)$ is an $\mathbf{A}$-epimorphism.

Proof. 

Clearly, if $\mathbf{B}$ is bicoreflective in $\mathbf{A}$, then the $\mathbf{B}$-coreflection of $r\left(\mathbb{Z}\right)$ is an $\mathbf{A}$-epimorphism. Assume that the $\mathbf{B}$-coreflection $c:cr\left(\mathbb{Z}\right)\to r\left(\mathbb{Z}\right)$ of $r\left(\mathbb{Z}\right)$ is an epimorphism. We will show that the $\mathbf{B}$-coreflection $c^{\prime }:cG\to G$ for an arbitrary group G from $\mathbf{A}$ is an epimorphism. Let H be a group from $\mathbf{A}$ and $f_1,f_2:G\to H$ be homomorphisms such that $f_1\circ c^{\prime }=f_2\circ c^{\prime }$. For every $g\in G$ let $G_g$ be a group isomorphic to $r\left(\mathbb{Z}\right)$ and $i_g:r\left(\mathbb{Z}\right)\cong G_g\to G$ be the homomorphism given by $i_g\left(1\right)=g$. Moreover, let $c{G}_g\to G_g$ be the $\mathbf{B}$-coreflection of $G_g$. Then $h:{\coprod }_{g\in G}^{\mathbf{A}}c{G}_g\to {\coprod }_{g\in G}^{\mathbf{A}}{G}_g\to G$ is an epimorphism. There exists a unique homomorphism $\overline{h}:{\coprod }_{g\in G}^{\mathbf{A}}c{G}_g\to cG$ such that the following diagram commutes:

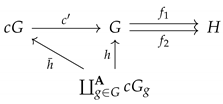
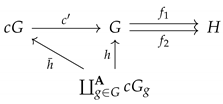
We have $f_1\circ h=f_1\circ c^{\prime }\circ \overline{h}=f_2\circ c^{\prime }\circ \overline{h}=f_2\circ h$. But h is an epimorphism, therefore $f_1=f_2$ and $c^{\prime }$ is an epimorphism. □

In the following example we show that Lemma 1 does not hold in general.

Example 1.

Let Z be the group of integers with the topology generated by the subgroup $\{2n:n\in Z\}$ and $\mathbf{A}$ be the smallest epireflective subcategory containing Z. Then $\mathbf{A}$ consists of subgroups of products of the form ${\prod }_{i\in I}{G}_i$, where each $G_i$ is isomorphic to the group Z. Let $\mathbf{B}$ be the subcategory consisting of all indiscrete groups from $\mathbf{A}$. The $\mathbf{B}$-coreflection of $r\left(\mathbb{Z}\right)\cong Z$ is $c:cr\left(\mathbb{Z}\right)\to r\left(\mathbb{Z}\right)$, where $cr\left(\mathbb{Z}\right)$ is the indiscrete group of integers and $c\left(1\right)=2$. Clearly, c is an $\mathbf{A}$-epimorphism. Hence, by Lemma 2, $\mathbf{B}$ is bicoreflective in $\mathbf{A}$, but it does not contain the group $r\left(\mathbb{Z}\right)$.

Consider a finite cyclic semitpological group $Z_n$. The closure of $\left\{0\right\}$ in $Z_n$ is a subgroup of $Z_n$ and it is the smallest (with respect to inclusion) open neighborhood of 0. The same holds for the group of integers with a non-$T_0$ topology. Moreover, we have the following simple fact:

Lemma 3.

Let G and H be cyclic semitopological groups, either finite or infinite and non-$T_0$. Let $n,k\in \mathbb{N}$ be such that $\overline{\left\{0\right\}}=⟨n⟩$ in G and $\overline{\left\{0\right\}}=⟨k⟩$ in H. Consider the subgroup $⟨\left(1,1\right)⟩$ of $G{\times }^{*}H$. Then $\overline{\left\{(0,0)\right\}}=⟨\left(m,m\right)⟩$, where m is the least common multiple of n and k.

Proof. 

Let U be an open neighborhood of $\left(0,0\right)$ in $G{\times }^{*}H$. Then $V=U\cap G{\times }^{*}\left\{0\right\}$ is open in $G{\times }^{*}\left\{0\right\}$. Therefore V (and hence also U) contains $⟨n⟩{\times }^{*}\left\{0\right\}$. Analogously, U contains $\left\{0\right\}{\times }^{*}⟨k⟩$. Hence U contains $⟨n⟩{\times }^{*}⟨k⟩$. Therefore every neighborhood of $\left(0,0\right)$ in $⟨\left(1,1\right)⟩$ contains $⟨\left(m,m\right)⟩$. The subgroup $⟨\left(m,m\right)⟩$ is open in $⟨\left(1,1\right)⟩$, since $⟨n⟩\times ⟨k⟩$ is open in $G{\times }^{*}H$. □

Clearly, the above lemma can be generalized to any finite number of groups.

The following proposition is a generalization of [4] (Proposition 4.9).

Proposition 1.

Let $\mathbf{A}$ be an epireflective subcategory of $\mathbf{STopGr}$ such that $\mathbf{A}\subseteq \mathbf{STopAb}$ and $r\left(\mathbb{Z}\right)=Z_n$, where $n=p_1^{{\alpha }_1}\cdots p_k^{{\alpha }_k}$ is the prime factorization of n. For $i\in \{1,\dots ,k\}$, consider the group $Z_{p_i^{{\alpha }_i}}$ with the subspace topology induced from $r\left(\mathbb{Z}\right)$. Let $m_i$ be the natural number such that $\overline{\left\{0\right\}}=⟨p_i^{m_i}⟩$ in $Z_{p_i^{{\alpha }_i}}$. We define the subcategories ${\mathbf{B}}_i$ and ${\mathbf{C}}_i$ of $\mathbf{A}$ as follows:

1. 

If every cyclic group from $\mathbf{A}$ of order $p_i^{{\alpha }_i}$ is homeomorphic to $Z_{p_i^{{\alpha }_i}}$ with the subspace topology induced from $r\left(\mathbb{Z}\right)$ or there exists a cyclic group $Z_{p_i^{{\beta }_i}}$ (where ${\beta }_i<{\alpha }_i$) from $\mathbf{A}$ such that $\overline{\left\{0\right\}}=⟨p_i^{m_i}⟩$ in $Z_{p_i^{{\beta }_i}}$, then let ${\mathbf{B}}_i$ be the subcategory consisting precisely of those groups from $\mathbf{A}$ that do not have an element of order $p_i^{{\alpha }_i}$.

2. 

If the subgroup $Z_{p_i^{{\alpha }_i}}$ of $r\left(\mathbb{Z}\right)$ is not indiscrete, let ${\mathbf{C}}_i$ be the subcategory consisting precisely of such groups G from $\mathbf{A}$ that if H is a cyclic subgroup of G of order $p_i^{{\beta }_i}$, where ${\beta }_i\le {\alpha }_i$, then the index of $\overline{\left\{e_H\right\}}$ in H is less than $p_i^{m_i}$.

Then ${\mathbf{B}}_i$ and ${\mathbf{C}}_i$ are maximal hereditary coreflective subcategories of $\mathbf{A}$ that are not bicoreflective in $\mathbf{A}$.

Note that there does not need to be a subcategory ${\mathbf{B}}_i$ or ${\mathbf{C}}_i$ for every $i\in \{1,\dots ,k\}$.

Proof. 

Clearly, the subcategories ${\mathbf{B}}_i$ and ${\mathbf{C}}_i$ are hereditary and, by Lemma 1, they are not bicoreflective in $\mathbf{A}$. The subcategories ${\mathbf{B}}_i$ are coreflective in $\mathbf{A}$.

We need to show that also the subcategories ${\mathbf{C}}_i$ are coreflective in $\mathbf{A}$. Let ${\left\{G_j\right\}}_{j\in I}$ be a family of groups from ${\mathbf{C}}_i$ for some $i\in \{1,\dots ,k\}$, ${\coprod }_{j\in I}{G}_j\to G$ be an extremal $\mathbf{A}$-epimorphism and f be the homomorphism ${⨁}_{j\in J}^{*}{G}_j\to {\coprod }_{j\in I}{G}_j\to G$. Assume that G has a subgroup H homeomorphic to $Z_{p_i^{{\alpha }_i}}$ with the subspace topology induced from $r\left(\mathbb{Z}\right)$. Let x be an element of ${⨁}_{j\in I}^{*}{G}_j$ such that $⟨f\left(x\right)⟩=H$. Then the subgroup $⟨x⟩$ is also homeomorphic to $Z_{p_i^{{\alpha }_i}}$. Without loss of generality we may assume that $⟨x⟩=⟨\left(x_1,\dots ,x_m\right)⟩$ is a subgroup of $⟨x_1⟩{\times }^{*}\cdots {\times }^{*}⟨x_m⟩$, where each $x_l$ belongs to some $G_{j_l}\in {\left\{G_j\right\}}_{j\in I}$. By Lemma 3, the topology of $⟨x⟩$ is coarser then the topology of $Z_{p_i^{{\alpha }_i}}$, a contradiction.

Lastly we show that every hereditary coreflective subcategory of $\mathbf{A}$ that is not bicoreflective in $\mathbf{A}$ is contained in one of the subcategories ${\mathbf{B}}_i$ or ${\mathbf{C}}_i$. If a subcategory $\mathbf{D}$ is hereditary and coreflective in $\mathbf{A}$, but not bicoreflective in $\mathbf{A}$, then it does not contain the group $r\left(\mathbb{Z}\right)$. Therefore it does not contain one of its subgroups $Z_{p_i^{{\alpha }_i}}$. Hence, it either does not contain a cyclic group of order $p_i^{{\alpha }_i}$ (and then $\mathbf{D}\subseteq {\mathbf{B}}_i$) or it does not contain the group $Z_{p_i^{{\alpha }_i}}$ with $\overline{\left\{0\right\}}=⟨p_i^{m_i}⟩$. Then it also does not contain a cyclic group $Z_{p_i^{{\beta }_i}}$, where ${\beta }_i\le {\alpha }_i$, with $\overline{\left\{0\right\}}=⟨p_i^{m_i}⟩$, and then $\mathbf{D}\subseteq {\mathbf{C}}_i$. □

In [4] we presented examples of such epireflective subcategories $\mathbf{A}$ of $\mathbf{STopGr}$ that every hereditary coreflective subcategory of $\mathbf{A}$ that contains a group with a non-indiscrete topology is bicoreflective in $\mathbf{A}$. Here we give another example of subcategories of $\mathbf{STopGr}$ with this property. Note that if the subcategory $\mathbf{A}$ from the following example consists only of abelian groups, then we easily obtain the following result from the above proposition.

Example 2.

Let $\mathbf{A}$ be an epireflective subcategory of $\mathbf{STopGr}$ such that $r\left(\mathbb{Z}\right)$ is the discrete cyclic group ${\mathbb{Z}}_p$, where p is a prime number. Then every hereditary coreflective subcategory $\mathbf{B}$ of $\mathbf{A}$ that contains a group with a non-indiscrete topology is bicoreflective in $\mathbf{A}$. Let G be a non-indiscrete group from $\mathbf{B}$ and U be an open neighborhood of $e_G$ such that $U\ne G$. Choose an element $x\in G\setminus U$. The order of x is p and the subgroup $⟨x⟩$ of G is discrete, therefore $⟨x⟩\cong {\mathbb{Z}}_p$ belongs to $\mathbf{B}$ and $\mathbf{B}$ is bicoreflective in $\mathbf{A}$.

Proposition 2.

Let $\mathbf{A}$ be an epireflective subcategory of $\mathbf{STopGr}$ such that $\mathbf{A}\subseteq \mathbf{PTopAb}$ and $r\left(\mathbb{Z}\right)$ is the group of integers with the topology generated by its subgroups of the form $⟨p^n⟩$, where $n\in \mathbb{N}$, $p\in P$ and P is a given set of prime numbers. Let $p\in P$ and ${\mathbf{B}}_p$ be the subcategory of $\mathbf{A}$ consisting precisely of such groups G from $\mathbf{A}$ that if H is an infinite cyclic subgroup of G then there exists an $n\in \mathbb{N}$ such that the subgroup of index $p^n$ is not open in H. Then those ${\mathbf{B}}_p$ that contain a group with an element of infinite order are maximal hereditary coreflective subcategories of $\mathbf{A}$ that are not bicoreflective in $\mathbf{A}$. If all ${\mathbf{B}}_p$ contain only torsion groups, then they are all equal to the subcategory $\mathbf{B}$ of all torsion groups from $\mathbf{A}$ and $\mathbf{B}$ is the largest hereditary coreflective subcategory of $\mathbf{A}$ that is not bicoreflective in $\mathbf{A}$.

Proof. 

Obviously, the subcategory $\mathbf{B}$ is hereditary and coreflective, but not bicoreflective in $\mathbf{A}$. If all subcategories ${\mathbf{B}}_p$ contain only torsion groups, then for every group G from $\mathbf{A}$ and every element $g\in G$ of infinite order we have $⟨g⟩\cong r\left(\mathbb{Z}\right)$. Therefore every hereditary coreflective subcategory of $\mathbf{A}$ that is not bicoreflective in $\mathbf{A}$ is contained in $\mathbf{B}$ and the subcategory $\mathbf{B}$ is maximal with this property.

Now assume that at least one of the subcategories ${\mathbf{B}}_p$ contains a group with an element of infinite order. Clearly, every subcategory ${\mathbf{B}}_p$ is hereditary. It does not contain the group $r\left(\mathbb{Z}\right)$, and therefore, by Lemma 1, it is not bicoreflective in $\mathbf{A}$.

We show that the subcategories ${\mathbf{B}}_p$ are coreflective in $\mathbf{A}$. Let $p\in P$, ${\left\{G_i\right\}}_{i\in I}$ be a family of groups from ${\mathbf{B}}_p$ and $f:{\coprod }_{i\in I}^{\mathbf{A}}{G}_i\to G$ be an extremal $\mathbf{A}$-epimorphism. Let x be an element of ${\coprod }_{i\in I}^{\mathbf{A}}{G}_i$ such that the subgroup of index $p^n$ is open in $⟨f\left(x\right)⟩$ for every $n\in \mathbb{N}$. Then also the subgroup of index $p^n$ of $⟨x⟩$ is open in $⟨x⟩$ for every $n\in \mathbb{N}$. Without loss of generality we may assume that $⟨x⟩=⟨\left(x_1,\dots ,x_k\right)⟩$ is a subgroup of $⟨x_1⟩\bigsqcup \cdots \bigsqcup ⟨x_k⟩=⟨x_1⟩\times \cdots \times ⟨x_k⟩$, where $⟨x_1⟩\times \cdots \times ⟨x_k⟩$ is the product with the usual topology and each $x_j$ belongs to some $G_{i_j}\in {\left\{G_i\right\}}_{i\in I}$. For every $j\in \{1,\dots ,k\}$ there exists a natural number $n_j$ such that the subgroup of index $p^{n_j}$ is not open in $⟨x_j⟩$. Then the subgroup of $⟨x⟩$ of index $p^{n_{j_0}}$, where $n_{j_0}$ is the largest from $n_1,\dots ,n_k$, is not open in $⟨x⟩$, a contradiction.

Next we show that every hereditary coreflective subcategory of $\mathbf{A}$ that is not bicoreflective in $\mathbf{A}$ is contained in some ${\mathbf{B}}_p$. Let $\mathbf{C}$ be a hereditary coreflective subcategory of $\mathbf{A}$ that is not bicoreflective in $\mathbf{A}$. Then $\mathbf{C}$ does not contain the group $r\left(\mathbb{Z}\right)$. If $\mathbf{C}$ contains only torsion groups, then $\mathbf{C}\subseteq {\mathbf{B}}_p$ for every $p\in P$. Otherwise $\mathbf{C}$ contains the group of integers with a topology such that its subgroup of index $p^n$ is not open for some $p\in P$ and $n\in \mathbb{N}$. Therefore $\mathbf{C}$ is contained in ${\mathbf{B}}_p$. □

Proposition 3.

Let $\mathbf{A}$ be an epireflective subcategory of $\mathbf{STopGr}$ such that $\mathbf{A}\subseteq \mathbf{STopAb}$ and $r\left(\mathbb{Z}\right)$ is the group of integers with a non-$T_0$ topology. Let the closure of $\left\{0\right\}$ in $r\left(\mathbb{Z}\right)$ be the subgroup $⟨n⟩$. Then the following holds:

1. 

If the embedding $⟨n⟩\to r\left(\mathbb{Z}\right)$ is an $\mathbf{A}$-epimorphism, then the subcategory $\mathbf{B}$ of all torsion groups from $\mathbf{A}$ is the largest hereditary coreflective subcategory of $\mathbf{A}$ that is not bicoreflective in $\mathbf{A}$.

2. 

For every minimal natural number k such that $k|n$ and the embedding $⟨k⟩\to r\left(\mathbb{Z}\right)$ is not an $\mathbf{A}$-epimorphism let ${\mathbf{B}}_k$ be the subcategory consisting of such groups G from $\mathbf{A}$ that if H is a cyclic subgroup of G then the index of $\overline{\left\{e_H\right\}}$ in H is at most $\frac{n}{k}$. The subcategories ${\mathbf{B}}_k$ are maximal hereditary coreflective subcategories of $\mathbf{A}$ that are not bicoreflective in $\mathbf{A}$.

Assume that for every minimal natural number k such that $k|n$ and the embedding $⟨k⟩\to r\left(\mathbb{Z}\right)$ is not an $\mathbf{A}$-epimorphism, $\mathbf{A}$ contains a finite cyclic group $G_k$ such that the index of $\overline{\left\{e_{G_k}\right\}}$ in $G_k$ is greater than $\frac{n}{k}$. Then the subcategory $\mathbf{B}$ of all torsion groups from $\mathbf{A}$ is also a maximal hereditary coreflective subcategory of $\mathbf{A}$ that is not bicoreflective in $\mathbf{A}$.

Proof. 

Assume that the closure of $\left\{0\right\}$ in $r\left(\mathbb{Z}\right)$ is the subgroup $⟨n⟩$ and the embedding $i:⟨n⟩\to r\left(\mathbb{Z}\right)$ is an $\mathbf{A}$-epimorphism. Clearly, the subcategory $\mathbf{B}$ is hereditary and coreflective, but not bicoreflective in $\mathbf{A}$. We need to show that it is maximal with this property. Let $\mathbf{C}$ be a hereditary coreflective subcategory of $\mathbf{A}$ that contains the group Z with some topology and $c:cr\left(\mathbb{Z}\right)\to r\left(\mathbb{Z}\right)$ be the $\mathbf{B}$-coreflection of $r\left(\mathbb{Z}\right)$. Assume that $c\left(1\right)=k$. Let $f:Z\to r\left(\mathbb{Z}\right)$ be the homomorphism given by $f\left(1\right)=n$. Then f is continuous. There exists a unique homomorphism $\overline{f}:Z\to cr\left(\mathbb{Z}\right)$ such that $f=c\circ \overline{f}$. Hence $k>0$ and $k|n$. Therefore c is an $\mathbf{A}$-epimorphism and, by Lemma 2, the subcategory $\mathbf{B}$ is bicoreflective in $\mathbf{A}$.

Now assume that the embedding $i:⟨n⟩\to r\left(\mathbb{Z}\right)$ is not an $\mathbf{A}$-epimorphism. The subcategory $\mathbf{B}$ is hereditary and coreflective in $\mathbf{A}$, but not bicoreflective in $\mathbf{A}$. Let k be minimal such that $k|n$ and the embedding $⟨k⟩\to r\left(\mathbb{Z}\right)$ is not an $\mathbf{A}$-epimorphism. Clearly, the subcategory ${\mathbf{B}}_k$ is hereditary. For the ${\mathbf{B}}_k$-coreflection $c:cr\left(\mathbb{Z}\right)\to r\left(\mathbb{Z}\right)$ we have $c\left(1\right)\ge k$. Therefore it is not an epimorphism and ${\mathbf{B}}_k$ is not bicoreflective in $\mathbf{A}$.

We need to show that ${\mathbf{B}}_k$ is coreflective in $\mathbf{A}$. Let ${\left\{G_i\right\}}_{i\in I}$ be a family of groups from ${\mathbf{B}}_k$, ${\coprod }_{i\in I}^{\mathbf{A}}{G}_i\to G$ be an extremal $\mathbf{A}$-epimorphism and f be the homomorphism ${⨁}_{i\in I}^{*}{G}_i\to {\coprod }_{i\in I}^{\mathbf{A}}{G}_i\to G$. Assume that x is an element of ${⨁}_{i\in I}^{*}{G}_i$ such that the index of $\overline{\left\{e_{⟨f\left(x\right)⟩}\right\}}$ in $⟨f\left(x\right)⟩$ is greater than $\frac{n}{k}$. Then also the index of $\overline{\left\{e_{⟨x⟩}\right\}}$ in $⟨x⟩$ is greater than $\frac{n}{k}$. Without loss of generality we may assume that $⟨x⟩=⟨\left(x_1,\dots ,x_m\right)⟩$ is a subgroup of $⟨x_i⟩{\times }^{*}\cdots {\times }^{*}⟨x_m⟩$, where each $x_j$ is an element of some $G_{i_j}$. The index of $\overline{\left\{e_{⟨x_j⟩}\right\}}$ in $⟨x_j⟩$ is a divisor of $\frac{n}{k}$ for every $j\in \{1,\dots ,m\}$. Then, by Lemma 3, the index of $\overline{\left\{e_{⟨x⟩}\right\}}$ in $⟨x⟩$ is at most $\frac{n}{k}$, a contradiction.

Lastly, we show that every hereditary coreflective subcategory of $\mathbf{A}$ that is not bicoreflective in $\mathbf{A}$ is contained in $\mathbf{B}$ or ${\mathbf{B}}_k$. Let $\mathbf{C}$ be a hereditary coreflective subcategory of $\mathbf{A}$ that is not bicoreflective in $\mathbf{A}$. Let $c:cr\left(\mathbb{Z}\right)\to r\left(\mathbb{Z}\right)$ be the $\mathbf{C}$-coreflection of $r\left(\mathbb{Z}\right)$. If it is a trivial homomorphism, then $\mathbf{C}$ is contained in $\mathbf{B}$. Otherwise $c\left(1\right)\ge k$, where k is minimal such that $k|n$ and the embedding $⟨k⟩\to r\left(\mathbb{Z}\right)$ is not an $\mathbf{A}$-epimorphism. Assume that G is a cyclic group from $\mathbf{C}$ that does not belong to ${\mathbf{B}}_k$. Then the index of $\overline{\left\{e_G\right\}}$ in G is greater than $\frac{n}{k}$. Then $\mathbf{C}$ contains the group of integers Z with a topology such that the index of $\overline{\left\{0\right\}}$ in Z is greater than $\frac{n}{k}$ (a subgroup of $cr\left(\mathbb{Z}\right)\bigsqcup G$). Then there exists a homomorphism $f:Z\to r\left(\mathbb{Z}\right)$ such that $f\left(1\right)<k$. Then also $c\left(1\right)<k$, a contradiction. Therefore $\mathbf{C}$ is contained in ${\mathbf{B}}_k$. Note that if for some minimal natural number k such that $k|n$ and the embedding $⟨k⟩\to r\left(\mathbb{Z}\right)$ is not an $\mathbf{A}$-epimorphism, $\mathbf{A}$ does not contain a finite cyclic group G such that the index of $\overline{\left\{e_G\right\}}$ in G is greater than $\frac{n}{k}$, then the subcategory $\mathbf{B}$ is contained in ${\mathbf{B}}_k$, and therefore it is not maximal. □