Abstract
Using the defined notion of the inference with multiply-conclusion rules, we show that in the logics enjoying the disjunction property, any derivable rule can be inferred from the single-conclusion rules and a single multiple-conclusion rule, which represents the disjunction property. Also, the conversion algorithm of single- and multiple-conclusion deductive systems into each other is studied.
1. Introduction
The question “What is inference rule?” is almost as profound as the question “What is truth?.” Speaking very generally, inference rules are the acceptable means of reasoning. They give us a way to go from a set of accepted statements (propositions, judgments) to an acceptable statement (proposition, judgment). Rules can be given in different forms: Aristotle used rules in a form of moduses like [1] (§1 (6))
Nowadays, we would write such a rule as
In this paper, we consider only propositional logics. Thus, the premises and conclusions are propositions (propositional formulas). But even in this case, one may consider different forms of modus ponens [2]:
As we see, the former rule is about conditional, while the latter rule is about entailment. Clearly, the second form of modus ponens is a rule of meta-logic rather than a rule of logic. In this paper we confine ourselves to rules of the first form: a finitary structural inference rule or a modus rule is given by an ordered pair , where is a finite (maybe empty) set of formulas and A is a formula, and we use or to denote such a pair. Any pair constitutes the modus rule that allows for any substitution , to infer from .
Let us note that curiously enough, the rule of substitution “for any substitution, , from A infer ” is not structural: it allows to infer formula q from formula p, where p and q are propositional variables, but the structural rule would allow to infer any formula from any formula.
By logic we understand a (finitary structural) consequence relation defined in the following way; for all sets of formulas , and every formula A
Given a logic , we define a set of theorems of to be
It is customary to define a logic by a deductive system—a set of rules and axioms. Because axioms can be viewed as rules without premises, we assume that a deductive system is a set of rules and a procedure for derivation such that if and only if A can be derived from by rules .
We extend the notion of the deductive system by allowing to use multiple-conclusion rules. This requires to extend the notion of derivation, and we discuss this generalization in Section 3. Let us stress out that we do not consider multiple-conclusion logics in the sense of Shoesmith and Smiley [3], Carnap’s logics of junctives [4], or hyperformulas [5]. Instead, we study regular logics defined by the deductive systems that admit multiple-conclusion rules. For instance, one can use the following rules to define the classical logic [3] (2.3) and further discussions in Chapter 18 of this book):
The idea of using multiple-conclusion rules can be traced back at least to Carnap [6]. Much earlier, Peirce introduced the dialogisms, which are essentially the multiple-conclusion rules, but he preferred to replace them with the single-conclusion rules [7]. Gentzen’s sequent also can be viewed as a multiple-conclusion construction. The following quotation from the authors of [3] explains why Carnap, and not Gentzen, perhaps, should be regarded as the one who introduced multiple-conclusion rules: “Its germ can be found in Gerhard Gentzen’s celebrated Untersuchungen über das logische Schliessen (1934) if one is prepared to interpret his calculus of ‘sequents’ as a metatheory for a multiple-conclusion logic, but this is contrary to Gentzen’s own interpretation, and it was Rudolf Carnap who first consciously broached the subject in his book Formalization of logic (1943)” [3] (Section 2.1, the historical note).
Carnap’s motivation for introducing multiple-conclusion rules was as follows: if we want to syntactically characterize a two-valued classical semantics, this syntactical system should be valid (up to matrix isomorphisms) only in the two-element Boolean matrix. Let us consider matrices depicted in Figure 1 (the designated elements are marked by a bullet). It is not hard to see that any rule which is valid in matrix , is valid in all matrices for all .
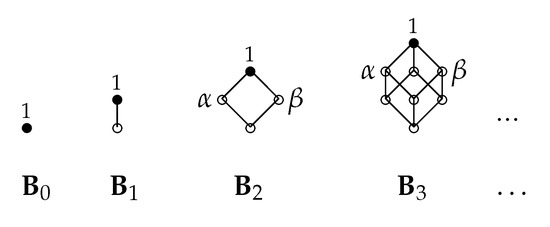
Figure 1.
Boolean matrices.
Carnap’s solution was to employ the rules of a different kind: a (structural) multiple-conclusion rule (or multiple-alternative rule, or m-rule for short) is an ordered pair of finite sets of formulas. m-rule is valid in a logical matrix if for any valuation such that for all , there is such that , that is,
Let us consider the m-rules
Then, if we consider logical matrices from Figure 1, we can see that
Thus, if we employ m-rules and as inference rules together with modus ponens and axioms of the Classical Logic , there is only one logical matrix in which all these rules and axioms are valid, namely .
In 1932 Gödel stated without proof (the proof is due to Gentzen) that intuitionistic propositional logic enjoys the disjunction property: for any formulas , if formula is a theorem, then at least one of the formulas must be a theorem. It is not true for the classical propositional logic: formula is a theorem, while neither p, nor are theorems. Let us point out that even though the classical logic does not enjoy the disjunction property, the rule can be used as an inference rule without expanding the set of theorems.
In what follows, rule plays a special role. In the setting of natural deduction, ∨-elimination rule is as depicted in Figure 2:
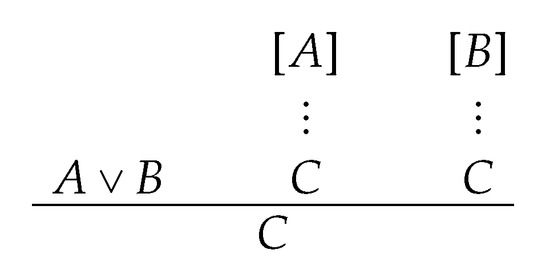
Figure 2.
∨-Elimination as a natural deduction rule.
That is, if we can derive and we can derive C separately from A and from B, then we can derive C.
In the multiple-conclusion setting (with the use of ) ∨-elimination can be expressed in a more natural way as depicted below in Figure 3:
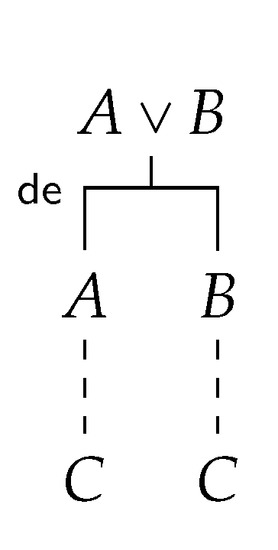
Figure 3.
∨-Elimination as a multiple-conclusion rule.
In this paper, we study how admissibility of can be used to construct bases of admissible rules.
Let us recall that a rule is called admissible for a given logic if for every substitution ,
It is not hard to see that a rule is admissible for logic defined by rules if and only if rules define a logic such that .
We can extend the notion of admissibility to m-rules as follows; an m-rule is admissible for a given logic if every substitution ,
The topic of the paper is the relations between the m-rules and and admissibility of rules. We divide m-rules into three categories: if is an m-rule, then
A rule that has a nonempty set of alternatives is called proper. For instance,
and and are proper m-rules.
Successive application of rules leads to a notion of inference: from a given set of formulas —assumptions—we infer a formula, A. Inferences from the empty set of assumptions (or from the axioms) are proofs.
In this paper, we focus on logics for which the ∨-elimination m-rule is admissible (for instance, it is admissible for the intuitionistic logic and it is not admissible for the classical logic). Additionally, we will show that all m-rules except, perhaps, for and , can be eliminated from any base of admissible m-rules for such a logic.
2. Preliminaries
Let be a set of all (propositional) formulas built in a usual way from a denumerable set of (propositional) variables and a finite set of connectives . The maps are called substitutions. Given a substitution and a formula A, denotes the result of replacing each variable p occurring in A with formula , and if is a set of formulas, then .
Let be a class of all ordered pairs of finite (possibly empty) subsets of . The members of are called multiple-conclusion rules, or multiple-alternative rules (m-rules for short). In the sequel, means that is a finite subset of , and if , the rule is denoted as . The members of are called premises, while the members of are called alternatives or conclusions. If is an m-rule, we drop curly brackets and write . Also, if , we write to denote .
If is an m-rule and is a substitution, then is again an m-rule which is called an instance of .
Let us note that m-rules allow empty sets of premises and alternatives/conclusions, and ∅ has a different meaning depending on whether it is a set of premises or a set of conclusions. To make it easier, we use ▼ for ∅ as a premise and we use ▲ for ∅ as a conclusion. We also assume that for every substitution , and . Symbols ▼ are ▲ are merely notations and they are not elements of the language or metalanguage.
Formula A is valid in a given logic (-valid for short) or A is a theorem of if (or ), otherwise, A is called refuted in .
We call logic consistent if not every formula from is a theorem of . Let us note that because of structurality, i.e., because obeys (S) from (1), a logic is consistent if and only if , where q is a variable.
Let us observe that a rule is admissible for logic (in symbols, ) if any substitution that refutes A, refutes at least one member of . If , then rule is admissible for if and only if [8]. For m-rules, an m-rule is admissible for (in symbols ) if every substitution that refutes all formulas from , refutes at least one formula from [8]. Thus, the rule ▼/▲ is not admissible in any logic.
If is a set of all conclusive rules admissible for logic , then defines a logic that has the same set of theorems as . It is not hard to see that is the biggest logic that has the same theorems as , and we call an admissible completion of . In the book by Rybakov [9] (Definition 1.7.3), the term “admissible closure” is used; in our view, the latter term is a bit ambiguous, because “admissible closure” can refer to a consequence closure operator. Let us note that if is a set of all conclusive rules admissible for and is a set of all m-rules admissible for , then and define the same logic, namely, . Indeed, it is clear that a conclusive rule is admissible for if and only if is admissible for as m-rule.
If is a logic defined by m-rules and is a rule, by we denote the smallest logic extending and containing . It is not hard to see that if is admissible for , then .
Admissibility of a rule can be expressed in terms of -unifiability. A set of formulas is unifiable in (or -unifiable) if 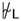 ▲, otherwise is nonunifiable in . In other words, formulas are -unifiable if and only if there is such a substitution , that , and in this case, is said to be an -unifier of . Thus, an m-rule is admissible for if and only if every -unifier of unifies at least one formula from .
▲, otherwise is nonunifiable in . In other words, formulas are -unifiable if and only if there is such a substitution , that , and in this case, is said to be an -unifier of . Thus, an m-rule is admissible for if and only if every -unifier of unifies at least one formula from .
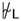 ▲, otherwise is nonunifiable in . In other words, formulas are -unifiable if and only if there is such a substitution , that , and in this case, is said to be an -unifier of . Thus, an m-rule is admissible for if and only if every -unifier of unifies at least one formula from .
▲, otherwise is nonunifiable in . In other words, formulas are -unifiable if and only if there is such a substitution , that , and in this case, is said to be an -unifier of . Thus, an m-rule is admissible for if and only if every -unifier of unifies at least one formula from .Logic is strongly consistent if there is a finite set of formulas such that , that is, is nonunifiable in . Note that if is a nonunifiable in finite set of formulas, then any rule (including ) is trivially admissible in . The m-rules with nonunifiable set of premises are called passive (passive rules were introduced in [10]).
Example 1.
Throughout the paper we will use the examples from the following well-known logics.
and normal modal logics [11]. All these logics are consistent: formula p, where p is a propositional variable, is not a theorem. And all of them, except for , are strongly consistent: formula is not unifiable, while in every nonempty set of formulas is unifiable (substitute each variable with ).
3. Derivation
An m-inference (or m-derivation) of an m-rule from a given set of m-rules will be a generalization of a regular notion of Hilbert style inference (for instance, like in [12]). Since we allow to use the multiple-conclusion rules, inference cannot be a sequence anymore, and it is a tree: application of any inconclusive rule triggers branching. Each derived alternative shall be considered individually, like a separate case in a proof by cases. The introduced below notion of m-inference with use of m-rules reflects our everyday practice of making derivations from a set of assumptions: at each step we either refer to an assumption, or we apply a rule of inference and derive an (intermediate) conclusion, or we use a proof by cases and we lay down a set of alternatives that will be considered separately. The latter is captured by application of some inconclusive rule, when instead of a single conclusion we arrive at a set of alternatives to be considered (for different flavors of formalization of the proofs by cases can be fond in [13]). Our definition of m-inference slightly differs from the definition in [8,14]. An alternative approach to derivation in the multiple conclusion setting the reader can find in [15].
3.1. Basic Definitions: Derivation Trees
By (finite) tree we understand a partially ordered set that has the biggest element (called a root) and for each , the segment is a chain. Labeling of a tree is a map , where ▼ is allowed only in the root and ▲ is allowed only in a leaf. Moreover, the root is always labeled by ▼. A tree together with labeling (that is the pair tree-labeling) is called a labeled tree. When we draw a labeled tree, to simplify notation, instead of node we will use its label . For instance, instead of left-hand side tree depicted in Figure 4 with labeling
we use the right-hand side tree
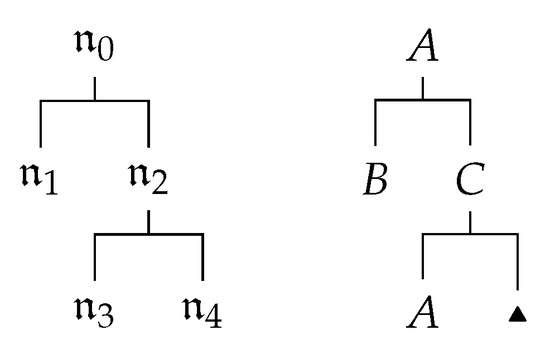
Figure 4.
Labeling.
If is a node of a labeled tree, we let and
. Nodes from are predecessors of and nodes from are successors of . A successor of a node is called immediate if there are no nodes strongly between and ;. By we denote the set of all leaves of , that is, is the set of all minimal elements of .
If , then . For instance, is a set of all formulas labeling all predecessors of , and is a set of all formulas labeling all leaves of the tree .
A leaf labeled by ▲ is a terminal leaf, otherwise, the leaf is called extendable.
3.2. Definition of m-Inference
Now, we can introduce the notion of m-inference in the setting of m-rules. Our definition of m-inference is slightly different from the one introduced in works by the authors of [3,14], but as Theorem 2 shows, the classes of derivable m-rules coincide.
Definition 1.
Let be a set of m-rules and be a set of formulas (which may be empty). An m-inference from by (or -inference for short) is a finite labeled tree, defined by induction:
- (a)
- A tree containing only a root labeled by ▼ is a -inference;
- (b)
- If I is a -inference, then a tree obtained from I by adjoining to an extendable leaf an immediate successor labeled by a formula from is a -inference;
- (c)
- If I is a -inference, and is an extendable leaf, then a tree, obtained from I by adjoining to immediate successors labeled by formulas , is -inference, provided there is an instance of a rule from such that
- (d)
- If I is a -inference and is an expendable leaf, then a tree, obtained from I by adjoining to immediate successors labeled by ▲, is -inference, provided there is an instance of a rule from such that
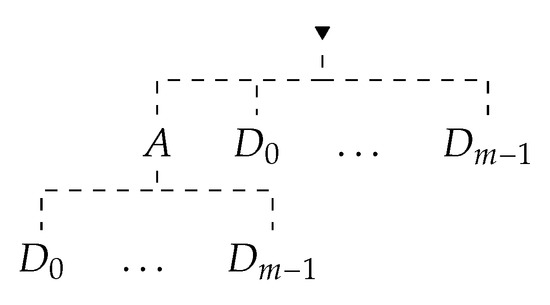
For instance, suppose and is an instance of a rule from . Then, if a tree depicted in Figure 5 is a -inference, then the trees depicted in Figure 6 are -inferences, provided for (a) that , and for (b), that all premises can be found on the branch between leaf and the root.
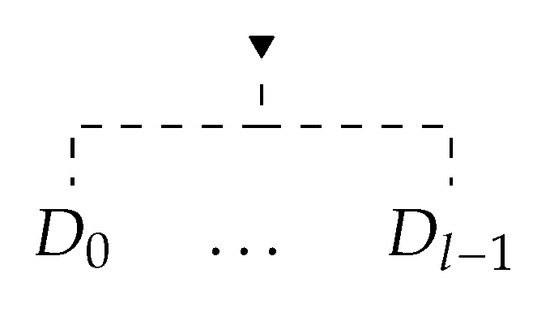
Figure 5.
Initial inference.
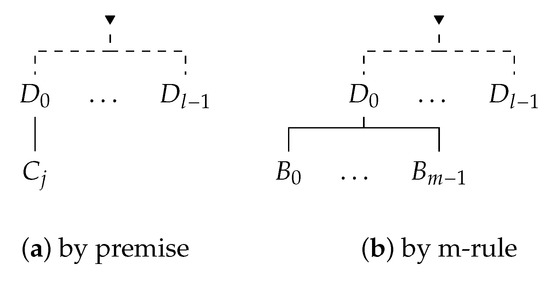
Figure 6.
Examples of Inferences.
Let us observe the following simple but important property of m-inferences.
Proposition 1.
Suppose that I and are -inferences. Then the following assertions hold:
- (a)
- a labeled tree obtained from I by omitting all successors of a given node is a -inference;
- (b)
- if we remove the root of and adjoin the remainder of to a leaf of I, the obtained labeled tree is a -inference;
- (c)
- for any substitution σ, the tree obtained from I by replacing in every node the labeling formula A by , is a -inference.
The proof follows immediately from the definition of m-inference.
3.3. Derivations of m-Rules
Using the notion of m-inference from assumptions, we can define the notion of m-inference of m-rule.
Definition 2.
Let be a set of m-rules and be an m-rule. We say that is derivable from rules (in symbols ) if there is a -inference I such that , i.e., every leaf is labeled by a formula from or by.
The following proposition is an immediate consequence of the definition.
Proposition 2.
Let be a finite set of formulas and be a set of m-rules. Then any -inference I is a derivation of m-rule where , i.e., is a set of all formulas labeling all leaves of I.
Corollary 1.
Suppose that I is an m-inference of an m-rule from a set of m-rules . Then if a formula labels a node n that is not a leaf, the tree obtained from I by omitting all nodes strongly below , is also an m-inference of from .
In other words, if , then there is a -inference, such that formulas from label only leaves.
Theorem 1.
Suppose that and are sets of m-rules, while and are m-rules. Then the following hold;
- (i)
- if , then ;
- (ii)
- if , then ;
- (iii)
- if and , then .
Proof.
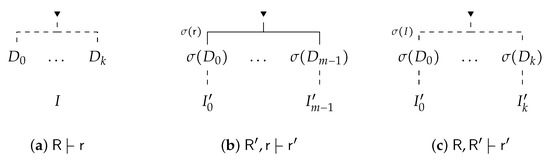
The proofs of (i) and (ii) are straightforward. Let us prove (iii).
Suppose that and . By assumption, there is a -inference of , which we denote by I, and there is a -inference of , which we denote by . To prove (iii) it suffices to observe that any application of rule in can be replaced by an instance of the proof I (see Figure 7).

Figure 7.
Proof of (iii).
Properties of m-Inference
Theorem 2.
Let be a set of m-rules, be an m-rule and A be a formula. Then
Proof.
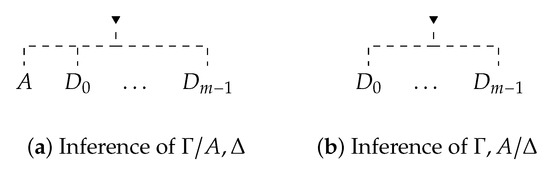
Indeed, if A is a formula, then the tree that consists of a root, labeled by ▼, and its single immediate successor, labeled by A, is an m-inference of the rule from . Thus, (R) holds.
It follows immediately from the definition of inference that if I is an inference of a rule from , then I is at the same time an inference of the rule for any finite sets of formulas . That is, (M) holds.
Also straight from the definition it follows that if I is an inference of a rule from and is a substitution, then the tree , obtained from I by replacing every label A with , is an inference of from . Thus, (S) holds.
To demonstrate (T) we will show that, given an m-inferences of rules and from , we can construct an m-inference of the rule .
Suppose and we have inferences of and from depicted respectively in Figure 8a,b:
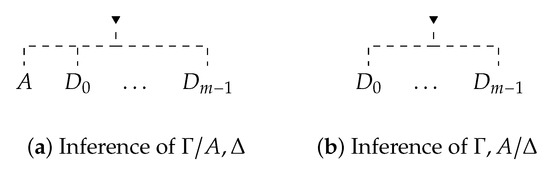
Figure 8.
Proof of (T): the premises.
By Corollary 1, we can assume that A labels only leaves. Then we can construct an inference of from by adjoining inference (b) to every leaf labeled by A as depicted below in Figure 9:

Figure 9.
Proof of (T): the result.
and in such a way to obtain an m-inference of . □
Let us also note the following property of passive rules which immediately follows from (M).
Corollary 2.
Let be a set of m-rules containing rule . Then, for any finite set of formulas ,
Corollary 3.
If is a set of m-rules admissible for logic and is an m-rule such that , then is also admissible for .
Proof.
Suppose that and is a substitution such that . By virtue of (S), there is an m-inference of from . From the definition of m-inference and admissibility of rules from , any application of rule from has at least one conclusion, which is a theorem of . Hence, contains a theorem of , and hence rule is admissible for . Let us note that if some rule from is terminating, its admissibility entails that is not consistent and hence, every rule is admissible for it. □
3.4. m-Deductive Systems
Theorem 2 ensures that for any set of m-rules , the restriction of to the single-conclusion relation is a consequence relation. Thus, every set of m-rules can be regarded as an m-deductive system . Recall that is the set of theorems: .
Let us point out that m-deductive systems lack some properties of regular deductive systems. For instance, a join of m-deductive systems with the same sets of theorems may be an m-deductive system with a strongly larger set of theorems. That is,
We assume that the reader is familiar with Heyting algebras as models of intermediate logics.
Let us consider deductive system defined by all formulas valid in algebra depicted in Figure 10 and the rule (we regard formulas as rules of type ); we constructed two m-deductive systems:
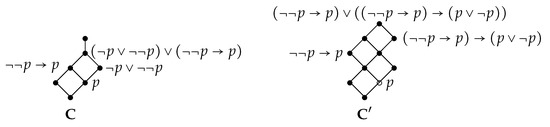
Figure 10.
Example.
Our goal is to verify that and formula is not a theorem of and , while A is a theorem of , that is, .
We start with an observation that algebra (see Figure 10) is (isomorphic to) a Lindenbaum algebra of on one variable. Hence, both algebras and are models for .
Next, we observe (and we left for the reader to perform this routine check) that (a) rules and are valid in , hence, is a model of ; (b) rules and are valid in , hence, is a model of ; and (c) all three m-logics have the same sets of theorems, that is,
Also, as we can see in Figure 10, formula A is refuted in and hence, and . Thus, we only need to show that .
Indeed, because algebra is a Lindebaum algebra of on one variable and any formula in one variable is a theorem of precisely when it is valid on the generator of depicted as ∘. Thus, because formula is valid on this generator, it is a theorem of , as well as it is a theorem of and . Thus, we can construct an m-inference of A from , which is presented in Figure 11.
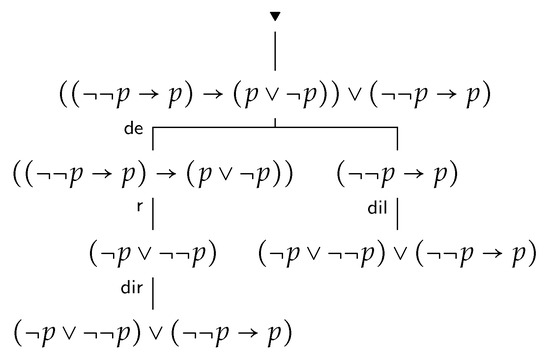
Figure 11.
m-Inference of formula A.
Thus, formula A is a theorem of .
3.5. Admissible Bases
Suppose that is a logic, is a set of m-rules and is an m-rule. We say that is derivable from m-rules relative to m-logic (in symbols ) if .
Let us observe that, by Corollary 3, if is a set of admissible for m-rules and , then is admissible for m-rule. Thus, we can use m-inferences to axiomatize admissible completion of logics.
Definition 3.
Suppose is a logic and is a set of admissible for conclusive rules. Then is an admissible relative to base if every admissible for conclusive rule is derivable from relative to , that is,
Example 2.
For the Visser rules
where , form a relative admissible base (cf. the work by the authors of [16]).
In a natural way, the notion of admissible base can be extended to m-rules.
Definition 4.
Suppose is a logic and is a set of admissible for m-rules. Then is an admissible relative to m-base if every admissible for m-rule is derivable from relative to , that is,
And an admissible m-base for is independent if neither proper subset of is an admissible m-base for .
Definition 5.
Suppose is a logic and is a set of admissible for m-rules. Then is an admissible relative to extended base if every admissible for conclusive rule is derivable from relative to , that is,
And an admissible extended base for is independent if neither proper subset of is an admissible m-base for .
In Section 5 and Section 6 we see that in the logics with the disjunction property, the admissible bases and m-bases are closely related.
Remark 1.
There is a difference in the properties of admissible conclusive and inconclusive rules. Namely, in contrast to conclusive rules, an inconclusive rule can be derivable and not admissible. Indeed, if is the logic defined by axiom schemes of the classical logic and as a single inference rule and , then, : it is clear that , on the other hand, every theorem of is valid in the two-element Boolean algebra, because all axioms and rules of are valid in it. Thus, rule is trivially derivable in but it is not admissible: , while and .
4. Introducing Meta-Disjunction
If our language contains disjunction with regular properties, m-Rule
plays a very special role in constructing deductive systems. Indeed, if is a set of proper m-rules such that , we can replace the set of m-rules by and the set of conclusive rules
where . Indeed, if in an inference we apply m-rule , instead, we can apply rule , and then apply times m-rule (where ). In this section, we discuss the sufficient conditions for logics to have an analog of ∨-elimination.
4.1. m-Protodisjunction
Let be a formula (a nonempty finite set of formulas) in two variables (in the sequel we write to make the meaning more transparent). Then we let
In the case when ∇ contains more then one formula,
We will use the following rules capturing the properties of ∇.
Let
be the set of rules representing the properties of ∇.
Proposition 3.
The following hold;
Proof.
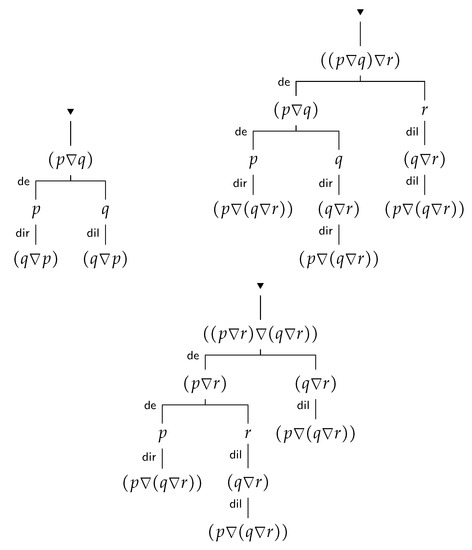
The proofs of (DC), (DRA), and (DD) are depicted in Figure 12. Proof of (DLA) is similar to the proof of (DRA), and (DI) is an immediate consequence of and the definition of m-inference. □

Figure 12.
Proof of .
Definition 6.
A set of m-rules is m-disjunctive if for some formula (some nonempty finite set of formulas) in two variables, rules , and are derivable from , and we call formula(s) an m-protodisjunction for (comp. with the notion of protodisjunction in works by the authors of [13,17]).
Definition 7.
An m-logic has the disjunction property ( for short) if rules , , and are admissible in , that is, if is m-disjunctive.
For instance, modal logic has the Disjunction property relative to m-protodisjunction .
Let us observe that if is an m-disjunctive set (or enjoys the ), then rules are derivable from (or respectively, these rules are admissible for ).
It is important that m-protodisjunction is defined uniquely up to -equivalence in the following sense.
Let be a set of m-rules. Sets of formulas and are said to be -equivalent if
Proposition 4.
Let be an m-disjunctive set of rules, and and be m-protodisjunctions for . Then and are -equivalent.
Proof.
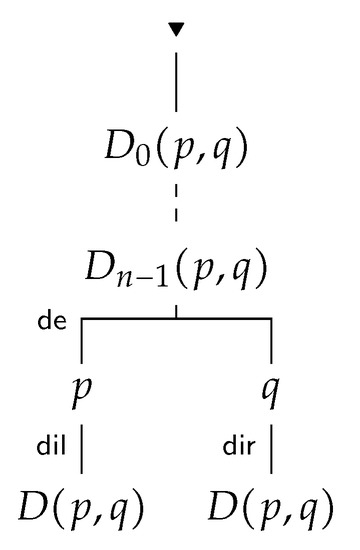
Suppose that and . An m-inference of D from is depicted in Figure 13. □
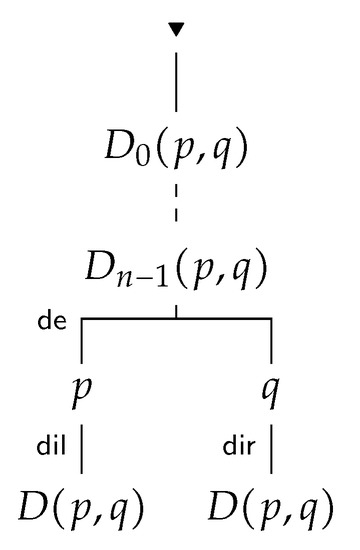
Figure 13.
Proof of Proposition 4.
Let us note, that if a logic has conjunction with regular properties, can be reduced to a single formula.
Note 1.
In order not to add an extra layer of complexity, in this paper we consider only the case when consists of a single formula, even though the main results hold in a general case.
If is an m-disjunctive set of m-rules or if is an m-logic with the , we always assume that meta-disjunction is expressible by a formula .
Example 3.
Let us consider intuitionistic propositional logic and normal modal logic . For we can take . For we can take . It is clear that rules and are derivable in these logics, that is, and , where , and all three rules (, , and ) are admissible for and [11]. For logic one can take . Let us point out that rule is admissible for , but it is not derivable [18] (Theorem 4.2).
4.2. Properties of m-Protodisjunction
In this section, we prove that with respect to , m-protodisjunction has the properties which disjunction is expected to have.
Proposition 5.
Suppose is an m-protodisjunction for a set of m-rules . Then for any formulas , and any ,
Proof.
One can apply to and obtain two cases to consider: and . In each of these cases one can derive . □
Immediately from Proposition 5 it follows that if is an m-logic enjoying the , then for any formulas and any ,
and consequently,
and
If is a finite set of formulas, we let
Thus, ∇ converts any finite nonempty set of formulas into a single formula.
m-Protodisjunction has the following property.
Corollary 4.
Suppose is a nonempty finite set of formulas and is a set of m-rules with m-protodisjunction (or is an m-logic with the ). Then
(accordingly, if and only if for some ).
Proof.
The corollary can be proven by a simple induction on cardinality of . □
Let us introduce the following notations: suppose that A is a formula, are sets of formulas, , and q is a variable not occurring in A and formulas from and . Then
If is a set of m-rules and q is a variable not occurring in any m-rule from ,
Remark 2.
Note that if is a terminating rule and , then, and the latter is a conclusive rule. Thus, for any m-rule and any , the rule is always a conclusive rule: even if , we have and (cf. Equation (8)). If is a conclusive rule, the rules and coincide. Hence, if is a set of conclusive rules, .
Example 4.
If , then
Rule is admissible for any extension of [19], while rule is admissible for any extension of enjoying the disjunction property.
If , then
Rule is admissible for any normal modal logic extending [10], while rule is admissible for any normal modal logic extending enjoying the disjunction property.
Proposition 6.
Let be a set of conclusive rules, Γ be a finite set of formulas and be formulas. Then,
Proof.
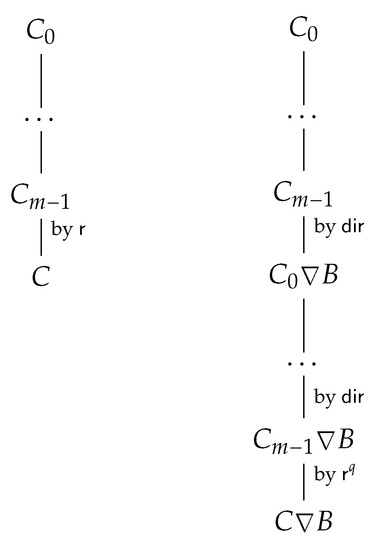
Let I be a single-conclusion inference of C from . Then C is the last formula in I. There are three cases to consider: (a) ; (b) ; (c) C is obtained from some preceding formulas by a conclusive rule from .
Case (a). Is trivial.
Case (b). If , then by the definition of m-inference, . Thus, and, by , we get .
Case (c). Suppose C is obtained by an instance of some rule . Then,
is an instance of and we can easily convert inference I into the inference of (see Figure 14). □

Figure 14.
Proof of Prop. 6.
Corollary 5.
Let be a set of conclusive rules, Γ be a finite set of formulas and be formulas. Then, for any ,
Proof.
Indeed, for we can take and use Proposition 6. In the case when , we can use commutativity and associativity of and reduce this case to the case . □
5. From Admissible m-Base to Admissible Base
Our goal is to demonstrate that for any consistent m-logic with the , the problem of admissibility of any given proper m-rule can be reduced to the problem of admissibility of some conclusive rule.
Theorem 3.
Suppose is a consistent m-logic with the . Let be a proper m-rule and q be a variable not occurring in . Then the following are equivalent.
- (a)
- m-Rule is admissible for ;
- (b)
- m-Rule is admissible for ;
- (c)
- Rule is admissible for ;
- (d)
- Rule is admissible for .
Proof.
(a) ⇒ (b). Assume that proper m-rule is admissible for . Because is proper, . Let us consider the three following cases:
- , that is, and ;
- , that is .
Case. Admissibility of entails that there is such that and consequently, for every substitution , . Hence, because is admissible for , for every substitution , we have and therefore, rule is admissible for .
Case. We need to prove that for any substitution ,
Let be a unifier of , that is for all . Let us consider two subcases:
- (i)
- unifies ;
- (ii)
- does not unify .
Proof of (i).
Recall that is admissible for . Therefore, if unifies , that is, holds for all , by admissibility, there is such that . Hence, because rule is admissible for , we can apply it and obtain . □
Proof of (ii).
Suppose that does not unify . Then, there is such that σ(A). On the other hand, unifies and hence, . Then, by the Disjunction Property, . Rule is admissible for , hence, entails for every . □
(b) ⇒ (c). Suppose m-rule is admissible for . We need to prove that rule is admissible for . Let be a substitution which unifies , that is, makes all premises derivable. Then, our assumption entails that holds for some . Hence, by virtue of Corollary 4, which means that holds.
(c) ⇒ (d). Suppose that rule is admissible for . We need to prove that rule is admissible for . Let us consider two cases: and .
Case, that is, rule is admissible for . Hence, if consists of a single formula B, we have . If contains more than one formula, by the disjunction property, there is a formula such that . If we take into account that q and apply the disjunction property to , we can conclude that holds and hence, holds for every substitution . Thus, rule is admissible for .
Case and we need to show that rule is admissible for . Let be a substitution that unifies , that is for all .
Recall that is consistent, therefore there is a formula C such that C. Take the substitution
Because q does not occur in formulas from , for all , , and, consequently, . By the assumption, , and hence by , , that is, . Thus, unifies . Now, we can apply the assumption that rule is admissible, and we can conclude that for some formula , formula is derivable. Thus, because , formula is a theorem. Recall that we selected C not to be a theorem, hence, by the Disjunction Property, formula is a theorem. And because variable q does not occur in B, we have , and it means that is a theorem and rule is admissible.
(d) ⇒ (a). Suppose that the rule is admissible for . Let be a unifier for . Then, by the admissibility of , we have . Now, we can apply Corollary 4 and conclude that for some , . Thus, the rule is admissible in . □
Remark 3.
For any consistent m-logic with the disjunction property, the rules and are either both admissible, or both not admissible. Moreover, can be derived from , while the converse needs not to be true: the restricted Visser rule is derivable from the Visser rule [20], while the converse does not hold [21] (Corollary 2). If the m-rules , , and are not just admissible (which is required by the disjunction property), but they are derivable in , then is derivable from .
Logic is a-decidable if the problem of admissibility of conclusive rules in is decidable, and logic is am-decidable if the problem of admissibility of m-rules in is decidable.
Corollary 6.
For every consistent m-logic with the DP, the problems of a- and am-admissibility are equivalent.
Example 5.
It is well known from [11] that logics enjoy the DP. Therefore, because the problem of a-admissibility for them is decidable [22,23,24], the problem of m-admissibility for these logics is decidable too. In algebraic terms, for each of these logics, the universal theory of the Lindenbaum algebra is decidable [24] (Theorem 10).
5.1. A Note on Terminating Rules
The goal of this section is to show that terminating rules can be eliminated from any m-inference of any proper rule.
If is a set of m-rules, by we denote a set of proper m-rules obtained from by replacing every terminating rule with conclusive rule , where q does not occur in any of formulas
Proposition 7.
Suppose that there is an m-inference I of a proper rule from . Then, there is an inference of from that does not contain terminal leaves.
Proof.
Let I be an m-inference of from . By assumption, rule is proper, hence, is not empty. Suppose that .
Let us observe that, by the definition of m-inference, application of any terminating rule gives a leaf of this m-inference. Thus, if and is an instance of that we have been used in I, instead, we can use the instance of a proper rule that belongs to . And in such a way, we can eliminate all applications of the terminating rules from I. □
From Proposition 7 it immediately follows that for strongly consistent logics any m-base (finite m-base) can be converted into an m-base (finite m-base) containing at most one terminating m-rule.
Proposition 8.
Let be an m-base (a relative m-base) of strongly consistent m-logic in which formula A is not unifiable and let . Then is an m-base (relative m-base).
Proof.
First, from Proposition 7, it follows that every conclusive admissible rule is derivable from . Next, if m-rule is admissible, then rule is admissible too, and hence it is derivable from . Thus, m-rule is derivable from . □
5.2. Converting Admissible m-Base into Admissible Base
To convert a given relative admissible m-base of a given logic with the into a relative base, one can do the following: convert every rule from into rule ; the obtained set of rules we denote . The set consists of conclusive rules (cf. Remark 2). From Theorem 3 we know that each rule from remains admissible. Below, we show that every admissible for conclusive rule can be derived from . Let us note that as a result of such a conversion some m-rules become trivial, for instance, :
Theorem 4.
Suppose that is a logic with the and is an admissible m-base (a relative m-base) of , then, is an admissible base (respectively, a relative base) of .
To prove Theorem 4, we prove a bit more general Theorem 5, which holds not only for the logics enjoying the . Recall from Proposition 3 that all rules from (cf. Equation (3)) representing the properties of ∇ are derivable in any logic with the . Hence, we can take in Theorem 5 to be a singleton, and we will obtain Theorem 4 as a corollary.
Theorem 5.
Suppose is a set of proper m-rules, and is a proper rule. If
then
In other words, any m-inference of from can be converted into inference of from which is a single-conclusion inference, because all rules from and are conclusive.
Proof.
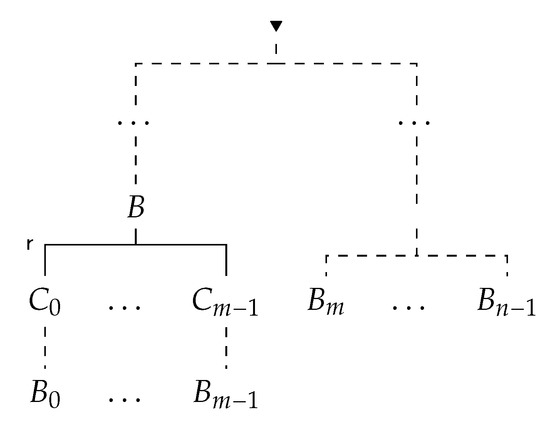
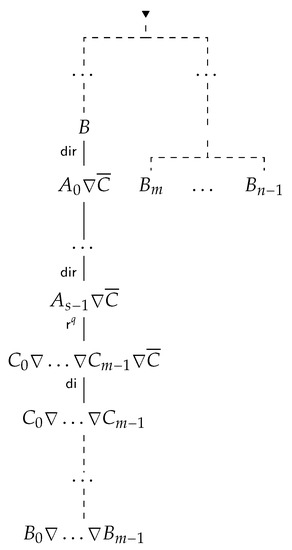
Let I be a -inference and is a set of formulas which appear in the leaves of I. Without loss of generality we can assume that each formula from appears in a leaf of the inference: if , after we have derived , we can apply (multiple times if necessary) rule and derive .
Let k be the number of nodes of I having more than one immediate successor (in other words, k represents the number of applications of inconclusive rules). By induction on k we prove that for any -inference, such that , there is a -inference, , such that . Let us note that because all members of are conclusive rules, is a linear inference and has a single leaf labeled by .
Basis. If , then I is a linear inference. By the assumption, is a set of proper m-rules and therefore, it does not contain any terminating rules. Hence, the leaf of I contains a formula D from , and using the rules from one can easily extend I to derive .
Assumption. Assume that for any -inference I having less than k branching nodes, there is an - inference the leaf of which contains .
Step. Let I be a -inference having k branching nodes. Let be a branching node having no branching successors. Suppose that is a list of formulas in the leaves below , and is a list of all formulas in the leaves that are not successors of . Assume also that (see Figure 15) and alternatives are obtained by application of inconclusive rule from .

Figure 15.
Prop. 5: Initial Inference.
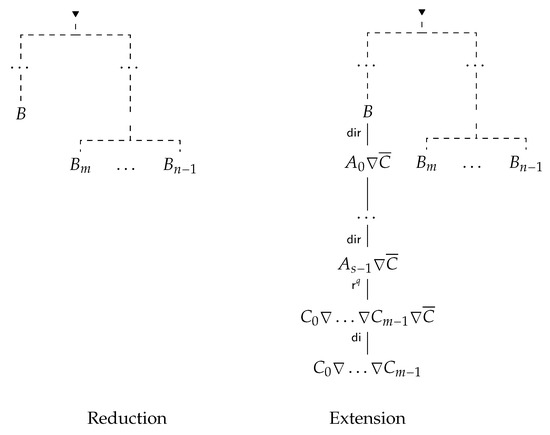
Let us remove all successors of from I. By Proposition 1(a), the resulting tree is also a -inference with in its leaves (see the left-hand side of Figure 16).

Figure 16.
Theorem 5: Step.
Observe that , hence
where , is an instance of . As all formulas are in the nodes preceding , we can extend the reduced inference (see Figure 16).
By Corollary 5, from we can derive
Then we can apply Corollary 5 again and get
And so on, until we got
In such a way we obtain the inference depicted in Figure 17.

Figure 17.
Theorem 5: Finishing Step.
Let us observe that the obtained inference contains branching nodes, therefore we can apply the induction assumption and convert the obtained inference into an inference of , using, if necessary, rules from . □
Corollary 7.
Suppose that is a logic enjoying the . Then, if has a finite admissible m-base (relative m-base), then, has a finite admissible base (relative base).
Example 6.
It was proven in [22] by Rybakov that logics and have no finite relative admissible bases. Hence, these logics have no finite relative admissible m-bases either.
6. From Admissible Base to Admissible m-Base
In the previous section we saw how to convert a given (relative) admissible m-base of a logic with the into a (relative) admissible base . In this section, we show how to convert a given (relative) admissible base into a (relative) admissible m-base.
Theorem 6.
Suppose that is a logic and is an admissible base (relative base). Then, if is strongly consistent and there is a nonunifiable in finite set of formulas , the set is an admissible m-base (relative m-base); otherwise, is an admissible m-base (relative m-base).
Proof.
First, let us prove that every proper admissible rule is derivable from for . Indeed, suppose that is a proper m-rule admissible in . If consists of a single formula, m-rule is a conclusive rule, and hence by the definition of the base, is derivable from . Suppose . Let us consider rule . By Theorem 3(d), is admissible for , and hence, is derivable from . Now, we can times apply and obtain . Thus, is derivable from .
For relative bases one can take a set of conclusive rules and repeat the preceding argument.
Next, we prove that if is a finite nonunifiable in set of formulas, then every admissible for terminating m-rule can be derived from .
Indeed, suppose that m-rule is admissible for . Then, is a nonunifiable in finite set of formulas and hence, conclusive rule is admissible in for every formula A. In particular, m-rules are admissible for each . Therefore, because is a base, rule is derivable from for each . Thus, each premise of rule is derivable from and by transitivity of consequence relation, is derivable from .
For relative bases one can take a set of conclusive rules and repeat the preceding argument. □
Corollary 8.
Suppose that is a logic enjoying the . Then, if has a finite admissible base (relative base), then has a finite admissible m-base (relative m-base).
Combining together Corollaries 7 and 8, we obtain the following.
Corollary 9.
A logic with the has a finite admissible base (relative base) if and only if it has a finite admissible m-base (relative m-base).
7. Some Applications
(1) Logics are a-decidable [9]. Hence, by Corollary 6, all these logics are am-decidable.
(2) Logics and are a-decidable [25]; hence, by Corollary 6, these logics are am-decidable.
(3) A relative admissible base for conclusive rules for was established in [16]. Adding m-rules and to this relative base (or any relative base for this matter) gives us a relative m-base described in [26].
(4) It is known from [19] that Medvedev’s logic (which enjoys the ) is structurally complete. Hence, m-rules and form a relative to admissible m-base.
(5) Gabbay-de Jongh logics enjoy the DP [27]. The relative m-bases for these logics have been constructed in [28] (Theorem 5.36):
where . By Theorem 4, (or , because rules are conclusive) gives a relative admissible base for :
Note that we did not include and because these rules are trivial:
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Ukasiewicz, J. Aristotle’s Syllogistic from the Standpoint of Modern Formal Logic; Clarendon Press: Oxford, UK, 1951; p. xi+141. [Google Scholar]
- Scott, D.S. Rules and derived rules. In Logical Theory and Semantic Analysis, Essays dedicated to Stig Kanger; Stenlund, S., Ed.; D.Reidel Publishing Company: Dordrecht, The Netherlands, 1974; pp. 147–161. [Google Scholar]
- Shoesmith, D.J.; Smiley, T.J. Multiple-Conclusion Logic; Reprint of the 1978 original [MR0500331]; Cambridge University Press: Cambridge, UK, 2008; p. xiv+396. [Google Scholar]
- Carnap, R. Formalization of Logic; Harvard University Press: Cambridge, MA, USA, 1943; p. xviii+159. [Google Scholar]
- Bezhanishvili, N.; Ghilardi, S. Multiple-conclusion rules, hypersequents syntax and step frames. In Advances in Modal Logic; College Publications: London, UK, 2014; Volume 10, pp. 54–73. [Google Scholar]
- Carnap, R. Introduction to Semantics; Harvard University Press: Cambridge, MA, USA, 1942; p. xii+263. [Google Scholar]
- Chris, B. A Note on Peirce and Multiple Conclusion Logic. Trans. Charles S. Peirce Soc. 1982, 18, 349–351. [Google Scholar]
- Iemhoff, R. On rules. J. Philos. Log. 2015, 44, 697–711. [Google Scholar] [CrossRef]
- Rybakov, V.V. Admissibility of Logical Inference Rules; Studies in Logic and the Foundations of Mathematics; North-Holland Publishing Co.: Amsterdam, The Netherlands, 1997; Volume 136, p. ii+617. [Google Scholar]
- Rybakov, V.V.; Terziler, M.; Gencer, C. Unification and passive inference rules for modal logics. J. Appl. Non-Class. Logics 2000, 10, 369–377. [Google Scholar] [CrossRef]
- Chagrov, A.; Zakharyaschev, M. Modal Logic; Oxford Logic Guides; Oxford Science Publications; The Clarendon Press: Oxford, UK; Oxford University Press: New York, NY, USA, 1997; Volume 35, p. xvi+605. [Google Scholar]
- Wójcicki, R. Theory of Logical Calculi; Synthese Library; Kluwer Academic Publishers Group: Dordrecht, The Netherlands, 1988; Volume 199, p. xviii+473. [Google Scholar]
- Cintula, P.; Noguera, C. The proof by cases property and its variants in structural consequence relations. Stud. Log. 2013, 101, 713–747. [Google Scholar] [CrossRef]
- Iemhoff, R. Consequence relations and admissible rules. J. Philos. Log. 2015, 1–22. [Google Scholar] [CrossRef]
- Skura, T.; Wiśniewski, A. A system for proper multiple-conclusion entailment. Log. Log. Philos. 2015, 24, 241–253. [Google Scholar] [CrossRef]
- Iemhoff, R. On the admissible rules of intuitionistic propositional logic. J. Symb. Log. 2001, 66, 281–294. [Google Scholar] [CrossRef]
- Tommaso, M. A study of truth predicates in matrix semantics. arXiv 2019, arXiv:1908.01661. [Google Scholar]
- Kowalski, T. BCK is not structurally complete. Notre Dame J. Form. Log. 2014, 55, 197–204. [Google Scholar] [CrossRef]
- Prucnal, T. On two problems of Harvey Friedman. Stud. Log. 1979, 38, 247–262. [Google Scholar] [CrossRef]
- Iemhoff, R. Intermediate logics and Visser’s rules. Notre Dame J. Form. Log. 2005, 46, 65–81. [Google Scholar] [CrossRef]
- Citkin, A. A note on admissible rules and the disjunction property in intermediate logics. Arch. Math. Log. 2012, 51, 1–14. [Google Scholar] [CrossRef]
- Rybakov, V.V. Bases of admissible rules of the logics S4 and Int. Algebra Log. 1985, 24, 87–107. [Google Scholar] [CrossRef]
- Rybakov, V.V. Logical equations and admissible rules of inference with parameters in modal provability logics. Stud. Log. 1990, 49, 215–239. [Google Scholar] [CrossRef]
- Rybakov, V.V. Decidability of logical equations in the modal system Grz and in intuitionistic logic. Sib. Mat. Zh. 1991, 32, 140–153, 213. [Google Scholar] [CrossRef]
- Odintsov, S.; Rybakov, V. Unification and admissible rules for paraconsistent minimal Johanssons’ logic J and positive intuitionistic logic IPC+. Ann. Pure Appl. Log. 2013, 164, 771–784. [Google Scholar] [CrossRef]
- Jeřábek, E. Admissible rules of modal logics. J. Log. Comput. 2005, 15, 411–431. [Google Scholar] [CrossRef]
- Gabbay, D.M.; De Jongh, D.H.J. A sequence of decidable finitely axiomatizable intermediate logics with the disjunction property. J. Symb. Log. 1974, 39, 67–78. [Google Scholar] [CrossRef]
- Goudsmit, J. Intuitionistic Rules Admissible Rules of Intermediate Logics. Ph.D. Thesis, Utrech University, Utrecht, The Netherlands, 2015. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).