1. Introduction
Systems of nonlinear equations must usually be solved when nonlinear models, appearing in Science and Engineering, are discretized. There are no analytical techniques for solving these systems, so we approach their solutions by using iterative schemes. Although the most known iterative procedure is Newton’s scheme, in recent years, the focus of this area of research has been in constructing new iterative methods, trying to improve Newton’s one, in terms of convergence, efficiency, and stability (see, for example, some third-order schemes in References [
1,
2,
3,
4,
5,
6], or higher-order ones in References [
7,
8,
9,
10,
11,
12]). The key fact to get the most efficient methods is to evaluate as few Jacobian matrices as possible, per iteration (see Reference [
13] and the references therein).
In 2016, the authors of [
14] proposed a parametric class of iterative schemes with fourth-order of convergence, including a very efficient fifth-order procedure. The efficiency index used is defined as
, where
p is the order of convergence of the method,
d the number of functional evaluations per iteration, and
the number of products/quotients used for obtaining a new iterate. This class combined three evaluations of the nonlinear function and only one of the Jacobian matrix, per iteration. In addition to the study of the local convergence and the computational cost of an iterative method, we must analyze its dependence on the set of initial estimations used. This analysis was made in Reference [
15].
In this manuscript, we modified this class of iterative methods to avoid the calculation of Jacobian matrices, getting two different families, whose difference is based on the order of the estimation of the Jacobian matrix. Then, using the real multidimensional dynamics, we studied the behavior of the elements of the family (usually with the same order of convergence) and decided which ones are the best, from this point of view. Specifically, we studied the multipliers of the strange fixed points, analyzed the asymptotical behavior of the free critical points, and found different kinds of strange attractors using bifurcation diagrams. At the end, the dynamical planes are shown to check the theoretical results.
Introductory Concepts
Now, let us recall some concepts that we will use along this manuscript. Let
be a system of
n equations with
n variables, where
, with coordinate functions
,
. Our aim is to find a solution
as a fixed point of the iteration method:
being the initial guess.
Let us denote with
the vectorial fixed-point rational function associated to the iterative method applied to n-variable polynomial system
,
,
. Most of the following concepts are direct extensions of those considered in complex dynamics (see, for example, [
16,
17]). The orbit of
is defined as
. A point
is a fixed point of
G if
, and its stability is characterized in a result from Robinson ([
16], p. 558), stating that the character of a period-k point
depends on the eigenvalues of
,
. It is attracting if all
, repelling if all
(
)), and unstable or saddle if at least one
exists such that
. In addition, a fixed point is called hyperbolic if all the eigenvalues
of
have
.
On the other hand, if an iterative scheme has at least order two, then the zeroes of the function are superattracting fixed points of G. We call a strange fixed point to that not being a zero of . The basin of attraction of an attracting fixed point of G, is .
A point is a critical point of G if the eigenvalues of are null. Therefore, if satisfies for all , then x is a critical point. If it is not a root of polynomial , it is called a free critical point.
In this manuscript, we apply these techniques (as it has been previously made, for example, in Reference [
17]), to a couple of Jacobian-free families of iterative schemes. Specifically, we study the strange fixed points and their stability, prove the existence of free critical points, and find different chaotic behaviors (strange attractors, period-doubling cascades, etc.). In the last section, some basins of attraction are shown to visualize the performance of the elements of the family. Some numerical results are presented.
2. Jacobian-Free Parametric Families
We propose the following Jacobian-free version of a fourth-order iterative class designed by the authors of [
14], denoted by M41, whose iterative expression is:
being
.
Because of the technique used in the proof, these methods have an order of convergence four in a neighborhood of
, where
is nonsingular. The following result shows its local convergence, using the notation about the Taylor expansion of
and
around
, introduced in Reference [
18]. To get the Taylor expansion of the divided difference operator
(see Ortega-Rheimboldt [
19]), its integral expression is used (known as the Genochi–Hermite formula):
Theorem 1. Let be a zero of , a sufficiently differentiable Frechét function in an open convex set D. Let us assume that is nonsingular and let be an initial estimation near to . Class (2) has fourth-order of convergence for any , . The error equation of the family is:being , , , , and I denotes the identity matrix. Proof. The Taylor development of
around
is:
being also the expansion of its successive derivatives:
Then, denoting by
and
:
By forcing that
, it is obtained that:
Then, the expansion of error at the first step of the iterative process
is:
and, therefore:
In a similar way, the Taylor expansion of the error at the second step
is:
Finally, the error equation of the method can be expressed as:
that, expressed in terms of powers of
and after some algebraic simplifications, results in:
proving the fourth-order of convergence of all the elements of the family for any real
. □
Now, if a second-order estimation of the Jacobian matrix is made in the original M4 family of Reference [
14] in a similar way to that in Reference [
20], then it can be expressed as:
where
, which we denote as M42. The following result shows its local order of convergence.
Theorem 2. Let be a zero of , a sufficiently differentiable Frechét function in an open convex set D. Let us assume that is nonsingular, and let be an initial estimation near to . If , the family defined by (3) has, at least, fourth-order of convergence for any , being fifth-order convergent when . The error equation of the class is:being , and , . Proof. By denoting
and
and in a similar way as in the proof of Theorem 1, the Taylor expression of the second-order divided difference and its inverse can be expressed as:
and:
Then, the error at the first step is:
and again:
Thus, the expansion of the error at the second step is:
Finally, the error equation of the method can be expressed as:
that, expressed in terms of
and simplifying:
proving that all the members of the class have, at least, fourth-order of convergence, except the element corresponding to
, which is fifth-order convergent. □
In the following sections, we use the properties of the discrete dynamical systems associated to these families in order to select their most stable members.
3. Multidimensional Dynamical Analysis
In the following, we denote by
,
the fixed point function associated to M41 and M42 classes, respectively, applied on
n-dimensional quadratic polynomial
, where:
3.1. Class M41
As the polynomial system has separated variables, all the components of
(for a fixed
) have the same expression, with the only difference of the sub-index corresponding to the component of
x. In the case of method M41, the coordinate functions of the multidimensional rational operator can be expressed as:
for
.
All the information about the stability analysis of these fixed points appears in the next result.
Theorem 3. The roots of are superattracting fixed points of the rational function associated to M41. This operator also has a different number of real strange fixed points whose values depend on β:
If , six roots of , denoted by , are real, being their respective eigenvalues of the associate Jacobian matrix , and .
If , five roots of , are real, being their respective eigenvalues of the associate Jacobian matrix , and .
For , there are four real roots of , being their respective eigenvalues of the associate Jacobian matrix , and if , for and if .
If , three roots of are real, being their respective eigenvalues of the associate Jacobian matrix , and .
For and , there are two real roots of satisfying , .
If , four roots of are real, being their respective eigenvalues of the associate Jacobian matrix , and , .
When , there are four real roots of satisfying , .
Proof. By solving the equation
, the fixed points of the multidimensional rational function are obtained:
that is, they are
and also the roots of the polynomial
, provided that
.
However, as most six of the strange fixed points roots of
are real, depending on the value of
, let us denote them by
to
. In order to analyze the stability of these fixed points, the eigenvalues of the associated Jacobian matrix:
being
, are studied for
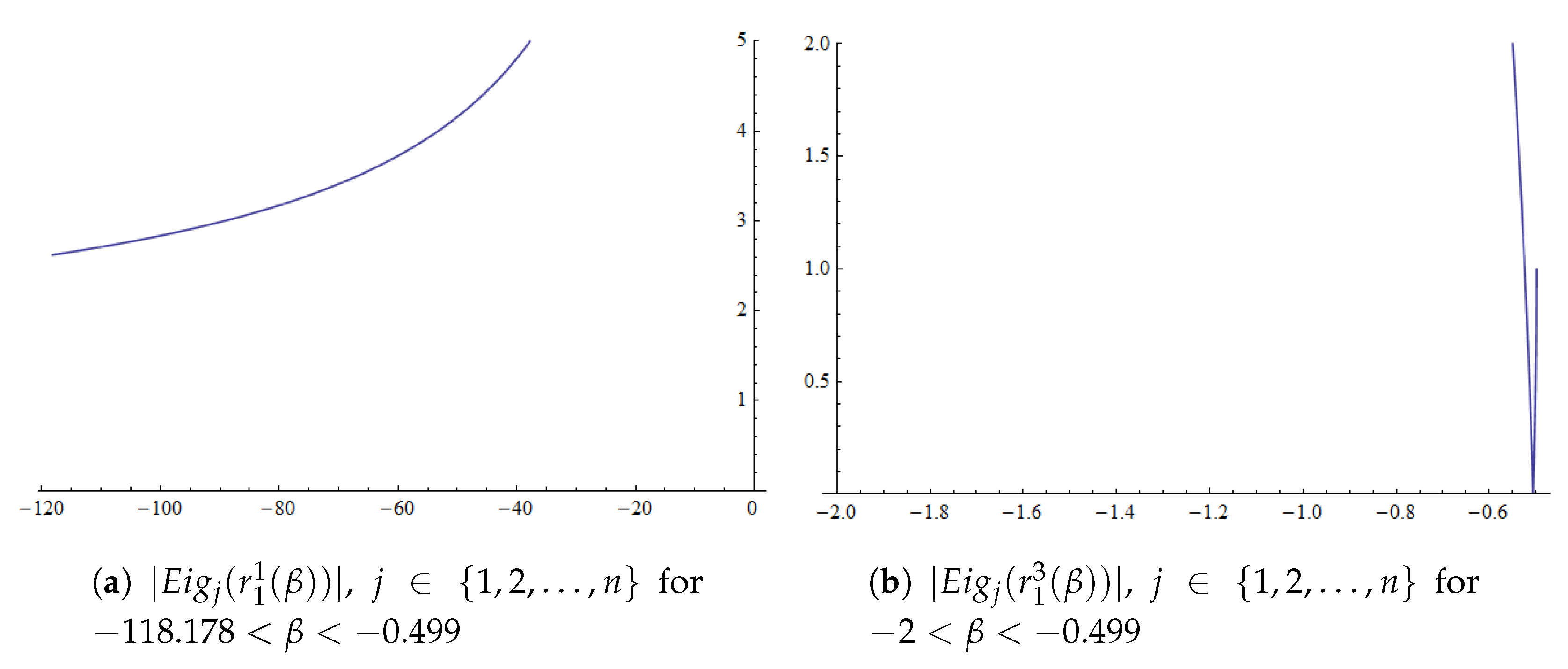
. In each interval where the number of real strange fixed points changes, the Jacobian matrix is evaluated on them and the absolute value of their respective eigenvalues is analyzed. This procedure states the stability of the fixed points (see
Figure 1a) for
as a component of the fixed point,
, if
and
for
.
Taking these results into account, those fixed points whose components are and/or for are attracting. In a similar way, all the fixed points whose components are and for are attracting. If a fixed point is composed exclusively by and out of these intervals of , or by , , and/or for all values of , it is repulsive. In any other case, the strange fixed point is classified as saddle. □
Now, we make a similar study for the second Jacobian-free class of iterative methods.
3.2. Family M42
When the rational operator associated to method M42 on
is analyzed, its coordinate functions can be expressed as:
for
.
To calculate the fixed points of the multidimensional rational function, we get the roots of
. We obtain again
and also the real roots of the polynomial
. It can be checked that
only has, at most, two real roots, which are denoted by
and
. However, the rational function
is the same as that analyzed in Reference [
15], corresponding to the original fourth-order iterative class designed by the authors of [
14], who use Jacobian matrices in its iterative expression applied on
.
Although the classes of iterative methods are different (that of Reference [
14] uses Jacobian matrices and the proposed one is Jacobian-free), the second order estimation of the Jacobian matrix has the same effect on quadratic polynomial systems. So, the following result coincides with that of [
14].
Theorem 4. The roots of are superattracting fixed points of the rational function associated to M42. This operator also has a different number of real strange fixed points whose values depend on β:
- (a)
If or , and are real, being their respective eigenvalues of the associate Jacobian matrix , .
- (b)
For , the only real fixed points are the roots of ; thus, there are no strange fixed points.
There also exist two free critical points with components , , for .
In the next section, we delve into the bifurcation analysis of these free critical points in order to locate other undesirable behaviors, such as attracting periodic orbits, strange attractors, etc.
4. Critical Points and Bifurcation Diagrams
Firstly, we analyze the case of class M41, that is, the rational function and its critical points.
Theorem 5. The components of the free critical points of operator are the only ones making null all the partial derivatives of , for , that is, the solutions of and also the real zeroes of the tenth-degree polynomial depending on β, denoted by , :
- (a)
only four of them being real for ;
- (b)
six for , , and and;
- (c)
there exist eight free different components of the critical points of for .
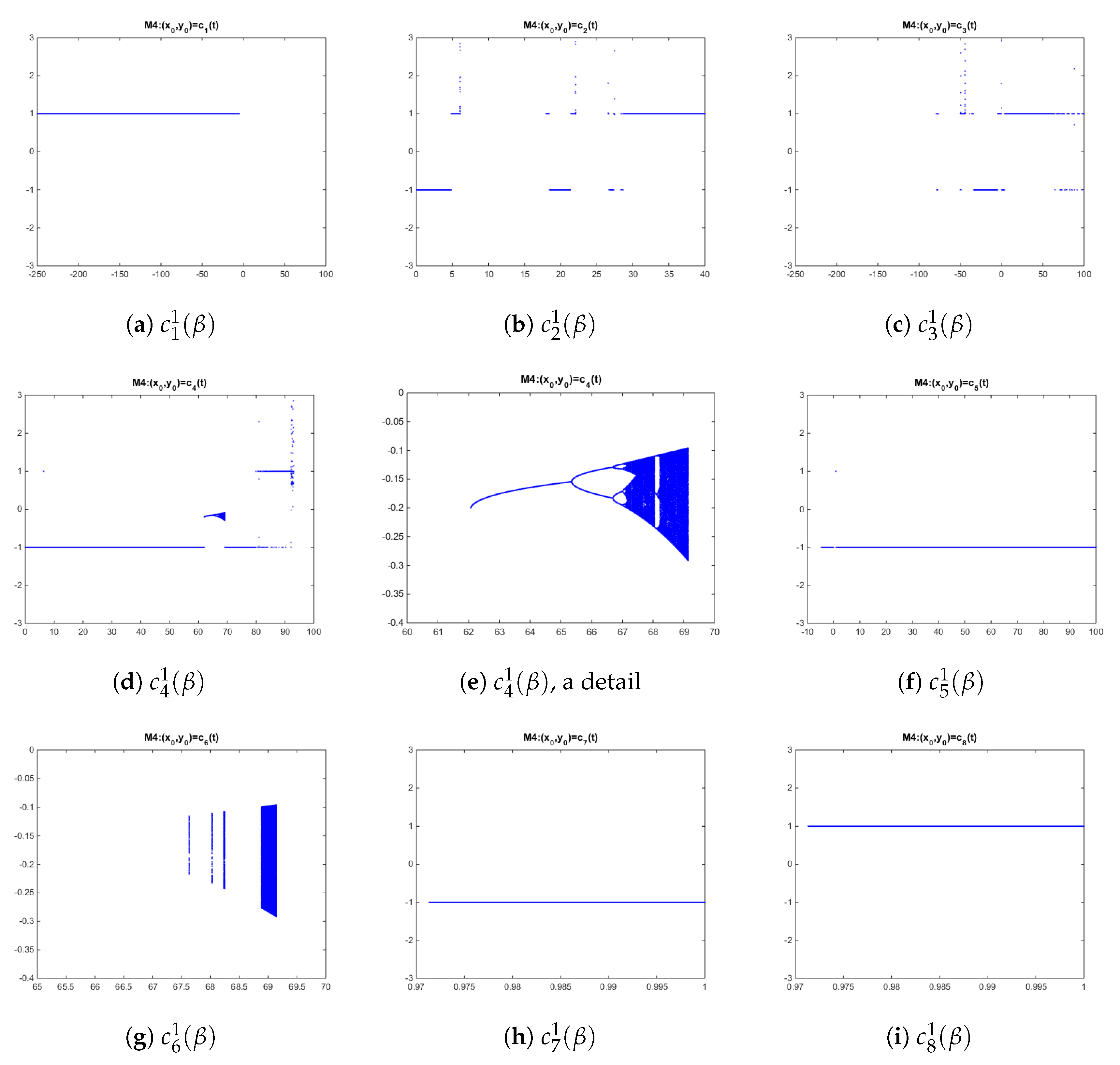
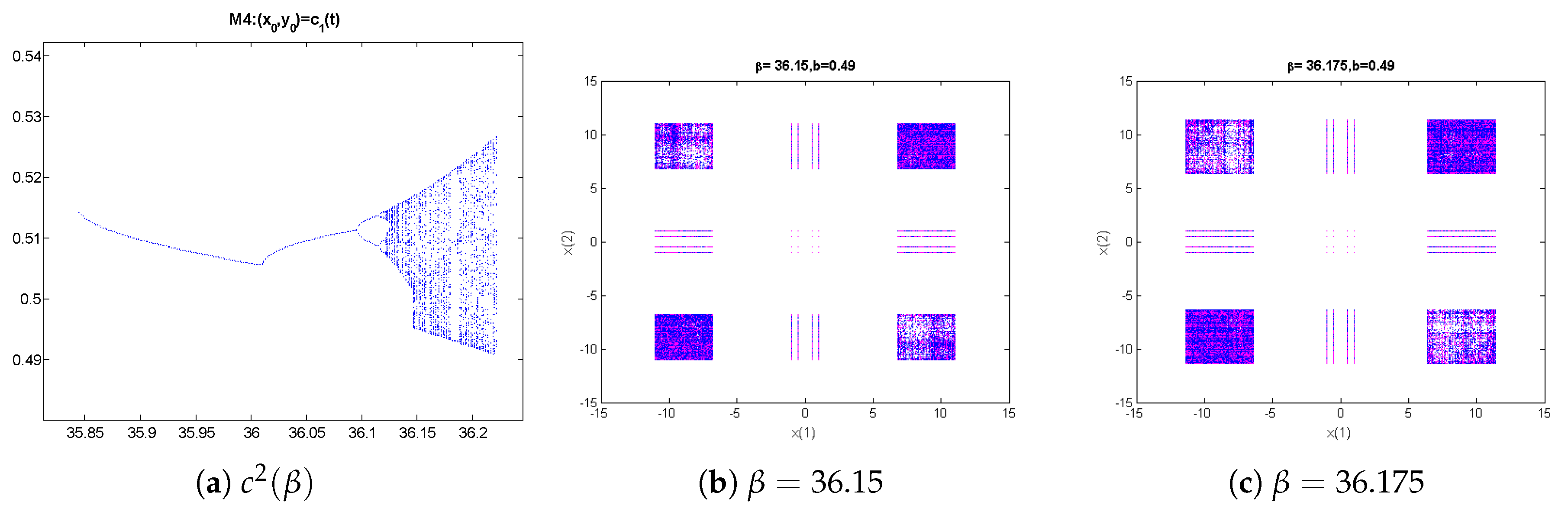
We use Feigenbaum diagrams to analyze the bifurcations of the map related to each family on system
using each one of the free critical points of the map as a starting point and observing their behavior for different ranges of
. When the rational function is iterated on these critical points, different behavior can be found after 1000 iterations of the method corresponding to each value of
in a mesh of 3000 subintervals. The resulting behavior is from convergence to the roots to periodic orbits or even other attractors. In the case of class M41, we observe in
Figure 2 the orbits of these critical points, in the range of
where each one of them is real.
A clear convergent behavior to the roots in the intervals is observed where the critical points are real, except inside the interval
, where a chaotic region can be seen where a strange fixed point has bifurcated (for
, there is change in the number of strange fixed points, two of them parabolic, see Theorem 3) into period-doubling cascades. Further, some blue regions appear associated with chaotic behavior. In them, strange attractors can be found (in the bidimensional case,
). To do it, we plotted in the
-space the iteration of
, for values of
in the blue area. For each fixed value of parameter
, 1000 different initial estimations have been used and, for each of them, the iterates have been plotted following this code color: The first 100 iterations are not plotted, while the following 400 are plotted in blue color, the next 400 in green color, and the last hundred in magenta color. This can be observed in
Figure 3a,b, as the strange fixed point bifurcates in periodic orbits of increasing period, until the chaotic behavior appears (
Figure 3c,d, where the orbits are dense in a small rectangular region of the
space).
Regarding M42 class, let us remark that there exist only two different free critical points
and by
(see Theorem 4). In
Figure 4a,b, a clear symmetry in the convergence to the roots is observed, and we can also see nonconvergent behavior to the roots for elements corresponding to
. We see in
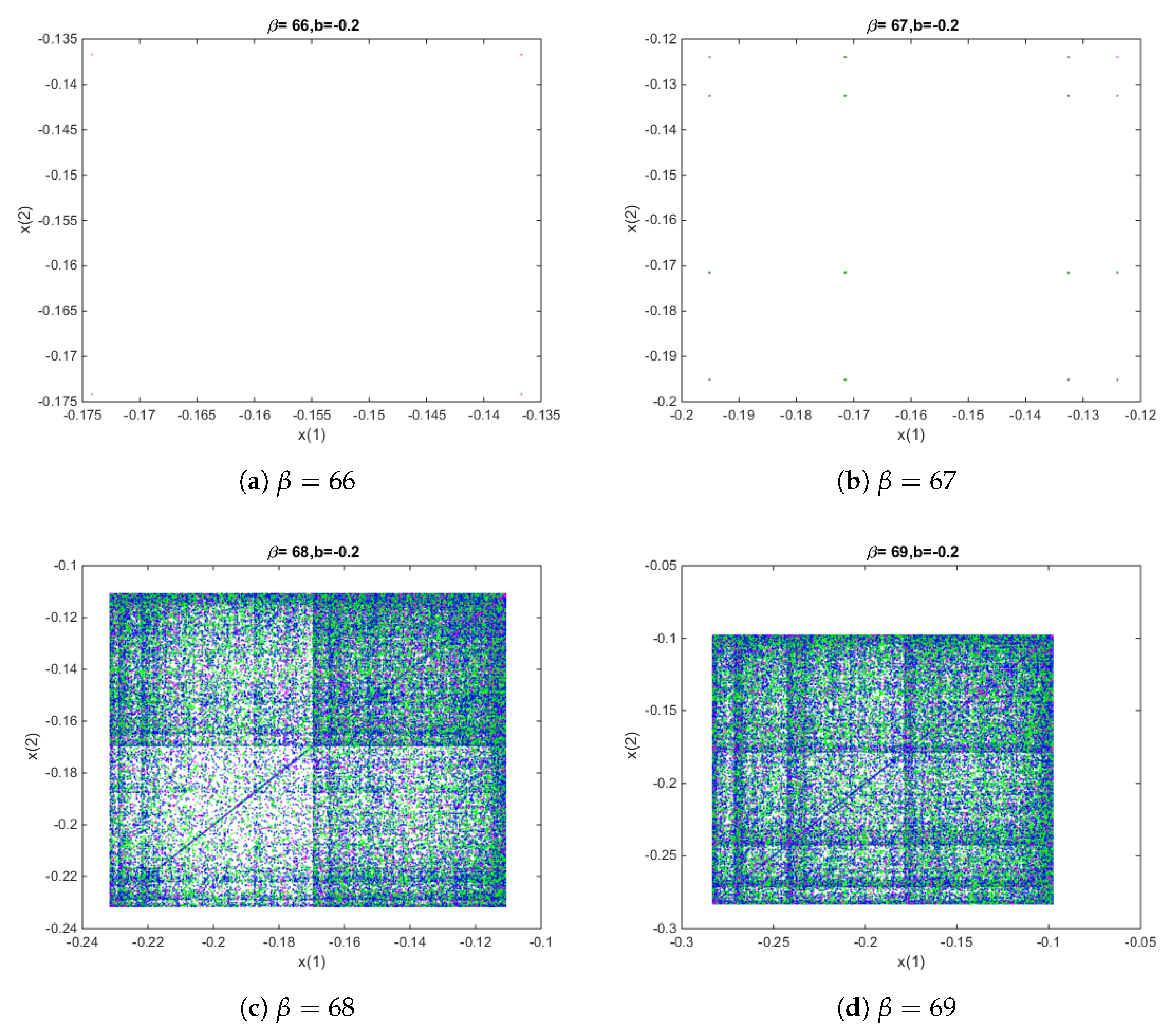
Figure 4c four period-doubling bifurcation areas where the repulsive fixed points have bifurcated into period-doubling orbits.
In order to better visualize this behavior, we plotted in the
-plane the iteration of
, for
in the blue area of
Figure 5a near to
. Then, symmetric strange attractors appear (see
Figure 5b,c).
As in this case, the four strange attractors must be separately identified, the way these pictures have been obtained is slightly different than that used in case M41 family: Fixing the value of parameter , 1000 different initial estimations have been taken in small rectangles close to the origin. For each specific value of , the method has been used on each of them, plotting one point per iteration. The code color used is as follows: The first 800 iterations do not appear, while the following 100 appear in blue color and the last hundred are shown in magenta color. The resulting plots show how the four attracting fixed points change into attracting areas, being disjoint or not depending on . Nevertheless, the set of starting guesses belonging to their respective basins of attraction is very small, as well as the interval of real values of inducing this performance.
5. Dynamical Planes for
In this section, we compare the sensitivity of the proposed classes to the initial estimation, depending on some values of the parameter that have resulted to provide stable or unstable behavior, for each one of the families.
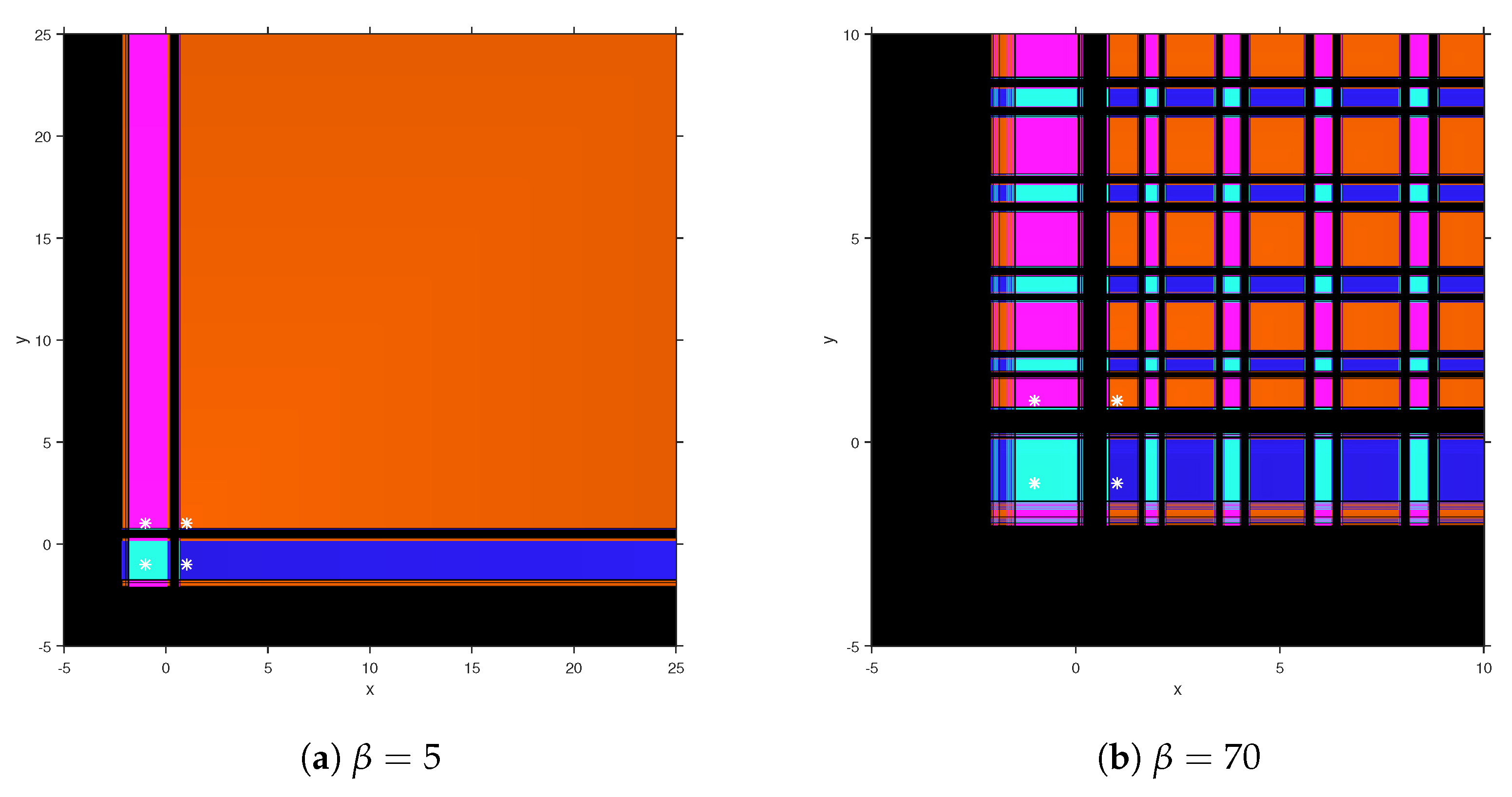
In
Figure 6 and
Figure 7, we plotted the dynamical planes corresponding to M41 for several values of
. They were obtained using the routines appearing in Reference [
21]. A mesh of
points was used, the maximum number of iterations employed was 40, and the stopping criterium has a tolerance of
. We plotted a point of this mesh of different colors depending on the root they converge to. Moreover, the color is brighter when the number of iterations used is lower. It is plotted in black color if it reaches the maximum number of iterations without converging to any of the roots.
We observe in
Figure 6 that the four roots of the vectorial polynomial have their respective wide basins of attraction (colored in orange, cyan, blue, and purple), with several connected components for each root, separated by the Julia set. There are also four repulsive fixed points and 16 saddle points. In case
, there exist four superattracting fixed points, sixteen repulsive, and other sixteen saddle fixed points. It can be observed in
Figure 6b that the number of connected components in the plotted area is much higher, and the immediate basin of attraction (the component holding the fixed point) is smaller in general.
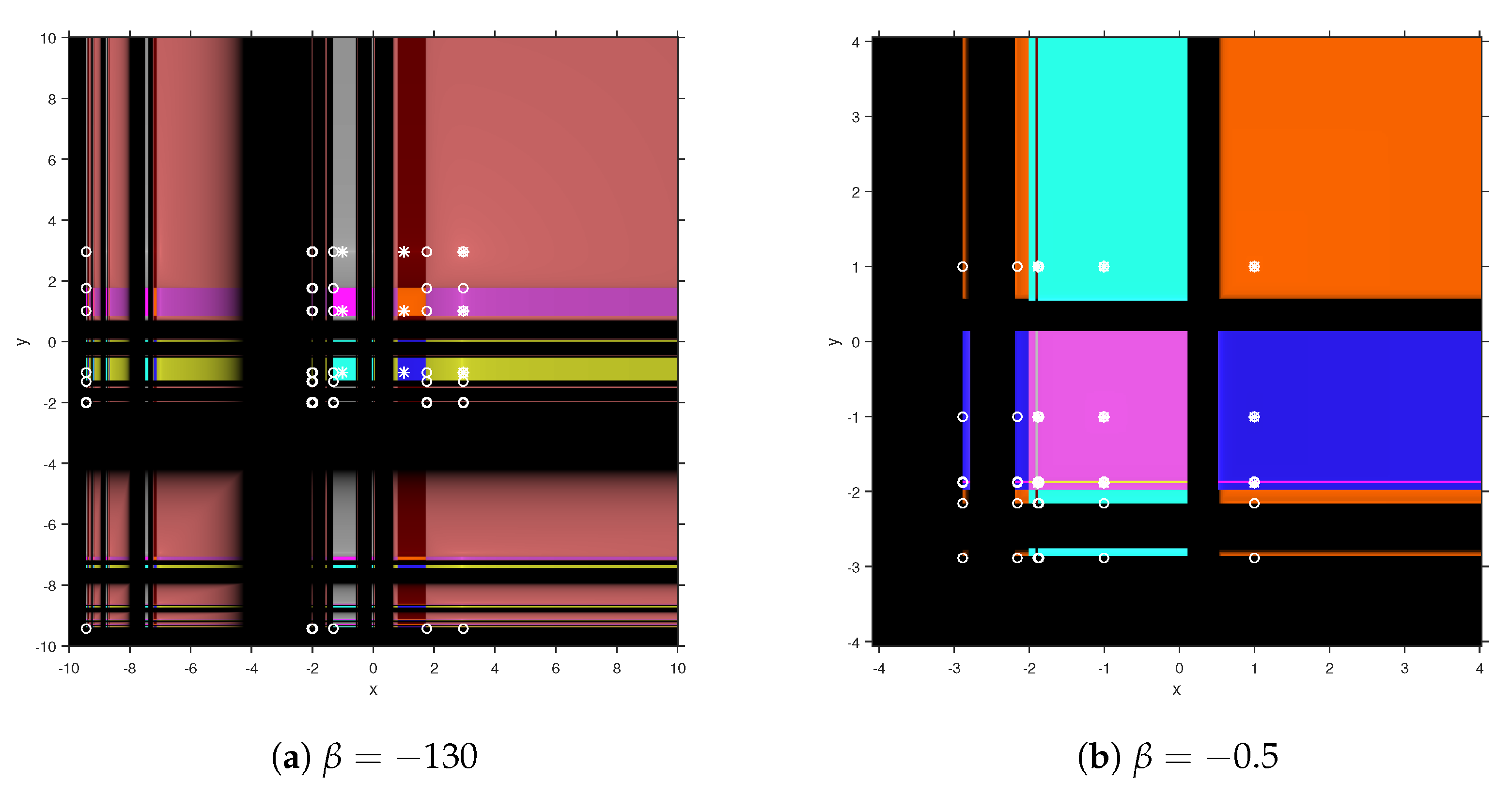
On the other hand, unstable behavior appears in
Figure 7, corresponding to the values
and
, where nine strange attracting fixed points had been found, in both cases. They are located in the colored areas of no convergence to the roots, presented in yellow, brown, gray, pink, and green, among others. There are also 25 repulsive and 30 saddle fixed points for
and, in the case of
, there are 9 repulsive and 18 saddle fixed points. Regarding the symbols, fixed points are marked with a white circle, while those attracting are shown with a white star. Let us remark that repulsive and nonhyperbolic points are always in the Julia set, and attracting ones lay in their respective basin of attraction.
To sum up, the stability of the members of Jacobian-free class M41 of iterative schemes has been analyzed for a quadratic multivariate polynomial. Unstable behavior, in terms of attracting strange fixed points, has been located for , the rest of elements being stable, with wide sets of convergent initial estimations.
Class M42
The dynamical planes related to the M42 class on
for different values of parameter
are shown in
Figure 8 and
Figure 9.
We see in
Figure 8a, for
, that the basins of attraction of the four zeroes of the polynomial form a balanced division of the real plane into four parts (with only a connected component for each root). The fifth-order case
(
Figure 8b) is also stable, but the number of basins of attraction increases slightly with the value of the parameter, and they are divided in several connected components.
Finally, the unstable behavior is shown in
Figure 9a,b, for
and
, respectively, where strange attractors appear. They are located in the black regions, showing no convergence to the zeroes.
To summarize, the stability of the elements of classes M41 and M42 of iterative methods were studied for quadratic multivariate polynomial. The only unstable behavior was located in small intervals where attracting periodic orbits or dense attracting regions were found, and the rest of the elements were stable, the most stable ones being clearly stated. This is numerically checked in the following section.
6. Numerical Performance
The numerical results shown in this section were obtained using Matlab R2014b, with variable precision arithmetics with 200 digits of mantissa. In each table of results, the residual
and the difference between consecutive iterations
are presented for the first three iterations. The approximated computational order of convergence (ACOC) is also calculated, by means of (see [
5]):
The nonlinear systems used in these tests, , are defined by the following coordinate functions, joint with the corresponding size and the estimated solution to be found:
, , ,
;
, , ,
.
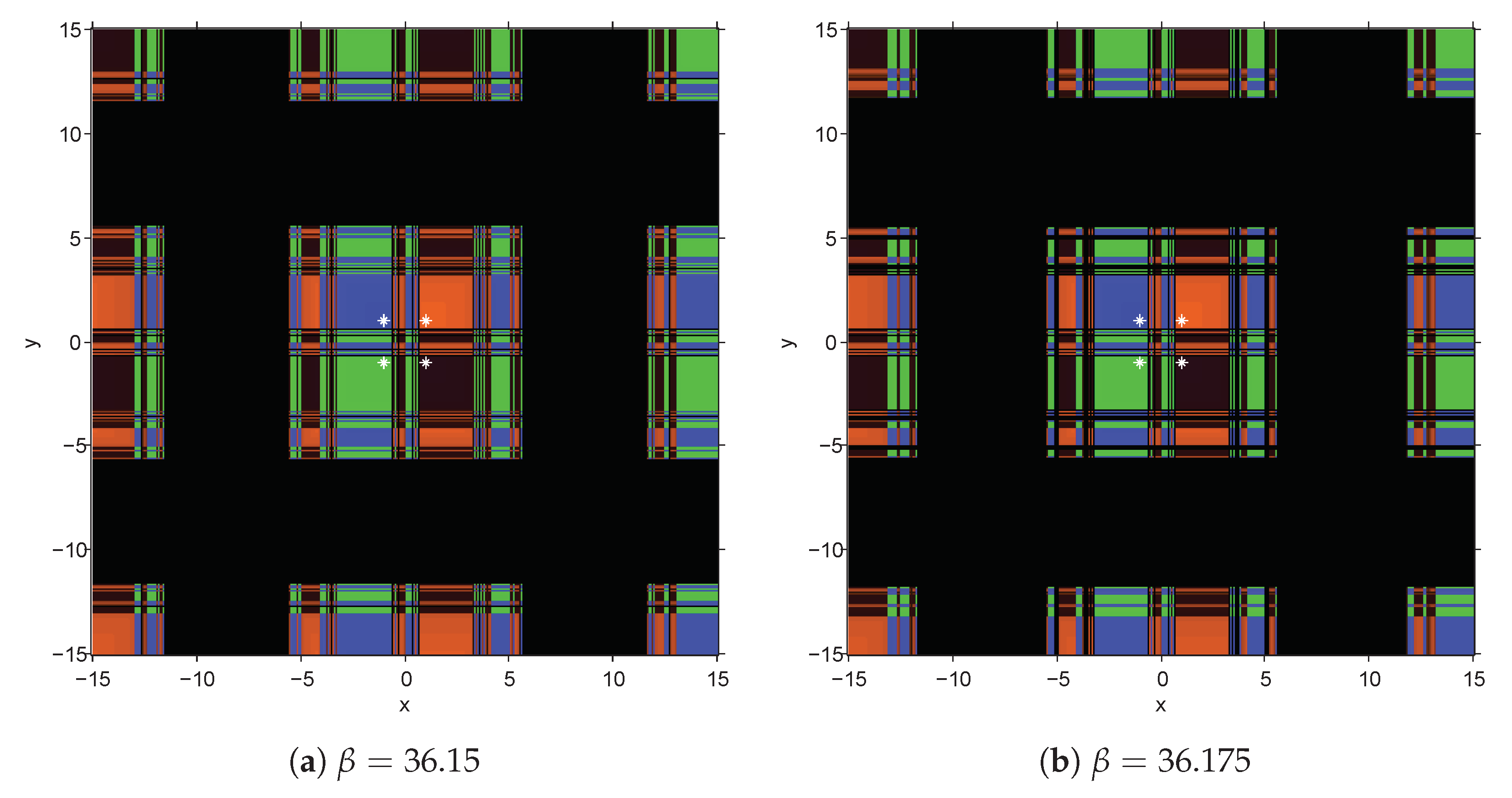
For each Jacobian-free class, M41 and M42, two stable elements were used ( and for M41 and and for M42), and also two respective unstable elements ( and for M41 and and for M42), expecting to see their performance on nonpolynomial functions.
In both examples of nonpolynomial systems, it is observed that, being good results in general, those obtained using values of parameter
that have shown to be stable in the dynamical analysis give more precise results than those that are considered unstable, as can be checked in
Table 1 and
Table 2.
7. Conclusions
Two highly efficient Jacobian-free classes of iterative methods were designed, and it has been proven that their order of convergence is four, except for a fifth-order particular case at for the second class. The real multidimensional stability of the members of both classes of iterative schemes was analyzed for quadratic polynomial systems. For the first family, only two real components of strange fixed points that can yield attracting points different from the roots appear. In the second one, there are no attracting strange fixed points. On the other hand, free real critical points fall in chaotic behavior only in small intervals for both cases. The rest of the members are stable, being the most similar performance to Newton’s scheme located around . Finally, numerical experiments confirm the theoretical results, showing good performance in all cases but having lower residual errors in those cases that correspond to the stable values of the parameter.
Author Contributions
The contribution of the authors to this manuscript can be defied as: Conceptualization, A.C. and J.R.T.; Validation, J.G.M. and M.P.V.; Formal Analysis, J.R.T.; Investigation, M.P.V.; Resources, J.G.M.; Writing—Original Draft Preparation, A.C.; Writing—Review & Editing, J.R.T.
Funding
This research was partially supported by Ministerio de Economía y Competitividad under grants PGC2018-095896-B-C22, Generalitat Valenciana PROMETEO/2016/089 and FONDOCYT 027-2018 and 029-2018, Dominican Republic.
Acknowledgments
The authors would like to thank the anonymous reviewers for their comments and suggestions that have improved the final version of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Frontini, M.; Sormani, E. Third-order methods from quadrature formulae for solving systems of nonlinear equations. Appl. Math. Comput. 2004, 149, 771–782. [Google Scholar] [CrossRef]
- Homeier, H.H.H. A modified Newton method with cubic convergence: The multivariable case. J. Comput. Appl. Math. 2004, 169, 161–169. [Google Scholar] [CrossRef]
- Noor, M.A.; Waseem, M. Some iterative methods for solving a system of nonlinear equations. Comput. Math. Appl. 2009, 57, 101–106. [Google Scholar] [CrossRef]
- Xiao, X.; Yin, H. A new class of methods with higher order of convergence for solving systems of nonlinear equations. Appl. Math. Comput. 2015, 264, 300–309. [Google Scholar] [CrossRef]
- Cordero, A.; Torregrosa, J.R. Variants of Newton’s method using fifth-order quadrature formulas. Appl. Math. Comput. 2007, 190, 686–698. [Google Scholar] [CrossRef]
- Darvishi, M.T.; Barati, A. A third-order Newton-type method to solve systems of nonlinear equations. Appl. Math. Comput. 2007, 187, 630–635. [Google Scholar] [CrossRef]
- Sharma, J.R.; Guha, R.K.; Sharma, R. An efficient fourth order weighted-Newton method for systems of nonlinear equations. Numer. Algor. 2013, 62, 307–323. [Google Scholar] [CrossRef]
- Narang, M.; Bhatia, S.; Kanwar, V. New two-parameter Chebyshev-Halley-like family of fourth and sixth-order methods for systems of nonlinear equations. Appl. Math. Comput. 2016, 275, 394–403. [Google Scholar] [CrossRef]
- Behl, R.; Sarría, I.; Crespo, R.G.; Magreñán, Á.A. Highly efficent family of iterative methods for solving nonlinear models. Comput. Appl. Math. 2019, 346, 110–132. [Google Scholar] [CrossRef]
- Amorós, C.; Argyros, I.K.; González, R.; Magreñán, Á.A.; Orcos, L.; Sarría, I. Study of a high order family: Local convergence and dynamics. Mathematics 2019, 7, 225. [Google Scholar] [CrossRef]
- Argyros, I.K.; González, D. Local convergence for an improved Jarratt-type method in Banach space. IJIMAI 2015, 3, 20–25. [Google Scholar] [CrossRef][Green Version]
- Sharma, J.R.; Gupta, P. An efficient fifth order method for solving systems of nonlinear equations. Comput. Math. Appl. 2014, 67, 591–601. [Google Scholar] [CrossRef]
- Cordero, A.; Torregrosa, J.R.; Vassileva, M.P. Design, Analysis, and Applications of Iterative Methods for Solving Nonlinear Systems. In Nonlinear Systems—Design, Analysis, Estimation and Control; InTechOpen: London, UK, 2016; Chapter 5; pp. 87–116. [Google Scholar]
- Cordero, A.; Gutiérrez, J.M.; Magreñán, Á.A.; Torregrosa, J.R. Stability analysis of a parametric family of iterative methods for solving nonlinear models. Appl. Math. Comput. 2016, 285, 26–40. [Google Scholar] [CrossRef]
- Cordero, A.; Chicharro, F.I.; Torregrosa, J.R. Real stability of an efficient family of iterative methods for solving nonlinear systems. In Proceedings of the Conference CEDYA + CMA 2017, Cartagena, Spain, 26–30 June 2017; pp. 213–218. [Google Scholar]
- Robinson, R.C. An Introduction to Dynamical Systems, Continous and Discrete; Americal Mathematical Society: Providence, RI, USA, 2012. [Google Scholar]
- Cordero, A.; Soleymani, F.; Torregrosa, J.R. Dynamical analysis of iterative methods for nonlinear systems or how to deal with the dimension? Appl. Math. Comput. 2014, 244, 398–412. [Google Scholar] [CrossRef]
- Cordero, A.; Hueso, J.L.; Martínez, E.; Torregrosa, J.R. A modified Newton-Jarratt’s composition. Numer. Algor. 2010, 55, 87–99. [Google Scholar] [CrossRef]
- Ortega, J.M.; Rheimboldt, W.C. Iterative Solutions of Nonlinear Equations in Several Variables; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Argyros, I.K.; George, S. Ball convergence for Steffensen-type fourth-order methods. IJIMAI 2015, 3, 37–42. [Google Scholar] [CrossRef][Green Version]
- Chicharro, F.I.; Cordero, A.; Torregrosa, J.R. Drawing dynamical and parameters planes of iterative families and methods. Sci. World 2013, 2013, 780153. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
Stability of the fixed points.
Figure 1.
Stability of the fixed points.
Figure 2.
Feigenbaum diagrams of , .
Figure 2.
Feigenbaum diagrams of , .
Figure 3.
Strange attractors of M41 class for values in the period-doubling cascade region.
Figure 3.
Strange attractors of M41 class for values in the period-doubling cascade region.
Figure 4.
Feigenbaum diagrams of , .
Figure 4.
Feigenbaum diagrams of , .
Figure 5.
Strange attractors of M42 class for values in the period-doubling cascade region.
Figure 5.
Strange attractors of M42 class for values in the period-doubling cascade region.
Figure 6.
Dynamical planes for stable values of of class M41 on .
Figure 6.
Dynamical planes for stable values of of class M41 on .
Figure 7.
Dynamical plane for unstable values of of class M41 on .
Figure 7.
Dynamical plane for unstable values of of class M41 on .
Figure 8.
Dynamical planes for stable values of of class M42 on .
Figure 8.
Dynamical planes for stable values of of class M42 on .
Figure 9.
Dynamical planes for stable values of of class M42 on .
Figure 9.
Dynamical planes for stable values of of class M42 on .
Table 1.
, , , .
Table 1.
, , , .
| Class | | | | | | | | ACOC |
|---|
| M41 | 5 | 1.357 | 0.2225 | 0.08254 | 2.895 | 1.066 | 5.868 | 4.0309 |
| M41 | 10 | 1.246 | 0.07772 | 0.02856 | 4.087 | 1.506 | 3.546 | 3.9913 |
| M41 | 68 | 0.9315 | 0.9567 | 0.3453 | 0.005465 | 0.002014 | 2.314 | 3.7328 |
| M41 | −130 | 0.8917 | 1.071 | 0.3819 | 0.03454 | 0.001272 | 8.167 | 3.4626 |
| M42 | −10 | 0.8471 | 1.1990 | 0.4278 | 4.169 | 1.536 | 1.384 | 3.5685 |
| M42 | 5 | 1.3470 | 0.1941 | 0.07197 | 5.116 | 1.885 | 7.685 | 4.9915 |
| M42 | 36 | 1.0120 | 0.7287 | 0.2630 | 2.376 | 8.752 | 3.015 | 3.7659 |
| M42 | 36.15 | 1.0130 | 0.7261 | 0.2621 | 2.391 | 8.809 | 3.109 | 3.7672 |
Table 2.
, , , .
Table 2.
, , , .
| Class | | | | | | | | ACOC |
|---|
| M41 | 5 | 1.233 | 3.827 | 1.522 | 4.672 | 1.858 | 1.039 | 4.0 |
| M41 | 10 | 0.01233 | 2.747 | 1.093 | 9.852 | 3.919 | 1.629 | 4.0 |
| M41 | 68 | 1.237 | 8.575 | 3.411 | 1.913 | 7.608 | 4.684 | 4.0005 |
| M41 | −130 | 1.228 | 1.434 | 5.704 | 5.968 | 2.374 | 1.82 | 3.9990 |
| M42 | −10 | 1.212 | 5.273 | 2.097 | 7.529 | 2.994 | 6.357 | 3.9687 |
| M42 | 5 | 1.293 | 1.492 | 5.94 | 8.504 | 3.382 | 2.075 | 5.2587 |
| M42 | 36 | 1.367 | 3.346 | 1.333 | 4.298 | 1.709 | 1.395 | 4.1567 |
| M42 | 36.15 | 1.367 | 3.347 | 1.333 | 4.325 | 1.72 | 1.438 | 4.1569 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).