Lipschitz Stability for Non-Instantaneous Impulsive Caputo Fractional Differential Equations with State Dependent Delays
Abstract
1. Introduction
- Lipschitz stability;
- state dependent delays (note a special case is time varying delays); and
- models with non-instantaneous impulses.
2. Notes on Fractional Calculus
- -
- Riemann–Liouville (RL) fractional derivative:where denotes the Gamma function.
- -
- Caputo fractional derivativeNote that for a constant m the equality holds. However, for any given , we denote .
- -
- The Grünwald–Letnikov fractional derivative is given byand the Grünwald–Letnikov fractional Dini derivative bywhere and denotes the integer part of the fraction .
3. Statement of the Problem and Basic Definitions
- -
- Unchangeable lower limit of the Caputo fractional derivative: the lower limit of the fractional derivative is equal to the initial time on the whole interval of consideration.
- -
- Changeable lower limit of the Caputo fractional derivative: the lower limit of the fractional derivative is equal to the left end on the interval without impulses.
- A1.
- The function is such that for any the inclusion holds.
- A2.
- The function and for any the inequalities holds.
- A3.
- The functions .
- A4.
- The function .
- A5.
- The function for and for .
- -
- Uniformly Lipschitz stable if there exists and such that, for any for any initial time and any initial function , the inequality implies for where is a solution of Equation (1).
- -
- Globally uniformly Lipschitz stable if there exists such that, for any initial time and any initial function , the inequality implies for
4. Lyapunov Functions and Their Derivatives among Nonlinear Non-Instantaneous Caputo Delay Fractional Differential Equations
- -
- The function is continuous on and it is locally Lipschitz with respect to its second argument.
- -
- For each and , there exist finite limits
- -
- First type: the Caputo fractional derivative of the function defined bywhere is a solution of Equation (1).
- -
- Second type: Dini fractional derivative of the Lyapunov function among Equation (1): Let and for a non-negative integer k. Then,where and for any . We note that, because of Assumption A2, the inequality holds (), i.e is well defined.The derivative of Equation (4) keeps the concept of fractional derivatives because it has a memory.
- -
- Third type: Caputo fractional Dini derivative of a Lyapunov function among Equation (1): Let the initial function be given and the function and for a non-negative integer k. Then,or its equivalenceThe derivative given by Equation (6) depends significantly on both the fractional order q and the initial data of IVP for FrDDE (Equation (1)) and it makes this type of derivative close to the idea of the Caputo fractional derivative of a function.
5. Comparison Results
- A6.
- The function is strictly decreasing with respect to its second argument, and for any the functions are nondecreasing with respect to their second argument.
- A7.
- The function for and for any the function for .
- A8.
- For all , the functions satisfies .
- 1.
- Assumptions A1–A4 and A6 are satisfied.
- 2.
- The function is a solution of Equation (1) where , .
- 3.
- The function is such that
- (i)
- For any and for , the inequalityholds.
- (ii)
- For all the inequalityholds.
6. Main Results
- 1.
- Assumptions A1–A8 are fulfilled.
- 2.
- There exist a function and
- (i)
- The inequalitiesholds, where , , ;
- (ii)
- For any initial data and any solution of Equation (1) defined on such that for any , k is a non-negative integer, such that and for the inequalityholds.
- (iii)
- For any and the inequalityholds.
- 3.
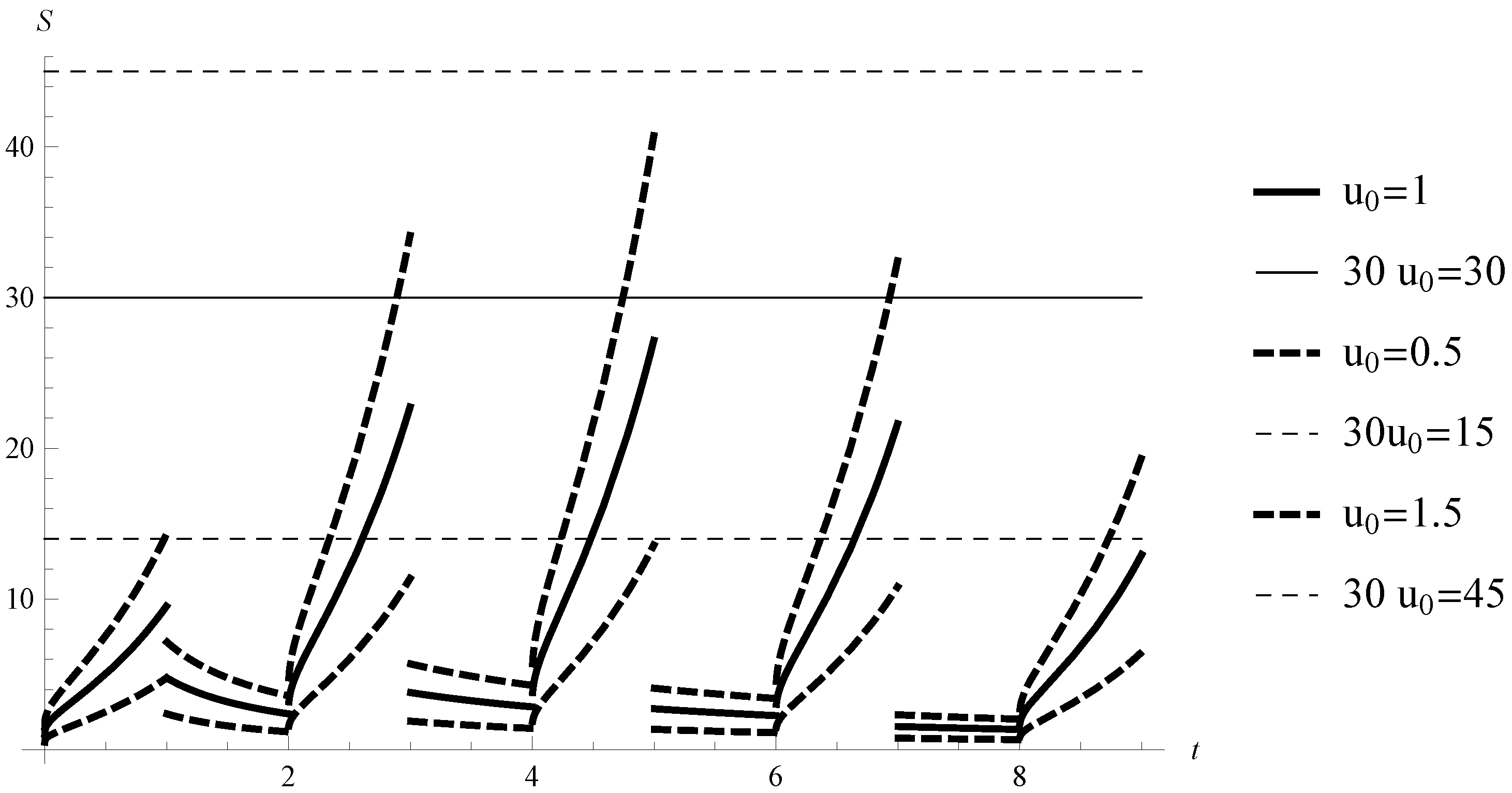
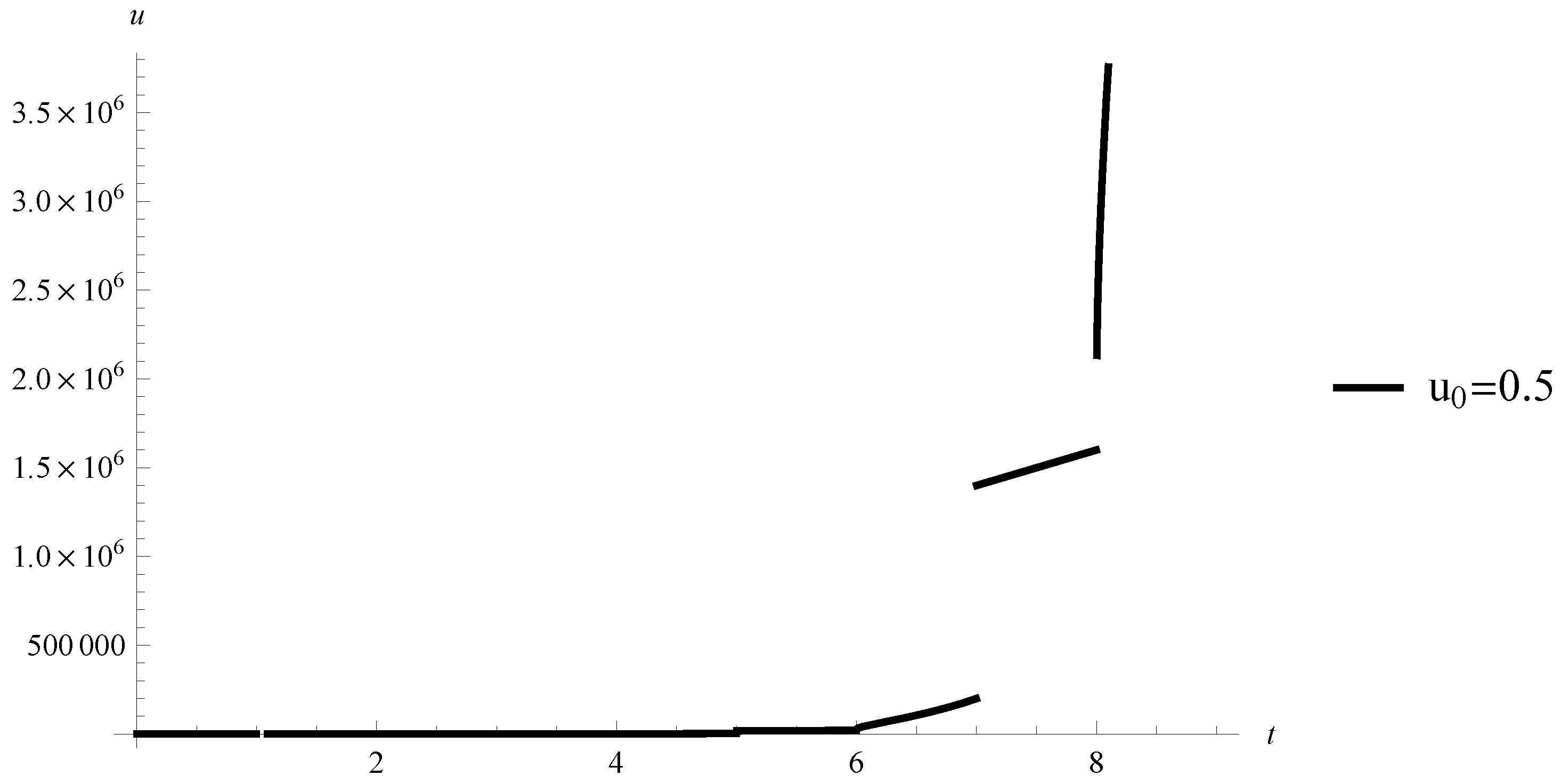
- The zero solution of Equation (10) is uniformly Lipschitz stable (uniformly globally Lipschitz stable).
- 1.
- Assumptions A1–A8 are fulfilled.
- 2.
- There exist a function , and
- (i)
- The inequalitiesholds, where , .
- (ii)
- (iii)
- For any and the inequalityholds.
- 3.
- The zero solution of Equation (10) is uniformly Lipschitz stable (uniformly globally Lipschitz stable).
Author Contributions
Funding
Conflicts of Interest
References
- Dannan, F.M.; Elaydi, S. Lipschitz stability of nonlinear systems of differential equations. J. Math. Anal. Appl. 1986, 113, 562–577. [Google Scholar] [CrossRef]
- Zavoli, A.; Giulietti, F.; Avanzini, G.; De Matteis, G. Spacecraft dynamics under the action of Y-dot magnetic control. Acta Astronaut. 2016, 122, 146–158. [Google Scholar] [CrossRef]
- Agarwal, R.; Hristova, S.; O’Regan, D. Lyapunov Functions and Stability of Caputo Fractional Differential Equations with Delays. Differ. Equ. Dyn. Syst. 2018, 1–22. [Google Scholar] [CrossRef]
- Hernandez, E.; O’Regan, D. On a new class of abstract impulsive differential equations. Proc. Am. Math. Soc. 2013, 141, 1641–1649. [Google Scholar] [CrossRef]
- Agarwal, R.; Hristova, S.; O’Regan, D. Non-Instantaneous Impulses in Differential Equations; Springer: Berlin, Germany, 2017. [Google Scholar]
- Agarwal, R.; Hristova, S.; O’Regan, D. Non-instantaneous impulses in Caputo fractional differential equations. Fract. Calc. Appl. Anal. 2017, 20, 595–622. [Google Scholar] [CrossRef]
- Bai, L.; Nieto, J.J. Variational approach to differential equations with not instantaneous impulses. Appl. Math. Lett. 2017, 73, 44–48. [Google Scholar] [CrossRef]
- Nieto, J.J.; Uzal, J.M. Pulse positive periodic solutions for some classes of singular nonlinearities. Appl. Math. Lett. 2018, 86, 134–140. [Google Scholar] [CrossRef]
- Agarwal, R.; Hristova, S.; O’Regan, D. Lyapunov Functions to Caputo Fractional Neural Networks with Time-Varying Delays. Axioms 2018, 7, 30. [Google Scholar] [CrossRef]
- Agarwal, R.P.; O’Regan, D.; Hristova, S. Stability of Caputo fractional differential equations by Lyapunov functions. Appl. Math. 2015, 60, 653–676. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, D.; Cao, J. Asymptotic Stability of Caputo Type Fractional Neutral Dynamical Systems with Multiple Discrete Delays. Abstr. Appl. Analys. 2014, 2014, 138124. [Google Scholar] [CrossRef]
- Das, S. Functional Fractional Calculus; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Pandey, D.N.; Das, S.; Sukavanam, N. Existence of solutions for a second order neutral differential equation with state dependent delay and not instantaneous impulses. Intern. J. Nonlinear Sci. 2014, 18, 145–155. [Google Scholar]
- Lakshmikantham, V.; Bainov, D.; Simeonov, P. Theory of Impulsive Differential Equations; World Scientific: Singapore, 1989. [Google Scholar]
- Lakshmikantham, V.; Leela, S.; Devi, J.V. Theory of Fractional Dynamic Systems; CSP: Cambridge, UK, 2009; 170p. [Google Scholar]
- Sadati, S.J.; Ghaderi, R.; Ranjbar, A. Some fractional comparison results and stability theorem for fractional time delay systems. Rom. Rep. Phy. 2013, 65, 94–102. [Google Scholar]
- Stamova, I.; Stamov, G. Lipschitz stability criteria for functional differential systems of fractional order. J. Math. Phys. 2013, 54, 043502. [Google Scholar] [CrossRef]
- Stamova, I.; Stamov, G. Functional and Impulsive Differential Equations of Fractional Order: Qualitative Analysis and Applications; CRC Press: Boca Raton, FL, USA, 2016; 276p. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agarwal, R.; Hristova, S.; O’Regan, D. Lipschitz Stability for Non-Instantaneous Impulsive Caputo Fractional Differential Equations with State Dependent Delays. Axioms 2019, 8, 4. https://doi.org/10.3390/axioms8010004
Agarwal R, Hristova S, O’Regan D. Lipschitz Stability for Non-Instantaneous Impulsive Caputo Fractional Differential Equations with State Dependent Delays. Axioms. 2019; 8(1):4. https://doi.org/10.3390/axioms8010004
Chicago/Turabian StyleAgarwal, Ravi, Snezhana Hristova, and Donal O’Regan. 2019. "Lipschitz Stability for Non-Instantaneous Impulsive Caputo Fractional Differential Equations with State Dependent Delays" Axioms 8, no. 1: 4. https://doi.org/10.3390/axioms8010004
APA StyleAgarwal, R., Hristova, S., & O’Regan, D. (2019). Lipschitz Stability for Non-Instantaneous Impulsive Caputo Fractional Differential Equations with State Dependent Delays. Axioms, 8(1), 4. https://doi.org/10.3390/axioms8010004






