On the Degree-Based Topological Indices of the Tickysim SpiNNaker Model

Abstract

Tickysim is a clock tick-based simulator for the inter-chip interconnection network of the SpiNNaker architecture. Network devices such as arbiters, routers, and packet generators store, read, and write forward data through fixed-length FIFO buffers. At each clock tick, every component executes a “read” phase followed by a “write” phase. The structures of any finite graph which represents numerical quantities are known as topological indices. In this paper, we compute degree-based topological indices of the Tickysim SpiNNaker Model ($TSM$) sheet.

1. Introduction

Neural networks are applicable in many solutions for classification, prediction, control, etc. The variety of purposes is growing but with each new application the expectations are higher. We want neural networks to be more precise independently of the input data. Efficiency of the processing in a large manner depends on the training algorithm. Basically this procedure is based on the random selection of weights in which neurons connections are burdened. During training process we implement a method which involves modification of the weights to minimize the response error of the entire structure see details in [1,2].

Convolutional neural network (CNN) is an essential model to achieve high accuracy in various machine learning applications, such as image recognition and natural language processing. One of the important issues for CNN acceleration with high energy efficiency and processing performance is efficient data reuse by exploiting the inherent data locality. Recurrent neural networks (RNNs) are powerful models of sequential data. They have been successfully used in domains such as text and speech. However, RNNs are susceptible to overfitting; regularization is important [3]. Motivated by these networks we consider the Tickysim SpiNNaker Model(network) for utilization its topological properties.

In this paper all graphs are finite, simple, and undirected. Let $V\left(G\right)$ and $E\left(G\right)$ be the vertex set and edge set of a graph G. The vertices $u,v\in V\left(G\right)$ are adjacent (or neighbors) if u and v are endpoints of $e\in E\left(G\right)$ and e is incident with the vertices u and v and e is said to connect u and $v.$ The set of all neighbors of a vertex u of G denoted by $N\left(u\right)$ is called the neighborhood of $v.$ The degree of a vertex in an undirected simple graph is the number of edges incident with it. The degree of the vertex u is denoted by $\zeta \left(u\right)$ and $S_u$ is the sum of degrees of all vertices adjacent to the vertex $u.$ In other words, $S_u={\displaystyle \sum _{v\in N\left(u\right)}}{d}_v,$ where $N\left(u\right)=\{v\in V(G):uv\in E(G\left)\right\}.$ All the concepts of graph theory and combinatorics are used from the book of Harris et al. [4,5].

The application of molecular structure descriptors is now a standard procedure in the study of structure–property relations, especially in QSPR/QSAR study. In the past couple of years, the amount of proposed nuclear descriptors is rapidly increases as a result of the significance of the creation of these descriptors. They interface the particular physico-substance properties of mixture blends. A most seasoned, considered, and prominent topological record among all degree-based topological lists is the Randić index, which was presented by Randić in 1975 [6]. This record was discovered to be reasonable with the end goal of a medication plan [7]. The numerical elements of the Randić index incorporates its association with the standardized Laplacian framework [8,9,10]. The formal definition of the Randić index of a graph G is given as follows:

$$R\left(G\right)=\sum _{uv\in E\left(G\right)}\frac{1}{\sqrt{\zeta \left(u\right)\times \zeta \left(v\right)}}.$$

(1)

Soon after the discovery of Randić index, the general Randić index was introduced. It is denoted by $R_{\alpha }\left(G\right)$, and its formula is given as:

$$R_{\alpha }\left(G\right)=\sum _{uv\in E\left(G\right)}{(\zeta \left(u\right)\times \zeta \left(v\right))}^{\alpha },$$

(2)

where $\alpha$ is a nonzero real number. Zhou et al. [11] introduced the general sum-connectivity index ${\chi }_{\alpha }\left(G\right)$ and defined it as:

$${\chi }_{\alpha }\left(G\right)=\sum _{uv\in E\left(G\right)}{(\zeta \left(u\right)+\zeta \left(v\right))}^{\alpha },$$

(3)

where $\alpha$ is a real number. Shirdel et al. introduced a new degree-based Zagreb index named the “hyper-Zagreb index” which is defined in [12], and is also known as general sum-connectivity index ${\chi }_2\left(G\right).$ The first general Zagreb index was studied in [13].

$$M_{\alpha }\left(G\right)=\sum _{u\in V\left(G\right)}{\left(\zeta \left(u\right)\right)}^{\alpha }.$$

(4)

Estrada et al. invented the atom-bond connectivity index, abbreviated as the $ABC$ index [14]. $ABC$ index is of much importance due to its correlation with the thermodynamic properties of alkanes (see [15,16]). The definition of the $ABC$ index is as follows:

$$ABC\left(G\right)=\sum _{uv\in E\left(G\right)}\sqrt{\frac{\zeta \left(u\right)+\zeta \left(v\right)-2}{\zeta \left(u\right)\times \zeta \left(v\right)}}.$$

(5)

The fourth version of the $ABC$ index was introduced by Ghorbani and Hosseinzadeh [17], and is defined as:

$$AB{C}_4\left(G\right)=\sum _{uv\in E\left(G\right)}\sqrt{\frac{S_u+S_v-2}{S_u{S}_v}}.$$

(6)

Another important degree-based topological index is the geometric-arithmetic index ($GA$ index) and is of much importance due to its application to acyclic, unicyclic, and bicyclic molecular graphs [18]. The formal definition of the $GA$ index is as follows:

$$GA\left(G\right)=\sum _{uv\in E\left(G\right)}\frac{2\sqrt{\zeta \left(u\right)\times \zeta \left(v\right)}}{\zeta \left(u\right)+\zeta \left(v\right)}.$$

(7)

Recently, the fifth version of $GA$ was introduced by Graovac el al. [19], defined as:

$$G{A}_5\left(G\right)=\sum _{uv\in E\left(G\right)}\frac{2\sqrt{S_u{S}_v}}{S_u+S_v}.$$

(8)

In [20], Ghorbani and Azimi defined first multiple Zagreb index $P{M}_1\left(G\right)$ and second multiple Zagreb index $P{M}_2\left(G\right)$, defined as:

$$P{M}_1\left(G\right)=\prod _{uv\in E\left(G\right)}(\zeta \left(u\right)+\zeta \left(v\right)),$$

(9)

$$P{M}_2\left(G\right)=\prod _{uv\in E\left(G\right)}(\zeta \left(u\right)\times \zeta \left(v\right)).$$

(10)

These multiple Zagreb indices are studied for some chemical structures in [21,22,23,24,25]. The first Zagreb polynomial $M_1(G,x)$ and second Zagreb polynomial $M_2(G,x)$ are defined as:

$$M_1(G,x)=\sum _{uv\in E\left(G\right)}{x}^{\left(\zeta \right(u)+\zeta (v\left)\right)},$$

(11)

$$M_2(G,x)=\sum _{uv\in E\left(G\right)}{x}^{\left(\zeta \right(u)\times \zeta (v\left)\right)}.$$

(12)

2. Applications of Topological Indices

To relate with certain physico-concoction properties, the $GA$ index has much preferred prescient control over the prescient energy of the Randić connectivity index [26]. The first and second Zagreb indexes were found to be helpful for calculation of the aggregate $\pi$-electron energy of the particles inside particular rough articulations [27]. These are among the graph invariants that were proposed for estimation of the skeleton of stretching of the carbon atom [28]. The Randić index is a topological descriptor that has related with a great deal of the synthetic qualities of atoms and has been discovered parallel to processing the boiling point and Kovats constants of the particles. The particle bond network $\left(ABC\right)$ index gives a decent connection to the security of direct alkanes and also the stretched alkanes and for processing the strain vitality of cyclo alkanes [29,30].

In the past two decades, analysts contemplated certain substance diagrams and arrangement s and processed their particular indices. W. Gao and M. R. Farahani figured degree-based indices of synthetic structures by utilizing an edge-separated technique [31]. Gao et al. [32] contemplated concoction structures in medications and some medication structures, and processed the overlooked topological indices. Some different utilizations of the atomic descriptors of sub-atomic diagrams and systems are given in the reference list and the references [33]. These applications and writing survey inspired us to investigate some new substance diagrams and process their topological indices [34,35,36,37].

3. Materials and Methods

At the highest level of abstraction, inter-chip architectures are basically mathematical graphs where each device is considered as vertex and the topology used between these devices reflects the edges and in total nature of graph. One of the network topologies used in this model is 12 × 12 hexagonal torus. In this topology, each node is connected to six incident nodes. We also consider the finite Tickysim SpiNNaker Model sheet which is obtained by hexagonal torus. For more details, see [38].

The Second of the network topology consists of a set of a hexagonal segments of a hexagonal mesh of nodes. Each node in the simulation represents a SpiNNaker chip that contains a router, packet generator, packet consumer, and a tree of two-input round-robin arbiters which arbitrates between the inputs to the router. The router always consists of a four-stage pipeline. If a packet cannot be forwarded to its requested output after 50 cycles at the head of the router, it is dropped. The packet generator generates packets for each node of the system. If the output buffer is full, the packet generator waits until a space becomes available. The packet consumer receives incoming packets immediately, but the packet consumer will wait 10 cycles before accepting another packet. The arbiter tree is based on SpiNNaker’s NoC aspects. In each cycle, the arbiter selects a waiting packet on one of its inputs and forwards it to its output if there is space in the output buffer.

The graph $TSM$ of a Tickysim SpiNNaker Model sheet is shown in Figure 1. The number of vertices in the Tickysim SpiNNaker Model sheet are $mn$, and the vertex partition of the graph $TSM$ sheet based on the degree of vertices is shown in Table 1.

Figure 1. Graph of the Tickysim SpiNNaker Model sheet for m = n = 12.

Table 1. The vertex partition of the graph $TSM$ sheet based on the degree of vertices.

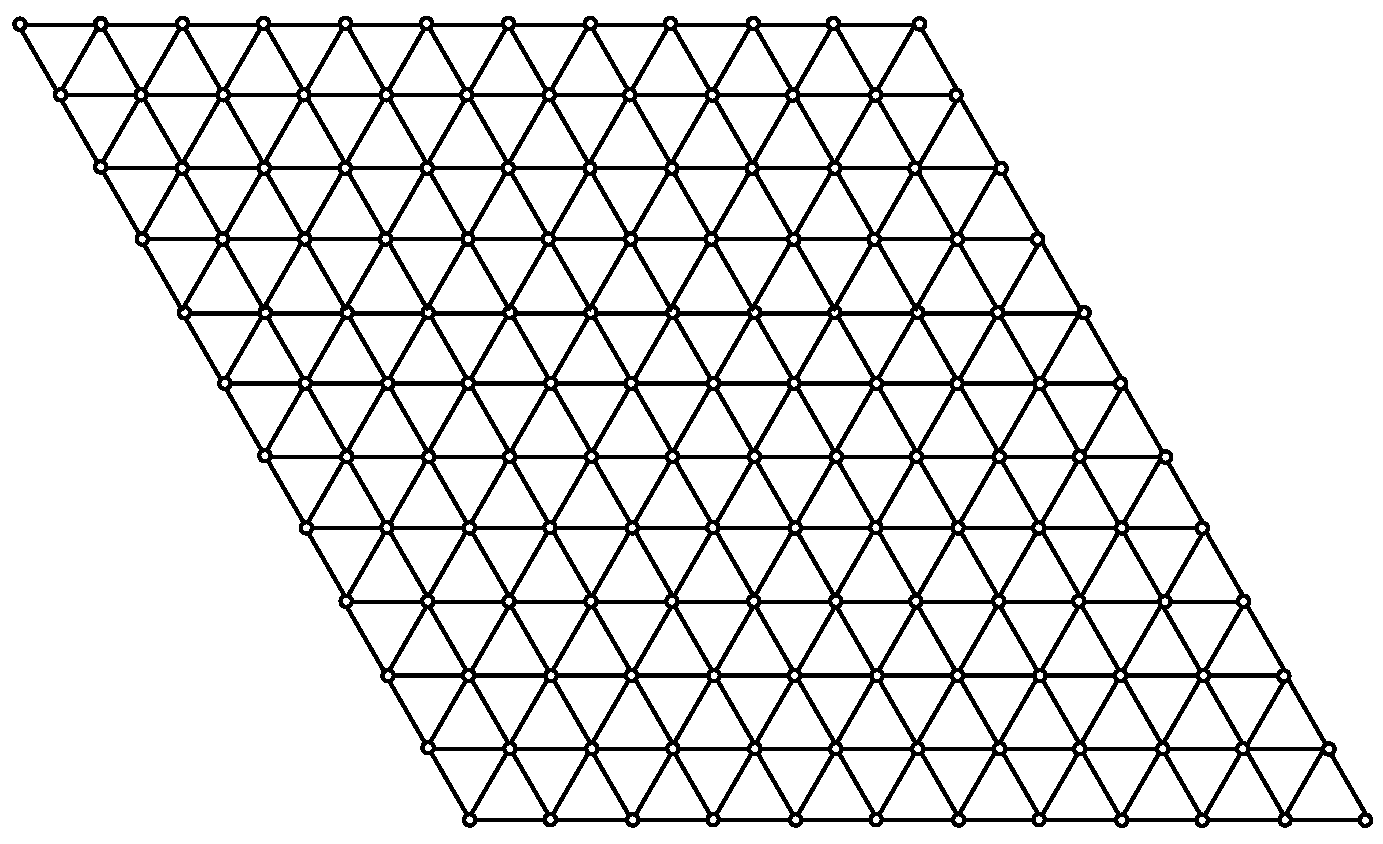
Degree of Vertex	Number of Vertices
2	2
3	2
4	$2m+2n-8$
6	$mn-2m-2n+4$
Total	$mn$

4. Main Results

Theorem 1.

Let $TSM$ be a Tickysim SpiNNaker Model sheet, then

1. 

$M_{\alpha }\left(TSM\right)=2^{\alpha +1}+2\times 3^{\alpha }+(m+n-4)2^{2\alpha +1}+(mn-2m-2n+4)6^{\alpha }$,

2. 

$R_{\alpha }\left(TSM\right)=2^{3\alpha +2}+2^{2\alpha +2}\times 3^{\alpha }+2^{\alpha +1}\times 3^{2\alpha }+2^{3\alpha +1}(m+n-5)(2^{\alpha }+2.3^{\alpha })+6^{2\alpha }(3mn-8m-8n+21)$,

3. 

${\chi }_{\alpha }\left(TSM\right)=4\times 6^{\alpha }+4\times 7^{\alpha }+2\times 3^{2\alpha }+(m+n-5)2^{3\alpha +1}+4(m+n-5){\left(10\right)}^{\alpha }+(3mn-8m-8n+21){\left(12\right)}^{\alpha }$,

where α is a real number.

Proof. 

The number of edges of the $TSM$ sheet graph is $3mn-2m-2m+1.$ The edge partition based on the degree of the end vertices of each edge are shown in Table 2. Since the formula of the general Randić index is

$$R_{\alpha }\left(TSM\right)=\sum _{uv\in E\left(TSM\right)}{\left(\zeta \left(u\right)\zeta \left(v\right)\right)}^{\alpha },$$

it implies that

$$\begin{array}{ccc}\hfill R_{\alpha }\left(TSM\right)& =& e_{2,4}{(2\times 4)}^{\alpha }+e_{3,4}{(3\times 4)}^{\alpha }+e_{3,6}{(3\times 6)}^{\alpha }\hfill \\ & +& e_{4,4}{(4\times 4)}^{\alpha }+e_{4,6}{(4\times 6)}^{\alpha }+e_{6,6}{(6\times 6)}^{\alpha }\hfill \\ & =& \left(4\right){\left(8\right)}^{\alpha }+\left(4\right){\left(12\right)}^{\alpha }+\left(2\right){\left(18\right)}^{\alpha }+(2m+2n-10){\left(16\right)}^{\alpha }\hfill \\ & +& (4m+4n-20){\left(24\right)}^{\alpha }+(3mn-8m-8n+21){\left(36\right)}^{\alpha }\hfill \\ & =& 2^{3\alpha +2}+2^{2\alpha +2}\times 3^{\alpha }+2^{\alpha +1}\times 3^{2\alpha }\hfill \\ & +& 2^{3\alpha +1}(m+n-5)(2^{\alpha }+2\times 3^{\alpha })+6^{2\alpha }(3mn-8m-8n+21),\hfill \end{array}$$

and the formula of the general sum-connectivity index is

$${\chi }_{\alpha }\left(TSM\right)=\sum _{uv\in E\left(TSM\right)}{(\zeta \left(u\right)+\zeta \left(v\right))}^{\alpha },$$

which implies that

$$\begin{array}{ccc}\hfill {\chi }_{\alpha }\left(TSM\right)& =& e_{2,4}{(2+4)}^{\alpha }+e_{3,4}{(3+4)}^{\alpha }+e_{3,6}{(3+6)}^{\alpha }\hfill \\ & +& e_{4,4}{(4+4)}^{\alpha }+e_{4,6}{(4+6)}^{\alpha }+e_{6,6}{(6+6)}^{\alpha }\hfill \\ & =& \left(4\right){\left(6\right)}^{\alpha }+\left(4\right){\left(7\right)}^{\alpha }+\left(2\right){\left(9\right)}^{\alpha }+(2m+2n-10){\left(8\right)}^{\alpha }\hfill \\ & +& (4m+4n-20){\left(10\right)}^{\alpha }+(3mn-8m-8n+21){\left(12\right)}^{\alpha }\hfill \\ & =& 4\times 6^{\alpha }+4\times 7^{\alpha }+2\times 3^{2\alpha }+(m+n-5)2^{3\alpha +1}\hfill \\ & +& 4(m+n-5){\left(10\right)}^{\alpha }+(3mn-8m-8n+21){\left(12\right)}^{\alpha }.\hfill \end{array}$$

Table 2. The edge partition of a graph $TSM$ sheet based on the degree of end vertices of each edge.

$\left(\mathit{\zeta }\right(\mathit{u}),\mathit{\zeta }(\mathit{v}\left)\right)$, where $\mathit{uv}\in \mathit{E}\left(\mathit{TSM}\right)$	Number of Edges
$(2,4)$	4
$(3,4)$	4
$(3,6)$	2
$(4,4)$	$2m+2n-10$
$(4,6)$	$4m+4n-20$
$(6,6)$	$3mn-8m-8n+21$
Total	$3mn-2m-2n+1$

This completes the proof. □

Theorem 2.

The atom-bond connectivity index $TSM$ sheet is given by

$$\begin{array}{ccc}\hfill ABC\left(TSM\right)& =& \frac{1}{2}\sqrt{10}\mathit{mn}+2\sqrt{2}+\frac{2}{3}\sqrt{15}+\frac{1}{3}\sqrt{14}+\frac{1}{4}\left(2m+2n-10\right)\sqrt{6}\hfill \\ & +& \frac{1}{3}\left(4m+4n-20\right)\sqrt{3}+\frac{1}{6}\left(-8m-8n+21\right)\sqrt{10}.\hfill \end{array}$$

Proof. 

The number of $e_{2,4},e_{3,4},e_{3,6},e_{4,4},e_{4,6}$, and $e_{6,6}$ edges are mentioned in Table 2. Since the atom-bond connectivity index is defined as

$$ABC\left(TSM\right)=\sum _{uv\in E\left(TSM\right)}\sqrt{\frac{\zeta \left(u\right)+\zeta \left(v\right)-2}{\zeta \left(u\right)\times \zeta \left(v\right)}},$$

it implies that

$$\begin{array}{ccc}\hfill ABC\left(TSM\right)& =& e_{2,4}\sqrt{\frac{2+4-2}{2\times 4}}+e_{3,4}\sqrt{\frac{3+4-2}{3\times 4}}+e_{3,6}\sqrt{\frac{3+6-2}{3\times 6}}\hfill \\ & +& e_{4,4}\sqrt{\frac{4+4-2}{4\times 4}}+e_{4,6}\sqrt{\frac{4+6-2}{4\times 6}}+e_{6,6}\sqrt{\frac{6+6-2}{6\times 6}}\hfill \\ & =& \frac{1}{2}\sqrt{10}\mathit{mn}+2\sqrt{2}+\frac{2}{3}\sqrt{15}+\frac{1}{3}\sqrt{14}+\frac{1}{4}\left(2m+2n-10\right)\sqrt{6}\hfill \\ & +& \frac{1}{3}\left(4m+4n-20\right)\sqrt{3}+\frac{1}{6}\left(-8m-8n+21\right)\sqrt{10}.\hfill \end{array}$$

This completes the proof. □

Theorem 3.

The geometric-arithmetic index $GA$ of the $TSM$ sheet is given by

$$GA\left(TSM\right)=4\sqrt{2}+\frac{16}{7}\sqrt{3}-6m-6n+11+\frac{2}{5}\left(4m+4n-20\right)\sqrt{6}+3\mathit{mn}.$$

Proof. 

The numbers of $e_{2,4},e_{3,4},e_{3,6},e_{4,4},e_{4,6}$, and $e_{6,6}$ edges are mentioned in Table 2. Since the geometric-arithmetic index is defined as

$$GA\left(TSM\right)=\sum _{uv\in E\left(TSM\right)}\frac{2\sqrt{\zeta \left(u\right)\times \zeta \left(v\right)}}{\zeta \left(u\right)+\zeta \left(v\right)},$$

it implies that

$$\begin{array}{ccc}\hfill GA\left(TSM\right)& =& e_{2,4}\frac{2\sqrt{2\times 4}}{2+4}+e_{3,4}\frac{2\sqrt{3\times 4}}{3+4}+e_{3,6}\frac{2\sqrt{3\times 6}}{3+6}\hfill \\ & +& e_{4,4}\frac{2\sqrt{4\times 4}}{4+4}+e_{4,6}\frac{2\sqrt{4\times 6}}{4+6}+e_{6,6}\frac{2\sqrt{6\times 6}}{6+6}\hfill \\ & =& 4\frac{2\sqrt{2\times 4}}{2+4}+4\frac{2\sqrt{3\times 4}}{3+4}+2\frac{2\sqrt{3\times 6}}{3+6}\hfill \\ & +& (2m+2n-10)\frac{2\sqrt{4\times 4}}{4+4}+(4m+4n-20)\frac{2\sqrt{4\times 6}}{4+6}\hfill \\ & +& (3mn-8m-8n+21)\frac{2\sqrt{6\times 6}}{6+6}\hfill \\ & =& 4\sqrt{2}+\frac{16}{7}\sqrt{3}-6m-6n+11+\frac{2}{5}\left(4m+4n-20\right)\sqrt{6}+3\mathit{mn}.\hfill \end{array}$$

This completes the proof. □

In the next two theorems, we calculated the fourth atom-bond connectivity index $AB{C}_4$ and the fifth geometric-arithmetic index $G{A}_5$. There are eighteen types of edges on the degree-based sum of neighbors vertices of each edge in the Tickysim SpiNNaker Model sheet. We used this partition of edges to calculate $AB{C}_4$ and $G{A}_5$ indices. Table 3 gives such types of edges of the Tickysim SpiNNaker Model sheet. The edge set $E\left(TSM\right)$ is divided into eighteen edge partitions based on the degree of end vertices. The edge partition $E_{u,v}\left(TSM\right)$ contains $m_{u,v}$ edges $uv,$ where $S_u=u$, $S_v=v$, and $m_{u,v}=\left|E_{u,v}\left(TSM\right)\right|.$

Table 3. The edge partition of the graph $TSM$ sheet based on the degree sum of neighbor vertices of the end vertices of each edge.

$({\mathit{S}}_{\mathit{u}},{\mathit{S}}_{\mathit{v}})$, where $\mathit{uv}\in \mathit{E}\left(\mathit{TSM}\right)$	Number of Edges
$(8,16)$	4
$(14,19)$	4
$(14,29)$	2
$(16,16)$	2
$(16,20)$	4
$(16,28)$	4
$(19,20)$	4
$(19,29)$	4
$(19,32)$	4
$(20,20)$	$2m+2n-20$
$(20,28)$	4
$(20,32)$	$4m+4n-36$
$(28,32)$	4
$(29,32)$	4
$(29,36)$	2
$(32,32)$	$2m+2n-18$
$(32,36)$	$4m+4n-36$
$(36,36)$	$3mn-14m-14n+65$
Total	$3mn-2m-2n+1$

Theorem 4.

The fourth atom-bond connectivity index $AB{C}_4$ of the Tickysim SpiNNaker Model sheet is given by

$$\begin{array}{ccc}\hfill AB{C}_4\left(TSM\right)& =& \frac{1}{12}\sqrt{70}\mathit{mn}+\frac{1}{2}\sqrt{11}+\frac{2}{133}\sqrt{8246}+\frac{1}{203}\sqrt{16646}\hfill \\ & +& \frac{1}{8}\sqrt{30}+\frac{1}{10}\sqrt{170}+\frac{1}{2}\sqrt{6}+\frac{2}{95}\sqrt{3515}+\frac{4}{551}\sqrt{25346}\hfill \\ & +& \frac{7}{38}\sqrt{38}+\frac{1}{20}\left(2m+2n-20\right)\sqrt{38}+\frac{1}{35}\sqrt{1610}\hfill \\ & +& \frac{1}{8}\left(4m+4n-36\right)\sqrt{5}+\frac{43}{406}\sqrt{203}+\frac{1}{58}\sqrt{3422}+\frac{1}{32}\left(2m+2n-18\right)\sqrt{62}\hfill \\ & +& \frac{1}{24}\left(4m+4n-36\right)\sqrt{33}+\frac{1}{36}\left(-14m-14n+65\right)\sqrt{70}.\hfill \end{array}$$

Proof. 

Let $m_{i,j}$ denote the number of edges of the Tickysim SpiNNaker Model sheet with $i=S_u$ and $j=S_v.$ It is easy to see that the summation of the degree of the edge endpoints of a given graph has eighteen edge types $m_{8,16},m_{14,19},m_{14,29},m_{16,16},m_{16,20},m_{16,28},m_{19,20},$ $m_{19,29},m_{19,32},m_{20,20},m_{20,28},m_{20,32},m_{28,32},m_{29,32},$ $m_{29,36},m_{32,32},m_{32,36}$, and $m_{36,36}$, which are shown in Table 3. The fourth atom-bond connectivity index $AB{C}_4$ is defined as:

$$AB{C}_4\left(TSM\right)=\sum _{uv\in E\left(TSM\right)}\sqrt{\frac{S_u+S_v-2}{S_u\times S_v}}.$$

This implies that

$$\begin{array}{ccc}\hfill AB{C}_4\left(TSM\right)& =& m_{8,16}\sqrt{\frac{8+16-2}{8\times 16}}+m_{14,19}\sqrt{\frac{14+19-2}{14\times 19}}+m_{14,29}\sqrt{\frac{14+29-2}{14\times 29}}+m_{16,16}\sqrt{\frac{16+16-2}{16\times 16}}\hfill \\ & +& m_{16,20}\sqrt{\frac{16+20-2}{16\times 20}}+m_{16,28}\sqrt{\frac{16+28-2}{16\times 28}}+m_{19,20}\sqrt{\frac{19+20-2}{19\times 20}}\hfill \\ & +& m_{19,29}\sqrt{\frac{19+29-2}{19\times 29}}+m_{19,32}\sqrt{\frac{19+32-2}{19\times 32}}+m_{20,20}\sqrt{\frac{20+20-2}{20\times 20}}\hfill \\ & +& m_{20,28}\sqrt{\frac{20+28-2}{20\times 28}}+m_{20,32}\sqrt{\frac{20+32-2}{20\times 32}}+m_{28,32}\sqrt{\frac{28+32-2}{28\times 32}}\hfill \\ & +& m_{29,32}\sqrt{\frac{29+32-2}{29\times 32}}+m_{29,36}\sqrt{\frac{29+36-2}{29\times 36}}+m_{32,32}\sqrt{\frac{32+32-2}{32\times 32}}\hfill \\ & +& m_{32,36}\sqrt{\frac{32+36-2}{32\times 36}}+m_{36,36}\sqrt{\frac{36+36-2}{36\times 36}}.\hfill \\ & =& \frac{1}{12}\sqrt{70}\mathit{mn}+\frac{1}{2}\sqrt{11}+\frac{2}{133}\sqrt{8246}+\frac{1}{203}\sqrt{16646}+\frac{1}{8}\sqrt{30}\hfill \\ & +& \frac{1}{10}\sqrt{170}+\frac{1}{2}\sqrt{6}+\frac{2}{95}\sqrt{3515}+\frac{4}{551}\sqrt{25346}+\frac{7}{38}\sqrt{38}\hfill \\ & +& \frac{1}{20}\left(2m+2n-20\right)\sqrt{38}+\frac{1}{35}\sqrt{1610}+\frac{1}{8}\left(4m+4n-36\right)\sqrt{5}\hfill \\ & +& \frac{43}{406}\sqrt{203}+\frac{1}{58}\sqrt{3422}+\frac{1}{32}\left(2m+2n-18\right)\sqrt{62}+\frac{1}{24}\left(4m+4n-36\right)\sqrt{33}\hfill \\ & +& \frac{1}{36}\left(-14m-14n+65\right)\sqrt{70}.\hfill \end{array}$$

This completes the proof. □

Theorem 5.

The fifth geometric-arithmetic index $G{A}_5$ of the Tickysim SpiNNaker Model sheet is given by

$$\begin{array}{ccc}\hfill G{A}_5\left(TSM\right)& =& 29+\frac{32}{51}\sqrt{38}-10n+\frac{8}{33}\sqrt{266}+\frac{4}{43}\sqrt{406}+1/6\sqrt{551}\hfill \\ & +& \frac{4}{13}\left(4m+4n-36\right)\sqrt{10}+\frac{12}{17}\left(4m+4n-36\right)\sqrt{2}\hfill \\ & +& \frac{16}{11}\sqrt{7}+\frac{16}{9}\sqrt{5}+\frac{16}{15}\sqrt{14}+\frac{8}{3}\sqrt{2}-10m+3\mathit{mn}\hfill \\ & +& \frac{16}{39}\sqrt{95}+\frac{2}{3}\sqrt{35}+\frac{32}{61}\sqrt{58}+\frac{24}{65}\sqrt{29}.\hfill \end{array}$$

Proof. 

Let $m_{i,j}$ denote the number of edges of the Tickysim SpiNNaker Model sheet with $i=S_u$ and $j=S_v.$ It is easy to see that the summation of the degree of edge endpoints of given graph has eighteen edge types $m_{8,16},m_{14,19},m_{14,29},m_{16,16},m_{16,20},m_{16,28},m_{19,20},m_{19,29},m_{19,32},m_{20,20},$ $m_{20,28},m_{20,32},m_{28,32},m_{29,32},$ $m_{29,36},m_{32,32},m_{32,36}$, and $m_{36,36}$, which are shown in Table 3. The fifth geometric-arithmetic index $G{A}_5$ is defined as:

$$G{A}_5\left(TSM\right)=\sum _{uv\in E\left(TSM\right)}\frac{2\sqrt{S_u\times S_v}}{S_u+S_v}.$$

This implies that

$$\begin{array}{ccc}\hfill G{A}_5\left(TSM\right)& =& m_{8,16}\frac{2\sqrt{8\times 16}}{8+16}+m_{14,19}\frac{2\sqrt{14\times 19}}{14+19}+m_{14,29}\frac{2\sqrt{14\times 29}}{14+29}\hfill \\ & +& m_{16,16}\frac{2\sqrt{16\times 16}}{16+16}+m_{16,20}\frac{2\sqrt{16\times 20}}{16+20}+m_{16,28}\frac{2\sqrt{16\times 28}}{16+28}\hfill \\ & +& m_{19,20}\frac{2\sqrt{19\times 20}}{19+20}+m_{19,29}\frac{2\sqrt{19\times 29}}{19+29}+m_{19,32}\frac{2\sqrt{19\times 32}}{19+32}\hfill \\ & +& m_{20,20}\frac{2\sqrt{20\times 20}}{20+20}+m_{20,28}\frac{2\sqrt{20\times 28}}{20+28}+m_{20,32}\frac{2\sqrt{20\times 32}}{20+32}\hfill \\ & +& m_{28,32}\frac{2\sqrt{28\times 32}}{28+32}+m_{29,32}\frac{2\sqrt{29\times 32}}{29+32}+m_{29,36}\frac{2\sqrt{29\times 36}}{29+36}\hfill \\ & +& m_{32,32}\frac{2\sqrt{32\times 32}}{32+32}+m_{32,36}\frac{2\sqrt{32\times 36}}{32+36}+m_{36,36}\frac{2\sqrt{36\times 36}}{36+36}\hfill \\ & =& 29+\frac{32}{51}\sqrt{38}-10n+\frac{8}{33}\sqrt{266}+\frac{4}{43}\sqrt{406}+1/6\sqrt{551}\hfill \\ & +& \frac{4}{13}\left(4m+4n-36\right)\sqrt{10}+\frac{12}{17}\left(4m+4n-36\right)\sqrt{2}+\frac{16}{11}\sqrt{7}\hfill \\ & +& \frac{16}{9}\sqrt{5}+\frac{16}{15}\sqrt{14}+\frac{8}{3}\sqrt{2}-10m+3\mathit{mn}+\frac{16}{39}\sqrt{95}\hfill \\ & +& \frac{2}{3}\sqrt{35}+\frac{32}{61}\sqrt{58}+\frac{24}{65}\sqrt{29}.\hfill \end{array}$$

This completes the proof. □

We compute the hyper-Zagreb index $HM\left(G\right),$ first multiple Zagreb index $P{M}_1\left(G\right),$ second multiple Zagreb index $P{M}_2\left(G\right),$ and Zagreb polynomials $M_1(G,x),M_2(G,x)$ for the Tickysim SpiNNaker Model sheet in the following theorem.

Theorem 6.

Let $TSM$ be a Tickysim SpiNNaker Model sheet, then

1. 

$HM\left(TSM\right)=886-624m-624n+432\mathit{mn},$

2. 

$P{M}_1\left(TSM\right)=252047376\left(2^{6mn-6m-6n-8}\times 3^{3mn-8m-8n+21}\times 5^{4m-4n-20}\right),$

3. 

$P{M}_2\left(TSM\right)=27518828544\left(2^{6mn+4m+4n-58}\times 3^{6mn-12m-12n+22}\right),$

4. 

$M_1(TSM,x)=4x^6+4x^7+2x^9+(2m+2n-10)x^8+(4m+4n-20)x^{10}+(3mn-8m-8n+21)x^{12},$

5. 

$M_2(TSM,x)=4x^8+4x^{12}+2x^{18}+(2m+2n-10)x^{16}+(4m+4n-20)x^{24}+(3mn-8m-8n+21)x^{36}.$

Proof. 

Let $TSM$ be a Tickysim SpiNNaker Model sheet. The edge set $E\left(TSM\right)$ is divided into six edge partitions based on degree of end vertices. The first edge partition $E_1\left(TSM\right)$ contains 4 edges $uv,$ where $\zeta \left(u\right)=2,\zeta \left(v\right)=4.$ The second edge partition $E_2\left(TSM\right)$ contains m edges $uv,$ where $\zeta \left(u\right)=3$, $\zeta \left(v\right)=4.$ The third edge partition $E_3\left(TSM\right)$ contains 2 edges $uv,$ where $\zeta \left(u\right)=3,\zeta \left(v\right)=6.$ The fourth edge partition $E_4\left(TSM\right)$ contains $2m+2n-10$ edges $uv,$ where $\zeta \left(u\right)=\zeta \left(v\right)=4.$ The fifth edge partition $E_5\left(TSM\right)$ contains $4m+4n-20$ edges $uv,$ where $\zeta \left(u\right)=4,\zeta \left(v\right)=6.$ The sixth edge partition $E_6\left(TSM\right)$ contains $3mn-8m-8n+21$ edges $uv,$ where $\zeta \left(u\right)=\zeta \left(v\right)=6.$

Since

$$\begin{array}{cc}\hfill HM\left(TSM\right)=& \sum _{uv\in E\left(TSM\right)}{\left(\zeta \left(u\right)+\zeta \left(v\right)\right)}^2\hfill \\ \hfill =& \sum _{uv\in E_1\left(TSM\right)}{\left[\zeta \left(u\right)+\zeta \left(v\right)\right]}^2+\sum _{uv\in E_2\left(TSM\right)}{\left[\zeta \left(u\right)+\zeta \left(v\right)\right]}^2+\sum _{uv\in E_3\left(TSM\right)}{\left[\zeta \left(u\right)+\zeta \left(v\right)\right]}^2\hfill \\ \hfill +& \sum _{uv\in E_4\left(TSM\right)}{\left[\zeta \left(u\right)+\zeta \left(v\right)\right]}^2+\sum _{uv\in E_5\left(TSM\right)}{\left[\zeta \left(u\right)+\zeta \left(v\right)\right]}^2+\sum _{uv\in E_6\left(TSM\right)}{\left[\zeta \left(u\right)+\zeta \left(v\right)\right]}^2\hfill \\ \hfill =& e_{2,4}{(2+4)}^2+e_{3,4}{(3+4)}^2+e_{3,6}{(3+6)}^2+e_{4,4}{(4+4)}^2+e_{4,6}{(4+6)}^2\hfill \\ \hfill +& e_{6,6}{(6+6)}^2,\hfill \end{array}$$

after putting the values of edge partitions, we get

$$HM\left(G\right)=886-624m-624n+432\mathit{mn}.$$

Since,

$$\begin{array}{cc}\hfill P{M}_1\left(TSM\right)=& \prod _{uv\in E\left(TSM\right)}(\zeta \left(u\right)+\zeta \left(v\right))\hfill \\ \hfill =& \prod _{uv\in E_1\left(TSM\right)}(\zeta \left(u\right)+\zeta \left(v\right))\times \prod _{uv\in E_2\left(TSM\right)}(\zeta \left(u\right)+\zeta \left(v\right))\times \prod _{uv\in E_3\left(TSM\right)}(\zeta \left(u\right)+\zeta \left(v\right))\hfill \\ \hfill \times & \prod _{uv\in E_4\left(TSM\right)}(\zeta \left(u\right)+\zeta \left(v\right))\times \prod _{uv\in E_5\left(TSM\right)}(\zeta \left(u\right)+\zeta \left(v\right))\times \prod _{uv\in E_6\left(TSM\right)}(\zeta \left(u\right)+\zeta \left(v\right))\hfill \\ \hfill =& {(2+4)}^{|E_1\left(TSM\right)|}\times {(3+4)}^{|E_2\left(G\right)|}\times {(3+6)}^{|E_3\left(TSM\right)|}\times {(4+4)}^{|E_4\left(TSM\right)|}\hfill \\ \hfill \times & {(4+6)}^{|E_5\left(G\right)|}\times {(6+6)}^{|E_6\left(TSM\right)|}\hfill \\ \hfill =& {\left(6\right)}^4\times {\left(7\right)}^4\times {\left(9\right)}^2\times {\left(8\right)}^{2m+2n-10}\times {\left(10\right)}^{4m+4n-20}\times {\left(12\right)}^{3mn-8m-8n+21}\hfill \\ \hfill =& 252047376\left(2^{6mn-6m-6n-8}\times 3^{3mn-8m-8n+21}\times 5^{4m-4n-20}\right).\hfill \end{array}$$

Now, since

$$\begin{array}{cc}\hfill P{M}_2\left(G\right)=& \prod _{uv\in E\left(TSM\right)}(\zeta \left(u\right)\times \zeta \left(v\right))\hfill \\ \hfill =& \prod _{uv\in E_1\left(TSM\right)}(\zeta \left(u\right)\times \zeta \left(v\right))\times \prod _{uv\in E_2\left(TSM\right)}(\zeta \left(u\right)\times \zeta \left(v\right))\times \prod _{uv\in E_3\left(TSM\right)}(\zeta \left(u\right)\times \zeta \left(v\right))\hfill \\ \hfill \times & \prod _{uv\in E_4\left(TSM\right)}(\zeta \left(u\right)\times \zeta \left(v\right))\times \prod _{uv\in E_5\left(TSM\right)}(\zeta \left(u\right)\times \zeta \left(v\right))\times \prod _{uv\in E_6\left(TSM\right)}(\zeta \left(u\right)\times \zeta \left(v\right))\hfill \\ \hfill =& {(2\times 4)}^{|E_1\left(TSM\right)|}\times {(3\times 4)}^{|E_2\left(G\right)|}\times {(3\times 6)}^{|E_3\left(TSM\right)|}\times {(4\times 4)}^{|E_4\left(TSM\right)|}\hfill \\ \hfill \times & {(4\times 6)}^{|E_5\left(G\right)|}\times {(6\times 6)}^{|E_6\left(TSM\right)|}\hfill \\ \hfill =& {\left(8\right)}^4\times {\left(12\right)}^4\times {\left(18\right)}^2\times {\left(16\right)}^{2m+2n-10}\times {\left(24\right)}^{4m+4n-20}\times {\left(36\right)}^{3mn-8m-8n+21}.\hfill \end{array}$$

After simplification, we get

$$P{M}_2\left(TSM\right)=27518828544\left(2^{6mn+4m+4n-58}\times 3^{6mn-12m-12n+22}\right).$$

As,

$$\begin{array}{cc}\hfill M_1(TSM,x)=& \sum _{uv\in E\left(TSM\right)}{x}^{\left(\zeta \right(u)+\zeta (v\left)\right)}\hfill \\ \hfill =& \sum _{uv\in E_1\left(TSM\right)}{x}^{\left(\zeta \right(u)+\zeta (v\left)\right)}+\sum _{uv\in E_2\left(TSM\right)}{x}^{\left(\zeta \right(u)+\zeta (v\left)\right)}+\sum _{uv\in E_3\left(TSM\right)}{x}^{\left(\zeta \right(u)+\zeta (v\left)\right)}\hfill \\ \hfill +& \sum _{uv\in E_4\left(TSM\right)}{x}^{\left(\zeta \right(u)+\zeta (v\left)\right)}+\sum _{uv\in E_5\left(TSM\right)}{x}^{\left(\zeta \right(u)+\zeta (v\left)\right)}+\sum _{uv\in E_6\left(TSM\right)}{x}^{\left(\zeta \right(u)+\zeta (v\left)\right)}\hfill \\ \hfill =& \sum _{uv\in E_1\left(TSM\right)}{x}^{2+4}+\sum _{uv\in E_2\left(TSM\right)}{x}^{3+4}+\sum _{uv\in E_3\left(TSM\right)}{x}^{3+6}\hfill \\ \hfill +& \sum _{uv\in E_4\left(TSM\right)}{x}^{4+4}+\sum _{uv\in E_5\left(TSM\right)}{x}^{4+6}+\sum _{uv\in E_6\left(TSM\right)}{x}^{6+6}\hfill \\ \hfill =& |E_1\left(TSM\right)|x^6+|E_2\left(TSM\right)|x^7+\left|E_3\left(TSM\right)\right|x^9\hfill \\ \hfill +& |E_4\left(TSM\right)|x^8+|E_5\left(TSM\right)|x^{10}+\left|E_6\left(TSM\right)\right|x^{12}\hfill \\ \hfill =& 4x^6+4x^7+2x^9+(2m+2n-10)x^8\hfill \\ \hfill +& (4m+4n-20)x^{10}+(3mn-8m-8n+21)x^{12}.\hfill \end{array}$$

As

$$\begin{array}{cc}\hfill M_2(TSM,x)=& \sum _{uv\in E\left(TSM\right)}{x}^{\left(\zeta \right(u)\times \zeta (v\left)\right)}\hfill \\ \hfill =& \sum _{uv\in E_1\left(TSM\right)}{x}^{\left(\zeta \right(u)\times \zeta (v\left)\right)}+\sum _{uv\in E_2\left(TSM\right)}{x}^{\left(\zeta \right(u)\times \zeta (v\left)\right)}+\sum _{uv\in E_3\left(TSM\right)}{x}^{\left(\zeta \right(u)\times \zeta (v\left)\right)}\hfill \\ \hfill +& \sum _{uv\in E_4\left(TSM\right)}{x}^{\left(\zeta \right(u)\times \zeta (v\left)\right)}+\sum _{uv\in E_5\left(TSM\right)}{x}^{\left(\zeta \right(u)\times \zeta (v\left)\right)}+\sum _{uv\in E_6\left(TSM\right)}{x}^{\left(\zeta \right(u)\times \zeta (v\left)\right)}\hfill \\ \hfill =& \sum _{uv\in E_1\left(TSM\right)}{x}^8+\sum _{uv\in E_2\left(TSM\right)}{x}^{12}+\sum _{uv\in E_3\left(TSM\right)}{x}^{18}\hfill \\ \hfill +& \sum _{uv\in E_4\left(TSM\right)}{x}^{16}+\sum _{uv\in E_5\left(TSM\right)}{x}^{24}+\sum _{uv\in E_6\left(TSM\right)}{x}^{36}.\hfill \end{array}$$

By inserting the values, we obtain

$$M_2(G,x)=4x^8+4x^{12}+2x^{18}+(2m+2n-10)x^{16}+(4m+4n-20)x^{24}+(3mn-8m-8n+21)x^{36}.$$

This completes the proof. □

5. Conclusions

In this paper, we deal with a Tickysim SpiNNaker Model sheet and study its topological indices. We determined the first general Zagreb index $M_{\alpha }$, general Randić connectivity index $R_{\alpha }$, general sum-connectivity index ${\chi }_{\alpha }$, atom-bond connectivity index $ABC$, geometric-arithmetic index $GA$, fourth atom-bond connectivity index $AB{C}_4$, fifth geometric-arithmetic index $G{A}_5$, hyper-Zagreb index $HM\left(G\right)$, first multiple Zagreb index $P{M}_1\left(G\right)$, second multiple Zagreb index $P{M}_2\left(G\right)$, and Zagreb polynomials $M_1(G,x),M_1(G,x).$

In the future, we are interested in designing some incipient architectures/networks and then studying their topological indices, which will be quite auxiliary to understanding their underlying topology.