Efficient Implementation of ADER Discontinuous Galerkin Schemes for a Scalable Hyperbolic PDE Engine
Abstract
1. Introduction
2. High Order ADER Discontinuous Galerkin Finite Element Schemes
2.1. Unlimited ADER-DG Scheme and Riemann Solvers
2.2. Space-Time Predictor and Suitable Initial Guess
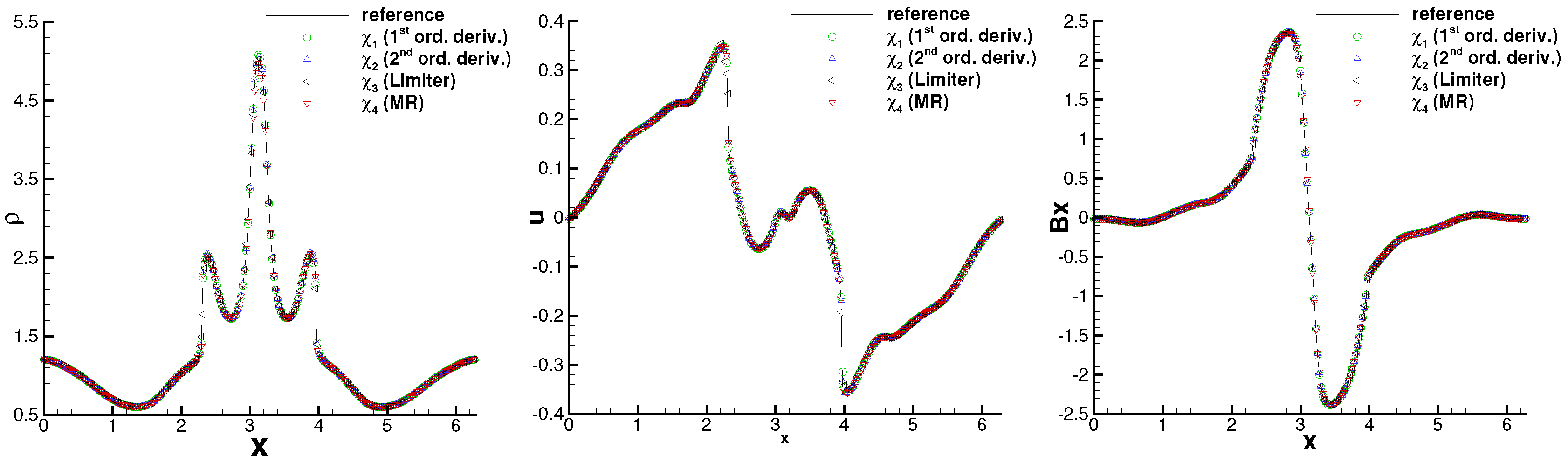
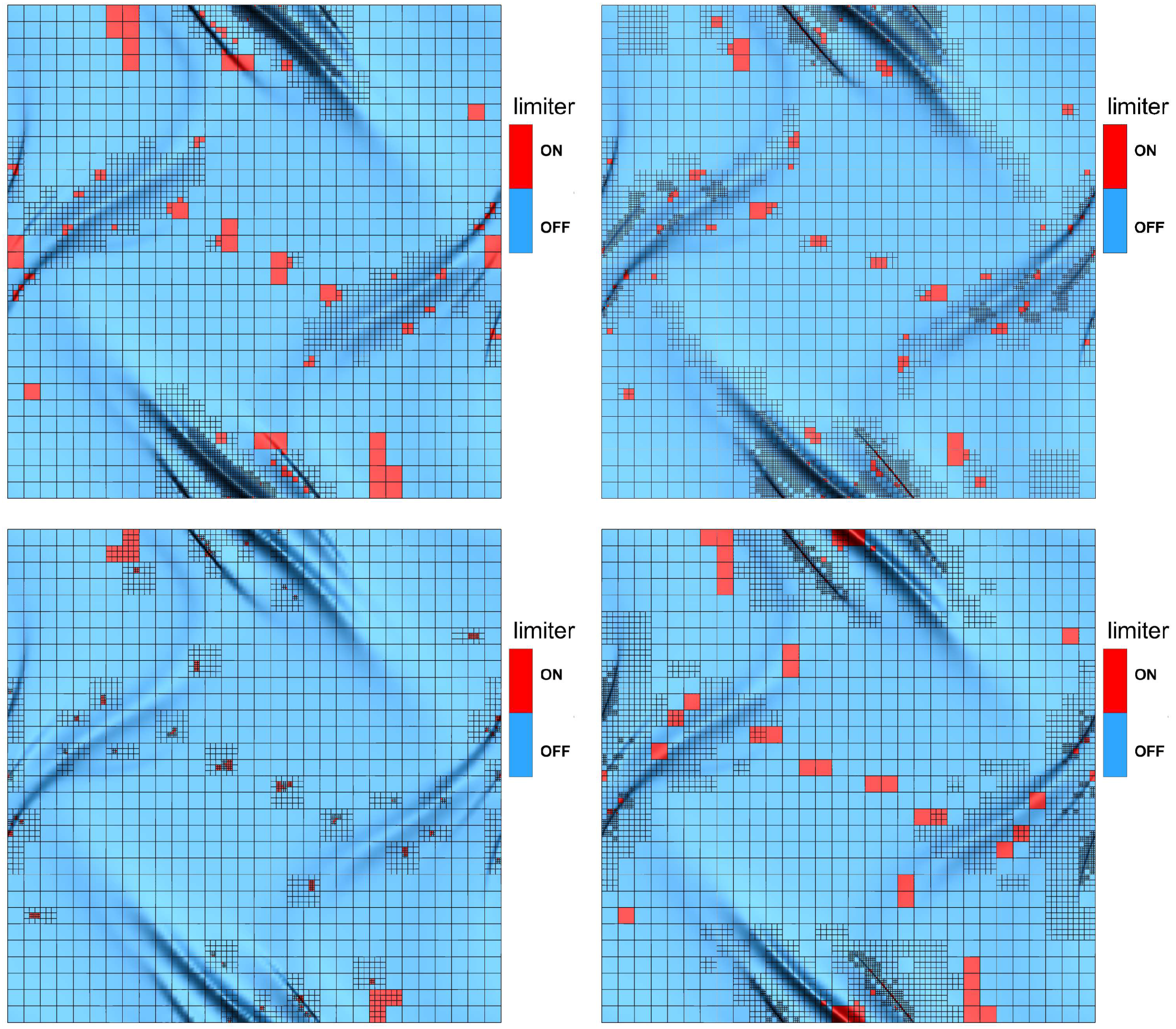
2.3. A Posteriori Subcell Finite Volume Limiter
3. Some Examples of Typical PDE Systems Solved With the ExaHyPE Engine
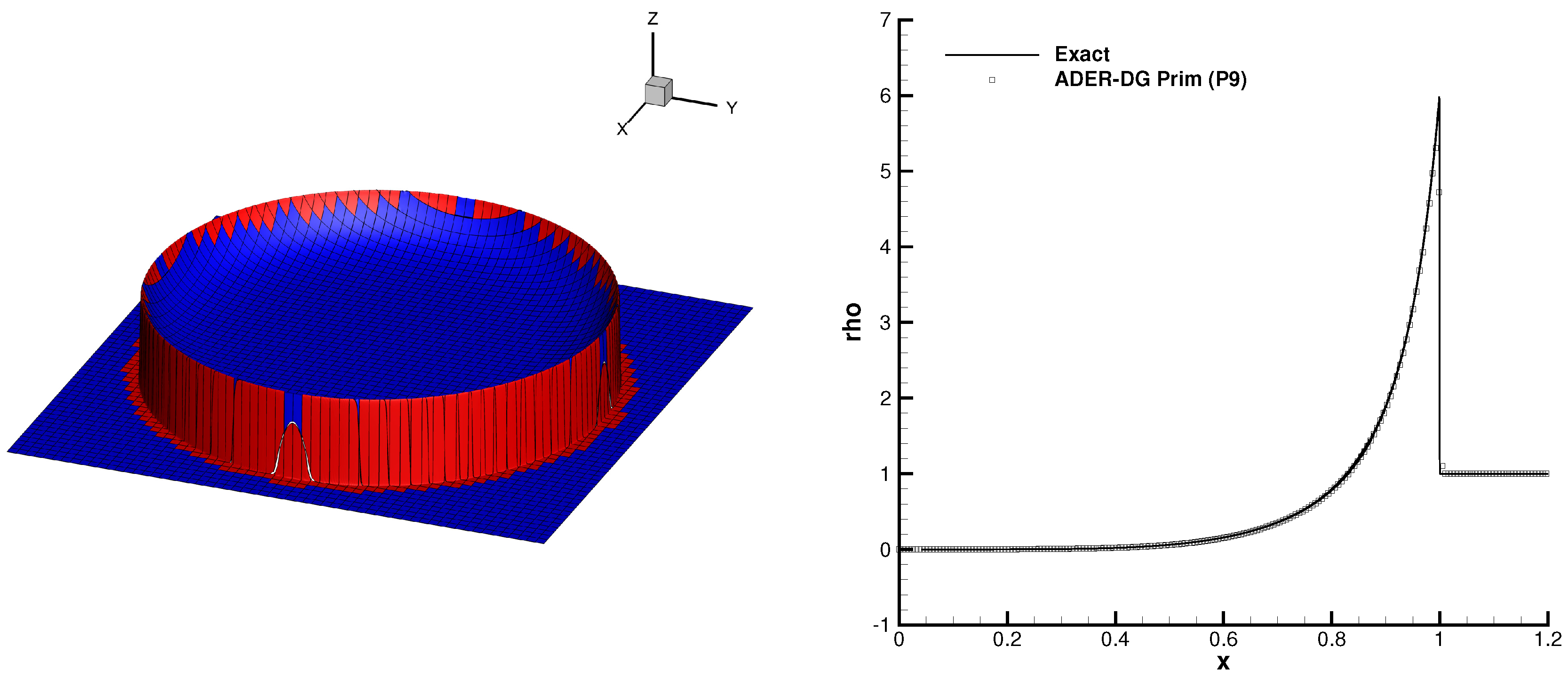
3.1. The Euler Equations of Compressible Gas Dynamics
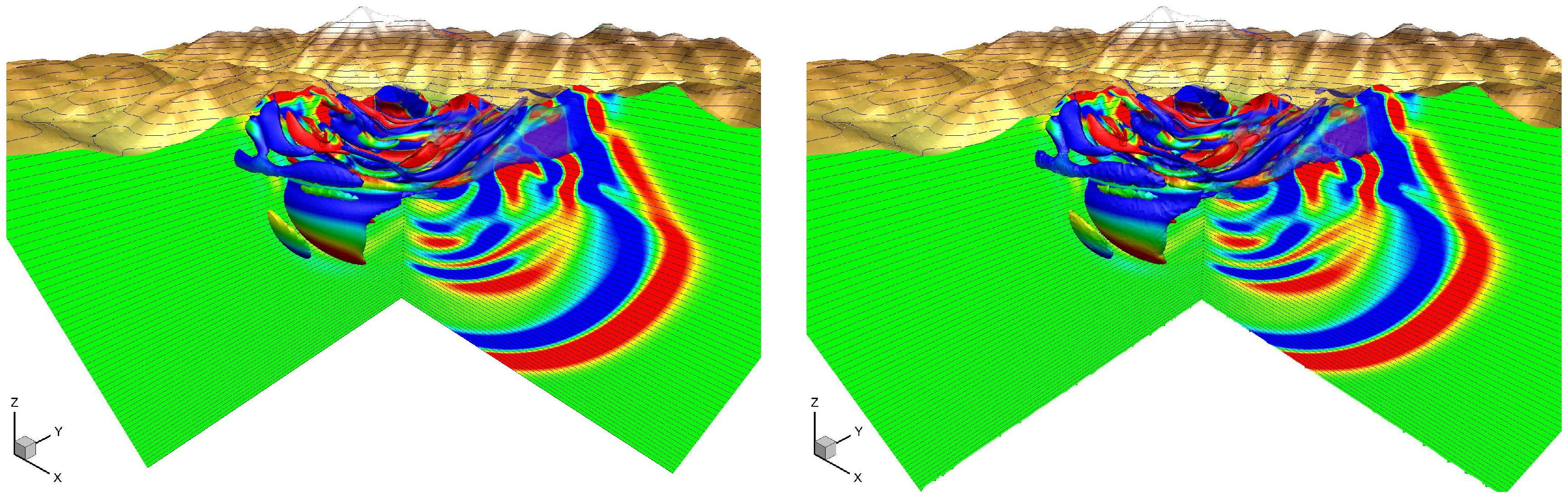
3.2. A Novel Diffuse Interface Approach for Linear Seismic Wave Propagation in Complex Geometries
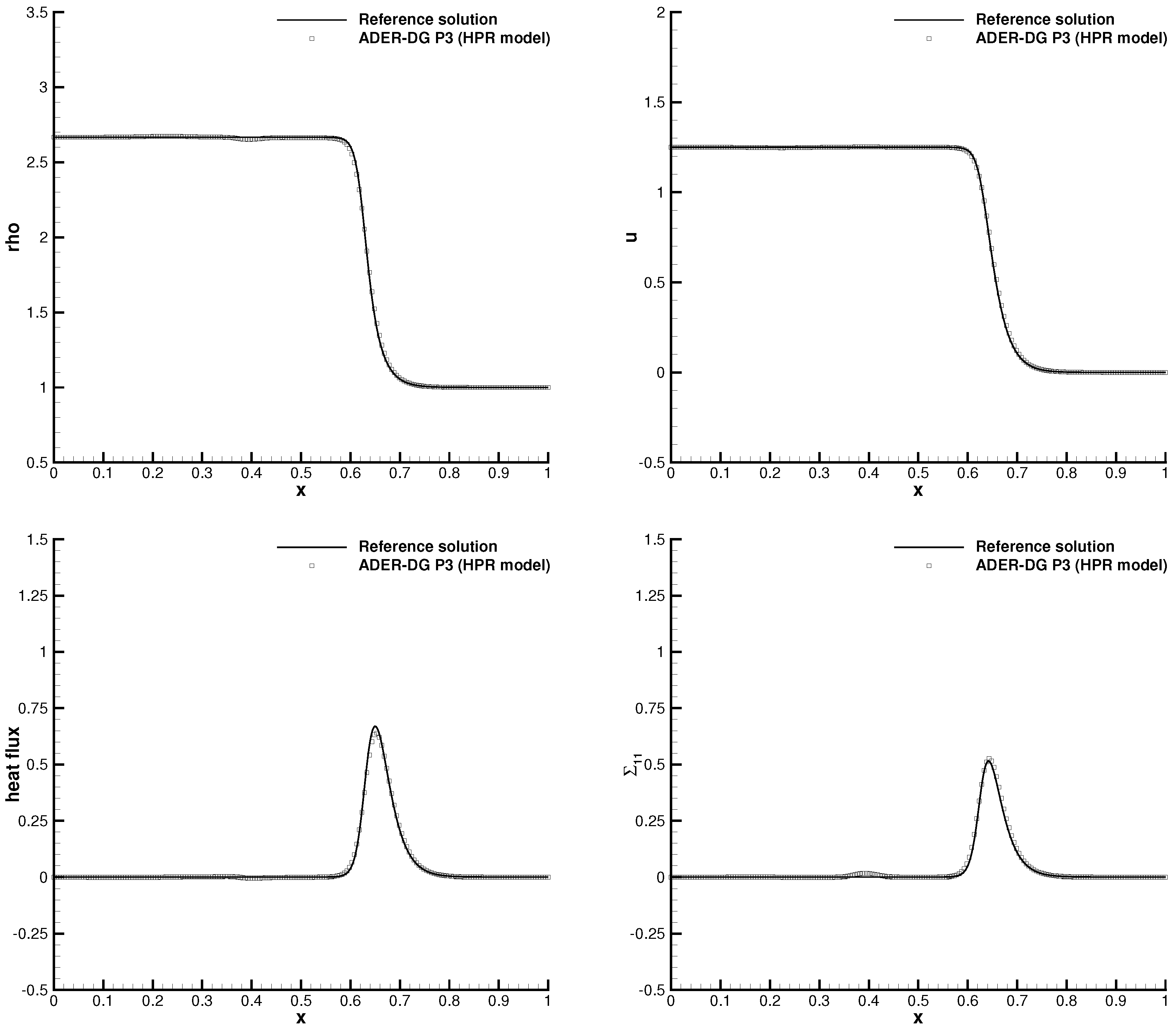
3.3. The Unified Godunov-Peshkov-Romenski Model of Continuum Mechanics (GPR)
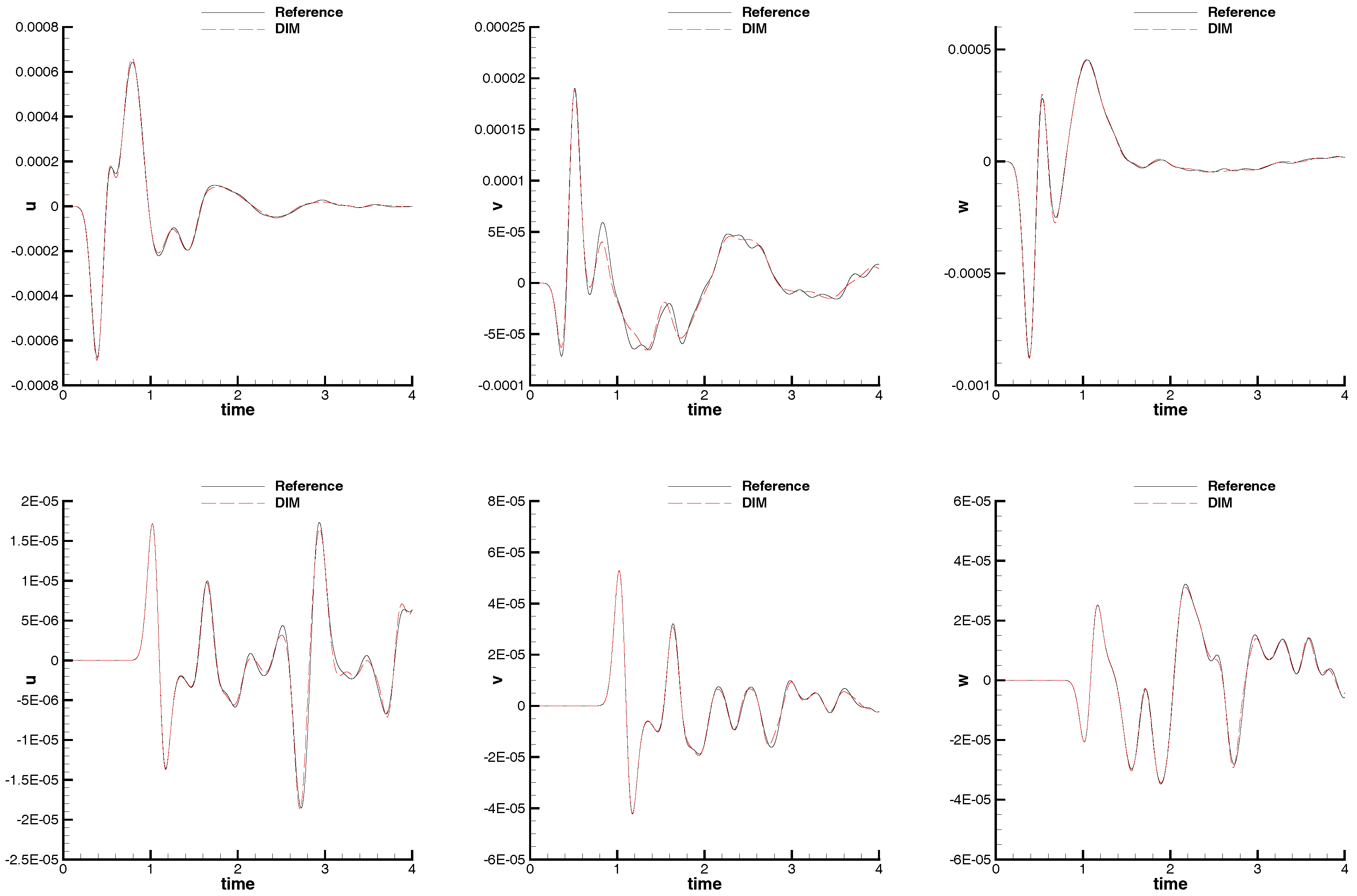
3.4. The Equations of Ideal General Relativistic Magnetohydrodynamics (GRMHD)
3.5. A Strongly Hyperbolic First Order Reduction of the CCZ4 Formulation of the Einstein Field Equations (FO-CCZ4)
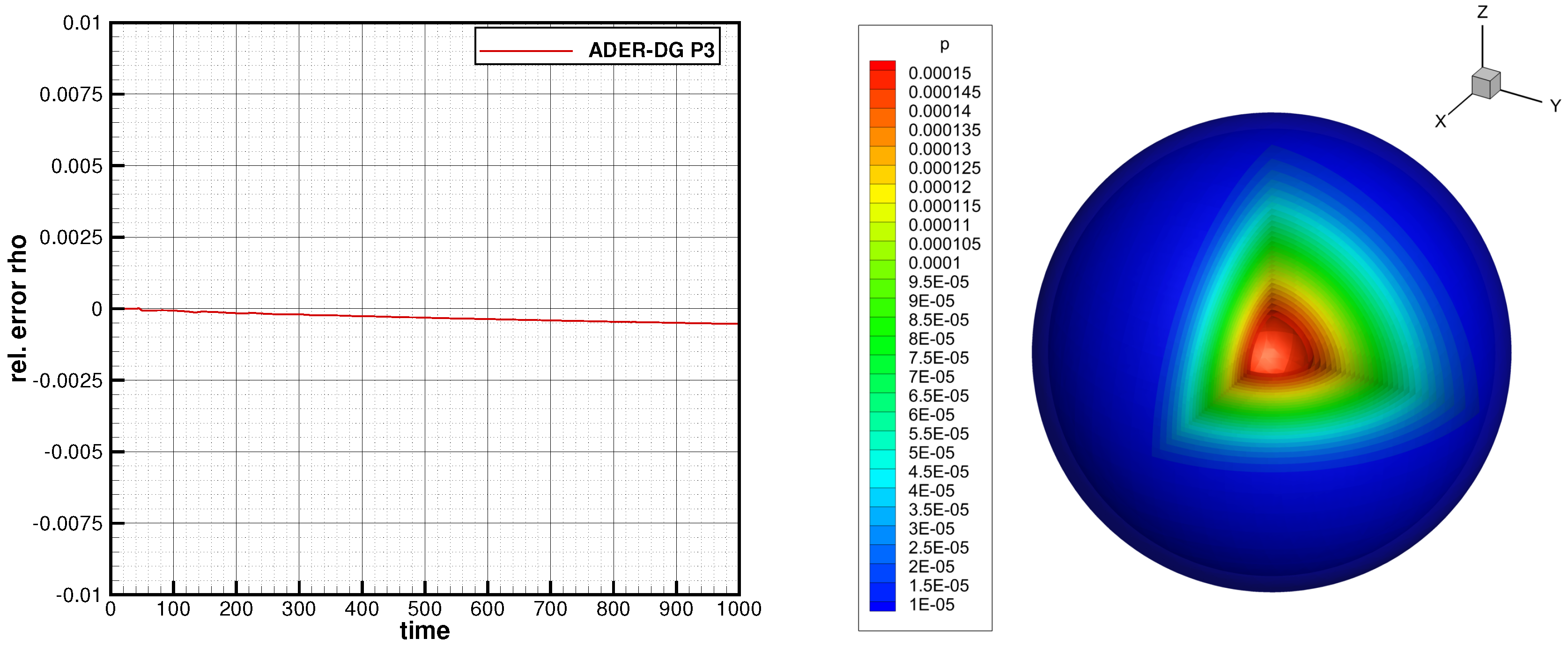
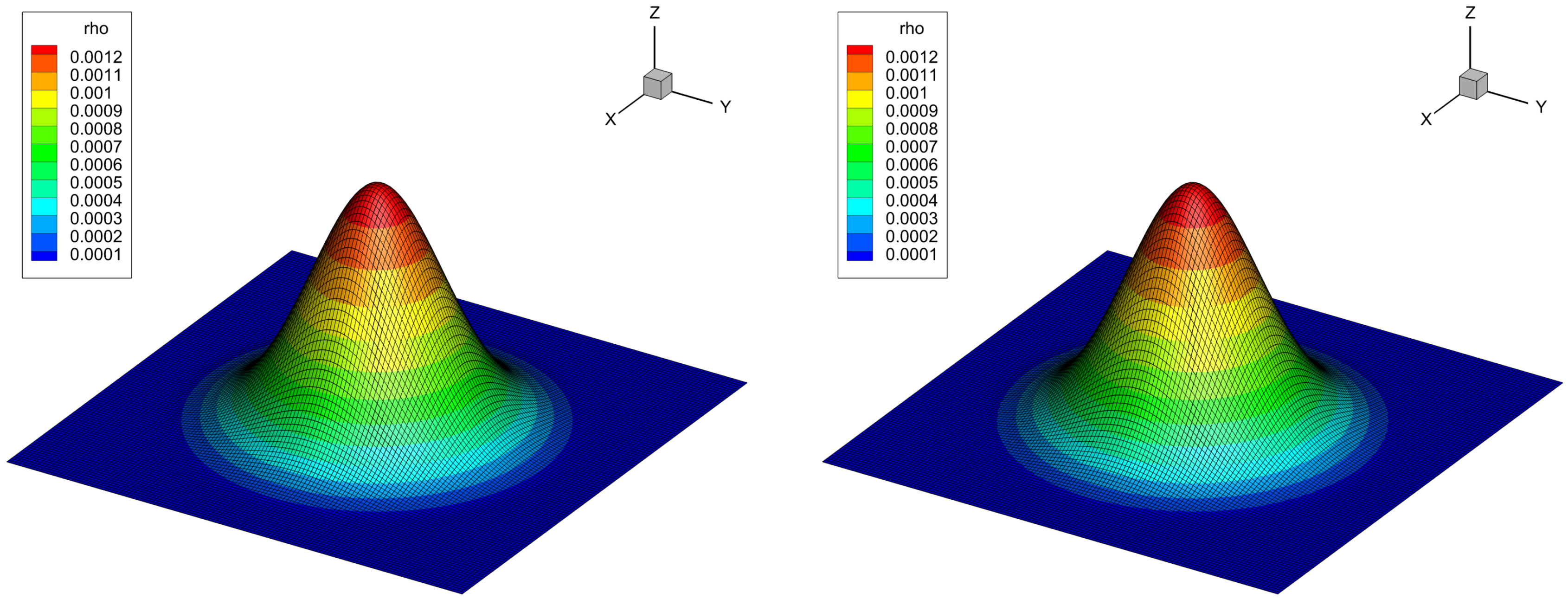
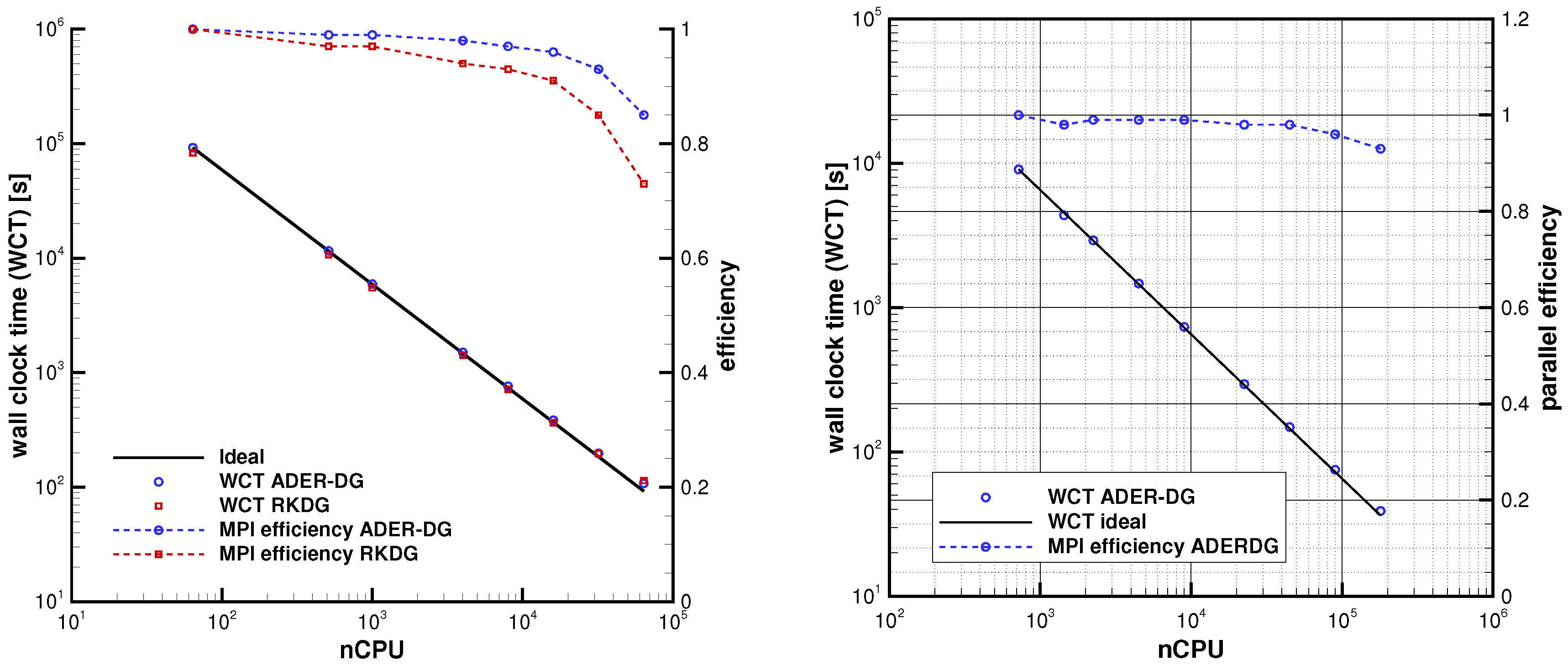
4. Strong MPI Scaling Study for the FO-CCZ4 System
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Riemann, B. Über die Fortpflanzung ebener Luftwellen von Endlicher Schwingungsweite; Göttinger Nachrichten: Göttingen, Germany, 1859; Volume 19. [Google Scholar]
- Riemann, B. Über die Fortpflanzung ebener Luftwellen von endlicher Schwingungsweite. Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen 1860, 8, 43–65. [Google Scholar]
- Noether, E. Invariante Variationsprobleme. In Nachrichten der königlichen Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse; Weidmannsche Buchhandlung: Berlin, Germany, 1918; pp. 235–257. [Google Scholar]
- Courant, R.; Friedrichs, K.; Lewy, H. Über die partiellen Differenzengleichungen der mathematischen Physik. Math. Annal. 1928, 100, 32–74. [Google Scholar] [CrossRef]
- Courant, R.; Isaacson, E.; Rees, M. On the solution of nonlinear hyperbolic differential equations by finite differences. Commun. Pure Appl. Math. 1952, 5, 243–255. [Google Scholar] [CrossRef]
- Courant, R.; Hilbert, D. Methods of Mathematical Physics; John Wiley and Sons, Inc.: New York, NY, USA, 1962. [Google Scholar]
- Courant, R.; Friedrichs, K.O. Supersonic Flows and Shock Waves; Springer: Berlin, Germany, 1976. [Google Scholar]
- Friedrichs, K. Symmetric positive linear differential equations. Commun. Pure Appl. Math. 1958, 11, 333–418. [Google Scholar] [CrossRef]
- Godunov, S. An interesting class of quasilinear systems. Dokl. Akad. Nauk SSSR 1961, 139, 521–523. [Google Scholar]
- Friedrichs, K.; Lax, P. Systems of conservation equations with a convex extension. Proc. Natl. Acad. Sci. USA 1971, 68, 1686–1688. [Google Scholar] [CrossRef] [PubMed]
- Godunov, S.; Romenski, E. Thermodynamics, conservation laws, and symmetric forms of differential equations in mechanics of continuous media. In Computational Fluid Dynamics Review 95; John Wiley: New York, NY, USA, 1995; pp. 19–31. [Google Scholar]
- Godunov, S.; Romenski, E. Elements of Continuum Mechanics and Conservation Laws; Kluwer Academic/Plenum Publishers: New York, NY, USA, 2003. [Google Scholar]
- Godunov, S. Symmetric form of the magnetohydrodynamic equation. Numer. Methods Mech. Contin. Med. 1972, 3, 26–34. [Google Scholar]
- Godunov, S.; Romenski, E. Nonstationary equations of the nonlinear theory of elasticity in Euler coordinates. J. Appl. Mech. Tech. Phys. 1972, 13, 868–885. [Google Scholar] [CrossRef]
- Romenski, E. Hyperbolic systems of thermodynamically compatible conservation laws in continuum mechanics. Math. Comput. Model. 1998, 28, 115–130. [Google Scholar] [CrossRef]
- Peshkov, I.; Romenski, E. A hyperbolic model for viscous Newtonian flows. Contin. Mech. Thermodyn. 2016, 28, 85–104. [Google Scholar] [CrossRef]
- Dumbser, M.; Peshkov, I.; Romenski, E.; Zanotti, O. High order ADER schemes for a unified first order hyperbolic formulation of continuum mechanics: Viscous heat-conducting fluids and elastic solids. J. Comput. Phys. 2016, 314, 824–862. [Google Scholar] [CrossRef]
- Dumbser, M.; Peshkov, I.; Romenski, E.; Zanotti, O. High order ADER schemes for a unified first order hyperbolic formulation of Newtonian continuum mechanics coupled with electro-dynamics. J. Comput. Phys. 2017, 348, 298–342. [Google Scholar] [CrossRef]
- Boscheri, W.; Dumbser, M.; Loubère, R. Cell centered direct Arbitrary-Lagrangian-Eulerian ADER-WENO finite volume schemes for nonlinear hyperelasticity. Comput. Fluids 2016, 134–135, 111–129. [Google Scholar] [CrossRef]
- Neumann, J.V.; Richtmyer, R.D. A method for the numerical calculation of hydrodynamic shocks. J. Appl. Phys. 1950, 21, 232–237. [Google Scholar] [CrossRef]
- Godunov, S.K. A finite difference Method for the Computation of discontinuous solutions of the equations of fluid dynamics. Math. USSR Sbornik 1959, 47, 357–393. [Google Scholar]
- Kolgan, V.P. Application of the minimum-derivative principle in the construction of finite-difference schemes for numerical analysis of discontinuous solutions in gas dynamics. Trans. Central Aerohydrodyn. Inst. 1972, 3, 68–77. (In Russian) [Google Scholar]
- Van Leer, B. Towards the Ultimate Conservative Difference Scheme II: Monotonicity and conservation combined in a second order scheme. J. Comput. Phys. 1974, 14, 361–370. [Google Scholar] [CrossRef]
- Van Leer, B. Towards the Ultimate Conservative Difference Scheme V: A second Order sequel to Godunov’s Method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Harten, A.; Osher, S. Uniformly high–order accurate nonoscillatory schemes I. SIAM J. Num. Anal. 1987, 24, 279–309. [Google Scholar] [CrossRef]
- Jiang, G.; Shu, C. Efficient Implementation of Weighted ENO Schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef]
- Cockburn, B.; Shu, C.W. TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws II: General framework. Math. Comput. 1989, 52, 411–435. [Google Scholar]
- Cockburn, B.; Lin, S.Y.; Shu, C. TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws III: One dimensional systems. J. Comput. Phys. 1989, 84, 90–113. [Google Scholar] [CrossRef]
- Cockburn, B.; Hou, S.; Shu, C.W. The Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws IV: The multidimensional case. Math. Comput. 1990, 54, 545–581. [Google Scholar]
- Cockburn, B.; Shu, C.W. The Runge-Kutta discontinuous Galerkin method for conservation laws V: Multidimensional systems. J. Comput. Phys. 1998, 141, 199–224. [Google Scholar] [CrossRef]
- Cockburn, B.; Shu, C.W. The Local Discontinuous Galerkin Method for Time-Dependent Convection Diffusion Systems. SIAM J. Numer. Anal. 1998, 35, 2440–2463. [Google Scholar] [CrossRef]
- Cockburn, B.; Shu, C.W. Runge-Kutta Discontinuous Galerkin Methods for Convection-Dominated Problems. J. Sci. Comput. 2001, 16, 173–261. [Google Scholar] [CrossRef]
- Shu, C. High order WENO and DG methods for time-dependent convection-dominated PDEs: A brief survey of several recent developments. J. Comput. Phys. 2016, 316, 598–613. [Google Scholar] [CrossRef]
- Dumbser, M.; Balsara, D.; Toro, E.; Munz, C. A Unified Framework for the Construction of One-Step Finite–Volume and discontinuous Galerkin schemes. J. Comput. Phys. 2008, 227, 8209–8253. [Google Scholar] [CrossRef]
- Dumbser, M.; Castro, M.; Parés, C.; Toro, E. ADER Schemes on Unstructured Meshes for Non–Conservative Hyperbolic Systems: Applications to Geophysical Flows. Comput. Fluids 2009, 38, 1731–1748. [Google Scholar] [CrossRef]
- Dumbser, M.; Zanotti, O.; Loubère, R.; Diot, S. A posteriori subcell limiting of the discontinuous Galerkin finite element method for hyperbolic conservation laws. J. Comput. Phys. 2014, 278, 47–75. [Google Scholar] [CrossRef]
- Zanotti, O.; Fambri, F.; Dumbser, M.; Hidalgo, A. Space-time adaptive ADER discontinuous Galerkin finite element schemes with a posteriori sub-cell finite volume limiting. Comput. Fluids 2015, 118, 204–224. [Google Scholar] [CrossRef]
- Dumbser, M.; Loubère, R. A simple robust and accurate a posteriori sub-cell finite volume limiter for the discontinuous Galerkin method on unstructured meshes. J. Comput. Phys. 2016, 319, 163–199. [Google Scholar] [CrossRef]
- Titarev, V.; Toro, E. ADER: Arbitrary High Order Godunov Approach. J. Sci. Comput. 2002, 17, 609–618. [Google Scholar] [CrossRef]
- Toro, E.; Titarev, V. Solution of the generalized Riemann problem for advection-reaction equations. Proc. R. Soc. Lond. 2002, 458, 271–281. [Google Scholar] [CrossRef]
- Titarev, V.; Toro, E. ADER schemes for three-dimensional nonlinear hyperbolic systems. J. Comput. Phys. 2005, 204, 715–736. [Google Scholar] [CrossRef]
- Toro, E.F.; Titarev, V.A. Derivative Riemann solvers for systems of conservation laws and ADER methods. J. Comput. Phys. 2006, 212, 150–165. [Google Scholar] [CrossRef]
- Bungartz, H.; Mehl, M.; Neckel, T.; Weinzierl, T. The PDE framework Peano applied to fluid dynamics: An efficient implementation of a parallel multiscale fluid dynamics solver on octree-like adaptive Cartesian grids. Comput. Mech. 2010, 46, 103–114. [Google Scholar] [CrossRef]
- Weinzierl, T.; Mehl, M. Peano-A traversal and storage scheme for octree-like adaptive Cartesian multiscale grids. SIAM J. Sci. Comput. 2011, 33, 2732–2760. [Google Scholar] [CrossRef]
- Khokhlov, A. Fully Threaded Tree Algorithms for Adaptive Refinement Fluid Dynamics Simulations. J. Comput. Phys. 1998, 143, 519–543. [Google Scholar] [CrossRef]
- Baeza, A.; Mulet, P. Adaptive mesh refinement techniques for high-order shock capturing schemes for multi-dimensional hydrodynamic simulations. Int. J. Numer. Methods Fluids 2006, 52, 455–471. [Google Scholar] [CrossRef]
- Colella, P.; Dorr, M.; Hittinger, J.; Martin, D.F.; McCorquodale, P. High-order finite-volume adaptive methods on locally rectangular grids. J. Phys. Conf. Ser. 2009, 180, 012010. [Google Scholar] [CrossRef]
- Bürger, R.; Mulet, P.; Villada, L. Spectral WENO schemes with Adaptive Mesh Refinement for models of polydisperse sedimentation. ZAMM J. Appl. Math. Mech. Z. Math. Mech. 2013, 93, 373–386. [Google Scholar] [CrossRef]
- Ivan, L.; Groth, C. High-order solution-adaptive central essentially non-oscillatory (CENO) method for viscous flows. J. Comput. Phys. 2014, 257, 830–862. [Google Scholar] [CrossRef]
- Buchmüller, P.; Dreher, J.; Helzel, C. Finite volume WENO methods for hyperbolic conservation laws on Cartesian grids with adaptive mesh refinement. Appl. Math. Comput. 2016, 272, 460–478. [Google Scholar] [CrossRef]
- Semplice, M.; Coco, A.; Russo, G. Adaptive Mesh Refinement for Hyperbolic Systems based on Third-Order Compact WENO Reconstruction. J. Sci. Comput. 2016, 66, 692–724. [Google Scholar] [CrossRef]
- Shen, C.; Qiu, J.; Christlieb, A. Adaptive mesh refinement based on high order finite difference WENO scheme for multi-scale simulations. J. Comput. Phys. 2011, 230, 3780–3802. [Google Scholar] [CrossRef]
- Dumbser, M.; Zanotti, O.; Hidalgo, A.; Balsara, D. ADER-WENO Finite Volume Schemes with Space-Time Adaptive Mesh Refinement. J. Comput. Phys. 2013, 248, 257–286. [Google Scholar] [CrossRef]
- Dumbser, M.; Hidalgo, A.; Zanotti, O. High Order Space-Time Adaptive ADER-WENO Finite Volume Schemes for Non-Conservative Hyperbolic Systems. Comput. Methods Appl. Mech. Eng. 2014, 268, 359–387. [Google Scholar] [CrossRef]
- Zanotti, O.; Fambri, F.; Dumbser, M. Solving the relativistic magnetohydrodynamics equations with ADER discontinuous Galerkin methods, a posteriori subcell limiting and adaptive mesh refinement. Mon. Not. R. Astron. Soc. 2015, 452, 3010–3029. [Google Scholar] [CrossRef]
- Fambri, F.; Dumbser, M.; Zanotti, O. Space-time adaptive ADER-DG schemes for dissipative flows: Compressible Navier-Stokes and resistive MHD equations. Comput. Phys. Commun. 2017, 220, 297–318. [Google Scholar] [CrossRef]
- Fambri, F.; Dumbser, M.; Köppel, S.; Rezzolla, L.; Zanotti, O. ADER discontinuous Galerkin schemes for general-relativistic ideal magnetohydrodynamics. Mon. Not. R. Astron. Soc. 2018, 477, 4543–4564. [Google Scholar] [CrossRef]
- Berger, M.J.; Oliger, J. Adaptive Mesh Refinement for Hyperbolic Partial Differential Equations. J. Comput. Phys. 1984, 53, 484–512. [Google Scholar] [CrossRef]
- Berger, M.J.; Jameson, A. Automatic adaptive grid refinement for the Euler equations. AIAA J. 1985, 23, 561–568. [Google Scholar] [CrossRef]
- Berger, M.J.; Colella, P. Local adaptive mesh refinement for shock hydrodynamics. J. Comput. Phys. 1989, 82, 64–84. [Google Scholar] [CrossRef]
- Leveque, R. Clawpack Software. Available online: http://depts.washington.edu/clawpack/ (accessed on 23 August 2018).
- Berger, M.J.; LeVeque, R. Adaptive mesh refinement using wave-propagation algorithms for hyperbolic systems. SIAM J. Numer. Anal. 1998, 35, 2298–2316. [Google Scholar] [CrossRef]
- Bell, J.; Berger, M.; Saltzman, J.; Welcome, M. Three-dimensional adaptive mesh refinement for hyperbolic conservation laws. SIAM J. Sci. Comput. 1994, 15, 127–138. [Google Scholar] [CrossRef]
- Quirk, J. A parallel adaptive grid algorithm for computational shock hydrodynamics. Appl. Numer. Math. 1996, 20, 427–453. [Google Scholar] [CrossRef]
- Coirier, W.; Powell, K. Solution-adaptive Cartesian cell approach for viscous and inviscid flows. AIAA J. 1996, 34, 938–945. [Google Scholar] [CrossRef]
- Deiterding, R. A parallel adaptive method for simulating shock-induced combustion with detailed chemical kinetics in complex domains. Comput. Struct. 2009, 87, 769–783. [Google Scholar] [CrossRef]
- Lopes, M.M.; Deiterding, R.; Gomes, A.F.; Mendes, O.; Domingues, M.O. An ideal compressible magnetohydrodynamic solver with parallel block-structured adaptive mesh refinement. Comput. Fluids 2018, 173, 293–298. [Google Scholar] [CrossRef]
- Dezeeuw, D.; Powell, K.G. An Adaptively Refined Cartesian Mesh Solver for the Euler Equations. J. Comput. Phys. 1993, 104, 56–68. [Google Scholar] [CrossRef]
- Balsara, D. Divergence-free adaptive mesh refinement for magnetohydrodynamics. J. Comput. Phys. 2001, 174, 614–648. [Google Scholar] [CrossRef]
- Teyssier, R. Cosmological hydrodynamics with adaptive mesh refinement. A new high resolution code called RAMSES. Astron. Astrophys. 2002, 385, 337–364. [Google Scholar] [CrossRef]
- Keppens, R.; Nool, M.; Tóth, G.; Goedbloed, J.P. Adaptive Mesh Refinement for conservative systems: Multi-dimensional efficiency evaluation. Comput. Phys. Commun. 2003, 153, 317–339. [Google Scholar] [CrossRef]
- Ziegler, U. The NIRVANA code: Parallel computational MHD with adaptive mesh refinement. Comput. Phys. Commun. 2008, 179, 227–244. [Google Scholar] [CrossRef]
- Mignone, A.; Zanni, C.; Tzeferacos, P.; van Straalen, B.; Colella, P.; Bodo, G. The PLUTO Code for Adaptive Mesh Computations in Astrophysical Fluid Dynamics. Astrophys. J. Suppl. Ser. 2012, 198, 7. [Google Scholar] [CrossRef]
- Cunningham, A.; Frank, A.; Varnière, P.; Mitran, S.; Jones, T.W. Simulating Magnetohydrodynamical Flow with Constrained Transport and Adaptive Mesh Refinement: Algorithms and Tests of the AstroBEAR Code. Astrophys. J. Suppl. Ser. 2009, 182, 519. [Google Scholar] [CrossRef][Green Version]
- Keppens, R.; Meliani, Z.; van Marle, A.; Delmont, P.; Vlasis, A.; van der Holst, B. Parallel, grid-adaptive approaches for relativistic hydro and magnetohydrodynamics. J. Comput. Phys. 2012, 231, 718–744. [Google Scholar] [CrossRef]
- Porth, O.; Olivares, H.; Mizuno, Y.; Younsi, Z.; Rezzolla, L.; Moscibrodzka, M.; Falcke, H.; Kramer, M. The black hole accretion code. Comput. Astrophys. Cosmol. 2017, 4, 1–42. [Google Scholar] [CrossRef]
- Dubey, A.; Almgren, A.; Bell, J.; Berzins, M.; Brandt, S.; Bryan, G.; Colella, P.; Graves, D.; Lijewski, M.; Löffler, F.; et al. A survey of high level frameworks in block-structured adaptive mesh refinement packages. J. Parallel Distrib. Comput. 2014, 74, 3217–3227. [Google Scholar] [CrossRef]
- Stroud, A. Approximate Calculation of Multiple Integrals; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1971. [Google Scholar]
- Castro, M.; Gallardo, J.; Parés, C. High-order finite volume schemes based on reconstruction of states for solving hyperbolic systems with nonconservative products. Applications to shallow-water systems. Math. Comput. 2006, 75, 1103–1134. [Google Scholar] [CrossRef]
- Parés, C. Numerical methods for nonconservative hyperbolic systems: A theoretical framework. SIAM J. Numer. Anal. 2006, 44, 300–321. [Google Scholar] [CrossRef]
- Rhebergen, S.; Bokhove, O.; van der Vegt, J. Discontinuous Galerkin finite element methods for hyperbolic nonconservative partial differential equations. J. Comput. Phys. 2008, 227, 1887–1922. [Google Scholar] [CrossRef]
- Dumbser, M.; Hidalgo, A.; Castro, M.; Parés, C.; Toro, E. FORCE Schemes on Unstructured Meshes II: Non–Conservative Hyperbolic Systems. Comput. Methods Appl. Mech. Eng. 2010, 199, 625–647. [Google Scholar] [CrossRef]
- Müller, L.O.; Parés, C.; Toro, E.F. Well-balanced high-order numerical schemes for one-dimensional blood flow in vessels with varying mechanical properties. J. Comput. Phys. 2013, 242, 53–85. [Google Scholar] [CrossRef]
- Müller, L.; Toro, E. Well-balanced high-order solver for blood flow in networks of vessels with variable properties. Int. J. Numer. Methods Biomed. Eng. 2013, 29, 1388–1411. [Google Scholar] [CrossRef] [PubMed]
- Gaburro, E.; Dumbser, M.; Castro, M. Direct Arbitrary-Lagrangian-Eulerian finite volume schemes on moving nonconforming unstructured meshes. Comput. Fluids 2017, 159, 254–275. [Google Scholar] [CrossRef]
- Gaburro, E.; Castro, M.; Dumbser, M. Well balanced Arbitrary-Lagrangian-Eulerian finite volume schemes on moving nonconforming meshes for the Euler equations of gasdynamics with gravity. Mon. Not. R. Astron. Soc. 2018, 477, 2251–2275. [Google Scholar] [CrossRef]
- Toro, E.; Hidalgo, A.; Dumbser, M. FORCE Schemes on Unstructured Meshes I: Conservative Hyperbolic Systems. J. Comput. Phys. 2009, 228, 3368–3389. [Google Scholar] [CrossRef]
- Dumbser, M.; Toro, E.F. A Simple Extension of the Osher Riemann Solver to Non-Conservative Hyperbolic Systems. J. Sci. Comput. 2011, 48, 70–88. [Google Scholar] [CrossRef]
- Castro, M.; Pardo, A.; Parés, C.; Toro, E. On some fast well-balanced first order solvers for nonconservative systems. Math. Comput. 2010, 79, 1427–1472. [Google Scholar] [CrossRef]
- Dumbser, M.; Toro, E.F. On Universal Osher–Type Schemes for General Nonlinear Hyperbolic Conservation Laws. Commun. Comput. Phys. 2011, 10, 635–671. [Google Scholar] [CrossRef]
- Einfeldt, B.; Roe, P.L.; Munz, C.D.; Sjogreen, B. On Godunov-type methods near low densities. J. Comput. Phys. 1991, 92, 273–295. [Google Scholar] [CrossRef]
- Dumbser, M.; Balsara, D. A New, Efficient Formulation of the HLLEM Riemann Solver for General Conservative and Non-Conservative Hyperbolic Systems. J. Comput. Phys. 2016, 304, 275–319. [Google Scholar] [CrossRef]
- Dumbser, M.; Enaux, C.; Toro, E. Finite Volume Schemes of Very High Order of Accuracy for Stiff Hyperbolic Balance Laws. J. Comput. Phys. 2008, 227, 3971–4001. [Google Scholar] [CrossRef]
- Dumbser, M.; Zanotti, O. Very High Order PNPM Schemes on Unstructured Meshes for the Resistive Relativistic MHD Equations. J. Comput. Phys. 2009, 228, 6991–7006. [Google Scholar] [CrossRef]
- Harten, A.; Engquist, B.; Osher, S.; Chakravarthy, S. Uniformly high order essentially non-oscillatory schemes, III. J. Comput. Phys. 1987, 71, 231–303. [Google Scholar] [CrossRef]
- Dumbser, M.; Käser, M.; Titarev, V.; Toro, E. Quadrature-Free Non-Oscillatory Finite Volume Schemes on Unstructured Meshes for Nonlinear Hyperbolic Systems. J. Comput. Phys. 2007, 226, 204–243. [Google Scholar] [CrossRef]
- Taube, A.; Dumbser, M.; Balsara, D.; Munz, C. Arbitrary High Order Discontinuous Galerkin Schemes for the Magnetohydrodynamic Equations. J. Sci. Comput. 2007, 30, 441–464. [Google Scholar] [CrossRef]
- Hidalgo, A.; Dumbser, M. ADER Schemes for Nonlinear Systems of Stiff Advection-Diffusion-Reaction Equations. J. Sci. Comput. 2011, 48, 173–189. [Google Scholar] [CrossRef]
- Jackson, H. On the eigenvalues of the ADER-WENO Galerkin predictor. J. Comput. Phys. 2017, 333, 409–413. [Google Scholar] [CrossRef]
- Zanotti, O.; Dumbser, M. Efficient conservative ADER schemes based on WENO reconstruction and space-time predictor in primitive variables. Comput. Astrophys. Cosmol. 2016, 3, 1. [Google Scholar] [CrossRef]
- Owren, B.; Zennaro, M. Derivation of efficient, continuous, explicit Runge–Kutta methods. SIAM J. Sci. Stat. Comput. 1992, 13, 1488–1501. [Google Scholar] [CrossRef]
- Gassner, G.; Dumbser, M.; Hindenlang, F.; Munz, C. Explicit one-step time discretizations for discontinuous Galerkin and finite volume schemes based on local predictors. J. Comput. Phys. 2011, 230, 4232–4247. [Google Scholar] [CrossRef]
- Heinecke, A.; Pabst, H.; Henry, G. LIBXSMM: A High Performance Library for Small Matrix Multiplications. Technical Report, SC’15: The International Conference for High Performance Computing, Networking, Storage and Analysis, Austin (Texas), 2015. Available online: https://github.com/hfp/libxsmm (accessed on 23 August 2018).
- Breuer, A.; Heinecke, A.; Bader, M.; Pelties, C. Accelerating SeisSol by generating vectorized code for sparse matrix operators. Adv. Parallel Comput. 2014, 25, 347–356. [Google Scholar]
- Breuer, A.; Heinecke, A.; Rettenberger, S.; Bader, M.; Gabriel, A.; Pelties, C. Sustained petascale performance of seismic simulations with SeisSol on SuperMUC. Lect. Notes Comput. Sci. (LNCS) 2014, 8488, 1–18. [Google Scholar]
- Charrier, D.; Weinzierl, T. Stop talking to me—A communication-avoiding ADER-DG realisation. arXiv, 2018; arXiv:1801.08682. [Google Scholar]
- Boscheri, W.; Dumbser, M. Arbitrary–Lagrangian–Eulerian Discontinuous Galerkin schemes with a posteriori subcell finite volume limiting on moving unstructured meshes. J. Comput. Phys. 2017, 346, 449–479. [Google Scholar] [CrossRef]
- Clain, S.; Diot, S.; Loubère, R. A high-order finite volume method for systems of conservation laws—Multi-dimensional Optimal Order Detection (MOOD). J. Comput. Phys. 2011, 230, 4028–4050. [Google Scholar] [CrossRef]
- Diot, S.; Clain, S.; Loubère, R. Improved detection criteria for the Multi-dimensional Optimal Order Detection (MOOD) on unstructured meshes with very high-order polynomials. Comput. Fluids 2012, 64, 43–63. [Google Scholar] [CrossRef]
- Diot, S.; Loubère, R.; Clain, S. The MOOD method in the three-dimensional case: Very-High-Order Finite Volume Method for Hyperbolic Systems. Int. J. Numer. Methods Fluids 2013, 73, 362–392. [Google Scholar] [CrossRef]
- Loubère, R.; Dumbser, M.; Diot, S. A New Family of High Order Unstructured MOOD and ADER Finite Volume Schemes for Multidimensional Systems of Hyperbolic Conservation Laws. Commun. Comput. Phys. 2014, 16, 718–763. [Google Scholar] [CrossRef]
- Levy, D.; Puppo, G.; Russo, G. Central WENO schemes for hyperbolic systems of conservation laws. M2AN Math. Model. Numer. Anal. 1999, 33, 547–571. [Google Scholar] [CrossRef]
- Levy, D.; Puppo, G.; Russo, G. Compact central WENO schemes for multidimensional conservation laws. SIAM J. Sci. Comput. 2000, 22, 656–672. [Google Scholar] [CrossRef]
- Dumbser, M.; Boscheri, W.; Semplice, M.; Russo, G. Central weighted ENO schemes for hyperbolic conservation laws on fixed and moving unstructured meshes. SIAM J. Sci. Comput. 2017, 39, A2564–A2591. [Google Scholar] [CrossRef]
- Hu, C.; Shu, C. Weighted essentially non-oscillatory schemes on triangular meshes. J. Comput. Phys. 1999, 150, 97–127. [Google Scholar] [CrossRef]
- Sedov, L. Similarity and Dimensional Methods in Mechanics; Academic Press: New York, NY, USA, 1959. [Google Scholar]
- Kamm, J.; Timmes, F. On Efficient Generation of Numerically Robust Sedov Solutions; Technical Report LA-UR-07-2849; LANL: Los Alamos, NM, USA, 2007. [Google Scholar]
- Tavelli, M.; Dumbser, M.; Charrier, D.; Rannabauer, L.; Weinzierl, T.; Bader, M. A simple diffuse interface approach on adaptive Cartesian grids for the linear elastic wave equations with complex topography. arXiv, 2018; arXiv:1804.09491. [Google Scholar]
- Dumbser, M.; Käser, M. An arbitrary high-order discontinuous Galerkin method for elastic waves on unstructured meshes—II. The three-dimensional isotropic case. Geophys. J. Int. 2006, 167, 319–336. [Google Scholar] [CrossRef]
- Godunov, S.K.; Zabrodin, A.V.; Prokopov, G.P. A Difference Scheme for Two-Dimensional Unsteady Aerodynamics. J. Comp. Math. Math. Phys. USSR 1961, 2, 1020–1050. [Google Scholar]
- Antón, L.; Zanotti, O.; Miralles, J.A.; Martí, J.M.; Ibáñez, J.M.; Font, J.A.; Pons, J.A. Numerical 3+1 general relativistic magnetohydrodynamics: A local characteristic approach. Astrophys. J. 2006, 637, 296. [Google Scholar] [CrossRef]
- Zanna, L.D.; Zanotti, O.; Bucciantini, N.; Londrillo, P. ECHO: An Eulerian Conservative High Order scheme for general relativistic magnetohydrodynamics and magnetodynamics. Astron. Astrophys. 2007, 473, 11–30. [Google Scholar] [CrossRef]
- Löhner, R. An adaptive finite element scheme for transient problems in CFD. Comput. Methods Appl. Mech. Eng. 1987, 61, 323–338. [Google Scholar] [CrossRef]
- Radice, D.; Rezzolla, L.; Galeazzi, F. High-order fully general-relativistic hydrodynamics: New approaches and tests. Class. Quantum Gravity 2014, 31, 075012. [Google Scholar] [CrossRef]
- Bermúdez, A.; Vázquez, M. Upwind methods for hyperbolic conservation laws with source terms. Comput. Fluids 1994, 23, 1049–1071. [Google Scholar] [CrossRef]
- Alic, D.; Bona-Casas, C.; Bona, C.; Rezzolla, L.; Palenzuela, C. Conformal and covariant formulation of the Z4 system with constraint-violation damping. Phys. Rev. D 2012, 85, 064040. [Google Scholar] [CrossRef]
- Dedner, A.; Kemm, F.; Kröner, D.; Munz, C.D.; Schnitzer, T.; Wesenberg, M. Hyperbolic Divergence Cleaning for the MHD Equations. J. Comput. Phys. 2002, 175, 645–673. [Google Scholar] [CrossRef]
- Gundlach, C.; Martin-Garcia, J. Symmetric hyperbolic form of systems of second-order evolution equations subject to constraints. Phys. Rev. D 2004, 70, 044031. [Google Scholar] [CrossRef]
- Dumbser, M.; Guercilena, F.; Köppel, S.; Rezzolla, L.; Zanotti, O. Conformal and covariant Z4 formulation of the Einstein equations: Strongly hyperbolic first–order reduction and solution with discontinuous Galerkin schemes. Phys. Rev. D 2018, 97, 084053. [Google Scholar] [CrossRef]

| Error | Error | Error | Order | Order | Order | Theor. | ||
|---|---|---|---|---|---|---|---|---|
| 25 | — | — | — | 4 | ||||
| 50 | 4.39 | 4.38 | 4.26 | |||||
| 75 | 4.55 | 4.30 | 4.17 | |||||
| 100 | 4.46 | 4.17 | 4.01 | |||||
| 20 | — | — | — | 5 | ||||
| 30 | 5.32 | 5.37 | 5.75 | |||||
| 40 | 5.39 | 5.31 | 4.92 | |||||
| 50 | 5.50 | 5.39 | 5.69 | |||||
| 10 | — | — | — | 6 | ||||
| 20 | 5.96 | 6.22 | 6.55 | |||||
| 30 | 6.45 | 6.33 | 5.96 | |||||
| 40 | 5.77 | 5.93 | 5.82 |
| Error | Order | WCT [s] | Error | Order | WCT [s] | ||
|---|---|---|---|---|---|---|---|
| ADER-DG () | RKDG () | ||||||
| 8 | 0.093 | 8 | 0.107 | ||||
| 16 | 5.44 | 1.371 | 16 | 5.14 | 1.394 | ||
| 24 | 2.34 | 6.854 | 24 | 2.81 | 6.894 | ||
| 32 | 6.48 | 21.642 | 32 | 5.81 | 21.116 | ||
| ADER-DG () | RKDG () | ||||||
| 8 | 0.363 | 8 | 0.456 | ||||
| 16 | 4.88 | 5.696 | 16 | 4.86 | 6.666 | ||
| 24 | 4.76 | 28.036 | 24 | 4.78 | 29.186 | ||
| 32 | 5.17 | 89.271 | 32 | 5.13 | 87.115 | ||
| ADER-DG () | RKDG () | ||||||
| 8 | 1.090 | 8 | 1.219 | ||||
| 16 | 6.14 | 16.710 | 16 | 6.14 | 17.310 | ||
| 24 | 5.78 | 84.425 | 24 | 5.80 | 83.777 | ||
| 32 | 6.01 | 263.021 | 32 | 5.97 | 260.859 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dumbser, M.; Fambri, F.; Tavelli, M.; Bader, M.; Weinzierl, T. Efficient Implementation of ADER Discontinuous Galerkin Schemes for a Scalable Hyperbolic PDE Engine. Axioms 2018, 7, 63. https://doi.org/10.3390/axioms7030063
Dumbser M, Fambri F, Tavelli M, Bader M, Weinzierl T. Efficient Implementation of ADER Discontinuous Galerkin Schemes for a Scalable Hyperbolic PDE Engine. Axioms. 2018; 7(3):63. https://doi.org/10.3390/axioms7030063
Chicago/Turabian StyleDumbser, Michael, Francesco Fambri, Maurizio Tavelli, Michael Bader, and Tobias Weinzierl. 2018. "Efficient Implementation of ADER Discontinuous Galerkin Schemes for a Scalable Hyperbolic PDE Engine" Axioms 7, no. 3: 63. https://doi.org/10.3390/axioms7030063
APA StyleDumbser, M., Fambri, F., Tavelli, M., Bader, M., & Weinzierl, T. (2018). Efficient Implementation of ADER Discontinuous Galerkin Schemes for a Scalable Hyperbolic PDE Engine. Axioms, 7(3), 63. https://doi.org/10.3390/axioms7030063





