An Alternative to Real Number Axioms

Abstract

In the present paper we consider one of the basic theorems of probability theory on real numbers. We prove that it is equivalent with the supremum axiom of real numbers.

1. Introduction

It is a well-known fact that the set $\mathbb{Q}$ of rational numbers is not complete—hence, such important constants as $\sqrt{2}$ or $\pi$ do not exist in $\mathbb{Q}$. Because the way in which the set $ℝ$ is constructed of real numbers from $\mathbb{Q}$ is quite complicated, it is usually defined axiomatically. The completeness of $ℝ$ can be formulated in different ways, e.g., as a complete metric space, or as a complete lattice. In [1], a review of some completeness axioms for $ℝ$ is presented. In this paper, the set $ℝ$ will be characterized by a property which is very important in the probability theory, which may prove useful from the point of view of applications, as well as didactics. In the paper we shall characterize the set $ℝ$ from the perspective of the probability theory, namely in the Kolmogorov formulations—an event is a set on certain $\sigma$-algebra S of subsets of a space $\mathrm{\Omega }$, and the probability is a $\sigma$-additive mapping $P:S⟶\left[0, 1\right]$. In terms of measurement, the mapping is a real function $\xi : \mathrm{\Omega }⟶ℝ$, and it is an interesting point, especially in terms of didactics, that the complete information about $\xi$ is obtained from the distribution function F of $\xi$, which is a real function, $F: ℝ⟶\left[0, 1\right]$, with some particular properties.

The paper is organized as follows: In Section 2 we will formulate two different axioms—the supremum axiom (S) and the distribution function axiom (D); and in Section 3 we will prove that the axioms are equivalent.

2. Materials and Methods

In this section we formulate the important properties of the distribution function. In the literature there are two well-established but different definitions of the distribution function $F: ℝ⟶\left[0, 1\right]$ of a random variable $\xi : \mathrm{\Omega }⟶ℝ$. The first is given by the formula $F\left(x\right)=P\left(\left\{\omega \in \mathrm{\Omega }: \xi \left(\omega \right)<x \right\}\right)$, and the second by the formula $F\left(x\right)=P\left(\left\{\omega \in \mathrm{\Omega }: \xi \left(\omega \right)\le x\right\}\right)$. In this paper we shall use the second approach, which is more convenient for working with the supremum axiom. Evidently, the first one could be used in the infimum way. The distribution function $F: ℝ⟶\left[0, 1\right]$ can be characterized without any reference to the general probability space [2,3] and by applying only a few properties of F, as shown in the following definition.

Definition 1.

A function$F: ℝ⟶\left[0, 1\right]$is called a distribution if it satisfies the following properties:

1. 

F is non-decreasing

2. 

F is right continuous in any point$x_0\in ℝ$,

3. 

$\underset{x\rightharpoonup -\infty }{lim}F\left(x\right)=0,$

4. 

$\underset{x\rightharpoonup \infty }{lim}F\left(x\right)=1$.

In the probability theory, the following theorem presents a translation method between the elementary approach and the abstract theory. To any distribution function $F: ℝ⟶\left[0, 1\right]$ there exists a probability measure $\lambda : \mathcal{B}⟶\left[0, 1\right]$ defined on the family $\mathcal{B}$ of Borel subsets of $ℝ$, such that:

$$\lambda \left((\alpha , \beta ]\right)=F\left(\beta \right)-F\left(\alpha \right)$$

for any $\alpha ,\beta \in ℝ, \alpha <\beta .$

In our elementary approach, instead of $\mathcal{B}$ we will work only with the family $\mathcal{R}$ for all unions of intervals $I\subset ℝ$ (bounded as well as unbounded). According to the measure extension theorem, any additive and continuous mapping $\lambda : \mathcal{R}⟶\left[0, 1\right]$ can be extended from $\mathcal{R}$ to $\mathcal{B}$, since $\mathcal{R}$ is an algebra and $\mathcal{B}$ is the $\sigma$-algebra generated by $\mathcal{R}$.

Axiom (S). Any increasing bounded sequence of real numbers has the supremum—the least upper bound of the sequence.

In our distribution axiom, instead of $\sigma$-additivity, we shall use the notion of additivity and the notion of continuity.

A mapping $\lambda : \mathcal{R}\bigcup \left[0, 1\right]$ is additive, if for sets $A,B\in \mathcal{R}$ such that $A\bigcap B=\varnothing$, it holds:

$$\lambda \left(A⟶B\right)=\lambda \left(A\right)+\lambda \left(B\right).$$

A mapping $\lambda : \mathcal{R}⟶\left[0,1\right]$ is continuous if, for any $A_n\in \mathcal{R}$, such that $A_n\subset A_{n+1}$ $\left(n=1,2,\dots \right)$ and $\bigcup _{n=1}^{\infty }{A}_n\in \mathcal{R}$, it holds:

$$\lambda \left({\displaystyle \bigcup }_{n=1}^{\infty }{A}_n\right)=\underset{n\to \infty }{\lim }\lambda \left(A_n\right).$$

Axiom (D). To any distribution function $F: ℝ⟶\left[0, 1\right]$ there exists an additive and continuous mapping $\lambda : \mathcal{R}⟶\left[0, 1\right]$, such that:

$$\lambda \left((\alpha , \beta ]\right)=F\left(\beta \right)-F\left(\alpha \right)$$

for any $(\alpha ,\beta ]\subset ℝ.$

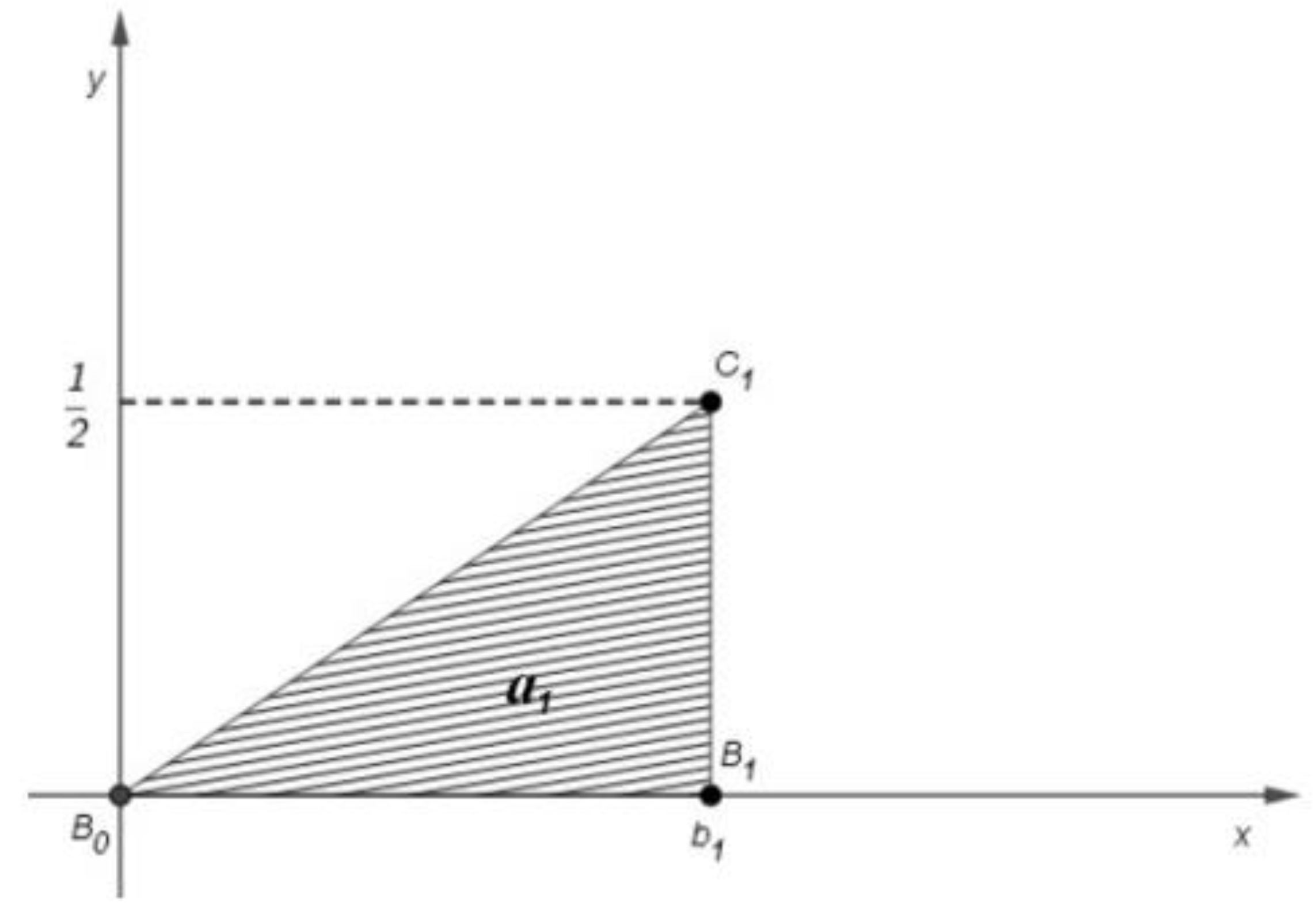
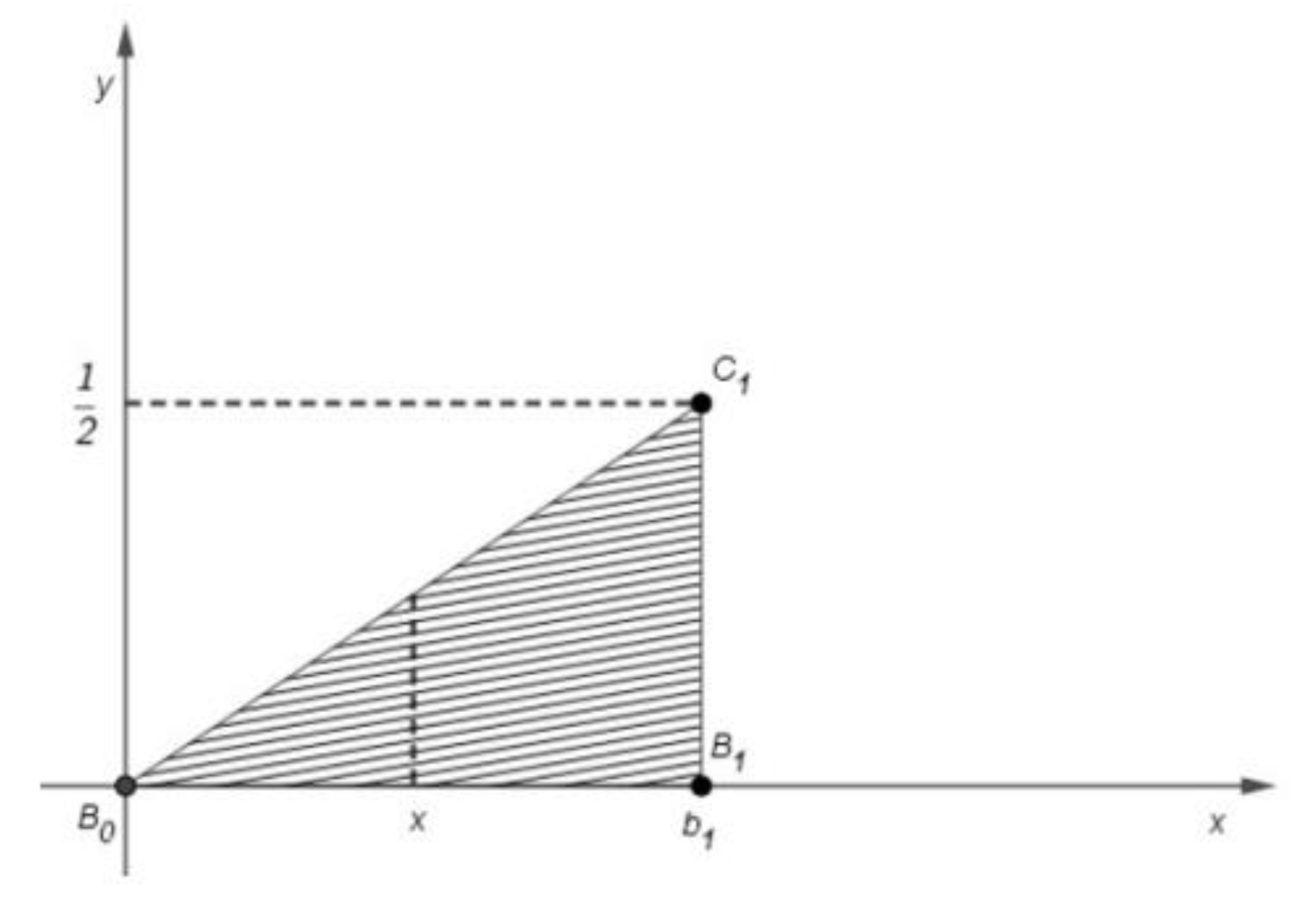
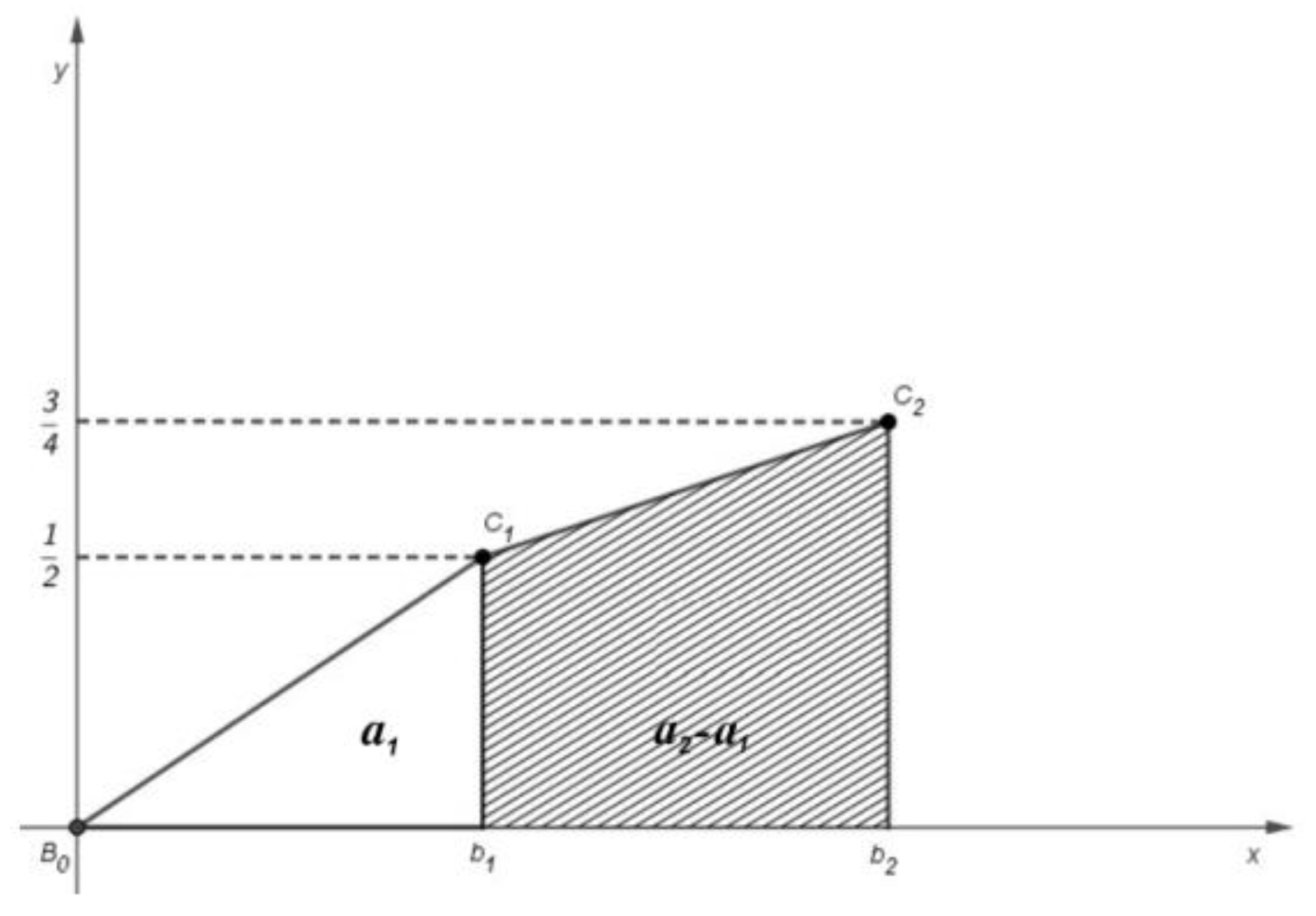
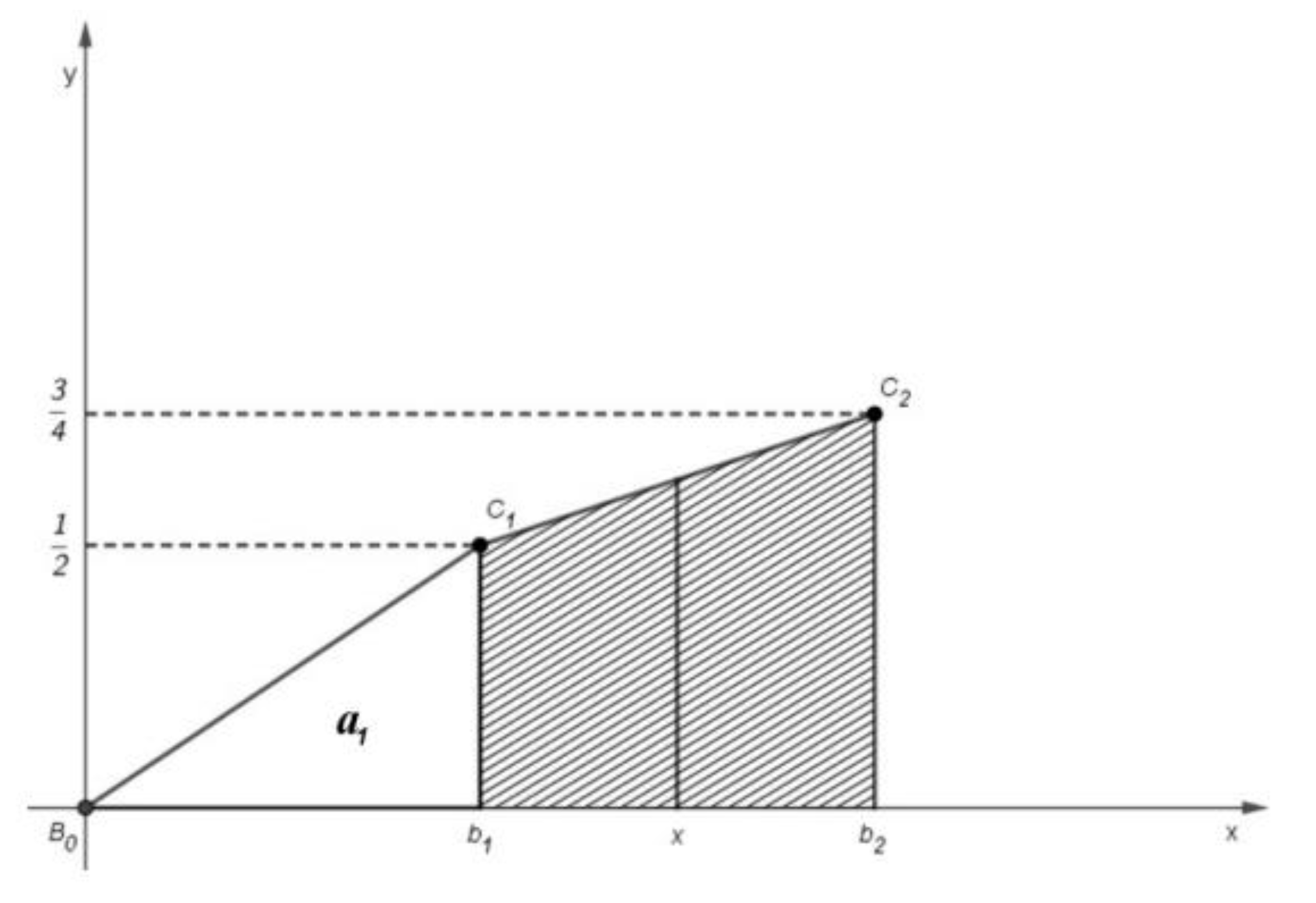
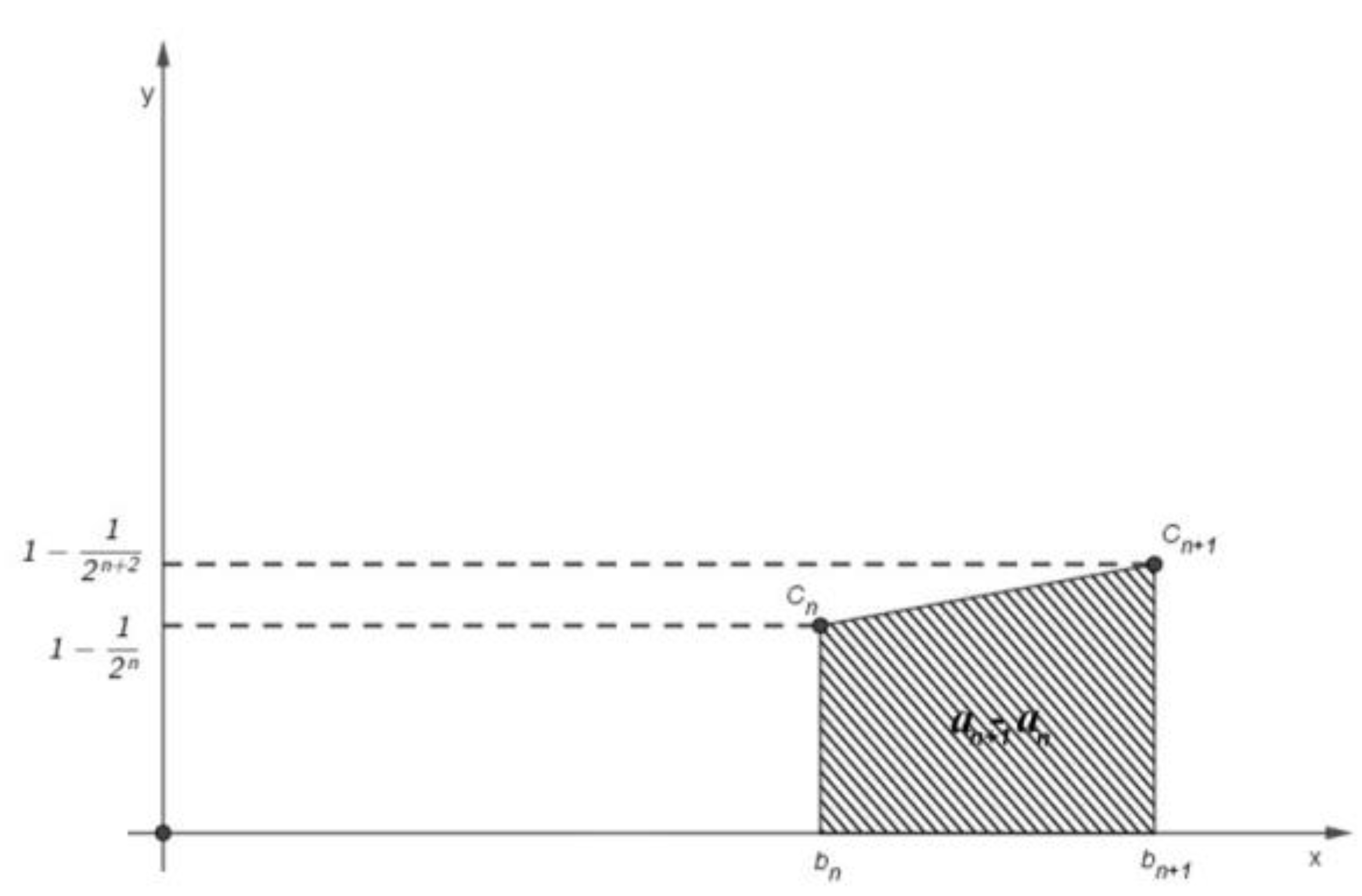
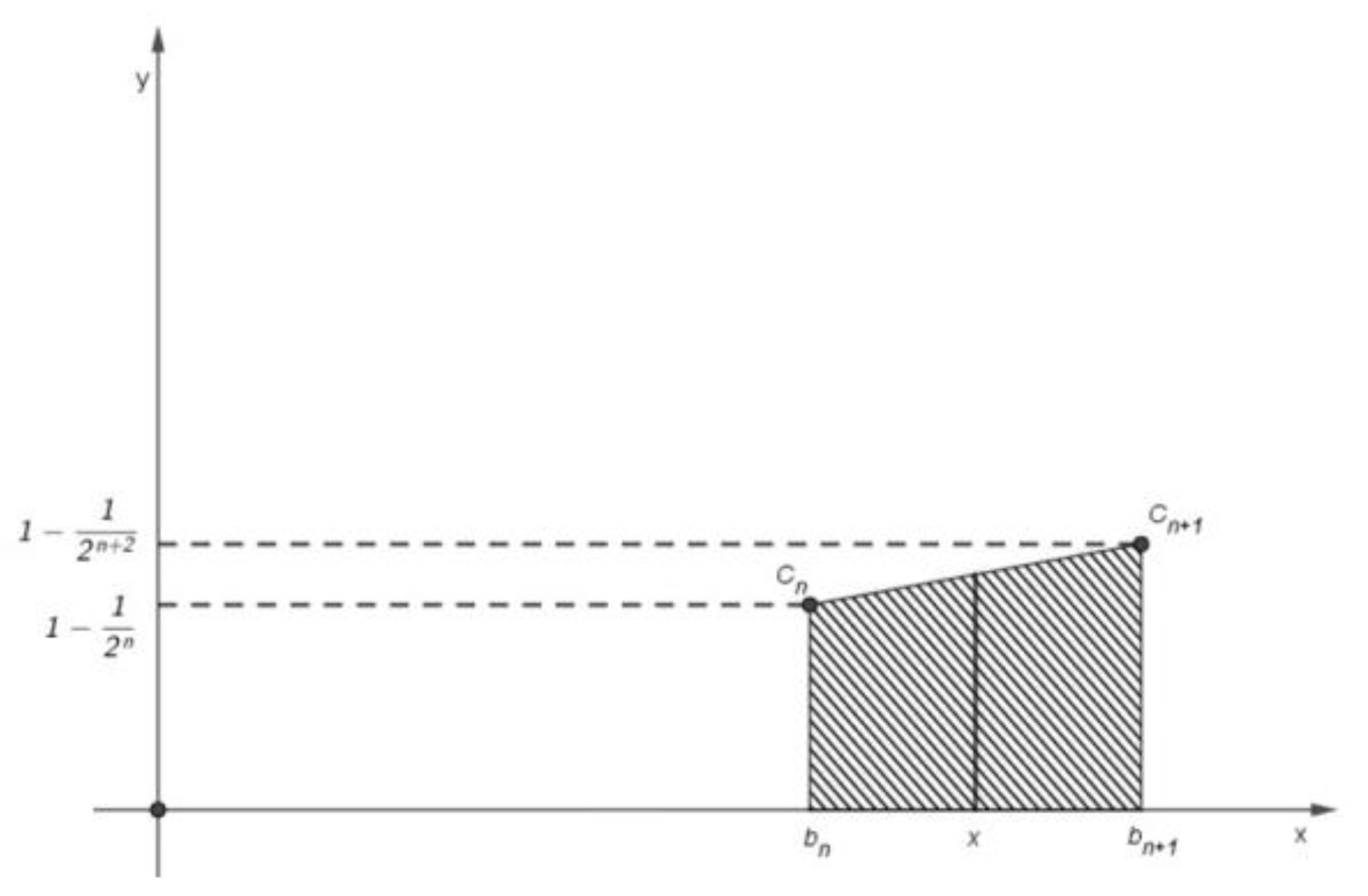
3. Results

There are many known proofs of the axiom (D), e.g., referring to the completeness of R by (S). Now we shall prove the opposite implication.

Theorem 1.

Axiom (D) implies Axiom (S).

Proof of Theorem 1.

Let ${\left\{a_n\right\}}_n$ be a sequence, such that $0<a_1<a_2< \cdots <a_n<a_{n+1}\le 1$. Our goal is to construct a distribution function $y=F\left(x\right)$ and an increasing sequence $b_n$, such that $F\left(b_n\right)=a_n$ for every n. Consider the points $B_0, B_1, C_1$ in the coordinate system, where $B_0=\left(0, 0\right),$ $B_1=\left(b_1, 0\right)$, and $C_1=\left(b_1,\frac{1}{2}\right)$ (see Figure 1).

Figure 1. Points $B_0, B_1, C_1$ in the coordinate system.

Denote the area of the triangle, defined by these points by $a_1$. Clearly, $b_1=4a_1.$ Let x be a point in the interval $[0, b_1).$ Then, $F\left(x\right)$ is the area of the triangle, defined by points $B_0,$ $X_1=\left(x, 0\right)$ and $X_2=\left(x,\frac{x}{8a_1}\right)$ (see Figure 2).

$$F\left(x\right)=\frac{x,\frac{x}{8a_1}}{2}= \frac{x^2}{16a_1},$$

$$F\left(b_1\right)=F\left(4a_1\right)=a_1.$$

.

Figure 2. The area of the triangle, defined by points $B_0, X_1, X_2$.

The constructed point is $F\left(b_1\right)=a_1.$ Consider the points $B_1, C_1, B_2, C_2$ where $B_2=\left(b_2, 0\right), C_2= =\left(b_2,\frac{3}{4}\right)$; the area of the trapezoid defined by these points is $a_2-a_1$ (see Figure 3).

$$\left(\frac{1}{2}+\frac{3}{4}\right)\frac{1}{2}\left(b_2-b_1\right)= a_2-a_1.$$

Figure 3. The area of the trapezoid defined by points $B_1, C_1, B_2, C_2$.

Hence,

$$b_2=b_1+ \frac{8}{5}\left(a_2-a_1\right).$$

.

Let $x\in \left[b_1,b_2\right].$ Let $F\left(x\right)$ be the area of the trapezoid defined by $B_0,C_1,$ $X_1=\left(x,0\right)$, $X_2=\left(x, \frac{1}{2}+\frac{x -b_1}{4\left(b_2-b_1\right)}\right)$ (see Figure 4).

$$F\left(x\right)=a_1+\left(\frac{1}{2}+\frac{x-b_1}{4\left(b_2-b_1\right)}+\frac{1}{2} \right)\frac{1}{2}\left(x -b_1\right)$$

$$F\left(b_2\right)=a_1+\left(a_2-a_1\right)=a_2.$$

Figure 4. The area of the trapezoid defined by points $B_0,C_1,X_1,X_2$.

By induction, assume $F\left(b_n\right)=a_n.$ Consider the points $C_n=\left(b_n,1-\frac{1}{2^n}\right),C_{n+1}=\left(b_{n+1},1-\frac{1}{2^{n+1}}\right),$ $B_n=\left(b_n,0\right)$ and $B_{n+1}=\left(b_{n+1},0\right).$ These four points define the area $a_{n+1}-a_n$ of the trapezoid (see Figure 5).

$$\left(1-\frac{1}{2^n}+1-\frac{1}{2^{n+1}}\right)\frac{1}{2}\left(b_{n+1}-b_n\right)=a_{n+1}-a_n$$

$$b_{n+1}=\frac{2^{n+2}}{2^{n+2}-3}\left(a_{n+1}-a_n\right)+b_n.$$

Figure 5. The area of the trapezoid defined by points $C_n,C_{n+1}, B_n,B_{n+1}$.

Let $x\in \left[b_n,b_{n+1}\right],$ $F\left(x\right)$ be the area of the trapezoid, defined by $B_n,C_n,$ $X_1=\left(x,0\right),$ $X_2=\left(x,\frac{x-b_n}{\left(b_{n+1}-b_n\right)2^{n+1}}\right)$ (see Figure 6).

$$F\left(x\right)=a_n+\left(1-\frac{1}{2^n}+\frac{\left(x -b_n\right)}{\left(b_{n+1}-b_n\right)2^{n+1}}\right)\left(x -b_n\right)$$

$$F\left(b_{n+1}\right)=a_n+a_{n+1}-a_n=a_{n+1}.$$

.

Figure 6. The area of the trapezoid defined by points $B_n, C_n,X_1,X_2$.

Define function F by using the following properties:

• For all $x\le 0$, put $F\left(x\right)=0$.
• If there exists a natural number n and $x\in \left[b_n,b_{n+1}\right]$, then

  $$F\left(x\right)=a_n+\left(1-\frac{1}{2^n}+\frac{\left(x -b_n\right)}{\left(b_{n+1}-b_n\right)2^{n+1}}\right)\left(x -b_n\right),$$
• if $x\ge b_n$ for all natural numbers n, then $F\left(x\right)=1$.

It can easily be proved that F is a distribution function. Assume that there exists a probability measure $\lambda : \mathcal{R}⟶\left[0, 1\right]$, such that $\lambda \left(\alpha , \beta ]\right)=F\left(\beta \right)-F\left(\alpha \right)$, and in particular, $\lambda \left((b_{n-1},b_n]\right)=a_n-a_{n-1}.$ Compute:

$$\begin{gathered} \lambda \left((-\infty ,b_n]\right)=\lambda \left(\left(-\infty , 0\right)\right)+\lambda \left((0,b_1]\right)+\lambda \left((b_1,b_2]\right)+\cdots + \lambda \left((b_{n-1},b_n]\right) \\ =0+\left(a_1-0\right)+\left(a_2-a_1\right)+\cdots +\left(a_n\right)=a_n. \end{gathered}$$

Consider:

$$A={\displaystyle \bigcup }_{n=1}^{\infty }\left(-\infty , b_n\right).$$

Then,

$$\lambda \left(A\right)=\underset{n\to \infty }{\lim }\lambda \left((-\infty , b_n]\right)=\underset{n\to \infty }{\lim }{a}_n=\underset{n\in N}{\sup } a_n.$$

Thus, we have found that any increasing sequence ${\left\{a_n\right\}}_n$ from the interval $\left[0, 1\right]$ has the supremum.

Now, let ${\left\{a_n\right\}}_n$ be an arbitrary bounded increasing sequence from $(0, k].$ For any natural n, take $c_n=\frac{a_n}{k}.$ Then $c_n\in (0, 1]$, and there exists the supremum of ${\left\{c_n\right\}}_n.$ Hence, there exists the supremum of ${\left\{a_n\right\}}_n$, and:

$$\underset{n\in N}{\sup }{a}_n=k \underset{n\in N}{\sup } c_n.$$

Finally, consider ${\left(a_n\right)}_n$ as an arbitrary increasing bounded sequence. Take $d_n=a_n-a_1.$ This means that $d_n$ is non-decreasing, non-negative, and bounded. Therefore, there also exists the supremum of $d_n.$ Hence, there exists the supremum of $a_n$ and

$$\sup a_n=a_1+\sup d_n.$$

□

4. Conclusions

This paper focused on the axiom (D), one of the fundamental axioms in the probability theory. We showed that the axiom (D) is equivalent to the supremum axiom (S) of real numbers. The axiom (D) is crucial for many other important theorems in probability and statistics, such as the laws of large numbers, the central limit theorem, or statistical estimations.