Axioms 2018, 7(3), 57; https://doi.org/10.3390/axioms7030057
Single-Valued Neutrosophic Clustering Algorithm Based on Tsallis Entropy Maximization
1
School of Science, Xi’an Polytechnic University, Xi’an 710048, China
2
Department of Mathematics, University of New Mexico, Gallup, NM 87301, USA
3
School of Textile and Materials, Xi’an Polytechnic University, Xi’an 710048, China
*
Author to whom correspondence should be addressed.
Received: 10 May 2018 / Revised: 19 July 2018 / Accepted: 20 July 2018 / Published: 17 August 2018
Abstract
Data clustering is an important field in pattern recognition and machine learning. Fuzzy c-means is considered as a useful tool in data clustering. The neutrosophic set, which is an extension of the fuzzy set, has received extensive attention in solving many real-life problems of inaccuracy, incompleteness, inconsistency and uncertainty. In this paper, we propose a new clustering algorithm, the single-valued neutrosophic clustering algorithm, which is inspired by fuzzy c-means, picture fuzzy clustering and the single-valued neutrosophic set. A novel suitable objective function, which is depicted as a constrained minimization problem based on a single-valued neutrosophic set, is built, and the Lagrange multiplier method is used to solve the objective function. We do several experiments with some benchmark datasets, and we also apply the method to image segmentation using the Lena image. The experimental results show that the given algorithm can be considered as a promising tool for data clustering and image processing. View Full-Text
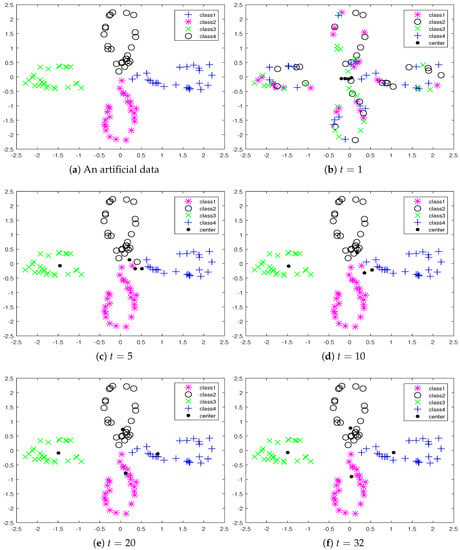
Figure 1
This is an open access article distributed under the Creative Commons Attribution License which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited (CC BY 4.0).
Share & Cite This Article
MDPI and ACS Style
Li, Q.; Ma, Y.; Smarandache, F.; Zhu, S. Single-Valued Neutrosophic Clustering Algorithm Based on Tsallis Entropy Maximization. Axioms 2018, 7, 57.
Note that from the first issue of 2016, MDPI journals use article numbers instead of page numbers. See further details here.