Certain Notions of Energy in Single-Valued Neutrosophic Graphs
Abstract
:1. Introduction
2. Energy of Single-Valued Neutrosophic Graphs
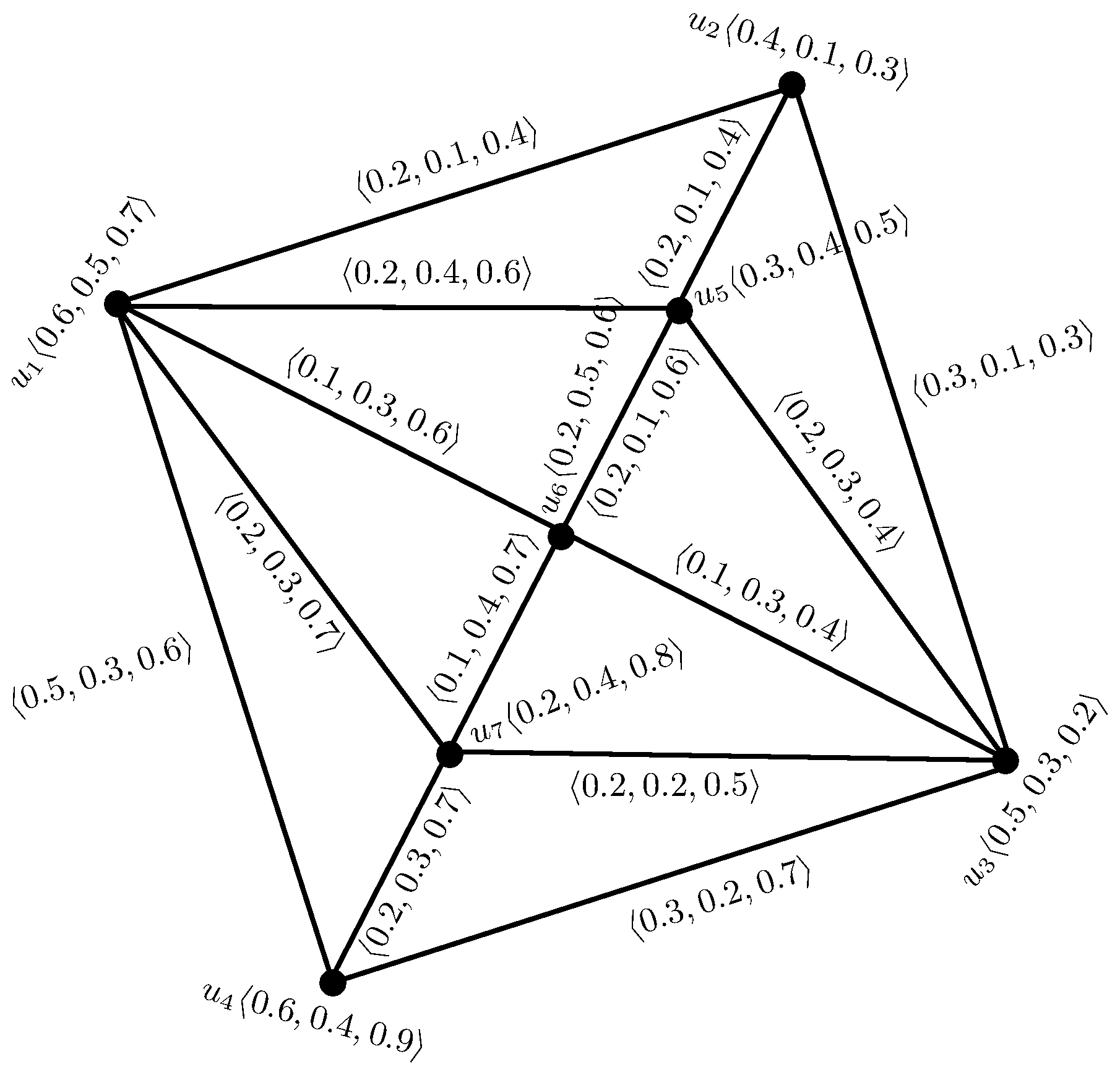
| X | u1 | u2 | u3 | u4 | u5 | u6 | u7 |
| 0.6 | 0.4 | 0.5 | 0.6 | 0.3 | 0.2 | 0.2 | |
| 0.5 | 0.1 | 0.3 | 0.4 | 0.4 | 0.5 | 0.4 | |
| 0.7 | 0.3 | 0.2 | 0.9 | 0.5 | 0.6 | 0.8 |
| Y | u1u2 | u2u3 | u3u4 | u4u1 | u1u5 | u1u6 | u1u7 | u3u5 | u3u6 | u3u7 | u2u5 | u5u6 | u6u7 | u4u7 |
| 0.2 | 0.3 | 0.3 | 0.5 | 0.2 | 0.1 | 0.2 | 0.2 | 0.1 | 0.2 | 0.2 | 0.2 | 0.1 | 0.2 | |
| 0.1 | 0.1 | 0.2 | 0.3 | 0.4 | 0.3 | 0.3 | 0.3 | 0.3 | 0.2 | 0.1 | 0.1 | 0.4 | 0.3 | |
| 0.4 | 0.3 | 0.7 | 0.6 | 0.6 | 0.6 | 0.7 | 0.4 | 0.4 | 0.5 | 0.4 | 0.6 | 0.7 | 0.7 |
- and
- , and .
- Since is a symmetric matrix whose trace is zero, so its eigenvalues are real with zero sum.
- By matrix trace properties, we havewhereHence Analogously, we can show that and . ☐
- (i)
- (ii)
- (iii)
3. Laplacian Energy of Single-Valued Neutrosophic Graphs
- and
- , and .
- Since is a symmetric matrix with non-negative Laplacian eigenvalues, such thatSimilarly, it is easy to show that, and
- By definition of Laplacian matrix, we have
- (i)
- (ii)
- (iii)
- .
- (i)
- (ii)
- (iii)
- .
- (i)
- (ii)
- ;
- (iii)
- (i)
- (ii)
- (iii)
4. Signless Laplacian Energy of Single-Valued Neutrosophic Graphs
- 1.
- and
- 2.
- , and .
5. Relation among Energy, Laplacian Energy and Signless Laplacian Energy of SVNGs
6. Application of Energy of SVNGs in Group Decision-Making
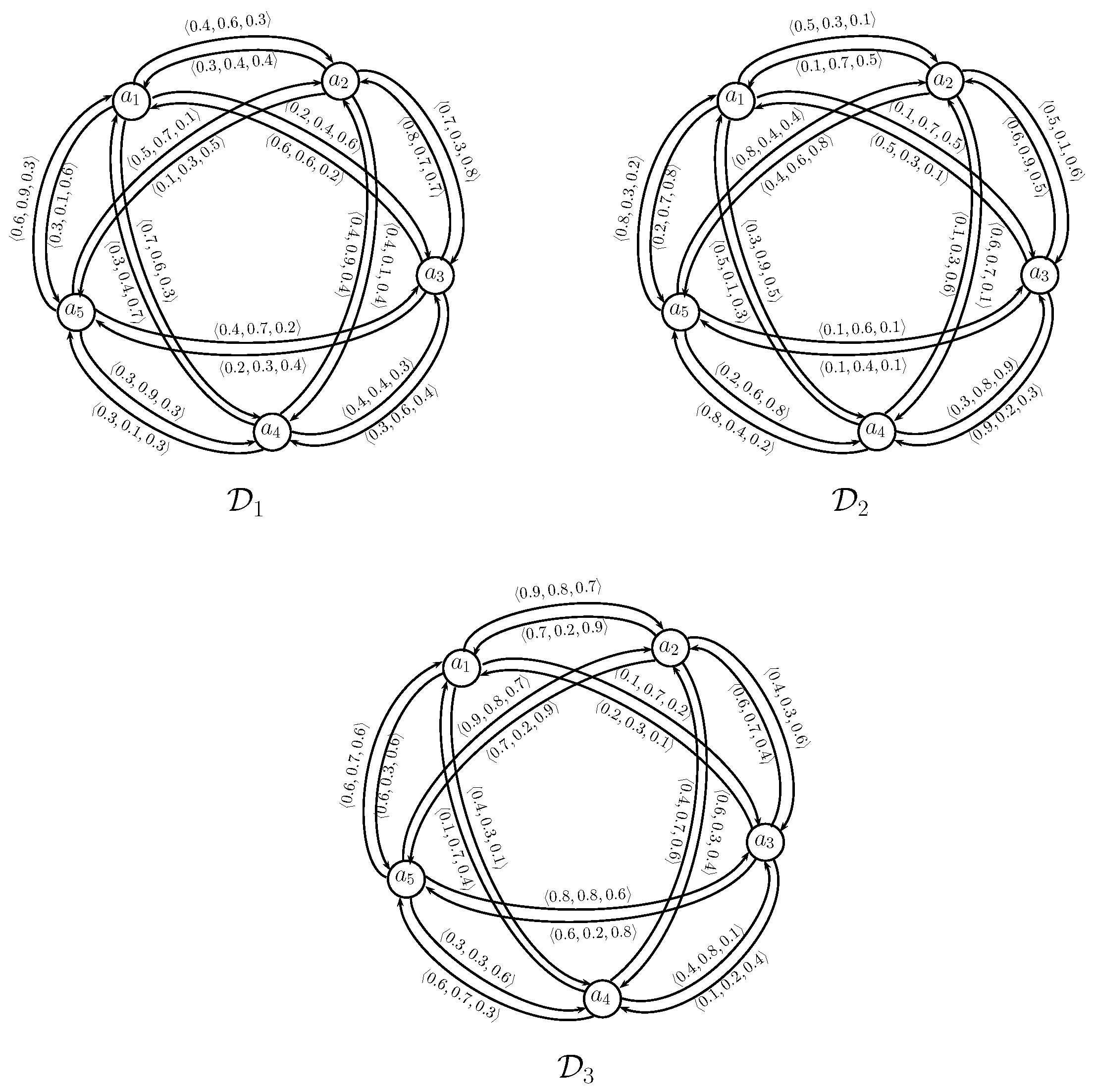
Alliance Partner Selection of a Software Company
7. Real Time Example
- Spec,
- Spec,
- Spec,
- , , .
- Therefore,
- Laplasian Spec,
- Laplacian Spec,
- Laplacian Spec,
- , , .
- Therefore,
- Signless Laplacian Spec,
- Signless Laplacian Spec,
- Signless Laplacian Spec,
- , , .
- Therefore,
- Spec,
- Spec,
- Spec,
- , , .
- Therefore, .
- Laplacian Spec,
- Laplacian Spec,
- Laplacian Spec,
- , , .
- Therefore,
- Signless Laplacian Spec,
- Signless Laplacian Spec,
- Signless Laplacian Spec,
- , , .
- Therefore,
- Spec,
- Spec,
- Spec,
- , ,
- Therefore,
- Laplacian Spec
- Laplacian Spec
- Laplacian Spec
- , , .
- Therefore, .
- Signless Laplacian Spec
- Signless Laplacian Spec
- Signless Laplacian Spec
- , , .
- Therefore, .
- Spec,
- Spec,
- Spec,
- , , .
- Therefore,
- Laplacian Spec,
- Laplacian Spec,
- Laplacian Spec,
- , , .
- Therefore,
- Signless Laplacian Spec,
- Signless Laplacian Spec,
- Signless Laplacian Spec,
- , , .
- Therefore,
8. Conclusions
Author Contributions
Conflicts of Interest
References
- Smarandache, F. A unifying field in logics. In Neutrosophy: Neutrosophic Probability, Set and Logic; American Research Press: Rehoboth, DE, USA, 1999. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Y.Q.; Sunderraman, R. Single-valued neutrosophic sets. Multisp. Multistruct. 2010, 4, 410–413. [Google Scholar]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar]
- Bhattacharya, S. Neutrosophic information fusion applied to the options market. Invest. Manag. Financ. Innov. 2005, 1, 139–145. [Google Scholar]
- Aggarwal, S.; Biswas, R.; Ansari, A.Q. Neutrosophic modeling and control. In Proceedings of the 2010 International Conference on Computer and Communication Technology, Allahabad, India, 17–19 September 2010; pp. 718–723. [Google Scholar]
- Guo, Y.; Cheng, H.D. New neutrosophic approach to image segmentation. Pattern Recognit. 2009, 42, 587–595. [Google Scholar]
- Ye, J.; Fu, J. Multi-period medical diagnosis method using a single-valued neutrosophic similarity measure based on tangent function. Comput. Methods Programs Biomed. 2016, 123, 142–149. [Google Scholar]
- Ye, J. Multicriteria decision-making method using the correlation coefficient under single-valued neutrosophic environment. Int. J. Gen. Syst. 2013, 42, 386–394. [Google Scholar]
- Naz, S.; Rashmanlou, H.; Malik, M.A. Operations on single-valued neutrosophic graphs with application. J. Intell. Fuzzy Syst. 2017, 32, 2137–2151. [Google Scholar]
- Ashraf, S.; Naz, S.; Rashmanlou, H.; Malik, M.A. Regularity of graphs in single-valued neutrosophic environment. J. Intell. Fuzzy Syst. 2017, 33, 529–542. [Google Scholar]
- Gutman, I. The energy of a graph. Ber. Math. Stat. Sekt. Forsch. Graz. 1978, 103, 1–22. [Google Scholar]
- Gutman, I. The Energy of a Graph: Old and New Results, Algebraic Combinatorics and Applications; Springer: Berlin/Heidelberg, Germany, 2001; pp. 196–211. [Google Scholar]
- Gutman, I.; Zhou, B. Laplacian energy of a graph. In Linear Algebra and Its Applications; Elsevier: New York, NY, USA, 2006; Volume 414, pp. 29–37. [Google Scholar]
- Gutman, I.; Robbiano, M.; Martins, E.A.; Cardoso, D.M.; Medina, L.; Rojo, O. Energy of line graphs. In Linear Algebra and Its Applications; Elsevier: New York, NY, USA, 2010; Volume 433, pp. 1312–1323. [Google Scholar]
- Erdos, P. Graph theory and probability, canad. J. Math. 1959, 11, 34–38. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar]
- Kaufmann, A. Introduction a la Theorie des Sour-Ensembles Flous; Masson et Cie: Paris, France, 1973; p. 1. [Google Scholar]
- Rosenfeld, A. Fuzzy Graphs, Fuzzy Sets and Their Applications; Zadeh, L.A., Fu, K.S., Shimura, M., Eds.; Academic Press: New York, NY, USA, 1975; pp. 77–95. [Google Scholar]
- Anjali, N.; Mathew, S. Energy of a fuzzy graph. Ann. Fuzzy Maths Inform. 2013, 6, 455–465. [Google Scholar]
- Sharbaf, S.R.; Fayazi, F. Laplacian energy of a fuzzy graph. Iran. J. Math. Chem. 2014, 5, 1–10. [Google Scholar]
- Parvathi, R.; Karunambigai, M.G. Intuitionistic fuzzy graphs. In Computational Intelligence, Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2006; pp. 139–150. [Google Scholar]
- Akram, M. Bipolar fuzzy graphs. Inf. Sci. 2011, 181, 5548–5564. [Google Scholar]
- Akram, M.; Davvaz, B. Strong intuitionistic fuzzy graphs. Filomat 2012, 26, 177–196. [Google Scholar]
- Akram, M.; Malik, H.M.; Shahzadi, S.; Smarandache, F. Neutrosophic soft rough graphs with application. Axioms 2018, 7, 14. [Google Scholar]
- Akram, M.; Siddique, S. Neutrosophic competition graphs with applications. J. Intell. Fuzzy Syst. 2017, 33, 921–935. [Google Scholar]
- Akram, M.; Sitara, M.; Smarandache, F. Graph structures in bipolar neutrosophic environment. Mathematics 2017, 5, 60–80. [Google Scholar]
- Naz, S.; Ashraf, S.; Akram, M. A novel approach to decision-making with Pythagorean fuzzy information. Mathematics 2018, 6, 1–28. [Google Scholar]
- Ishfaq, N.; Sayed, S.; Akram, M.; Smarandache, F. Notions of rough neutrosophic digraphs. Mathematics 2018, 6, 18. [Google Scholar]
- Sayed, S.; Ishfaq, N.; Akram, M.; Smarandache, F. Rough neutrosophic digraphs with application. Axioms 2018, 7, 5. [Google Scholar]
- Akram, M.; Ishfaq, N.; Sayed, S.; Smarandache, F. Decision-making approach based on neutrosophic rough information. Algorithms 2018, 11, 59. [Google Scholar]
- Naz, S.; Malik, M.A.; Rashmanlou, H. Hypergraphs and transversals of hypergraphs in interval-valued intuitionistic fuzzy setting. J. Mult.-Valued Logic Soft Comput. 2018, 30, 399–417. [Google Scholar]
- Praba, B.; Chandrasekaran, V.M.; Deepa, G. Energy of an intutionistic fuzzy graph. Ital. J. Pure Appl. Math. 2014, 32, 431–444. [Google Scholar]
- Basha, S.S.; Kartheek, E. Laplacian energy of an intuitionistic fuzzy graph. Ind. J. Sci. Technol. 2015, 8, 1–7. [Google Scholar]
- Broumi, S.; Smarandache, F.; Talea, M.; Bakali, A. Single-valued neutrosophic graphs: degree, order and size. In Proceedings of the 2016 IEEE International Conference on Fuzzy Systems, Vancouver, BC, Canada, 24–29 July 2016; pp. 2444–2451. [Google Scholar]
- Broumi, S.; Bakali, A.; Talea, M.; Smarandache, F.; Kishore, K.K.; Sahin, R. Shortest path problem under interval valued neutrosophic setting. J. Fundam. Appl. Sci. 2018, 10, 168–174. [Google Scholar]
- Hamidi, M.; Saeid, A.B. Accessible single-valued neutrosophic graphs. J. Appl. Math. Comput. 2017, 1–26. [Google Scholar] [CrossRef]
- Stanujkic, D.; Zavadskas, E.K.; Smarandache, F.; Brauers, W.K.; Karabasevic, D. A neutrosophic extension of the MULTIMOORA method. Informatica 2017, 28, 181–192. [Google Scholar]
- Smarandache, F.; Ye, J. Summary of the Special Issue “Neutrosophic Information Theory and Applications” at “Information Journal”. Information 2018, 9, 49. [Google Scholar]
- Tripathi, G. A matrix extension of the Cauchy-Schwarz inequality. Econ. Lett. 1999, 63, 1–3. [Google Scholar]
- Akram, M.; Shahzadi, S. Neutrosophic soft graphs with application. J. Intell. Fuzzy Syst. 2017, 32, 841–858. [Google Scholar]
- Fan, Z.P.; Liu, Y. An approach to solve group decision-making problems with ordinal interval numbers. IEEE Trans. Syst. Man Cybern. B Cybern. 2010, 40, 1413–1423. [Google Scholar]
- Biswas, P.; Pramanik, S.; Giri, B.C. TOPSIS method for multi-attribute group decision-making under single-valued neutrosophic environment. Neural Comput. Appl. 2016, 27, 727–737. [Google Scholar]

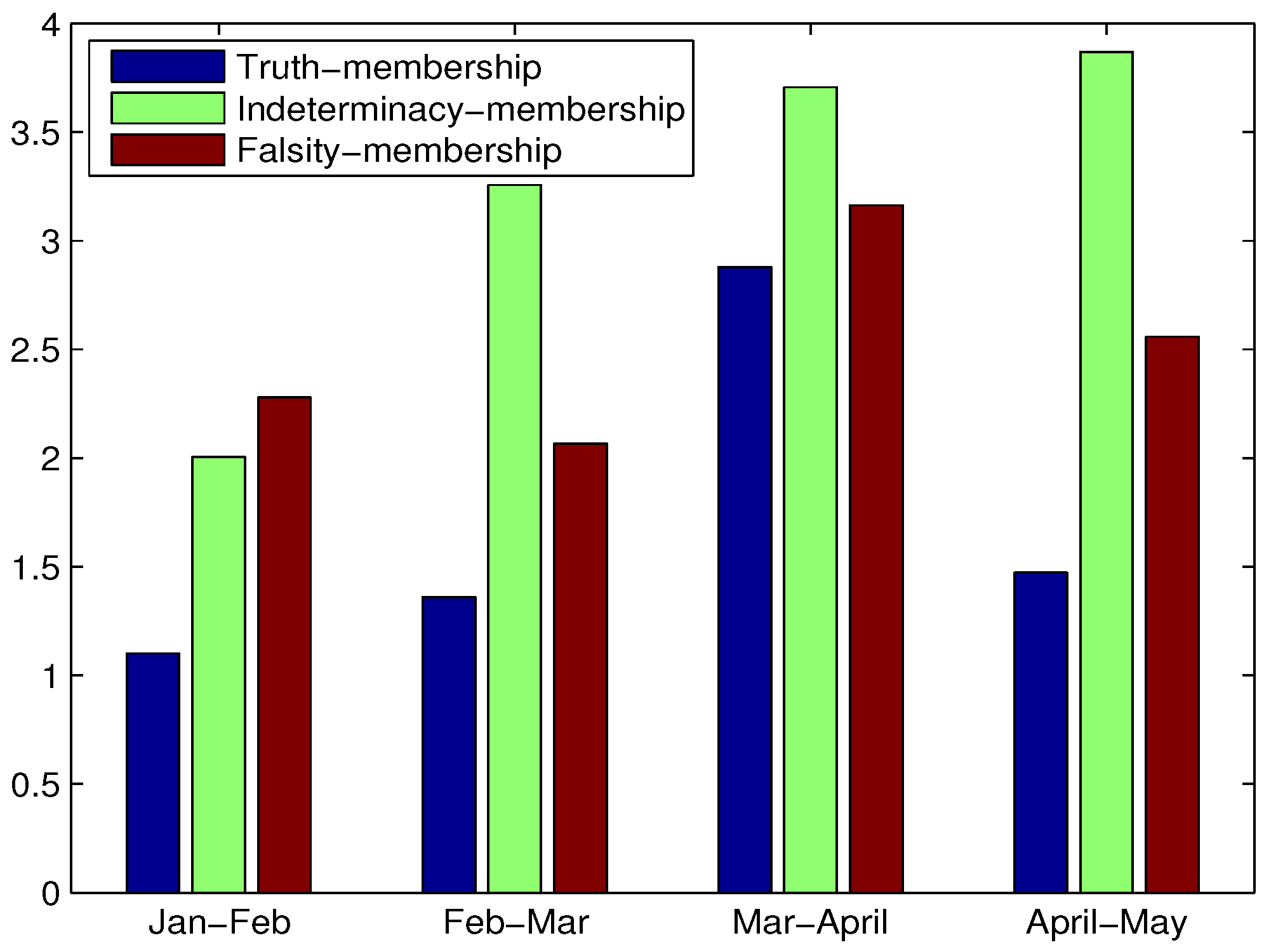
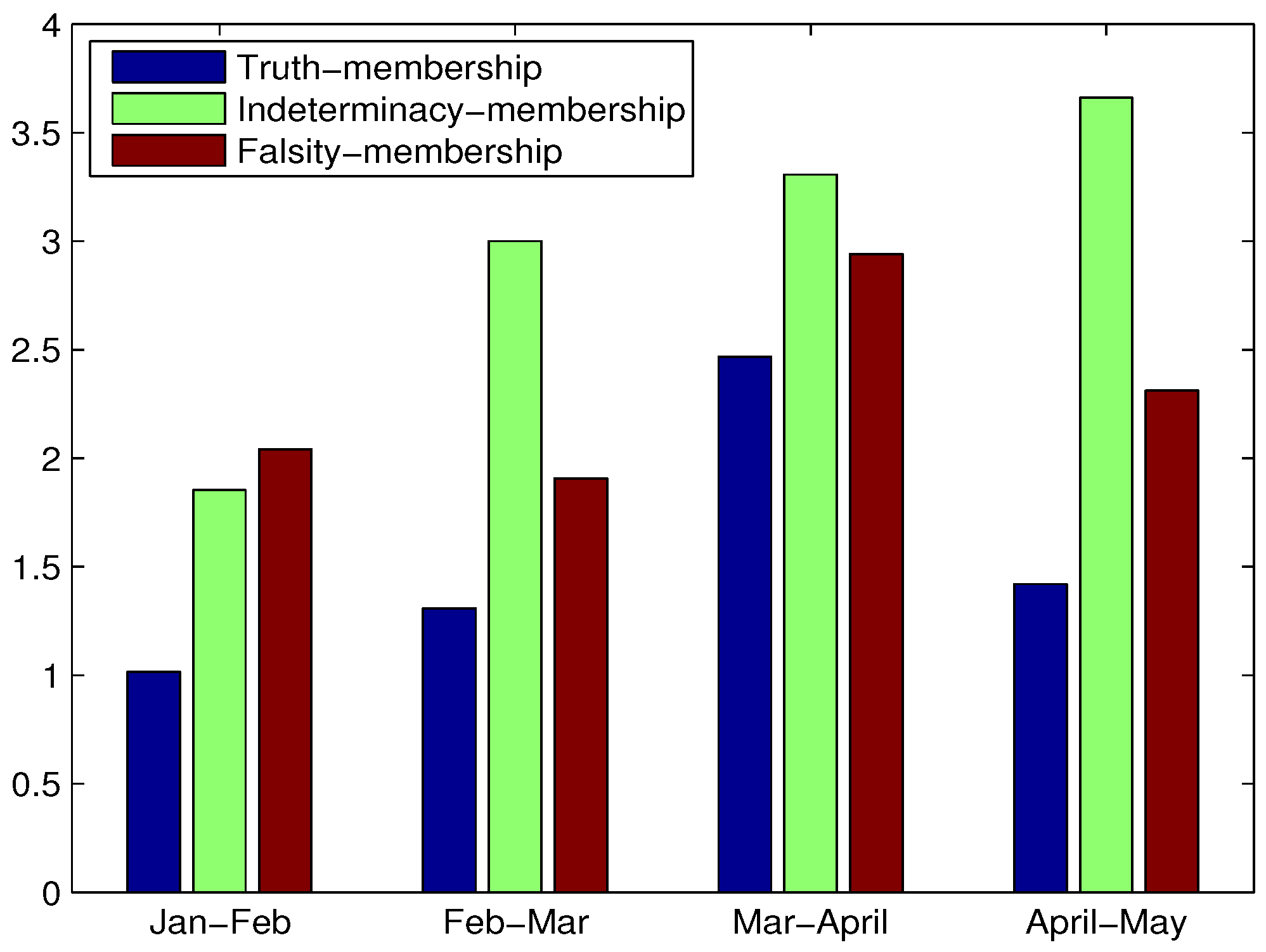
| R | |||||
|---|---|---|---|---|---|
| R | |||||
|---|---|---|---|---|---|
| R | |||||
|---|---|---|---|---|---|
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naz, S.; Akram, M.; Smarandache, F. Certain Notions of Energy in Single-Valued Neutrosophic Graphs. Axioms 2018, 7, 50. https://doi.org/10.3390/axioms7030050
Naz S, Akram M, Smarandache F. Certain Notions of Energy in Single-Valued Neutrosophic Graphs. Axioms. 2018; 7(3):50. https://doi.org/10.3390/axioms7030050
Chicago/Turabian StyleNaz, Sumera, Muhammad Akram, and Florentin Smarandache. 2018. "Certain Notions of Energy in Single-Valued Neutrosophic Graphs" Axioms 7, no. 3: 50. https://doi.org/10.3390/axioms7030050
APA StyleNaz, S., Akram, M., & Smarandache, F. (2018). Certain Notions of Energy in Single-Valued Neutrosophic Graphs. Axioms, 7(3), 50. https://doi.org/10.3390/axioms7030050






