1. Introduction
Recent progress in technology and science has driven interest to studies of heat conduction beyond common Fourier law [
1]:
, where
k is the thermal diffusivity,
T is the temperature; Fourier law describes heat conduction in homogeneous matter at normal conditions well. New heat sources, such as lasers, microwaves etc, are employed in medicine, science and material processing for melting, welding, cutting, drilling, etc. Often heat source and treated media are in motion. Some of modern materials and media have one or two dimensions: ultra-thin films, layers and nano-wires. Highly inhomogeneous porous and multilayered media are also common in industry. First major deviations from Fourier law were found in liquid Helium and in some solid crystal dielectrics at low temperatures <25 ° K [
2,
3,
4,
5]. Proper phenomenon was called Second Sound [
6]; its satisfactory qualitative mathematical description was proposed by Cattaneo and Vernotte [
7], who supposed phonon heat transport in addition to Fourier heat diffusion. In terms of temperature it can be put as follows:
where
kF is the Fourier thermal diffusivity,
is the relaxation time of the heat waves propagation, which relates the moments of the temperature change and of the respective heat flux change. Cattaneo-Vernotte constitution implies a phase lag between the heat flux vector and the temperature gradient; in addition to heat diffusion the temperature perturbation propagates in matter like damped sound-wave at finite speed
. The relaxation time
τ is associated with the phonon–phonon interaction time; at normal conditions it is very small:
τ ≈ 10
−13 s. The Cattaneo Equation (1) is the particular case of the telegrapher’s equation (TE).
which takes its name because it describes the electric signal propagation in long electric lines without radiation [
8]. For heat conduction we have
,
,
and
in Equation (1); the source term,
, describes heat exchange with the environment of low excess temperatures. However, precise quantitative description of the Second Sound with Equation (1) was not successful. There are reports on non-Fourier heat transport in highly inhomogeneous matter even at normal conditions [
9,
10,
11,
12,
13,
14,
15,
16,
17], in fuel droplets [
18], in biomaterials [
19], in energy saving and insulating materials [
20], in graphene, nanofibers, carbon nanotubes, silicon wires, etc. [
21,
22,
23,
24,
25,
26,
27]. Heat transport in these cases was found close to that described by Guyer and Krumhansl (GK) in [
28,
29]. In the one-dimensional case in terms of temperature alone it has the following form:
In its pure form the Guyer–Krumhansl law has
κ = 0. The following formulation:
involves the parameters
,
,
, and
, where the latter,
kb, is the ballistic type heat conductivity. The parameters in the above Equations (3) and (4) have the following dimensions:
,
,
,
,
,
,
, and
.
Despite GK equation is usually associated with ballistic properties, which manifest when the characteristic system scale
L is comparable or less than the mean free path
l of the phonons
L <
l, contradictory opinions on it exist [
30,
31,
32]. In particular, the term “ballistic” is questioned in the context of GK type heat conduction in macroscopic inhomogeneous materials at room temperature [
10,
11]. Moreover, more complicated system of equations was proposed for the ballistic heat transport in [
30], while heat propagation in highly inhomogeneous materials was reported to be close to GK law [
9,
11].
Solutions to Hyperbolic Heat Conduction Equation (HHCE) can be obtained both analytically and numerically [
33,
34,
35,
36,
37,
38,
39,
40], although numerical methods seem to be more commonly used [
41,
42,
43,
44]. Analytical study gives deeper insight in the problem; operational analytical approach and solutions to HHE were developed in [
45,
46,
47,
48,
49,
50]. This method easily handles also other linear DE of high order and fractional DE [
51,
52,
53,
54,
55,
56,
57,
58]. Use of the exponential differential operators, such as the heat operator
[
59] allows operational solution of GK-type Equation (4) as demonstrated in [
47,
48,
49,
50].
In what follows we will obtain some exact solutions to non-Fourier heat transfer in GK-type equation with the substantial derivative, where the speed of the media is constant, and will obtain some particular operational solutions to modified GK-type equation in this case. Moreover, we will study the important case of periodic initial conditions, which occur, for example, in polymer electrolyte fuel cells (PEFCs) [
60,
61,
62,
63,
64,
65,
66,
67,
68], as well as in thin membranes and highly inhomogeneous porous periodic structures, in printed wired heating boards [
69] etc. We will analyze the solutions for the heat transport, described by the system of inhomogeneous partial derivative equation, and use the Knudsen number to account for the ballistic conditions in 1- and 2-dimensional structures [
70].
2. Ballistic Heat Transport Equations with Substantial Derivative
For ultra-thin films and wires neither pure GK nor Cattaneo laws describe exactly heat transport phenomena, but their combination with Fourier law; it forms the following inhomogeneous system of differential equations for the ballistic
and diffusive component
of the complete dimensionless quasi-temperature
(see [
30]):
where indices
b and
d stand for “ballistic” and “diffusive”, respectively. The dimensionless quasi-temperature
θ can be described as the non-dimensional energy, associated with the internal energy; the quantities
and
must therefore be understood to quasi-temperatures, defined as a measure of corresponding internal energy components
and
, respectively to which they are related by the simple relations
(see [
30] for details), where
c is the heat capacity.
It should be understood though, that the ballistic heat transport is effectively described by both contributions in
,
and
are distinguished for convenience. It is easy to see that the above Equations (5) and (6) are of GK-type (5) and of telegrapher’s type (6); the inhomogeneous right hand side (r.h.s.) of Equation (6) is given by the solution of (5). In the above equations and in all following equations the space- and time-coordinates are obviously dimensionless as well as the proper coefficients in the equations are. The dimensionless form of equations for the temperature is useful at least because of the space-time temperature distribution is expressed in our work explicitly in terms of
x and
t. Proper renormalization in SI units or else how is elementary (see, for example, [
30] for details) and good, especially in view of heavy notations in the analytical solutions, which we will obtain in what follows.
Low-dimensional system is characterized by the dimensionless Knudsen number
, which for the phonon heat transport describes the ratio of the free mean path of the phonons
l to the characteristic scale of the system
L. Knudsen number usually arises in problems, where the scale of the system and the characteristic scale of the processes in it compare with each other, such as for gas flow in ultra-narrow channels [
71], etc. In distinct ballistic case in (5),
Kn = 1, we have
α = 3.333,
δ = 3,
ε = 2,
κ = −1 in (3) and
kF = 5/3,
Db = 3/2,
τ = 1/2,
μ = −1/2 in (4). We assume dimensionless equations here and in what follows. In the weak ballistic case,
Kn = 0.1, we get
α = 0.03333,
δ=0.03,
ε = 2,
κ = −1 in (3) and
kF = 0.01666,
kb = 0.015,
τ = 1/2,
μ = −1/2 in (4). In the distinct ballistic case,
Kn = 1, all heat transport terms in GK-type equation contribute more or less equally, in the weak ballistic case,
Kn = 0.1, the Cattaneo wave-term prevails. The inhomogeneous system of PDE (5) and (6) for ballistic heat transport thin film was studied numerically in [
30]; based on the periodic analytical solutions to GK-type equation [
72] some solutions to (5) and (6) were obtained in [
73,
74].
Above Equations (5) and (6), as well as Equations (2)–(4), describe non-Fourier heat transport in stationary media. In the case when the observer moves relatively to the media with constant speed
, the substantial derivative
should be used instead of the time-derivative
to describe the variation of quantity
F along a path. Generally speaking, both the material equations and the energy, mass and momentum conservation equations in case of moving observer should be considered with account for the substantial derivative, resulting in a proper heat conduction equation for the temperature alone. This is relatively simple in the case of Fourier heat diffusion and even for relativistic heat equation [
75,
76], some more complicated for GK-type equation. While not intending to rigorously derive a set of equations for the heat transport in case of moving observer, accounting for the relativistic heat flux, the energy balance, etc., we will solve the extended form of the known GK-type equation with the simple substantial derivative. Derivation of a physically comprehensive one-dimensional analogue of GK-equation in case of moving observer remains beyond the scope of the present study. The following modified form of GK-type equation arises upon the use of the substantial time derivative:
This simply presumes that the temperature as a function of time is recorded by a floating instrument in a flow, such as a weather balloon in meteorology and oceanography, which implies the substantial derivative along the pathline traveled. With this said, we notice that the above Equation (7) differs from GK-type Equation (4) by some additional terms: the second mixed time-space derivative in the left hand side (l.h.s.) and the third- and first-order space-derivatives in the r.h.s. We need to emphasize that this equation is related to a rigid domain meanwhile the observer is moving with speed
. Moreover, the coefficient for the second-order space-derivative in the r.h.s. now contains the speed
, which can compensate
α, eliminating the second-order space-derivative, if
, or invert the sign of this term, if
. Telegrapher’s equation accordingly modifies as follows:
Differently from GK-type equation with substantial derivative (7), TE (8) has only second-order differential operators; both GK-type and TE can be solved by the operational method, employing exponential differential operators
and involving the heat operator
[
59]. The operational solution to the third-order PDE (7) apparently involves exponential differential operator of the third order
. However, in what follows we will demonstrate as this solution effectively reduces to the shift of the solution in a stationary media. Considering thin films, we have obvious relations between the coefficients in (7) and (5):
,
,
,
, while for Equation (6) we see that
,
. For heat transport in moving thin film, the system of DE (5) and (6) for the complete quasi-temperature
takes the following form:
In what follows we will approach the GK-type equation with substantial derivative (7) operationally, and will also provide exact analytical harmonic solution to the system of PDE (9) and (10), describing ballistic heat transfer with substantial derivative.
3. Operational Approach to Transport Equations
The above Equations (7) and (8) are the particular cases of the following DE with the coordinate-dependent operators
and
:
which can be solved using the operational method. Equation (11) models a broad spectrum of physical phenomena. It becomes telegrapher’s equation for
and constant
ε term and further reduces to Cattaneo heat equation for
; GK-type equation appears when
. Some of these equations were studied in [
45,
46,
47,
48,
49,
50]. Other second-order PDE and fractional DE were explored with the help of the operational approach in [
51,
52,
53,
54,
55,
56,
57,
58]. The formal converging particular operational solution to (11) reads as follows:
where
can be obtained from the initial condition
. The particular form of the initial function will be chosen below. The other branch of the solution contains the positive argument in the exponential,
. No Laplace transforms exist for it. However, symmetry with respect to inversion,
, allows writing the other solution to Equation (7), based on the one we obtain with the help of the Laplace transforms
The solution has the following integral form, provided it converges:
The ability to perform analytical integration in (14) depends on the explicit form of the operators
,
and of the initial function
; the numerical calculation can be done though. Accounting for the explicit form of the operators
and
in Equation (7), we obtain from (14) the following integral:
which benefits from the use of the operational identity for
,
(see [
59,
77]):
and yields
Applying formula (17) to the fourth-order exponential differential operator
, we get the heat operator [
59]
; collecting the second-order derivative terms in the exponential, we get
. This yields the following particular bounded solution to GK-type heat equation with substantial derivative (7):
which involves the shift operator
, where
, and the heat operator
, where
. The shift operator produces the translation along
x and the heat operator produces Gauss transforms (17) and operational relations [
59], so that the solution with account for the motion contains the translation
of the stationary solution.
Let us consider the initial polynomial function
. The particular solution (18) to GK-type equation with substantial derivative (7) arises upon the application of the operational rule
which is easy to prove [
57,
58]. For
we immediately obtain the following integral:
where
The above integral can be taken in elementary functions if we account for the explicit form of the Hermite polynomials:
For example, for
the solution reads as follows:
More general case of the exponential-polynomial function
is cumbersome and we omit proper expressions for conciseness. However, we have performed the integration explicitly in Wolfram Mathematica program and below we give the example of the solution for
:
Evidently, all the values in the above expressions are dimensionless as well as the coordinate x and the time t.
In the harmonic ansatz the evolution of the initial function
can be easily obtained from (18) as follows:
Other solutions and their detailed study will be performed in forthcoming publications. All the above solutions to equations with substantial derivative contain the shift, , respectively to the solution in a stationary media, which depends on x. Further examples can be easily considered with the help of the operational approach. In the following chapter we will explore in details the particular case of the harmonic solution. Evidently, it can be easily generalized for any periodic solution, expandable in Fourier series. Similarly, the Fourier integral transforms technique apply.
4. Exact Periodic Solutions to GK-Type Equation with Substantial Derivative
An exact harmonic solution
for the inhomogeneous system of PDE (9) and (10) can be obtained straight from the operational solution (18) (see (25)), or by separating the variables:
. GK-type equation with substantial derivative (7) in the harmonic ansatz,
reduces to the following ordinary differential equation for
:
where
,
, and
. The function
is introduced here for clarity of notations. The exact solution to GK equation with substantial derivative (7) then easily follows from the solution to (26):
where the constants
are determined either from the initial or boundary conditions. According to the theory of separation of variables, the whole solution has to satisfy initial or boundary conditions. Evidently, telegrapher’s equation with substantial derivative in the harmonic ansatz similarly reads
and differs from (26) by the substitutions
,
,
. It’s solution
is evidently (27), where
δ = 0.
Consider, for example, the Cauchy initial conditions
In the stationary case,
v = 0, the Cauchy conditions (37), where initially
, have the meaning of zero heat flux
q if
B = 0 for both ballistic and diffusive components of quasi-temperature [
30]. If
v ≠ 0, then the dimensionless equation
describes the one-dimensional energy balance. The initially zero heat flux
q then corresponds to
.
Then, GK-type Equation (7) with substantial derivative in the harmonic ansatz has the solution (27), satisfying ODE (26), where the coefficients
are determined from the Cauchy conditions (29):
and
, and read as follows:
TE with substantial derivative (8) has the harmonic solution, whose time-dependent part
satisfies ODE (28):
where the coefficients
are obtained from the Cauchy initial conditions (29):
Now, let us consider the Dirichlet boundary conditions in the moments of time
and
:
The harmonic solutions (27) and (31) satisfy respectively GK Equation (7) and telegrapher’s Equation (8) with substantial derivative with the coefficients, determined by Equation (33):
and
Similarly, we can consider evolution of any function, expandable in Fourier series.
Note, that for some values of the coefficients α and δ the quantities U and u can assume negative values. Albeit it is not very obvious in the form of the harmonic solution (27) to GK-type equation with substantial derivative (26) and the solution (31) to TE with substantial derivative (28), these solutions remains real at any moment of time for a real initial function, because of the complex exponential is compensated by proper complex parts in the coefficients and .
5. Exact Periodic Solutions to Ballistic Heat Transport in Thin Films
Ballistic heat transport in thin films is described by the system of PDE (9) and (10). In order to obtain the exact solution to this problem we reduced GK-type Equation (9) in the harmonic ansatz to (26) and solved it (see (27)); the result naturally involves the particular solution (25). This solution now constitutes the r.h.s. of Equation (10) for
. Consider the Cauchy initial problem for
:
and the Cauchy conditions for
:
The quasi-temperature component
is in fact given by Equation (27):
where
,
,
,
,
,
,
,
is the speed of the media; for the Cauchy initial conditions (36) (see (29) with
) the coefficients
are given by Equation (30). The solution (38) for
contributes to the r.h.s. of the telegrapher’s Equation (6) for the component
. The exponential differential operators
do not bring new harmonics to the initial content,
, and Equation (6) reduces to the following inhomogeneous ODE for
:
where
where
are given by Equation (30). The above Equation (39) for
possesses analytical solution, which, in turn, yields the evolving in time harmonic solution for the diffusive quasi-temperature component
in the following form:
where the constants
are determined from the Cauchy initial conditions (37) for
:
The exact analytical harmonic solutions for the
is given by (38) and (30), and for
, it is given by (41)–(44); their sum represents the complete solution for the ballistic heat transfer in thin films [
30] with the Cauchy initial conditions (36), (37), valid for arbitrary values of the Knudsen numbers
. Note, that a real initial distribution of quasi-temperature
evolves in real domain even for imaginary exponentials in the solutions due to complex coefficients
and
.
Now let us consider the Dirichlet conditions at the boundaries
where
(see also Equation (33)). The evolution of
is given by Equation (38), where
are set by Equation (34). The evolution of the counterpart
is governed by Equations (39) and (40). The r.h.s. of Equation (39) is set by Equation (38) for the ballistic component
, where
are given by (34). The explicit solution
to inhomogeneous DE (39) is possible, although it is much more cumbersome than in the Cauchy case:
where
The solution for in the form (46), (47) explicitly involves the Dirichlet conditions and together with the solution for , given in the Dirichlet case by (38) and (34), they describe the evolution of the complete harmonic quasi-temperature .
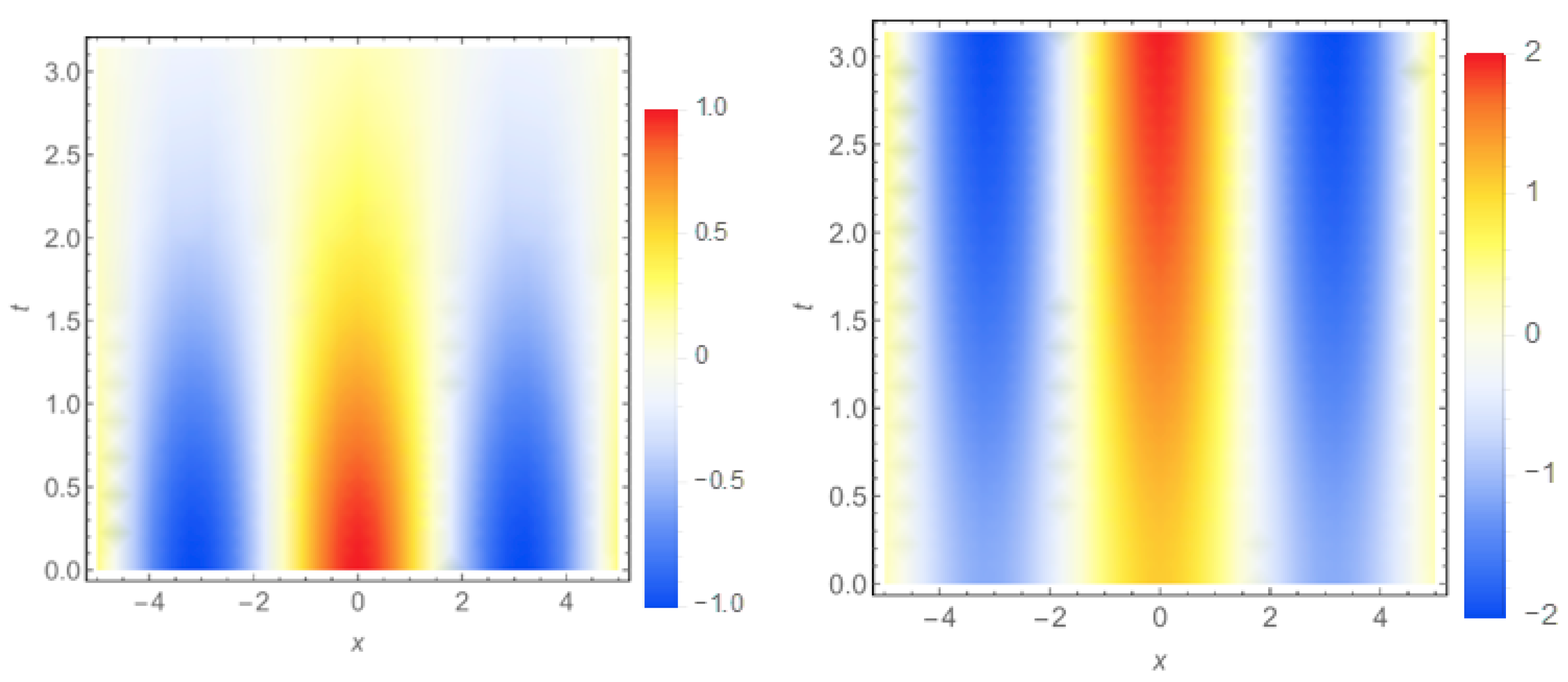
Let us now consider some examples of the harmonic solutions to GK-type heat equation with substantial derivative. Consider, for example, the Cauchy problem with initial conditions
,
. Let’s first consider
. Proper solutions for
,
and
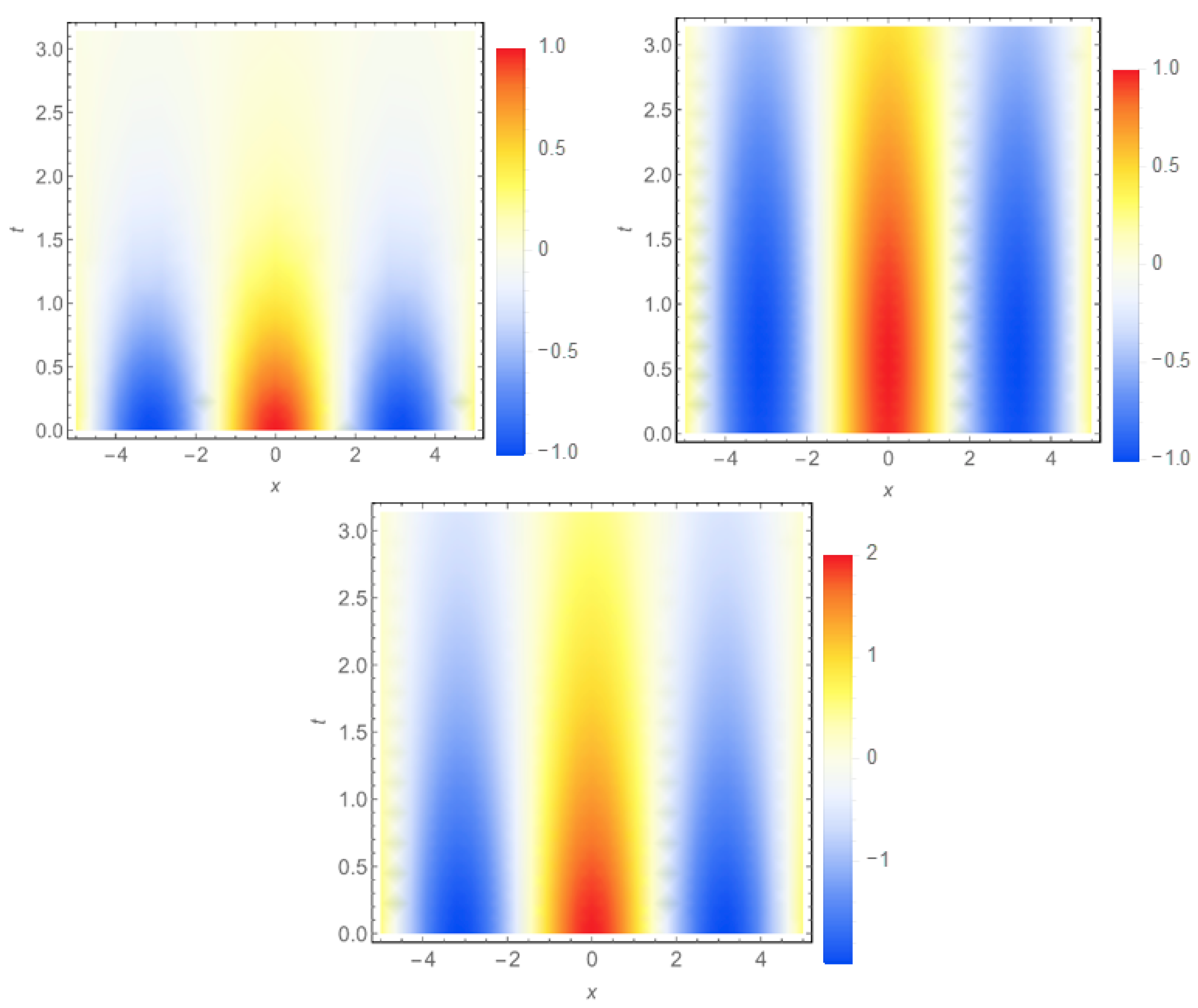
in the stationary media are presented in
Figure 1.
It can be seen in the top left plot in
Figure 1 as the ballistic component
rapidly relaxes to the stationary state. The diffusive component
behaves similarly, but the relaxation process takes much more time. The behavior of ballistic and diffusive components in the domain is more distinct for
. The complete quasi-temperature
(see bottom plot in
Figure 1) follows the behavior of both the ballistic
and diffusive
constituents. However, the latter, being the solution of Equation (39), is strongly influenced by the solution (38) for the ballistic component
, which sets the inhomogeneous part in Equation (39). Thus, the evolution of the quasi-temperature
in thin films has two speeds: the ballistic constituent
develops rapidly and sets the r.h.s. in Equation (39) for the diffusive constituent
. The evolution of
is much slower: after the first instances it proceeds under the influence of already relaxed true ballistic constituent
.
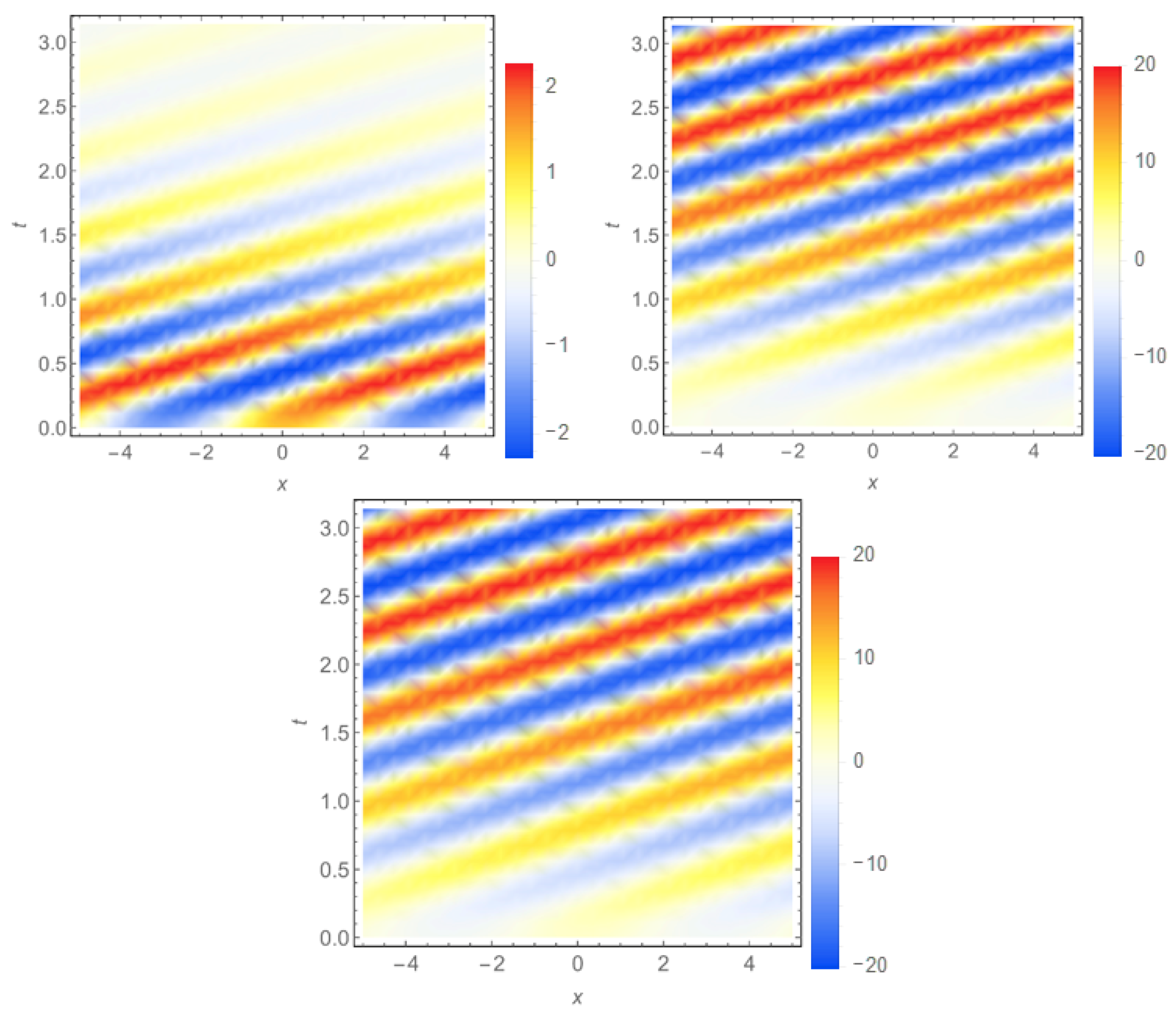
In the case when the rate of change of temperature for a given position in a field depends both on the instantaneous rate of change of temperature at that location (∂/∂
t) as well as on the rate at which the temperature is convected to that location by the fluid motion, the behaviors of the solutions change significantly. The solutions for
Knd =
Knb = 1 and
v = 10, are presented in
Figure 2, for
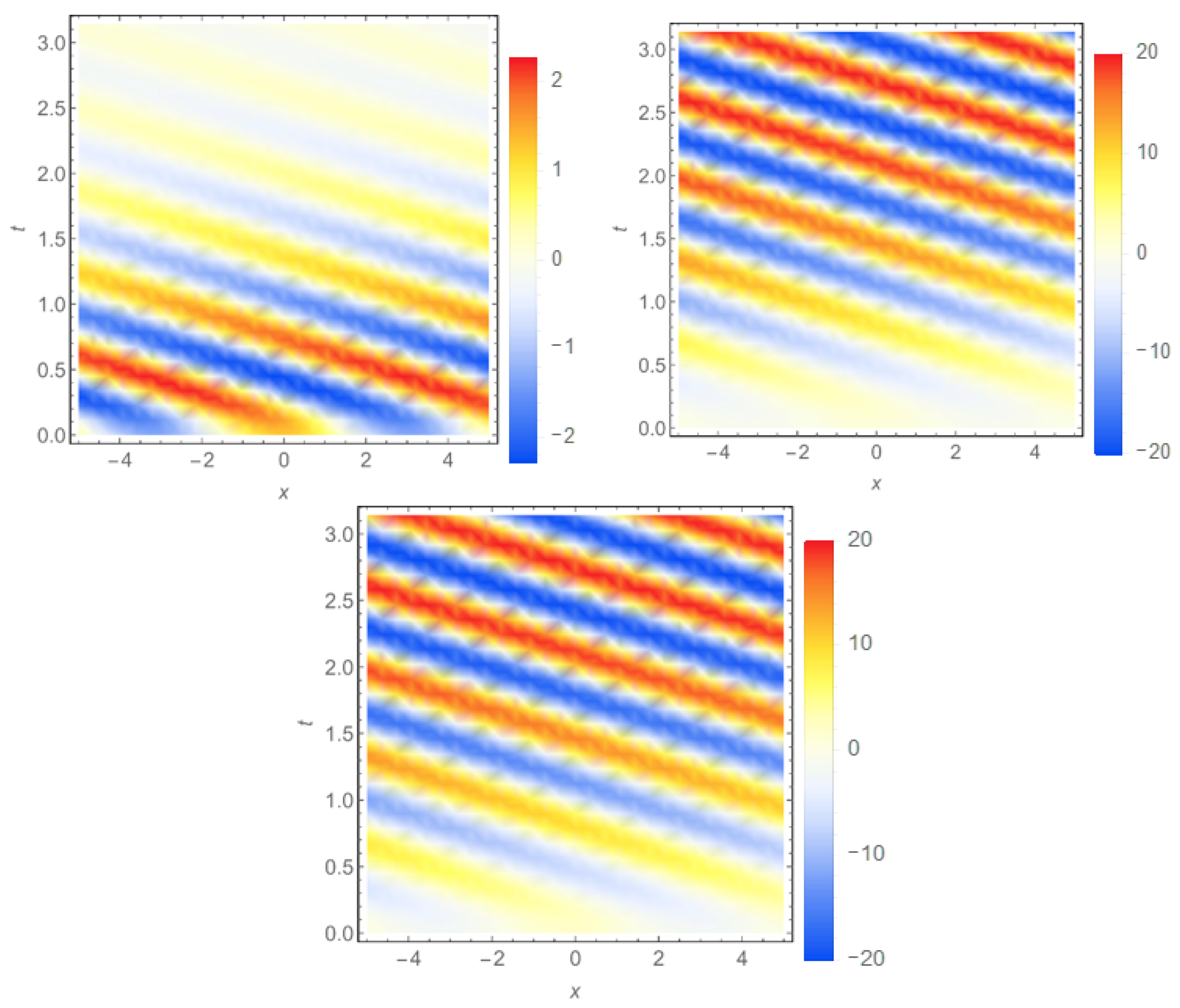
v = −10 in
Figure 3.
The ballistic constituent
rapidly vanishes with time; the direction of the colorful waves in the plot depends on the sign of the speed
v (see top left plots in
Figure 2 and
Figure 3). Diffusive counterpart of the complete quasi-temperature
has waves of increasing amplitude as seen in top right plots in
Figure 2 and
Figure 3. The complete quasi-temperature
has obvious non-Fourier behavior, which largely follows that of
.
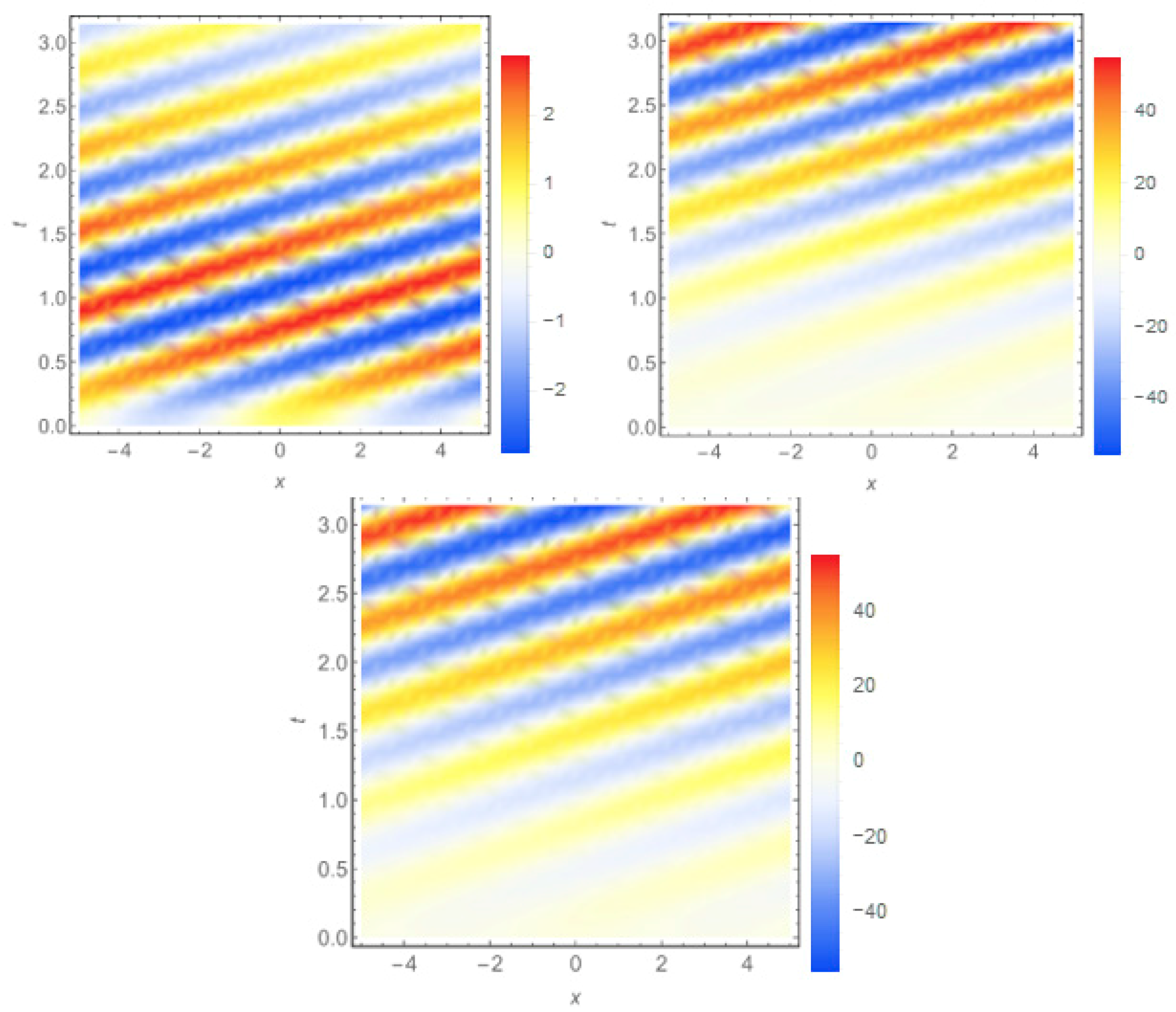
For smaller values of Knudsen number,
, the behavior of the harmonic solutions to ballistic heat propagation in thin films, obeying the Eqs. system (9) and (10) with Cauchy conditions (36) (37), has less distinctive wave interference with slower fade of the solution for
and weaker amplitude increase speed for
; proper solutions for
v = +10 are presented in
Figure 4.
It is important to note, that the whole system is symmetric under the speed inversion, which becomes obvious with account for formulae (38)–(44).
Note, that for
Knb =
Knd = 0.1
and
constituents behave differently (see
Figure 4). The diffusive constituent slowly grows as the ballistic constituent shows gradual amplitude decrease, as shown in
Figure 5. Moreover, for
v = 10 the complete quasi-temperature
monotonously increases, following the behavior of the diffusive constituent as shown in
Figure 5. The maximum principle, established though for parabolic equations, is violated for the diffusive component and complete quasi-temperature with Cauchy conditions for non-Fourier ballistic heat transport in thin films. In all of the cases, the evolution of
occurs faster than that of
; the two-speed heat propagation process can be seen in every set of plots in
Figure 1,
Figure 2,
Figure 3,
Figure 4 and
Figure 5.
The exploration of the solutions for Dirichlet conditions will be done elsewhere.
It should be noted that the one-dimensional energy balance equation yields zero value for the initial heat flux, if . Above we have obtained the solutions, which allow nonzero initial conditions on the first time derivative; we have investigated some examples while writing this paper. For example, for the case of , v = 10 the maximum principle is violated for both zero and nonzero initial conditions imposed on the first time-derivative of the ballistic component; however, there was no significant qualitative difference in the behaviors of the diffusive component in this case.
Explicit study for the solution in thin films with zero initial heat flux and non-zero velocity will be done in forthcoming publications.
6. Conclusions
In the present work we have studied and analytically solved one-dimensional heat transport equations of Cattaneo- and Guyer–Krumhansl-type with substantial derivative. Exponential differential operators and the operational method were used to obtain integral forms of exact particular solutions to heat transport equations. The media speed is accounted for by the exponential differential operator , which produces a shift . Together with the heat operator they transform the initial temperature profile and determine its evolution. Their action on the initial polynomial yields sums of the Hermite polynomials ; the action on the monomial-exponential function yields more complicated sums of Hermite polynomials. Proper exact operational solutions were obtained in the sums of converging integrals of elementary functions. Several examples were considered, the solutions for , and were given. The solutions exactly satisfy the heat transport equations, which has been proven by direct substitution.
The equations with substantial derivative of Guyer-Krumhansl-type and of telegrapher’s-type are demonstrated to have similar structure in the harmonic ansatz. Their exact harmonic solutions have been obtained by both operational method and the separation of variables. The latter reduces these PDEs to ODEs. We have shown that the harmonic solutions may have local and global extremums in the domain due to the interference of the Cattaneo heat waves; proper second-order time-derivative term also insures finite speed of the temperature perturbation propagation. We have shown that in a GK-type equation with dominant ballistic term δ, the Cattaneo heat waves are damped.
We have obtained the exact analytical solution to the ballistic heat transport in thin films by solving the system of inhomogeneous PDEs [
30] in the harmonic ansatz; both Cauchy and Dirichlet conditions were explored. We found that true ballistic constituent of quasi-temperature,
, evolves much faster than the diffusive counterpart of quasi-temperature,
. We have studied the evolution of the complete quasi-temperature
under the ballistic conditions; the latter apply when the phonon mean free path
l is comparable with the system scale
L. The quasi-temperature
first senses fast evolving true ballistic part
. The contribution of
sets the r.h.s. in the inhomogeneous DE for the component
. After relatively fast relaxation of
, further evolution of the complete quasi-temperature
follows the diffusive constituent
. Thus the initial fast-developing true ballistic component
determines the evolution of the complete quasi-temperature of the system
by imposing distribution for the diffusive quasi-temperature
at the beginning of the process.
The obtained harmonic solutions for the Cauchy problem (9), (10), (36), (37) were applied for the study of the temperature patterns in thin films for the Knudsen number values
Kn = 0.1 and
Kn = 1. In the stationary case
v = 0, the true ballistic component
monotonously relaxes (see
Figure 1 and
Figure 5); its diffusive counterpart
behavior shows noticeable dependence on the value of the Knudsen numbers: for
Kn = 1 it slowly relaxes (see
Figure 5) and for
Kn = 0.1 it droningly grows (see
Figure 1). The effect of the speed of the observer on the perceived heat transport in thin films is distinguished for the pure ballistic and diffusive quasi-temperature constituents. In the presence of the motion, the extremum of the ballistic component
occurs inside the domain after the initial moment
t = 0 (see
Figure 2,
Figure 3 and
Figure 4). The diffusive quasi-temperature component monotonously grows in the domain both in the weak ballistic (see
Figure 4) and strong ballistic cases (see
Figure 2 and
Figure 3). This behavior contrasts common Fourier heat diffusion, for which the maximum principle holds. It is also noticeable that the system shows symmetric behavior while the value of the speed is reversed, which does not contradict the Second law. The Knudsen number variation from 0.1 to 1 in the presence of the speed
v = 10, are practically not sensed by the system. Thus the speed of the observer
v influences the registered temperature rather than the ballistic heat transport contribution.