Mathematical Modeling of Rogue Waves: A Survey of Recent and Emerging Mathematical Methods and Solutions
Abstract
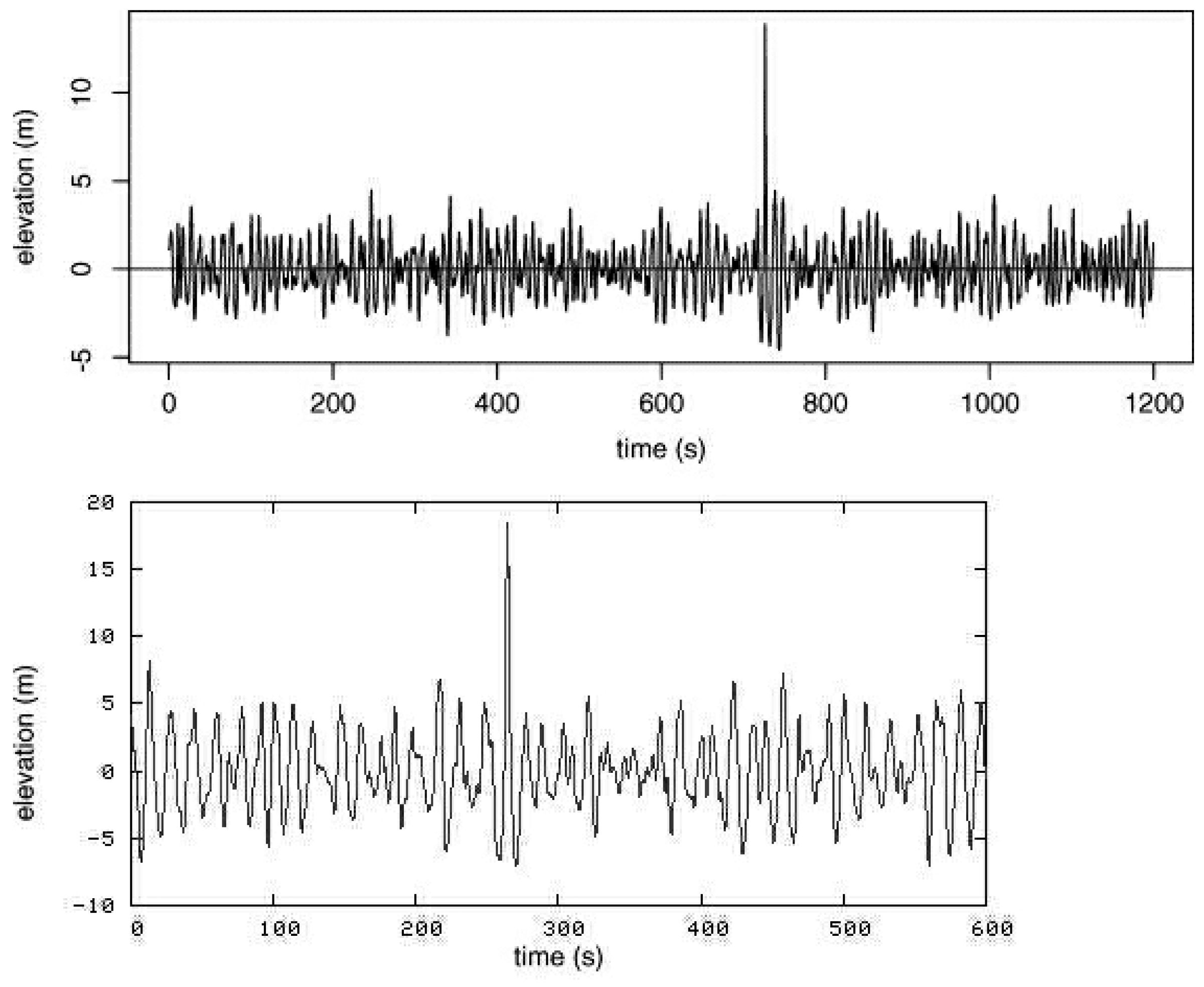
1. Introduction
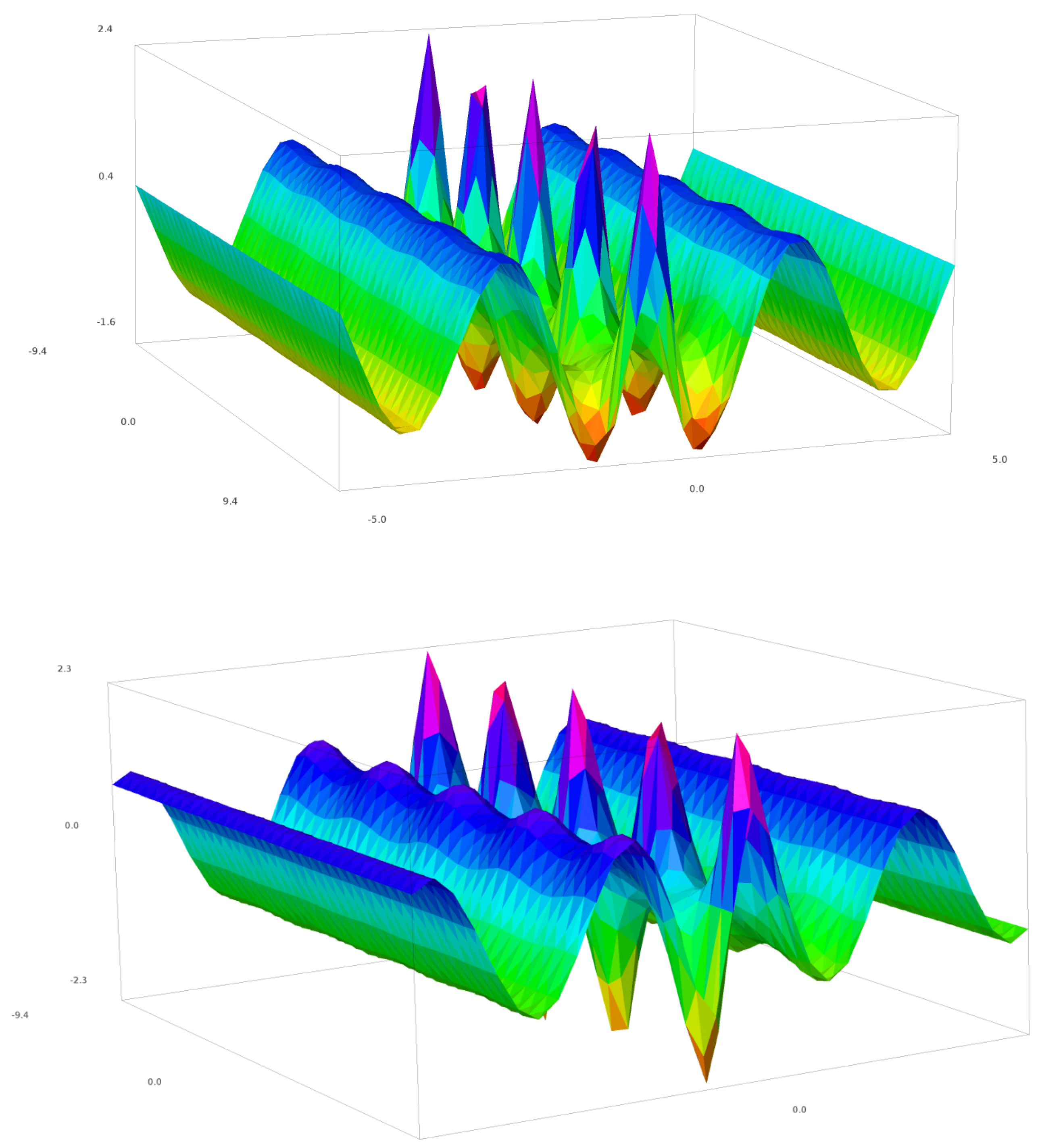
2. The Non-Linear Schrödinger Equation in the Prediction of Rogue Waves
The Solutions to the NLSE
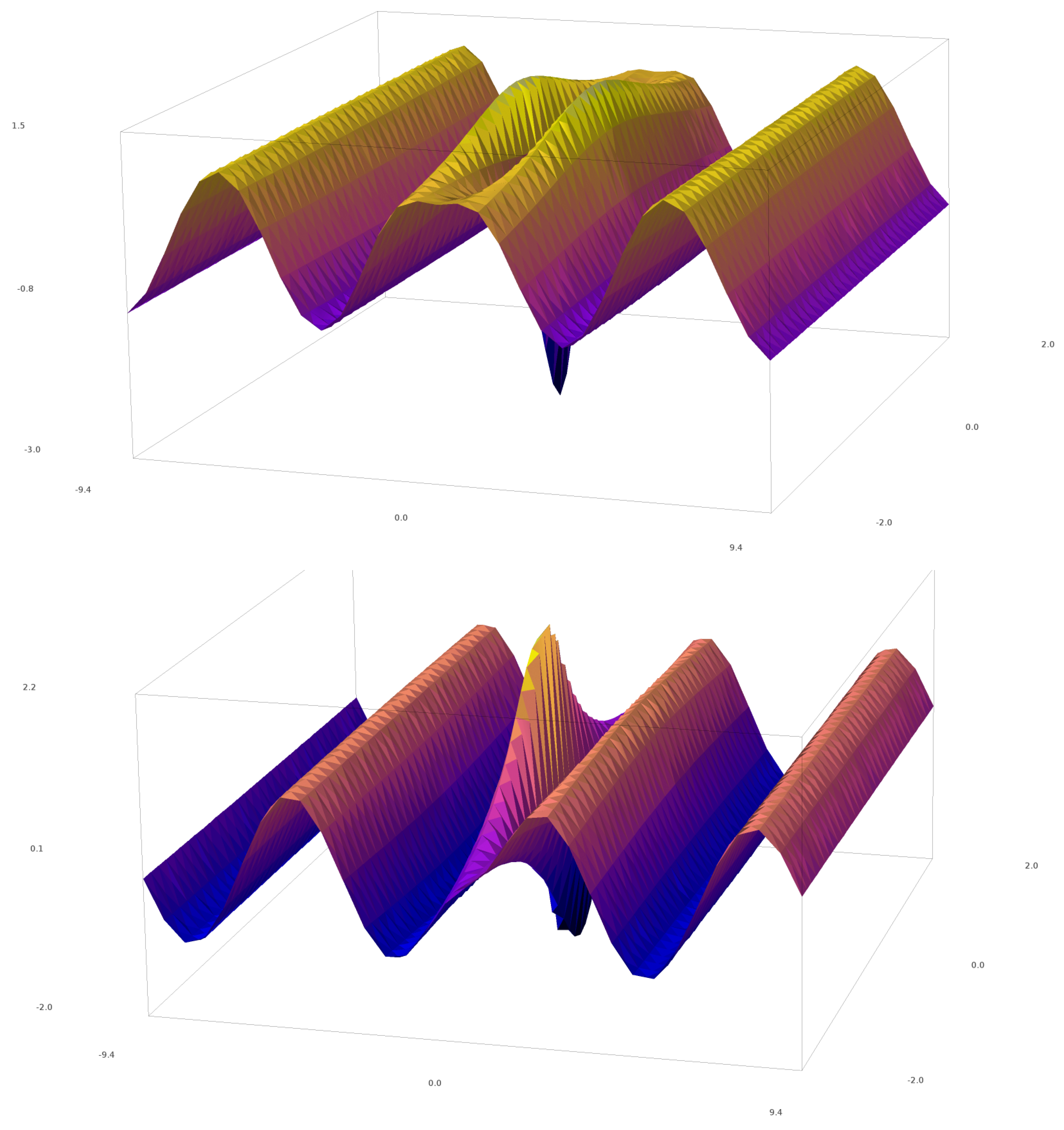
3. The Korteweg–de Vries Equation
4. The Extended Dysthe Equation
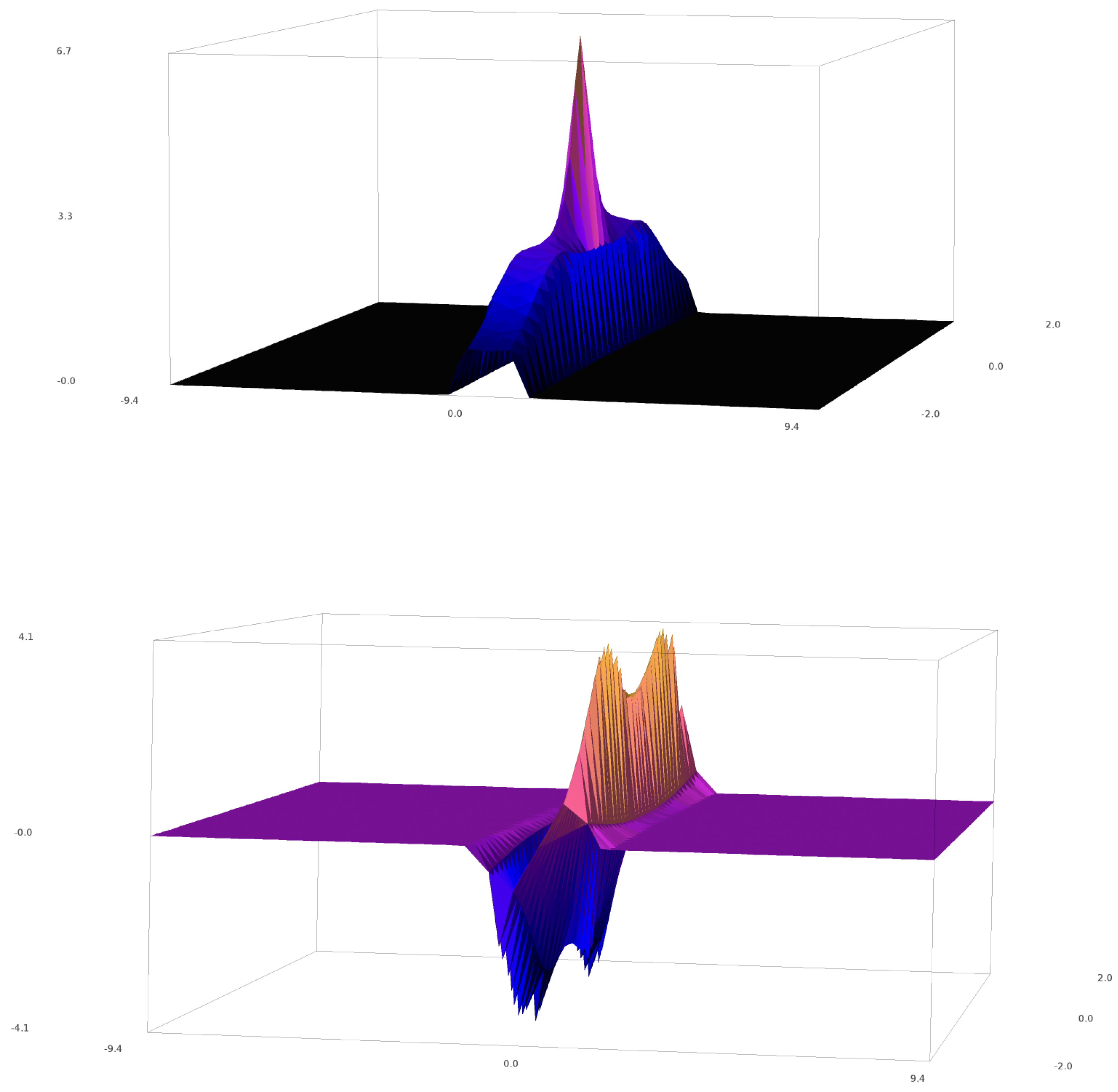
5. The MMT Model
6. The Hirota Equation
7. The Ablowitz–Musslimani Models: Non-Local Rogue Waves
8. Conclusions
Funding
Conflicts of Interest
Abbreviations
| MMT | Majda–McLaughlin–Tabak |
| AKNS | Ablowitz–Kaup–Newell–Segur |
References
- Lehner, S.; Schulz-Stellenfleth, J.; Niedermeier, A.; Horstmann, J.; Rosenthal, W. Extreme waves detected by satellite borne synthetic aperture radar. In Proceedings of the ASME 2002 21st International Conference on Offshore Mechanics and Arctic Engineering, Oslo, Norway, 23–28 June 2002; American Society of Mechanical Engineers: New York, NY, USA, 2002; pp. 251–256. [Google Scholar]
- Rosenthal, W.; Lehner, S. Rogue waves: Results of the MaxWave project. J. Offshore Mech. Arct. Eng. 2008, 130, 021006. [Google Scholar] [CrossRef]
- Didenkulova, I.; Slunyaev, A.; Pelinovsky, E.; Kharif, C. Freak waves in 2005. Nat. Hazards Earth Syst. Sci. 2006, 6, 1007–1015. [Google Scholar] [CrossRef]
- Haver, S. A possible freak wave event measured at the Draupner Jacket January 1 1995. In Proceedings of the 2004 Rogue Waves, Brest, France, 20–22 October 2004; pp. 1–8. [Google Scholar]
- Stansell, P. Distributions of freak wave heights measured in the North Sea. Appl. Ocean Res. 2004, 26, 35–48. [Google Scholar] [CrossRef]
- Dysthe, K.; Krogstad, H.E.; Müller, P. Oceanic rogue waves. Annu. Rev. Fluid Mech. 2008, 40, 287–310. [Google Scholar] [CrossRef]
- Weisse, R. Marine Climate and Climate Change: Storms, Wind Waves and Storm Surges; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Solli, D.; Ropers, C.; Koonath, P.; Jalali, B. Optical rogue waves. Nature 2007, 450, 1054. [Google Scholar] [CrossRef] [PubMed]
- Stenflo, L.; Marklund, M. Rogue waves in the atmosphere. J. Plasma Phys. 2010, 76, 293–295. [Google Scholar] [CrossRef]
- Moslem, W.; Shukla, P.; Eliasson, B. Surface plasma rogue waves. Europhys. Lett. 2011, 96, 25002. [Google Scholar] [CrossRef]
- Tlidi, M.; Gandica, Y.; Sonnino, G.; Averlant, E.; Panajotov, K. Self-Replicating spots in the brusselator model and extreme events in the one-dimensional case with delay. Entropy 2016, 18, 64. [Google Scholar] [CrossRef]
- Kibler, B.; Fatome, J.; Finot, C.; Millot, G.; Dias, F.; Genty, G.; Akhmediev, N.; Dudley, J.M. The Peregrine soliton in nonlinear fibre optics. Nat. Phys. 2010, 6, 790–795. [Google Scholar] [CrossRef]
- Levi-Civita, T. Determination rigoureuse des ondes permanentes d’ampleur finie. Math. Ann. 1925, 93, 264–314. [Google Scholar] [CrossRef]
- Nekrasov, A. On waves of permanent type. Izv. Ivanovo-Voznesensk. Politekhn. Inst. 1921, 3, 52–65. [Google Scholar]
- Smith, R. Giant waves. J. Fluid Mech. 1976, 77, 417–431. [Google Scholar] [CrossRef]
- Zakharov, V.E. Collapse of Langmuir waves. Sov. Phys. JETP 1972, 35, 908–914. [Google Scholar]
- Dai, C.Q.; Wang, Y.Y.; Tian, Q.; Zhang, J.F. The management and containment of self-similar rogue waves in the inhomogeneous nonlinear Schrödinger equation. Ann. Phys. 2012, 327, 512–521. [Google Scholar] [CrossRef]
- Akhmediev, N.; Soto-Crespo, J.M.; Ankiewicz, A. Extreme waves that appear from nowhere: on the nature of rogue waves. Phys. Lett. A 2009, 373, 2137–2145. [Google Scholar] [CrossRef]
- Akhmediev, N.; Ankiewicz, A.; Soto-Crespo, J. Rogue waves and rational solutions of the nonlinear Schrödinger equation. Phys. Rev. E 2009, 80, 026601. [Google Scholar] [CrossRef] [PubMed]
- Akhmediev, N.; Ankiewicz, A.; Soto-Crespo, J.; Dudley, J.M. Rogue wave early warning through spectral measurements? Phys. Lett. A 2011, 375, 541–544. [Google Scholar] [CrossRef]
- Chabchoub, A.; Hoffmann, N.; Branger, H.; Kharif, C.; Akhmediev, N. Experiments on wind-perturbed rogue wave hydrodynamics using the Peregrine breather model. Phys. Fluids 2013, 25, 101704. [Google Scholar] [CrossRef]
- Cousins, W.; Sapsis, T.P. Quantification and prediction of extreme events in a one-dimensional nonlinear dispersive wave model. Phys. D Nonlinear Phenom. 2014, 280, 48–58. [Google Scholar] [CrossRef]
- Cousins, W.; Sapsis, T.P. Unsteady evolution of localized unidirectional deep-water wave groups. Phys. Rev. E 2015, 91, 063204. [Google Scholar] [CrossRef] [PubMed]
- Cousins, W.; Sapsis, T.P. Reduced-order precursors of rare events in unidirectional nonlinear water waves. J. Fluid Mech. 2016, 790, 368–388. [Google Scholar] [CrossRef]
- Tlidi, M.; Panajotov, K. Two-dimensional dissipative rogue waves due to time-delayed feedback in cavity nonlinear optics. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 013119. [Google Scholar] [CrossRef] [PubMed]
- Lugiato, L.A.; Lefever, R. Spatial dissipative structures in passive optical systems. Phys. Rev. Lett. 1987, 58, 2209. [Google Scholar] [CrossRef] [PubMed]
- Panajotov, K.; Clerc, M.G.; Tlidi, M. Spatiotemporal chaos and two-dimensional dissipative rogue waves in Lugiato-Lefever model. Eur. Phys. J. D 2017, 71, 176. [Google Scholar] [CrossRef]
- Akhmediev, N.; Kibler, B.; Baronio, F.; Belić, M.; Zhong, W.P.; Zhang, Y.; Chang, W.; Soto-Crespo, J.M.; Vouzas, P.; Grelu, P.; et al. Roadmap on optical rogue waves and extreme events. J. Opt. 2016, 18, 063001. [Google Scholar] [CrossRef]
- Dai, C.; Wang, Y.; Yan, C. Chirped and chirp-free self-similar cnoidal and solitary wave solutions of the cubic-quintic nonlinear Schrödinger equation with distributed coefficients. Opt. Commun. 2010, 283, 1489–1494. [Google Scholar] [CrossRef]
- Haghgoo, S.; Ponomarenko, S.A. Self-similar pulses in coherent linear amplifiers. Optics Express 2011, 19, 9750–9758. [Google Scholar] [CrossRef] [PubMed]
- Kruglov, V.; Peacock, A.; Harvey, J. Exact self-similar solutions of the generalized nonlinear Schrödinger equation with distributed coefficients. Phys. Rev. Lett. 2003, 90, 113902. [Google Scholar] [CrossRef] [PubMed]
- Kruglov, V.; Peacock, A.; Harvey, J. Exact solutions of the generalized nonlinear Schrödinger equation with distributed coefficients. Phys. Rev. E 2005, 71, 056619. [Google Scholar] [CrossRef] [PubMed]
- Fermann, M.; Kruglov, V.; Thomsen, B.; Dudley, J.; Harvey, J. Self-similar propagation and amplification of parabolic pulses in optical fibers. Phys. Rev. Lett. 2000, 84, 6010. [Google Scholar] [CrossRef] [PubMed]
- Hamedi, H.R. Optical bistability and multistability via magnetic field intensities in a solid. Appl. Opt. 2014, 53, 5391–5397. [Google Scholar] [CrossRef] [PubMed]
- Munk, W.; Snodgrass, F. Measurements of southern swell at Guadalupe Island. Deep Sea Res. 1957, 4, 272–286. [Google Scholar] [CrossRef]
- Kruglov, V.; Peacock, A.; Dudley, J.; Harvey, J. Self-similar propagation of high-power parabolic pulses in optical fiber amplifiers. Opt. Lett. 2000, 25, 1753–1755. [Google Scholar] [CrossRef] [PubMed]
- Osborne, A.R.; Onorato, M.; Serio, M. The nonlinear dynamics of rogue waves and holes in deep-water gravity wave trains. Phys. Lett. A 2000, 275, 386–393. [Google Scholar] [CrossRef]
- Zakharov, V.E. Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 1968, 9, 190–194. [Google Scholar] [CrossRef]
- Serkin, V.; Hasegawa, A.; Belyaeva, T. Nonautonomous solitons in external potentials. Phys. Rev. Lett. 2007, 98, 074102. [Google Scholar] [CrossRef] [PubMed]
- Dai, C.Q.; Wang, D.S.; Wang, L.L.; Zhang, J.F.; Liu, W. Quasi-two-dimensional Bose–Einstein condensates with spatially modulated cubic–quintic nonlinearities. Ann. Phys. 2011, 326, 2356–2368. [Google Scholar] [CrossRef]
- Peregrine, D. Water waves, nonlinear Schrödinger equations and their solutions. ANZIAM J. 1983, 25, 16–43. [Google Scholar] [CrossRef]
- Zakharov, V.; Shabat, A. Interaction between solitons in a stable medium. Sov. Phys. JETP 1973, 37, 823–828. [Google Scholar]
- Matveev, V.B.; Matveev, V. Darb. Trans. Solitons; Springer-Verlag: Berlin, Germany, 1991. [Google Scholar]
- Akhmediev, N.; Korneev, V. Modulation instability and periodic solutions of the nonlinear Schrödinger equation. Theor. Math. Phys. 1986, 69, 1089–1093. [Google Scholar] [CrossRef]
- Dysthe, K.B.; Trulsen, K. Note on breather type solutions of the NLS as models for freak-waves. Phys. Scr. 1999, 1999, 48. [Google Scholar] [CrossRef]
- Voronovich, V.V.; Shrira, V.I.; Thomas, G. Can bottom friction suppress ‘freak wave’formation? J. Fluid Mech. 2008, 604, 263–296. [Google Scholar] [CrossRef]
- Benjamin, T.B.; Feir, J. The disintegration of wave trains on deep water Part 1. Theory. J. Fluid Mech. 1967, 27, 417–430. [Google Scholar] [CrossRef]
- Bespalov, V.; Talanov, V. Filamentary structure of light beams in nonlinear liquids. ZhETF Pisma Redaktsiiu 1966, 3, 471. [Google Scholar]
- Kim, D.S.; Markowsky, G.; Lee, S.G. Mobile Sage-Math for linear algebra and its application. Electron. J. Math. Technol. 2010, 4, 285–298. [Google Scholar]
- SageMath Mathematics Software, Version 6.5. 2015. Available online: http://www.sagemath.org/ (accessed on 5 June 2017).
- Kharif, C.; Pelinovsky, E. Physical mechanisms of the rogue wave phenomenon. Eur. J. Mech. B Fluids 2003, 22, 603–634. [Google Scholar] [CrossRef]
- Matsuno, Y. Bilinear Transformation Method; Elsevier: New York, NY, USA, 1984. [Google Scholar]
- Hirota, R. A new form of Bäcklund transformations and its relation to the inverse scattering problem. Prog. Theor. Phys. 1974, 52, 1498–1512. [Google Scholar] [CrossRef]
- Matveev, V.B. Positons: Slowly decreasing analogues of solitons. Theor. Math. Phys. 2002, 131, 483–497. [Google Scholar] [CrossRef]
- Osborne, A. Soliton physics and the periodic inverse scattering transform. Phys. D Nonlinear Phenom. 1995, 86, 81–89. [Google Scholar] [CrossRef]
- Osborne, A. Solitons in the periodic Korteweg–de Vries equation, the FTHETA-function representation, and the analysis of nonlinear, stochastic wave trains. Phys. Rev. E 1995, 52, 1105. [Google Scholar] [CrossRef]
- Dysthe, K.B. Note on a modification to the nonlinear Schrödinger equation for application to deep water waves. Proc. R. Soc. Lond. A 1979, 369, 105–114. [Google Scholar] [CrossRef]
- Longuet-Higgins, M. The instability of gravity waves of infinite amplitude in deep water. II. Subharmonics. Proc. R. Soc. Lond. A 1978, 360, 489–506. [Google Scholar] [CrossRef]
- Trulsen, K.; Dysthe, K. Freak waves—A three-dimensional wave simulation. In Proceedings of the 21st Symposium on Naval Hydrodynamics, Trondheim, Norway, 24–28 June 1996; National Academy Press: Washington, DC, USA, 1997; Volume 550, p. 558. [Google Scholar]
- Trulsen, K.; Dysthe, K.B. A modified nonlinear Schrödinger equation for broader bandwidth gravity waves on deep water. Wave Motion 1996, 24, 281–289. [Google Scholar] [CrossRef]
- Trulsen, K.; Kliakhandler, I.; Dysthe, K.B.; Velarde, M.G. On weakly nonlinear modulation of waves on deep water. Phys. Fluids 2000, 12, 2432–2437. [Google Scholar] [CrossRef]
- Majda, A.; McLaughlin, D.; Tabak, E. A one-dimensional model for dispersive wave turbulence. J. Nonlinear Sci. 1997, 7, 9–44. [Google Scholar] [CrossRef]
- Pushkarev, A.; Zakharov, V. Quasibreathers in the MMT model. Phys. D Nonlinear Phenom. 2013, 248, 55–61. [Google Scholar] [CrossRef]
- Zakharov, V.; Dias, F.; Pushkarev, A. One-dimensional wave turbulence. Phys. Rep. 2004, 398, 1–65. [Google Scholar] [CrossRef]
- Zakharov, V.; Guyenne, P.; Pushkarev, A.; Dias, F. Wave turbulence in one-dimensional models. Phys. D Nonlinear Phenom. 2001, 152, 573–619. [Google Scholar] [CrossRef]
- Komen, G.J.; Cavaleri, L.; Donelan, M. Dynamics and Modelling of Ocean Waves; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Lavrenov, I. The wave energy concentration at the Agulhas current off South Africa. Nat. hazards 1998, 17, 117–127. [Google Scholar] [CrossRef]
- Zakharov, V.; Kuznetsov, E. Optical solitons and quasisolitons. J. Exp. Theor. Phys. 1998, 86, 1035–1046. [Google Scholar] [CrossRef]
- Tao, Y.; He, J. Multisolitons, breathers, and rogue waves for the Hirota equation generated by the Darboux transformation. Phys. Rev. E 2012, 85, 026601. [Google Scholar] [CrossRef] [PubMed]
- Ablowitz, M.J.; Kaup, D.J.; Newell, A.C.; Segur, H. Method for solving the sine-Gordon equation. Phys. Rev. Lett. 1973, 30, 1262. [Google Scholar] [CrossRef]
- Ankiewicz, A.; Soto-Crespo, J.; Akhmediev, N. Rogue waves and rational solutions of the Hirota equation. Phys. Rev. E 2010, 81, 046602. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Zhang, H.; Wang, L.; Porsezian, K.; Fokas, A. Generating mechanism for higher-order rogue waves. Phys. Rev. E 2013, 87, 052914. [Google Scholar] [CrossRef] [PubMed]
- Ablowitz, M.J.; Musslimani, Z.H. Integrable nonlocal nonlinear Schrödinger equation. Phys. Rev. Lett. 2013, 110, 064105. [Google Scholar] [CrossRef] [PubMed]
- Ablowitz, M.J.; Musslimani, Z.H. Inverse scattering transform for the integrable nonlocal nonlinear Schrödinger equation. Nonlinearity 2016, 29, 915. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Musslimani, Z.H. Integrable nonlocal nonlinear equations. Stud. Appl. Math. 2017, 139, 7–59. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Musslimani, Z.H. Integrable discrete P T symmetric model. Phys. Rev. E 2014, 90, 032912. [Google Scholar] [CrossRef] [PubMed]
- Musslimani, Z.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N. Optical Solitons in P T Periodic Potentials. Phys. Rev. Lett. 2008, 100, 030402. [Google Scholar] [CrossRef] [PubMed]
- Ablowitz, M.J.; Chakravarty, S.; Takhtajan, L.A. A self-dual Yang-Mills hierarchy and its reductions to integrable systems in 1+1 and 2+1 dimensions. Commun. Math. Phys. 1993, 158, 289–314. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Luo, X.D.; Musslimani, Z.H. Inverse scattering transform for the nonlocal nonlinear Schrödinger equation with nonzero boundary conditions. J. Math. Phys. 2018, 59, 011501. [Google Scholar] [CrossRef]
- Yang, B.; Yang, J. General rogue waves in the nonlocal PT-symmetric nonlinear Schrodinger equation. arXiv, 2017; arXiv:1711.05930. [Google Scholar]
- Yu, F. Dynamics of nonautonomous discrete rogue wave solutions for an Ablowitz–Musslimani equation with PT-symmetric potential. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 023108. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manzetti, S. Mathematical Modeling of Rogue Waves: A Survey of Recent and Emerging Mathematical Methods and Solutions. Axioms 2018, 7, 42. https://doi.org/10.3390/axioms7020042
Manzetti S. Mathematical Modeling of Rogue Waves: A Survey of Recent and Emerging Mathematical Methods and Solutions. Axioms. 2018; 7(2):42. https://doi.org/10.3390/axioms7020042
Chicago/Turabian StyleManzetti, Sergio. 2018. "Mathematical Modeling of Rogue Waves: A Survey of Recent and Emerging Mathematical Methods and Solutions" Axioms 7, no. 2: 42. https://doi.org/10.3390/axioms7020042
APA StyleManzetti, S. (2018). Mathematical Modeling of Rogue Waves: A Survey of Recent and Emerging Mathematical Methods and Solutions. Axioms, 7(2), 42. https://doi.org/10.3390/axioms7020042