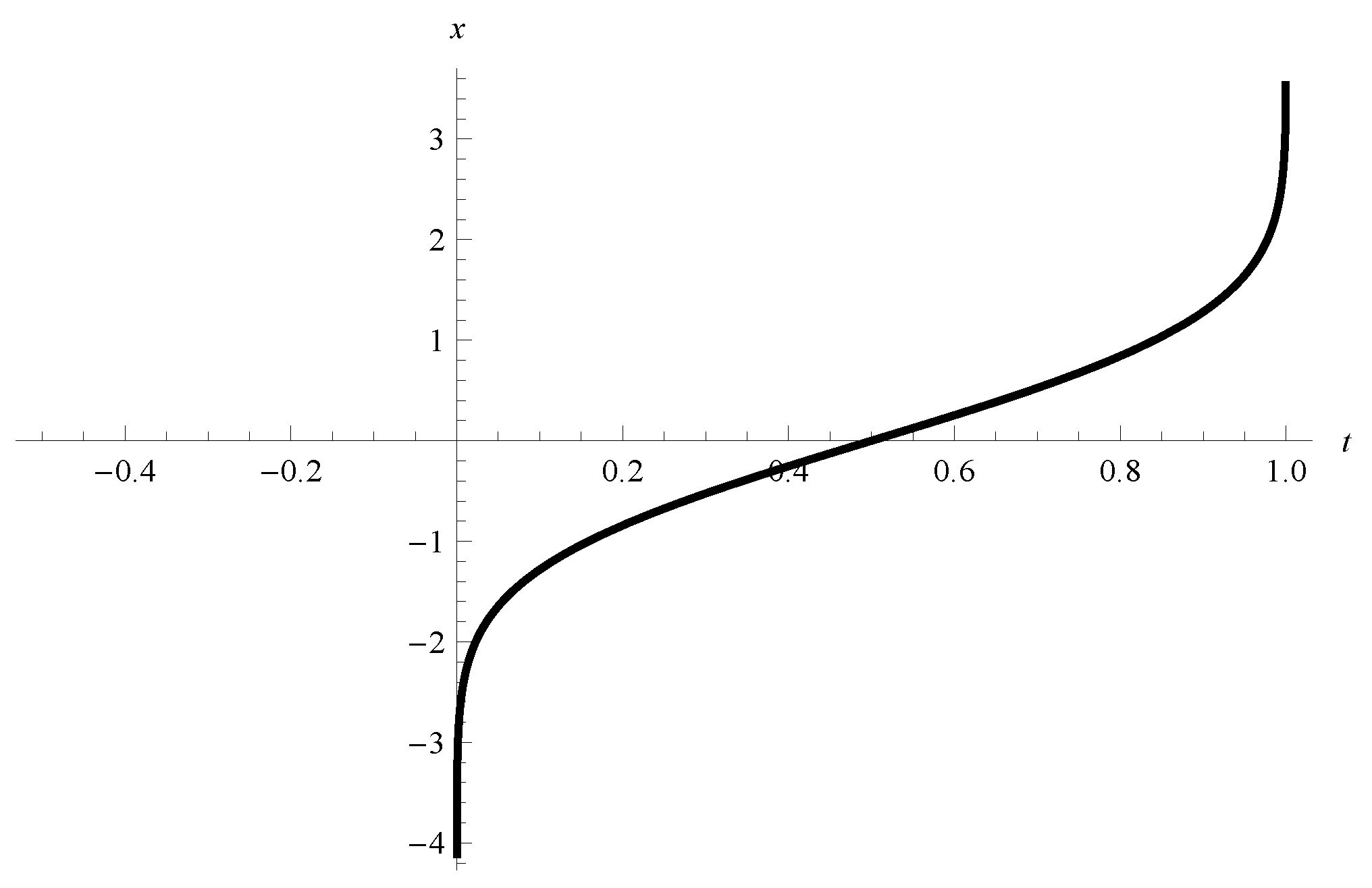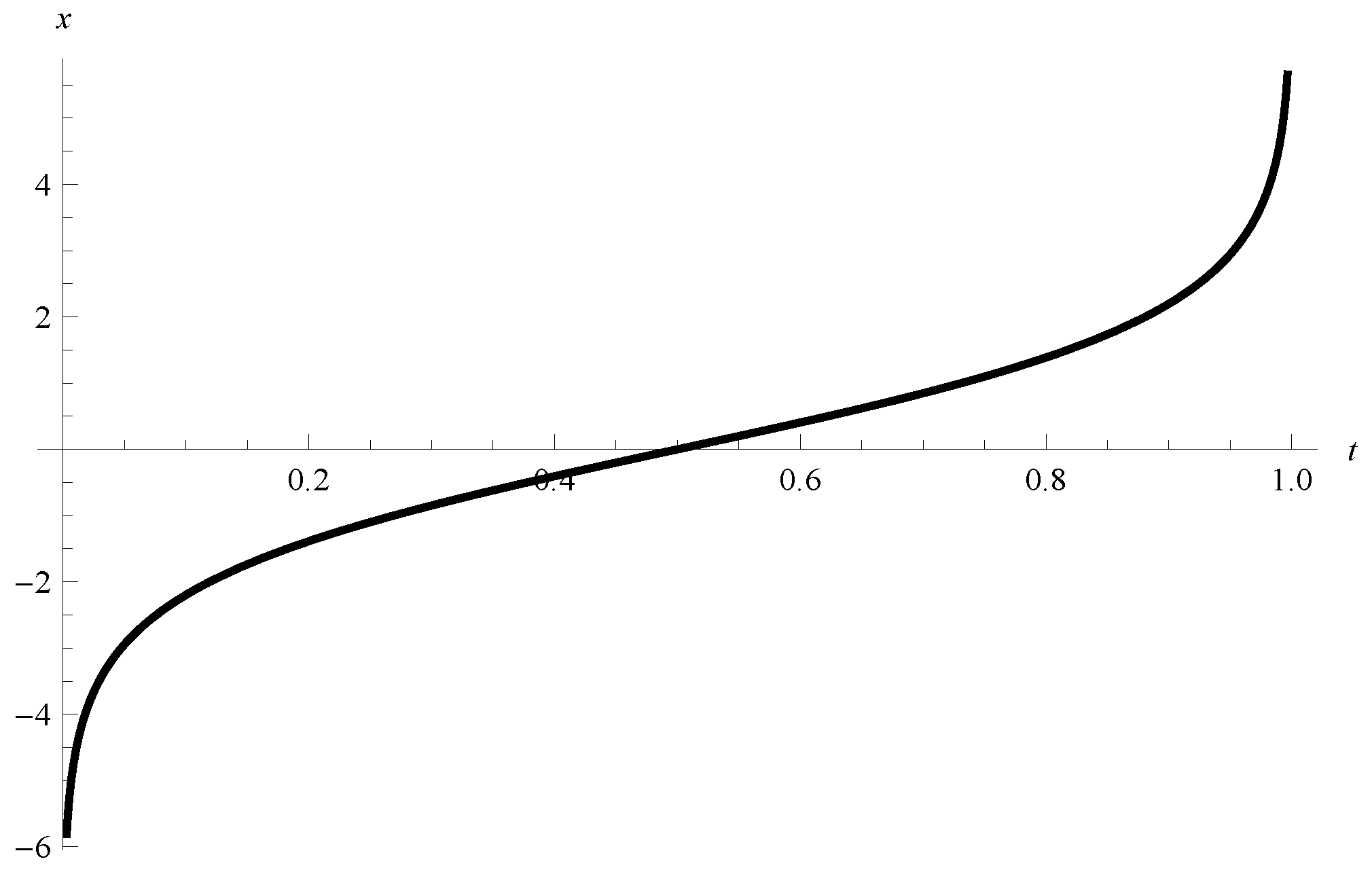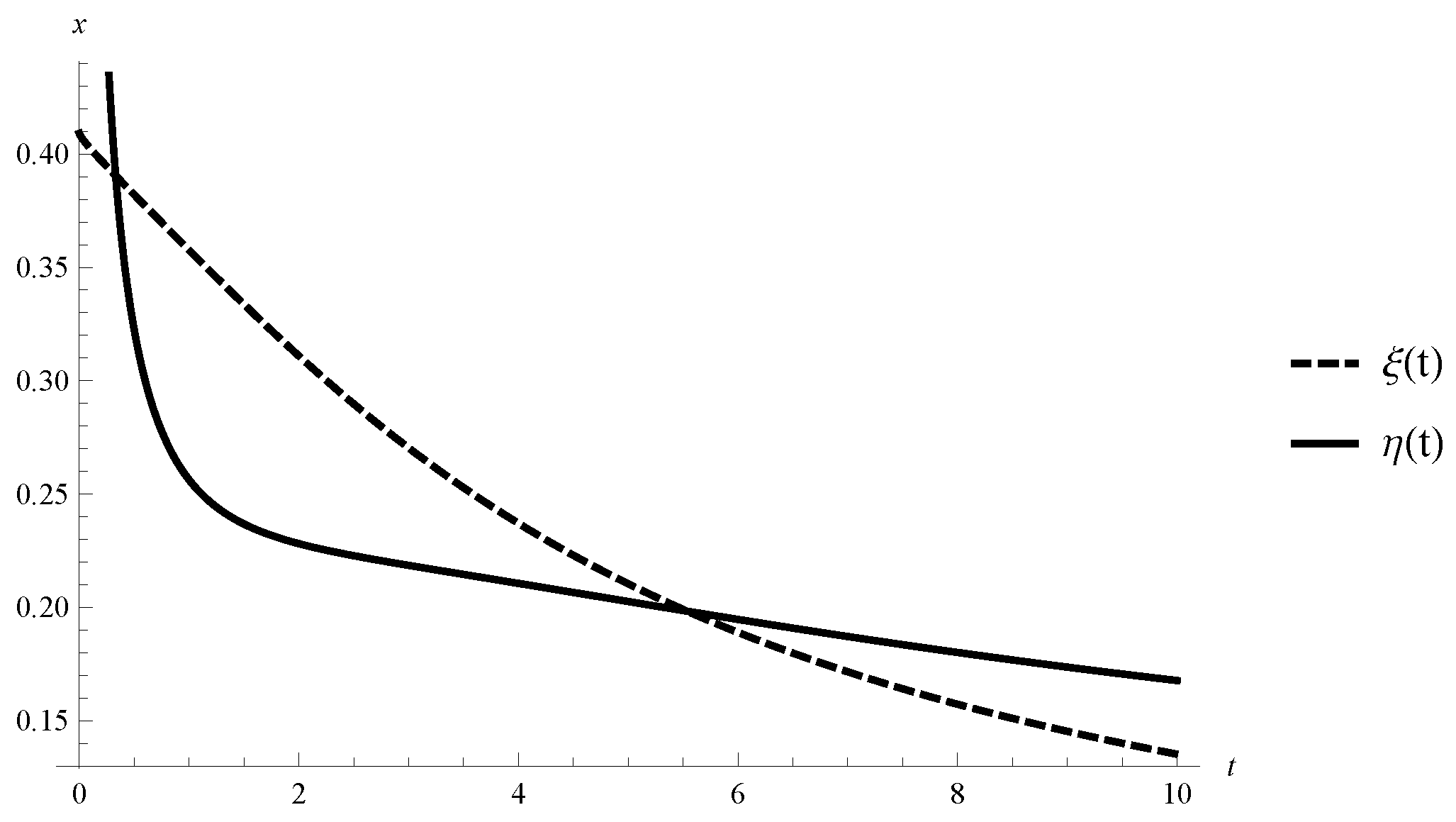1. Introduction
Neural networks have a wide range of applications in pattern recognition, associative memory, combinatorial optimization, etc. Delays are incorporated into the model equations of the networks because of the finite speeds of the switching and transmission of signals in a network and this leads to time delays in a working network. It was observed both experimentally and numerically in [
1] that time delay could induce instability, causing sustained oscillations which may be harmful to a system. Additionally, when one considers memory and hereditary properties of various materials and processes ([
2]), it is natural to consider fractional derivatives in the model. Neural networks in biology, coupled lasers, wireless communication and power-grid networks in physics and engineering ([
3,
4,
5,
6]) are modeled by fractional order differential equations.
In controlling nonlinear systems, the Lyapunov second method provides a way to analyze the stability of the system without explicitly solving the differential equations. Stability results concerning integer-order neural networks can be found in [
7,
8,
9] and recently Lyapunov stability theory for fractional order systems was discussed (see [
10,
11]). Fractional order Lyapunov stability theory was applied for various types of fractional neural networks using quadratic Lyapunov functions (see [
2,
12,
13,
14]) and stability analysis of fractional-order delay neural networks can be found in [
15,
16,
17,
18,
19], for example. Finite-time stability of fractional-order neural networks with constant transmission delay and constant self-regulating parameters is studied in [
20,
21] and for distributed delays and constant self-regulating parameters see [
22].
The main goal of this paper is to study stability properties of Caputo fractional order neural networks with delays. We study the general case of time varying transmission delays as well as time varying self-regulating parameters of all units and time varying functions of the connection between two neurons in the network. Note that usually in the literature the activation functions in the models are Lipschitz with constant Lipschitz coefficients. In this paper, the cases of time varying Lipschitz coefficients as well as nonLipschitz activation functions are studied. The investigation is based on the fractional Lyapunov method. It is worth pointing out that the Lyapunov functional method can not be easily generalized to fractional order systems. It is mainly connected with the derivative taken in the given fractional system. Taking these factors into consideration, we present a brief overview of the existing literature on the various definitions of fractional order derivatives of Lyapunov functions among Caputo fractional differential equations with variable delays and we compare them in several examples, discussing their advantages and disadvantages. Using the appropriate fractional derivative of Lyapunov functions, some stability sufficient criteria are provided and illustrated with examples.
2. Lyapunov Functions and Their Derivatives among the Delay Fractional Differential Equation
We first consider the derivative of Lyapunov functions among the delay fractional differential equation.
In this paper we consider Caputo fractional derivatives with order
defined by (see, for example [
23])
where
denotes the Gamma function.
Consider the initial value problem (IVP) for the nonlinear Caputo fractional delay differential equations (FrDDE)
where
,
is the initial time,
is the initial function,
and for any
the notation
is used.
Let
be a solution of the IVP for the FrDDE (
1) and let
be a Lyapunov function, i.e.,
is continuous and locally Lipschitzian with respect to its second argument, where
.
In the literature there are three types of derivatives of Lyapunov functions among solutions of fractional differential equations used to study stability properties:
- -
first type–Let
be a solution of IVP for FrDDE (
1). Then the
Caputo fractional derivative of the Lyapunov function
is defined by
This type of derivative is applicable for continuously differentiable Lyapunov functions. It is used mainly for quadratic Lyapunov functions to study several stability properties of fractional differential equations (see, for example [
10]).
- -
second type–this type of derivative of
among FrDDE (
1) was introduced by I. Stamova, G. Stamov (Definition 1.12 [
24]):
where
and the notation
is used.
Note that the operator defined by (
3) has no memory (the memory is typical for fractional derivatives) (see Case 2.1 of Example 1 and Case 2.2 of Example 2).
Remark 1. In general where is a solution of (1). Now, let us recall the remark in [
25] concerning definition (
3) where
is defined by
where
.
Following this notation the fractional derivative of the Lyapunov function is defined by
The derivative (
4) has memory and it depends on the initial time
. It is closer to both the Grunwald-Letnikov fractional derivative and the Riemann-Liouville fractional derivative, than to the Caputo fractional derivative of a function. We will call the derivative (
4) the
Dini fractional derivative of the Lyapunov function. The Dini fractional derivative is applicable for continuous Lyapunov functions.
Remark 2. In the general case .
- -
third type–for any
the derivative of the Lyapunov function
among IVP for FrDDE (
1) with initial point
and initial function
is defined by:
or its equivalent
The derivative (
6) depends significantly on both the fractional order
q and the initial data
of IVP for FrDDE (
1) and this type of derivative is close to the idea of the Caputo fractional derivative of a function.
We call the derivative given by (
5) or its equivalent (
6) the
Caputo fractional Dini derivative. This type of derivative is applicable for continuous Lyapunov functions (see, for example [
26,
27,
28]).
Remark 3. The equalityholds for any and for any initial data : Remark 4. Note that in the case of delays in the differential equations, the derivative of the Lyapunov function is considered for functions and points t such that . This condition is called the Razumikhin condition.
We will illustrate the application of the above given derivatives on the quadratic Lyapunov function (used in stability of neural networks [
2,
12,
13,
14]).
Example 1. Let . Consider the quadratic Lyapunov function i.e., .
Case 1. First type of derivative. Let be a solution of the IVP for FrDDE (1). According to [29] we get Case 2. Second type of derivative.
Case 2.1: Let the function . From Formula (3) we obtain It is seen that the derivative does not depend on any initial data of the fractional equation.
Case 2.2: Dini fractional derivative. Let the function . From Formula (4) we obtain The Dini fractional derivative depends on both the fractional order q and initial time.
Case 3. Third type of derivative. Caputo fractional Dini derivative. According to Remark 4 and Case 2.2 the inequalityholds. The Caputo fractional Dini derivative depends on both the fractional order q and initial data .
From the literature we note that one of the sufficient conditions for stability is connected with the sign of the derivative of the Lyapunov function of the equation.
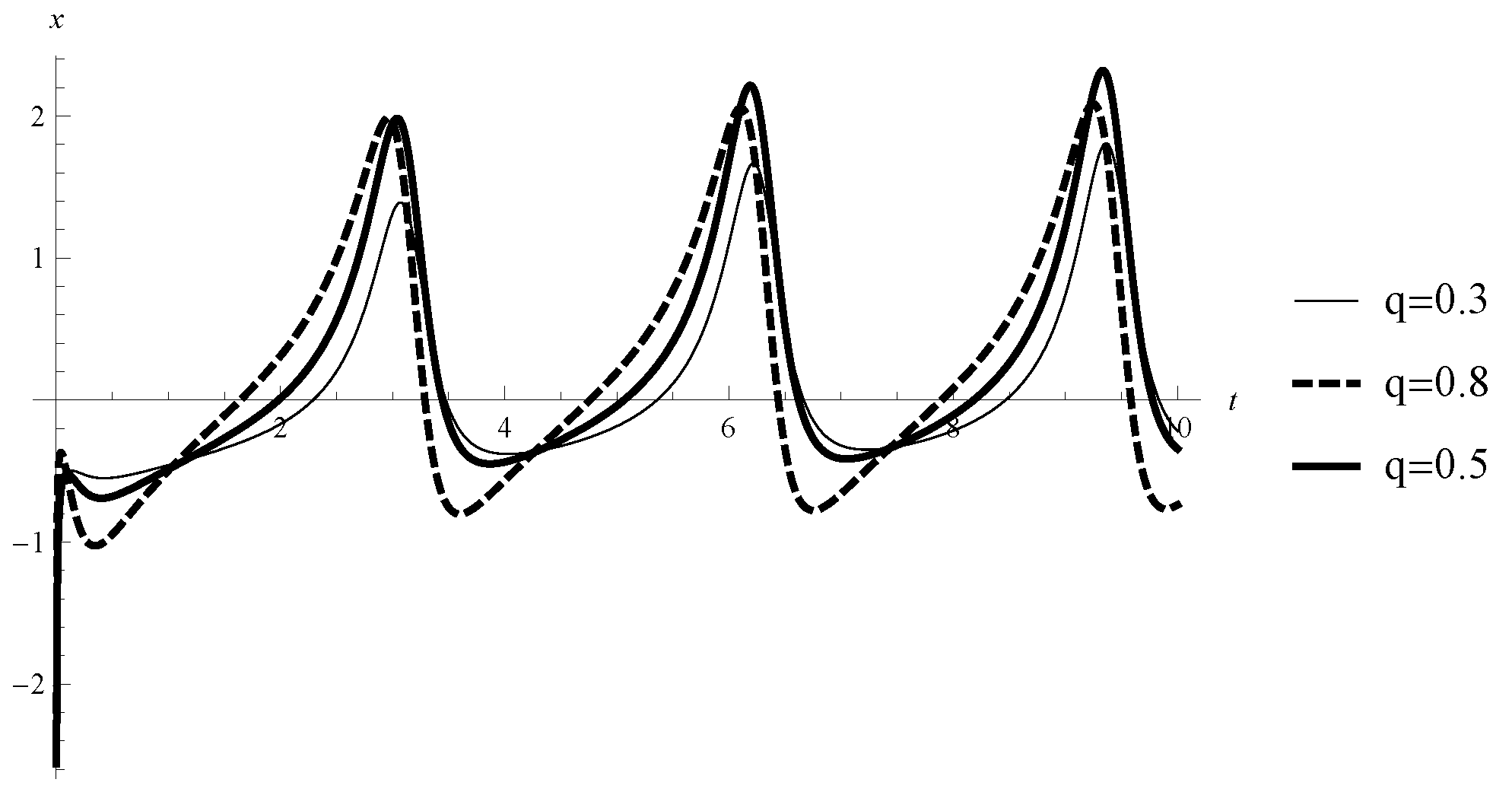
Example 2. Consider the IVP for the scalar linear FrDDEwhere , . Case 1. Consider the quadratic Lyapunov function [12,13,14]) i.e., . Let be a solution of IVP for FrDDE (14) and be such that . Then according to [29] we get The sign of is changeable (the graph of the function for various values of q is given on Figure 1). Case 2. Consider the function .
Case 2.1: Caputo fractional derivative. Let be a solution of IVP for FrDDE (14). From Equation (2) we obtain The fractional derivative of this function V is difficult to obtain so it is difficult to discuss its sign.
Case 2.2: Use Formula (3) and for any function and any point such that we obtaini.e., the sign of the derivative is changeable. Case 2.3: Dini fractional derivative. For any function and such that we apply Formula (4) and obtain Case 2.4: Caputo fractional Dini derivative. According to Remark 4 and Case 2.3 the inequalityholds. Therefore, for (14) both the Dini fractional derivative and the Caputo fractional Dini derivative seem to be more applicable than the Caputo fractional derivative of Lyapunov function. Remark 5. The above example notes that the quadratic function for studying stability properties of neural network might not be successful (especially when the right hand side depends directly on the time variable). Formula (3) is not appropriate for applications to fractional equations. The most general derivatives for non-homogenous fractional differential equations are Dini fractional derivatives and Caputo fractional Dini derivatives. 3. Remarks on Some Applications of Derivatives of Lyapunov Functions
Some authors use the derivative defined by (
3) to study stability properties of delay fractional differential equations ([
24,
30]) and delayed reaction-diffusion cellular neural networks of fractional order ([
31]). The proofs are based on the following result:
Lemma 1. - 1.
The function is continuous in and is nondecreasing in u for each .
- 2.
The maximal solution of the IVP for scalar Caputo fractional differential equation exists on .
- 3.
The Lipschitz function is such that for the inequalityis valid whenever for where . Then implies , where is the solution of (1) with initial data .
The claim of Lemma 1 is not true. We will give a counterexample.
Example 3. Consider the IVP for FrDDE (1) with , , , , , , and where with is the general hypergeometric function or Aomoto-Gelfand hypergeometric function [32]. We denote its solution by . Consider the Lyapunov function . According to Example 1, Case 2.1, Equation (11) we get . The function is a solution of the IVP for the comparison scalar fractional differential equation Then but the inequalitydoes not hold for . The application of the derivative
defined by (
3) is not appropriate in studying stability properties of neural networks of fractional order (as presented in [
31]). We will consider fractional neural networks with delays and using Lyapunov functions and their Caputo fractional derivative, Dini fractional derivative or Caputo fractional Dini derivative (and without applying Lemma 1) we study stability.
4. Stability for Caputo Fractional Order Neural Networks with Time Varying Delays
4.1. System Description
Consider the general model of fractional order neural networks with time varying delay (FODNN)
where
,
n represents the number of units in the network,
is the pseudostate variable of the
i-th unit of master system,
,
is the self-regulating parameters of the
i-th unit, ,
correspond to the connection of the
i-th neuron to the
j-th neuron at times
t and
respectively,
and
denote the activation functions of the neurons at time
t and
, respectively,
,
and
is an external bias vector,
is the transmission delay.
The initial conditions of the given system (
15) are listed as
where
,
with the norm
.
Remark 6. The problem of existence and uniqueness of equilibrium states of fractional-order neural networks was investigated by several authors; for sufficient conditions which guarantee the existence and uniqueness of solutions for FODNN with constant delays we refer the reader to [15]. Definition 1. A vector is an equilibrium point of Caputo FODNN (15), if the equalities hold for all . We will discuss the equilibrium points on some FODNN with various activation functions. It will be useful for stability analysis.
Example 4. Consider the system of FODNN (15) with , , with the activation functions , and and . Then the point is an equilibrium point iff . Example 5. Let , c is a constant and consider the scalar FODNN Case 1. Let and the activation function be the cosine function (see [33]). The point is an equilibrium point of FODNN(17) because for all . Case 2. Let and the activation function be the Probit function (see Figure 2) where is the error function. Then . The point is an equilibrium point of FODNN(17) because for all . Case 3. Let and the activation function be the Logit function (see Figure 3). Then . The point is an equilibrium point of Caputo FODNN (17) because for all . Assumption 1. Let the Caputo FODNN (15) have an equilibrium point . If Assumption 1 is satisfied then we can shift the equilibrium point
of system (
15) to the origin. The transformation
is used to put system (
15) in the following form:
where
.
We will give the Dini fractional derivative of a Lyapunov function depending directly on the time
t among the FODNN (
18) which will be used in the proofs of some of the main results.
Example 6. Consider the IVP for FODNN (18). Consider the function where for where are constants. Let and be such that . Then from Formula (4) we obtain for the Dini fractional derivative: 4.2. Some Results for Caputo Fractional Differential Equations
We will give some results for fractional derivatives of Lyapunov functions among Caputo fractional differential equations which will be used for our main results concerning the stability of FODNN.
Lemma 2. ([29]). Let be constant, symmetric and positive definite matrix and be a function with the Caputo fractional derivative existing. Then
Lemma 3. (Theorem 3.1 [16]). Let be nondecreasing functions, for , , us strictly increasing and there exists a continuously differentiable Lyapunov function such that - (i)
- (ii)
for any such that the inequalityholds where is a solution of (1) with .
Then the equilibrium point of (1) is uniformly stable. For the Caputo fractional Dini derivative we have:
Lemma 4. (Theorem 6 [34]). Assume be an equilibrium point for (1) with and there exists a Lyapunov function such that - (i)
for
where are strictly increasing and .
- (ii)
for any initial data and any function such that if for a point we have for then the inequalityholds.
Then the equilibrium point of (1) is uniformly stable. 4.3. Stability Analysis
We will study stability properties of several different types of FODNN (
1) using different types of Lyapunov functions and their fractional derivatives given in
Section 2.
4.3.1. Lipschitz Activation Functions and Quadratic Lyapunov Functions
The stability analysis of the fractional-order neural networks with constant delays and Lipschitz active functions was studied in [
35] and the argument was based on topological degree theory, nonsmooth analysis and a nonlinear measure method. We will apply the Lyapunov method to derive some sufficient conditions for stability in the case of variable delays.
We assume the following:
Assumption 2. The neuron activation functions are Lipschitz, i.e., there exist positive numbers such that and for .
Assumption 3. There exists positive numbers such that , for .
Remark 7. If Assumption 2 is satisfied then the functions in FODNN (18) satisfy for any . The case of multiple time constant delays and the functions of the connection of the
i-th neuron to the
j-th neuron at time
t in FODNN (
15) are constants studied using the quadratic Lyapunov function in [
14]. We will study the case of variable bounded functions of connection.
Theorem 1. Let and Assumptions 1–4 are satisfied.
Then the equilibrium point of Caputo FODNN (15) is uniformly stable. Proof. Consider the quadratic functions
. Let the point
be such that
where
is a solution of the FODNN (
18). Then since
we have
. Applying Lemma 2 we get
Inequality (
20) and Lemma 3 prove the claim. ☐
Example 7. Consider the system of FODNN (15) with , , with the activation functions , the delay and where are given by The point is an equilibrium point of Caputo FODNN (15) if (see Example 4). Then and , . Therefore, if then according to Theorem 1 the zero equilibrium is uniformly stable.
4.3.2. Non-Lipschitz Activation Functions and Quadratic Lyapunov Functions
There are many types of activation functions which are not Lipschitz (see Example 2, Cases 2 and 3). In this case we assume:
Assumption 5. There exists a function such that for any solution of the FODNN (18) and any point and the inequalityholds. Assumption 6. There exists a function such that Theorem 2. Let Assumptions 1, 5 and 6 be satisfied with .
Then the equilibrium point of Caputo FODNN (15) is uniformly stable. Proof. Consider the quadratic functions
. Let
be a solution of the FODNN (
18). Let
be such that
. Then applying Lemma 2, we get for the Caputo fractional derivative
From inequality (
24) and Lemma 3 the claim follows. ☐
Example 8. Let and consider the scalar nonlinear FODNNwhere , , , the functions and the activation function is the Probit function or the Logit function (see Example 6). Then the Equation (25) has an equilibrium point (see Example 5). Neither of the activation functions are Lipschitz and Theorem 1 cannot be applied. Let be such that .
Consider the following possible cases:
- -
Let and . Since we obtain and from the monotonicity property of the function f we get and . Then applying we get - -
Let and . Then and applying we obtain - -
Let . Then and from monotonicity property of the function f it follows . Therefore,
Therefore, the Assumption 5 is satisfied. Then, according to Theorem 2 the equilibrium point of FODNN (25) is uniformly stable for all . 4.3.3. Non-Lipschitz Activation Functions and Time-Depended Lyapunov Functions
In the case the function in Assumption 6 not being large enough, we introduce
Assumption 7. There exists a continuous positive function such that and the fractional derivative exists for .
In this case, Assumption 5 could be weakened to
Assumption 8. There exists a function such that for any function and be such that the inequalityholds. Theorem 3. Let the Assumptions 1, 6–8 be satisfied and Then the equilibrium point of Caputo FODNN (15) is uniformly stable. Proof. In this case the quadratic function does not work.
Consider the function
where the function
is defined in Assumption 7. Then, according to Assumption 7 condition (i) of Lemma 4 is satisfied with
and
. Let
and
be such that
Then from Formula (
4) and Example 6 we obtain for the Dini fractional derivative:
According to Remark 3 and inequality (
28) we get the inequality
i.e., condition (ii) of Lemma 4 is satisfied. Applying Lemma 4 we prove the claim. ☐
Example 9. Let and consider the scalar FODNN (17) with , , , the activation functions are the Continuous Tan-Sigmoid Function , and the equilibrium point . Theorem 1 is not applicable since the coefficient before x is not a constant.
Let be a solution of FODNN (17). Then using the inequality we get . In addition, let be such that then and i.e., Assumption 5 is satisfied with . However the inequality is not satisfied (see Figure 4 for ). Therefore, Theorem 2 cannot be applied. Consider the function . Then we get the inequality According to Theorem 3 the equilibrium point of Caputo FODNN (17) is uniformly stable. Therefore, in the case that the activation functions are not Lipschitz and the coefficients are not constants in FODNN, we can use Lyapunov function depending directly on the time variable; its Caputo fractional Dini derivative is applicable to study the stability.
5. Conclusions
Several sufficient conditions are given for stability of the equilibrium point of Caputo fractional order neural networks with delays of order . We study the general case when
- -
the transmission delays are time variables;
- -
the self-regulating parameters of all units are variable in time;
- -
the functions of the connection between two neurons in the network are variable in time bounded functions;
- -
the activation function is nonLipschitz (usually in the literature only the case of Lipschitz activation functions is studied).
The investigation is based on applying the fractional Lyapunov approach and various types of Lyapunov functions are discussed (not only the quadratic one as is usually considered in the literature). The presence of the fractional derivative in the model requires an appropriate defined and used derivative of Lyapunov functions among the fractional model. A brief overview of the existing literature and the main types of derivatives among Caputo fractional equations are presented. These types of derivatives are used as an apparatus to study stability properties of the considered Caputo fractional order neural networks for different types of activation functions. Many examples with different types of activation functions such as tanh function, Logit function, continuous Tan-Sigmoid function, are provided to illustrate the practical application of the obtained sufficient conditions.