NN-Harmonic Mean Aggregation Operators-Based MCGDM Strategy in a Neutrosophic Number Environment
Abstract
:1. Introduction
2. Preliminaries
2.1. Harmonic Mean and Weighted Harmonic Mean
2.2. NNs
- If yI = 0, then z is degenerated to the determinate component z = x
- If x = 0, then z is degenerated to the indeterminate component z = yI
- If IL = IU, then z is degenerated to a real number.
- (1)
- I2 = I
- (2)
- I.0 = 0
- (3)
- I/I = Undefined
- (4)
- z1 + z2 = x1 + x2 + (y1 + y2)I = [x1 + x2 + (y1 + y2)IL, x1 + x2 + (y1 + y2)IU]
- (5)
- z1 − z2 = x1 − x2 + (y1 − y2)I = [x1 − x2 + (y1 − y2)IL, x1 − x2 + (y1 − y2)IU]
- (6)
- z1 z2 = x1x2 + (x1y2 + x2y1)I + y1y2I2 = x1x2 + (x1y2 + x2y1 + y1y2)I
- (7)
- (8)
- (9)
- (10)
- If S(z1) > S(z2), then z1 > z2
- If S(z1) = S(z2) and A(z1) < A(z2), then z1 < z2
- If S(z1) = S(z2) and A(z1) = A(z2), then z1 = z2.
3. Harmonic Mean Operators for NNs
3.1. NN-Harmonic Mean Operator (NNHMO)
3.2. NN-Weighted Harmonic Mean Operator (NNWHMO)
4. Cosine Function for Determining Unknown Criteria Weights
- P1.
- , if
- P2.
- , if
- P3.
- , if xij of P > xij of Q or yij of P < yij of Q or both.
- P1.
- P2.
- P3.
- For, xij of P > xij of Q
- ⇒
- Determinate part of P > Determinate part of Q
- ⇒
- .For, yij of P < yij of Q
- ⇒
- Indeterminacy part of P < Indeterminacy part of Q
- ⇒
- .For, xij of P > xij of Q and yij of P < yij of Q
- ⇒
- (Real part of P > Real part of Q) & (Indeterminacy part of P < Indeterminacy part of Q)
- ⇒
- . ☐
5. Multi-Criteria Group Decision-Making Strategies Based on NNHMO and NNWHMO
5.1. MCGDM Strategy 1 (Based on NNHMO)
5.2. MCGDM Strategy 2 (Based on NNWHMO)
6. Simulation Results
6.1. Solution Using MCGDM Strategy 1
6.2. Solution Using MCGDM Strategy 2
7. Comparison Analysis and Contributions of the Proposed Approach
7.1. Comparison Analysis
7.2. Contributions of the Proposed Approach
- NNHMO and NNWHMO in NN environment are firstly defined in the literature. We have also proved their basic properties.
- We have proposed score and accuracy functions of NN numbers for ranking. If two score values are same, then accuracy function can be used for ranking purpose.
- The proposed two strategies can also be used when observations/experiments contribute is disproportionate amount to the arithmetic mean. The harmonic mean is used when sample values contain fractions and/or extreme values (either too small or too big).
- To calculate unknown weights structure of criteria in NN environment, we have proposed cosine function.
- Steps and calculations of the proposed strategies are easy to use.
- We have solved a numerical example to show the feasibility, applicability, and effectiveness of the proposed two strategies.
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hwang, L.; Lin, M.J. Group Decision Making under Multiple Criteria: Methods and Applications; Springer: Heidelberg, Germany, 1987. [Google Scholar]
- Hwang, C.; Yoon, K. Multiple Attribute Decision Making, Methods and Applications; Springer: New York, NY, USA, 1981; Volume 186. [Google Scholar]
- Chen, S.J.; Hwang, C.L. Fuzzy Multiple Attribute Decision-Making, Methods and Applications; Lecture Notes in Economics and Mathematical Systems; Springer: Berlin/Heidelberg, Germany, 1992; Volume 375. [Google Scholar]
- Chang, T.H.; Wang, T.C. Using the fuzzy multi-criteria decision making approach for measuring the possibility of successful knowledge management. Inf. Sci. 2009, 179, 355–370. [Google Scholar] [CrossRef]
- Krohling, R.A.; De Souza, T.T.M. Combining prospect theory and fuzzy numbers to multi-criteria decision making. Exp. Syst. Appl. 2012, 39, 11487–11493. [Google Scholar] [CrossRef]
- Chen, C.T. Extension of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets Syst. 2000, 114, 1–9. [Google Scholar] [CrossRef]
- Zhang, G.; Lu, J. An integrated group decision-making method dealing with fuzzy preferences for alternatives and individual judgments for selection criteria. Group Decis. Negot. 2003, 12, 501–515. [Google Scholar] [CrossRef]
- Krohling, R.A.; Campanharo, V.C. Fuzzy TOPSIS for group decision making: A case study for accidents with oil spill in the sea. Exp. Syst. Appl. 2011, 38, 4190–4197. [Google Scholar] [CrossRef]
- Xia, M.; Xu, Z. A novel method for fuzzy multi-criteria decision making. Int. J. Inf. Technol. Decis. Mak. 2014, 13, 497–519. [Google Scholar] [CrossRef]
- Mehlawat, M.K.; Guptal, P. A new fuzzy group multi-criteria decision making method with an application to the critical path selection. Int. J. Adv. Manuf. Technol. 2015. [Google Scholar] [CrossRef]
- Lin, L.; Yuan, X.H.; Xia, Z.Q. Multicriteria fuzzy decision-making based on intuitionistic fuzzy sets. J. Comput. Syst. Sci. 2007, 73, 84–88. [Google Scholar] [CrossRef]
- Liu, H.W.; Wang, G.J. Multi-criteria decision-making methods based on intuitionistic fuzzy sets. Eur. J. Oper. Res. 2007, 179, 220–233. [Google Scholar] [CrossRef]
- Pramanik, S.; Mondal, K. Weighted fuzzy similarity measure based on tangent function and its application to medical diagnosis. Int. J. Innov. Res. Sci. Eng. Technol. 2015, 4, 158–164. [Google Scholar]
- Pramanik, S.; Mukhopadhyaya, D. Grey relational analysis based intuitionistic fuzzy multi-criteria group decision-making approach for teacher selection in higher education. Int. J. Comput. Appl. 2011, 34, 21–29. [Google Scholar] [CrossRef]
- Mondal, K.; Pramanik, S. Intuitionistic fuzzy multi criteria group decision making approach to quality-brick selection problem. J. Appl. Quant. Methods 2014, 9, 35–50. [Google Scholar]
- Dey, P.P.; Pramanik, S.; Giri, B.C. Multi-criteria group decision making in intuitionistic fuzzy environment based on grey relational analysis for weaver selection in Khadi institution. J. Appl. Quant. Methods 2015, 10, 1–14. [Google Scholar]
- Ye, J. Multicriteria fuzzy decision-making method based on the intuitionistic fuzzy cross-entropy. In Proceedings of the International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 26–27 August 2009. [Google Scholar]
- Chen, S.M.; Chang, C.H. A novel similarity measure between Atanassov’s intuitionistic fuzzy sets based on transformation techniques with applications to pattern recognition. Inf. Sci. 2015, 291, 96–114. [Google Scholar] [CrossRef]
- Chen, S.M.; Cheng, S.H.; Chiou, C.H. Fuzzy multi-attribute group decision making based on intuitionistic fuzzy sets and evidential reasoning methodology. Inf. Fusion 2016, 27, 215–227. [Google Scholar] [CrossRef]
- Wang, J.Q.; Han, Z.Q.; Zhang, H.Y. Multi-criteria group decision making method based on intuitionistic interval fuzzy information. Group Decis. Negot. 2014, 23, 715–733. [Google Scholar] [CrossRef]
- Yue, Z.L. TOPSIS-based group decision-making methodology in intuitionistic fuzzy setting. Inf. Sci. 2014, 277, 141–153. [Google Scholar] [CrossRef]
- He, X.; Liu, W.F. An intuitionistic fuzzy multi-attribute decision-making method with preference on alternatives. Oper. Res Manag. Sci. 2013, 22, 36–40. [Google Scholar]
- Mondal, K.; Pramanik, S. Intuitionistic fuzzy similarity measure based on tangent function and its application to multi-attribute decision making. Glob. J. Adv. Res. 2015, 2, 464–471. [Google Scholar]
- Peng, H.G.; Wang, J.Q.; Cheng, P.F. A linguistic intuitionistic multi-criteria decision-making method based on the Frank Heronian mean operator and its application in evaluating coal mine safety. Int. J. Mach. Learn. Cybern. 2016. [Google Scholar] [CrossRef]
- Liang, R.X.; Wang, J.Q.; Zhang, H.Y. A multi-criteria decision-making method based on single-valued trapezoidal neutrosophic preference relations with complete weight information. Neural Comput. Appl. 2017. [Google Scholar] [CrossRef]
- Wang, J.Q.; Yang, Y.; Li, L. Multi-criteria decision-making method based on single-valued neutrosophic linguistic Maclaurin symmetric mean operators. Neural Comput. Appl. 2016. [Google Scholar] [CrossRef]
- Kharal, A. A neutrosophic multi-criteria decision making method. New Math. Nat. Comput. 2014, 10, 143–162. [Google Scholar] [CrossRef]
- Ye, J. Multiple attribute group decision-making method with completely unknown weights based on similarity measures under single valued neutrosophic environment. J. Intell. Fuzzy Syst. 2014, 27, 2927–2935. [Google Scholar]
- Mondal, K.; Pramanik, S. Multi-criteria group decision making approach for teacher recruitment in higher education under simplified neutrosophic environment. Neutrosophic Sets Syst. 2014, 6, 28–34. [Google Scholar]
- Biswas, P.; Pramanik, S.; Giri, B.C. A new methodology for neutrosophic multi-attribute decision-making with unknown weight information. Neutrosophic Sets Syst. 2014, 3, 44–54. [Google Scholar]
- Biswas, P.; Pramanik, S.; Giri, B.C. Cosine similarity measure based multi-attribute decision-making with trapezoidal fuzzy neutrosophic numbers. Neutrosophic Sets Syst. 2014, 8, 46–56. [Google Scholar]
- Mondal, K.; Pramanik, S. Neutrosophic decision making model for clay-brick selection in construction field based on grey relational analysis. Neutrosophic Sets Syst. 2015, 9, 64–71. [Google Scholar]
- Mondal, K.; Pramanik, S. Neutrosophic tangent similarity measure and its application to multiple attribute decision making. Neutrosophic Sets Syst. 2015, 9, 85–92. [Google Scholar]
- Pramanik, S.; Biswas, P.; Giri, B.C. Hybrid vector similarity measures and their applications to multi-attribute decision making under neutrosophic environment. Neural Comput. Appl. 2015. [Google Scholar] [CrossRef]
- Sahin, R.; Küçük, A. Subsethood measure for single valued neutrosophic sets. J. Intell. Fuzzy Syst. 2015, 29, 525–530. [Google Scholar] [CrossRef]
- Mondal, K.; Pramanik, S. Neutrosophic decision making model of school choice. Neutrosophic Sets Syst. 2015, 7, 62–68. [Google Scholar]
- Ye, J. An extended TOPSIS method for multiple attribute group decision making based on single valued neutrosophic linguistic numbers. J. Intell. Fuzzy Syst. 2015, 28, 247–255. [Google Scholar]
- Biswas, P.; Pramanik, S.; Giri, B.C. TOPSIS method for multi-attribute group decision-making under single-valued neutrosophic environment. Neural Comput. Appl. 2016, 27, 727–737. [Google Scholar] [CrossRef]
- Biswas, P.; Pramanik, S.; Giri, B.C. Value and ambiguity index based ranking method of single-valued trapezoidal neutrosophic numbers and its application to multi-attribute decision making. Neutrosophic Sets Syst. 2016, 12, 127–138. [Google Scholar]
- Biswas, P.; Pramanik, S.; Giri, B.C. Aggregation of triangular fuzzy neutrosophic set information and its application to multi-attribute decision making. Neutrosophic Sets Syst. 2016, 12, 20–40. [Google Scholar]
- Smarandache, F.; Pramanik, S. (Eds.) New Trends in Neutrosophic Theory and Applications; Pons Editions: Brussels, Belgium, 2016; pp. 15–161. ISBN 978-1-59973-498-9. [Google Scholar]
- Sahin, R.; Liu, P. Maximizing deviation method for neutrosophic multiple attribute decision making with incomplete weight information. Neural Comput. Appl. 2016, 27, 2017–2029. [Google Scholar] [CrossRef]
- Pramanik, S.; Dalapati, S.; Alam, S.; Smarandache, S.; Roy, T.K. NS-cross entropy based MAGDM under single valued neutrosophic set environment. Information 2018, 9, 37. [Google Scholar] [CrossRef]
- Sahin, R.; Liu, P. Possibility-induced simplified neutrosophic aggregation operators and their application to multi-criteria group decision-making. J. Exp. Theor. Artif. Intell. 2017, 29, 769–785. [Google Scholar] [CrossRef]
- Biswas, P.; Pramanik, S.; Giri, B.C. Multi-attribute group decision making based on expected value of neutrosophic trapezoidal numbers. New Math. Nat. Comput. 2017, in press. [Google Scholar]
- Smarandache, F. Introduction to Neutrosophic Measure, Neutrosophic Integral, and Neutrosophic, Probability; Sitech & Education Publisher: Craiova, Romania, 2013. [Google Scholar]
- Smarandache, F. Introduction to Neutrosophic Statistics; Sitech & Education Publishing: Columbus, OH, USA, 2014. [Google Scholar]
- Xu, Z. Fuzzy harmonic mean operators. Int. J. Intell. Syst. 2009, 24, 152–172. [Google Scholar] [CrossRef]
- Park, J.H.; Gwak, M.G.; Kwun, Y.C. Uncertain linguistic harmonic mean operators and their applications to multiple attribute group decision making. Computing 2011, 93, 47–64. [Google Scholar] [CrossRef]
- Wei, G.W. FIOWHM operator and its application to multiple attribute group decision making. Expert Syst. Appl. 2011, 38, 2984–2989. [Google Scholar] [CrossRef]
- Ye, J. Simplified neutrosophic harmonic averaging projection-based strategy for multiple attribute decision-making problems. Int. J. Mach. Learn. Cybern. 2017, 8, 981–987. [Google Scholar] [CrossRef]
- Ye, J. Multiple attribute group decision making method under neutrosophic number environment. J. Intell. Syst. 2016, 25, 377–386. [Google Scholar] [CrossRef]
- Liu, P.; Liu, X. The neutrosophic number generalized weighted power averaging operator and its application in multiple attribute group decision making. Int. J. Mach. Learn. Cybern. 2016, 1–12. [Google Scholar] [CrossRef]
- Zheng, E.; Teng, F.; Liu, P. Multiple attribute group decision-making strategy based on neutrosophic number generalized hybrid weighted averaging operator. Neural Comput. Appl. 2017, 28, 2063–2074. [Google Scholar] [CrossRef]
- Pramanik, S.; Roy, R.; Roy, T.K. Teacher selection strategy based on bidirectional projection measure in neutrosophic number environment. In Neutrosophic Operational Research; Smarandache, F., Abdel-Basset, M., El-Henawy, I., Eds.; Pons Publishing House: Bruxelles, Belgium, 2017; Volume 2, ISBN 978-1-59973-537-5. [Google Scholar]
- Majumdar, P.; Samanta, S.K. On similarity and entropy of neutrosophic sets. J. Intell. Fuzzy Syst. 2014, 26, 1245–1252. [Google Scholar]
- Biswas, P.; Pramanik, S.; Giri, B.C. Entropy based grey relational analysis strategy for multi-attribute decision-making under single valued neutrosophic assessments. Neutrosophic Sets. Syst. 2014, 2, 102–110. [Google Scholar]

| I | Sc(Ai) | Ranking Order |
|---|---|---|
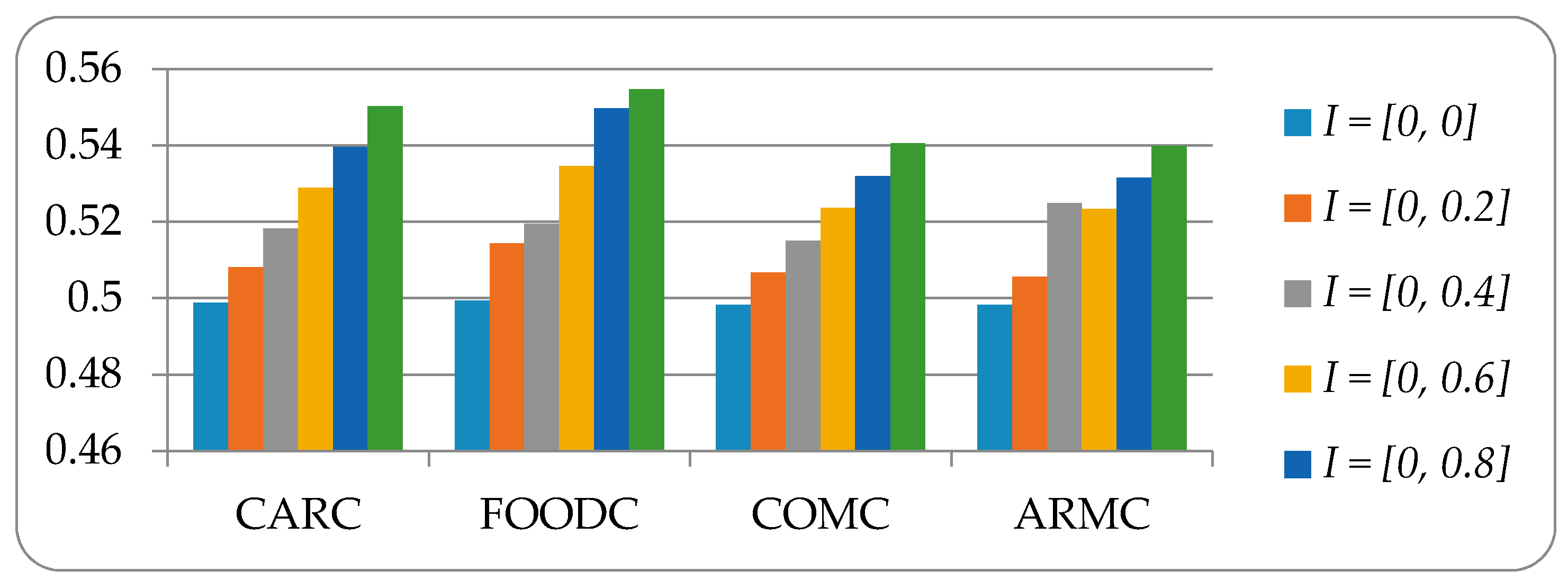
| I = [0, 0] | S(A1) = 0.4988, S(A2) = 0.4993, S(A3) = 0.4982, S(A4) = 0.4983 | A2 A1 A4 A3 |
| I [0, 0.2] | S(A1) = 0.5081, S(A2) = 0.5144, S(A3) = 0.5067, S(A4) = 0.5056 | A2 A1 A3 A4 |
| I [0, 0.4] | S(A1) = 0.5182, S(A2) = 0.5195, S(A3) = 0.5151, S(A4) = 0.5249 | A2 A1 A4 A3 |
| I [0, 0.6] | S(A1) = 0.5289, S(A2) = 0.5346, S(A3) = 0.5236, S(A4) = 0.5233 | A2 A1 A3 A4 |
| I [0, 0.8] | S(A1) = 0.5396, S(A2) = 0.5497, S(A3) = 0.5320, S(A4) = 0.5316 | A2 A1 A3 A4 |
| I [0, 1] | S(A1) = 0.5503, S(A2) = 0.5547, S(A3) = 0.5405, S(A4) = 0.5399 | A2 A1 A3 A4 |
| I | Sc(Ai) | Ranking Order |
|---|---|---|
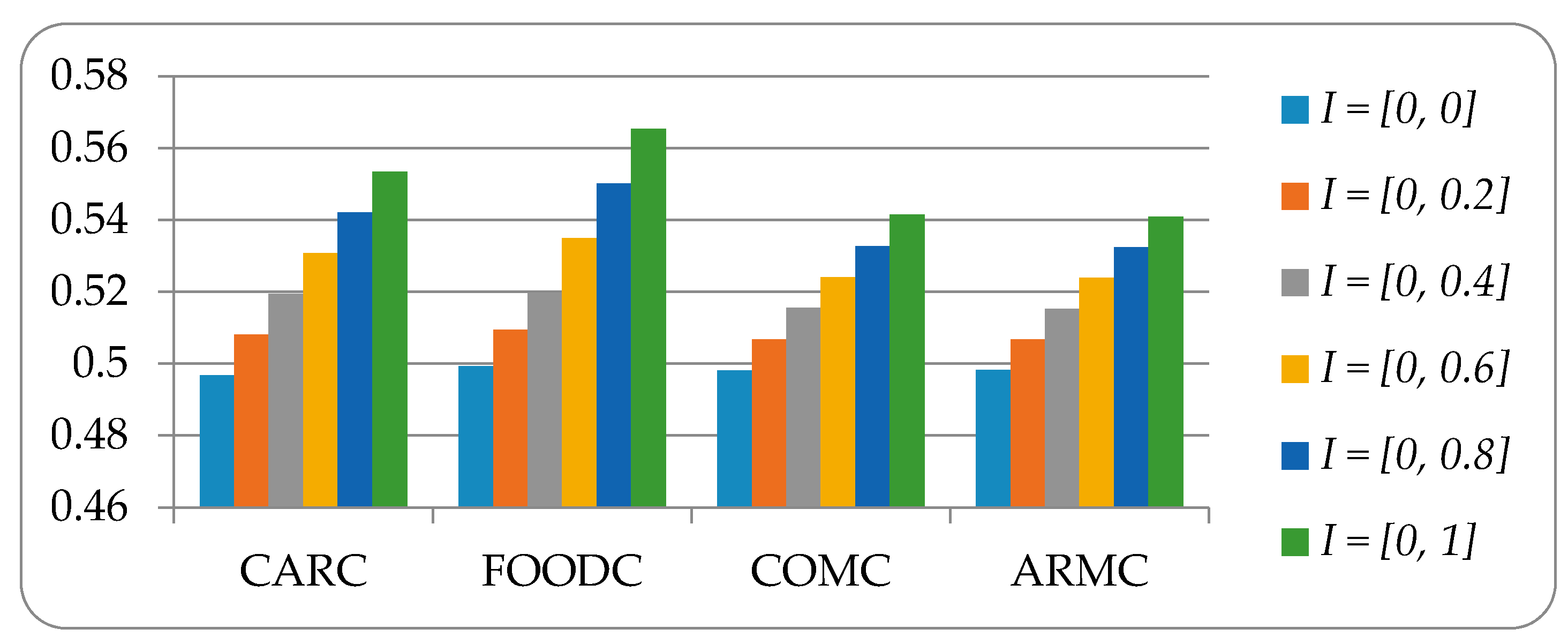
| I = 0 | S(A1) = 0.4968, S(A2) = 0.4993, S(A3) = 0.4981, S(A4) = 0.4982 | A2 A4 A3 A1 |
| I [0, 0.2] | S(A1) = 0.5081, S(A2) = 0.5095, S(A3) = 0.5068, S(A4) = 0.5067 | A2 A1 A4 A3 |
| I [0, 0.4] | S(A1) = 0.5195, S(A2) = 0.5198, S(A3) = 0.5155, S(A4) = 0.5153 | A2 A1 A3 A4 |
| I [0, 0.6] | S(A1) = 0.5308, S(A2) = 0.5350, S(A3) = 0.5241, S(A4) = 0.5239 | A2 A1 A3 A4 |
| I [0, 0.8] | S(A1) = 0.5421, S(A2) = 0.5502, S(A3) = 0.5328, S(A4) = 0.5324 | A2 A1 A3 A4 |
| I [0, 1] | S(A1) = 0.5535, S(A2) = 0.5654, S(A3) = 0.5415, S(A4) = 0.5410 | A2 A1 A3 A4 |
| I | Ye [52] | Zheng et al. [54] | Liu and Liu [53] | Proposed Strategy 1 | Proposed Strategy 2 |
|---|---|---|---|---|---|
| [0, 0] | A2 A4 A3 A1 | A2 A4 A3 A1 | A2 A4 A1 A3 | A2 A1 A4 A3 | A2 A4 A3 A1 |
| [0, 0.2] | A2 A4 A3 A1 | A2 A4 A3 A1 | A2 A3 A1 A4 | A2 A1 A3 A4 | A2 A1 A4 A3 |
| [0, 0.4] | A2 A4 A3 A1 | A2 A4 A3 A1 | A2 A3 A4 A1 | A2 A1 A4 A3 | A2 A1 A3 A4 |
| [0, 0.6] | A4 A2 A3 A1 | A4 A2 A3 A1 | A2 A3 A4 A1 | A2 A1 A3 A4 | A2 A1 A3 A4 |
| [0, 0.8] | A4 A2 A3 A1 | A4 A2 A3 A1 | A2 A3 A4 A1 | A2 A1 A3 A4 | A2 A1 A3 A4 |
| [0, 1] | A4 A2 A3 A1 | A4 A2 A3 A1 | A2 A4 A3 A1 | A2 A1 A3 A4 | A2 A1 A3 A4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mondal, K.; Pramanik, S.; Giri, B.C.; Smarandache, F. NN-Harmonic Mean Aggregation Operators-Based MCGDM Strategy in a Neutrosophic Number Environment. Axioms 2018, 7, 12. https://doi.org/10.3390/axioms7010012
Mondal K, Pramanik S, Giri BC, Smarandache F. NN-Harmonic Mean Aggregation Operators-Based MCGDM Strategy in a Neutrosophic Number Environment. Axioms. 2018; 7(1):12. https://doi.org/10.3390/axioms7010012
Chicago/Turabian StyleMondal, Kalyan, Surapati Pramanik, Bibhas C. Giri, and Florentin Smarandache. 2018. "NN-Harmonic Mean Aggregation Operators-Based MCGDM Strategy in a Neutrosophic Number Environment" Axioms 7, no. 1: 12. https://doi.org/10.3390/axioms7010012
APA StyleMondal, K., Pramanik, S., Giri, B. C., & Smarandache, F. (2018). NN-Harmonic Mean Aggregation Operators-Based MCGDM Strategy in a Neutrosophic Number Environment. Axioms, 7(1), 12. https://doi.org/10.3390/axioms7010012