Minimising subgroups have a structural characterisation which may be used to calculate the scale. Moreover, the proof of this characterisation involves a procedure for finding minimising subgroups. The characterisation and the procedure for finding minimising subgroups will now be described and then illustrated in several examples.
4.3. Tidy Subgroups and the Scale in Examples
Theorem 3 and the notion of tidy subgroup will now be illustrated by using them to compute the scale for the same automorphisms as in the previous section, as well as for some additional examples.
Example 2 (Revisited), let and be an automorphism as before. The tidying procedure will be applied with for an arbitrary vertex v in . For this, note that .
Since
is an automorphism, and is in particular injective, the subgroup
defined as in Equation (
2), is equal to
and the subgroup
defined as in Equation (
1) is equal to
. Hence,
is the fixator of the vertices
v,
, ...,
and
is the fixator of the vertices
,
. As before, the cases when
x is elliptic and when it is hyperbolic are treated separately.
x is elliptic. The orbit
,
is finite and so there is
k such that
is equal to this orbit. Choosing
, we then have that
and it is easily seen that
is equal to this subgroup as well. Hence, putting
we have that
. Hence,
V is tidy above. It follows that
as well and is closed. Therefore,
V is tidy for
. Of course,
x is hyperbolic. As before, let ℓ be the axis for x, suppose that x translates along ℓ through distance d, let c be the distance from v to ℓ, and let w be the vertex on ℓ that is closest to v. In addition, denote the neighbour of w closest to by and the neighbour of w closest to by .
The subgroup
U itself is not tidy for
. To see this, note that since
fixes all vertices
with
, it fixes
w and
as well. Similarly,
fixes
w and
. Hence
if
and
U is not tidy above. The same conclusion holds even when
because, while
U acts as the full permutation group
on the
neighbours of
w,
and
each fix one of the neighbours and
is not equal to the product of two such subgroups. We see too that, since
x fixes every vertex on the path from
v to
, the same calculation as in the earlier discussion yields that
which is strictly greater than
. Hence,
U is not minimising.
The subgroup
is tidy above however. Setting
, we have that
V fixes all vertices on the path from
w to
. Hence, the Tits independence property for
implies that
, where
and
are the fixators in
V of the components
and
of
formed when the path from
w to
is deleted and containing
and
w respectively. Since
, it follows that
V is tidy above. The index we are interested in may be calculated to be
which is strictly less than that found in (
3). However, it is not the minimum value calculated using the spectral radius formula unless
v happens to lie on
ℓ, or
and
. The second and third steps of the tidying procedure must therefore be implemented to find a minimising subgroup.
Carrying out these steps will require labelling some more vertices of . Denote the set of neighbours of w by and similarly for . Recall that and are neighbours of w on ℓ, and denote by the neighbour of w lying on the path from v to w. Then , and are neighbours of : is the neighbour closest to w; is closest to ; and lies on the path from to . The subgroup V found in the previous paragraph fixes all vertices on ℓ between w and as well as the vertices on the paths joining v to w and to , that is, all vertices on the path from v to . In particular, V acts on by fixing and and as the full symmetric group on ; and acts on by fixing and and as the full symmetric group on .
The definition of in Proposition 2 implies that y belongs to this subgroup if for all but finitely many n. Hence, tree automorphisms in fix all the vertices of ℓ and all vertices on paths joining to ℓ except for finitely many n. The action of on thus fixes and and permutes vertices in arbitrarily; and its action on fixes and and permutes vertices in arbitrarily. That the closure of is compact as claimed in Proposition 2 may be seen by observing that this closure is the fixator of all vertices on ℓ.
That the product
is not a group may be seen by considering its action on
. While
V and
both fix
w, we have that
fixes
and
and acts as
on the remaining vertices in
; and
V fixes
and
and acts as
on the remaining vertices; but the product
is not a subgroup of
. In the present example,
is compact and equal to the fixator of the path from
w to
, which is tidy for
. We shall see, however, that the procedure described in Proposition 3 produces a different tidy subgroup. According to this procedure, define
. To determine
, we apply the following lemma about finite permutation groups to the subgroups
and
of
.
Lemma 1. Let denote the permutation group . Then, Proof. Note that no permutation in sends 1 to q. On the other hand, if and does not fix q, then there is such that and there is such that . Then and is not in . ☐
It follows from Lemma 1 that
Since elements of
V fix
,
,
and
already,
It is easily seen that all elements of
V fixing
and
belong to
. Hence
. Then,
that is, elements of
W fix all vertices on the axis
ℓ between
and
.
To compute the scale of
using this tidy subgroup
W, observe that
fixes all vertices on
ℓ between
and
and
fixes all vertices between
and
. The distance on
ℓ between
and
is
d, and the orbit of
under
therefore has order
. Hence,
Regular trees are a particular type of
building—see [
16] for the definition—and automorphism groups of locally finite buildings are totally disconnected, locally compact groups. The calculation of the scale in terms of geometric data describing the building could also be carried out by a similar approach to that used for trees.
Example 3 (Revisited), let for some finite group F and be the shift automorphism as before. It has already been remarked that G is compact and invariant under and so . When the tidying procedure is applied with there is no change: in Step 1, we have and so in the next step; in Step 2, ; and in Step 3, and .
The tidying procedure will be illustrated by applying it to the compact open subgroup
where
X is a finite subset of
. When
, we recover the subgroup
considered previously.
Since is an automorphism, the group defined in Proposition 1 is equal to and the number N whose existence is guaranteed by the proposition depends on X.
In the case when
the subgroup
is already tidy above and
. To see this, note that
In this case, we have .
For another case, suppose that
. Then,
Hence,
. In other words,
and
. Moreover,
and
. Similar calculations apply for
and
. However,
which is tidy above, and
.
For any subgroup
with
we have
and
.
Lie groups over local fields are totally disconnected and locally compact as well, and the scale of elements in such groups, that is, of inner automorphisms of the groups, was computed by H. Glöckner in [
17]. His were the first calculations of the scale for groups that went beyond the basic cases seen in the previous examples.
Example 4. Let G be a Lie group over the field of p-adic numbers. Glöckner does not use the tidying procedure to find subgroups tidy for x (that is, for ) but instead describes and directly in terms of the normal form of the Lie algebra automorphism and calculates in terms of eigenvalues of (in a finite extension of ). This correspondence between the scale and tidy subgroups on one hand and eigenvalues and eigenspaces on the other is evidence that scale techniques are a substitute for Lie algebra techniques when studying t.d.l.c. groups that are not Lie groups over local fields.
The main ideas in [17] may be sketched as follows. Assume that V is tidy for x, then is closed and so is a Lie subgroup of G. Moreover, is an open subgroup of and , where is the automorphism of induced by conjugation by x and Δ
is the module function on automorphisms. The module of this automorphism of is then equal to the module of the automorphism induced on the Lie algebra of . Glöckner then describes this Lie algebra as a subalgebra of (the Lie algebra of G) in what he calls the contraction decomposition
of . This decomposition applies to any linear automorphism of a finite-dimensional vector space, L, over a local field of characteristic 0
, and expresses L aswhere Glöckner bases this decomposition on a variation on ([18] Lemma 3.4). Applying it when L is the Lie algebra of G and , he finds that is a subalgebra isomorphic to the Lie algebra of . Using this decomposition, Glöckner shows in ([17] Corollary 3.6) that, if G is a Lie group over a local field, K, of characteristic 0
and x is in G, thenwhere are the roots of the characteristic polynomial of in a splitting field, , for this polynomial and is the unique extension to of absolute value on K. Glöckner thus reduces the computation of the scale to finding eigenvalues and avoids the need to find tidy subgroups. He gives more explicit formulæ for the scale on linear algebraic groups. The formulæ and their relation to the methods for computing the scale previously discussed may be illustrated with the case when the group is and the element x has the property that its characteristic polynomial splits over , in which case there is a basis for with respect to which x has a diagonal matrix with entries , the eigenvalues of x. Consider the compact, open subgroup . Note that the condition that U is a group forces the determinant of each element of U to have p-adic absolute value equal to 1.
Applying powers of to U yields thatwhere . Thus, if , then and . Suppose that . (The case when is similar.) Then,and it may be calculated that Hence, by Theorem 2, , which is the same value as given in the last example in ([17] Corollary 3.6). The subgroup U is not tidy above for when because, as follows from (
5),
and the element belongs to U but not to . of the tidying procedure. The subgroupmay be verified to be tidy above by showing that every element of V is the product of an upper triangular and a lower triangular matrix. Proposition 1 thus holds with in this case. It may also be verified thatwhich is a closed subgroup of , and hence that V is also tidy below. That the tidying procedure terminates after the first step in this case is no accident: it is shown in ([19] Theorem 3.2) that that occurs for any automorphism α for which the contraction subgroup
,is closed and it is shown in ([18] Theorem 3.5) that that is always so for automorphisms of p-adic Lie groups. Glöckner has also calculated the scale in some cases for linear groups over a skew field, K, with positive characteristic, see [20]. He shows that, if x is a diagonalisable element in , , or , then the scale is given by the same formula as in the characteristic 0
case. He does so by writing down tidy subgroups for . In particular, he shows that, if the diagonal entries in x are in order of decreasing modulus, then certain compact, open subgroups may be written as the product of their subgroup of upper triangular matrices with their subgroup of lower triangular matrices and that this implies tidiness above. Tidiness below is again satisfied automatically, as in the previous paragraph, because contraction subgroups for inner automorphisms are closed. More is known about
p-adic Lie groups than for general t.d.l.c. groups but a key question remains unanswered even for these groups. If an element
x in a t.d.l.c. group satisfies that
, then subgroups tidy for
x are normalised by
x and, conversely, if
U is normalised by
x, then
. A t.d.l.c. group
G is
uniscalar if
for every
and it is shown in [
21], relying on a result in [
22], that a
p-adic Lie group that is compactly generated and uniscalar has a compact, open normal subgroup. There are uniscalar t.d.l.c. groups having no compact, open normal subgroups which are compactly generated, see [
23], and which are topologically simple, see [
24]. However, no examples are known of uniscalar t.d.l.c. groups which are topologically simple and compactly generated, or which are topologically simple (of necessity not compactly generated) and
p-adic Lie.
Another significant class of t.d.l.c. groups are the groups of
almost automorphisms of trees introduced by Yu. Neretin, [
25,
26], and shown to be simple by C. Kapoudjian, [
27]. Neretin groups are also studied in [
28], where it is shown that they do not contain a lattice, and the notation used here conforms with that paper. The papers [
29], on abstract commensurators, and [
30], on ‘germs of automorphisms’ are also relevant. Neretin’s groups are also the inspiration for the simple groups acting on trees recently constructed in [
31].
Example 5. An almost automorphism
of an infinite, locally finite tree is a bijection on the vertices of which preserves all but finitely many edge relations. The set of almost automorphisms forms a group under composition of bijections. This group has two subgroups which are important for this discussion: the group of automorphisms of ; and the group of finite permutations of the vertices of . Fix a vertex v in and let . Then, U is a compact group under the subspace topology of and each almost automorphism of commensurates some open subgroup of U to another open subgroup. Hence,is a sub-base of a group topology on the group of almost automorphisms of . Since U is open in this topology, the group of almost automorphisms is then a locally compact group. Since non-trivial elements of cannot be in U, the subgroup is closed in this topology and is easily seen to be normal as well. (It may be seen that is the quasi-centre
of the group of almost automorphisms, see [32] for the definition.) The quotient of the group of almost automorphisms by is therefore a locally compact group which will be denoted by . It is this quotient group which will from now on be referred to as the group of almost automorphisms of
. Alternative but equivalent definitions of are used elsewhere. For example, in [28], two almost automorphisms of are defined to be equivalent if they agree on the complement of some finite subtree of and is defined to be the set of equivalence classes of almost automorphisms. Since each finite set of vertices in spans a finite subtree, this is the same as the equivalence relation of two almost automorphisms agreeing modulo . Almost automorphisms of may be seen to be equivalent if and only if the actions they induce on the boundary, , of the tree agree. The group may thus be defined in terms of its action on . In these terms, is the full group
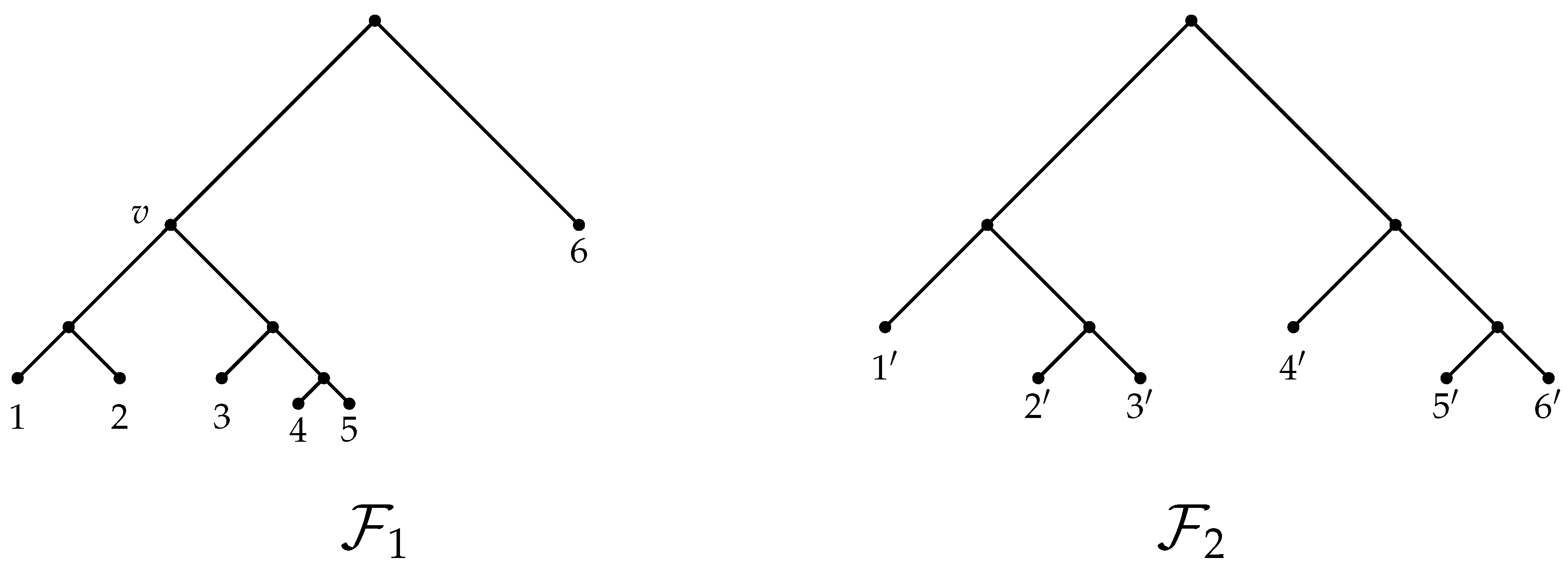
of the action on on . Almost automorphisms of the rooted tree , in which the root has r children and every other vertex has q children, have been studied extensively. In this notation, Neretin’s group of almost automorphisms is . The group has the Higman–Thompson group , see [33,34], as a dense subgroup and elements of may be represented (non-uniquely) as pairs, , of finite rooted subtrees of , see [33] or ([35] Section 3) for example. Since the scale is continuous, it therefore suffices, in order to compute the scale on , to compute it for elements represented by such pairs of finite trees. This calculation is intricate and the general case is not described in full detail here. Instead, the ideas will be illustrated by the calculation of for one element x in . Note, however, that this example only displays some of the intricacies arising in the calculation of the scale on . Let x be the element of (also known as Thompson’s group V) described by the pair of trees in Figure 1. When is embedded in , this element denotes the almost automorphism which sends the vertices labelled 1, ..., 6
in the tree on the left to the vertices with the corresponding labels , ..., in the tree on the right and copies across the subtrees below each of these vertices. Thus, the subtree of whose root is the vertex on level 3
and labelled 1
is raised to a subtree with root on level 2
, the subtrees with roots on level 3
and labelled 2
and 3
are copied across to two other subtrees with roots on level 3
, the subtrees with roots on level 4
and labelled 4
and 5
are raised to subtrees with roots on level 2
and 3
respectively, and the subtree with root on level 1
and labelled 6
is lowered to a vertex on level 3
. Let , so that U is a compact, open subgroup of , and let be the subgroup of U consisting of all automorphisms which fix the vertices labelled 1, ..., 6
in . Then, is the subgroup of U consisting of all automorphisms fixing the vertices labelled , ..., in . Since and are both subgroups of U, it follows that . The reverse inclusion may be verified by checking cases for automorphisms not in . For example, if interchanges the two vertices on level 1
of the tree, then maps the vertices of labelled 5
and 6
, whose only common ancestor is the root, to vertices which have the vertex labelled v as a common ancestor, and no such map is an automorphism of the tree. Hence, That this is not the minimum possible index will be seen by applying the tidying procedure to the subgroup U.
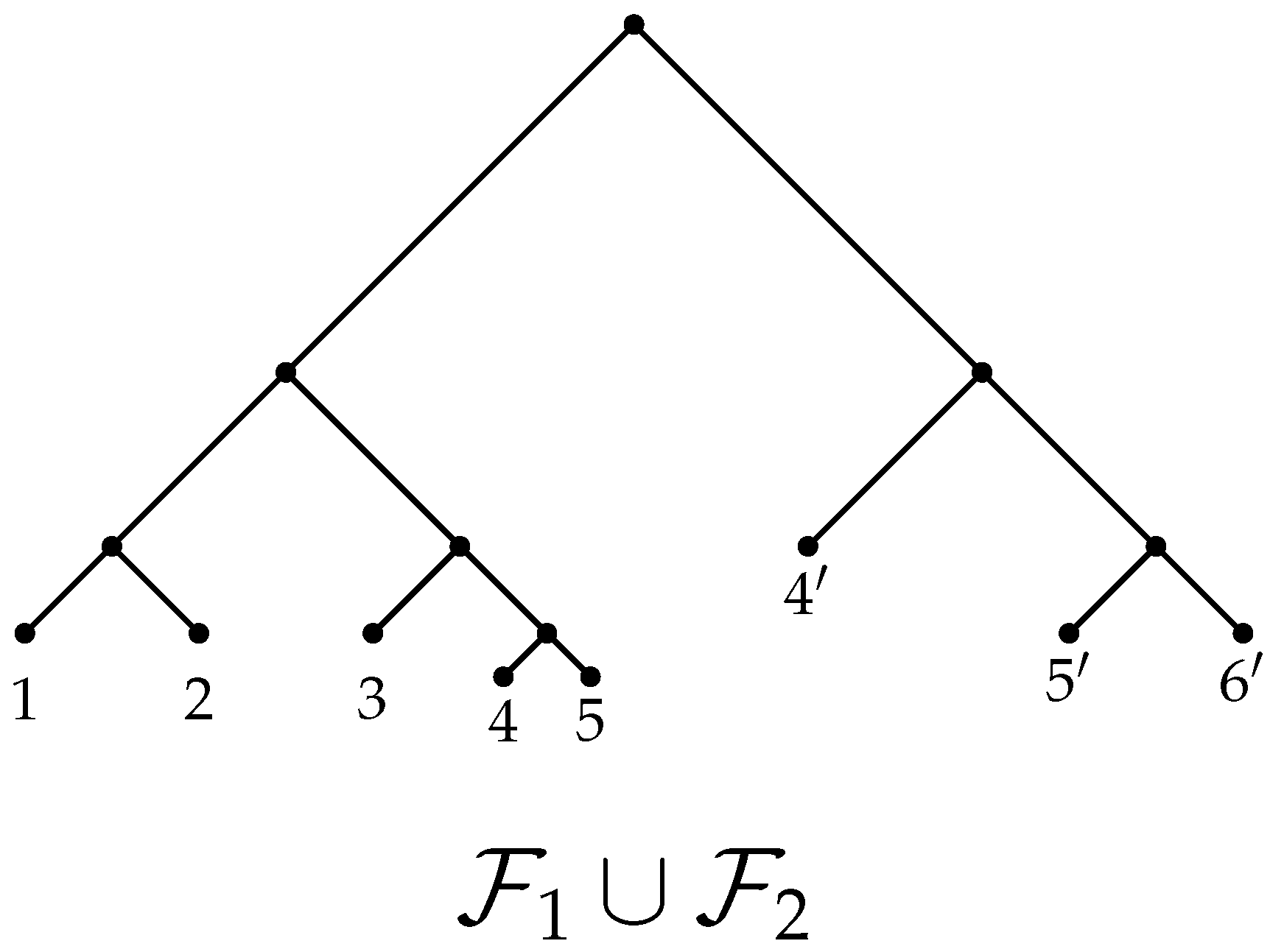
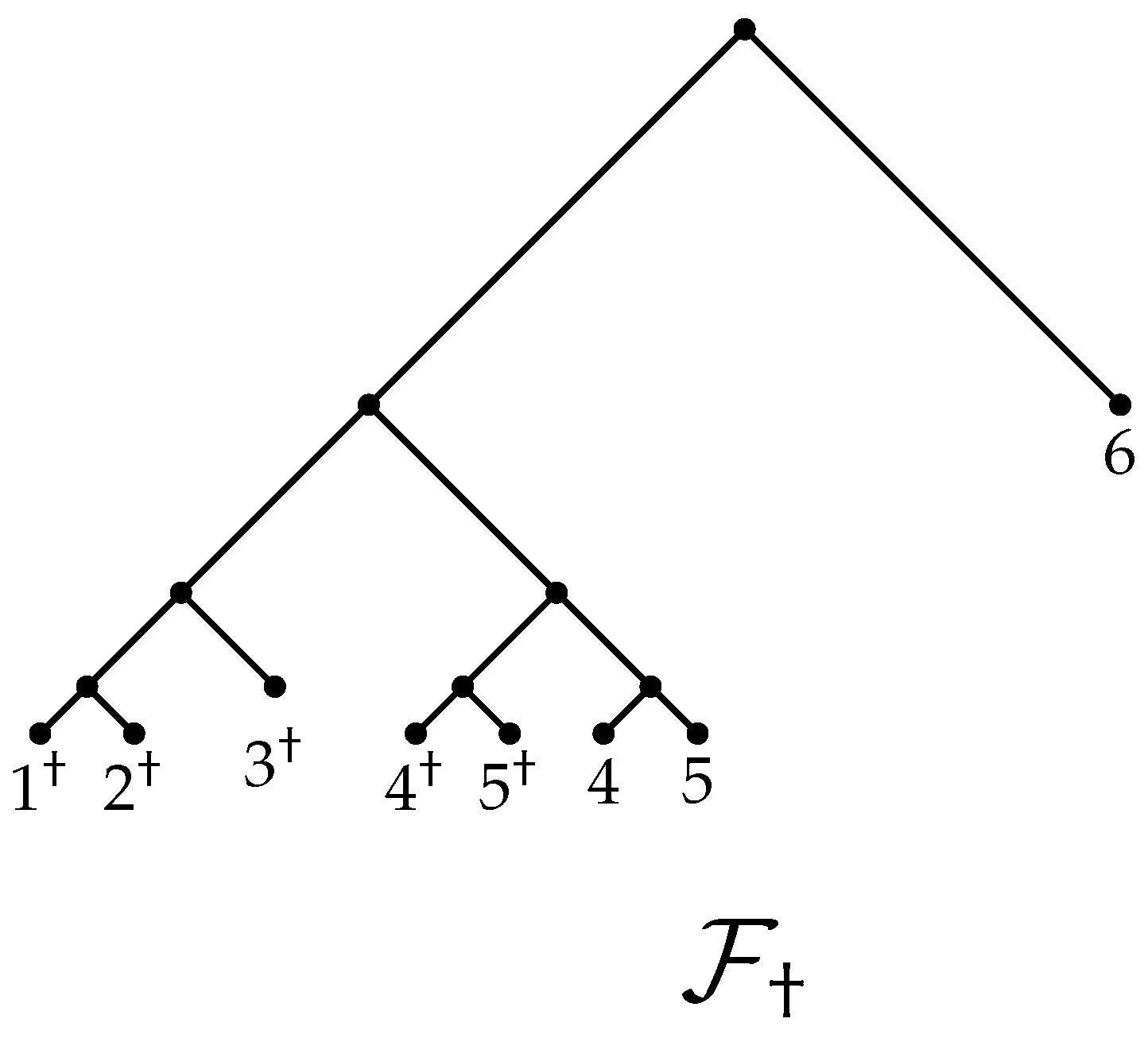
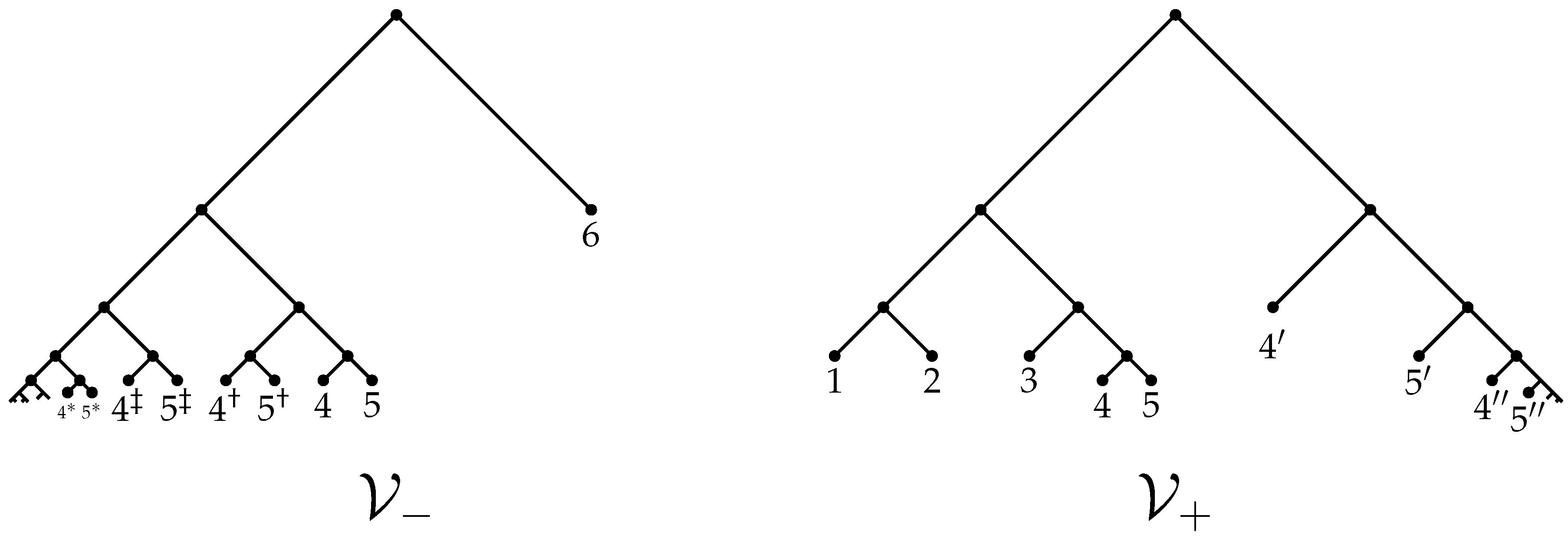
It turns out that is tidy above for x. To see this, Remark 1 tells us that it suffices to show that , where and . For this, observe that, since is the fixator of and is the fixator of , is the fixator of , see Figure 2. Furthermore, is the fixator of the tree shown in Figure 3 because x maps the vertices ,..., to the vertices 1,..., 5
; and is the fixator of the tree shown in Figure 4. ( includes the infinite path spanned by the images of the vertices 4
and 5
under positive powers of x. This is explained further in the next paragraph.) It follows that is the fixator of the tree . This intersection is equal to and so , which certainly contains . Therefore, is tidy above. To be consistent with the notation of Section 4.1, will now be denoted by V. It further turns out that , so that V (that is ) is tidy below as well. To see this, it suffices to show that, if and for some , then .
By definition, . As x is iterated, the vertices 4
and 5
are pushed down two levels of at a time and their images are at a distance 1
from a half-line descending from the vertex 6
, see Figure 4. This half-line is part of an “axis” for x that is translated down through distance 2
by x. Since V fixes the vertices 4
and 5
, the given element fixes the tree shown in Figure 4. By definition, . As x is iterated, the vertices 4
and 5
are carried across the tree until they are the children and of vertex 2
, and then pushed down one level of at a time, their images being at a distance 2
from a half-line descending from the vertex 1
, see Figure 4. This half-line is part of an “axis” for x that is translated up through distance 1
by x. Since V fixes the vertices 4
and 5
, fixes the tree , shown in Figure 4, which includes this half-line and all vertices within distance 2
of it. For the particular element v, we have that and so v fixes all vertices in below level N. Since v is a tree automorphism, it follows that v fixes all vertices on the half-line descending from vertex 1
. However, it does not follow that v fixes all images of vertices 4
and 5
above level N, and that must be shown in order to prove that . To show this, suppose for example that v interchanges the vertices and . Then, interchanges 4
and 5
, and so is in . However, interchanges and and so is not in . Similarly, does not belong to for any , which contradicts that . Hence, v fixes the vertices and . Similar arguments show that v fixes all images of 4
and 5
in , and hence that , as claimed. Since every for which there is with must be in , we have that and hence that V is tidy below for x. The scale of x is therefore equal to Just as for automorphism groups of trees, the calculation of the scale of the non-uniscalar involves identifying an ‘axis’ for x. This axis consists of two half-lines with finite trees attached, one of which is translated through distance 2
and determines an attracting end for x, while the other is translated through distance 1
and determines a repelling end. A dynamical description of the action of an almost automorphism may be used in general for the calculation of the scale, although the dynamics can be more complicated as there may be several (and different numbers of) attracting and repelling ends and the almost automorphism may permute some of them. As seen here, the scale depends on more than just the speed with which the axis is translated towards or away from the ends, but also on the “thickness” of the axis. A similar description of the dynamics of the action of almost automorphisms is given in [36], which develops ideas in [37].