Abstract
This paper gives a study of a two dimensional version of the theory of normal surfaces; namely, a study o normal curves and their relations with respect to geodesic curves. This study results with a nice discrete approximation of geodesics embedded in a triangulated orientable Riemannian surface. Experimental results of the two dimensional case are given as well.
1. Introduction
Motivated by the topological theory of normal surface we give in this paper a complete study of the relations between geodesic curves and normal curves embedded in a triangulated Riemannian surface.
Normal surface theory is a topological piecewise linear ( for short) counterpart of the differential geometric theory of minimal surfaces. This theory studies the ways surfaces intersect with a given triangulation of a 3-manifold. A surface is normal if it intersects the tetrahedra of a triangulation in a fairly simple manner. It was proved by Haken in [1] that every incompressible (i.e., topologically non trivial) surface embedded in a triangulated 3-manifold can be continuously deformed to a normal surface with respect to any given triangulation of the manifold.
Having the theory of normal surfaces, it is then desirable to interpret minimal surfaces in terms of normal surfaces. In this direction Jaco and Rubinstein presented in [2] a version, that is based on normal surfaces, of minimal and least area surfaces in a triangulated 3-manifold . It is shown in [2] that minimal and least area surfaces share many properties of classical minimal and least area surfaces. These results are the first to make precise the analogy between minimal and normal surfaces. However, the extent at which this analogy holds is far from being fully understood. For instance, the following two questions are very natural in this context, yet both of them are still open.
(I) Is it possible to subdivide a given triangulation of a 3-manifold arbitrarily fine, to obtain sequences of -minimal surfaces that converge in some suitable way to classical minimal surfaces?
An affirmative answer to the above question gives an alternative topological-combinatorial proof of many classical existence results of least area incompressible surfaces in 3-manifolds, such as those obtained for example in [3], using partial differential equations. Moreover, the use of existing algorithms for finding normal surfaces makes this topological-combinatorial result of computable algorithmic nature.
The second question is the following:
(II) Can every minimal surface in the smooth sense, be presented as a limit surface of a sequence of -minimal surfaces, appropriately constructed?
Answering these questions, at least partially will be the focus of two followup papers.
In this paper we will address these questions in one dimension lower. That is in the context of curves on surfaces. In particular the following theorems will be proved:
Theorem 1.
Let be a triangulated Riemannian surface. Then there exists a flow defined on the set of normal homotopy classes of curves that deforms each class to a geodesic curve in that class.
Theorem 2.
Let be a hyperbolic triangulated surface isometrically embedded in some . Let γ be a curve on Σ that is either a shortest geodesic between two given points p and q on Σ, in a homotopy class rel, or a shortest closed geodesic in a homotopy class in Σ. Then there exists a sequence of triangulated 2-submanifolds of , , each of them is a -approximation of Σ, and a sequence of -curves , each of which is normal with respect to so that converges to γ.
Theorem 1 gives rise to a curve shortening flow. Such flows are of major importance both theoretically and applicatively speaking, (see [4,5,6,7,8]). For instance, such flows are extensively used to identify malignant tissues in medical images and many other image segmentation problems.
In Section 2 we will give an essential preliminaries. This will include basic definitions and notations. In particular, normal curves will be defined in this section. Section 3 is devoted to the proof of Theorem 1. In Section 4 we will describe some experimental implementations of the curve shortening flow described in Section 3. These results will include some synthetic examples as well as examples in which this flow was tested on real data. In Section 5 Theorem 8 will be proved. In Section 6 we regard normal curves from the view point of the dual graph. Last, in Appendix A we will give a brief introduction to the theory of normal surfaces.
2. Preliminaries
2.1. Simplicial Complexes
Definition 1.
A collection K of simplices is called a simplicial complex if
- If , then .
- Let and let . Then .
- K is locally finite.
is called the underlying polyhedron (or polytope) of K.
Remark 1.
A triangulated manifold is regarded as a cell complex, and the complex structure is given by the triangulation.
Definition 2.
A complex is called a subdivision of K iff
- ;
- if , then there exists such that .
If is a subdivision of K we denote it by .
Let K be a simplicial complex and let . If L is a simplicial complex, then it is called a subcomplex of K.
Definition 3.
Let . Then
is called the star of .
If , then we define: .
Definition 4.
Let be a embedding of an m-complex K. Let be a positive continuous function. Then a map is called a δ-approximation to f if:
- There exists a subdivision of K such that
- , for any
- , for any and for all .
Definition 5.
Let be a triangulated m-manifold embedded in . Let be a simplex. The vertex map , is determined by , where v is a vertex of s. The linear extension of is called the secant map induced by , and it is denoted by .
2.2. Fat Triangulations
Definition 6.
- A triangle in is called -fat iff all its angles are larger than a prescribed value .
- A k-simplex , , is -fat if all its facets are -fat for some .
- A triangulation is fat if all its simplices are -fat for some .
The importance of fat triangulations is stressed by the following example.
Schwartz Lantern
The Schwartz lantern is given by the following:
Example 1.
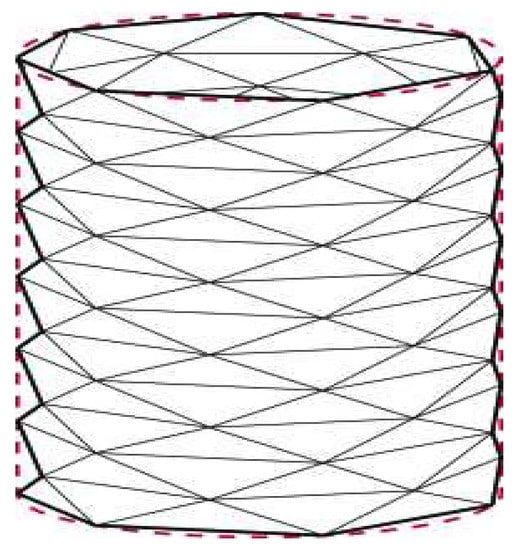
Let be the standard cylinder of hight 1 and radius 1 in . Let be the “lantern” that is given as the triangulated surface so that the vertices of its triangulation are placed on . Suppose the set of vertices of consists of points so that n points are evenly placed along the circle and points are placed along the vertical direction as indicated in the following Figure 1.

Figure 1.
Schwartz Lantern.
Simple computation shows that each of the triangles of has base length and hight . Following this, the area of the lantern thus satisfies:
As , , hence the following holds:
so blows up to ∞ as n goes to ∞. On the other hand, it can be shown that if the points are places so that the triangles of are fat then .
2.2.1. Existence Results
Existence of fat triangulations of Riemannian manifolds is guaranteed by the studies given in [9,10,11,12,13]. These are summarized below.
Theorem 3.
Every compact Riemannian manifold admits a fat triangulation [10].
Theorem 4.
Every open (unbounded) Riemannian manifold admits a fat triangulation [11].
Theorem 5.
Let be an n-dimensional Riemannian manifold with boundary, having a finite number of compact boundary components [13]. Then, any fat triangulation of can be extended to a fat triangulation of .
The motivation for having fat triangulations for manifolds in terms of -approximations is stressed by the following theorem.
Theorem 6.
Let be a triangulated m-manifold embedded in [14]. Then, for , there exist , such that, for any , fulfilling the following conditions:
- τ is -fat
then, the secant map is a δ-approximation of .
Definition 7.
Let be a Riemannian manifold. The Hausdorff metric is a metric defined on the set of compact subsets of by setting: , for any two compact subsets A and B, of , see [15].
2.3. Normal Curves
This section reviews essential background on normal curves. Most of definition and facts, even if some of them are new with respect to the existing literature, are merely obvious modifications of what is considered for surfaces, (See Appendix A). Along this subsection denotes a closed, smooth orientable surface , endowed with a triangulation , and a Euclidean or hyperbolic metric . We assume is a geodesic triangulation i.e., every edge of it is a geodesic arc between two vertices.
Definition 8.
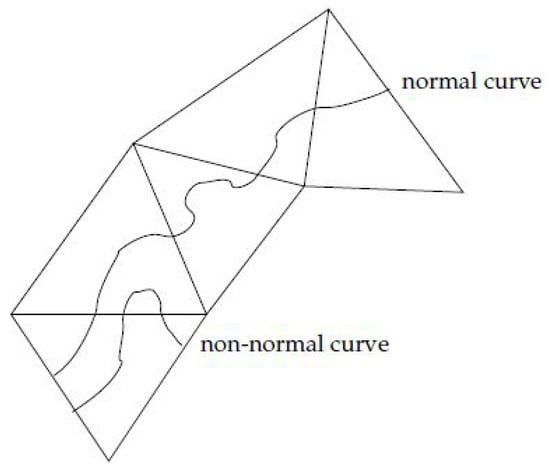
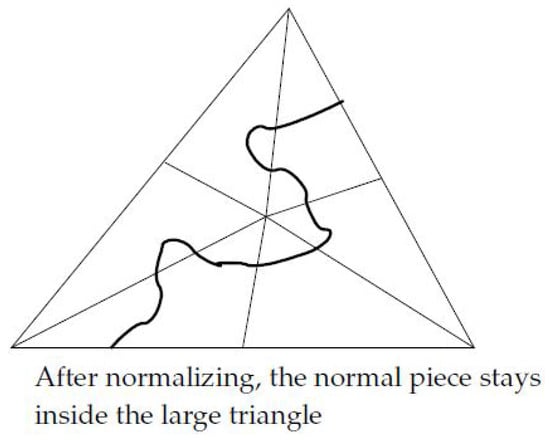
A normal curve is a curve so that each intersection arc of the curve with a 2-face is an arc that has its end points on two different edges of the 2-face. See Figure 2 below.

Figure 2.
Normal and not normal pieces.
2.4. Geometric Measures
2.4.1. Weight and Length
Let be a triangulated Riemannian surface and let be a rectifiable curve embedded in and transverse to . Define the weight of , to be the total number of intersection points of the curve with .
Definition 9.
- A curve embedded in Σ and transverse to will be called normally short iff its weight is minimal with respect to its homotopy class.
- A closed normal curve that is not null homotopic (a.k.a essential), is called normally shortest if its weight is minimal with respect to all homotopy classes of essential curves in Σ.
Unless mentioned otherwise, when dealing with curves with boundary, normally short/shortest will always be considered with respect to homotopy rel-∂-points.
Let be an embedded curve in transverse to . A local isotopy of is an isotopy which slides a non normal piece of across the edge intersected by this piece. Fix a given triangulation. Then the following facts hold:
- A normally short curve must be normal. This holds since if there exists a non-normal piece in some 2-face then it can be isotoped through the edge it intersects twice, thus reducing weight by at least two in contradiction to the minimality.
- For any close curve there exists a finite sequence of local isotopies which deforms the curve either to a normal curve or a curve which is completely included in just one triangle. In particular, if the curve is not null-homotopic, it is isotopic to a normal curve. This is true since the weight of a curve is an integer valued function which is bounded from below by zero, hence any curve is isotopic to some curve of minimal weight in its isotopy class which is either normal or has zero weight in which case it is entirely contained in a single 2-face.
2.4.2. Curvature
Definition 10.
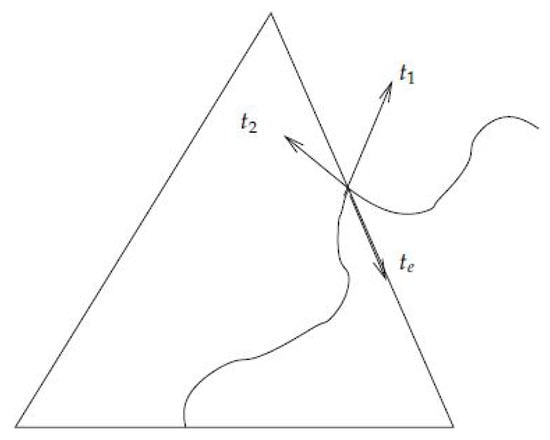
If Γ is a normal curve then its curvature , is defined as follows. At a point inside a 2-face it is given by the geodesic curvature at that point, and at a point which belongs to it is given by , where are the angles between the vectors , tangent to Γ, at that point, and the vector , which is tangent to the edge at this point. See Figure 3.

Figure 3.
Curvature at intersection with the 1-skeleton.
A normal curve is straight, if it has zero curvature at each intersection point with the edges of .
Lemma 1.
Let α be a piecewise smooth normal curve on a smooth triangulated surface . Suppose is an intersection point of the curve on the interior of some edge e, so that α is straight at x in the sense defined above. Assume, in addition, that the restriction of α to the two faces meeting along e are geodesic curves in these two triangles. Then the geodesic curvature of α at x exists and equals zero:
Proof.
Since the surface is smooth there exists well defined tangent plane for at x. Let be the tangent vector field defined along . Let the tangent vectors of and the tangent vector of e, all at the point x. Assuming that is a geodesic in both triangles meeting along e we have that , as , and the same holds while . In addition, since make an angle of at x, T is also well defined at x and we have that the covariant derivative of T w.r.t itself is given by
☐
Remark 2.
The curvature measure defined is a straight forward modification of the curvature measure defined in [2], for normal surfaces in 3-manifolds (see Appendix A), however Lemma 1 does not hold for surfaces in 3-manifolds. The difference between curves on surfaces and surfaces in 3-manifolds is basically the same as the difference between calculus in one variable to calculus in multiple variables.
Remark 3.
Following Cheeger and Ebin ([16]—Chapter 1), one has that if Γ is a rectifiable curve (i.e., of finite total length), which minimizes length with respect to small perturbations then it has to be straight at all intersection points with and each segment in , which connects two consecutive points in is a geodesic. Since each edge of is a geodesic segment, and since the surface Σ is hyperbolic, in particular there is a unique geodesic that connects every pair of points on Σ, it follows that if Γ is a curve which minimizes length then every segment of Γ either coincides with an edge of , or is a normal arc, or a union of such arcs.
3. Shortening Through Straightening
In this section we will present a new method for shortening curves that is defined on normal curves. We will show that this method gives rise to a flow under which a normal curve converges to a geodesic.
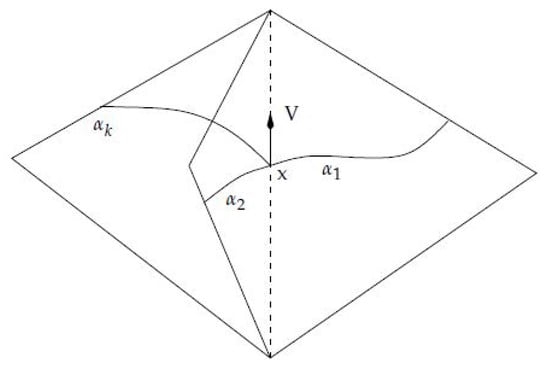
Let C be a rectifiable curve on a triangulated Riemannian surface . Before describing the following straightening procedure it is necessary to extend the definition of a straight curve so that the curve is allowed to go through a vertex. Suppose goes trough a vertex V of , then is straight at V if the two angles and , formed by at V, as shown in Figure 4, are equal.
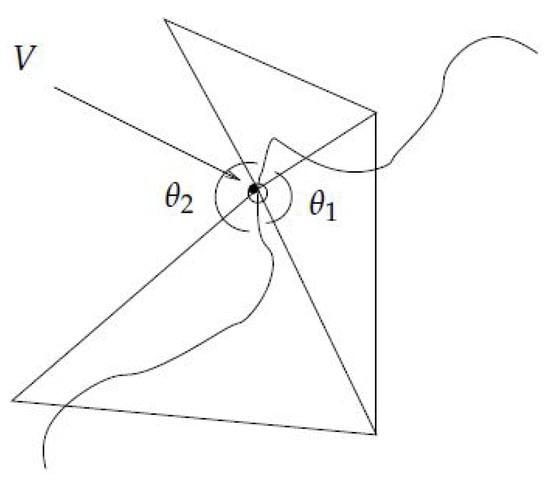
Figure 4.
Straight curve at a vertex.
Consider the following procedure.
- Normalize C with respect to . For the shortening procedure the definition of normal curves is altered a bit. A normal curve is allowed to go through a vertex of .
- Take a least-weight normal curve , isotopic to C.
- Straighten at all intersections with the edges of , except at vertices. If intersects a vertex then this point does not change.
- Subdivide , using the median subdivision, to obtain a new triangulation .
- Go to (1) while C is replaced by .
Remark 4.
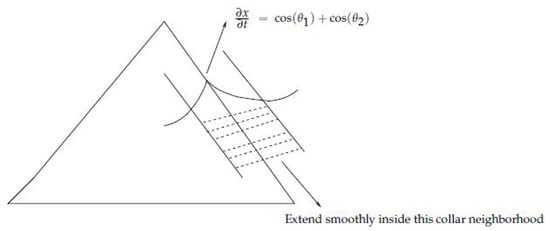
Step 3 is done by moving each internal point of a edge x, which belongs to according to,
where are as before. In particular case at which x is at an edge of angles and are measured with respect to some chosen direction vector on the tangent plane to Σ at x. Using a partition of unity we can smoothly extend this process inside some small collar neighborhood of , see Figure 5.

Figure 5.
Shortening by straightening.
Theorem 7.
The obtained sequence of straight curves converges to a smooth geodesic on Σ.
Proof.
Let denote the n-th subdivision where is the initial triangulation. Let be the mesh of . If x is an intersection point of with some edge of then the curvature at x is zero, for is assumed to be straight. Otherwise, x is a point on the interior of one of the normal pieces of inside some triangle . First, observe that at each iteration while normalizing is applied (Step above), each obtained normal arc is contained in the “parent” triangle of the triangle it pathes through, since it is a piece of a normal arc at the previous iteration, see Figure 6.

Figure 6.
A normalized piece.
Hence, since vertices are becoming dense in the surface, the obtained sequence of normal curves is a Cauchy sequence, so it converges to a limit curve in the topological completion of the space of normal curves on .
Claim 3.1.
The limit curve is a geodesic.
Proof.
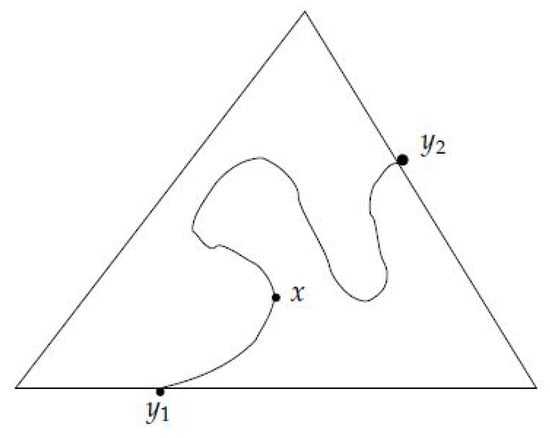
Let be some positive number. Let be some triangle of . Let be a normal piece inside , and let be the end points of that normal piece (Figure 7).

Figure 7.
The curvature inside a triangle.
According to Proposition of [17] since is rectifiable it has a Lipschitz parametrization, hence there exists a constant M so that,
In addition, since is a normal piece there is some so that is in the -neighborhood of in . Hence,
From Lemma 1 the curvature as defined is continuous, so there exists such satisfying,
therefore
Hence, if is the limit curve of the sequence , then at every point the geodesic curvature of is zero, so is a geodesic. ☐
This completes the proof of Theorem 7. ☐
Remark 5.
Normality of curves, is crucial and best illustrated by the lemma above for if the curve was not normal then we could not assume a bound on the arc length of its normal pieces, relative to the distance between and above, even when the division parameter λ gets very small.
4. Experimental Results
In this subsection some initial experimental results will be presented. This is the place to thank the students Chen Harel, Amir Gilad, Dima Serf and Gleb Lander from the Technion Electrical Engineering Department for their devoted work while programming the implementation of the curve shortening algorithm described above, in the course of their undergraduate studies. As an initial stage the dual graph of is built and a shortest path between the two triangles containing these points is found using the well known Dijekstra algorithm, see [18]. This shortest path in the dual graph corresponds to the minimal number of triangles one has to travel through in order to get from one point to the other. The obtained set of triangles is called the triangle path between the two points. A triangle path is illustrated in Figure 8 below, on a surface modelling a hand. In a second stage an initial guess for the shortest geodesic is chosen and then evolved according to the straightening algorithm above.
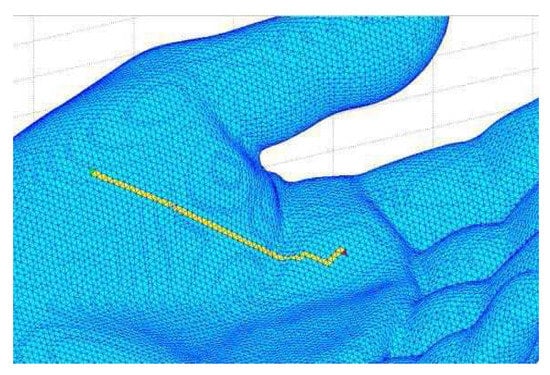
Figure 8.
Triangle path.
4.1. Synthetic Surfaces
The following two examples demonstrate the algorithm as tested on synthetic surfaces.
Example 2.
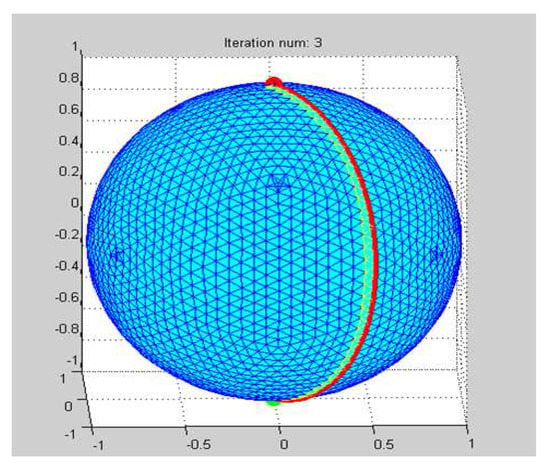
In Example 2 the algorithm is tested on a 2-sphere. Figure 9 shows the two antipodal points along with the obtained path are shown. The Path coincides with the half circle painted in red (the dark half circle following the bright one shown in the figure).

Figure 9.
Sphere.
Example 3.
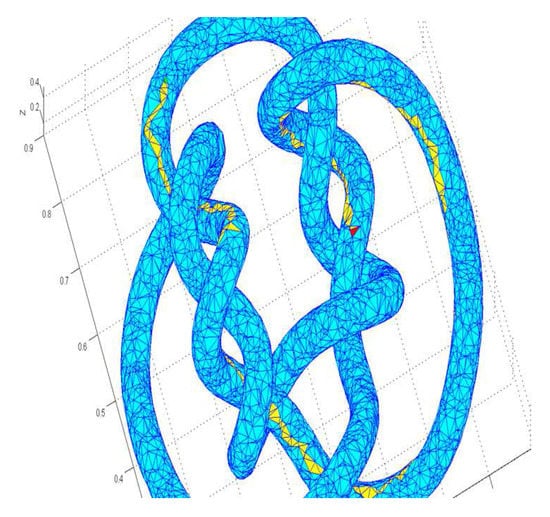
In Example 3 the algorithm is tested on a knotted torus. Figure 10 shows the obtained path.

Figure 10.
Knotted torus.
4.2. “Real” Data and Weighted Triangulation
As the Dijekstra algorithm for finding shortest path in a graph is suitable also to weighted graphs, where in this case a positive set of weights is assigned to the set of edges of the graph, and each weight reflects the cost of going through the specific edge. The algorithm above can be applied on weighted triangulations as well. A weighted triangulation is a triangulation endowed with a set of positive weights, assigned on the set of triangles, so that each weight reflects the cost it takes to path through the specific triangle when traveling from one chosen point to the other. Given this, the triangle path will be found using the weighted Dijekstra algorithm on the dual graph to the triangulation.
Example 4.
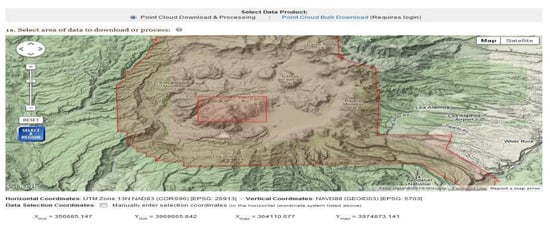
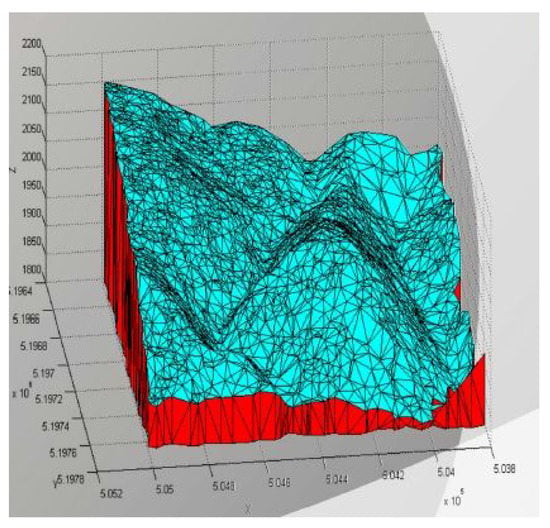
In Example 4 the algorithm is tested on a triangulated surface presenting a patch of the surface of the Earth. A chosen area in the Neveda Desert is represented as a triangulated surface. Figure 11 presents the overall area from which the examples are taken. Figure 12 shows an example of the extracted triangulated surface representing a chosen patch in the overall area.

Figure 11.
Overall area.

Figure 12.
Triangulated surface of the Earth.
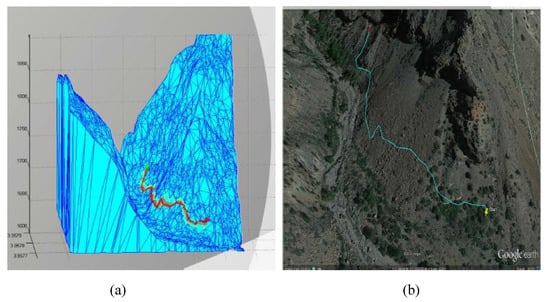
The weight on each triangle is proportional to its height. Figure 13 shows the obtained path between a chosen pair of points.

Figure 13.
Earth route.
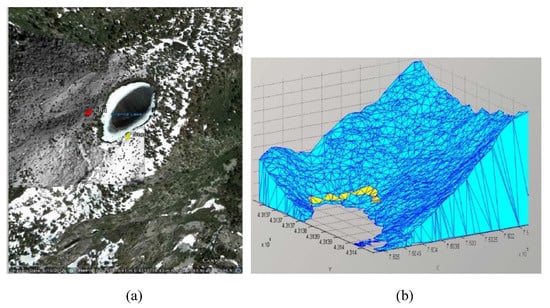
The Following Figure 14 shows the outcome of the algorithm in the presence of an obstacle. The chosen points are located on two sides of a lake, and the obtained route indeed avoids the lake.

Figure 14.
Walk around a lake.
5. Approximations of Geodesics
Theorem 8.
Let Σ be a hyperbolic surface isometrically embedded in some . Let γ be a curve on Σ that is either a shortest geodesic between two given points p and q on Σ or, a shortest closed geodesic in Σ. Then there exists a sequence of 2-submanifolds of , , each of them is a -approximation of Σ, and a sequence of -curves , each of which is normal with respect to so that converges to γ.
Proof.
The -approximation is given by the secant map as in Definition 5. Recall that according to Remark 3 every shortest path is a collection of normal pieces and pieces that coincide with edges of . Each normal piece of can be projected to a linear normal piece on a planar triangle of the secant approximation exactly in the same way as was done for surfaces. Every piece that coincides with an edge is projected onto the corresponding edge of the secant approximation of . This projection yields the sequence of curves that approximates . ☐
6. Reflections in the Dual Graph
Let be a normal curve on the triangulated surface . Suppose are two fixed points on interior in some two 2-cells, , respectively. It is possible that . Then naturally defines a weighted path in the dual graph of , in the following way.
- Each vertex of the dual path corresponds to a triangle intersected by .
- Each edge of is assigned to an edge of at which crosses from one 2-cell to an adjacent one.
- Each edge of is weighted according to the number of times crosses through the corresponding edge of .
- The length of is defined to be the sum of weights of all its edges.
Remark 6.
It is essential at this context to consider curves that are normally shortest, since while proving some of the following lemmas isotopy classes may change.
Lemma 2.
Let γ be a normally shortest curve that is either a simple closed curve or a curve that connects two given distinct points, p and q. Then, γ has at most one normal piece in every triangle of .
Proof.
Suppose conversely, that there is some triangle the intersection of which with is made of more than one normal piece. For simplicity suppose for the moment that it is made of two normal pieces. The general case will easily follow. Endowing the curve with an orientation, gives rise to four different types of such intersection patterns. In any of the following figures, the numbering of the points on the edges of is according to their order with respect to the chosen orientation.
- Two parallel intersections: passes through twice between the same two edges of with the same orientation.
- Anti parallel intersection: as in yet, with opposite orientations.
- Non parallel: Only one pair of points is on the same edge.
In any of the four cases the point 1 is connected to 4. A distinction will now be made between simple close curves and curves with boundary.
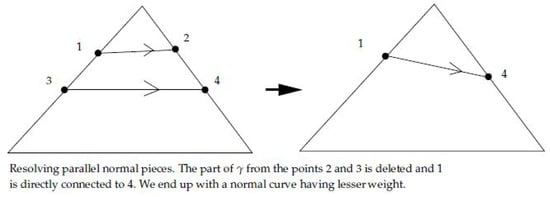
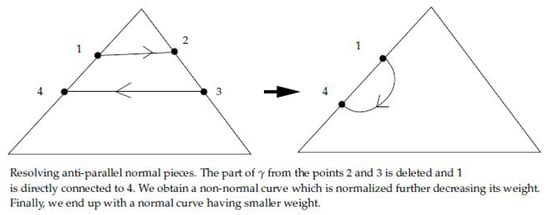
If , then by doing the above replacement another curve is obtained that also connects p to q which may or may not stay normal with respect to the triangulation yet, its weight is strictly smaller than the weight of . In case it is not normal it is normalized while further reducing weight. All in all, a normal curve is obtained, which connects the two ∂-points and has a lesser weight than in contradiction to the fact that is normally shortest. Refer to Figure 15 and Figure 16 for two typical examples.

Figure 15.
Resolving parallel components.

Figure 16.
Resolving non parallel components.
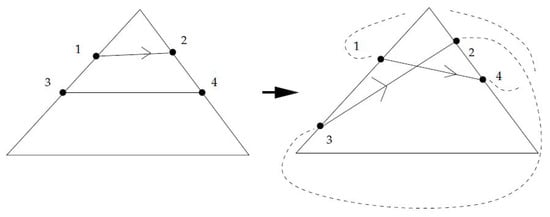
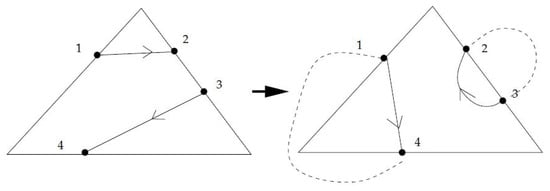
If is a simple close curve then in addition to connecting point 1 to 4, then the point 3 is connected to 2. This way two simple close curves and are obtained , that either intersect each other at some point inside or they are disjoint in , as seen in Figure 17 and Figure 18, showing the typical possibilities in this case. This of course depends on the way passes through .

Figure 17.
Intersecting closed curves.

Figure 18.
Disjoint closed curves.
Suppose . In this case both of them are normal with respect to , and it is necessary to show that at least one of them is essential. If say, is null homotopic in it must separate a disk in but then by the Jordan curve theorem it must intersect with at an additional point as well. This intersection point has to be outside of but, the parts of both and outside of the triangle coincide with the pieces of the initial curve , therefore has a self intersection point and this contradicts the assumption that it is simple.
Suppose now that and are disjoint from each other, and suppose both of them are null homotopic in . In this case the initial curve can be reproduced as a connected sum of and inside the triangle , thus making null homotopic in contradiction to its being essential. Suppose is essential. Still, as indicated in the Figure 18, it may happen that is not normal. In this case it is further normalized until a normal simple closed curve is obtained. This normal curve has strictly less weight than the initial curve , again forming a contradiction.
The same argument will go also for the general case of more than two normal pieces inside a triangle thus completing the proof. ☐
Lemma 3.
A path in the dual graph for which all weights along its edges are equal to 1 is realizable as a normal curve with respect to .
Proof.
The proof is obvious by assigning a normal piece to every pair of consecutive edges along the path. ☐
Theorem 9.
A normal curve is normally shortest if and only if its corresponding dual path is a shortest path according to the length function defined in Section 6.
Proof.
From Lemmas 2 and 3 there is a correspondence between unitary normal curves, i.e., curves that have at most one normal piece inside each triangle, and unitary pathes in the dual graph, i.e., paths for which the weight along each edge is one, so that, the weight of each normal curve, is equal to the length of its dual path and vice versa. The proof thus follows. ☐
Corollary 1.
There is an algorithm which finds in finite time a normally shortest curve on a triangulated surface.
Proof.
For a start find a least-weight dual curve in the dual graph using one of the numerous existing algorithms, such as the Dijekstra algorithm. Afterwards we use Theorem 9 to find its realization as a least-weight normal curve. A rough estimation on the complexity of this algorithm shows that it is in the order of the complexity of finding the least weighted curve in the dual graph times the complexity of building the dual graph. Building the dual graph is proportional to the number of triangles in the original triangulation while the complexity of say, Dijekstra algorithm is in the magnitude of , where n is the number of vertices in the dual graph which is equal to the number of triangles in the original graph. All in all a rough estimation of the complexity of the algorithm is . ☐
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. Normal Surfaces
In this section we will give some preliminary definitions and notations from normal surface theory that will be used later in this work.
Normal surfaces were first introduced in the study of 3-manifolds by H. Kneser [19], in the early 1930’s. Kneser used normal surfaces for his proof of the existence of prime decomposition of 3-manifolds. Normal surfaces were further used by W. Haken in the 1960’s [1], while giving Haken the possibility to develop a combinatorial viewpoint on topological problems such as the recognition of the unknot and other problems related to 3-manifolds, in the aim of producing computable algorithms. Nowadays, normal surfaces are extensively used and studied in overall aspects of 3-manifold topology and geometry, yielding more and more results and algorithms. The novice reader should look into [1,20]. Among other things, there is an algorithm that uses normal surfaces in order to decide in finite time whether or not a given 3-manifold is Haken, see [21].
Throughout this section will denote a 2-dimensional surface, , embedded in 3-manifold , which admits a triangulation, .
Definition A1.
An isotopy is a normal isotopy with respect to a given triangulation , if for every and for all simplices . We further say that two submanifolds of are normally isotopic if there exists a normal isotopy which carries one to the other.
Definition A2.
Let denote a tetrahedron of a given triangulation and let denote a face of . A normal arc in , is an arc properly embedded in , such that its end points are on two different edges of . A normal curve in , is a curve properly embedded in , transverse to the edges of , so that its intersection with each 2-face consists of collection of normal arcs. A normal disk is a disk , properly embedded in a tetrahedron such that , is a simple closed normal curve in . An elementary disk is a normal disk so that its boundary is either a triangle that separates one vertex on , from all three other vertices , or a quadrilateral (quad for short) that partitions the vertices of the tetrahedron into two separated pairs.
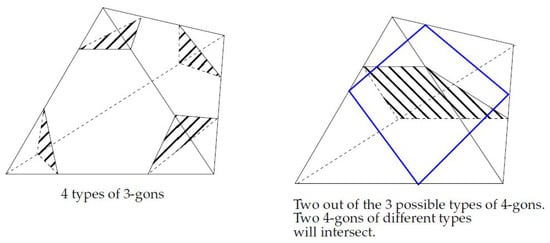
Elementary disks are illustrated in Figure A1, and they come in seven different types corresponding to seven possibilities to partition the set of vertices of a tetrahedron into subsets according to the definition. In the sequel we will sometimes refer to the boundary of an elementary disk as a 3-gon or 4-gon according to its being a triangle or a quad, and for a general normal disk we may refer to its boundary as an n-gon.
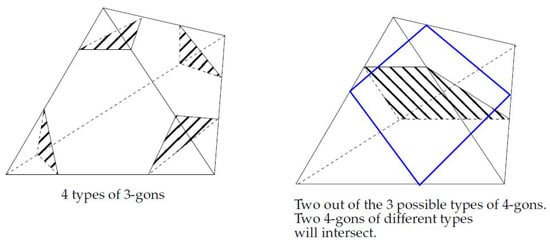
Figure A1.
Elementary disks.
Definition A3.
A surface properly embedded in is normal with respect to if it is transverse to the skeleta of , and if its intersections with any of the tetrahedra of is composed of a (possibly empty) collection of disjoint elementary disks.
Note that since the surface is embedded, we can have only one type of 4-gon at each tetrahedron.
Appendix B. Possible Normal Disk Types
The length of a normal curve is the number of normal arcs consisting it. Recall that the boundary of a normal disk is a simple closed normal curve on the boundary of a tetrahedron that forms a polygon. A thorough analysis of the possible length such a polygon can have, was done by Thompson and Stocking in [20,22] respectively. It is summarized as follows.
Lemma A1.
If is a normal disk then is an n-gon where n is either 3, 4 or an even number [20,22].
Figure A3 shows an example of a normal disk whose boundary is of length eight.
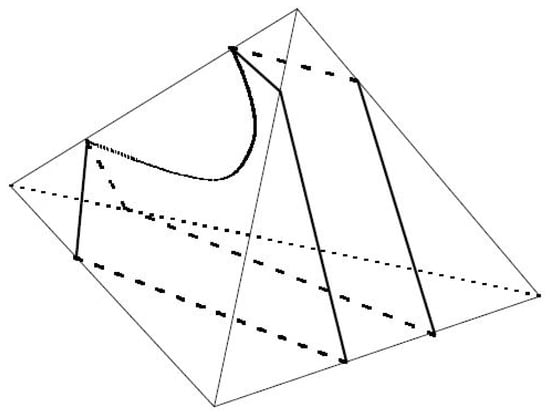
Figure A3.
Octagon normal disk.
Appendix C. Weight and Area
Definition A4.
Let be a surface properly embedded in and transverse to the skeleta of , ( needs not be normal).
- The weight , of is the total number of intersections of the surface with the 1-skeleton .
- A metric on each 2-face of is induced by identifying the face with an ideal triangle in the hyperbolic plane . As a result we can measure the length of each arc in . The length , of is defined as the total sum of lengths of all arcs in .
- The area of is defined as the ordered pair , lexicographically ordered.
Definition A5.
- A surface is called least weight iff its weight is minimal amongst all surfaces in its isotopy class.
- A normal surface is called a -minimal surface iff its length is a stationary point with respect to small variations in its normal isotopy class.
- A surface is of -least area surface iff its area is minimal in its isotopy class.
Definition A5 above is equivalent to the following. If , is a small variation of , and , and suppose . Then, is normally minimal if,
where, .
Notice that each two normally isotopic surfaces have the same weight. In addition, one can show that a least weight surface must be normal. Using this observation, the generality of normal surfaces is stressed by the following theorem,
Theorem A1.
([1,2]) Let be a surface properly embedded in a 3-manifold . Then, for any triangulation , of , there is a finite sequence of compressions, ∂-compressions and local isotopies, that deforms into a(possibly empty) set of surfaces that are normal, w.r.t. , and another (maybe empty) set of surfaces, each of which is entirely contained in a single tetrahedron of . In particular, if is irreducible, and is incompressible and ∂-incompressible, then it is isotopic to a normal surface.
Remark A1.
The natural candidate for a surface to be isotoped to, is a least weight surface in an isotopy class. From the proof of Theorem A1 one immediately obtains that a least weight surface is normal. Furthermore, Theorem A1 reflects nicely the analogy between normal surfaces and minimal surfaces. In [23,24,25] Meeks and Yau make a thorough study of minimal and least area surfaces in 3-manifolds and using partial differential equations techniques they show among other things that an incompressible surface is isotopic to a least area surface. Hence, in a way Theorem A1 can be regarded as a combinatorial counterpart of this result.
Appendix D. Curvature of Normal Surfaces
Let be a normal surface in the triangulated 3-manifold . In [2] a piecewise smooth mean curvature vector field, H, is defined on the intersection of a normal surface in the following way.
Definition A6.
Suppose α is some arc of and x is a point on α.
- If x is a point of lying in the interior of a 2-simplex, then definewhere here stands for the tangent vector of α at x and ∇ denotes covariant derivative. Hence, at an internal point is the geodesic curvature of α considered as an arc embedded in a triangular face of the triangulation (assume α is arc-length parameterized).
- If is an end point of α, let be all arcs of emanating from x, and definewhere is the tangent vector of at x and is a vector tangent to the edge e of T where x is included. here is the sum of all co-sines of the angles between the s and .
Using first and second variations, it is shown in [2] that is a PL minimal surface iff .
Appendix E. Mean Curvature Flow
As mentioned earlier classical results about the existence of least area surfaces such as [3] are based on techniques of partial differential equations. In particular, they are based on the analysis of the following mean curvature flow equation. Let be a smooth surface embedded in a Riemannian 3-manifold . Then the mean curvature flow is defined by the evolution equation, see [26]:
That is, every point of moves in the direction of the normal vector at that point, and at velocity that is proportional to the mean curvature at that point. In contrast, based on the definition of -minimal and -least area surfaces, as well as on the definition of curvature for normal surfaces, Jaco and Rubinstaein deduced, in [2], a version of the mean curvature flow. By the analysing it they where able to obtain the following existence theorem for -minimal surfaces: A vertex linking sphere in a triangulated 3-manifold is a normal 2-sphere that is the boundary of a small 3-ball around a vertex of .
Theorem A2.
([2]) In the normal homotopy class of any normal surface , that is not a vertex linking sphere, there exists a -minimal surface.
Remark A2.
In the theorem above Jaco-Rubinstein also claim uniqueness of the surface; however, since the definition of -minimal as well as -least area surfaces does not account for the interior of the normal disks, the uniqueness argument in [2] holds only with respect to the boundary of any normal disks while the interior of the disk may vary. In [27] the definition of a -minimal surface is altered by putting an additional constraint that the interior of each normal disk in , is a minimal surface in the usual differential geometric sense.
With this altered definition of -minimality it is shown,
Theorem A3 ([27])
There is exactly one -minimal surface in a normal homotopy class of any normal surface that is not a vertex linking sphere.
Appendix F. -Minimal Surfaces and Approximation of Least Area Surfaces
The above existence theorem gives hope that the answer to Question II, that was raised in the introduction, is affirmative. That is, it is possible to represent a least area surface as a limit surface of a sequence of -minimal surfaces. A seemingly natural approach to prove such an affirmative answer would be the following: Show it is possible to build a sequence of triangulations of the manifold , of decreasing mesh, so that the given least area surface is normal with respect to each of these triangulations. Then, based on the above theorem, take the -minimal representative of the least area surface, inside its normal homotopy class, with respect to each of the triangulations. This way one obtains a sequence of -minimal surfaces that should converge to the least area surface. However, as the mesh of the triangulations decreases it may very well happen that the given least area surface will become arbitrarily close to vertices of triangulations in the sequence. This pose a major problem. In the proof of Theorem A2 above it is shown that a surface which is -minimal with respect to some triangulation cannot get close to the vertices of that triangulation. Therefore, whenever the least area surface is close to a vertex it will remain far away from all -minimal surfaces. Since any natural way to define convergence of a sequence of surfaces to some limit surface will evidently require that the surfaces in the sequence will become close, in some natural manner, to the limit surface, the constrain presented here prevents us from obtaining an affirmative answer to Question II. In two consecutive papers Question I and II will be addressed in the case of normal surfaces.
References
- Haken, W. Theorie der normalflachen. Acta Math. 1961, 105, 245–375. [Google Scholar] [CrossRef]
- Jaco, W.; Rubinstein, J.H. PL-Minimal surfaces in 3-manifolds. J. Differ. Geom. 1988, 27, 493–524. [Google Scholar] [CrossRef]
- Meeks, W.H., III; Simon, L.; Yau, S.T. Embedded minimal surface, exotic spheres and manifolds with positive ricci curvature. Ann. Math. 1982, 116, 621–659. [Google Scholar]
- Caselles, V.; Kimmel, R.; Sapiro, G. Geodesic Active Countours. Int. J. Comput. Vis. 1997, 22, 61–79. [Google Scholar] [CrossRef]
- Grayson, M. Shortening embedded curves. Ann. Math. 1989, 129, 71–111. [Google Scholar] [CrossRef]
- Grayson, M. The heat equation shrinks embedded curves to round points. J. Differ. Geom. 1987, 26, 285–314. [Google Scholar] [CrossRef]
- Hass, J.; Scott, P. Shortening Curves on Surfaces. Topology 1994, 33, 25–43. [Google Scholar] [CrossRef]
- Kimmel, R.; Malladi, R.; Sochen, N. Images as embedded maps and minimal surfaces. Int. J. Comput. Vis. 2000, 39, 111–129. [Google Scholar] [CrossRef]
- Breslin, W. Thick triangulations of hyperbolic n-manifolds. Pacific J. Math. 2009, 241, 215–225. [Google Scholar] [CrossRef]
- Cairns, S.S. A simple triangulation method for smooth manifolds. Bull. Am. Math. Soc. 1961, 67, 389–390. [Google Scholar] [CrossRef]
- Peltonen, K. On the Existence of Quasiregular Mappings; Annales Academiae Scientiarum Fennicae. Series A. I, Mathematica, Dissertationes; Suomalainen Tiedeakatemia: Helsinki, Finland, 1992. [Google Scholar]
- Saucan, E. The existence of quasimeromorphic mappings in dimension 3. Conform. Geom. Dyn. 2006, 10, 21–40. [Google Scholar] [CrossRef]
- Saucan, E. Note on a theorem of Munkres. Mediterr. J. Math. 2005, 2, 215–229. [Google Scholar] [CrossRef]
- Munkres, J. Elementary differential topology; Princeton University Press: Princeton, NJ, USA, 1966. [Google Scholar]
- Morvan, J.-M.; Thibet, B. Approximation of the normal vector field and the area of a smooth surface. Disc. Comp. Geom. 2004, 32, 383–400. [Google Scholar] [CrossRef]
- Cheeger, J.; Ebin, D. Comparison Theorems in Riemannian Geometry; North-Holland Mathematical Library; American Mathematical Society: Providence, RI, USA, 1975; p. 9. [Google Scholar]
- Sullivan, J.M. Curves of finite total curvature. Disc. Diff. Geom. 2008, 38, 137–161. [Google Scholar]
- Dijekstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Kneser, H. Geschlossene flachen in drei-dimesnionalen Mannigfaltigkeiten. Jahresbericht der Deutschen Mathematiker-Vereinigung 1929, 38, 248–259. [Google Scholar]
- Thompson, A. Thin position and the recognition of 𝕊3. Math. Res. Lett. 1994, 1, 613–630. [Google Scholar] [CrossRef]
- Jaco, W.; Oertel, U. An Algorithm to decide if a 3-Manifold is a Haken Manifold. Topology 1984, 23, 195–209. [Google Scholar] [CrossRef]
- Stocking, M. Almost normal surfaces in 3-manifolds. Trans. Am. Math. Soc. 2003, 352, 171–207. [Google Scholar] [CrossRef]
- Meeks, W.H., III; Yau, S.T. Topology of three dimensional manifolds and the embedding problem in minimal surface theory. Ann. Math. 1980, 112, 441–484. [Google Scholar] [CrossRef]
- Meeks, W.H., III; Yau, S.T. The Classical Plateau problem and the topology of three dimensional manifolds. Topology 1982, 21, 409–442. [Google Scholar] [CrossRef]
- Meeks, W.H., III; Yau, S.T. The Existence of embedded minimal surfaces and the problem of uniqueness. Math. Z. 1982, 179, 151–168. [Google Scholar] [CrossRef]
- Huisken, G. Flow by mean curvaature of convex surfaces into spheres. J. Differ. Geom. 1984, 20, 237–266. [Google Scholar] [CrossRef]
- Ni, Y. Uniqueness of PL minimal surfaces. Acta Math. Sin. 2007, 23, 961–964. [Google Scholar] [CrossRef]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).