Tactical Size Unit as Distribution in a Data Farming Environment
Abstract
:1. Introduction
2. The Platoon as Entity in Simulation Models
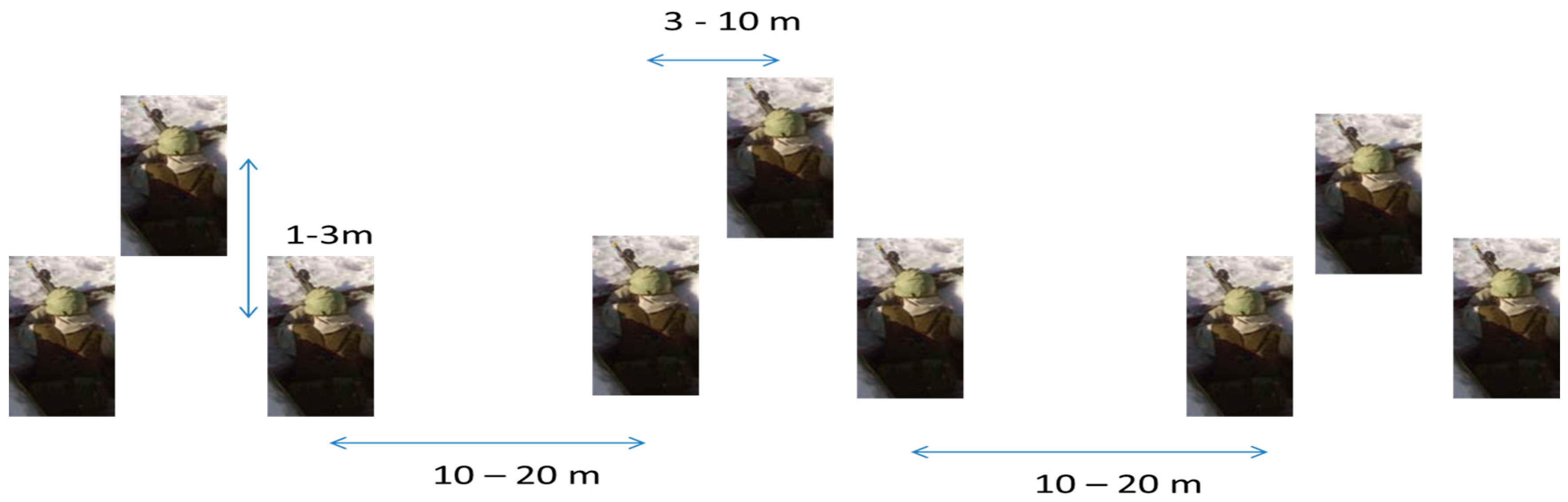
2.1. Conceptual Model of an Infantry Platoon
2.2. Computational Model
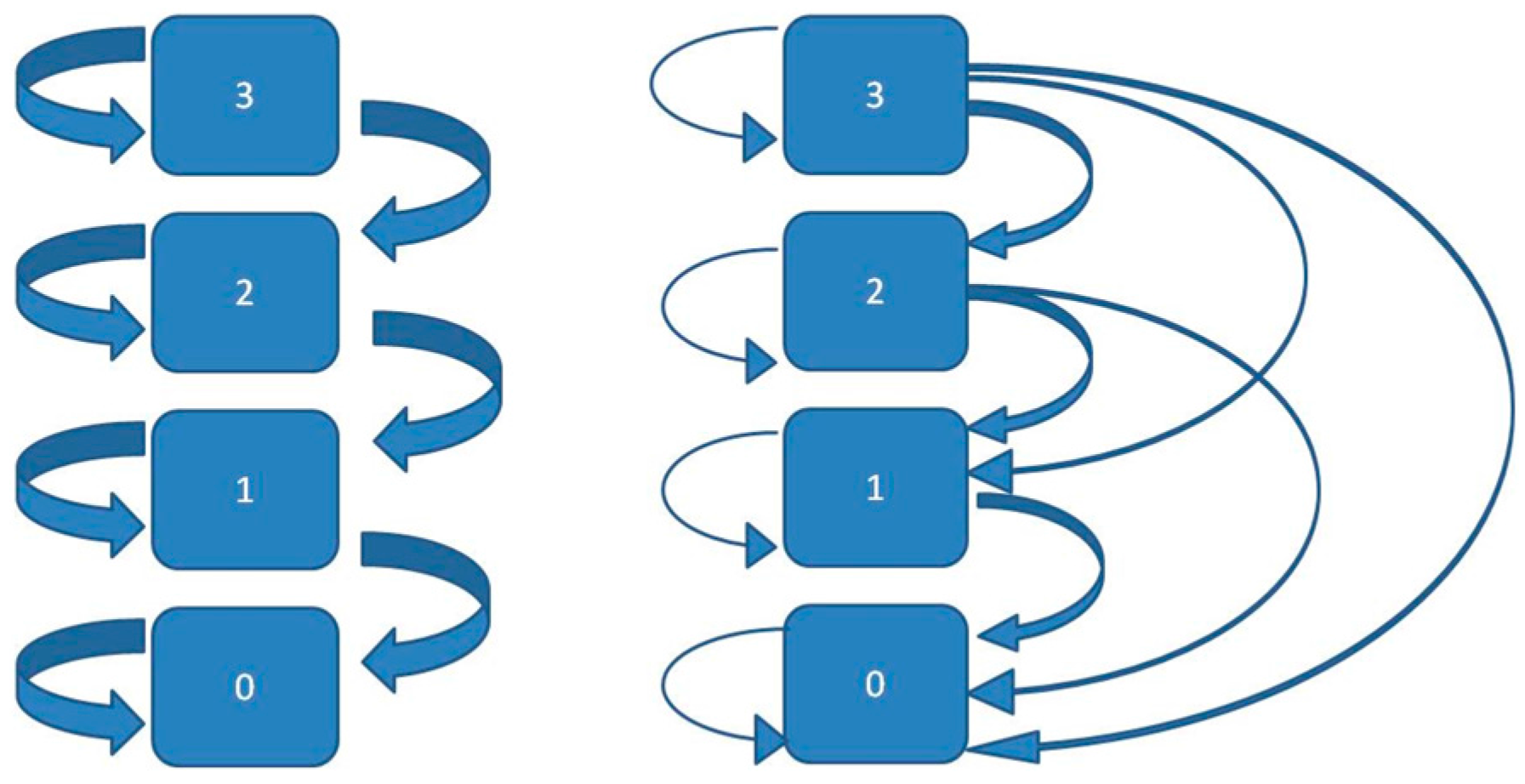
2.2.1. Markov Model for Strength Distributions
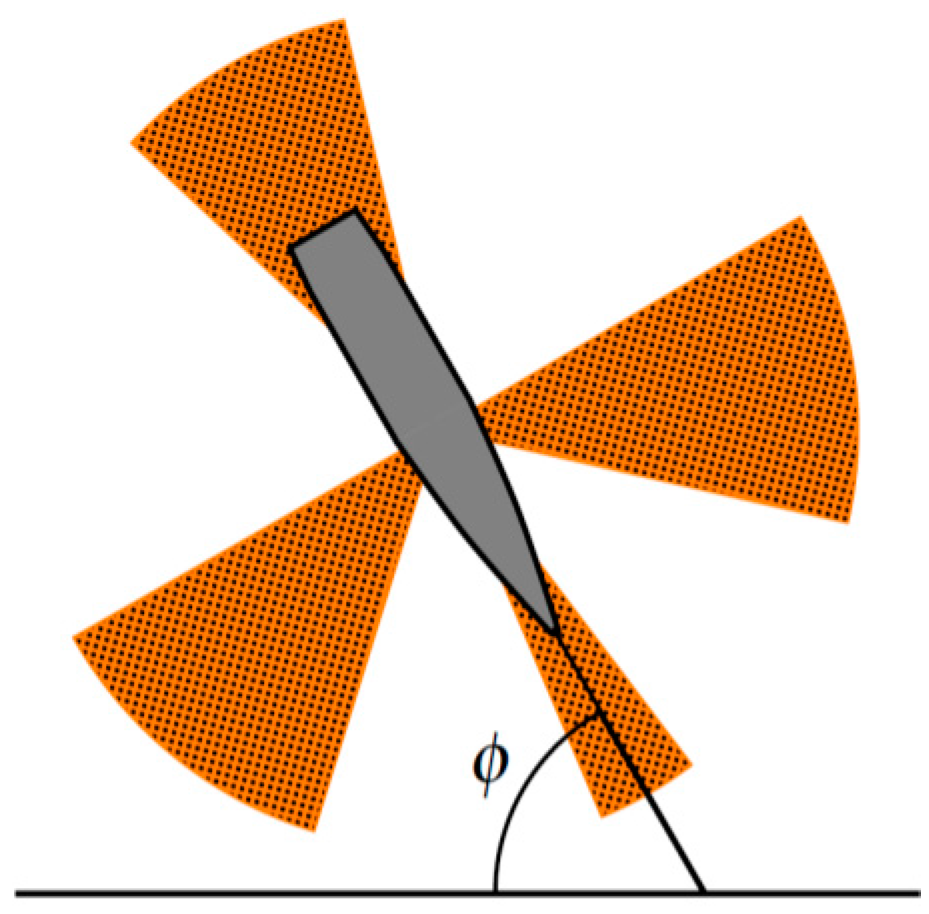
2.2.2. Model for Areal Distribution of the Unit
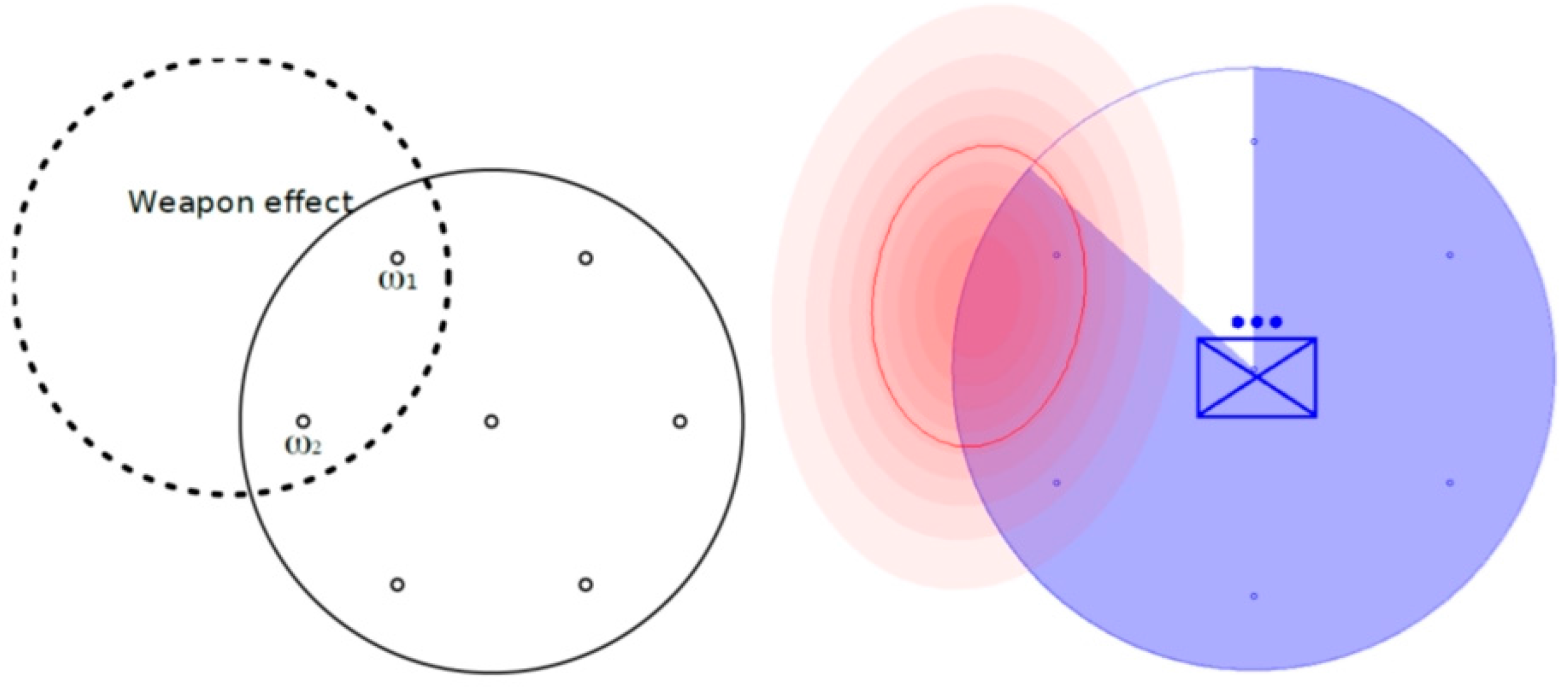
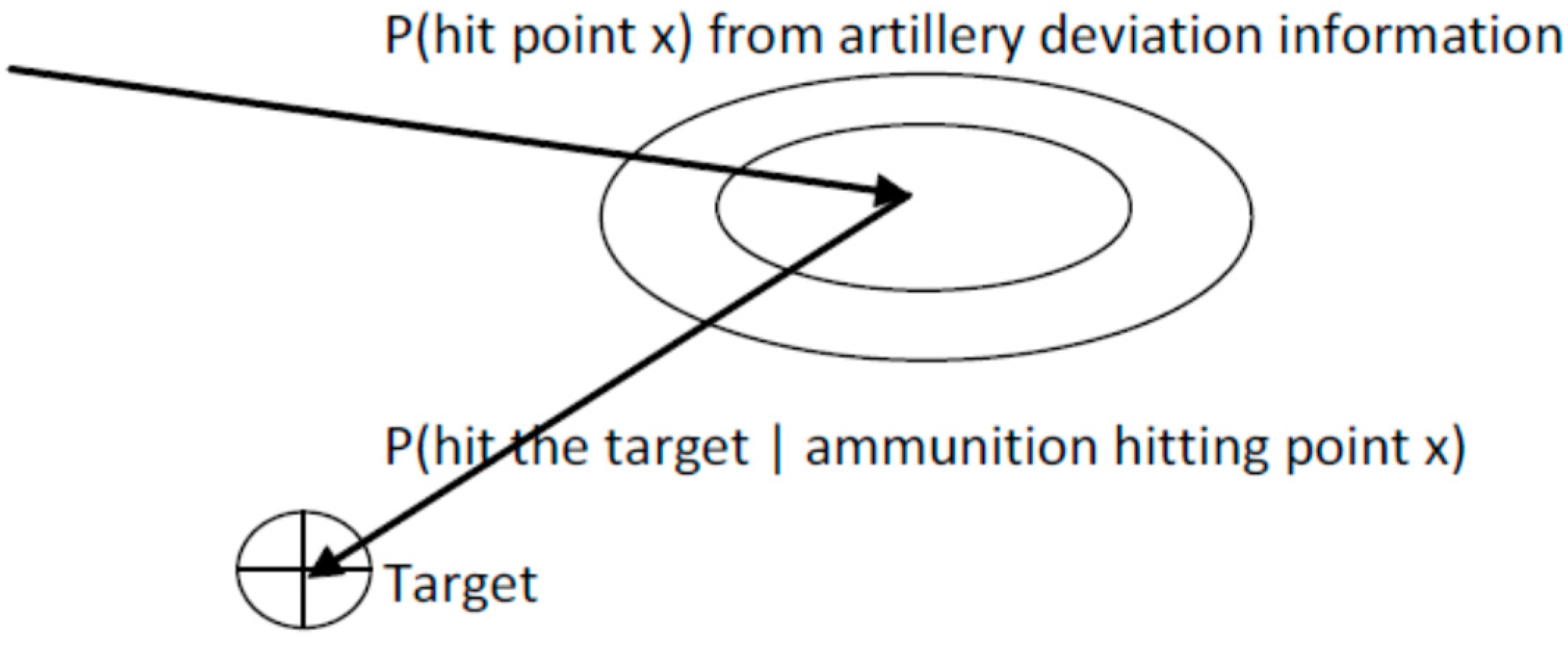
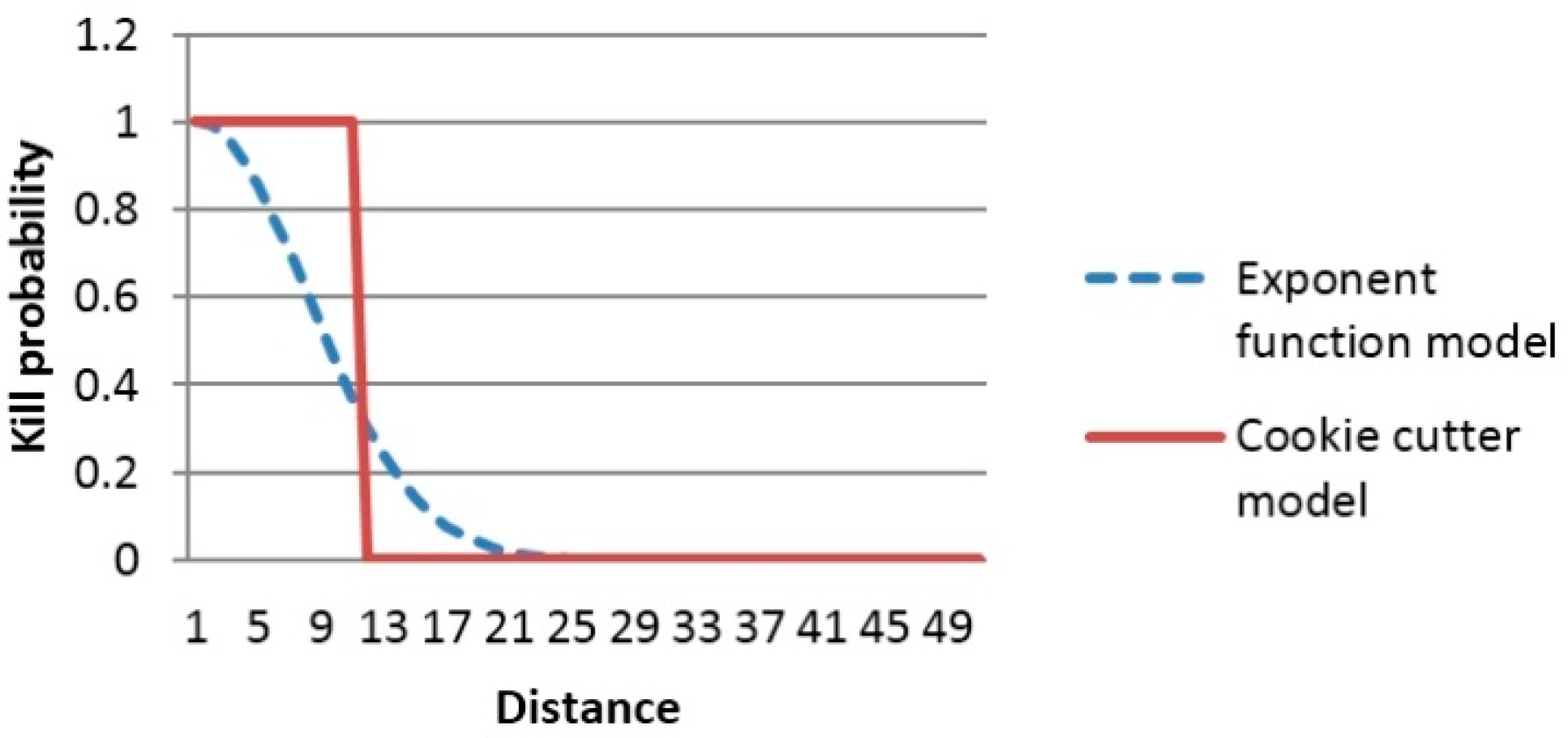
2.2.3. Model for Indirect Fire
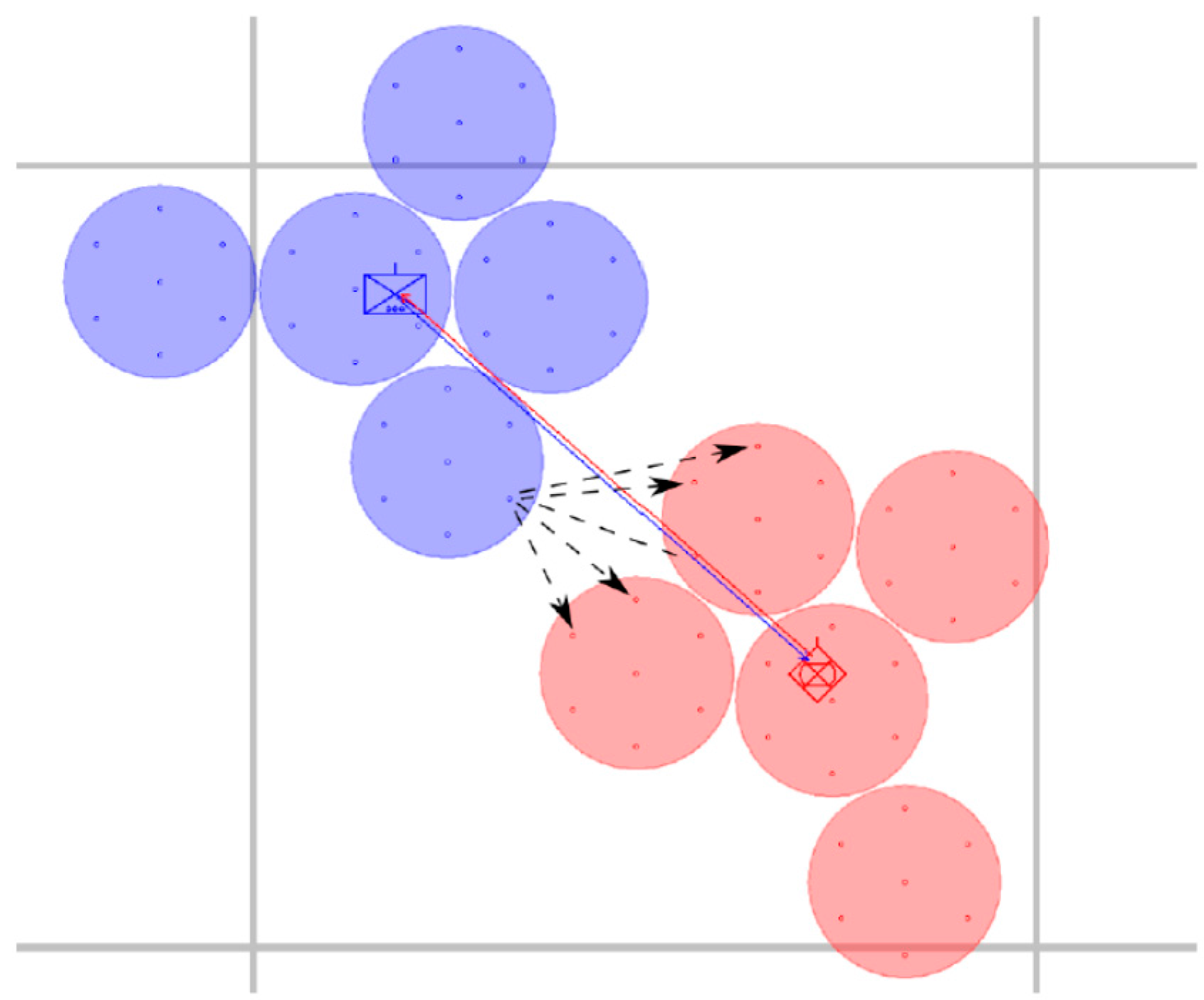
2.2.4. Optimal Target Selection of Calculation Points
3. Testing and Validation of the Model in a Data Farming Environment
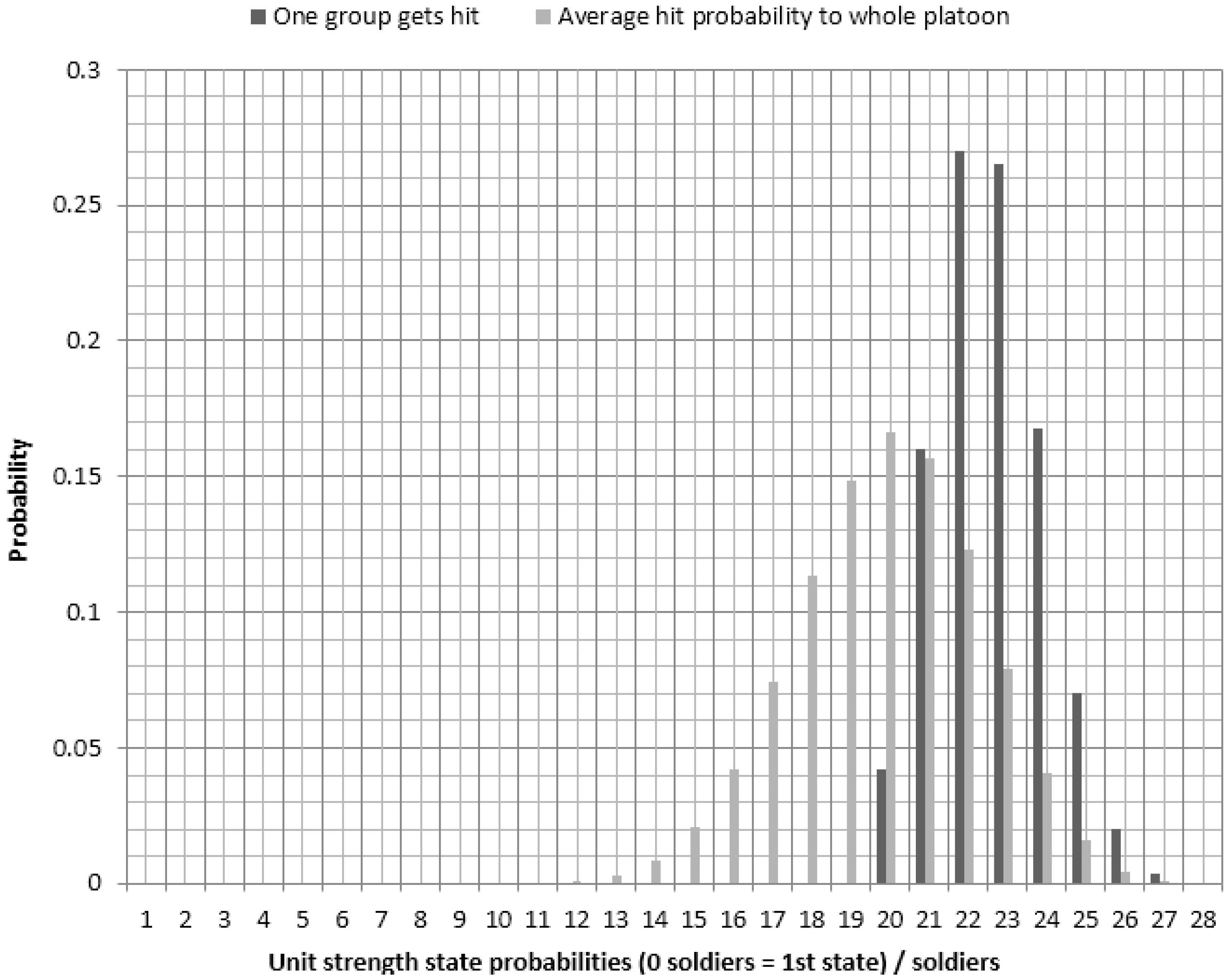
3.1. Some Simulated Cases with the Sandis Software
3.2. Verification and Validation of the Model
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References and Notes
- NATO Science and Technology Organization Modelling and Simulation Task Group 088. NATO MSG-088 Final Report—Data Farming in Support of NATO; STO Technical Report TR-MSG-088; Science and Technology Organization: Neuilly-sur-Seine Cedex, France, 2014. [Google Scholar]
- Geiger, A.; Choo, C.S.; Donnelly, T.; Erlenbruch, T.; Kallfass, D.; Schwierz, K.-P.; Wagner, G.; Seichter, S. Evaluation of Electro-optical Sensor Systems in Network Centric Operations using ABSEM 0.5. In Proceedings and Bulletin of the International Data Farming Community, Lisbon, Portugal, 19–24 September 2010; pp. 13–15.
- CAE Inc. CAE GESI™ Command & Staff Training; CAE Web Material. Available online: http://www.cae.com/uploadedfiles/content/businessunit/defence_and_security/media_centre/document/brochure.gesi.command.staff.training.pdf (accessed on 17 October 2015).
- Lappi, E. Computational Methods for Tactical Simulations. Ph.D. Thesis, National Defence University, Helsinki, Finland, 2012. [Google Scholar]
- Lappi, E.; Pakkanen, M.S.; Åkesson, B. An approximative method of simulating a duel. In Proceedings of the 2012 Winter Simulation Conference, Berlin, Germany, 9–12 December 2012.
- Lappi, E.; Pottonen, O. Combat parameter estimation in Sandis OA software. In Lanchester and Beyond—A Workshop on Operational Analysis Methodology; Hämäläinen, J.S., Ed.; Defence Forces Technical Research Centre: Riihimäki, Finland, 2006; pp. 31–38. [Google Scholar]
- Åkesson, B.M.; Lappi, E.; Pettersson, V.H.; Malmi, E.; Syrjänen, S.; Vulli, M.; Stenius, K. Validating indirect fire models with field experiments. J. Def. Model. Simul. 2013, 10, 425–434. [Google Scholar] [CrossRef]
- Lappi, E.; Urek, B.; Åkesson, B.; Arpiainen, J.; Roponen, J.; Jokinen, K.; Lappi, R. Comparing simulated results and actual battle events from 1944—A case study using Sandis software. In Tiede Ja Ase: Suomen Sotatieteellisen Seuran vuosijulkaisu n:o 72; Turunen, I., Ed.; The Finnish Society of Military Sciences: Helsinki, Finland, 2014; pp. 111–125. [Google Scholar]
- Taistelijan Opas [The Combatant Guide]. Maavoimien esikunta [Army Headquarters], Finnish Defence Forces, 2013. (In Finnish)
- Ryhmänjohtajan Opas [Squad Leaders Guide]. Pääesikunnan koulutusosasto [Defence Command Finland], Finnish Defence Forces, 1991. (In Finnish)
- Keinonen, Y. Jalkaväen Tulen Vaikutuksesta [On the Effect of Infantry Fire]; Pääesikunta [Defence Command Finland]: Helsinki, Finland, 1954. (In Finnish) [Google Scholar]
- Harinen, O. Sotilaiden Epäviralliset Ryhmänormit Kolmessa Jalkaväkikomppaniaa Koskeneessa Empiirisessä Tutkimuksessa (Knut Pipping, Roger Little, John Hockey); National Defence University: Helsinki, Finland, 2012. (In Finnish) [Google Scholar]
- Bhat, U. Elements of Applied Stochastic Models; Wiley and Sons, Inc.: Hoboken, NJ, USA, 1984. [Google Scholar]
- Kangas, L. Taistelun Stokastinen Mallinnus [Stochastic Modelling of Combat]. Master’s Thesis, Helsinki University of Technology, Espoo, Finland, 2005. [Google Scholar]
- Lappi, E.; Bruun, R.; Jokinen, K. Direct fire target selection in Sandis combat simulation. In Proceedings of the IFAC Workshop on Control Applications of Optimization, Jyväskylä, Finland, 6–8 May 2009; pp. 242–245.
- Lappi, E.; Pottonen, O.; Mäki, S.; Jokinen, K.; Saira, O.-P.; Åkesson, B.M.; Vulli, M. Simulating indirect fire—A numerical model and validation through field tests. In Proceedings of the 2nd Nordic Military Analysis Symposium, Stockholm, Sweden, 17–18 November 2008.
- Lappi, E.; Sysikaski, M.; Åkesson, B.; Yildirim, U.Z. Effects of terrain in computational methods for indirect fire. In Proceedings of the 2012 Winter Simulation Conference, Berlin, Germany, 9–12 December 2012.
- Bruun, R.S.; Hämäläinen, J.S.; Lappi, E.I.; Lesnowicz, E.J., Jr. Data farming with SANDIS Software Applied to Mortar Vehicle Support for Convoys. In Proceedings of the 21st International Data Farming Workshop, Lisbon, Portugal, 19–24 September 2010; pp. 20–21.
- Lappi, E.; Åkesson, B.; Valtonen, J.; Koskinen, J.; Hämäläinen, J.; Pentti, J.; Roponen, J.; Urek, B.; Sivertun, Å. Data Farming of a Historical Battle of Loimola in Summer 1944. In Proceedings and Bulletin of the International Data Farming Community, Riihimäki, Finland, 16–20 March 2015; pp. 18–21.
- Hartley, D.S., III. Verification & Validation In Military Simulations. In Proceedings of the Winter Simulation Conference, Atlanta, GA, USA, 7–10 December 1997.
- Laitinen, M.; Lappi, E. Can Marksmanship Explain the Results from the Kollaa Front? In Proceedings of the 2nd Nordic Military OA Symposium, Stockholm, Sweden, 17–18 November 2008.
- Lappi, E.; Kaasinen, J. Genetic optimization of tactical parameters in Sandis combat simulator. In Proceedings of the EuroGen 2007, Jyväskylä, Finland, 11–13 June 2007.
- Keinonen, Y. 1944—Taistellen Takaisin; Kustannusosakeyhtiö Tammi: Helsinki, Finland, 1971. (In Finnish) [Google Scholar]


© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lappi, E.; Åkesson, B. Tactical Size Unit as Distribution in a Data Farming Environment. Axioms 2016, 5, 7. https://doi.org/10.3390/axioms5010007
Lappi E, Åkesson B. Tactical Size Unit as Distribution in a Data Farming Environment. Axioms. 2016; 5(1):7. https://doi.org/10.3390/axioms5010007
Chicago/Turabian StyleLappi, Esa, and Bernt Åkesson. 2016. "Tactical Size Unit as Distribution in a Data Farming Environment" Axioms 5, no. 1: 7. https://doi.org/10.3390/axioms5010007
APA StyleLappi, E., & Åkesson, B. (2016). Tactical Size Unit as Distribution in a Data Farming Environment. Axioms, 5(1), 7. https://doi.org/10.3390/axioms5010007




