1. Introduction
Relation algebra ([
1,
2]) allows one to formulate first order logic (and set theory) in a quantifier-free, purely algebraic (equational) way. It has found numerous applications in mathematics and computer science (see, e.g., [
3,
4,
5,
6,
7,
8])., Inin particular, it is a foundation for relational databases [
9]. A relation algebra without some additional structures is equivalent in expressivity to three variable fragment of first order logic [
1]. A crucial ingredient that allows one to express with relation algebra all of the first order logic is the existence of Cartesian products. These can be defined equationally, as so-called relational products, within the relation algebra. In fact, the existence of relational products is strongly related to the representability of abstract relation algebras,
i.e., the possibility of their realization as subalgebras of the algebra of actual binary relations.
Allegories are enriched categories generalizing a category of sets and binary relations. Accordingly, relational products in an allegory can be viewed as a more abstract version of Cartesian products. Recently allegories were used as a mathematical framework to model databases in [
10,
11]. There, the authors had to assume the existence of appropriate relational products in order to make the formalism applicable in other than most trivial cases, in particular, relational products allow one to define
n-ary relations using binary ones.
There is a well-established definition of a binary relational product valid both for abstract relation algebras (see e.g., [
3,
7,
12,
13]) and allegories (see e.g., [
14] or Definition 9 in
Section 2 of this paper). In the case of the allegory of sets and binary relations, this definition characterizes, up to an isomorphism, the usual Cartesian products. For general allegories, one proves easily [
14] that the relational product is a categorical product for the subcategory of maps of the given allegory, that is a subcategory consisting of those arrows (generalized relations) that behave like total functions. It should be noted that, unlike the categorical definition of the product, which involves both universal and existential quantification (for all maps, such that …there exists a unique map, such that …), the definition of a relational product involves no quantification—it is just equations, in terms of constant arrows and projection arrows, which projection arrows must satisfy. Moreover, the unique factorization, the existence of which the categorical definition asserts, is given explicitly by a simple algebraic formula in terms of projection arrows and the maps to be factorized through the product. Unfortunately, this definition of a relational product is too strong to be considered an algebraic characterization of categorical product; there are examples (see e.g., [
15]) of allegories in which a categorical product in the subcategory of maps does not satisfy all of the standard axioms of a relational product. In [
15] and [
16], a weakening (see also Definition 10 in this paper) of the standard relational product was investigated, which still provides a categorical product in the subcategory of maps.
It is surprisingly difficult to generalize the definition of a binary relational product to an
n-ary one for an arbitrary
n. The most obvious one does not yield a categorical product in the subcategory of maps. A non-inductive definition (
i.e., one that did not rely on the iteration of binary products) of the
n-ary relational product was given in [
17]. the paper (concerned with abstract relational algebra rather than with allegories) does not contain the proof that the
n-ary relational product yields the
n-ary categorical product for functions, though the author proves that the
n-ary relational products of the same objects must be isomorphic.
In this paper, we define and investigate the weakening of an
n-ary relational product from [
17], which for
is equivalent to the binary relational product defined in [
15]. We prove that a weak
n-ary relational product yields an
n-ary categorical product in the subcategory of maps. Furthermore, we generalize to the case of weak
n-ary relational products some of the results proven in [
15] for weak binary relational products. Finally, we show that by composing the weak
n-ary products, we again get weak
n-ary products.
2. Preliminaries
We assume that the reader is familiar with basic category theory, and an excellent introduction can be found in [
18]. We recall some basic categorical definitions in order to fix the clean, but somewhat idiosyncratic, notation we use. The bulk of the preliminaries is taken by introductory material on allegories, which are not widely known and for which [
14] is the basic textbook.
Note that we consciously utilize the term “set” where “class” might be more appropriate in order not to clutter the presentation with the set-theoretical considerations.
2.1. Categories and Graphs
A graph consists of a set of vertices , a set of arrows and a pair of maps , called the source and target, respectively. We denote by the set of arrows with source A and target B, where .
A category is a graph with associative arrow composition defined whenever (note the diagrammatic order) and identity map , such that for all . We write . When using single letter arrow names, we will often omit the semicolon composition operator abbreviating .
We will often declare the composability of arrows using diagrams, e.g.,
Note that unlike in [
14], the diagrams are not considered commutative by default.
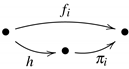
A categorical n-ary product is a family of arrows with a common source, such that for any other family of arrows with a common source and such that for all , there exists a unique arrow h, such that for all .
2.2. Allegories
An allegory [
14]
is a category enriched with intersection and reciprocation operators, respectively, for all
:
We require these operators to satisfy the following conditions: Intersections make each hom-set a meet-semilattice (see, e.g., [
19]), where we denote the associated partial order by ⊑,
i.e.,
, for all
. In addition,
and
are to satisfy:
For all
, such that the above formulas are well defined. Applying the reciprocation to both sides of the Equation (1d) (right semi-distributivity) and (1e) (right modular identity), using the Equations (1a)–(1c) and redefining symbols yields easily the following right versions:
Allegories generalize the allegory
of sets (objects) and binary relations (arrows). Because of this, we may refer to arrows in any allegory as “relations”. In
, we write
iff
. The identity in
is
, and the intersection is the set intersection,
i.e.,
, reciprocation is defined by
and composition of relations
such that
is defined by:
We distinguish the following classes of arrows in allegory:
If , then R is called total;
If , then R is called functional;
If R is functional and total, it is called a map. A set of all maps in an allegory is denoted by ;
If , then R is called injective;
If , then R is called surjective;
If and , then R is called coreflexive.
If is an isomorphism in an allegory , then both R and are maps, and . Note that for all is a map, and the composition of maps is a map. For any , we denote by the top element of , if it exists. In , we have .
An arrow T is called symmetric if . Some symmetric arrows might admit splittings:
Definition 1. An arrow R is called a splitting of a symmetric arrow T if and only if , .
We will make frequent use of the following results (
cf. [
14]):
Lemma 2. for all , such that R is functional. Similarly, for all , such that is functional.
Lemma 3. Define . Then, for all .
Lemma 4. Suppose that A is coreflexive. Then, (A is symmetric). Moreover, if B is another coreflexive arrow, such that and , then . In particular, this implies that , is again coreflexive (as obviously is) and that A is idempotent (i.e., ). Finally, A (and, hence, ) is functional, as .
Lemma 5. Maps are incomparable The ordering restricted to maps is discrete, that is for all .
Lemma 6. ([15]) Suppose that ![Axioms 03 00342 i001]() and that S is functional. Then,
and that S is functional. Then, .
2.3. Distributive and Division Allegories
A distributive allegory is an allegory
in which for all hom-sets
, there exists a bottom element
and a binary operation
, which together with
makes
a distributive lattice with
as the infimum and
as the supremum. In addition, we require that
and
satisfy:
for all
, such that the above formulae are type-correct.
A division allegory is a distributive allegory with a partial binary operation
(called a left division), defined if and only if both arguments have the same sources, and satisfying for all
![Axioms 03 00342 i001]()
Note that
is a division allegory with the union defined as set union,
i.e.,
, bottom
and a left division defined by:
2.4. A Functional Part of a Relation
The notion of a functional part
of a relation
R was introduced in [
3] and was later generalized to division allegories in [
15]. Let
be a division allegory, and let
. Then, the functional part of R [
3,
15] is defined by:
Note that in
, we have, for any
:
which, together with the following lemma, justifies interpreting
as the functional part of
R.
Lemma 7. ([3,15]) For any , where is a division allegory, we have that is functional, and moreover, R is functional if and only if .
The following result, which (slightly differently phrased) was proven in [
15], shows that, given relevant splittings, we can associate a map to any relation.
Lemma 8. Let be a division allegory, and let . Let also A be a coreflexive arrow, such that . Suppose that A has a splitting s, i.e., , . Then .
Proof. We provide the proof for completeness. Note first that s is functional as
. Furthermore,
is functional by Lemma 7. Hence,
must be functional, as well, being a composition of functional arrows. The arrow
is also total as:
☐
2.5. Relational Products
Here is a standard definition of a relational binary product in an allegory. Note that it is necessary to assume the existence of the top relation between objects that are supposed to be the components of the relational product.
Definition 9. ([14]) Let be an allegory. A pair of arrows is called a relational product if and only if it satisfies the following conditions:
The following is the weakening of the above definition formulated in [
15]:
Definition 10. ([15]) Let be an allegory. A pair of arrows is called a weak relational product if and only if it satisfies the following conditions: In [
15], it was proven that a weak relational product is a categorical product in the subcategory of maps. Additionally, it is immediate.
3. Weak n-Ary Relational Products
The following is a generalization of the characterization of binary relational products to the characterization of n-ary products.
Definition 11. ([17]) Let . A finite family of arrows with a common source C, that is, such that for all , is called an n-ary relational product if and only if it satisfies the following conditions: Before we present the weakening of the above definition, we need the following piece of notation. Let
be a finite family of arrows in an allegory
with a common source. We denote:
The following is the weakening of Definition 11:
Definition 12. Let . A finite family of arrows with a common source C, that is, such that for all , is called a weak n-ary relational product if and only if it satisfies the following conditions: An immediate corollary of Equations (8a) and (8c) is that arrows for all i are maps. Another immediate corollary is that an n-ary relational product is also a weak n-ary relational product. The following result shows that any categorical product in satisfies most of the Conditions (8):
Lemma 13. (cf. [15]). Let be an n-ary categorical product in . Then, satisfies Conditions (8a), (8b), (8d) and the “⊒” part of (8c). Proof. Condition (8a) and the “⊒” part of Condition (8c) are satisfied, because all
’s are maps, hence, respectively, functional and total. Let now
. Because
is a categorical
n-ary product, it follows that there exists a (unique) map
, such that
for all
. Hence, for all
:
which proves Condition (8b). Similarly, we prove Condition (8d). Let
, and let
. Tthen:
☐
Both the binary weak relational product and n-ary relational product are axiomatized using three axioms, two of which correspond to the properties (8a) and (8c) of a weak n-ary relational product. It is therefore interesting to check if the remaining properties (8b) and (8d) are really independent or if one of them implies the other in the presence of other axioms. The following two examples prove that neither implication holds:
Example 14. Consider the allegory of binary relations, and let be any set that is neither empty nor a singleton. It is immediate that the three maps satisfy the Conditions (8a), (8b) and (8c) (for ). They fail, however, to satisfy Condition (8d). Indeed, let , where and are both projections on the first component of a Cartesian product and is the projection on the second component. Then, we have that , and . However, as A is neither empty nor singleton, we must have , contradicting Condition (8d).
Example 15. Consider the allegory , with two distinct objects, A and B, and with:where π satisfies: This allegory can be realized in by setting, e.g., Let now , and let . It is immediate that both Equations (8a) and (8c) are satisfied by the ’s. To check the remaining two axioms of n-ary weak relational product, first note that contains only two families of maps : one obtained by setting ; the other one by setting . Both families satisfy property (8d); however, setting provides a counterexample to Equation (8b).
The following two lemmas are crucial for proving the main result of this paper:
Lemma 16. Let , and let be a weak n-ary relational product. Let . Define , for all . Then, for all and , the totality of implies that .
Proof. Let
and
. Assume that
is total. Then:
☐
Lemma 17. Let , and let be a weak n-ary relational product. Let . Then, is total for all .
Proof. We prove the lemma using induction on
J. For the base case, note that for all
:
Suppose now that we have proven for some
that
is total. Note that
is equivalent with R being total. We have:
☐
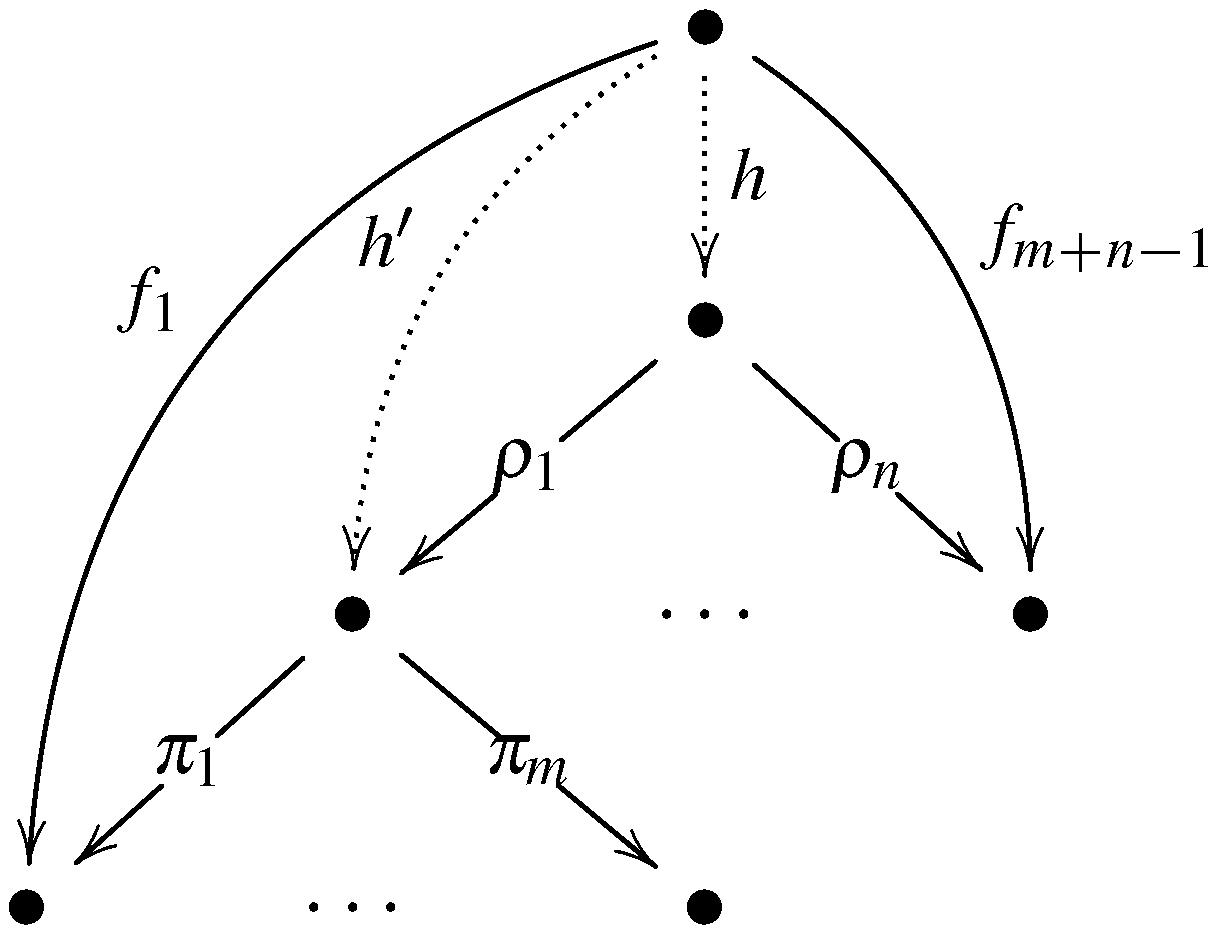
The following result, which is the main result of this paper, shows that an n-ary weak relational product is in fact a categorical product for maps.
Theorem 18. Suppose that is a weak n-ary relational product. Let an arrow and family of maps be such that for all , we have ![Axioms 03 00342 i003]()
.
Note that the diagram in the assumptions of the above theorem above implicitly implies that all of the maps have a common source.
Proof. (Theorem 18) First, assume that
and
for all
. Then:
Assume now that
. Then:
The arrow
h is functional, that is
. Indeed, for all
:
The arrow h is total, that is . Indeed, this is stated in Lemma 17.
Equality
holds for all i. Indeed,
On the other hand, we have already proven that h is a map, and so, both and are maps; hence, by Lemma 5, implies . ☐
Let us also note that our definition of a weak
n-ary relational product is a generalization of a weak binary relational product,
i.e., a pair of arrows
,
with a common source in an allegory
is a weak binary relational product (Definition 10) if and only if it is a weak two-ary relational product (Definition 12). Indeed, by Theorem 18 and ([
15], Theorem 2), a pair of arrows satisfying conditions of either of these two definitions is a categorical product for maps. Then, by Lemma 13 and ([
15], Lemma 5) a categorical product satisfies all of the conditions of Definitions 10 and 12 apart from the “⊑” part of Equations (5b) and (8c), which in this case, are identical anyway.
An example given in [
15] shows that there are indeed allegories
for which a categorical product in
does not satisfy the “⊑” part of Equation (8c); hence, one needs to assume something more about
to ensure that
n-ary categorical products in
satisfy all Conditions (8). The following result is a generalization of ([
15], Lemma 6) to the case of weak
n-ary relational products.
Lemma 19. Suppose that , is an n-ary categorical product in . If there exists a splitting of , then is an n-ary weak relational product.
Proof. The basic idea of the proof is the same as of the proof of ([
15], Lemma 6): we first prove that
is a weak
n-ary relational product, and then, we use this result to prove that
must be a weak
n-ary relational product, too. Let us denote
for all
. The family
satisfies Condition (8a). Indeed, we have (
cf. the proof of ([
15], Lemma 6)) that for all
:
Note that
implies that
is functional. Observe that for all
:
It follows that
satisfies (
cf. the proof of ([
15], Lemma 6)):
On the other hand, for all
, we have that [
15]
, as
is total, for all
; hence, also,
. Thus, the family
satisfies Condition (8c).
In order to see that the family
satisfies Condition (8b), note first that
and that
is by assumption a categorical product in
and, thus, by Lemma 13, satisfies all of Condition (8) but the “⊑” part of Condition (8c). Hence, for all families
, we have:
In order to see that the family
satisfies Condition (8d), note first that, for any
, as
is, by assumption, a categorical product in
, there exists a map h, such that
for all
. Furthermore, note that, as, by Lemma 13,
satisfies “⊒” part of Condition (8c) and R is a splitting of
, we must have
. Then, it follows that, for all
and
, we have:
By Theorem 18, we know now that
is a categorical product in
and that the arrow
is a map satisfying
for all
. On the other hand, as
is a categorical product in
by assumption, the standard argument shows that g must be an isomorphism. In any allegory, the inverse of an isomorphism equals the reciprocation of this isomorphism and both the isomorphism and its inverse are maps; hence, in particular
. Denote by C the common source of
’s. Putting it together, the argument being almost identical to the proof of ([
15], Lemma 6) shows that the family
satisfies the “⊑” part of Condition (8c):
This ends the proof, as, by Lemma 13, the family satisfies all of the other conditions of Definition 12 by virtue of being the categorical product in . ☐
In Conditions (8b) and (8d) the range of universal quantification was restricted to maps. The following result, which is the adaptation to
n-ary weak relational products of ([
15], Lemma 7), shows that we can modify those conditions, so that the range of quantification is restricted only by source-target considerations from the whole set of arrows in the allegory under consideration.
Lemma 20. (cf. ([15], Lemma 7)) Let be a division allegory in which all partial identities split. A family , where , of arrows in with a common source is an n-ary weak relational product if and only if it satisfies Conditions (8a) and (8c), as well as:for all families of arrows in with a common source and such that for all .
Proof. The basic idea of the proof is adapted from the proof of ([
15], Lemma 7). It is immediate that if a family
satisfies Conditions (8a) and (8c), as well as Conditions (10), then it is a weak
n-ary relational product, because for any
, we have
by Lemma 7 and
for all
, and thus, Conditions 10 subsume trivially Conditions (8b) and (8d). Hence, it remains to prove that Conditions (8b) and (8d) imply Conditions (10).
Assume that
is an
n-ary weak relational product, and let
be a family
with a common source
C and such that
for all
. Denote for brevity:
and let s be a splitting of
ı,
i.e.,
and
. By Lemma 8,
is a map for all
. Now, the families
and
satisfy Condition (10a) as, for all
:
We prove Condition (10b) similarly. Let
and
. Then:
☐
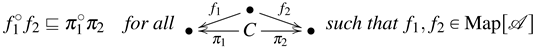
 .
.