1. Introduction
The problem of calculating the derivative of a function is an ill-posed problem, in the sense that, when a function involving noise,
, is given instead of a smooth function
and the derivative
is calculated, the error is enhanced. In the numerical solution of an ill-posed problem, Murio [
1] proposed the method of mollification. In that method, we calculate the mollified function
by
and we adopt
as an approximate of
. As the mollifier
, Murio [
1] uses a Gaussian probability density function. Hào
et al. [
2] proposed to use the de la Vallée Poussin kernel for the mollifier, in the calculation of fractional derivative.
In a preceding paper [
3], the present authors proposed to use the expansion in the orthogonal set of the rapidly decaying harmonic wavelets (rdH-wavelets), which were developed in [
4,
5]. The wavelets are characterized by a scaling function that we denote by
. When the expansion in wavelets is truncated at a stage, the truncated expansion is expressed by an expansion in a system of
, where
is the scaled scaling function given by
for
, and
denotes the set of all integers. Here
ν is the scale at the stage of truncation. In [
3], it was shown that an average of the expansion is expressed as Equation (
1) if we put
where
In [
3], a series of Meyer’s wavelets ([
6] [p. 49]), which are special ones of the rdH-wavelets, are studied. It was shown that the use of the simplest of Meyer’s wavelets agrees with the use of de la Vallée Poussin kernel adopted by Hào
et al. [
2].
In [
2,
3], the calculation of fractional derivative
for
was studied, which is generally an ill-posed problem. When
involving noise is given in place of smooth
f, we calculate
, which approximates
. In [
2,
3], we estimate how the error of this approximation can be reduced by the choice of the scale on which
μ depends.
In [
3], numerical examples of calculations are given, where we note that the Gibbs phenomenon is observed. In [
7], seeking the wavelets for which noise is reduced and the Gibbs phenomenon is not observed, we studied this problem in the standpoint of Fourier series, where we know various attempts suppressing the Gibbs phenomenon. We took up Fejer’s sum ([
8] [p. 111]) and the method of Lanczos’
σ-factor ([
8] [p. 109ff]) and its extensions ([
8] [p. 132]). Noting that Fejer’s sum can be regarded as the mollification based on a special one of the rdH-wavelets, we found one desired example. Noting that the use of the Haar wavelet is regarded as an extension of the method of Lanczos’
σ-factor, we found another desired example. For those choices, the estimations of the error of approximation (EA) given in [
3] do not apply. The primary purpose of the present paper is to give new estimations which apply to them.
When we look the estimations given in [
3] and those given below, we find that the condition of orthogonality of the wavelets, which was used in deriving the mollification based on wavelets, is not necessary. Hence we now consider also examples of non-orthogonal set of wavelets.
In
Section 2, we give a brief review of the derivation of the mollification based on orthogonal wavelets, and then give revised estimations of EA applicable to the mollifications based on the rdH-wavelets and the Haar wavelet, which are studied in [
7]. In
Section 3, we study these mollifications, and then mollifications based on unorthogonalized system of B-splines, in particular unorthogonalized Franklin’s wavelet ([
6] [p. 40]). In
Section 4, we study the derivative of a function involving noise. Numerical calculations are performed by using discrete Fourier transform (DFT), which is explained in
Appendix B.
We use notation
to represent the sets of all real numbers. We also use
for
and
. For
, the space of those functions
f that
and
are locally integrable and integrable, respectively, on
, is denoted by
. The Fourier transform of function
is denoted by
or
so that
and
and
are used to denote the norms in the space
and
, respectively. We denote the Heaviside step function by
, so that
,
and
for
.
3. Mollifiers Based on Wavelets
We use the following three requirements in judging whether the mollifier
is desirable or not. The first two were mentioned in [
7], as Criterions 1 and 2.
Requirement 1 is essentially zero for higher than a threshold frequency.
If this is satisfied, noise reduction is expected, since high frequency contribution is important in noise. This is concluded from Equation (6).
Requirement 2 is nonnegative for all .
If this is satisfied, the Gibbs phenomenon does not appear.
Requirement 3 The region where takes nonzero values is narrow.
If the region is narrower, the mollified function is less smeared.
In discussing the Gibbs phenomenon, we now use the function
given by
Requirement 2 is concluded by using the first Equation of (
6) for
when
is always nonnegative, since it follows that
.
Figure 1,
Figure 2 and
Figure 3 show the graphs of
,
and
, for the
that we consider in thepresent paper.
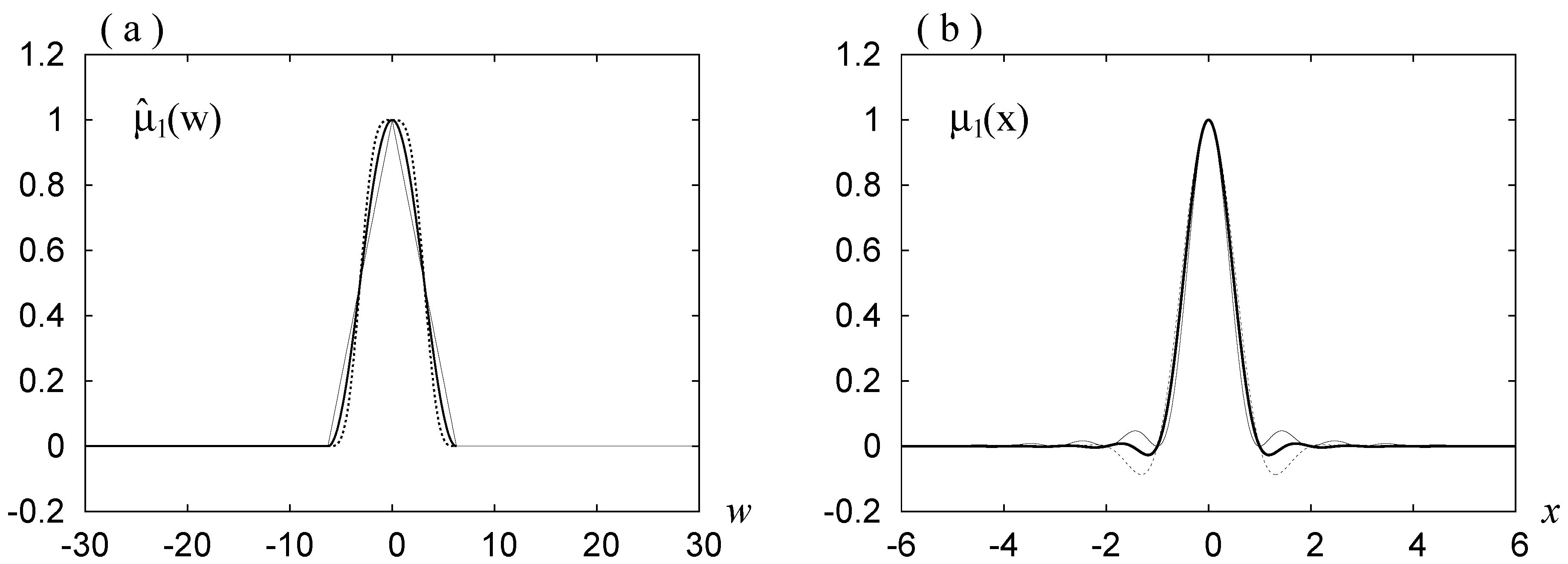
Figure 1.
and for the mollifiers based on the rdH-wavelets with . The three curves for with , 2, and 3, are shown by thin solid, thick solid, and dashed lines, respectively.
Figure 1.
and for the mollifiers based on the rdH-wavelets with . The three curves for with , 2, and 3, are shown by thin solid, thick solid, and dashed lines, respectively.
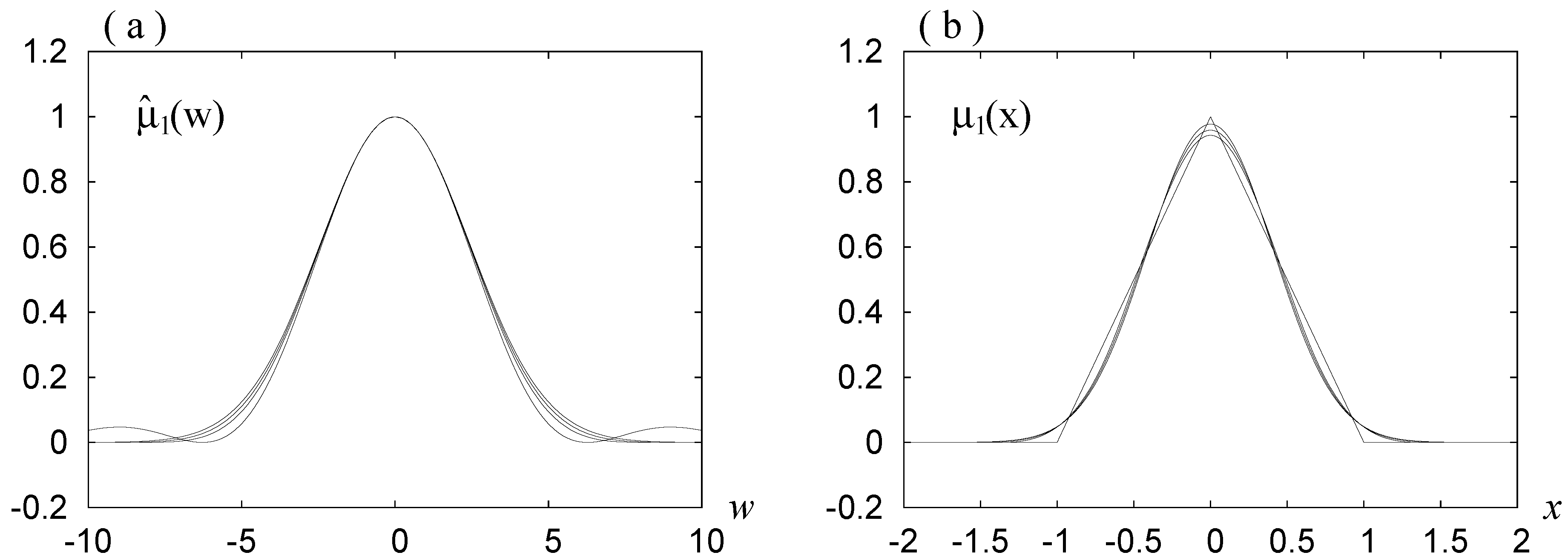
Figure 2.
(a) for the mollifiers based on the rdH-wavelet with , and (b) those based on the scaled B-spline wavelets of order , 2. In (a), the three curves for with , 2, and 3, are shown by thin solid, thick solid, and dashed lines, respectively. In (b), two curves almost overlap. is also drawn both in (a) and in (b).
Figure 2.
(a) for the mollifiers based on the rdH-wavelet with , and (b) those based on the scaled B-spline wavelets of order , 2. In (a), the three curves for with , 2, and 3, are shown by thin solid, thick solid, and dashed lines, respectively. In (b), two curves almost overlap. is also drawn both in (a) and in (b).
Figure 3.
and for the mollifiers based on the scaled B-spline wavelets of order , 2, 4, ∞. The curves take greater values as m increases at in (a), and at and in (b).
Figure 3.
and for the mollifiers based on the scaled B-spline wavelets of order , 2, 4, ∞. The curves take greater values as m increases at in (a), and at and in (b).
Lemma 4 If Requirement 2 is satisfied for , which appears in Definition 1, then and hence .
3.1. Rapidly Decaying Harmonic Wavelets
We consider rapidly decaying harmonic (rdH-) wavelets, which were presented in [
4,
5]. We assume that
, and that
is given by
Here
is assumed to satisfy the conditions that
,
,
and
for
.
Lemma 5 thus defined satisfies Condition 1.
As
for
, we use
for
, which are given by
Lemma 6 For the mollifiers based on the rdH-wavelets, Requirement 1 is satisfied.
Proof. This follows from
and Equation (
23). ☐
Remark 3 In [
3],
Meyer’s wavelets were studied, where and ,
2 and 3. In [
3,
7],
the Gibbs phenomenon is observed in these cases. Remark 4 If we put in Equation (
23),
,
and then .
This corresponds to truncation of Fourier series, and hence we expect the Gibbs phenomenon to occur if takes nonzero values at .
Figure 1 and
Figure 2a show the graphs for
. In [
7], it was argued that the use of
and
corresponds to the use of Fejer’s sum in the Fourier series, where the Gibbs phenomenon does not appear but the convergence is not good. The curve for
in
Figure 1b shows that Requirement 2 is satisfied, and the corresponding curve in
Figure 2a shows a poor convergence. The last demerit is due to the bumps outside the main peak for this case in
seen in
Figure 1b.
Figure 1b and
Figure 2a show that, when
and
, Requirement 2 is not strictly satisfied but is almost satisfied and the Gibbs phenomenon does not appear, and the convergence is good. These figures show also that, when
and
, Requirement 2 is not satisfied and the Gibbs phenomenon appears.
In [
7], it was stated that the best choice is
and
, where noise is reduced and the Gibbs phenomenon is not observed. In this case,
is given by
and hence
. Later in
Section 4, we adopt this choice as Mollifier 1.
3.2. B-Splines
The scaling function of the Haar wavelet is given by
We construct
for
from this
by
This
m is shifted by 1 from ([
6] [p. 48]).
is called the B-spline of order
m.
Use of
for
,
and
corresponds to use the Haar, the unorthogonalized (uo-) Franklin, and the uo-Battle–Lemarie wavelet ([
6] [p. 40, p. 48]), respectively.
We here define a shifted Haar wavelet, by its scaling function given by
We now construct
for
from
by
Adopting
,
is given by
and hence
. In particular, when
, we have
, where
When
, we have
, where
as seen in ([
11] [Section 4.1]).
Lemma 7 For the mollifiers based on the B-splines, , for which Requirement 2 is satisfied.
Proof. This follows from the fact that for all and by its construction. ☐
In [
7], the choice
was studied. It was noted that the Gibbs phenomenon does not occur and noise is reduced well, though not very well. In
Section 4, we adopt this as Mollifier 2.
Remark 5 In [
7],
the method of Lanczos’ σ-factor and its multiple applications ([
8] [p. 109ff, p. 132])
are called attention as a method of suppressing the Gibbs phenomenon in the Fourier series. It was noted there that Lanczos’ method corresponds to the present method using as the mollifier. Then is given by Equation (
28),
and hence noise reduction is not expected by Requirement 1. The extensions of Lanczos’ method correspond to the present method using for as the mollifier. Using and corresponds to the present studies for and .
3.3. Scaled B-Splines
In
Section 3.2, the use of
or
for
is mentioned. Then
, and as a probability density function (pdf), it has the variance
, by Equation (
29) and the theory of probability. In comparing two choices of
, it is desirable that the variances of them are equal or nearly equal with each other, in the respect of Requirement 3.
For
, we now adopt
or
, so that
or
. Then we have
, where
Now
.
By the central limit theorem, as
,
approaches the Gaussian pdf with the variance
, so that, in this limit,
If we adopt
for
, in the limit of
, we have
In
Figure 3a,b, the graphs of
and
, calculated by
and Equations (
30)–(
33), are shown for
, 2, 4 and ∞. The curves for
are not drawn. These are between the curves for
and those for
, and are very close to those for
. The curves of
are shown for
and 2 in
Figure 2b.
Figure 3a shows that Requirement 1 is well satisfied by the curves for
.
Figure 3b shows that Requirement 2 is satisfied by all the curves, and that Requirement 3 is satisfied slightly better by the curve for
. The estimations for the curves for
are nearly equal, but the best of them is for
. In
Section 4, we adopt this as Mollifier 3.
4. Numerical Computation
We are interested in numerically calculating a function that approximates
. The given data are the value of
λ and a function
involving noise, in place of
f. We adopt
as an approximation of
, where
. In order to calculate
, we only have to choose a mollifier
and a value of the scale
ν. The estimations in
Section 2.2 guarantee that the error can be made small if the error
is small. What we can practically do is to do the calculation for a number of values of
ν and to choose a reasonable one among them. We show some results of such an experiment for
.
In the numerical calculations, we choose sufficiently large values
and
, and consider discrete values of coordinates
for
. The integral
of a function
f is approximated by
, where
; See
Appendix B.
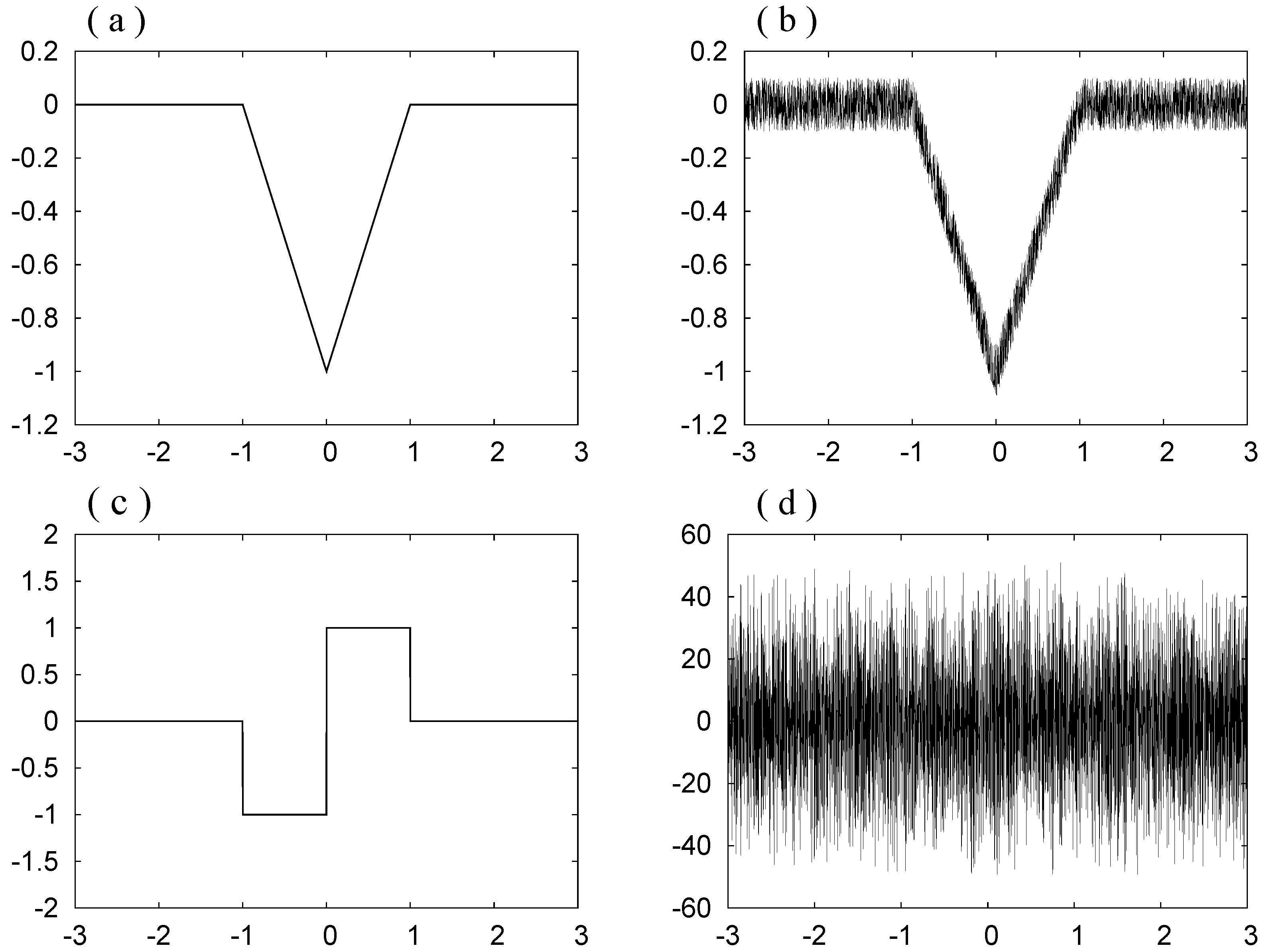
We now consider the V-shaped function
, which is given by
and noisy data
for
, where
for each
k is a random number chosen from the uniform distribution in the interval
. In
Figure 4a,b, the functions
and
are shown.
Figure 4c,d shows
and the central difference approximate
given by
We calculate
by
where we put
for
. This quantity is differentiable and its derivative is denoted by
.
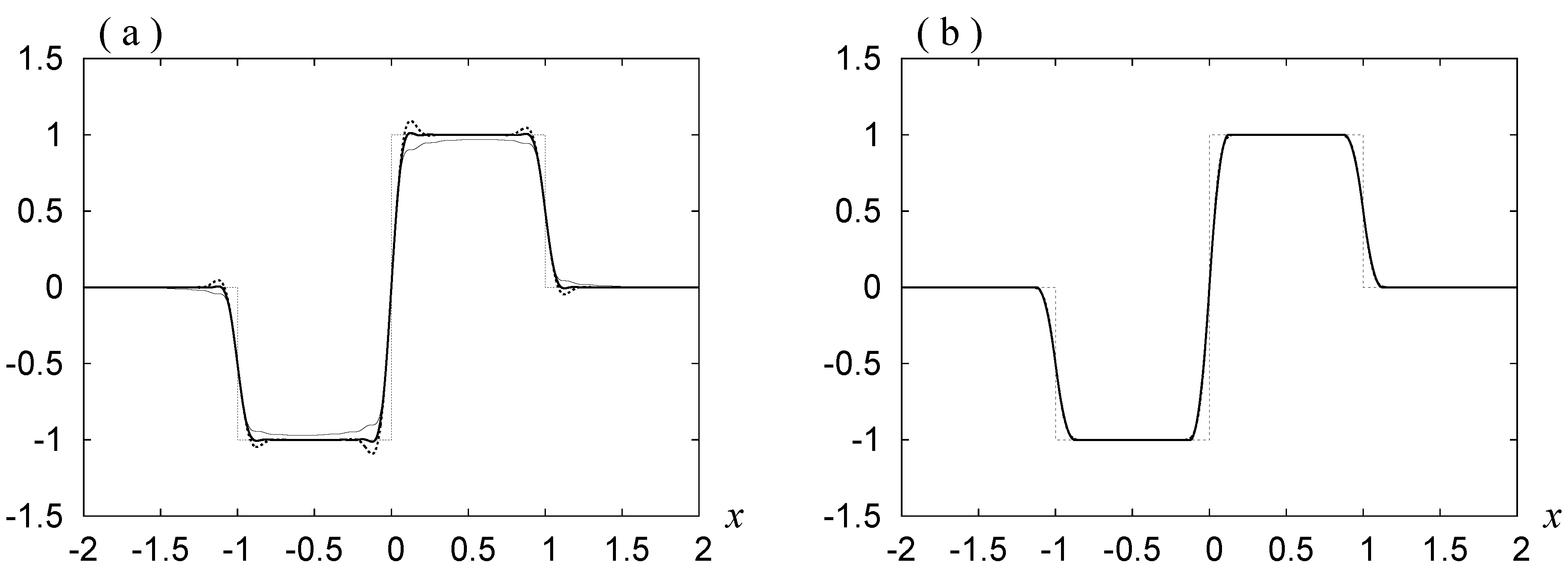
In
Figure 5,
Figure 6 and
Figure 7,
,
,
and
are shown for the following three choices of mollifier.
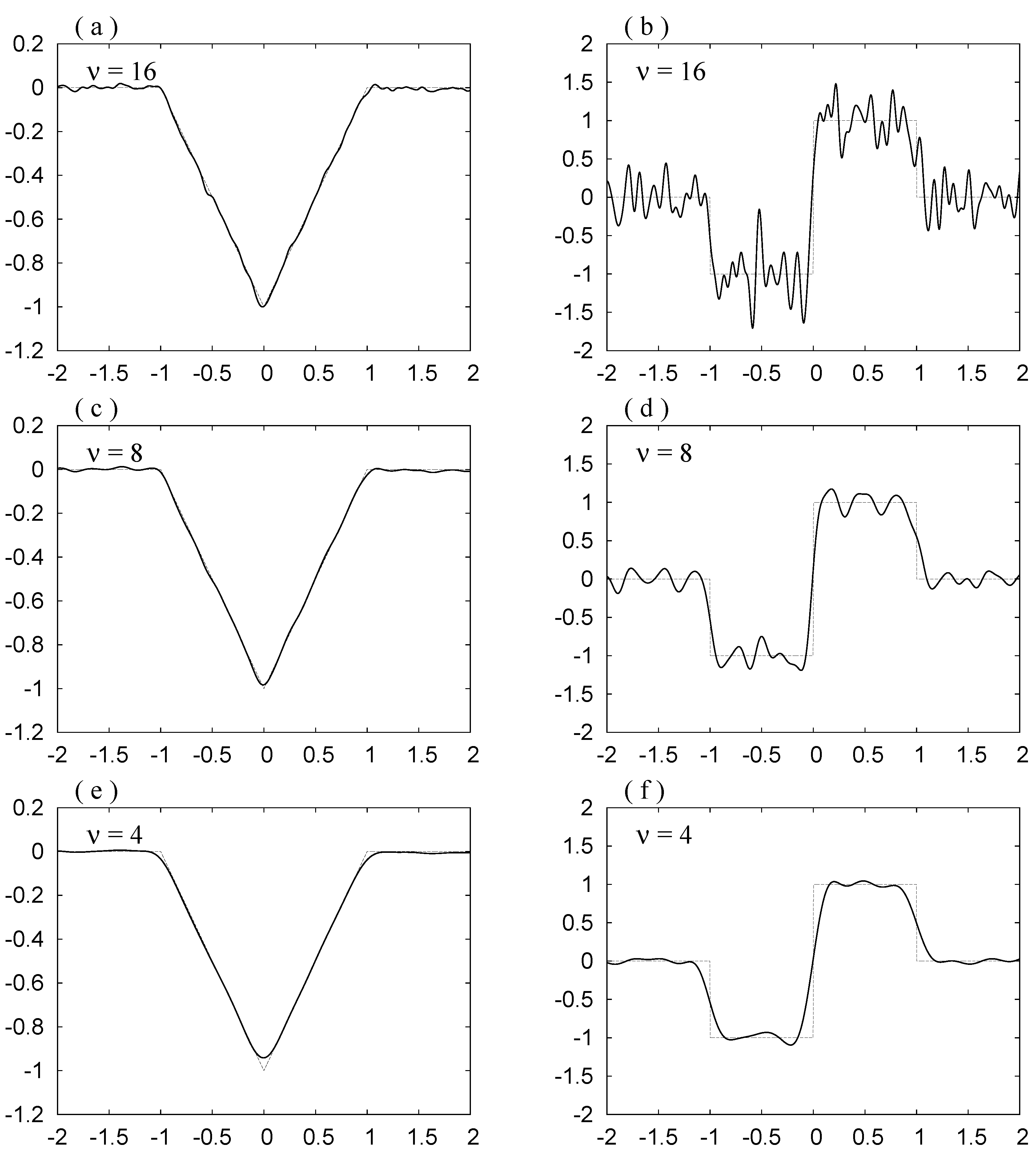
Mollifier 1 The mollifier based on the rdH-wavelet using and ,
given by Equation (
25)
in Section 3.1, where and .
Mollifier 2 The mollifier based on the Haar wavelet, given by in Section 3.2, where is given by Equation (
31),
and and .
Mollifier 3 The mollifier based on the scaled uo-Franklin wavelet, given by in Section 3.3, where is given by (
33)
and (
32),
and and .
Figure 4.
(a) ; (b) ; (c) ; (d) .
Figure 4.
(a) ; (b) ; (c) ; (d) .
Here
denotes the variance of the mollifier. In each of
Figure 5,
Figure 6 and
Figure 7, (a) and (b) are for
, (c) and (d) are for
, and (e) and (f) are for
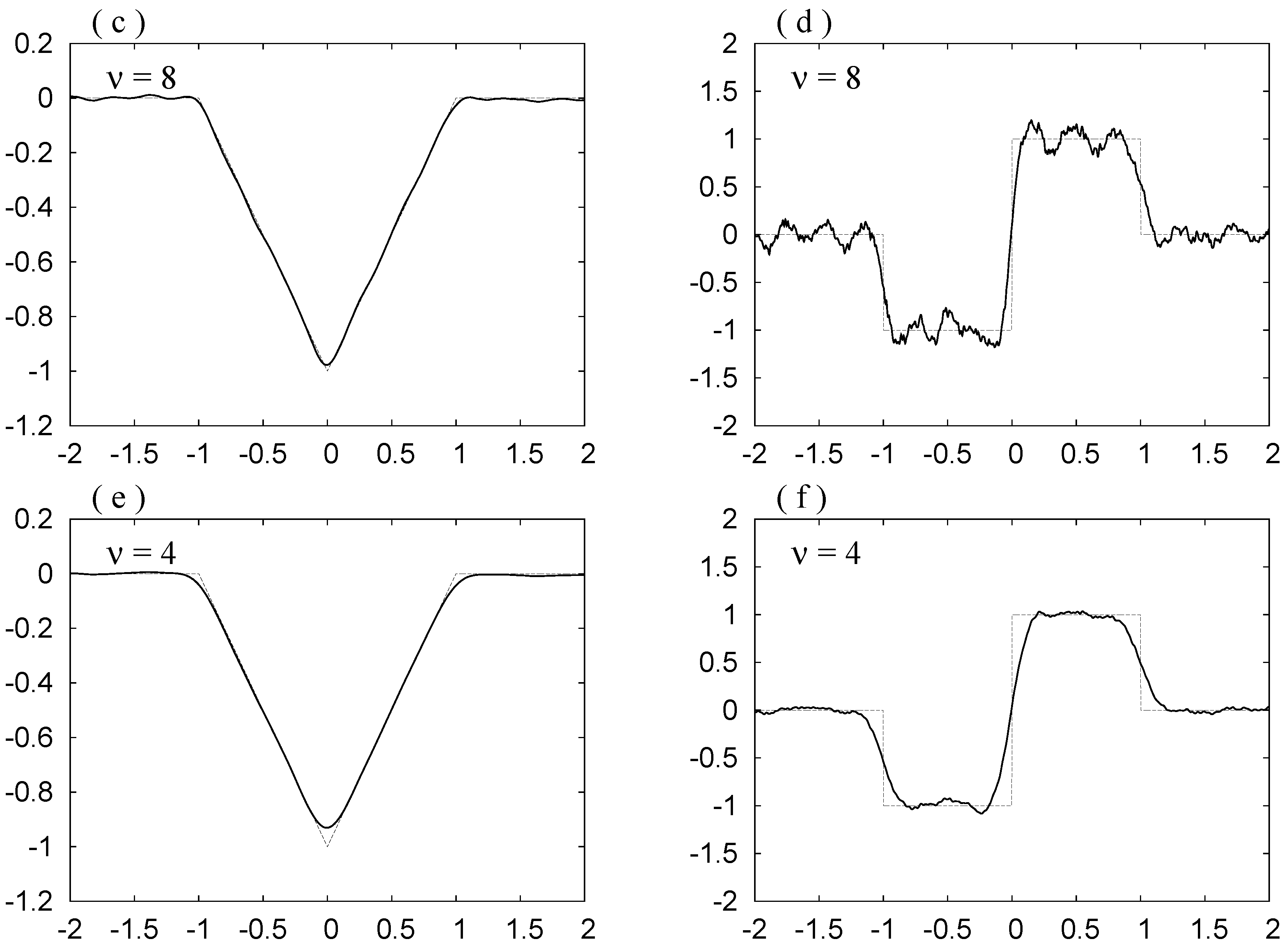
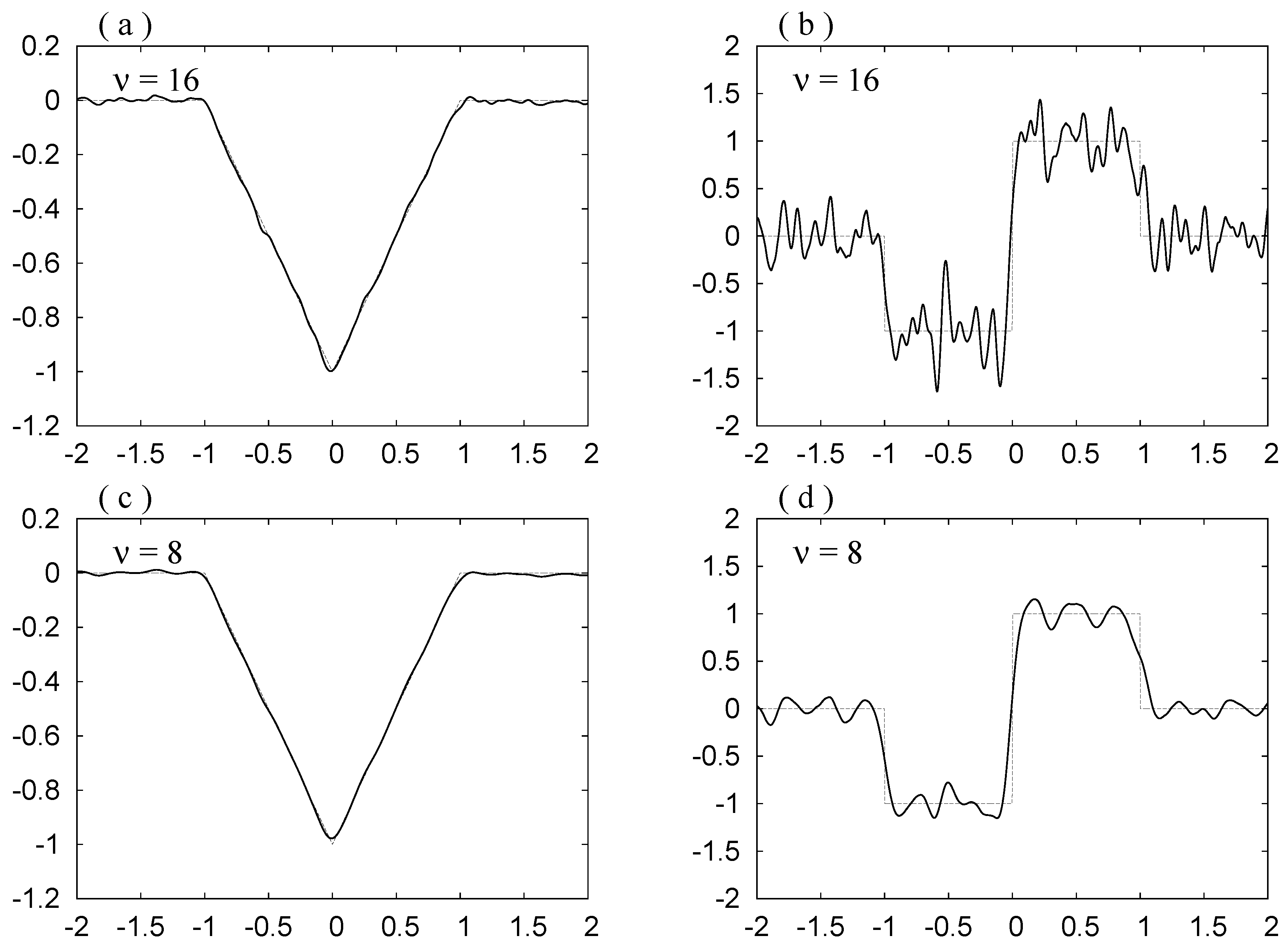
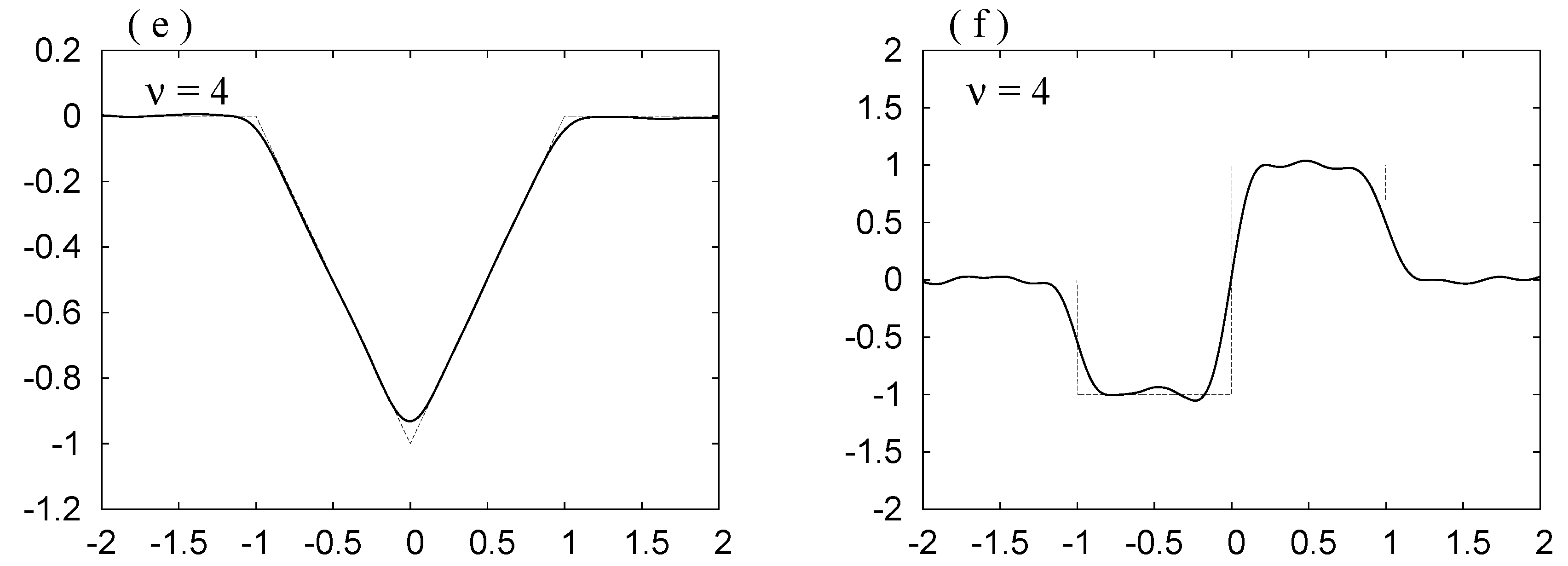
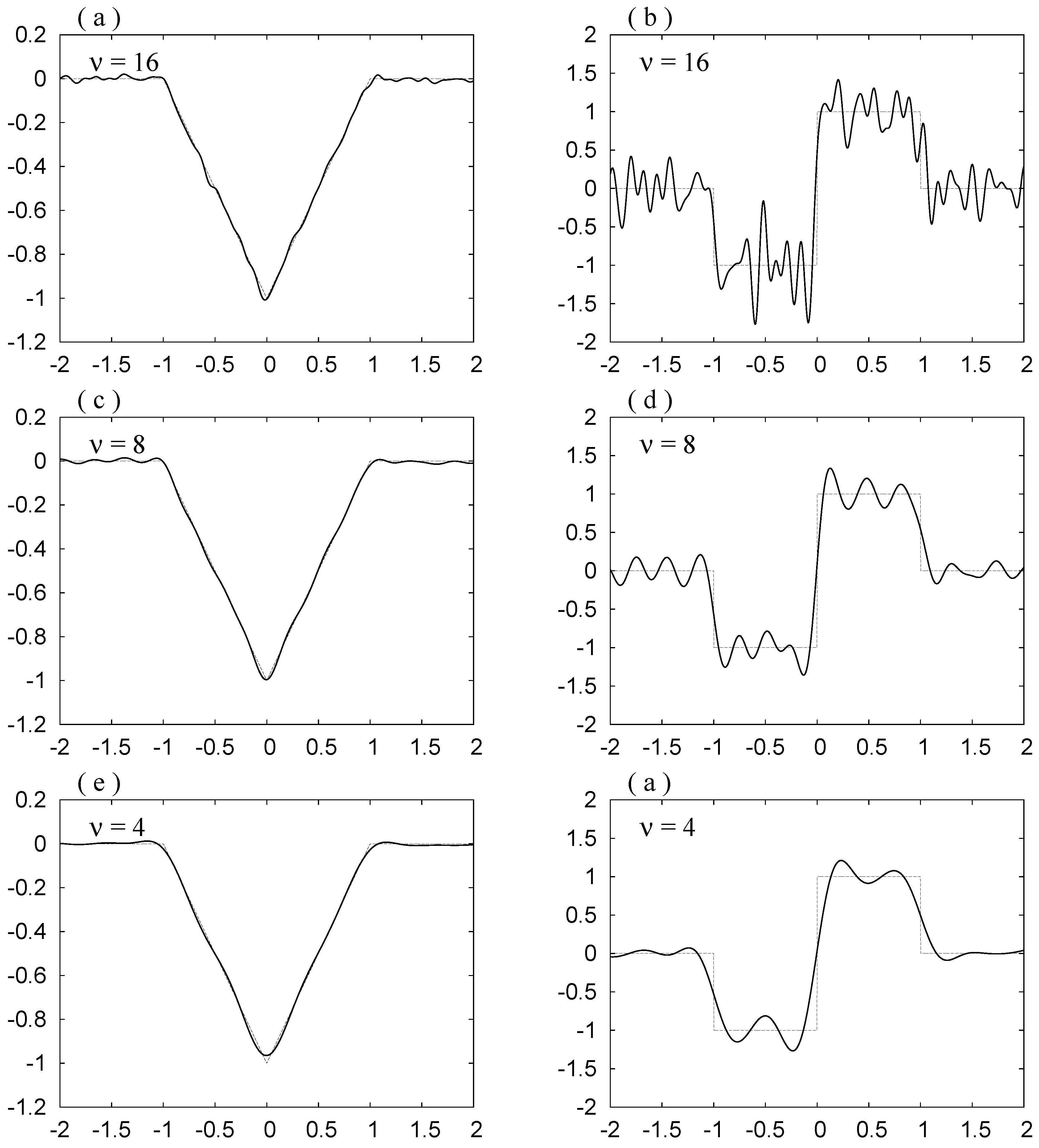
. We do not observe the Gibbs phenomenon in these curves. The noise is reduced as
ν decreases.
As
ν decreases, the noise is depressed, but also the bottom in (a), (c) and (e) becomes rounder, and the slope at
in (b), (d) and (f) becomes smaller. Hence in order to see the original forms shown in
Figure 4a,c clearly, we have to draw the curves for
,
and
. By Requirement 3, this smearing is governed by the width of the mollifier
. The width may be estimated by the value of the standard deviation
σ. The value is slightly smaller for the first choice.
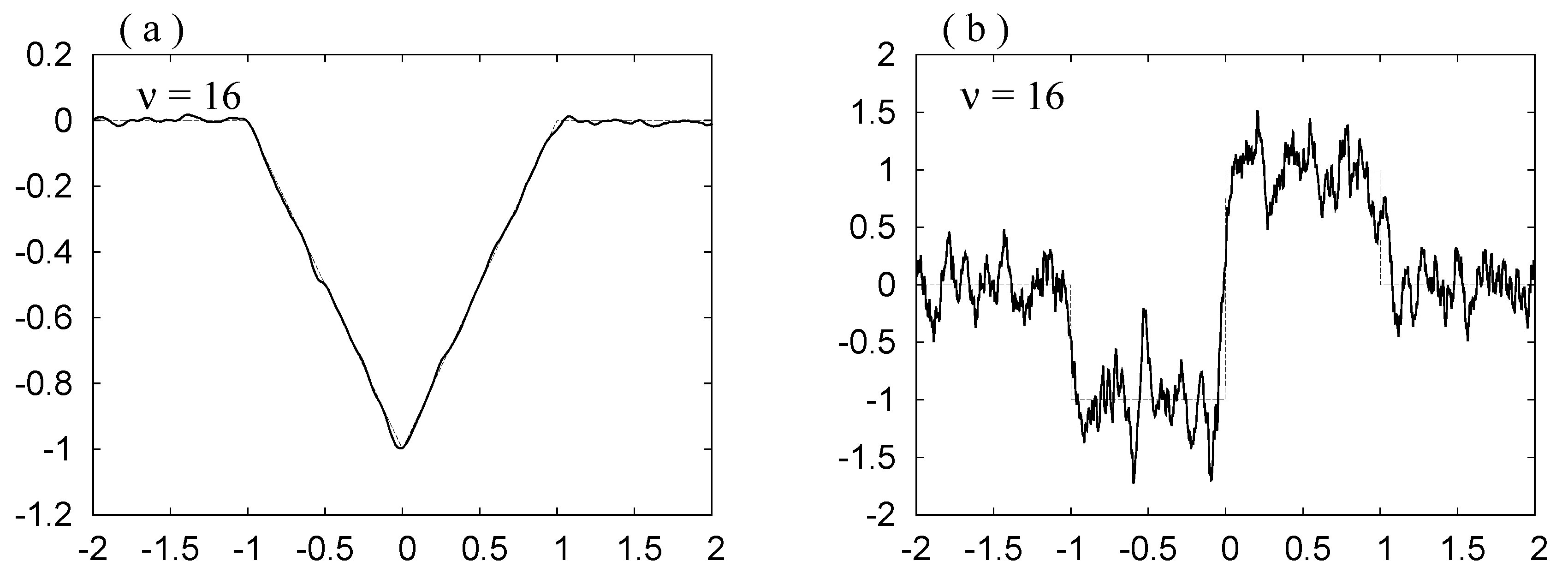
In
Figure 8, we show the curves for the choice specified by
and
for the rdH-wavelet. In this case, the Gibbs phenomenon is clearly seen, which is expected in Remark 3.
Figure 5.
(a), (c), (e): , ; (b), (d), (f): and , for Mollifier 1. The thinner curves show and .
Figure 5.
(a), (c), (e): , ; (b), (d), (f): and , for Mollifier 1. The thinner curves show and .
Figure 6.
(a), (c), (e): , ; (b), (d), (f): and , for Mollifier 2. The thinner curves show and .
Figure 6.
(a), (c), (e): , ; (b), (d), (f): and , for Mollifier 2. The thinner curves show and .
Figure 7.
(a), (c), (e): , ; (b), (d), (f): and , for Mollifier 3. The thinner curves show and .
Figure 7.
(a), (c), (e): , ; (b), (d), (f): and , for Mollifier 3. The thinner curves show and .
Figure 8.
(a), (c), (e): , ; (b), (d), (f): and , for the mollifier based on the rdH-wavelet using and . The thinner curves show and .
Figure 8.
(a), (c), (e): , ; (b), (d), (f): and , for the mollifier based on the rdH-wavelet using and . The thinner curves show and .
5. Concluding Remarks
In
Section 4, we study three mollifiers called Mollifiers 1, 2 and 3. In [
3], propositions are given for estimating the fractional derivative of a function, when the function given involves noise. Noting that those propositions are not applicable to the three mollifiers, we present revised propositions in
Section 2. We here note that the new estimations are applicable to the three mollifiers.
We first confirm that Condition 3 is applicable to Mollifiers 1, 2 and 3, by choosing β satisfying , and , respectively. We next confirm that the conditions , in Propositions 1 and 2 are satisfied if λ satisfies , and , respectively, for Mollifiers 1, 2 and 3.
The last fact for Mollifier 2 is confirmed by noting that
exists only when
for
given by Equation (
31), since we then have
The corresponding calculation for Mollifier 3 is done by using
with the aid of Equation (
32).
In the present method of mollification, we remove high frequency component of data, regarding it to be noise. Hence if noise involves low frequency component, it will not be removed, and if high frequency component in the data is not desired to be erased, the present method will not be useful.
In the present paper, we study an example of calculating the first order derivative. In [
3], the derivative of order
is calculated as an example, where the mollification based on an orthogonal rapidly decaying wavelet is used.