1. Introduction
There have been many studies that have postulated an interaction of asset prices and economic activity. A large body of the literature basically focused on the interlinkages of the stock market and output. Yet, as has recently been shown it is not so much the linkage between stock market and output that is relevant for macroeconomics, but the relationship between the bond market and economic activity [
1,
2]. The tightness of credit and the credit spreads in bond markets have been shown not only to interact but also to have exacerbating or even destabilizing effects on economic activity. (There are earlier non-conventional studies that view the role of credit as significantly amplifying forces [
3,
4,
5]. In [
3] it is the instability of credit and in [
4,
5] it is the way financing becomes delinked from collaterals that contributes to a downward spiral once large real or financial shocks occur.)
On the other hand, credit spreads are traditionally dealt with in corporate finance. In traditional corporate finance theory [
6] one viewed debt as a credit derivative and argued that the leverage of the economic units (firms, households) creates a default risk so that the degree of leverage as well as the volatility of the value of the underlying assets will explain the risk premium. Merton [
6] correspondingly spoke not about the term structure of interest rates, but the risk structure of interest rates. Each firm‘s risk characteristics are different and so would be its risk premium.
Recently an alternative to traditional corporate finance view has been developed that led to the term “finance premium”, which was defined using the theory of the “financial accelerator”. The financial accelerator theory developed by Bernanke
et al. [
7] has been put forward to explain the linkage of the risk premium and economic activity. The idea of the financial accelerator is in that tradition since, using information economics and the theory of costly state verification, it is argued that the risk premium reflects a finance premium according to which it rises with falling net worth, and falls with rising net worth. For example, for higher default risk a greater cost of state verification is needed, giving rise to a higher finance premium. If there are no possible losses and no verification cost, the constant (risk free) interest rate will be charged. In this tradition the financial accelerator theory has mainly been applied to firms and households.
The recent meltdown over the years 2007–2009 has also expedited the application of the financial accelerator theory to financial intermediaries. The financial accelerator is applied to the balance sheets and in particular to the net worth of banks. There is the important work by Adrian and Shin [
8] and Brunnermeier and Pederson [
9] where borrowing by financial intermediaries depends on their balance sheets. When asset prices get depressed, and net worth falls, margin requirements in the money market rise. This forces the financial intermediaries to pay a higher default premium and reduce their leverage further, entailing a further fall of asset prices and so on. The depressed asset prices, possibly entailing a fire sale of assets by some intermediaries, have external effects on the industry and bank runs can exacerbate this effect [
10]. (There was a large body of literature that has shown that there might be a downward spiral through interconnectedness, interlinkages and contagion. Such studies have started with Greenwald and Stiglitz [
11] and continued with Adrian and Shin [
8,
12], Gorton [
10], and Brunnermeier and Sannikov [
13].) Here too the financial accelerator is seen to be operative and affecting the macroeconomy. But once the empirical measure of a finance premium was introduced into the macroeconomic literature, the traditional corporate finance measures for credit spreads came back to the fore front of macroeconomics [
2,
14]. One of the most commonly used measures for credit spread, measuring default risk, is the Baa-Aaa spread. Of course, since real interest rate movements are not captured in the Baa-Aaa bond spread, the real interest rate has to be taken into account as well. Besides that in empirical macroeconomic research another important financial market variable is the term structure of interest rates. The term structure of interest rates not only indicates expected inflation rates and output, as predictor for future output [
15], but also the stance of the central banks with respect to future interest rates. So beside the bond spread and current real interest rates the yield curve was considered important too.
Econometric works, however, by using the bond spread, the real interest rate and the term structure of the interest rate as predictors for future output resulted only in modest success [
2,
14]. In their empirical study they obtain some success for some macroeconomic variables, for example, investment and to a lesser extent employment, but the Baa-Aaa spread usually is not significant in predicting output over a short forecast horizon (3 months) or even over a long forecast horizon (12 months). With respect to the credit spread variable their coefficients are insignificant for both the longer time period (1973:1–2009:12) as well for a shorter time horizon and using quarterly data (1985:1–2009:4). It is apparent that this less successful result for the usual credit spread variable, measured by the Baa-Aaa spread, gave some incentive to introduce a new credit spread variable. Their computed “spread variable" takes the same maturity for the treasury bonds as for the risky bonds, issued by firms. When they use this new spread (called GZ) in the same econometric forecasting exercise they get significant coefficients on the new measure for risk premia so that they claim they have found a variable that, jointly with the real interest rate and the term structure, can successfully be used for forecasting future economic activity.
In our paper we do not intend to judge the validity of their econometric results, as this has already been done by Swanson [
16]. Instead, we choose to exploit the multi resolution ability of wavelet analysis to separate specific frequency components of a signal in order to evaluate the information content of different monetary and financial indicators (real interest rate, term spread and credit spread) for economic activity. First, we perform wavelet-based exploratory data analysis to determine which frequencies are dominant in certain time intervals and to get an indication about the presence of specific highly localized patterns at certain scales. We exploit the potential of wavelets to detect structural breaks by identifying the scale and localizing the time at which sudden variations and discontinuities occur along a time scale for the different series through the test of homogeneity of variance. Finally, we measure the individual effects of financial and monetary variables for output at different horizons using the “double residuals" regression analysis on a scale-by-scale basis. Our results show that we are able to disentangle and isolate the factors that drive output at different horizons. In particular, relative to the aggregate analysis, scale-by-scale regressions indicate that the predictive content for economic activity of various financial indicators changes substantially across scales, with the current and future stances of monetary policy also displaying coefficient sign reversal behavior.
The remainder of the paper is organized as follows.
Section 2 provides motivation on the potential role of wavelets for the analysis of the information content of money and credit spreads for aggregate output.
Section 3 presents the results from wavelet exploratory data analysis using CWT and MODWT. Detection and location of structural breaks and “double residuals” regression analysis using wavelets are presented and discussed in
Section 4 and
Section 5, respectively.
Section 6 concludes.
2. Financial Indicators and Economic Activity in the Standard Classical Approach
In the standard classical approach the information content of different financial indicators for economic activity is examined using a simple regression framework. An interesting example is provided by a recent paper presented at FRB/JMCB conference “Financial Markets and Monetary Policy”, held at the Federal Reserve Board, Washington D.C., in which Gilchrist
et al. [
14] “attempts to quantify the role of financial frictions in business cycle fluctuations by estimating a DSGE model with the financial accelerator mechanism that links balance sheet conditions to the real economy through movements in the external finance premium”. Therefore, following Gilchrist
et al. [
14] and Gilchrist and Zakrajsek [
2] we estimate the following univariate forecasting specification:
where
Y denotes real GDP,
the “term spread”, that is the slope of the Treasury yield curve, defined as the difference between the three-month constant-maturity Treasury yield and the 10-year constant-maturity yield,
denotes the real federal funds rate, and
denotes a credit spread defined as the difference between the long-term Baa-rated corporate bonds and the yield on the constant-maturity 10-year Treasuries. (Data for real GDP are quarterly seasonally adjusted billions of chained 2005 Dollars, while interest rates data are monthly converted to quarterly averages. The source for interest rates data is “Selected Interest Rates” (H.15) federal Reserve statistics release. The real federal funds rate is calculated as in Gilchrist
et al. [
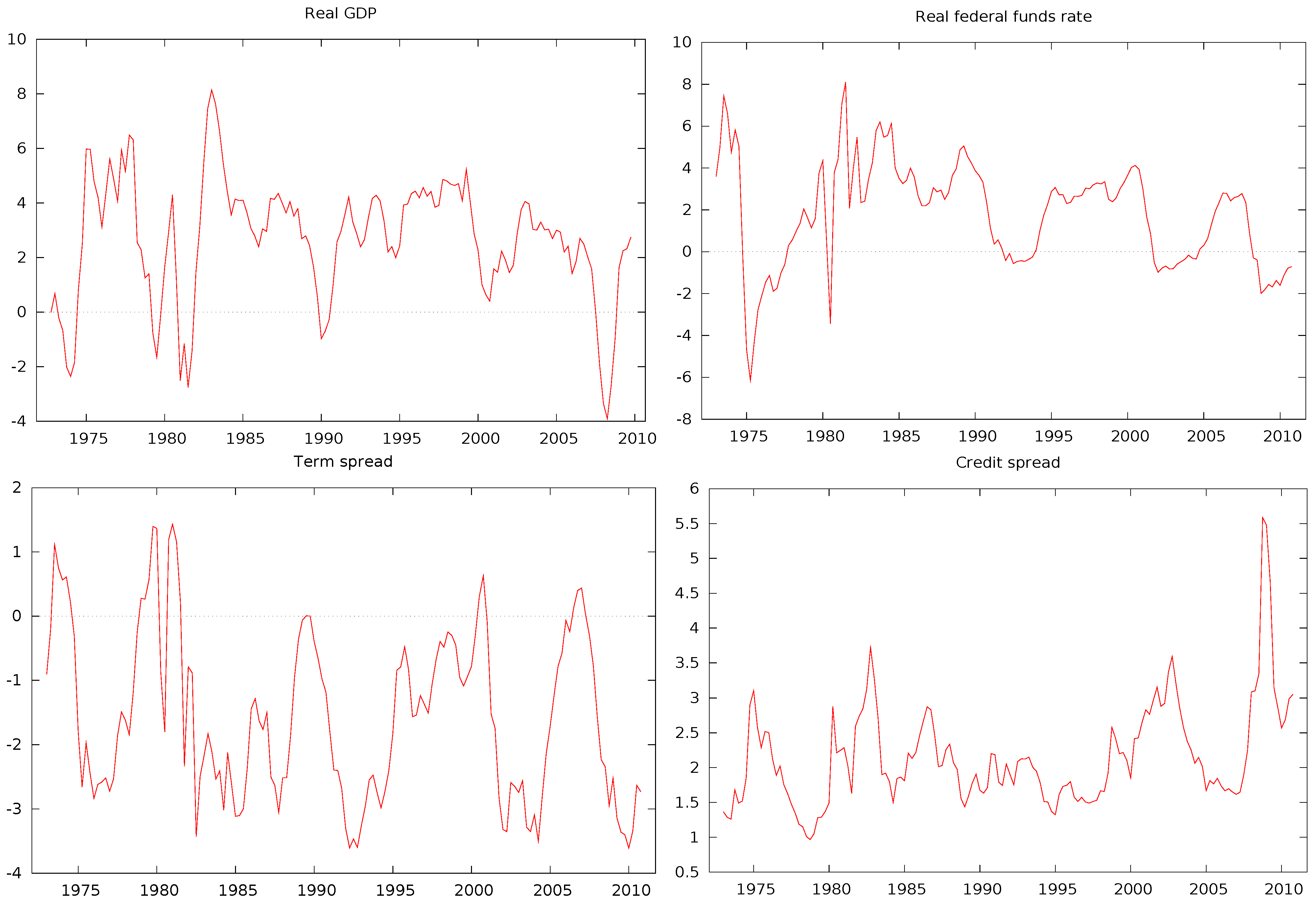
14].) The raw series are presented in
Figure 1.
The results of the estimated equation are presented in
Table 1. They show that the current slope of the yield curve is the only statistically and economically significant predictor of future changes of real GDP. In particular, a one-percentage-point increase in the term spread in quarter
t reduces the year-ahead real GDP growth by almost three-quarter percentage points. Neither the real interest rate nor the credit spread provide additional explanatory power for GDP growth. (Similar findings are reported in [
2,
14].)
The results of diagnostic tests on these regressors indicate that the residuals are autocorrelated and heteroskedastic and that the estimated relationship is unstable. (In fact, Bai-Perron’s [
17,
18] test on the basis of the breakpoint selection procedure based on the Bayesian Information Criterion (minimum BIC) identifies three structural breakpoints in the forecasting output equation according to the sequential test statistics,
, by using the 5% significance level and setting the maximum number of breaks
M equal to 5 and the trimming percentage to 15% in all cases. The estimated break dates are 1981:2, 1990:3 and 2003:2.)
Based on these “unpleasant" findings, especially as regards the predictive power of credit spreads, the strategy adopted in this strand of the literature is to look for various corporate bond spreads differing over the trading market, security type and issuer. For example, Gilchrist and his coauthors [
2,
14] construct “bond portfolios" based on secondary market prices of outstanding senior unsecured corporate bonds issued by non financial firms and compare their information and predictive contents for economic activity relative to the standard credit spread indicators at short-term and long-term forecast horizons.
Figure 1.
Raw series: Quarterly aggregate data from 1973:1 to 2009:4.
Figure 1.
Raw series: Quarterly aggregate data from 1973:1 to 2009:4.
Table 1.
Aggregate quarterly regression analysis.
Table 1.
Aggregate quarterly regression analysis.
| OLS-Dependent variable: ; 1973:4–2009:4 |
|---|
| | Coefficients | HAC s.e. | t-Ratio | p-Value |
|---|
| const | 1.737 | 1.125 | 1.543 | 0.125 |
| 0.471 | 0.278 | 1.697 | 0.092 * |
| 0.138 | 0.190 | 0.729 | 0.467 |
| –0.070 | 0.215 | –0.326 | 0.745 |
| 0.124 | 0.254 | 0.488 | 0.626 |
| –0.087 | 0.140 | –0.625 | 0.533 |
| –0.703 | 0.203 | –3.461 | 0.001 ** |
| –0.141 | 0.516 | –0.274 | 0.785 |
| = 0.235 - s.e. reg. = 1.986 - DW = 0.45 |
| LM test up to order 4 = 123.1 (p-value = 1.04e–43) |
| Breusch-Pagan test-LM = 20.01 (p-value = 0.005) |
| Test RESET-F(1, 136) = 3.52 (p-value = 0.063) |
Although the concepts of the “short-run” and of the “long-run” are central in economic analysis, variation in the relationships across time scales is seldom analyzed. By contrast, we begin by recognizing, for each relationship postulated by the underlying economic theory, the possibility that
where
is the dependent variable at scale “
s”,
(.) are arbitrary functions specified by the theory, which might differ across scales,
represents the codependent variables at scale “
s”, and
represents exogenous variables
at scale “
s”; that is, the relationships between economic variables may well be scale dependent.
Wavelets multi-resolution decomposition analysis can provide an effective solution to such a situation. The key insight is that wavelets provide a complete decomposition of the original series into several orthogonal components, each reflecting the evolution through time of the signal at a particular range of frequencies as determined by the inverse of the corresponding period expressed in terms of dyadic expansions. One of the most important properties of the wavelet transform is its ability to obtain the frequency content of a process as a function of time, that is to provide a time-scale (time-frequency) representation of a signal. In particular, wavelets have good frequency and time localization properties since they display good time resolution and poor frequency resolution at high frequencies, and good frequency resolution but poor time resolution for low frequencies. This property accords with our requirements, as most of the signals of practical interest in economics and finance have high frequency components for very short periods and low frequency components for long durations.
These time-frequency properties make wavelet analysis a powerful tool for exploratory data analysis because we can get an idea about the non-stationarity and the dominant scales of variation present in the series. First of all, the wavelet transform can be used to indicate how the power of the projection of the signal varies with the scale of observation. In addition, much information about the structure of the data can be obtained by comparing how the local power scales varies over time. As a result wavelet analysis can be used to look for (highly localized) patterns, possibly only at certain scales, and to reveal potentially interesting structure, like characteristic scales, in the data. Specifically, using wavelets for exploratory data analysis we try to investigate the major scales occurring in economic and financial data, i.e., letting the data indicate the major scales by choosing coefficients of maximal energy which is measured by maximum wavelet coefficient variance.
Most economic and financial time series exhibit quite complicated patterns like abrupt changes, jumps and volatility clustering. There may be purely local changes in the time domain, global changes in the frequency domain, and there may be also changes in the variance parameters. These processes evolve in a nonlinear fashion over time, are non-stationary and their frequency characteristics are time-dependent, that is the importance of the various frequency components is unlikely to remain stable over time. In such a case a locally adaptive filter like the wavelet transform is particularly well suited for evaluation of the models.
Although spectral methods have been by far the most important filter processing tool in economics for many years the role of wavelets has by now become familiar in empirical economic analysis. (After the first applications of wavelet analysis in economics and finance provided by Ramsey and his co-authors [
20,
21,
22,
23,
24], the number of wavelet applications in economics and finance has rapidly increased in the last few years. A variety of economic examples of the use of wavelets are provided from Gençay
et al. [
25,
26], Kim and In [
27], Fernandez [
28], Gallegati and Gallegati [
29], Crowley and Mayes [
30], Ramsey
et al. [
31], Gallegati
et al. [
32] among the others.) Wavelets, their generation, and their potential usefulness for economic analysis are discussed in intuitive terms in Ramsey [
33]. Gençay
et al. [
34] and Crowley [
35] generate an excellent development of wavelet analysis and provide many interesting economic examples. Percival and Walden [
36] provides a more technical exposition with many examples of the use of wavelets in a variety of fields, but not in economics.
3. Wavelet-Based Exploratory Data Analysis
In this section we perform exploratory data analysis using wavelets because the wavelet transforms offers a powerful tool for exploratory data analysis given its ability to handle non-stationary and complex signals and detect the dominant scales of variation in the data. The aim of exploratory data analysis (Exploratory data analysis [
37] is an alternative approach for data analysis through which we aim to obtain a preliminary indication about the characteristics of the data and the nature of further analysis.) is to gain new insights on the underlying structure,
i.e., to explore relationships, patterns, and detect outliers and anomalies, postponing the usual assumptions about what kind of model the data follow to the results of the same data analysis process. Indeed, when there are no (or incomplete) a priori notions of the expected relationships among the variables, preliminary investigation of data can provide a useful a pre-step from which new hypotheses can be generated and then subsequently tested with confirmatory approaches. (In addition, exploratory data analysis can reveal modeling problems that could have been anticipated theoretically but were not.)
3.1. Continuous Wavelet Transform
The essential characteristics of wavelets are best illustrated through the development of the continuous wavelet transform (CWT). A wavelet is a function
defined over the real axis that integrates to zero and is square integrable (have unit energy):
For any arbitrary mother wavelet function
ψ, the continuous wavelet transform of the given function
is:
where
represents a set of wavelet daughters obtained by scaling and translating the mother wavelet
ψ (see [
36]).
Let
be the continuous wavelet transform of a signal
, with respect to the wavelet
ψ, where
λ is a scaling or dilation factor that controls the length of the wavelet and
τ a location parameter that indicates where the wavelet is centered,
represents the wavelet power and depicts the local variance of
. The wavelet power spectrum provides an unfolding of the characteristics of a process in the scale-space plane and can be quite revealing about the structure of a particular process, as it can clearly show the presence of multiscale features and can easily identify their temporal locations. As a result wavelet analysis can be used to look for (highly localized) patterns, possibly only at certain scales, and to reveal potentially interesting structure, like characteristic scales, in the data. (It is worth noting that methods have been developed to account for the time-varying nature of the second moment at different scales [
38].)
Among the several types of wavelet families available such as, Morlet, Mexican hat, Haar, Daubechies,
etc., we choose to employ a widely used wavelet such as the Morlet wavelet, (The Morlet wavelet, consisting of a plane wave modulated by a Gaussian, has optimal joint time frequency concentration as it attains the minimum possible uncertainty of the corresponding Heisenberg box.) defined as
The Morlet wavelet is a complex wavelet that produces complex transforms and thus can provide us with information on both amplitude and phase. We use the Morlet wavelet with
(where
is a dimensionless frequency) since this particular choice provides a good balance between time and frequency localization and also simplifies the interpretation of the wavelet analysis because the wavelet scale,
λ, is inversely related to the frequency,
[
39].
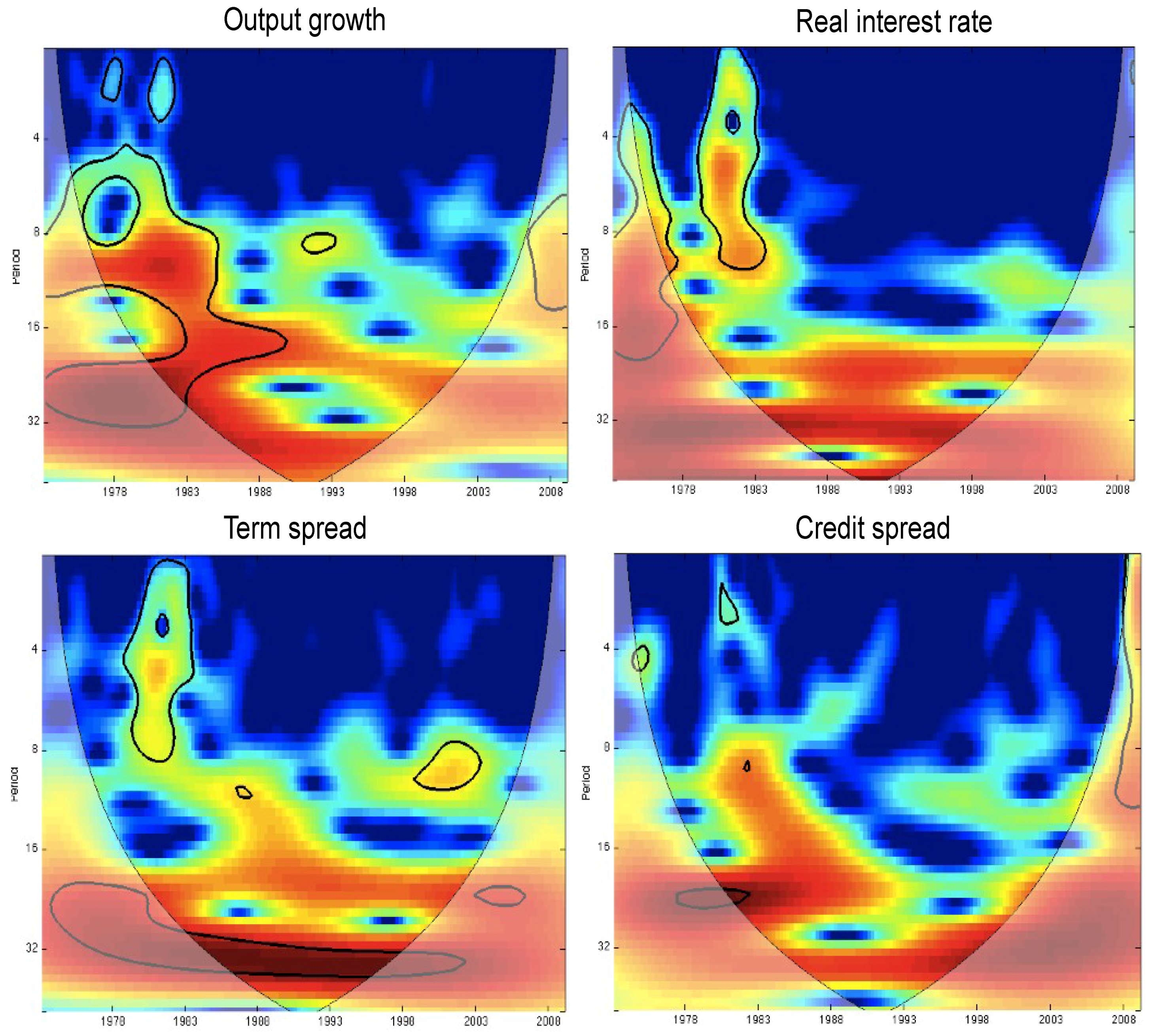
In
Figure 2 we see the plot of a continuous wavelet transform of the several variables using the Morlet wavelet. Time is recorded on the horizontal axis and the scale of the wavelet transform is recorded on the vertical axis. Reading across the graph at a given value for the wavelet scaling, one sees how the power of the projection varies across the time domain, while reading down the graph at a given point in time, one sees how the power varies with the scaling of the wavelet [
20]. We may evaluate the scaling characteristics of the data by examining the color plots of the continuous wavelet transform because the power of the projection of the signal onto the wavelet transform at the indicated level of scaling is indicated by color coding. The color code for power ranges from white (low power) to red (high power), with red (white) regions corresponding to higher (lower) wavelet transform coefficients. Significant regions are associated with warmer colors (red, orange and bright green). This color coding can provide an objective method for determining the principal timescales present in a signal and also for providing information about the scales at which important features provide a significant contribution.
A black contour line testing the wavelet power significance level against a white noise null is displayed as is the cone of influence, represented by a shaded area corresponding to the region affected by edge effects. (As with other types of transforms, the CWT applied to a finite length time series inevitably suffers from border distortions; this is due to the fact that the values of the transform at the beginning and the end of the time series are always incorrectly computed, in the sense that they involve “missing" values of the series which are then artificially prescribed; the most common choices are zero padding extension of the time series by zeros or periodization. Since the “effective support" of the wavelet at scale s is proportional to s, these edge effects also increase with s. The region in which the transform suffers from these edge effects is called the cone of influence. In this area of the time frequency plane the results are unreliable and have to be interpreted carefully.)
Figure 2.
CWT plot for real output, real interest rate, term spread and credit spread (from top to bottomt). The color code for power ranges from blue (low power) to red (high power) with significant regions associated with warmer colors (red, orange and bright green). A black contour line testing the wavelet power 5% significance level against a white noise null is displayed as is the cone of influence, represented by a shaded area corresponding to the region affected by edge effects.
Figure 2.
CWT plot for real output, real interest rate, term spread and credit spread (from top to bottomt). The color code for power ranges from blue (low power) to red (high power) with significant regions associated with warmer colors (red, orange and bright green). A black contour line testing the wavelet power 5% significance level against a white noise null is displayed as is the cone of influence, represented by a shaded area corresponding to the region affected by edge effects.
Looking at the wavelet spectra of the several variables there seems to be some evidence of dominant scales of variations associated with scale. Specifically:
The power of the industrial production was very high at scales corresponding to business cycle frequencies, that is 2 to 10 years, until mid-1980s. After that, the power at all frequencies steadily decreased, with an exception in the last decade, when it was again quite high at the scale corresponding to a 6 years period (in the literature this evidence is referred to as the “Great Moderation” [
40]);
For the real interest rate there is evidence of high (orange) and very high (red) power at scales corresponding to periods greater than 4 years (and between 2 and 4 years at the very beginning of the sample,
i.e., 2nd half of the seventies); there is also evidence of a significant region at short scales, between 1 and 2 years in early 80s in correspondence with the structural change in the monetary policy, when the Fed implemented a very restrictive monetary policy as a reaction to the inflationary pressures of the second oil shock (Volcker disinflation period [
41]);
For the term spread there is clear evidence of very high and high power at scales between 4 and about 10 years, a sort of “optimal” scale, and, like in the real interest rate case, also evidence of power (bright green) at short scales, that is 1 to 2 years, in early 80s;
Finally, for the credit spread there is evidence of high power at scales corresponding to periods between 4 and 8 years, particularly at the beginning and end of the sample period.
As noted by Gençay
et al. [
34], the CWT, by representing each datum with a pair of data, designating time, or space, and scale, is a highly information redundant transform. As a consequence it is computationally impossible to analyze a signal using all wavelet coefficients. A one to one transformation is obtained by discretizing the transform over scale and over time. We therefore move to the discussion of the discrete wavelet transform (DWT), since the DWT, and in particular the MODWT, a variant of the DWT, is largely predominant in economic applications. (The number of the papers applying the DWT is far greater than those using the CWT. As a matter of fact, the preference for DWT in economic applications can be explained by the ability of the DWT to facilitate a more direct comparison with standard econometric tools than is permitted by the CWT (e.g., time scales regression analysis, homogeneity test for variance, nonparametric analysis, ....).)
3.2. Discrete Wavelet Transform
The DWT is based on similar concepts as the CWT, but is more parsimonious in its use of data [
42]. In order to implement the discrete wavelet transform on sampled signals we need to discretize the transform over scale and over time through the dilation and location parameters. Indeed, the key difference between the CWT and the DWT lies in the fact that the DWT uses only a limited number of translated and dilated versions of the mother wavelet to decompose the original signal. The idea is to select
τ and
λ so that the information contained in the signal can be summarized in a minimum number of wavelet coefficients. The number of observations at each scale is given by
The discretized transform is known as the discrete wavelet transform, DWT.
The general formulation for a continuous wavelet transform can be restricted to the definition of the “discrete wavelet transform”, by discretizing the time-scale parameters
λ and
τ. In order to obtain an orthonormal basis a transform of the scaling parameter,
, and the Nyquist sampling rule,
, are used. The generating wavelet functions are then
where
j and
k are integers. If
T is small enough and the computation is done octave by octave,
i.e.,
, the “mother wavelet” results in the following equation
This function represents a sequence of rescaleable functions at a scale of
and with time index
k,
. The wavelet transform coefficient of the projection of the observed function,
,
on the wavelet
is given by:
For a complete reconstruction of a signal
, one requires a scaling function,
, that represents the smoothest components of the signal. While the wavelet coefficients represent weighted “differences” at each scale, the scaling coefficients represent averaging at each scale. One defines the scaling function, also know as the “father wavelet”, by:
And the scaling function coefficients vector is given by:
By construction, we have an orthonormal set of basis functions, whose detailed properties depend on the choices made for the functions,
and
. See for example the references cited above as well as [
38] and [
43].
The discretization of the continuous time-frequency decomposition creates a discrete version of the wavelet power spectrum
in which the entire time-frequency plane is partitioned with rectangular cells of varying dimensions but constant area, called Heisenberg cells. (Their dimensions change according to their scale: The windows stretch for large values of
λ to measure the low frequency movements and compress for small values of
λ to measure the high frequency movements.)
Figure 3 shows the (gray level representation of the) time-frequency plot of our dataset obtained by applying a non-decimated discrete wavelet transform using the Haar wavelet. (This wavelet transform is a compromise between the CWT, with continuous variations in scale, and DWT where the power of the transform is highly localized. Moreover, it is a phase invariant transform is not restricted to limitations imposed by the dyadic expansion used by the DWT.) In this time-frequency plot, with time along the horizontal axis and frequency along the vertical axis, (As we proceed down the frequency scale from one band to the next, the bandwidth of the frequencies is halved and the temporal dispersion of the wavelets is doubled.) each wavelet coefficient is represented by a rectangular area with the modulus of the wavelet coefficient determining the gray level of each rectangle: Fine scale coefficients occupy tall thin boxes and coarse scale coefficients occupy flat wide boxes. In this way the differences in the grey-scale intensity shading of the rectangles provides a grey-level representation of the signal in which the significant small- and large-scale features as well as their temporal localization are easily identified through the darker regions of this two-dimensional plane graph.
Consistently with the results shown in
Figure 2, we find significant activity at coarse scales for all variables except credit spread, as evidenced by the dark horizontal strips in the bottom part of the plots corresponding to the smooth part of the signal. Moreover, there are evident small-scale features represented by the dark vertical regions in the upper-left part of the plot for output growth, real interest rate and term spread. (There are some large coefficients at both left and right boundaries that can be considered a consequence of boundary effects affecting DWT.) In particular, in the case of output growth there is much more activity in the initial years than the rest of the signal at both fine and coarse scales, a finding that is consistent with the evidence from the literature on the “Great Moderation”. Otherwise, in the case of the real interest rate and the term spread there is, especially in the former case, clear evidence of a significant high-frequency activity in the initial part of the signal, the early 80s, in coincidence with a sharp break in monetary policy with Volcker’s appointment.
The most notable features emerging from the time-frequency wavelet exploratory analysis displayed in
Figure 3 and
Figure 4 are:
Time-Scale analysis using scalograms and time-frequency plots provides clear evidence of the changing nature of the signals;
The continuous wavelet transform does a good job of revealing the scaling characteristic (major scales) present in the data;
The time-frequency plots are useful in detecting sharp changes in the high- frequency component of the data, like structural breaks.
In sum, we have showed that both CWT and DWT can be used to gain insights on the dynamics and the structure of economic time series. In particular, using wavelets for exploratory data analysis we can get evidence about the presence of dominant scales of variation in the series and are able to identify significant events that altered the structure or volatility of the sequences. Such ability in revealing the scaling characteristic (major scales) present in the data and detecting sharp changes in the high-frequency component of the data, like structural breaks, can be explained with the different time-frequency localization properties of the different types of wavelets used in each case, that is Morlet wavelet in the CWT and Haar wavelet in MODWT. (Indeed, the Haar wavelet has a better time localization, and consequently poorer frequency localization, capacity than the Morlet wavelet.)
Figure 3.
Time-Frequency plots: Time is measured along the horizontal axis and frequency along the vertical axis. Each wavelet coefficient is represented by a rectangular area with fine scale coefficients occupying tall thin boxes and coarse scale coefficients flat wide boxes. The modulus of the wavelet coefficient determines the gray level of each rectangle.
Figure 3.
Time-Frequency plots: Time is measured along the horizontal axis and frequency along the vertical axis. Each wavelet coefficient is represented by a rectangular area with fine scale coefficients occupying tall thin boxes and coarse scale coefficients flat wide boxes. The modulus of the wavelet coefficient determines the gray level of each rectangle.
In any event, the analysis discussed above can be seen as a first preliminary step and is to be regarded as “explorative” and “non-parametric” in nature. The process is meant to provide insight into the structure of the model used and its effectiveness in reproducing the data generating process. Estimation and hypothesis testing are to come later utilizing the knowledge gained through the initial analysis of the structure of the processes being examined. With these preliminary exploratory data analysis dealt with, we can proceed to analyze the usefulness of wavelet analysis for detection and location of structural breaks.
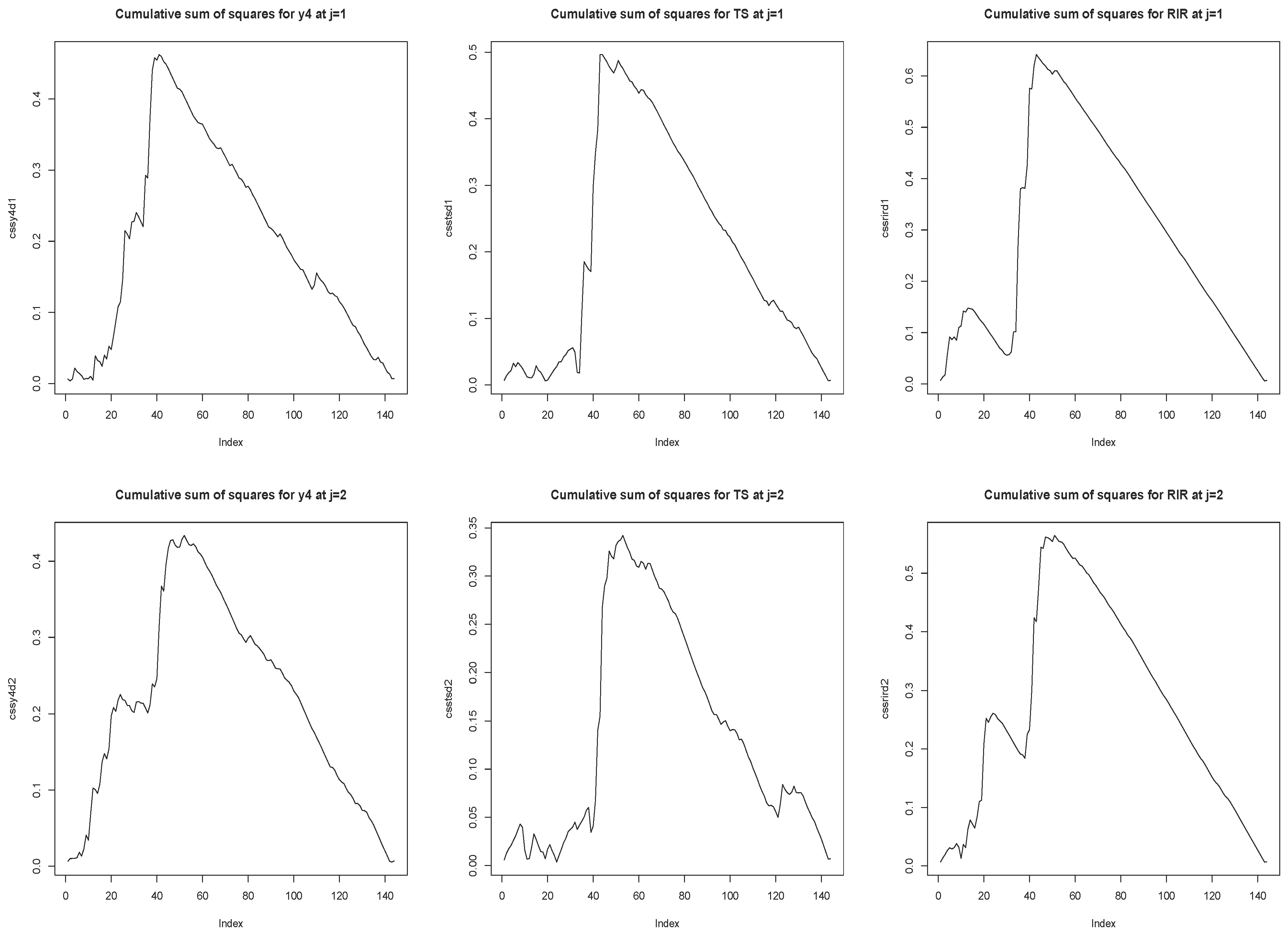
Figure 4.
The auxiliary test for j = 1 (upper panel) and j = 2 (lower panel) for output (left), term spread (center) and real interest rate (right).
Figure 4.
The auxiliary test for j = 1 (upper panel) and j = 2 (lower panel) for output (left), term spread (center) and real interest rate (right).
4. Detection and Location of Structural Breaks through the Test of Homogeneity of Variance
In this section we test for the presence of structural breaks in volatility by using a wavelet-based test for homogeneity of variance. Our interest in detecting wavelet variance change points location is motivated by the visual inspection of
Figure 2 and
Figure 3 where we observe a significant temporary increase in volatility at the beginning of the eighties for the real interest rate and the term spread. (Although these findings are well known in the literature, there is still room for wavelets to contribute to a deeper understanding of structural breaks with respect to standard classical analysis by taking advantage of the ability of wavelet analysis to identify the scale at which the inhomogeneity occurs.) Following the procedure suggested by Whitcher [
44] we first perform a test for homogeneity of variance using the normalized cumulative sum of squares test statistic from the DWT, and then, after the variance change has been detected, we estimate the time at which the variance of a time series changes on a particular scale by an auxiliary test statistic computed using the MODWT wavelet coefficients.
The wavelet-based test for homogeneity of variance [
44,
45] apply to wavelet coefficients obtained from the DWT the procedure based on an iterated cumulative sum of squares algorithm (ICSS) proposed by Inclan and Tiao [
46]. The statistical test for variance homogeneity is based on the hypothesis that the variance of the underlying stochastic process is constant and relies on two main properties of the discrete wavelet transform (DWT): The energy preservation and approximate decorrelation properties. (The first states that the variance of a time series is preserved and captured by the variance of its wavelet coefficients, so that the wavelet variance can partition the variance of a time series into different components, each associated with a specific scale or resolution. The latter refers to the fact that for any time series exhibiting both short and long memory characteristics the wavelet coefficients obtained by applying DWT can be assumed, for any scale, as approximately uncorrelated. This is not true for MODWT.) Based on the assumption that the DWT decorrelates colored noise processes, the interior wavelet coefficients (
) for scale
j at time
t can be regarded as a zero mean Gaussian white noise process with variance
. The null hypothesis for this test is
against the alternative:
where
k is the unknown time of a possible change in the variance and
represents the scale after all wavelet coefficients affected by boundary conditions have been discarded.
Given scale
j DWT coefficients
, the test statistic is based on a measure of variance accumulation as a function of time through the normalized sum of squares
:
from which
and
for
are computed and then used to form the
D-statistic,
.
The null hypothesis of homogeneity of variance can be rejected at conventional significance levels,
i.e.,
or
, if the observed
D-statistic is larger than the corresponding critical value. In
Table 2 we report the critical values for the
D-statistic obtained using Monte Carlo simulations for various sample sizes or large sample approximation to the distribution of
D under the assumption of white noise.
Table 2.
Monte Carlo simulation critical values.
Table 2.
Monte Carlo simulation critical values.
| D-Statistic critical values comparison: |
|---|
| WF | Scale | N | 10% | 5% | 1% |
|---|
| LA(8) | 1 | 27 | 0.3146 | 0.3509 | 0.4208 |
| | 2 | 61 | 0.2127 | 0.2361 | 0.2866 |
| D(4) | 1 | 30 | 0.2995 | 0.3336 | 0.3974 |
| | 2 | 63 | 0.2102 | 0.2346 | 0.2820 |
| Haar | 1 | 32 | 0.2908 | 0.3250 | 0.3903 |
| | 2 | 64 | 0.2086 | 0.2323 | 0.2796 |
After rejection of the null hypothesis of variance homogeneity the location of a variance change can be determined using the “nondecimated” DWT wavelet coefficients by (i) computing the rotated cumulative variance curve, (These plots show what can be thought of as deviations from the expected accumulation of sample variance across time for a stationary process [
47].) now using the MODWT wavelet coefficients; and (ii) recording the location of the wavelet coefficient from which the test statistic
D achieves its maximum [
48]. (The reason for using a variation of the DWT for determining the location of a variance change refers to the property of this highly redundant wavelet transform to have, unlike the classical DWT, a number of coefficients at each scale that equal the number of observations in the original time series.)
In general, wavelets that are zero phase, not very smooth, and have very few vanishing moments, like the Haar wavelet, would be most suitable for detecting regime shifts and discontinuities [
44]. Nonetheless, the Haar wavelet is a poor approximation to an ideal band-pass filter with respect to other wavelet filters like Daubechies’ extremal phase and least asymmetric wavelet filters because the level of approximation improves with the filter length. As a consequence, both the D(4) and the LA(8) filters are a much better approximation to an ideal band-pass filter than the Haar wavelet, (When filtering a time series via the DWT and using the Haar wavelet filter, significant amounts of low-frequency content may leak into the resulting wavelet coefficients [
48].) because they have better ability to capture the different frequency components (especially at scales greater than one). Thus, following Whitcher
et al. [
45,
48], instead of selecting a priori a specific wavelet function, we choose to use in our analysis all three different wavelet families, that is Haar, D(4), and LA(8).
In
Table 3 we report the results from applying the wavelet-based homogeneity test for variance using the Haar, D(4) and LA(8) wavelet filters. (In addition, Whitcher
et al. [
45,
48] recommend not to use levels greater than three because the power and size of the test decrease with the wavelet level. Thus, we restrict our detection and location analysis of variance changes to the lowest scale levels of wavelet coefficients,
i.e.,
and
.) There are only slight differences between the results from alternative wavelet filters in three out of four cases. The results are not sensitive to the choice of the wavelet family for the real interest rate and the term spread at scale 1 and 2, (The null hypothesis is rejected at
significance level of the term spread only using the D(4) wavelet filter.) and for output at scale 2, where the null hypothesis of variance homogeneity is always rejected. Contrasting results from the three wavelet filters are obtained for output at scale 1 with three different rejection results as the null hypothesis of variance homogeneity is rejected at all significance levels with the Haar filter and at the
and
significance level, respectively, with the
and
wavelet filters. Less conclusive findings than the previous ones are obtained for the credit spread, where the results indicate rejection of the variance homogeneity hypothesis at the
and
significance level at scale 1, but also span from acceptance to rejection of the null hypothesis at scale 2. (These differences in the test results for credit spread are likely to be related the occurrence of the break at the end of the sample period.) All in all, we can say that there is clear evidence that the volatility change phenomenon is localized in scale for both output and the real interest rate.
Table 3.
Results of testing for homogeneity of variance using the LA(8), D(4) and Haar wavelet filters.
Table 3.
Results of testing for homogeneity of variance using the LA(8), D(4) and Haar wavelet filters.
| D-Statistic: |
|---|
| WF | Scale | Output | Real int. rate | Term spread | Credit spread |
|---|
| LA(8) | 1 | 0.3980 * | 0.6584 | 0.5017 | 0.3445 ** |
| | 2 | 0.4289 | 0.5713 | 0.4726 | 0.1576 |
| D(4) | 1 | 0.3233 ** | 0.6343 | 0.4401 | 0.3364 * |
| | 2 | 0.5065 | 0.5866 | 0.2622 * | 0.3014 |
| Haar | 1 | 0.4233 | 0.6236 | 0.4143 | 0.3536 * |
| | 2 | 0.4406 | 0.4409 | 0.3399 | 0.2572 * |
As regards the detection of the location of the change point we can analyze the plot of
, the cumulative sum of squares from MODWT non-boundary wavelet coefficients, against
k in order to find the point
at which the maximum of
is attained. (For a variance stationary process its cumulative variance plot is expected to increase linearly with
k at approximately
, while when the variance of the process is not homogeneous a considerable divergence of the cumulative variance plot from the
line will be observed.)
Figure 4 displays a plot of the cumulative variance as a function of wavelet coefficient for the first two levels of each series for which the test has detected a variance change. The plot shows a sudden accumulation of variance followed by a sign of the slope change and a gradual tapering off of the variance (by construction the series must begin and end at zero). We see a pronounced peak and a drastic change around the 40th observation corresponding to the point where the variance changes to a smaller value. The change points are located at the beginning of the eighties for all variables and identify two already referred events characterizing the US economy in the early 80s: The “incredible Volcker disinflation” and the “Great Moderation”.
Table 4 shows the estimated locations of the variance change points, after adjusting for the phase shift of the different wavelet filters used, i.e., Haar, and . (MODWT wavelet coefficients are circularly shifted to better align features in the wavelet coefficients with the original series.) There is a very slight difference between and wavelet filters (two quarters for output at scale 1), the broader difference being with the Haar wavelet filter. At scale 1 the variance changes are located in 1982:III for the real interest rate and the term spread and between 1982:III and 1983:III for output, while at scale 2 they are located in 1982:IV for the real interest rate and in 1984:I for output (1981:III and 1984:IV, respectively, for the Haar wavelet filter).
Table 4.
Variance change location (phase shifted).
Table 4.
Variance change location (phase shifted).
| Scale 1 |
|---|
| WF | output | real int. | term |
| | | rate | spread |
| LA(8) | 83:I | 82:III | 82:III |
| D(4) | 82:III | 82:III | 82:III |
| Haar | 83:III | 82:II | 82:III |
| Scale 2 |
| WF | output | real int. | term |
| | | rate | spread |
| LA(8) | 84:I | 82:IV | 83:II |
| D(4) | 84:I | 82:IV | 83:II |
| Haar | 84:IV | 81:III | 82:IV |
The timing of the variance change for the real interest rate at scales 1 and 2 (1982:III and 1982:IV) is consistent with a monetary policy (negative) shock explanation: “The early Volcker era, for example, is a period of extreme volatility in both series" [
49], p. 1067. The series in question,
i.e., the new measure of monetary policy shocks and the change in the actual federal funds rate, that is the most commonly used indicator of monetary policy, present large swings in the early Volcker period (see Figure 1 in Romer and Romer [
49]). As a consequence of the Fed decision to use contractionary monetary policy to end inflation. The variance change point located in 1984:I at scale 2 is consistent with much of the existing empirical literature, specifically with both McConnell and Perez-Quiros [
50] and Kim and Nelson [
51] who established the first quarter of 1984 as the most likely time of the change in output volatility. The wavelet decomposition property can help in discriminating between the alternative explanations (Good luck, structural economic changes and better macroeconomic policies, particularly monetary policy, are the main competing hypotheses for the Great Moderation.) given for the moderation in the US output volatility through identification of the frequency ranges within which the changes have occurred. For example, the improved performance of macroeconomic policies, particularly monetary policy, can be associated to the scales containing business-cycle frequencies, while the good luck hypothesis can be associated to the scales corresponding to the highest frequencies. Thus, our finding seems to provide support for the hypothesis that improvements in monetary policy have probably been an important contribution not only to a lower and more stable inflation, but also to the reduced volatility of output.
5. Time Scale Relationships: Measuring Individual Effects at Different Horizons
The scale-by-scale decomposition provided by wavelet analysis allows the researcher answer to the following question: When examining the relationships between variables to what extent do we need to consider different scale compositions? Hence, the objective of this section is to clarify the benefits from using wavelets for the analysis of economic relationships at different time horizons.
The tendency of interest rate spreads to move together, especially during times of market distress, determines a pattern of intercorrelations among all three variables. In this case it is of interest to know how each independent variable is associated to the dependent variable after “controlling for",
i.e., partialling out, the other explanatory variables. Therefore, in this subsection we examine the relationship between each explanatory variable and aggregate output using the “double residuals" regression analysis. (This is the Frisch and Waugh’s famous result that partial regression coefficients are the same as multiple regression coefficients [
52].)
The “double residuals" regression analysis is performed by running a regression of residuals on residuals, with the aim of isolating a single coefficient in a regression after “partialling out" the effect of the other variables. In the first step, we remove or “partial out" from both the dependent variable and the independent variable of interest the effects of the other independent variables. The residuals from these regressions result in new measures of the dependent and independent variables that are uncorrelated with the excluded independent variables. In the second step we regress the residuals from the regression of the dependent variable on the residuals of the independent variable of interest.
As an example, consider the “net" relationship between aggregate output and the real interest rate. First, to partial out term and credit spreads from aggregate output and the real interest rate, we separately regress output (
) and the real interest rate (RIR) on the term spread (TS) and credit spread (CS)
producing two residual variables (
and
). These residuals represent measures of aggregate output and real interest rate uncorrelated with term and credit spreads. In particular, the residuals
(
) are the part of
(RIR) that is uncorrelated with TS and CS. We compute the linear association between the two residual variables,
and
, yielding the linear regression:
If these new measures of aggregate output and real interest rate are discovered to be related, the empirical association cannot be attributed to term and credit spreads since these two effects have been partialled out of the relationship.
In
Table 5 we present the results from the “double residuals" regression analysis between output and each explanatory variable defined in Equation (13), that is, the real interest rate, term spread and credit spread. In each panel of the table the top line reports aggregate results, while the next lines report scale-by-scale results. The aggregate results are consistent with previous findings presented in
Section 2 as we find that the term spread is the only significant variable for forecasting output. Relative to the aggregate, scale-by-scale regressions provide different insights. The results show that the predictive content for economic activity of widely-used financial indicators, such as the standard Baa-Treasury corporate credit spread, and indicators of the future and current stance of monetary policy, such as the shape of the yield curve or the real federal funds rate, changes widely across scales. In particular, the specific results can be summarized as follows:
The current stance of monetary policy, as measured by the real interest rate, is significantly negatively related to future output at the shortest scales, and , (associated to 4 and 8 quarters, respectively), but positively related in the long-run, (i.e., periods greater than 16 quarters);
The shape of the yield curve is positively related to future output in the shorter run, at scale , associated to 8 quarters, but at longest scales, i.e., and above, there is evidence of a negative relation between the term structure and future output;
The credit spread is significantly negatively related to future output at the longest scales only, i.e., and above.
In what follows we propose some theoretical interpretations for the results obtained for each regressor at different scales. Let us start with the positive long-run effects of real interest rate. The perceived existence of a negative relationship between interest rates and growth is one that pervades much economic thinking. The common view about the relationship between real interest rates and economic activity is that high real interest rates are deleterious because they choke off investment, while low real interest rates are desirable as they stimulate investment. This view is indeed partial since it takes into account only the cost of capital side of the investment story. The profitability side of firms’ investment behavior suggests a different interpretation: High real interest rates in periods of rapid growth may be a reflection of growing investment opportunities and thus booms can be seen as periods where both the profitability of capital and the demand for funds by firms are high. And since investment demand is more cyclical than income and savings (i.e., it increases more than income and savings in booms), high real interest rate may be a sign of a booming economy, just because the economy is a good place to invest during a boom. In sum, our results about the real interest rate indicate that while the cost of capital effect can be prevalent in the short and medium run (i.e., at the detail components level), profitability is likely to be prevailing in the long-run.
Our results, show a positive correlation of the term spread and future output at the shortest scales, from
to
, and a negative relation at the longest scales,
and
. This can be interpreted as follows. As to the shortest time scale, economic research has shown that the “yield curve spread" variable contains information about expectations of future inflation and the real interest rate [
15,
53]. Inflation and expected inflation tend to be positively correlated with economic activity and the expected interest rate is likely to be positively associated with future real growth via expectations of future changes in monetary policy; such as raising the future interest rate. Thus the positive correlation of the term spread and future output at the shortest scales, indicates the prevalence of the inflation effect in the shorter run. Such a positive correlation between the term structure and future output in the shorter run appears to be supported by recent studies on the relation of the term structure and output. For example, Estrella and Mishkin [
53] using a probit model show that there is a low probability of a recession when the term structure has a positive slope, but a high probability of a recession is indicated when there is a flat term structure. As to the longest time scale, concerning the negative relationship of the interest rate and output in the long-run, one can argue that in the long run high interest rates tend to indicate high real interest rates. Because households and above all firms’ spending decisions are mainly determined by long run interest rates, one would expect a negative relation between the term spread and future output at long time scales.
Table 5.
Scale-by-Scale “double residuals” OLS regressions.
Table 5.
Scale-by-Scale “double residuals” OLS regressions.
| Dependent variable: ; 1973:1–2009:4 (T = 144) |
|---|
| coeffs | HAC s.e. | t-ratio | p-value | Adj- |
| Aggregate | –0.0538 | 0.1515 | –0.3556 | 0.7226 | –0.0043 |
| 0.2584 | 0.0733 | 3.527 | 0.0006 *** | 0.1393 |
| –0.4196 | 0.2687 | –1.562 | 0.1206 | 0.0801 |
| –1.1956 | 0.2732 | –4.377 | 2.32e–05 *** | 0.2006 |
| –0.4962 | 0.1069 | –4.641 | 7.80e–06 *** | 0.1455 |
| –0.0652 | 0.1376 | –0.4740 | 0.6362 | –0.0036 |
| coeffs | HAC s.e. | t-ratio | p-value | Adj- |
| Aggregate | –0.8951 | 0.1944 | –4.604 | 8.95e- *** | 0.1721 |
| –0.8318 | 0.2100 | –3.961 | 0.0001 *** | 0.3766 |
| –1.0630 | 0.3390 | –3.135 | 0.0021 *** | 0.2514 |
| 1.0708 | 0.3278 | 3.267 | 0.0014 *** | 0.1196 |
| 0.3648 | 0.3096 | 1.179 | 0.2406 | 0.0179 |
| 0.1486 | 0.2085 | 0.7131 | 0.4770 | –0.0022 |
| coeffs | HAC s.e. | t-ratio | p-value | Adj- |
| Aggregate | –0.4913 | 0.5734 | –0.8568 | 0.3930 | 0.0143 |
| –1.1937 | 0.4244 | –2.813 | 0.0056 *** | 0.1392 |
| –1.9878 | 0.6594 | –3.015 | 0.0030 *** | 0.2302 |
| –1.3714 | 0.8000 | –1.714 | 0.0887 * | 0.0378 |
| –0.1250 | 0.4606 | –0.2714 | 0.7865 | –0.0055 |
| 0.0824 | 0.2141 | 0.3849 | 0.7009 | –0.0048 |
Concerning credit spreads, the coefficients estimates imply a robust economically significant negative relationship between credit spreads and real economic activity at the longest scales that is consistent with the current literature on financial markets. The relationship between credit spreads and future real activity can be motivated by financial theories that, like the “financial accelerator" theory developed by Bernanke and Gertler [
54] and Bernanke
et al. [
7,
55], depart from the Modigliani and Miller [
56] paradigm of perfect financial markets. These theories emphasize the role of balance sheet positions of borrower and lenders in causing an increase in the effective cost of external funds and widening of credit spreads. Movements in credit spreads are considered useful predictors of real activity as changes in the cost of borrowing lead to a variation in investment spending and hence in overall aggregate activity.
6. Conclusions
Wavelet methods provide a researcher with tools to identify easily features of data and relationships which would otherwise be difficult to detect using classical econometric techniques. In this paper we exploit the benefits from using wavelets for the analysis of economic relationships with scale effects by revisiting the forecasting power of a variety of monetary and financial indicators for economic activity. Our analysis differs from earlier studies that examine the predictive power of financial variables for measures of output in that we consider whether there are breakpoints and whether the forecasting ability varies across scales. We explore how the variables interact and whether we can observe accurately discontinuities in the variables at different time periods and time scales.
We examine the relationship between future output and a variety of financial indicators on a scale-by-scale basis using the “double residuals” regression analysis, that is “partialling out” the other explanatory variables, as such a procedure allows one to disentangle the individual power of different financial indicators in forecasting output. Relative to the aggregate analysis, scale-by-scale regressions provide evidence for the existence of transmission channels from financial conditions to real activity which are “scale-dependent”. Specifically, the results reveal that the predictive power of standard indicators of the stance of monetary policy, such as the shape of the yield curve, or the real federal funds rate, or credit spread, changes substantially across scales and also displays coefficient sign reversal as in the case of the current and future stances of monetary policy.
Wavelets can provide a deeper understanding of structural breaks with respect to standard classical analysis given their ability to identify the scale as well as the time period at which the inhomogeneity occurs. Following the procedure suggested by Whitcher [
44] we also perform a test for homogeneity of variance using the normalized cumulative sum of squares test statistic calculated from the DWT wavelet coefficients. We estimate the time at which the change occurs on a particular scale by an auxiliary test statistic computed using the MODWT wavelet coefficients. We are able to detect variance changes for all variables, except for the credit spread, and to locate the break dates in 1982:III at scale 1 for the real interest rate and the term spread, and for output in 1984:I at scale 2, in correspondence to two well known events characterizing the US economy in the early 80s: The “so-called” Great Moderation and the change of monetary policy conduct after 1979 under Fed Chairman Volcker. The timing of these variance changes can be helpful in understanding the break-down of the term spread as a leading indicator since the mid-1980s and discriminating amongst the alternative explanations given for the moderation in the US output volatility.
Our results show that we are able to disentangle and isolate the factors that drive output at different horizons. We note different short, medium and long run relations in the forecasting output equation and are able to identify the scale and localize the time at which regime shifts and discontinuities in variance changes in the data. All in all, we can conclude that allowing for different time scales of variation within the data one is able to provide a fruitful understanding of the complex dynamics of economic relationships [
57,
58]. Utilizing economic and financial time series with non-stationary or transient components, we obtain results that are certainly richer than those obtained using standard aggregate regression methods.