Abstract
This paper describes and tests a wavelet-based implicit numerical method for solving partial differential equations. Intended for problems with localized small-scale interactions, the method exploits the form of the wavelet decomposition to divide the implicit system created by the time-discretization into multiple smaller systems that can be solved sequentially. Included is a test on a basic non-linear problem, with both the results of the test, and the time required to calculate them, compared with control results based on a single system with fine resolution. The method is then tested on a non-trivial problem, its computational time and accuracy checked against control results. In both tests, it was found that the method requires less computational expense than the control. Furthermore, the method showed convergence towards the fine resolution control results.
1. Introduction
Wavelets are a versatile tool for representing and analyzing functions. Wavelet transforms can be continuous, though we will focus on the discrete form (for both, see [1,2], or any other textbook on the subject). The discrete transform decomposes a function via families of wavelets and wavelet-related basis functions. Wavelets can be orthogonal [3,4,5], and biorthogonal [6]. The greatest advantage of wavelet decompositions is that they combine multiple scales (much like different Fourier modes, or frequencies) with substantial localization. As a result, wavelets can be used directly to efficiently approximate the solution of partial differential equations, as in [7,8] (where wavelet decompositions are used in every spatial direction, as well as for the time discretization). The decomposition can also be used indirectly, as a tool to analyze a function and determine where greater resolution is necessary, like in [9,10]. Wavelets have been used to efficiently represent operators, as in [11]. Work has also been done adapting wavelets to the challenges inherent in solving partial differential equations, notably the introduction of second generation wavelets in [12]. Unlike first generation wavelets, these are not always equal to translates and scalings of a “mother” function, and so can be (more easily) made compatible with, for instance, the domain of a partial differential equation. Also, since the multi-resolution decomposition is usually the key property, multi-resolution representations have been developed that do not require a wavelet basis, see [13]. We will keep our model simple, and so use biorthogonal wavelets (symmetric, with finite support), with a few small modifications to satisfy any required boundary conditions.
The goal of this paper is to improve the efficiency of implicit methods for time-dependent partial differential equations. The basic premise is that the time step resulting from an implicit discretization can be calculated at multiple resolutions, with each resolution calculated separately (sequentially). If the problem requires fine resolution in small sub-domains, then this approach can significantly speed up implicit calculation of time steps. At its most basic, this method starts by calculating what we call the large-scale system: The time step over the entire domain Ω, at a coarse resolution. Next, some of those calculated wavelet coefficients are used in the small-scale system, a new set of calculations at a fine resolution in the sub-domain . Some of the coefficients from the small-scale system are then added to the large-scale system and the time step is complete.
The advantage to our approach is the ability to compute a time step at different resolutions, in different domains, sequentially. Solving a problem at multiple resolutions is an obvious way to exploit a multi-scale decomposition. As such, there are similar methods to be found throughout the literature. The most similar are those intended to be used to solve elliptic problems at multiple scales. One that is particularly connected to our own method, due to its use of biorthogonal wavelets, can be found in [14]. Others can be found in [15,16,17]. Our method is different from those in that it is intended to be used on time-dependent problems. More importantly, adaptive multi-scale solvers for elliptic problems use repeated iterations at each resolution to maintain consistency and reduce the error. Our method keeps the different levels of resolution, the different scales, consistent with each other. This means that no repeated iteration is needed for each time step, so the problem only needs to be calculated once for each scale. This is not an advantage in an elliptic solver, but when several thousand (if not million) time steps have to be calculated, it is advantageous to avoid having to repeatedly calculate individual time steps.
Another perspective on our method is that it allows, in effect, the problem to be solved in a different manner in the subdomain Λ than over the remainder of the full domain Ω. This difference is, at the moment, restricted to the use of a finer resolution, but it could well be that using a different time-discretization altogether could be an option (note that this is not yet tested). This means that our method has a property similar to that of domain decomposition methods. As with adaptive multi-scale solvers, domain decomposition methods typically require multiple iterations between the different domains. Furthermore, they typically require limited interaction across the interfaces between domains. Our method is not restricted by the extent of interaction across the interfaces, only by whether those interactions are adequately modeled by the large-scale (coarse) resolution.
2. Wavelet Decomposition
Our notation is largely based on [2], a good introductory source for wavelets, which bases its approach on [1]. Further discussion on the many applications of wavelets can be found in [18]. We use the terminology, and some formatting, based on the theory of first generation wavelets, but the key steps for our method require only a multi-resolution decomposition. The concept could be extended to second generation wavelets, or to alternative decompositions. For instance, the discrete data based multi-resolution decomposition introduced by Harten in [13] would be ideal, in many ways.
Our numerical examples each use a biorthogonal spline wavelet/scaling function pair (biorthogonal wavelets were introduced in [6]). The first example uses a scaling function φ equivalent to the fourth order spline function, which is shown in Figure 1, along with its second derivative and its dual . The figure also shows the corresponding wavelet ψ, along with its second derivative and its dual .
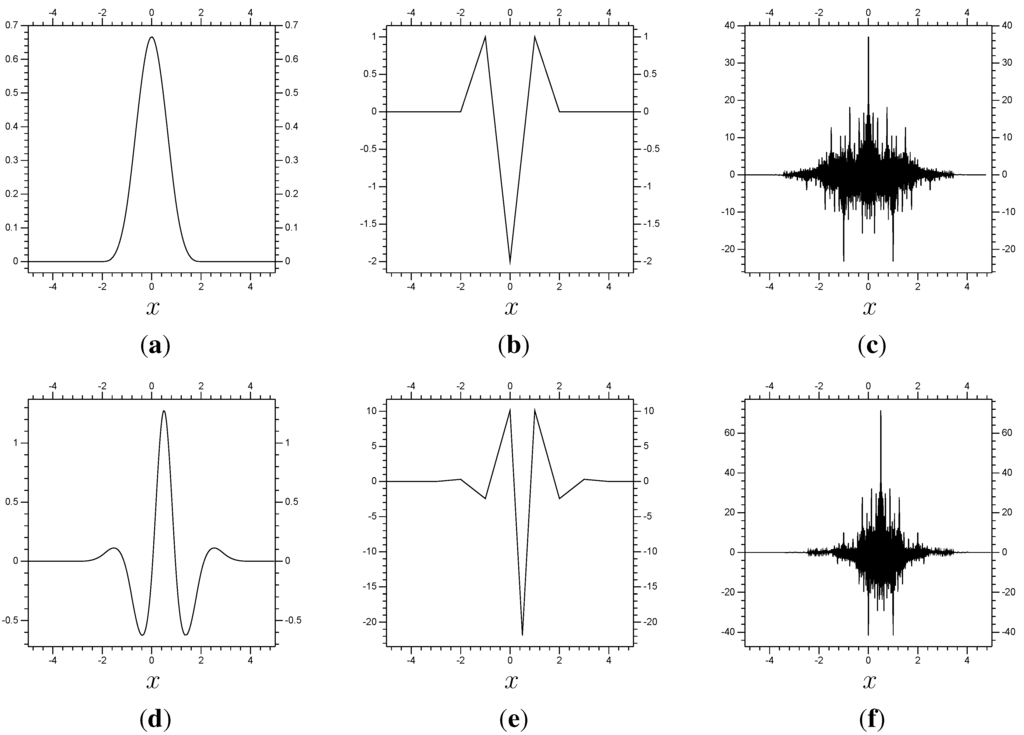
Figure 1.
Top: The wavelet pair corresponding to the spline function , its second derivative and dual re-centered at . Bottom: The same for the corresponding wavelet. (a) ; (b) ; (c) ; (d) ; (e) ; (f) .
A wavelet decomposition uses variants of the form
Notice that and for all (using the norm). Also, notice that the functions become more localized (i.e., have their support reduced) as j becomes more negative, while k determines the location of or . Notice also that and are equal except for a translation of one, and that and are equal except for a translation of . As a result, more negative values of j do not just make the functions and more localized, but also reduce the space between them. One key property of the scaling function, φ, and wavelet, ψ, is that they can be written in terms of the finer scaling functions , so
for constants and .
These functions create subspaces of of the form
This definition and (2.2) mean that and, more generally, for all . We also get , which in turn makes
As a result, any function () can be expressed using different, but equivalent, sets of basis functions from the spaces and . First, by the definition of ,
However, assuming that , we can write it in terms of , so
Continuing this pattern, we can get
which can be expanded to
and further. Basically, there is a starting function of the form
which is simply an approximation of f in the coarse resolution space . Then functions
are added to correct that approximation. So, any function has a unique component in (equal to the projection of f onto when orthogonal wavelets are used), an approximation containing only the coarser, large-scale, features of f. The finer, smaller scale, features of f are found in the spaces to .
3. Multi-Scale Method
We propose a new wavelet method for solving time-dependent partial differential equations, specifically multi-scale problems that require implicit time-discretization. The method exploits the form of the wavelet decomposition to divide the implicit system created by the time-discretization into multiple, smaller, systems that can be solved sequentially. One can, if certain requirements are taken into account, compute implicit time steps at multiple spatial resolutions. Most importantly, these resolutions are solved sequentially, and kept consistent so they need only be solved once per time step. For non-linear problems, where even a linearized scheme (such as that in Equation (7.2)) requires solving a new system every time step, this can greatly reduce computational expense. The key idea is to divide the system to be solved into two, smaller, systems that can be solved separately. First, we have a coarse resolution
over the whole domain Ω, called the large-scale system. The next system has the finer resolution
only covering the subset , called the small-scale system (with ). This arrangement allows the two systems to be solved sequentially. First, the large-scale system is solved, in over Ω, and the resulting coefficients that are within (or near) Λ are converted so that they can be expressed in terms of the small-scale. Those coefficients are included in the calculations for the new small-scale system. Next, the large-scale () components of the newly calculated small-scale system are converted to the form used in the large-scale, and added to the earlier large-scale values. This finishes the time step. Note that the two systems, large and small-scale, are solved separately.
Depending on how the discretization is implemented, the two systems can be the same size (that is, have the same number of coefficients). In fact, this arrangement can be done with any number of systems, possibly nested, as shown in Figure 2. As long as their domains are either nested or disjoint, any number of systems can be used. That the different systems can be solved separately is the advantage here. A pair of systems sized will be quicker to solve than a single system sized .
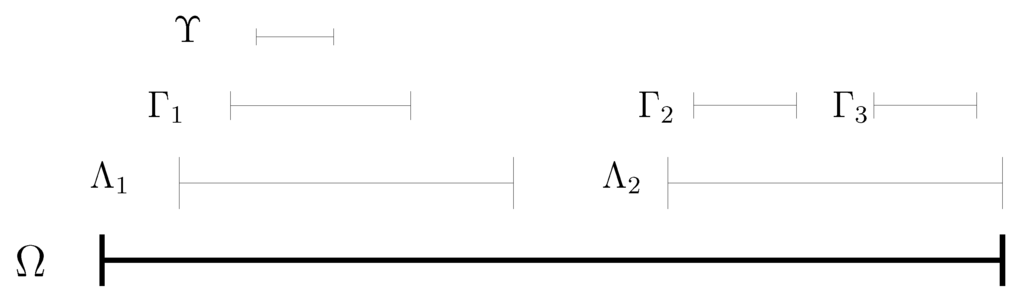
Figure 2.
A diagram of several nested small-scale systems of a domain Ω.
4. Implementation
In this section we describe the basic implementation of the method: The dividing of an implicit time step into two, separately calculated, systems. This concept should be compatible with many features of multi-scale methods, (i.e., making the large- and small-scale systems use adaptive decompositions). However, we will not include any, to avoid additional complications. The numerical experiments will be kept as simple as possible, as well.
To explain our method in detail requires a certain level of notation. We shall look at a one-dimensional example, though the general concept behind the method can be expanded to any number of dimensions. For instance, our second numerical example uses a decomposition of a two-dimensional domain Ω via tensor product between a Fourier decomposition in the x direction and a wavelet decomposition in the y direction. This allows the small-scale domain Λ to be of the form , i.e., to cover the entire x domain and a subset of the y domain. If the decomposition was via a tensor product with wavelet decompositions in both directions, then we could use a subdomain Λ that is smaller, with finer resolution, in either direction, or both.
The actual functions we shall be dealing with are those of the form
Recall that wavelet decompositions are in the spaces and , , as defined in (2.3) and (2.4). In Section 2 we discussed how there are multiple ways of expressing a function via wavelet decomposition. Since the specific form of the decomposition is relevant to any wavelet-related method, a means of expressing these differences becomes helpful.
All functions in the space and can be characterized in terms of the coefficients of their wavelets and scaling functions. The wavelet (ψ) coefficients are written , the scaling function (φ) coefficients are written , with j relating to resolution and k relating to location. The coefficients are best organized into vectors of the form
The same can be done with the sets of coefficients , creating vectors of the form
Any decomposition of the form in (4.1) has an equivalent vector
Any function can also be decomposed directly into via
with a vector , which has the same number of components as the vector in (4.4). The setup discussed in Section 3 focused on two different levels of resolution, and , with . One helpful way of writing this is to define a vector , containing all the necessary coefficients for , and a vector containing all the necessary coefficients for the spaces to . This setup, using and , would result in vectors of the form
The result of this setup is that any function in can be expressed in terms of a vector of the form , and any function in can be expressed in terms of a vector .
Next, we have two different domains to use: Ω and . The vector has all the coefficients from the space over the entire domain Ω. Now we must consider vectors relating only to . Whether a coefficient can be considered relating to Λ depends on its scaling function . We use biorthogonal scaling functions and wavelets that are symmetric, with finite support. As a result, we designate or to be within Λ if the center of the function’s support is strictly within Λ. Other options would probably work, such as defining or to be in Λ if their supports intersect Λ. A subscript Λ, for , restricts the coefficients in to those relating to the smaller domain Λ. This will be standard practice throughout this paper. If a subscript Λ is added to a vector or matrix, that means that the vector or matrix is restricted to the smaller domain Λ, with coefficients relating only to Λ.
Now we take a linear partial differential equation of the form
where L is a linear differential operator
As L is linear, we discretize it using a matrix M. The idea is for M to calculate the effect of L restricted to . So, if the function is expressed in terms of , then
This matrix M can be calculated via a Galerkin or collocation method, so long as it is accurate in approximating L. Our earliest tests of this method used a Galerkin method. In this paper, the examples will be calculated via a collocation method, discussed later in Subsection 7.2. Boundary conditions are a potential issue. To keep the equations in this section clean, we will be ignoring the boundary conditions, or assuming that they are satisfied via the wavelet decomposition and M. Our later examples use the method effectively on a problem with zero boundary conditions and on a problem with constant, non-zero, boundary conditions. Our approach for satisfying zero boundary conditions is discussed in Subsection 7.2.
The method is meant for use with an implicit time-discretization. Here, and in the rest of the paper, we shall illustrate the implementation of the method using the second order Adams-Moulton scheme for the time-discretization. This particular scheme is ideal since it is simple and, most importantly, implicit. Combining that time-discretization with the matrix M gives us the time step
We also use the block decomposition
Assume that the vectors and have and components, respectively. The matrix A will have rows and columns and D will have rows and columns. The matrix B will have rows and columns, and C will have rows and columns. Note that while A and D are square, they do not have to be equal in size. In fact, our main example will usually give A four times as many rows and columns as D.
Now we separate the time step in Equation (4.9) into two systems. First, we have the large-scale system, with functions in the space over Ω, characterized by vectors of the form . We also have the small-scale system with functions in over Λ, characterized by vectors of the form . Recall that has only the components of corresponding to the functions in Λ. The large-scale system is at the limited resolution , and so uses the matrix D to model the operator L from (4.7). The small-scale system is expressed in terms of a matrix of the form
where , , and are composed of the elements from A, B, C and D that are related to Λ.
Example 4.1
Using the domains and and the space , we shall take a look at getting from D.
In this example, the vector has 79 components: The functions are at points separated by a distance of , and so are at points , , … , . The matrix D, which is a discretization for the differential operator L restricted to , is a square matrix. Multiplication (on the left) by this matrix takes the coefficients from a function in the vector , creating the vector , the approximation of . We can write it as
The matrix only operates on the coefficients of functions restricted to Λ. As a result, the number of rows and columns of have to be equal to the number of coefficients in Λ. As a result, it is smaller:
The first step is to use a time-discretization to find a temporary approximation of , which we shall call . Using the second-order Adams-Moulton method yields the large-scale system
This calculates the time step on Ω at the large-scale resolution . What we want next is to calculate the time step on Λ at the small-scale resolution . However, and the newly calculated have to be included. So, we use the components of and that are in Λ, which we call and , respectively. These are used in the system
Note the presence of , a corrector term for the temporary approximation . The final step is to take , rewrite it in Ω as , and add it to for
This setup is consistent with the time-discretization. Since , the restriction of to Λ will be
Next, we will rewrite that expression using
The last term in (4.16) is going to be smaller than the others, considering the restriction to followed by a restriction to Λ. In the context of the small-scale system, the last term in (4.16) can be viewed as representing influences that are similar to boundary conditions: Influences consistent with the problem that come from outside the region being calculated (Λ, in this case). This term, being somewhat cumbersome to write and read, will not be written in the next expressions. We will simply replace the first term in (4.16) with the second (they are, at least, approximately equal). This substitution yields
which matches the second order Adams-Moulton discretization.
5. Error Sources
Now we take a closer look at the main sources of error. Recall, from (4.9), that the full resolution, full domain, time-discretization for a linear problem is
The multi-scale method makes use of the components of the vectors and , as well as the elements of the matrices A to D, that relate to the sub-domain Λ. Now we will have to discuss the sub-domain , and related vectors/matrices. We will now subdivide the vectors as follows:
with and the components from . The related matrix block decomposition is
and the same for C and D. The idea is to have
and so on. Written this way, the time-discretization becomes
Now compare that with the multi-scale method. The large-scale step is
Next we look at the small-scale system,
Combining those two steps results in the full time stepping scheme
So, the error inherent in the multi-scale system comes from three distinct sources:
- The vectors not being included at all. In order to keep the error below a specified tolerance, we would need to implement an adaptive procedure. This would involve calculating the values of the coefficients in that are adjacent to the domain Λ. The domain Λ would be expanded if these values were found to have exceeded the specified threshold. Other coefficients in , further from Λ, would also be calculated. If these were found to be above the specified threshold, then the large-scale system would be given a finer resolution.
- The matrices and from (5.6) being omitted from (5.9). This source of error is reduced by widening the vectors at the expense of (i.e., including extra large-scale coefficients in the calculation of the small-scale system). We call these “extra” terms, and they are explained in detail in Section 8. These terms reduce the error because the matrices A to D will be diagonally dominant (due to the fact that φ and ψ are well centered). Consider the block decomposition ofIncreasing the number of components in increases the number of elements in . It also reduces the number of elements in , , and . The matrix will have rows of elements removed, effectively restricting to the top right corner of C. Since the elements in C are smaller further from the diagonal, the result is a matrix that has both fewer elements and smaller valued elements. As a result, becomes smaller as is expanded.The best way to control this source of error is an adaptive scheme that checks the largest values of and . The number of “extra” terms would be increased if either calculation was above a given tolerance.
- The last type of error is from the last vector term in (5.9). This source of error is best managed via the “extra” terms, as well (i.e., by increasing the number of components in ). Including more “extra” terms will result in having fewer elements, as well as smaller elements (as with and above). One other thing to notice is that is a corrector term, and so, in general, is of smaller magnitude than . We haveso it is order , and a reasonable time step will keep its magnitude low.
Managing these sources of error should be sufficient to control the error stemming from the method itself, (i.e., control the error stemming from limiting the small-scale resolution to Λ and from dividing the time step into two different systems). Other sources of error, those that are not a direct result of the multi-scale method itself, would be addressed separately. If a particular approach for keeping the time step small enough (or the resolution fine enough) is compatible with a wavelet decomposition and an implicit time-discretization, it should prove compatible with our multi-scale method.
6. A Test Problem
To illustrate the application of the method, and confirm that it can work, we test it on a one dimensional problem involving Burgers’ equation. Burgers’ equation is appropriate because it is not linear, its expression is fairly simple, and because it can be easily set up to require fine resolution in a small region and so benefit from the method we are testing. Note that we are deliberately keeping things very simple. We will use fixed Λ subdomains, and fixed resolutions. The method looks to be compatible with many types of adaptive schemes, and other expansions. However, in this paper, we want to ensure that the method can deliver consistent results, with no additional complications. We therefore use the simplest version of the method, without these additional features.
We solve for the function , , , satisfying
with boundary and initial conditions
The function is plotted in Figure 3 (a). The exact value of is
using φ from Figure 1. This choice of initial condition will require some explanation. First, we use an initial condition in to simplify the required programs and to avoid any error at . This means that all different models/resolutions start at zero error. The general shape chosen relates to the behavior of Burgers’ equation, mainly the effect of the term. If we set the viscous parameter, ν, to zero then the solution becomes
meaning that the characteristics will start at points and have slopes equal to . Of course, if then this effect will be changed, but the basic nature, and directions, will be much the same. Now consider what this means for in Figure 3. As shown in this figure, the two peaks will approach each other as the time increases, colliding at . What happens when they meet depends on the magnitude of ν. If , then the characteristics will intersect, resulting in a singular solution. If then the peaks will collide, but not cause an infinite slope. Instead, the translation will cease, and the solution will converge to zero under the influence of the viscosity (see Figure 3). So, instead of an infinite slope at , the solution will have a finite slope dependent on the magnitude of ν. Increase ν and the resulting slope at will get smaller. Decrease ν and the slope at will be greater. A very steep slope at will make proper expression of the solution very difficult for a coarse resolution space. The results shown here, with , require at least for reasonable results (using our wavelet/scaling function pair).
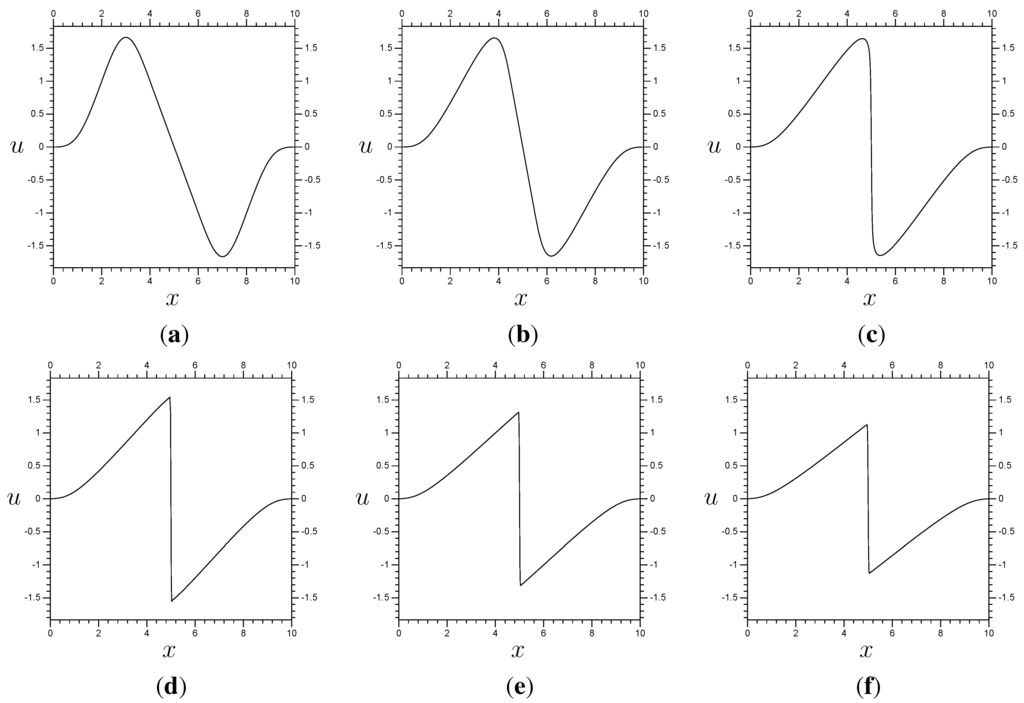
Figure 3.
Results for Burgers’ equation with resolution and time step . (a) ; (b) ; (c) ; (d) ; (e) ; (f) .
7. Calculation
7.1. Time-Discretization
As before, we shall use the second order Adams-Moulton method for our time-discretization:
meaning we consider the functions using the time step h. The main problem with this time-discretization is dealing with the non-linear term . To avoid additional complications arising from solving this non-linear system, we shall use the linearization
Using this, we have the time-discretization
with the non-linear term replaced by the linear operator applied to . Furthermore, since the approximation (7.2) has the same order as the time-discretization, the loss of accuracy should be negligible, especially for a small time step h.
7.2. Physical Decomposition
The physical decomposition is in a space , for , , using the functions φ and ψ in Figure 1. We use a collocation method, though the earliest experiments were done via a Galerkin method, and so both are compatible. Our collocation method involves matching the exact values of and from (7.3) at the points , . Since we are using the domain , with , that means points to calculate at every time step. The number of coefficients and used will be the same as the number of collocation points, that is for . Our standard model will use , so that is 639 coefficients.
The boundary conditions are zero, with as and , to maintain consistency with (6.1). We keep the decomposition consistent with these boundary conditions in the simplest way possible. To demonstrate, we will look to the boundary. What we do is reshape every supported at as follows:
rather than the usual . Note that all that is being changed is that is, effectively, being subtracted by , the function with the same shape but from exactly the other side of . Our scaling function, φ, is that from Figure 1. It is symmetric around zero, so this makes anti-symmetric around , so
The same change is made to the that are supported at . They have their counterpart from exactly the other side of subtracted from them, resulting in
The process for is much the same, with a small change because ψ is symmetric around , meaning will have to be modified by to keep .
The derivatives will be approximated using matrices, of course, created out of some common components. First, the Fast Wavelet Transform and Inverse Fast Wavelet Transform are calculated via
where is the resolution of the scaling functions used in the wavelet decomposition.
Next, we have , a matrix that when multiplied by will output a vector of values of (where contains the coefficients of u) at the collocation points. So, if
with the in , then will be a vector composed of values , .
Putting these together, we get
matrices that approximate the first and second x derivatives.
The collocation arrangement for the linearized term is based on the same matrices, and one more component:
We approximate the nonlinear terms via the operator
7.3. Results
The results obtained using are in Figure 3. These are what we will usually call our “control results”, which we will use for comparison with those using our multi-scale method (Section 4), which will use as their finest resolution. The multi-scale results will attempt to duplicate the control results while taking less computational time (the control results required approximately one second per time step). The error resulting only from the multi-scale method will be the difference between the multi-scale results and the control results, since that will be the effect of ignoring the fine resolution coefficients outside of Λ, and the effect of dividing the time step calculations into two systems. So, this “error” term, the difference between the control results and the multi-scale results, will be our main focus in calculations. However, the accuracy of these control results may provide some useful perspective. For comparison, we solved the problem numerically using a physical decomposition in (so four times as many coefficients), and with a time step size of (so five times as many time steps). The calculation of a single time step with this model was in excess of seventy seconds. At , the difference between the results and the control results was, in the indicated norms,
At it was
Plots of the results, and their differences with the control results, can be found in Figure 4.
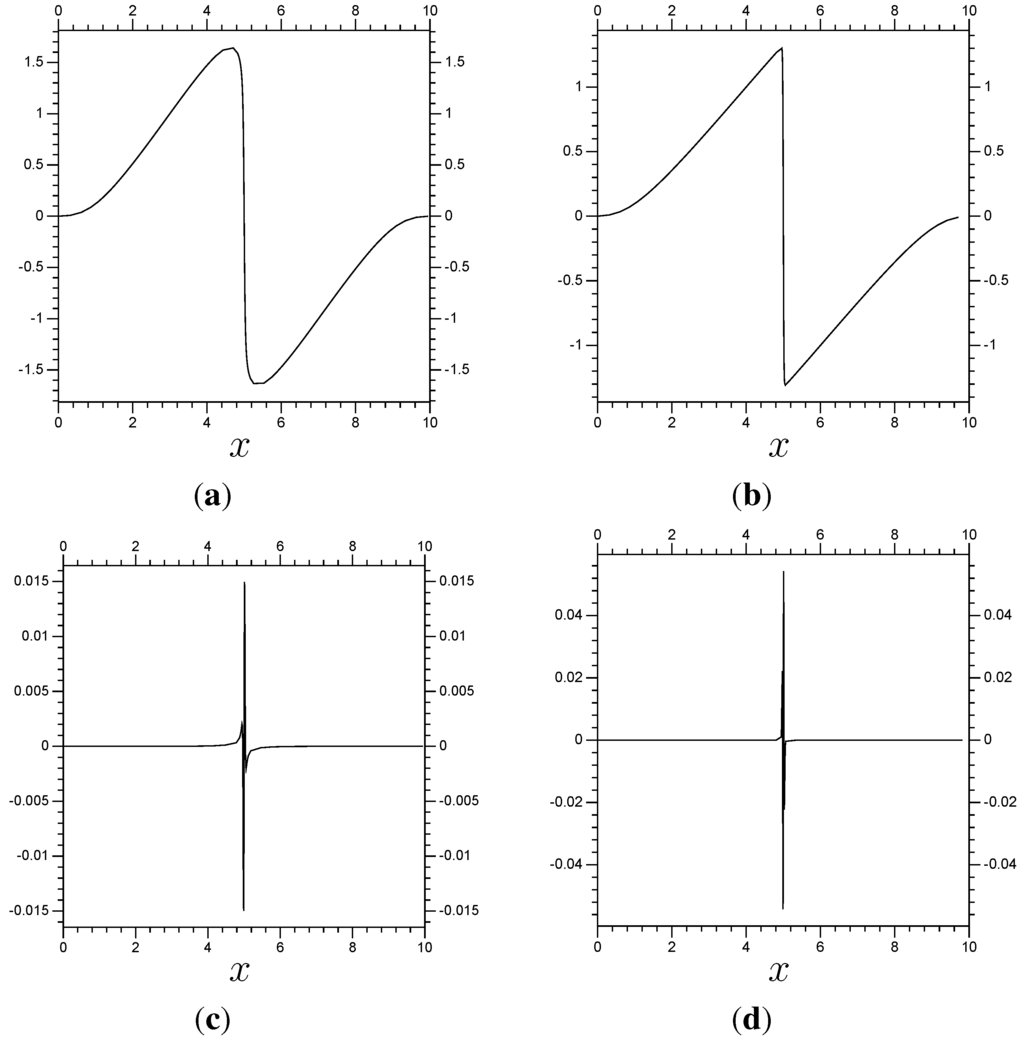
Figure 4.
Results for Burgers’ equation using , and time step size , (a) at and (b) at . Next, the difference between the results and the results, (c) at and (d) at .
Now we try to reduce the expense of calculating the results. The solution does not require fine resolution outside of the center. As a result, for smaller (more negative) values j, the coefficients away from will be very small. So, one could use the method from Section 4, with a resolution of over all and have and only on . This arrangement would have 159 elements for the large-scale system, as well as , and terms for the small-scale system on . This makes for a total of 287 elements, solved in two, similarly sized, systems. The control results have a full resolution on , so 639 coefficients, with many contributing very little to the accuracy.
8. Further Improvements
The basic outline of the method is only the beginning, and it will need to be improved for the actual implementation. First, the basic method is for a linear problem, but the test problem is non-linear. Although we linearized it using (7.2), there are still some non-trivial difficulties arising from the linearized terms. Properly calculating the linearized terms in the two systems, and keeping those calculations consistent with each other, will be the first improvement. The second improvement is more general, suitable for any problem, and relates to the coefficients in , those that are common to both the large and small-scale systems.
8.1. Non-Linear Terms
The method described in Section 4 was, from the beginning, set up using a single matrix discretization of the operator L: The matrix M is created at resolution and over all Ω. This is the best way to deal with linear operators. However, it is not a good option for dealing with any non-linear terms.
Recall that we use the linearization from (7.2),
to avoid having to solve a system involving the non-linear term . Using this approximation involves creating a linear operator that calculates the multiplication by , then applying that operator to the value in the time step. The linearization requires creating a new linear operator at every time step, of the form from (7.9). To do so at resolution over all Ω at every single time step would be time consuming. Instead, we create an operator at resolution on Ω, call it , and an operator at resolution on Λ, . These operators are created separately. The first one, , is used in the large-scale system
with positive rather than negative due to the form used in (7.9). Note that we are keeping the linear terms, discretized as in (4.8) and block decomposed as in (4.10), hence the inclusion of D.
The second operator, , created at the small-scale resolution over Λ, and so created independently of , is used in the small-scale system
Note that O here represents a zero matrix and is a zero vector. As usual, the last step is to compute .
One set of terms from (8.3),
needs to be discussed in more detail. Notice that is a matrix the same size as (see (4.11)), so the vector on the left of (8.4) has components in the spaces to so it is not of the form . These components are not included in Equation (8.2), since that calculation is restricted to the large-scale resolution , but these terms have to be included in the small-scale system. In this way, (8.4) is analogous to the term
found in Equation (4.13), applied to the linearized components of the problem. Both involve vectors used, and calculated, in the large-scale system, and their influence on the small-scale system. The linear version, (8.5), can be written as
which is of the same form as (8.4), with in place of and D in place of . The first term on the left in (8.6) is equal to , a term in the small-scale system. The second term in (8.6) is the vector restricted to the sub-domain Λ. Since this has already been included in the calculations (in the large-scale system), it needs to be subtracted here in order to avoid being included twice. Equation (4.13) uses a simplified form of (8.6). If is composed of elements of D, then (8.6) is equal to
the same as the last term in (4.13). This process is accurate in the linear case when the matrices are created together (i.e., since D and are both from M). This process does not work for the non-linear case since the operators and are created separately, so the restriction of to Λ is not equal to the large-scale related elements of (i.e., restricted to ). As a result, (8.4) is necessary for non-linear problems.
Note that taking the matrix M from (4.8) and block decomposing it as per (4.10) is not the only way to calculating the matrix D and the matrices to . It is just the most accurate option. One could, for instance, calculate the matrix E to approximate the operator L at the large-scale resolution over Ω and, separately, calculate the matrices to to approximate L on Λ. This actually saves time, as smaller domains and coarser resolution reduce the size of the resulting systems substantially. This setup yields the large-scale system
Next, we get the small-scale system
following the pattern from (8.6). If we, instead, assume that , then the small-scale system becomes
However, using (8.9) results in errors around the boundaries of Λ, and when it is applied to linear problems (or components of problems) the errors can manifest as instability. This is particularly common with even derivatives (for example, viscosity terms). Using (8.10) reduces the error (and instability) at the boundary of Λ. The downside to (8.10) is persistent error in the center of Λ. The solution is to use both approaches simultaneously. We need (8.9) at the boundary and (8.10) in the center, and it is easy to do just that. We use a diagonal matrix, J, to convert smoothly between the two vectors
What is needed is for J to be a diagonal matrix, with diagonal elements equal to one near the center, and zero at both ends, i.e., a diagonal matrix J with diagonal elements
In place of either terms in (8.11), we use
Consider the components from (8.13) (as those that could be written in the form of a vector ). The components nearest to the interface of Λ (in the current setup, those nearest to the top and bottom of the vector) will be equal to zero. Those in the center will be equal to . There is also a gradual transition between the central and outer components. So, we get the small-scale system
which uses (8.9) in the center of Λ, for accuracy, and (8.10) near the interface of Λ, for stability.
This will be applied to nonlinear terms, using a diagonal matrix , of similar form to the matrix J in (8.12). The related term becomes
(recall that the matrix is the same size as ). The full small-scale system is
As long as the matrices A, B, C and D are created from a single matrix M, there is no reason to use J on the linear terms from the problem.
8.2. “Extra” Terms
Our next modification to the systems is more complicated to implement than a matrix multiplication. Recall that our large-scale system is in the space over all Ω, and the small-scale system is in the finer space on the smaller domain Λ. By necessity, a lot of our focus is on the set of coefficients that they have in common, the set of coefficients of functions that are within both the large-scale system’s limited resolution and the small-scale system’s limited domain (so functions within Λ). These coefficients are where most of the interactions between the two systems occur, where the coefficients/components in one system have an effect on those in the other system. Getting accurate interactions between the large and small-scale systems is key to getting accurate results with the method. This particular modification is about expanding that region of interaction, increasing the number of coefficients included in the small-scale system. These extra coefficients (and their associated functions ) are treated exactly the same as those in Λ. However, these extra terms (we shall frequently refer to them as simply “extra” coefficients or “extra” functions ) are not actually in Λ itself. We do not include any additional coefficients to , and so we keep the small-scale resolution restricted to the domain Λ. As a result, the increase in the size of the small-scale system (in terms of number of coefficients) is small, at least in terms of the original size of the system. This new feature creates a new domain , with . The small-scale system calculates resolution coefficients within , but keeps the resolution within Λ itself. This is illustrated in Figure 5.
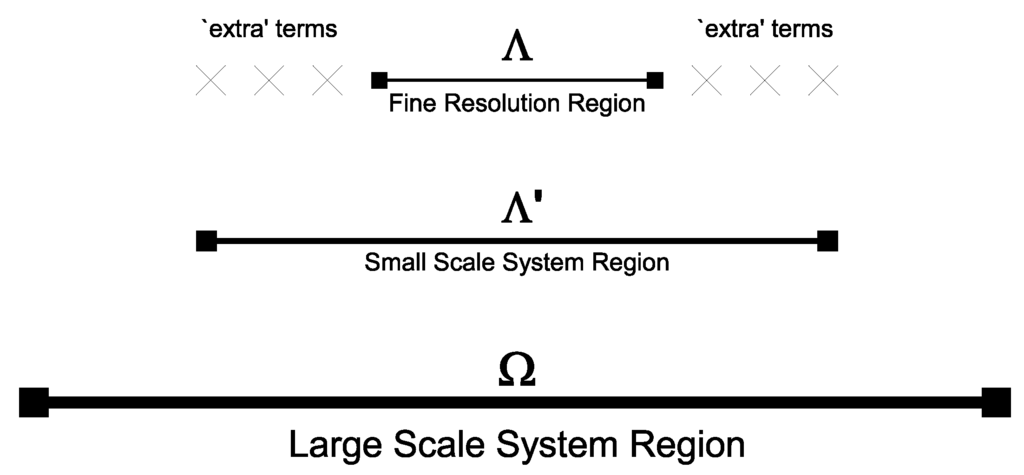
Figure 5.
A simple diagram showing Ω, Λ, and the location of the “extra” terms.
Including the “extra” terms in the time step calculation of the small-scale system, (4.13), results in some changes to the vectors and matrices in the equation, but no changes to how the equation itself is written. The inclusion of more coefficients in the small-scale system results in larger vectors , and a larger matrix . The matrix is larger as well, due to additional rows on top and bottom. The matrix has extra columns on the left and right. The matrix is unchanged.
Expanding the number of coefficients has a cost. First, there are those extra terms to solve in the time step calculation. Also, the matrix will have to be calculated over the expanded domain, . This would require including all the coefficients within . Thankfully, in our current, linearized, scheme, those terms are not included in the actual computation of the values for the time step, which is the most time consuming phase. They only come into play when setting up the operators themselves.
9. Results
The most accurate (and stable) results use linear components derived from a full operator decomposition matrix M (see Section 4). Doing so results in the term from (8.9) being equal to a zero matrix, so there is no need for a matrix J (see Subsection 8.1) for the linear components of L. A matrix (again, see Subsection 8.1), is required for the non-linear derivative terms. Our first set of multi-scale results use on and on . They also use three “extra” terms and
meaning that the non-linear effect on the “extra” terms in is removed entirely. The results are in Figure 6, and the error (difference between the multi-scale, from Figure 6, and control results, from Figure 3) is in Figure 7. They show little difference from the full resolution results. Remember that these results use half as many terms, in total, and the method solves them in approximately half sized sections. As a result, the average time step for the system takes about 0.988 seconds (on a 2.5 GHz processor, standard for the remainder of the paper), while the average time step for the / multi-scale system takes about 0.0337 s. So, the multi-scale system gives results differing by 0.001, and takes about 3.4% as much time to compute.
Next, we need to confirm that the method can converge towards the results of the fine resolution system. To do so, we use a full domain and compare it to a scheme using with localized . An increase in the size of Λ and the number of “extra” terms should cause the resulting error to decrease. The multiplier is set to have a zero for each “extra” term, then one more zero followed by , 1, and so on. The problem is the same, with , as is the size of the time step, . One interesting result is that the error in the interior of Λ becomes so small that it becomes insignificant next to the errors near and . See Figure 8, and notice that the error on the boundary stays constant as Λ increases in size. The error near and is due to lack of resolution around the boundary. No matter how large we make Λ, or how close Λ gets to the boundary of Ω, that error stays constant (to within machine precision). We are mostly interested in the accuracy near the center of the domain, the modeling of the collision between the peaks. Also, the translation from the boundary to the center is trivial, meaning that the accuracy near the boundary has a minimal effect on the interior. So, we shall simply ignore and when calculating the error. In Figure 9 we have a set of plots of the errors (numerically approximated using a resolution of elements per unit) of the different multi-scale systems, compared with the full domain system. These are calculated at , only on . Table 1 summarizes the Figure 9 results (notice that the “Terms” column relates to the horizontal axis for the plots on the left in Figure 9, and the “Time” column relates to those on the right). To put these results in perspective, the difference calculated in Subsection 7.3 between the control results and a much more accurate model has , and differences of , and , respectively, on the subdomain . Basically, we have found solid evidence that the error resulting from our multi-scale method is trivial next to the error stemming from using a limited resolution of .
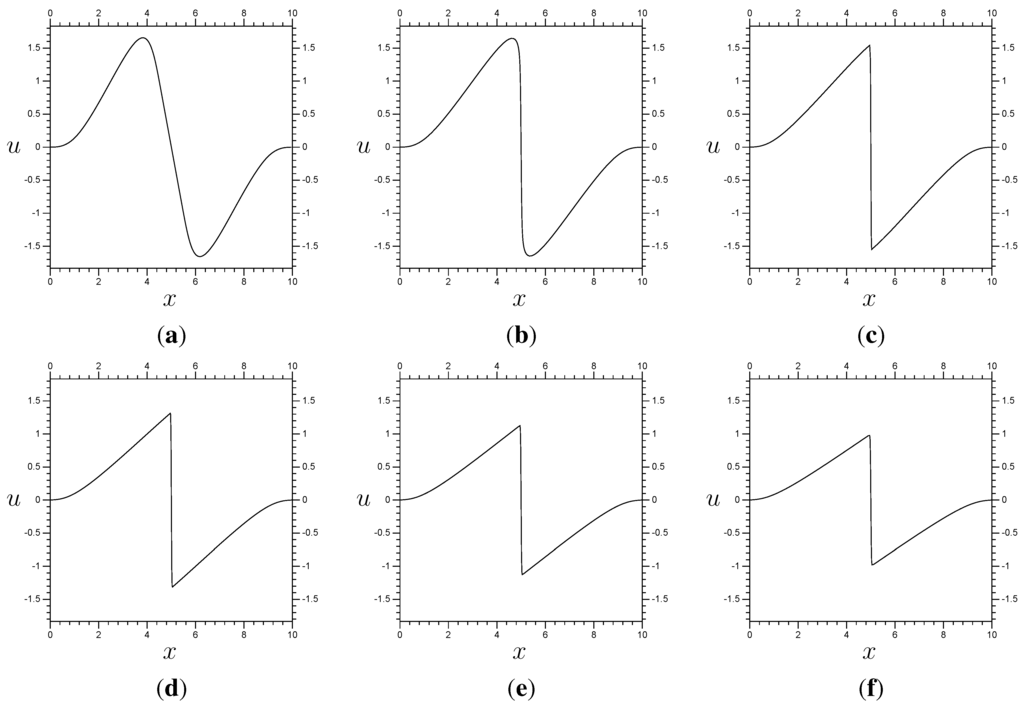
Figure 6.
Results for Burgers’ equation using the components from Section 8. These use with localized and three “extra” coefficients around . It also uses values of 0, 0, 0, 0, , 1, 1, etc. The time step size is . (a) ; (b) ; (c) ; (d) ; (e) ; (f) .
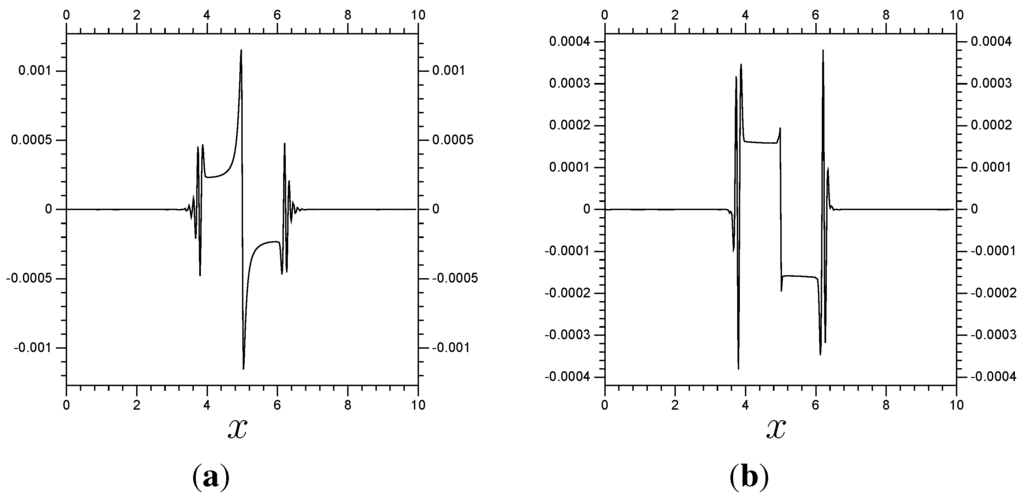
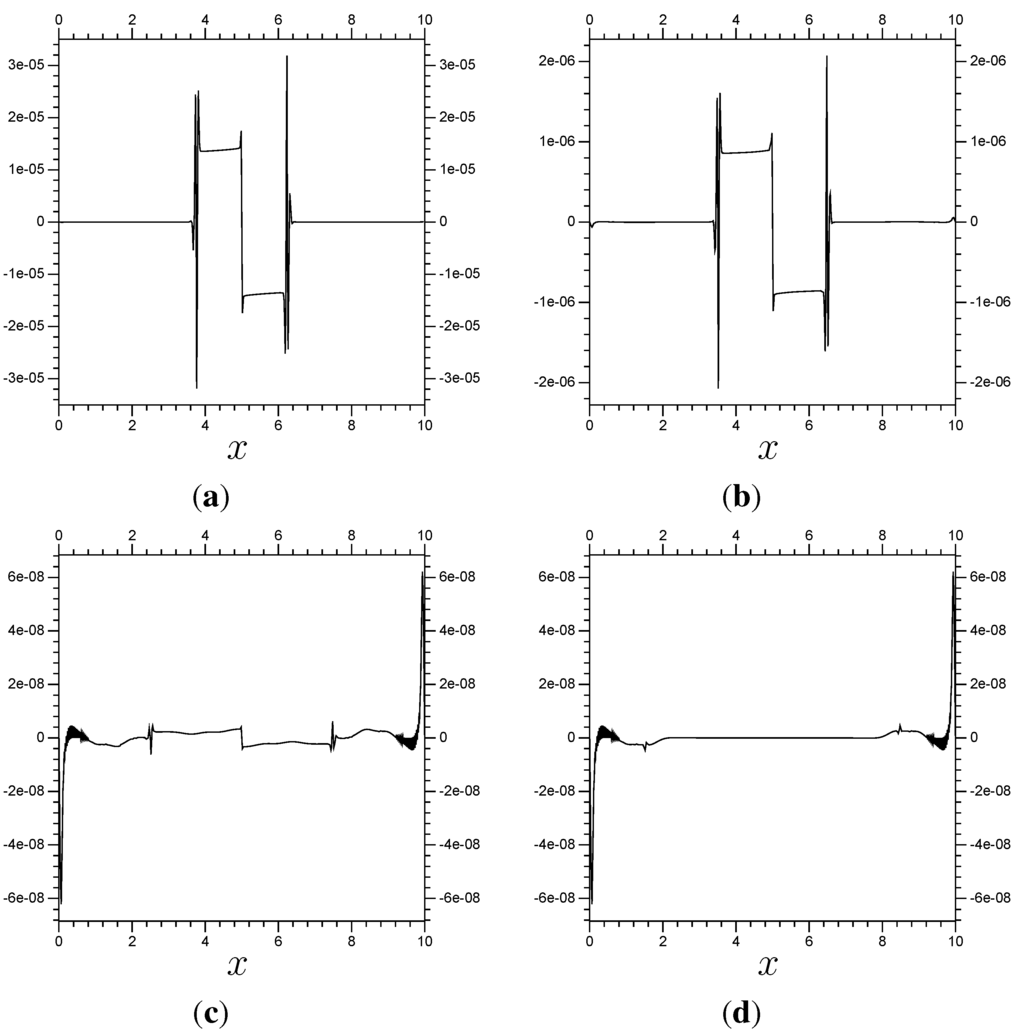
Figure 8.
Error from results using with localized . The error is the difference between the multi-scale results and the control results, all calculated at . The multi-scale results differ in their Λ sub-domains. All use 4 “extra” terms per boundary of Λ. (a) ; (b) ; (c) ; (d) .
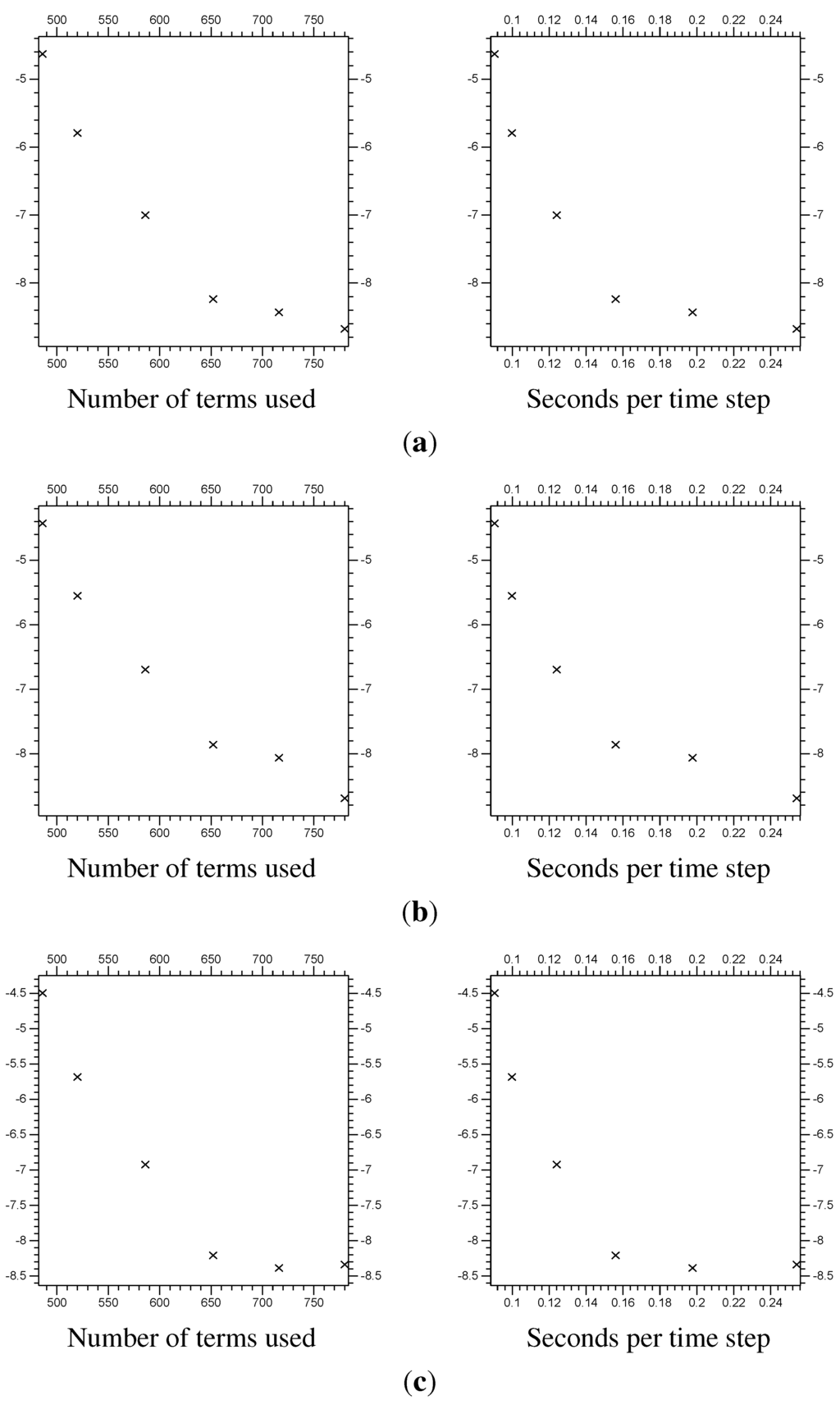
Figure 9.
Error from multi-scale systems, compared with system size and computational time. The system size is the total number of coefficients and used in the systems (also seen in Table 1). The computational time is the average time taken to calculate a single time step, in seconds (all using the same computer). The vertical axis is the of the error, the difference between the multi-scale results and the fine resolution control results on (1.5, 8.5). (a) of the error; (b) of the error; (c) of the error.

Table 1.
Burgers’ equation error for multi-scale systems. By “Time” we mean the average computing time (in seconds) per time step. Note that the errors are only calculated in the region .
| Λ | “extra” | Terms | Time | Error | Error | Error |
|---|---|---|---|---|---|---|
| 4 | 128 | 0.0904 | ||||
| 5 | 138 | 0.0998 | ||||
| 6 | 156 | 0.1241 | ||||
| 7 | 174 | 0.1560 | ||||
| 7 | 190 | 0.1977 | ||||
| 7 | 206 | 0.2541 | ||||
| control results | 0.9888 | |||||
10. A Further Test
Now we extend the method to a non-trivial problem, one that requires fine resolution in one of its two spatial dimensions. We shall use the same time stepping scheme, the same multi-scale method, and the same modifications (the “extra” terms and matrix J). However, the differential equation has a fourth spatial derivative, and so is best approached with a higher order scaling function and wavelet pair, seen in Figure 10.
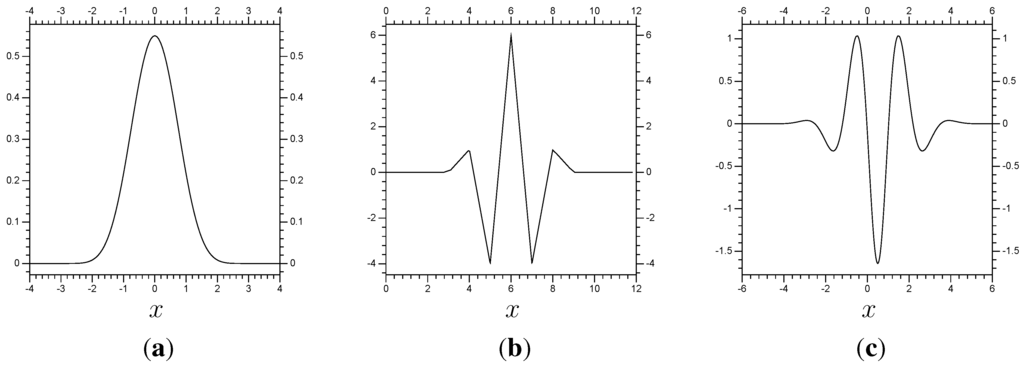
Figure 10.
The spline function , our scaling function. Next, and our wavelet, ψ. (a) ; (b) ; (c) .
10.1. The Rossby Wave Problem
The problem is time-dependent on an x, y, domain, with reference lengths and , respectively. There are periodic boundary conditions in the x-direction, and time-independent Dirichlet boundary conditions in the y-direction. First, we shall nondimensionalize the problem, converting the domain to and . The primary effect of this is that the Laplacian operator will be re-scaled to
For further details on the problem, see [19].
The problem is based on the nondimensionalized barotropic vorticity equation
(see ([20] [p. 637]) for details) with the (real) function the stream function on the domain (not a wavelet). The velocity component in the x-direction is equal to and the y component is equal to . The variable x represents longitude (east-west) and y the latitude (north-south). The coefficient β relates to planetary rotation and ν is the viscosity coefficient.
Next we decompose the stream function Ψ into two components,
with ϵ small relative to Ψ and . The function is the stream function of the basic flow. We are assuming that the basic flow is a shear flow, with velocity only in the x-direction, meaning that is a function of y only. We set , a known function. The Rossby waves are given by , the stream function representing small perturbations of the basic flow, with the matching vorticity perturbation .
Substituting (10.3) into (10.2), we obtain
which becomes
(with being the third derivative of ). We shall ignore the last y dependent term, since is small, and even when we shall keep ν much smaller than ϵ, so (10.5) becomes
Our examples will use , meaning the basic flow will be very nearly constant in the regions near and , (at and , respectively). Second, the basic flow velocity will be zero at . As we shall see, these properties of have interesting implications for P.
The boundary conditions are for and (recall that the boundary conditions are periodic in x). We shall have those boundary conditions phased in gradually (over or so) to smooth out the discontinuity, starting at zero and smoothly increasing to . Notice that the boundary conditions are all composed of , so they can be written in terms of . If we use the linear form of the problem (set ), then P (and Z) can be written using only functions in the x-direction (each multiplied by a function of y and t). The initial condition is simply .
Now we go to the simplest case, set along with ϵ. If we assume that the problem has a steady state, we can find that it will have the form
In the area immediately around , is approximately one and is approximately zero. The problem becomes
with a solution of the form , . As a result, recalling that the boundary condition at is , the steady state is
approximately, near . The more general observation is that the problem in (10.7) has a singularity when , so at . The singularity at means we require fine resolution at that location in order to accurately model the problem. The effect of the critical layer, the region around , on the problem is well known. The function P, which has the form of (10.9) near , will propagate downwards, curve slightly, then stop around (see Figure 11B). This behavior is consistent with that found in the literature: Figure 11B is consistent with all the P (equivalent) plots in [19], and virtually identical to ([19] [Figure 2a]). The behavior of the perturbation velocity is also fairly well known. Figure 11 contains plots of Z at different times. The general Z shape expected for the linear problem is the waves around , seen in Figure 11. Notice that the amplitude of Z near is much higher than that anywhere else, and that the waves in the center get more tightly concentrated as t increases. As we shall see, this results in a greater requirement for fine resolution in the center as t increases, which is what we would expect considering the singularity at . The shape of our Z plots in Figure 11 matches well with ([19] [Figure 18a]) and ([21] [Figure 4]), even though our results use different domains and boundary conditions.
Apart from P and Z, there is one more quantity we shall use to check the accuracy of our results. We shall be interested in the momentum of the system, specifically the averaged x directional momentum flux of the region . Information on momentum as it relates to fluid dynamics can be found in any text on the subject, such as ([20] [p. 88]). For our purposes, it suffices to say we calculate the momentum going in and out of the region via the integral
at and . The change in the x-averaged momentum flux across the region is equal to
although the first integral is approximately zero since for . In this particular system, there are some very clear expectations. First, the linear problem is expected to result in a positive flux at the beginning, so momentum flowing into the critical layer. In ([22] [Figure 5, line 1]) and ([19] [Figure 3]), the flux for the linear problem can be seen reaching its maximum early, then lowering and stabilizing at a positive value. This is the expected behavior of the linear problem, see Figure 11a. When the non-linear interactions are included, the critical layer is expected to reflect some of the momentum. The flux, as seen in ([22] [Figure 5, lines 2,3]) and ([19] [Figure 3b]), is expected to reach its maximum value early, then reduce down to zero and begin oscillating around zero. Later, we shall test our numerically derived results against these expectations.
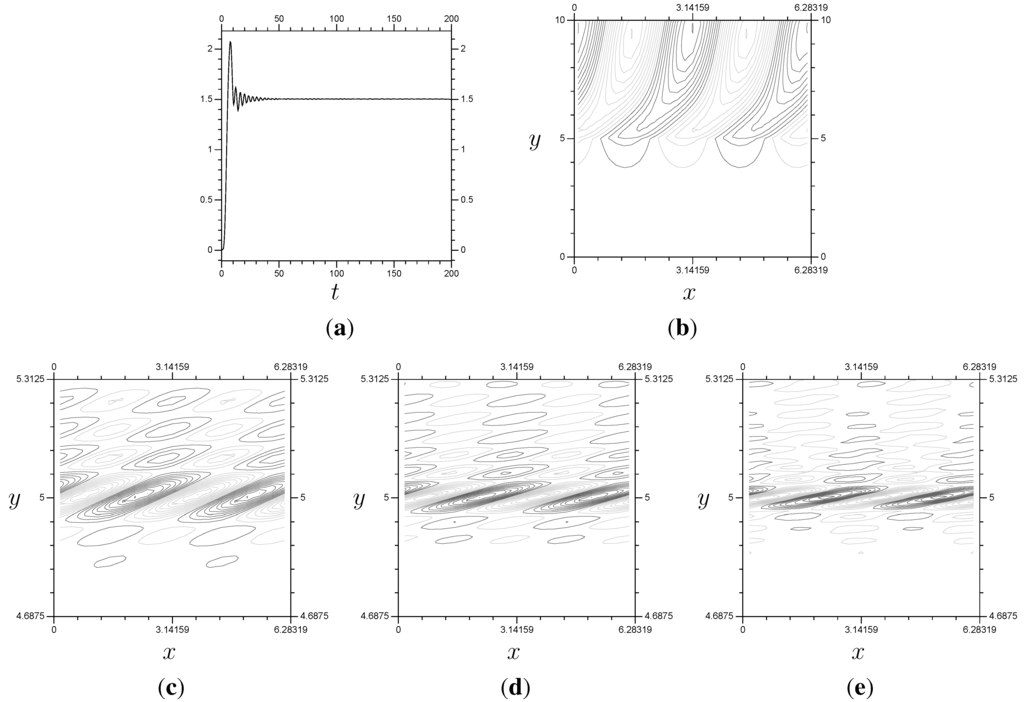
Figure 11.
(Top) The flux (a), steady state for P (b). (Bottom) the progression of Z at in the x-y plane, from left to right. These use , and . Notice that Z increases in amplitude and decreases in wavelength as time increases. (a) The Flux; (b) P; (c) Z, ; (d) Z, ; (e) Z, .
10.2. Linear Results
The key observation for the linear version of the problem (when ) is the steady state expected by the theory, briefly discussed in Subsection 10.1. As t increases, the linear solution eventually converges to the steady state given in Figure 11b (as long as we are using our usual ). However, as shown in Figure 11, this results in Z requiring very fine resolution around . As a result, what we actually see in numerical computation is the perturbation stream function P reaching the steady state (or close to it), holding, then, after some time, becoming completely inaccurate. Generally, without viscosity, our computed values of P are accurate up to approximately using resolution , as shown in Figure 12 and Figure 13.
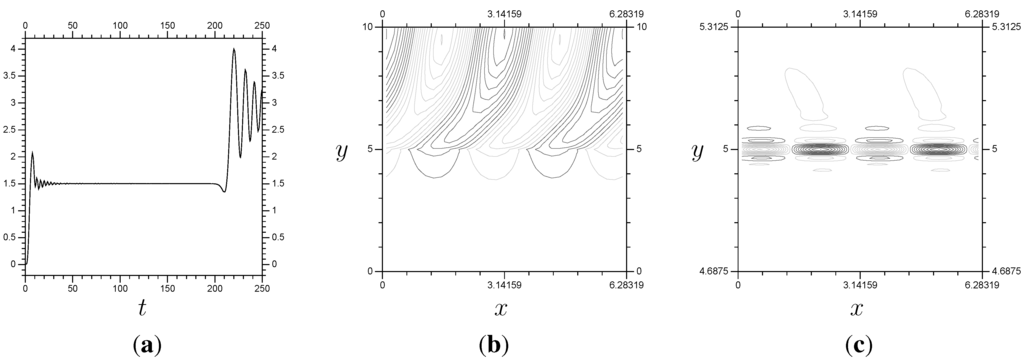
Figure 12.
The results from a linear system. Notice that (the x averaged momentum flux) remains stable until . These results use a “switch-on” function for the boundary condition values equal to , , , and no viscosity. (a) ; (b) P, ; (c) Z, .
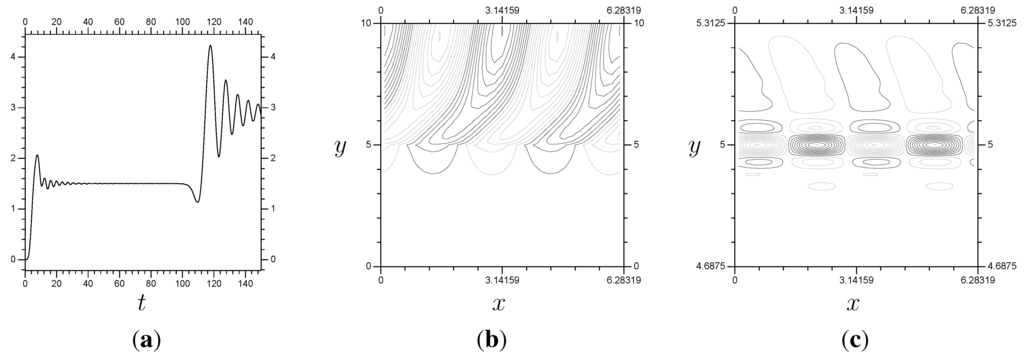
As seen in the Z plots, the key information is around , so that is the location for the small-scale system. The real test is whether the multi-scale results will be accurate (stable, etc.) over the same time frame. The single system results are accurate to approximately (Figure 12). In Figure 14, we have results using everywhere and on , showing an accurate solution of the problem up to , so the multi-scale method works for the linear problem. Note that the multi-scale arrangement has terms per Fourier mode, and the two systems are solved separately. The full system has 639 elements per Fourier mode, and the system has to be solved all at once.
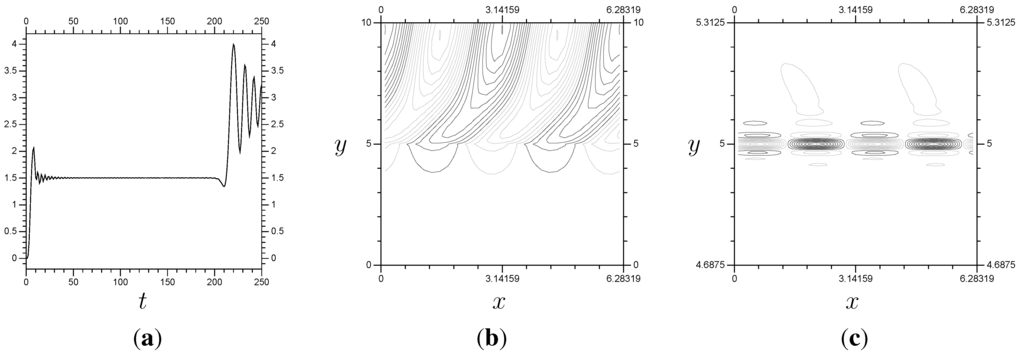
Figure 14.
Results from a with localized double system. The small-scale is over , and 3 “extra” terms are used over both interfaces of Λ. There is a little instability in the flux around , but this arrangement is very close to the full control system, found in Figure 12. (a) ; (b) P, ; (c) Z, .
10.3. Non-Linear Results
The actual benefits of the multi-scale system exist primarily for non-linear problems, so we shall switch to the non-linear version, with . The linearization scheme used on Burgers’ equation (see (7.2)) will be used again.
There is one more, significant, issue: We shall need many more Fourier coefficients to properly express the x direction when . With the boundary conditions just multiples of , and with initial conditions of zero, the linear problem’s solution can be written in terms of in the x direction. If we have with the same boundary and initial conditions, then the problem will require , , in the x direction. We use , so the even Fourier modes will be relevant. Obviously, we have to restrict the number of Fourier modes we calculate to a finite number, and use a pseudo Fourier scheme to approximate and . The functions P and Z are real, so modeling the Fourier modes (for ) requires K complex values and one real value to keep track of, which are effectively real values.
So, we have to create and solve a new linear system at every step, and the systems themselves will be significantly larger. As a result, we shall keep the y resolution down to a manageable , or 16 elements per interval of length one, so 159 total on . Combined with 11 elements for the x direction and that makes 1749 real coefficients in total. The boundary conditions are the same, and , as before. We shall include some viscosity, , to stabilize the system and make the resolution plausible. We use , and the size of the time step is .
Our multi-scale results use the method that was applied to Burgers’ equation in Section 8. We use three “extra” terms and a J multiplier with
The linear components of the calculation are derived the same way as in Section 8 as well, from a system using the finest resolution over all Ω.
As discussed at the end of Subsection 10.1, the flux for the non-linear problem is expected to reach its maximum early, then reduce down to zero and begin oscillating around zero. As for P, it is expected to develop waves similar to the linear problem, at least initially. As t increases, we can expect the tip of the waves in P, the parts near , to break from the rest and create separate, somewhat circular, shapes. This behavior is shown nicely in ([19] [Figure 2b and Figure 14b]). Other than the expectation of greater complexity, we shall say little of Z. We shall, however, use Z to check the accuracy of the multi-scale results.
When , the flux is expected to quickly reach the steady state of the linear system, then slowly reduce to zero and begin oscillating around zero. Take a look at Figure 15a–f. The value is not high enough for the flux to reach zero during , so instead we see a reduction towards zero for the model. We set as our top resolution, the results we want to duplicate efficiently with the multi-scale method. Our large-scale resolution is .
Now we discuss how this particular Rossby wave problem responds to the multi-scale method. The problem does seem to require a larger domain for the small-scale system, which cuts into the efficiency. The system took an average of about 9.55 s per time step. See Figure 16 for our multi-scale results with the smallest small-scale domain, . The double system requires approximately 3.51 s per time step, a significant improvement on the system. However, the results are not quite as close to the system as we would like. Including more elements above improves things. In fact, the results are visually indistinguishable to the control results in Figure 15. However, the model requires 3.90 s per time step, and requires 4.48 s per time step.
The multi-scale results were shown to be able to duplicate the results, using with a localized resolution. There was also a significant reduction in the effort, with the time step taking half as much time to compute. The resolution used was restricted to a coarse to keep computing requirements reasonable. The increase from to means that the small-scale system has approximately half of its coefficients be in , so coefficients that are also in the large-scale system. This is the least efficient form of the method, with only a single space worth of additional resolution in the small-scale system, and it still proved beneficial with the non-linear Rossby wave problem. The control results took about s per time step, while the, visually identical, multi-scale results with took 4.48 s per time step. So, we have accurate results with less than half the computational expense.
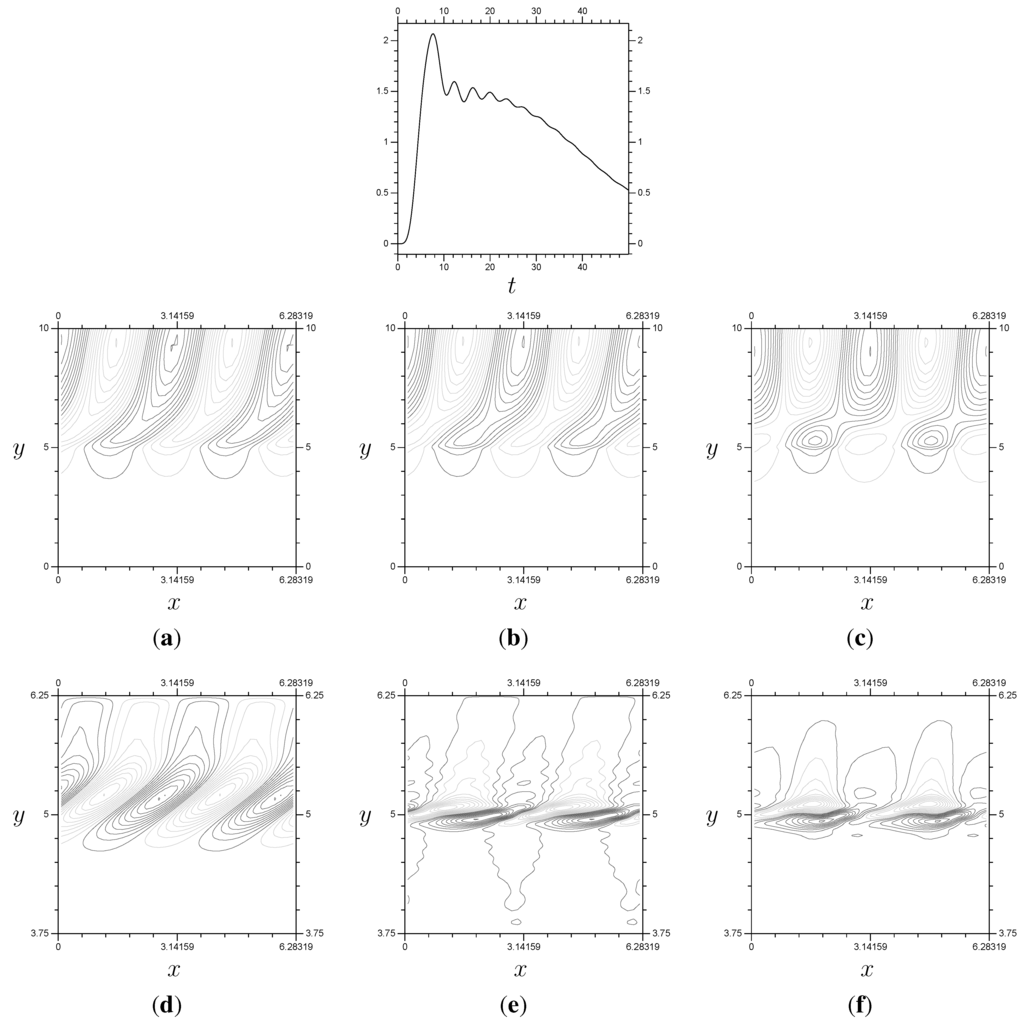
Figure 15.
Plots for the problem using . (Top) Flux; (Middle) P; (Bottom) Z. (a) P, ; (b) P, ; (c) P, ; (d) Z, ; (e) Z, ; (f) Z, .
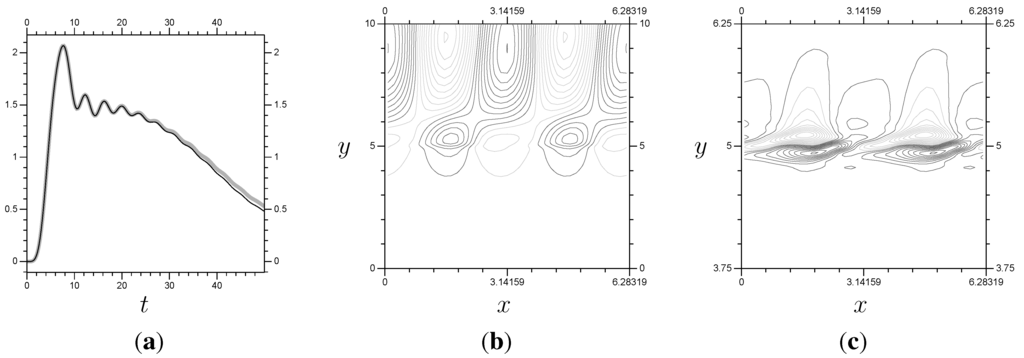
Figure 16.
Plots for multi-scale models of the Rossby wave problem. All use . The flux is plotted against that for the control results (the lighter, thicker line). The results using the larger and are omitted, as they are visually identical to the full control results from Figure 15. (a) ; (b) P at ; (c) Z at .
10.4. Convergence
The convergence of the Rossby wave problem is slightly restricted by the boundary conditions. Recall that the initial conditions are zero, while the boundary condition is equal to . Since Λ does not reach , the boundary conditions are modeled at the large-scale resolution. The lack of resolution for the boundary conditions results in error that cannot be removed without significant modifications to the method (including a second small-scale system at or incorporating the non-zero boundary conditions into Λ). As in the convergence related discussion in Section 9, we look at the effect of different Λ sizes and “extra” terms on the accuracy of multi-scale results. The control results are a resolution single system. The test systems use or over Ω and on Λ. Plots of the transformed error can be found in Figure 17. The summarized data is in Table 2.
Now we take a look at the convergence from the non-linear results in Section 10.3. The multi-scale results are calculated at with on differing small-scale domains Λ. They are compared with the full domain control results. The usual plots of the error against the number of and coefficients used, and the time required, for the multi-scale system can be found in Figure 18. The summarized data can be found in Table 3.
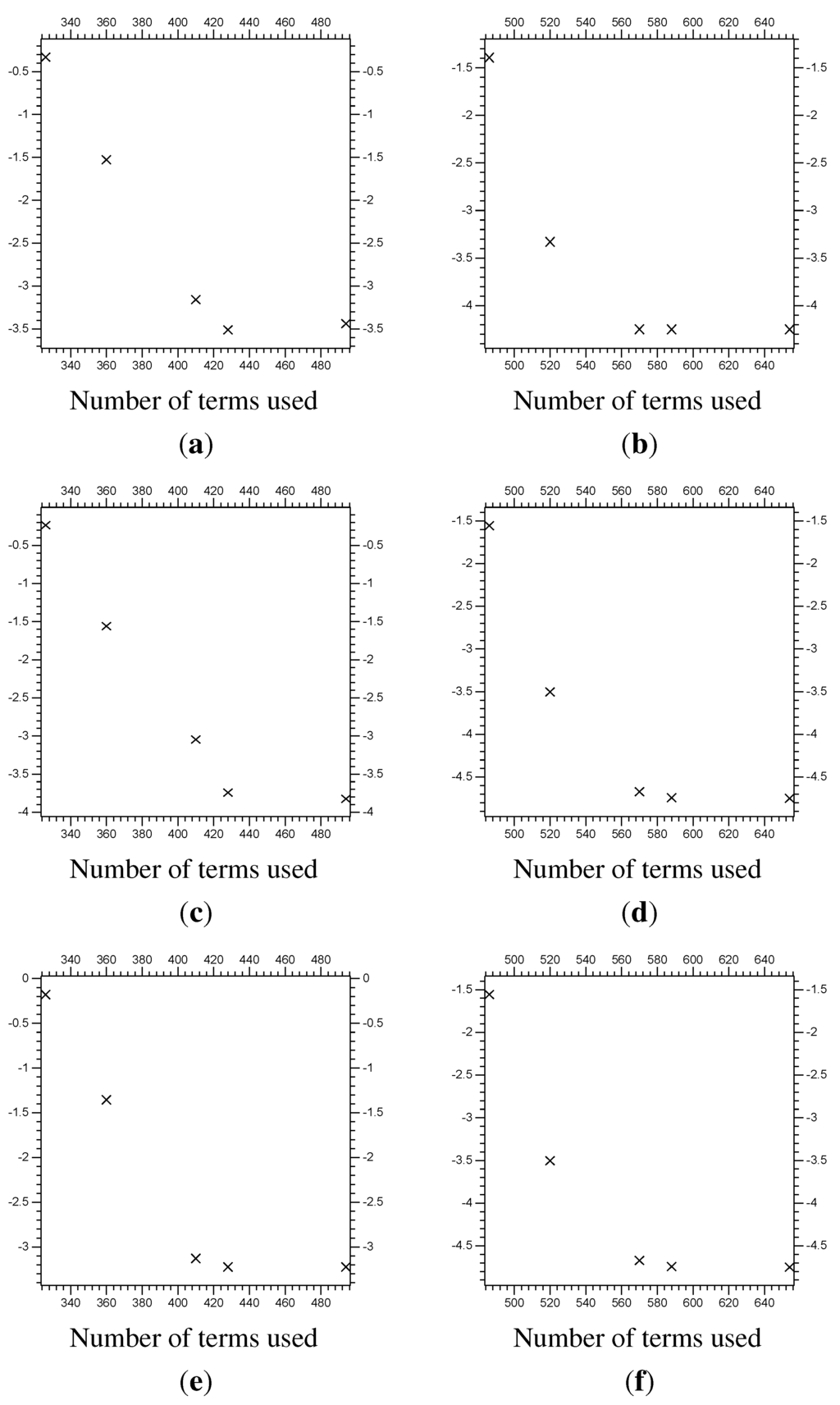
Figure 17.
The error at of the function Z from the linear problem. The vertical axis is the of the error (the difference between the multi-scale system results and the control results). The horizontal axis is the total number of and coefficients used for the y directional decomposition. (a) of the error for with on Λ; (b) of the error for with on Λ; (c) of the error for with on Λ; (d) of the error for with on Λ; (e) of the error for with on Λ; (f) of the error for with on Λ.

Table 2.
Error from multi-scale linear Rossby wave results.
| Λ | “extra” | Terms | Error | Error | Error | |
|---|---|---|---|---|---|---|
| [3.75,6.25] | 3 | 326 | ||||
| [3.50,6.50] | 4 | 360 | ||||
| [3.25,7.00] | 5 | 410 | ||||
| [3.00,7.00] | 6 | 428 | ||||
| [2.50,7.50] | 7 | 494 | ||||
| [3.75,6.25] | 3 | 486 | ||||
| [3.50,6.50] | 4 | 520 | ||||
| [3.25,7.00] | 5 | 570 | ||||
| [3.00,7.00] | 6 | 588 | ||||
| [2.50,7.50] | 7 | 654 |
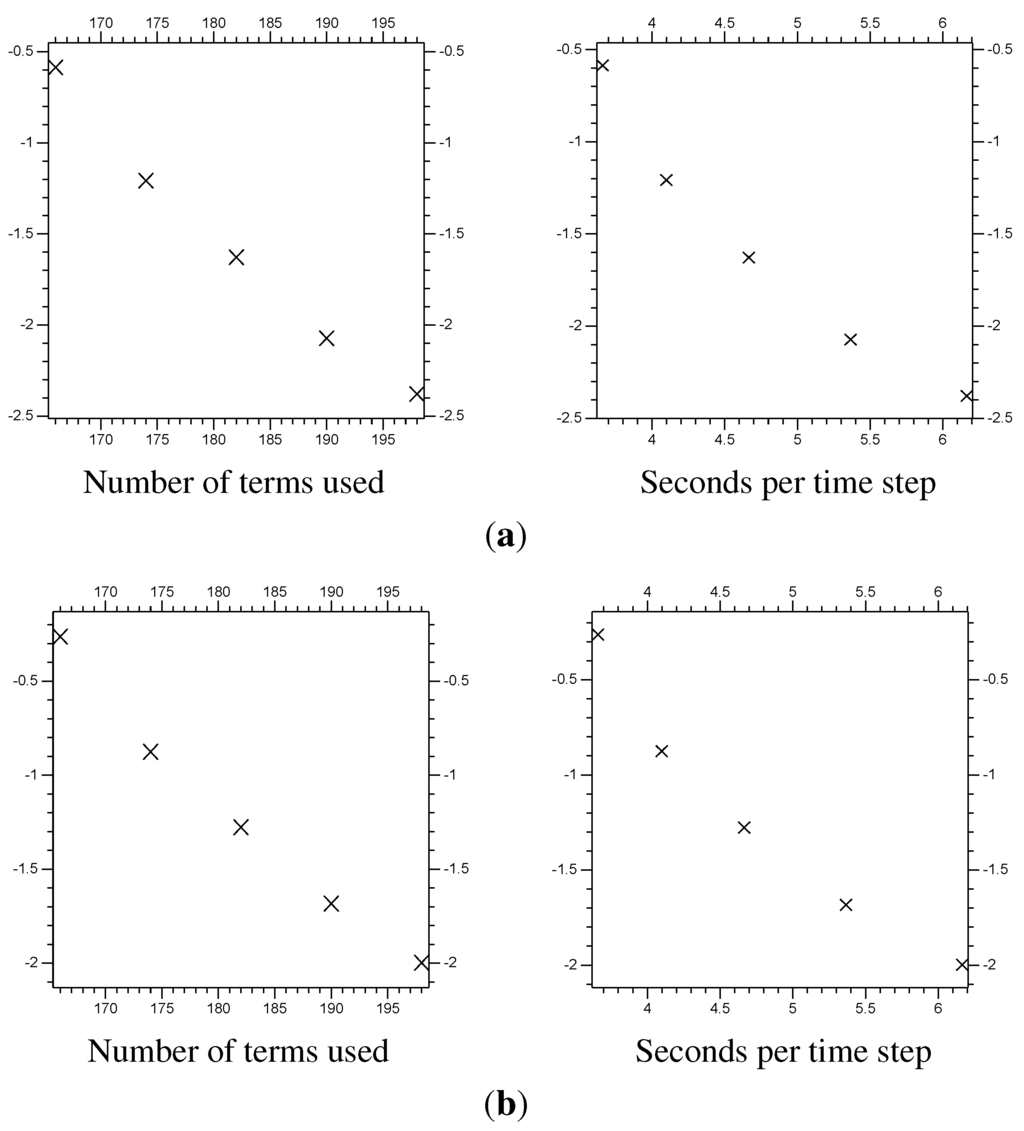
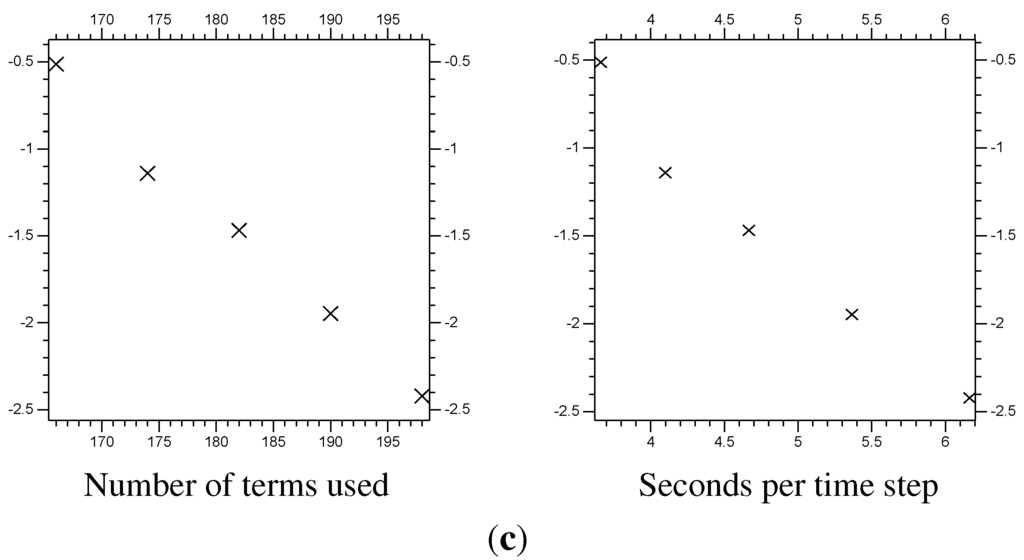
Figure 18.
The error at of the function Z from the non-linear () problem. The vertical axis is the of the error, the difference between the multi-scale results and the control results (see Figure 15). The horizontal axis is the total number of and coefficients used for the y directional decomposition. (a) of the error; (b) of the error; (c) of the error.

Table 3.
Error from non-linear multi-scale Rossby wave results. All but the control use and .
| Λ | “extra” | Terms | Time | Error | Error | Error |
|---|---|---|---|---|---|---|
| 4 | 168 | 3.66 | ||||
| 4 | 176 | 4.10 | ||||
| 4 | 184 | 4.67 | ||||
| 4 | 192 | 5.27 | ||||
| 4 | 200 | 6.16 | ||||
| Control | 9.25 | |||||
11. Conclusions
After some wavelet based preliminaries, we described a new method for partial differential equations at multiple scales, in Section 3. The small-scale resolution is restricted to a sub-domain Λ of the full domain Ω. The method divides the implicit system created by the time-discretization scheme into two smaller systems: One at a coarse resolution over the entire domain Ω and the other at fine resolution on the subset . This dividing of the system will typically result in significant computational savings.
Next we set up a test problem based on Burgers’ equation. The initial condition, Figure 3a, results in two peaks that approach each other and collide. The resulting collision requires a fine resolution to be properly expressed. A resolution of is required for stable and accurate results once the peaks collide (at approximately ). A resolution of causes instability (coefficients in the range of ). However, since the collision is at , the fine resolution is only required in a domain in the center. The calculations using a single resolution of over the entire domain Ω take 0.988 s per time step. The resolution of would be restricted to a sub-domain Λ in the center of Ω, where the peaks collide. The method required a few improvements beyond the basic setup, outlined in Section 8.
We first tested the resolutions on Ω and on , yielding a close approximation to the control results. The largest difference between them went briefly higher than 0.001, and otherwise was below 0.0005 (see Figure 7). These differences were found to be an order of magnitude smaller than the error stemming from the limited resolution () and time step () common to both the multi-scale and control results (see Subsection 7.3 and Figure 4). Furthermore, the multi-scale results required 0.0337 s per time step, while the control results required approximately one second per time step. So, the multi-scale results were not only just stable and much less expensive to calculate, but also accurate.
The next step was to check for convergence towards the control results, computed using a resolution of on the full domain. For this test we used on Ω and on several different subsets Λ of Ω. We had to control for the error near the boundaries of Ω (far from the Λ sub-domains), which was, in fact, identical for all the different Λ sub-domains. Using the , and norms, increasing the size of the small-scale system resulted in a smaller difference between the test systems and the control results. The eventual error was approaching machine precision.
Next, further confirmation was sought using a non-trivial problem. The Rossby wave problem is two dimensional, on , with small-scale interactions found towards the center of the domain in the y direction. First we tested the linear form of the problem, where fine resolution near is needed to accurately represent the correct solution over time. Without viscosity, the numerical results would fail to maintain consistency beyond a certain value of t, with a finer resolution allowing this value of t to be larger. Using the linear problem with no viscosity, a wavelet decomposition with a resolution of will show the correct result over the time frame , over , and over . The multi-scale method was used with on and everywhere else, as well as a total of 6 “extra” terms. The results were accurate on , just like the full domain control results. So, the method worked for the linear version of the problem.
The non-linear Rossby wave problem also responded well to the multi-scale method. Similarly to the tests in Section 9, a set of with localized were calculated, using different sub-domains Λ and different numbers of “extra” terms (see Subsection 8.2). These were compared with full domain control results. The , and norms of the differences between the multi-scale and control results were calculated. As in Section 9, the calculated differences between the test and control results showed a convergence to zero as the width of Λ was increased.
In Section 8 two modifications to the basic method are introduced, one necessary for accurate results with a non-linear problem, the other contributing to accuracy for any problem. There are several additional features beyond those in Section 8 that should be tested.
- First is the fact that both the large and small-scale systems should have adaptive decompositions. Due to how the systems are divided, there is no particular reason why the small-scale system in Λ could not follow any given adaptive scheme (that is compatible with an implicit time-discretization). Most of the changes in an adaptive scheme would be towards the finer resolution terms, which interact very little with the large-scale system. The real question is how to determine if a particularly tight concentration of fine resolution terms merits creating further small-scale systems.
- Giving the large-scale system an adaptive decomposition could be more complicated. Increasing the resolution of the large-scale system within Λ would probably be a bad idea. That would create duplicate terms (those that are calculated twice, once in each) to no net benefit. However, a few, isolated, small-scale calculations outside of Λ would obviously give greater accuracy, at limited expense. Again, the real question is when to decide that a set of small-scale terms would be best given its own small-scale system, and be calculated separately from the large-scale system.
- Our two dimensional example involves a sub-domain Λ that covers a small subset of the domain in the y direction, but covers the entire interval in the x direction. Basically, the example has two spatial dimensions, but the multi-scale method is only used in one of those dimensions. It would be instructive to test a problem requiring localization in two or more spatial dimensions. A turbulence related problem would be appropriate for testing purposes, or any problem from fluid dynamics that results in small-scale vortices.
- An analysis of the effect of our method on the stability of the underlying time-discretization. Preliminary testing was done in [23], showing a minimal effect on stability, but more is needed.
- Using multiple small-scale systems, either nested or discrete, as shown in Figure 2. If a problem requires high resolution in two regions, call them and , it may be possible to calculate them separately, after the calculation of the large-scale system. The large-scale system could have, for example, 800 elements, with 400 small-scale elements and 200 large-scale in each of and . Solving all of these together would involve 1200 elements. Solving them broken up into three systems would involve an 800 element system and two of 400. This should involve substantial savings.
- Using a different time step size for the small-scale system. Instead of calculating after each time step of the large-scale system, we could calculate then (or , , , then ). Doing so requires the intermediate large-scale vectors , which are relatively easy to calculate via interpolation. However, further experimentation is necessary to find how well this works, and what modifications may be necessary.
- Making the size of Λ, the resolutions used, and the number of “extra” terms adaptive. This requires analyzing the sources of error stemming from the boundaries of Λ and the lack of “extra” terms.
Additionally, the key steps and components of this method could be combined with other methods. The method should be compatible with any multi-scale decomposition, and any procedures for solving the resulting systems. As long as the partial differential equation is time based, and the time-discretization is implicit, our multi-scale method should be useable. The nature of the partial differential equation itself will determine if our method would be useful.
So, in summary, this multi-scale implicit method shows potential for solving certain partial differential equations, namely those that produce stiff decompositions and require fine resolution in small regions. The preliminary tests went well, but further testing of the method, and extensions to the method, are required.
Acknowledgements
Thanks are due to the anonymous referees, who provided helpful, pointed, and insightful reviews of the initial submission.
References
- Daubechies, I. Ten Lectures on Wavelets; SIAM: Philadelphia, PA, USA, 1992. [Google Scholar]
- Blatter, C. Wavelets, A Primer; A K Peters Ltd.: Natick, MA, USA, 1998. [Google Scholar]
- Meyer, Y. Ondelettes et Functions Splines; Séminaire EDP, Ecole Polytechnique: Paris, France, 1986. [Google Scholar]
- Lemarié, P.G. Ondelettes à localisation exponentielle. J. Math. Pures Appl. 1988, 67, 227–236. [Google Scholar]
- Daubechies, I. Orthonormal bases of compactly supported wavelets. Commun. Pure Appl. Math. 1988, 41, 909–996. [Google Scholar] [CrossRef]
- Cohen, A.; Daubechies, I.; Feauveau, J.-C. Biorthogonal bases of compactly supported wavelets. Commun. Pure Appl. Math. 1992, 45, 485–560. [Google Scholar] [CrossRef]
- Farge, M.; Schneider, K. Coherent Vortex Simulation (CVS), a semi-deterministic turbulence model using wavelets. Flow Turbul. Combust. 2001, 66, 393–426. [Google Scholar] [CrossRef]
- Alam, J.M.; Kevlahan, N.K.R.; Vasilyev, O.V. Simultaneous space-time adaptive wavelet solution of nonlinear parabolic differential equations. J. Comput. Phys. 2006, 214, 829–857. [Google Scholar] [CrossRef]
- Hesthaven, J.S.; Jameson, L.M. A wavelet optimized adaptive multi-domain method. J. Comput. Phys. 1998, 145, 280–296. [Google Scholar] [CrossRef]
- Léonard, S.; Terracol, M.; Sagaut, P. A wavelet-based adaptive mesh refinement criterion for large-eddy simulation. J. Turbul. 2006, 7. [Google Scholar] [CrossRef]
- Beylkin, G.; Coifman, R.; Rokhlin, V. Fast wavelet transforms and numerical algorithms I. Commun. Pure Appl. Math. 1991, 44, 141–183. [Google Scholar] [CrossRef]
- Sweldens, W. The lifting scheme: A construction of second generation wavelets. SIAM J. Math. Anal. 1998, 29, 511–546. [Google Scholar] [CrossRef]
- Harten, A. Multiresolution Representation and Numerical Algorithms: A Brief Review; ICASE/LaRC Interdisciplinary Series in Science and Engineering; Springer: Berlin, Germany, 1997; Volume 4, pp. 289–322. [Google Scholar]
- Vasilyev, O.V.; Kevlahan, N.K.-R. An adaptive multilevel wavelet collocation method for elliptic problems. J. Comput. Phys. 2005, 206, 412–431. [Google Scholar] [CrossRef]
- Vasilyev, O.V.; Paolucci, S. A dynamically adaptive multilevel wavelet collocation method for solving partial differential equations in a finite domain. J. Comput. Phys. 1996, 125, 498–512. [Google Scholar] [CrossRef]
- Müller, S.; Stiriba, Y. A multilevel finite volume method with multiscale-based grid adaptation for steady compressible flows. J. Comput. Appl. Math. 2009, 227, 223–233. [Google Scholar] [CrossRef]
- Mehra, M.; Kevlahan, N.K.-R. An adaptive multilevel wavelet solver for elliptic equations on an optimal spherical geodesic grid. SIAM J. Sci. Comput. 2008, 30, 3073–3086. [Google Scholar] [CrossRef]
- Tang, Y.Y.; Wickerhauser, V.; Yuen, P.C.; Li, C. Wavelet Analysis and Its Applications; Springer: New York, NY, USA, 2001. [Google Scholar]
- Campbell, L.J. Wave-Mean-Flow interactions in a forced rossby wave packet critical layer. Stud. Appl. Math. 2004, 112, 39–85. [Google Scholar] [CrossRef]
- Kundu, P.K.; Cohen, I.M. Fluid Mechanics, 3rd ed.; Elsevier Academic Press: New York, NY, USA, 2004. [Google Scholar]
- Campbell, L.J.; Maslowe, S.A. Forced rossby wave packets in baratropic shear flows with critical layers. Dyn. Atmos. Oceans 1998, 28, 9–37. [Google Scholar] [CrossRef]
- Béland, M. Numerical study of the nonlinear rossby wave critical level development in a barotropic zonal flow. J. Atmos. Sci. 1976, 33, 2066–2078. [Google Scholar] [CrossRef]
- McLaren, D.A. Sequential and Localized Implicit Wavelet-Based Solvers for Stiff Partial Differential Equations. Ph.D. Thesis, University of Ottawa, Ottawa, Canada, 2012. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).