Signal Estimation Using Wavelet Analysis of Solution Monitoring Data for Nuclear Safeguards
Abstract
:1. Introduction
2. Solution Monitoring for Nuclear Safeguards
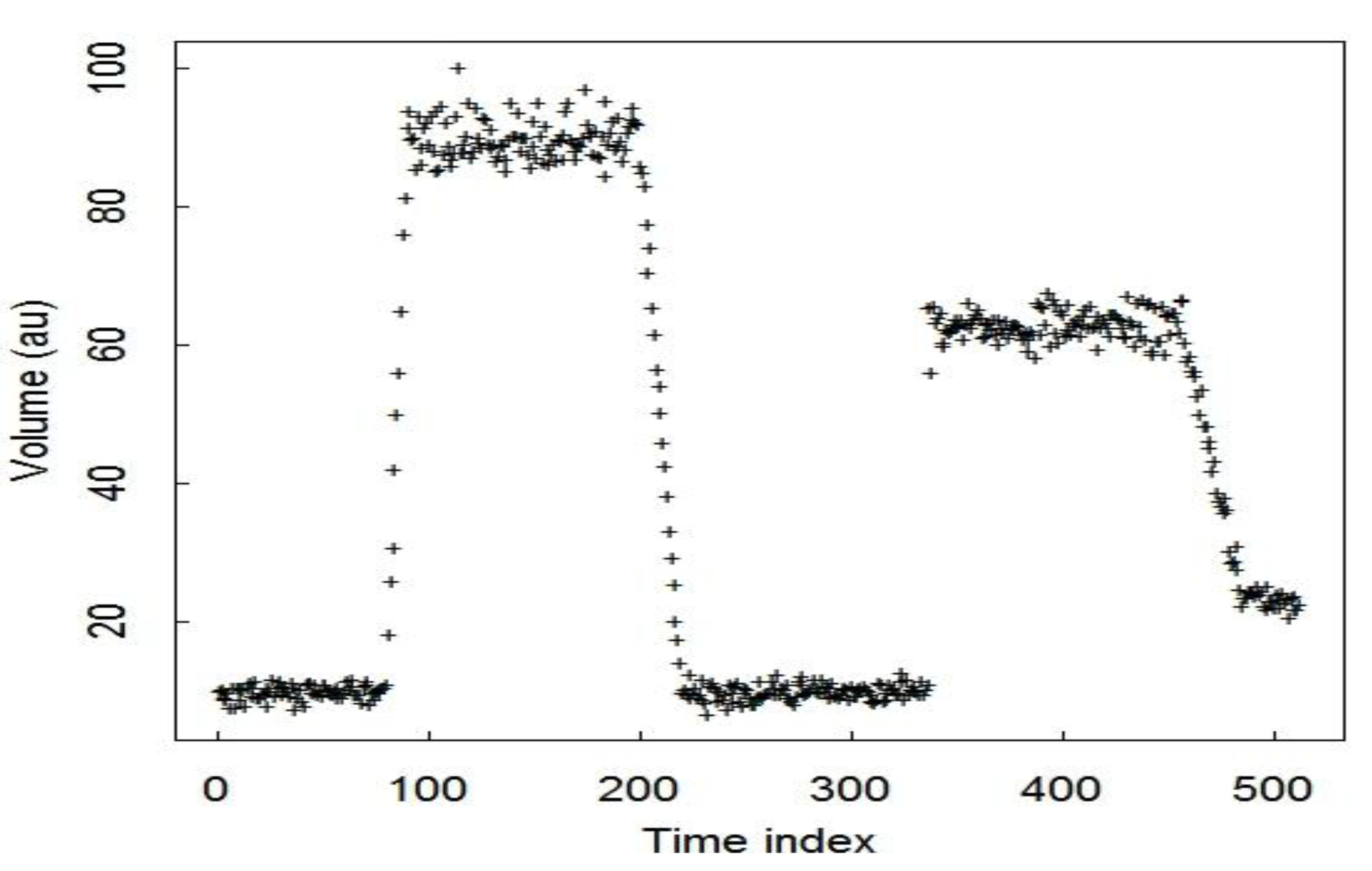
3. Simulated Data
4. Wavelets
- 1)
- M(t) is decomposed using a discrete wavelet transformation;whereare wavelet coefficients. Note that these coefficients are obtained from noisy data and are therefore also disturbed by noise withsuch that is error and are the true coefficients.
- 2)
- Using a wavelet thresholding method, an estimate of the true noiseless coefficients is found. These are denoted . Wavelet thresholding sets below a certain threshold to 0.
- 3)
- The data is reconstructed using an inverse discrete wavelet transform with to obtain and estimate of the noiseless dataOne requirement when using wavelets to approximate data is that the data must be of a dyadic length ( for ). SM data is plentiful so it is easy to break the data into dyadic sections. All simulated datasets have dyadic length (usually 256, 512, or 1024) to keep the analysis as simple as possible. Wavelet smoothing is easily implemented in R using any of several wavelet packages, such as wavethresh, which we use here.
4.1. The Gibbs Phenomenon in Wavelet Analysis
4.2. Mathematical Description of the Gibbs Phenomenon
4.3. Example of the Gibbs Phenomenon
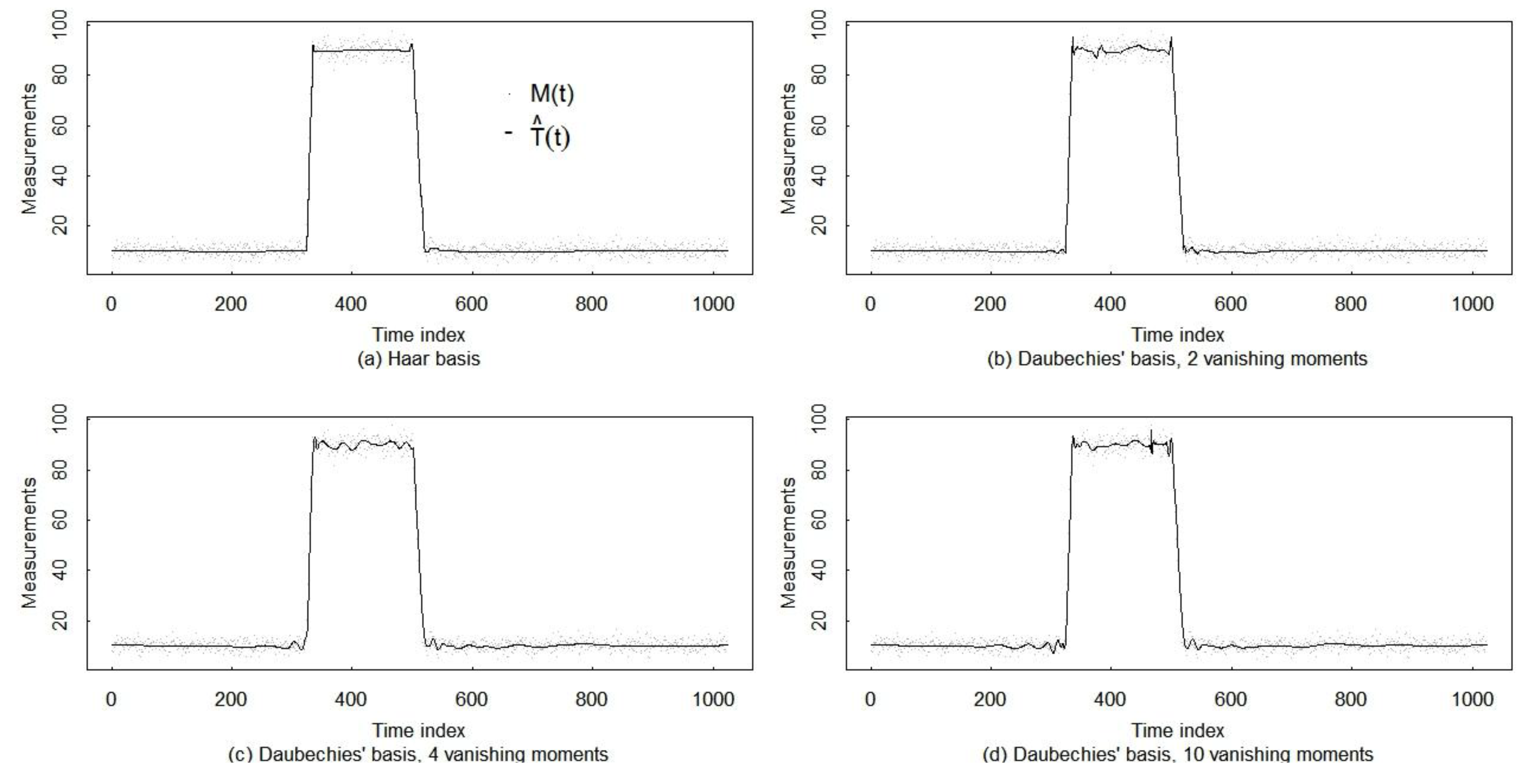
4.4. Mitigation of the Gibbs Phenomenon
5. Simulation Results
5.1. Wavelet Smoothing
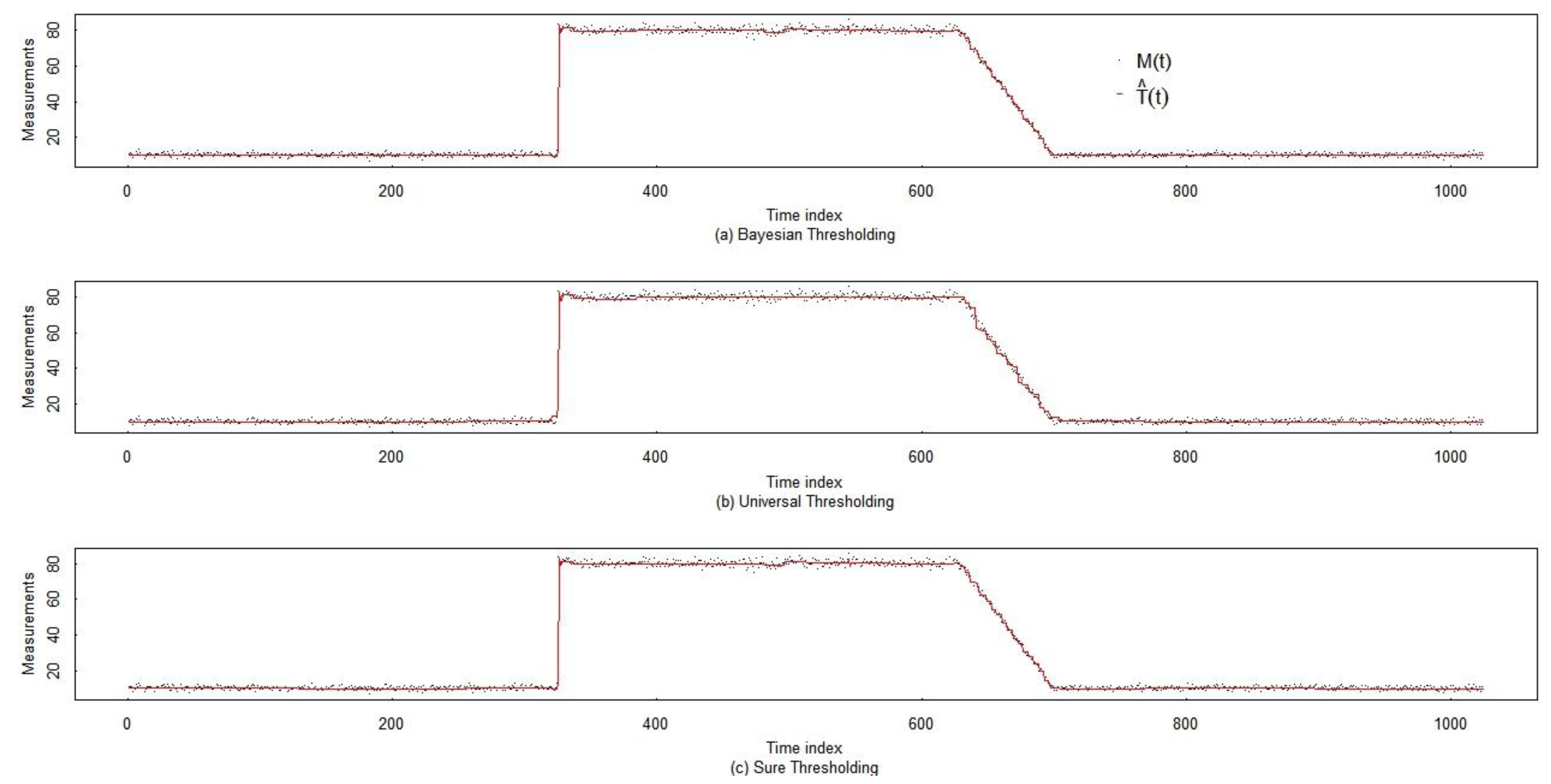
| Bayesian soft | Universal soft | Sure soft |
|---|---|---|
| 0.6822 ±0.008 | 0.8975 ±0.005 | 0.8079 ±0.007 |
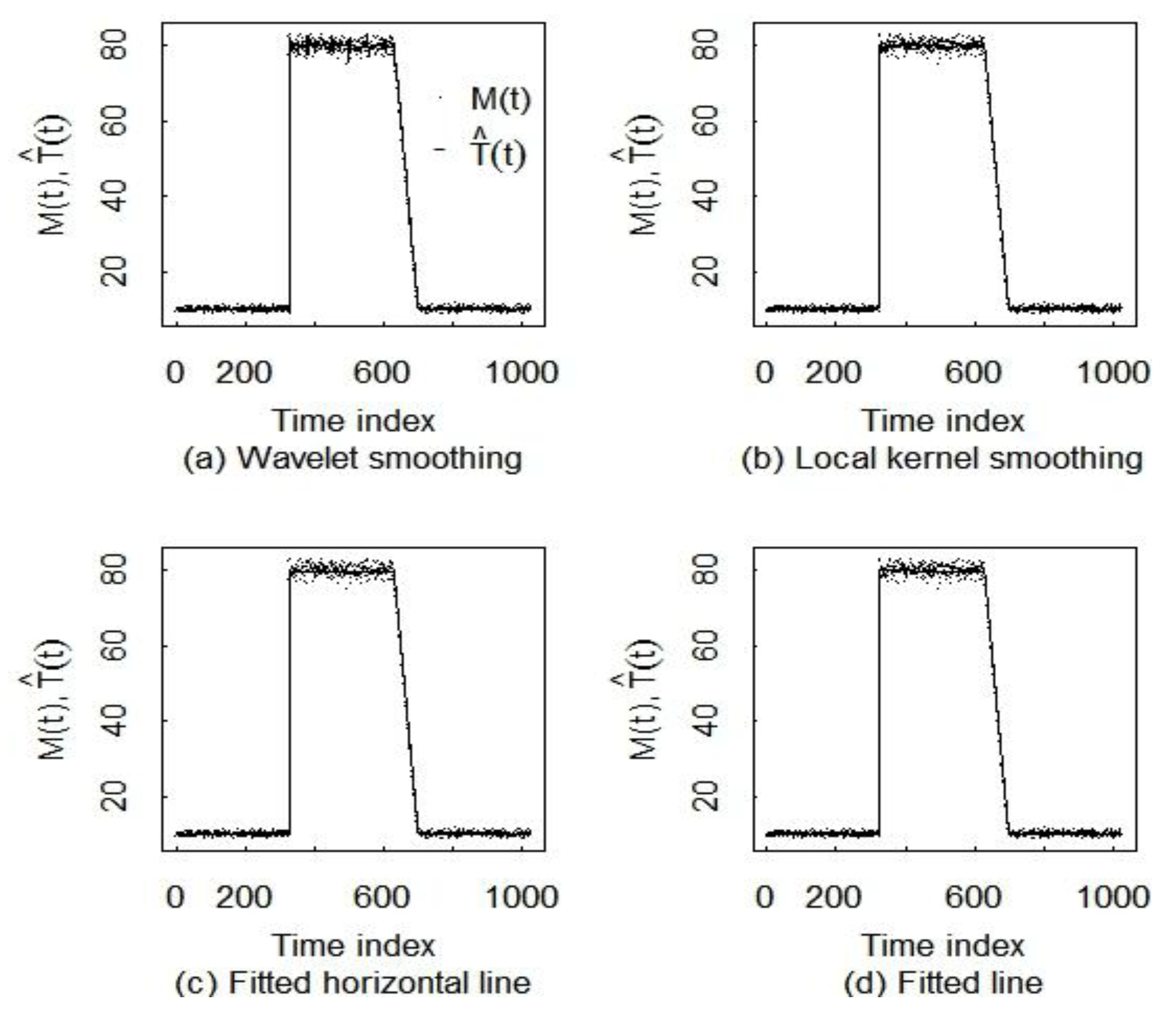
5.2. Comparison of Three Smoothing Methods
| Haar wavelets | lokerns | PLR (flat line) | PLR (any line) | |
|---|---|---|---|---|
| data length 210 | 0.46 ± 0.005 | 0.71 ± 0.002 | 0.057 ± 0.002 | 0.075 ± 0.002 |
| near change points | 0.91 ± 0.015 | 3.60 ± 0.015 | 0.118 ± 0.006 | 0.141 ± 0.006 |
| away from change points | 0.44 ± 0.003 | 0.31 ± 0.002 | 0.054 ± 0.003 | 0.069 ± 0.002 |
| Wave1 | Wave2 | Wave3 | Wave4 | lokerns | PLR1 | PLR2 | |
|---|---|---|---|---|---|---|---|
| All points | 0.007 | 0.012 | 0.017 | 0.017 | 0.018 | 0.003 | 0.004 |
| Near change points | 0.023 | 0.021 | 0.045 | 0.040 | 0.056 | 0.010 | 0.020 |
| Away from change points | 0.006 | 0.006 | 0.016 | 0.016 | 0.016 | 0.002 | 0.002 |
| Wave1 | Wave2 | Wave3 | Wave4 | lokerns | PLR1 | PLR2 | |
|---|---|---|---|---|---|---|---|
| All points | 0.008 | 0.015 | 0.021 | 0.022 | 0.027 | 0.022 | 0.004 |
| Near change points | 0.022 | 0.035 | 0.048 | 0.052 | 0.077 | 0.143 | 0.021 |
| Away from change points | 0.008 | 0.008 | 0.020 | 0.021 | 0.025 | 0.005 | 0.003 |
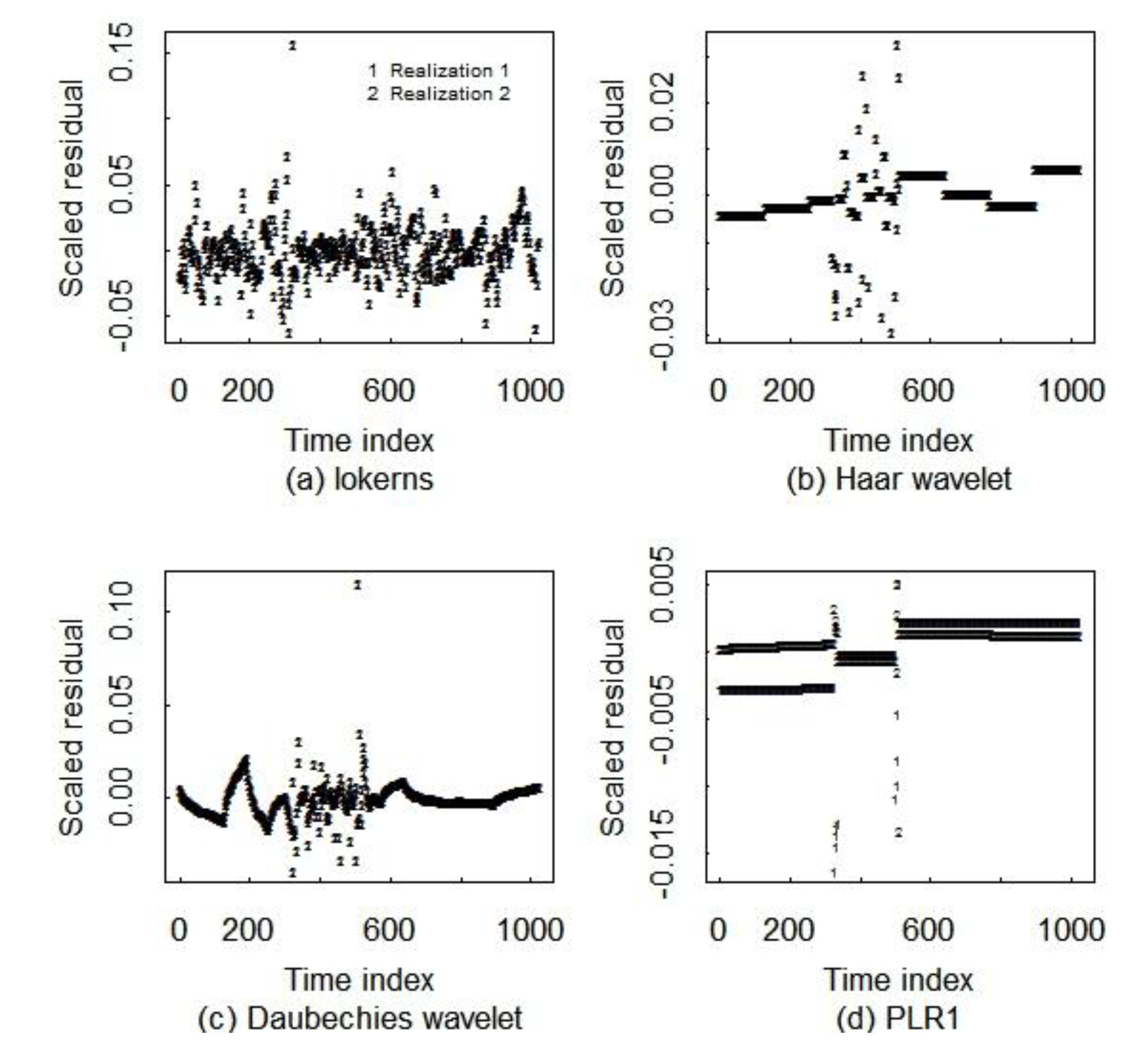
6. Conclusions
Acknowledgments
References and Notes
- Burr, T.; Hengartner, N.; Matzner-Lober, E.; Myers, S.; Rouviere, L. Smoothing low resolution NaI spectra. IEEE Trans. Nucl. Sci. 2010, 57, 2831–2840. [Google Scholar] [CrossRef]
- Kelly, S. Gibbs phenomenon for wavelets. Appl. Comput. Harmon. Anal. 1995, 3, 72–81. [Google Scholar] [CrossRef]
- Burr, T.; Suzuki, M.; Howell, J.; Hamada, M.; Longo, C. Signal estimation and change detection in tank data for nuclear safeguards. Nucl. Instrum. Methods Phys. Res. A 2011, 640, 200–221. [Google Scholar] [CrossRef]
- Burr, T.; Hamada, M.S.; Skurikhin, M.; Brian Weaver, B. Pattern recognition options to combine process monitoring and material accounting data in nuclear safeguards. Stat. Res. Lett. 2012, 1, 6–31. [Google Scholar]
- Binner, R.; Jahssens-Maenhous, J.H.G.; Sellinschegg, D.; Zhao, K. Practical issues relating to tank volume determination. Ind. Eng. Chem. Res. 2008, 47, 1533–1545. [Google Scholar] [CrossRef]
- Burr, T.; Howell, J.; Suzuki, M.; Crawford, J.; Williams, T. Evaluation of Loss Detection Methods in Solution Monitoring for Nuclear Safeguards. In Proceedings of American Nuclear Society Conference on Human-Machine Interfaces, Knoxville, TN, USA, 5–9 April 2009.
- Howell, J. Towards the re-verification of process tank calibrations. Trans. Inst. Meas. Control 2009, 31, 117–128. [Google Scholar] [CrossRef]
- Suzuki, M.; Hori, M.; Nagaoka, S.; Kimura, T. A study on loss detection algorithms using tank monitoring data. J. Nucl. Sci. Technol. 2009, 46, 184–192. [Google Scholar] [CrossRef]
- Aigner, H. International target values 2000 for measurement uncertainties in safeguarding nuclear materials. J. Nucl. Mater. Manag. 2002, 30. Available online: www.inmm.org/topics/publications (accessed on 11 March 2011). [Google Scholar]
- Burr, T.; Suzuki, M.; Howell, J.; Hamada, M. Loss detection results on simulated tank data modified by realistic effects. J. Nucl. Sci. Technol. 2012, 49, 209–221. [Google Scholar] [CrossRef]
- Miller, E.; Howell, J. Tank measurement data compression for solution Monitoring. J. Nucl. Mater. Manag. 1999, 28, 25–33. [Google Scholar]
- R Statistical Programming Language. Available online: www.r-project.org (accessed on 18 March 2012).
- Daubechies, I. Ten Lectures on Wavelets. In Proceedings of CBMS-NSF Regional Conference Series in Applied Mathematics, Philadelphia, PA, USA, 1992.
- Donoho, D.; Johnstone, I. Adapting to unknown smoothing via wavelet shrinkage. J. Am. Stat. Assoc. 1995, 90, 1200–1224. [Google Scholar] [CrossRef]
- Donoho, D.; Johnstone, I. Ideal spatial adaption by wavelet shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar] [CrossRef]
- Johnstone, I.; Silverman, B. Wavelet threshold estimators for data with correlated noise. J. R. Stat. Soc. Ser. B 1997, 59, 319–351. [Google Scholar] [CrossRef]
- Bakshi, B. Multiscale analysis and modeling using wavelets. J. Chemom. 1999, 13, 415–434. [Google Scholar] [CrossRef]
- Abramovich, F. Wavelet thresholding via a Bayesian approach. J. R. Stat. Soc. Ser. B 1998, 60, 725–749. [Google Scholar] [CrossRef]
- Abramovich, F.; Sapatinas, T.; Bailey, T. Wavelet analysis and its statistical applications. J. R. Stat. Soc. Ser. D 2000, 49, 1–29. [Google Scholar] [CrossRef]
- Nason, G. Wavelet Methods in Statistics with R; Springer: New York, NY, USA, 2008. [Google Scholar]
- Boggess, A.; Narcowich, G. A First Course in Wavelets with Fourier Analysis, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Sharifzadeh, M.; Azmoodeh, F.; Shahabi, C. Change Detection in Time Series Data Using Wavelet Footprints. In Proceedings of the 9th International Conference on Advances in Spatial and Temporal Databases, Angra dos Reis, Brazil, 22–24 August 2005; pp. 127–144.
- Longo, C.; Burr, T.; Myers, K. Wavelet change detection in solution monitoring data for nuclear safegaurds. Axioms 2013. submitted for publication. [Google Scholar]
- Gibbs, W. Fouriers’s series. Nature 1898, 29, 300. [Google Scholar]
- Jerri, A. Advances in the Gibbs Phenomenon; Σ Sampling Publishing: Potsdam, NY, USA, 2011. [Google Scholar]
- Gu, X.-H.; Cai, J.-H. Study of the Gibbs Phenomenon in De-Noising by Wavelets. In Proceedings of the 7th World Congress on Intelligent Control and Automation, Chongqing, China, 25–27 June, 2008.
- The “find-one-changepoint-at-a-time” version of breakpoints is easy to implement in R, highly accurate, and very fast. After finding the approximate location of a changepoint in a contiguous range of indices, tempindices, call the optimize function using:
- th = optimize(fnw, interval = tempindices, x = tempindices, y = y[temp.indices])$minimum with the function fnw defined as
- fnw = function(th, x, y, sigma.rel = 0.015, sigma.add = 1) {# conditional minimum SSQ given theta
- X = cbind(x, pmax(0, x − th))
- wts = 1/(sigma.add^2 + y^2*sigma.rel^2)
- sum(lsfit(X, y, wt = wts)$resid^2)
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Burr, T.; Longo, C. Signal Estimation Using Wavelet Analysis of Solution Monitoring Data for Nuclear Safeguards. Axioms 2013, 2, 44-57. https://doi.org/10.3390/axioms2010044
Burr T, Longo C. Signal Estimation Using Wavelet Analysis of Solution Monitoring Data for Nuclear Safeguards. Axioms. 2013; 2(1):44-57. https://doi.org/10.3390/axioms2010044
Chicago/Turabian StyleBurr, Tom, and Claire Longo. 2013. "Signal Estimation Using Wavelet Analysis of Solution Monitoring Data for Nuclear Safeguards" Axioms 2, no. 1: 44-57. https://doi.org/10.3390/axioms2010044
APA StyleBurr, T., & Longo, C. (2013). Signal Estimation Using Wavelet Analysis of Solution Monitoring Data for Nuclear Safeguards. Axioms, 2(1), 44-57. https://doi.org/10.3390/axioms2010044





