Ordering Planar Graphs by Their Signless Laplacian Spectral Radii

Abstract

A graph is planar if it can be embedded in the plane such that its edges intersect only at their common endpoints. In this paper, we determine the graphs attaining the second and third largest signless Laplacian spectral radii among all planar graphs of order $n\ge 398$. Furthermore, we apply this characterization to identify the planar graphs that achieve the first three largest values of the sum of the first and second largest signless Laplacian eigenvalues.

1. Introduction

In this paper, we discuss the graphs that are finite, undirected and simple. Let $G=\left(V\right(G),E(G\left)\right)$ be a graph where $V\left(G\right)$ is the vertex set of G and $E\left(G\right)$ is the edge set of G. Assuming that $\left|V\right(G\left)\right|=n\left(G\right)$ and $\left|E\right(G\left)\right|=m\left(G\right)$. Let $Q\left(G\right)=D\left(G\right)+A\left(G\right)$ denote the signless Laplacian matrix of a graph G, where $D\left(G\right)$ is the degree matrix of G and $A\left(G\right)$ is the adjacency matrix of G. The spectrum of $Q\left(G\right)$ is $\sigma \left(Q\left(G\right)\right)=\{q_1\left(G\right),\dots ,q_n\left(G\right)\}$. Supposing that $q_i\left(G\right)\ge q_{i+1}\left(G\right)\ge 0$ where $1\le i\le n-1$, and $q_1\left(G\right)$ is the first largest signless Laplacian eigenvalue (or Q-spectral radius) of G.

A graph that can be drawn on a plane so that its edges intersect only at vertices. For any planar graph, it is called maximal if the addition of any further edge would destroy its planarity. For any planar graph G with $n\ge 3$, $m\left(G\right)\le 3n-6$, and equality is attained precisely when G is a maximal planar graph. The studying of the first largest signless Laplacian eigenvalues of planar graphs reveals the structural properties of planar graphs, connecting a graph’s structure, spectrum, and various invariants. It represents a convergence point of structural graph theory and spectral graph theory and provides a key mathematical metric and optimization objective for network design (communication, transportation), prediction of chemical molecular properties, and graph machine learning algorithms [1].

During the last 20 years, there was a lot of research conducted on the first eigenvalue of planar graphs. Schwenk and Wilson [2] raised a question about the first largest eigenvalues of a planar graph. Assume that $G_1$ and $G_2$ are two vertex-disjoint graphs. Let $G_1\vee G_2$ denote the graph formed by taking the disjoint union of $G_1$ and $G_2$ and then connecting every vertex of $G_1$ to every vertex of $G_2$. Royle [3] and Cao [4] conjectured that among all planar graphs with $n\ge 9$ vertices, $K_2\vee P_{n-2}$ achieves the first largest signless Laplacian eigenvalue. In 2020, Zhai et al. [5] characterized the graphs with maximal Q-spectral radius subject to the size constraint. See [6,7,8] for related results. The second largest eigenvalue of the signless Laplacian matrix, denoted as $q_2\left(G\right)$, has attracted substantial research attention in graph theory. A necessary condition for graphs attaining the bound was established by Belardo et al. They further proposed the problem of characterizing all graphs G with $n\ge 2$ satisfying $q_2\left(G\right)=n-2$. For more details, see [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21] and the references within.

For any graph G with $e\left(G\right)$ edges, let $S_k={\sum }_{k=1}^n{q}_i\left(G\right)$ be the sum of k largest Laplacian eigenvalues of G. In 2013, Ashraf et al. [22] posited that $S_k\left(G\right)\le e\left(G\right)+{\displaystyle \frac{k^2+k}{2}}$ for $1\le k\le n$. We can learn more about the structure of graphs from the sum of the first and second largest signless Laplacian eigenvalues of planar graphs than just using the spectral radius. It represents a deepening of extremely spectral graph theory research and serves as a new and more comprehensive spectral metric for evaluating and optimizing the overall performance of planar networks (e.g., transportation networks, integrated circuits) and holds potential as a novel molecular descriptor in chemoinformatics. As an application of Theorem 1, we obtained the bounds of the sum of the first and second largest signless Laplacian eigenvalues of all planar graphs, and the bounds are significantly smaller than those predicted by Ashraf’s conjecture.

The remainder of this paper is structured in the following way: In Section 2, we introduce essential definitions and preliminary results that will be utilized in subsequent sections. In Section 3, we order planar graphs according to their first largest signless Laplacian eigenvalue among all planar graphs. As an application, we also find the planar graphs with the first three largest sums of the two largest signless Laplacian eigenvalues.

2. Preliminaries

A graph H is a subgraph of graph G, $H\subseteq G$, if $V\left(H\right)\subseteq V\left(G\right)$ and $E\left(H\right)\subseteq E\left(G\right)$. For $v\in V\left(G\right)$, $N_G\left(v\right)$ (or $N\left(v\right)$) is the neighborhood of v in G. The degree of a vertex $v\in V\left(G\right)$ is the number of vertices in G that are adjacent to v, denoted by $d_G\left(v\right)$ (simply $d\left(v\right)$). Especially, let $\Delta \left(G\right)$ denote the maximum degree of the vertices of G and ${\Delta }_2\left(G\right)$ denote the second largest degree of G.

Let $G-V_1$ be the graph obtained from G by deleting the vertices $V_1\subseteq V\left(G\right)$ and the edges adjacent to the vertices of $V_1$. Similarly, $G-e$ denotes the graph obtained from G by deleting an edge $e\in E\left(G\right)$. Let $G_1$ and $G_2$ be two vertex-disjoint graphs. The graph $G_1\cup G_2$ is the graph with vertex set $V\left(G_1\right)\cup V\left(G_2\right)$ and edge set $E\left(G_1\right)\cup E\left(G_2\right)$. As usual, let $P_n$ denote a path of order n, respectively. $K_{n_1,n_2}$ denotes the bipartite graph of $n_1+n_2$ vertices. For any connected graph G, the Perron eigenvector of its signless Laplacian matrix $Q\left(G\right)$ is the unique unit positive eigenvector associated with the largest signless Laplacian eigenvalue $q\left(G\right)$. We will introduce some lemmas that will be needed in the following.

Lemma 1

([9]). Assuming that G is a planar graph with $n\ge 456$, and $\Delta \left(G\right)\le n-3$. Then $q_1\left(G\right)\le n+2\le q_1\left(H_n\right)$, and equality if and only if $G\cong H_n$ where $H_n=K_2\vee P_{n-2}$, as shown in Figure 1. Moreover, if $n-2\le \Delta \left(G\right)\le n-1$, then $q_1\left(G\right)\le q_1\left(H_n\right)<n+3$.

Lemma 2

([11]). Assuming that A is a square, non-negative, irreducible real matrix with $n\times n$ and the largest eigenvalue is ρ. Suppose that for a non-negative real vector $y\ne 0$ and a real coefficient polynomial function f, the inequality $f\left(A\right)y\le ry$ holds for some $r\in R$. Then it follows that $f\left(\rho \right)\le r$.

Lemma 3

([11]). Let G be a graph of n vertices. Then,

$$q_2\left(G\right)\le n-2.$$

If the equality holds, then the complement $\overline{G}$ of G has at least one bipartite component.

Lemma 4

([12]). Let G be a graph with second maximum degree ${\Delta }_2$. Then,

$$q_2\left(G\right)\ge {\Delta }_2-1.$$

If the equality holds if and only if ${\Delta }_1={\Delta }_2$ and $u\sim v$, where $d\left(u\right)={\Delta }_1$ and $d\left(v\right)={\Delta }_2$.

Lemma 5

([12]). Let G be any connected graph with n vertices. Then,

$$q_2\left(G\right)\ge {\displaystyle \frac{{\Delta }_1+{\Delta }_2-\sqrt{{({\Delta }_1-{\Delta }_2)}^2+4}}{2}}.$$

Lemma 6

([23]). Let G be a connected graph. Then,

$$q_1\left(G\right)\le \underset{v\in V\left(G\right)}{max}\{d\left(v\right)+m\left(v\right)\},$$

where $d\left(v\right)$ is the degree of vertex v and $m\left(v\right)$ is the average of the degrees of the adjacent vertices of vertex v. Moreover, the equality holds if and only if G is a regular graph or G is a bipartite semi-regular graph.

Lemma 7

([24]). Let G be any connected graph. For any vertex $v\in V\left(G\right)$, we have

$$q_{i+1}\left(G\right)-1\le q_i(G-v)\le q_i\left(G\right),$$

where $1\le i\le n-1$, and the first equality holds if, and only if, v is an isolated vertex.

Lemma 8

([25]). Supposing that G is a connected graph with n vertices and H is any subgraph of G obtained from deleting an edge $e\in E\left(G\right)$. Then we have

$$q_1\left(G\right)\ge q_1\left(H\right)\ge q_2\left(G\right)\ge q_2\left(H\right)\ge \cdots \ge q_n\left(G\right)\ge q_n\left(H\right)\ge 0,$$

where $q_i\left(G\right)$ is the i-th largest signless Laplacian eigenvalue of the graph G.

We start to give a technical lemma, which will be used to calculate eigenvalues. Suppose that M is a real matrix with order $n\times n$, and $\mathcal{N}=\{1,2,\dots ,n\}$. Let $\pi :\mathcal{N}={\mathcal{N}}_1\cup {\mathcal{N}}_2\cup \cdots \cup {\mathcal{N}}_k$, in correspondence, M can be written in block form as

$$M=\left(\begin{array}{cccc}{M}_{1,1}& M_{1,2}& \cdots & M_{1,k}\\ M_{2,1}& M_{2,2}& \cdots & M_{2,k}\\ ⋮& ⋮& \dots & ⋮\\ M_{k,1}& M_{k,2}& \cdots & M_{k,k}\end{array}\right),$$

where $M_{i,j}$ is the sub-matrix of M with respect to rows in ${\mathcal{N}}_i$ and columns in ${\mathcal{N}}_j$. Let $B_{\pi }=\left(b_{i,j}\right)$ denote the quotient matrix of M based on $\pi$, where $b_{i,j}$ is the average row sum of $M_{i,j}$. If every block $M_{i,j}$ of the partitioned matrix M satisfies rows in that block sharing a common row sum $b_{i,j}$, then we call $\pi$ an equitable matrix. When $\pi$ is an equitable partition of M, the corresponding quotient matrix is also referred to as equitable.

Lemma 9

([26]). Let M be a real symmetric matrix and $B_{\pi }$ be an equitable quotient matrix of M. Then $\sigma \left(B_{\pi }\right)\subseteq \sigma \left(M\right)$. And, if M is non-negative and indecomposable, then

$${\lambda }_1\left(M\right)={\lambda }_1\left(B_{\pi }\right).$$

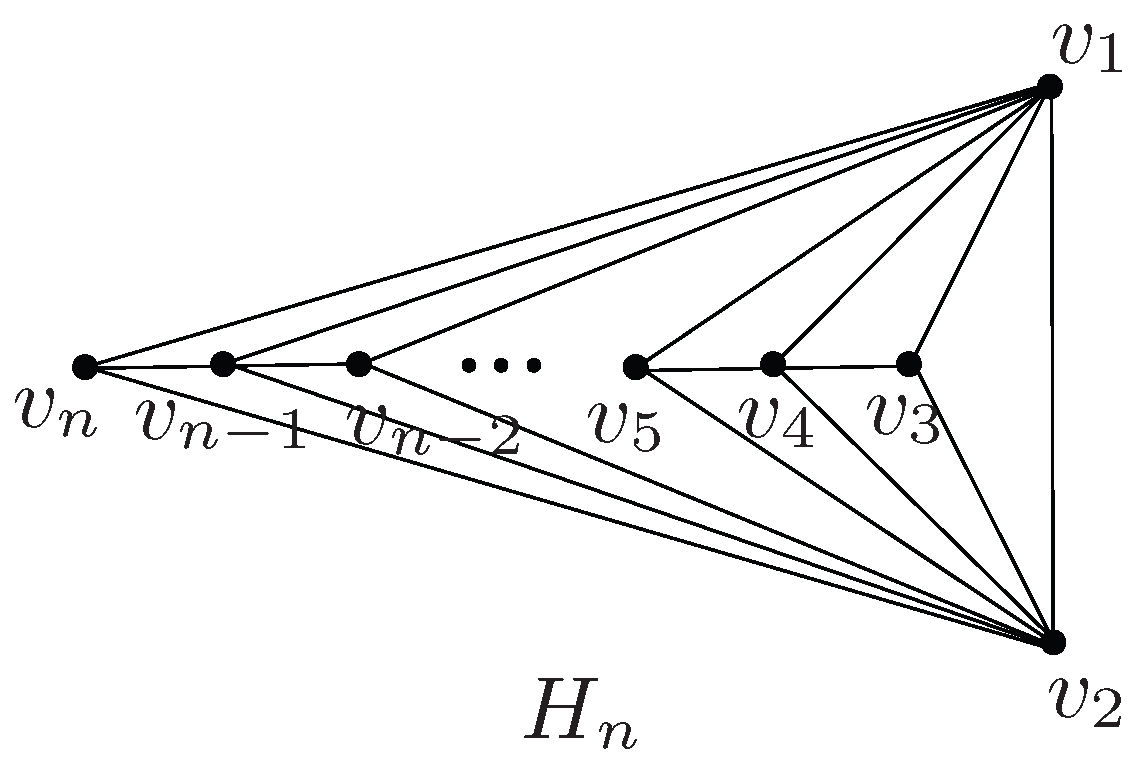
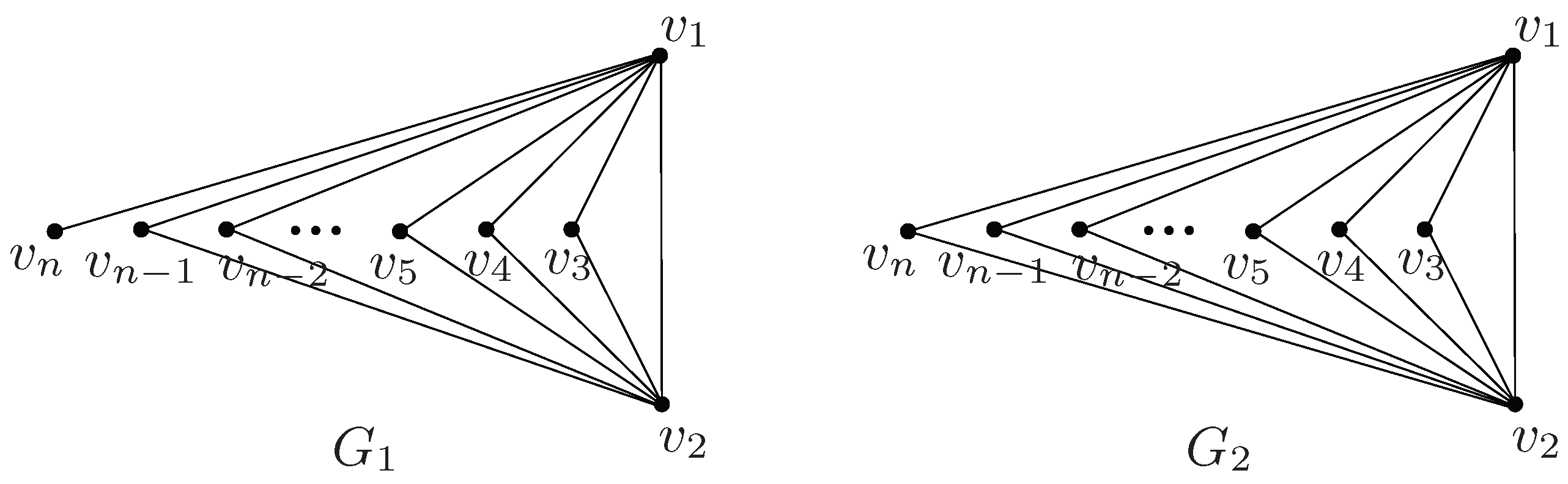
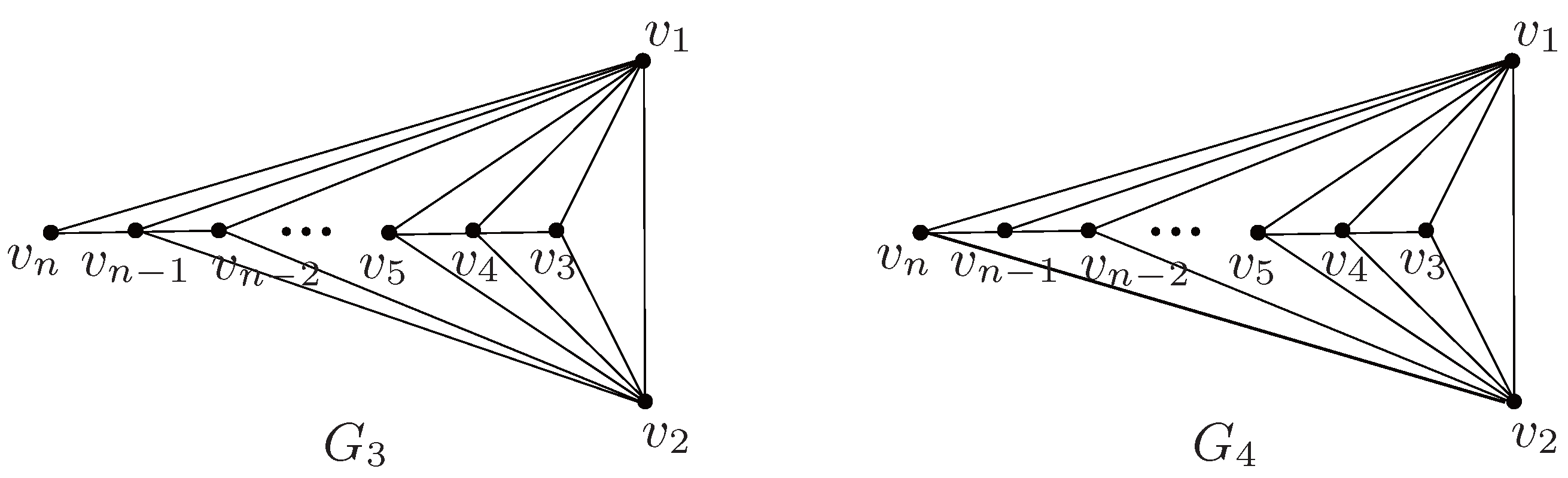
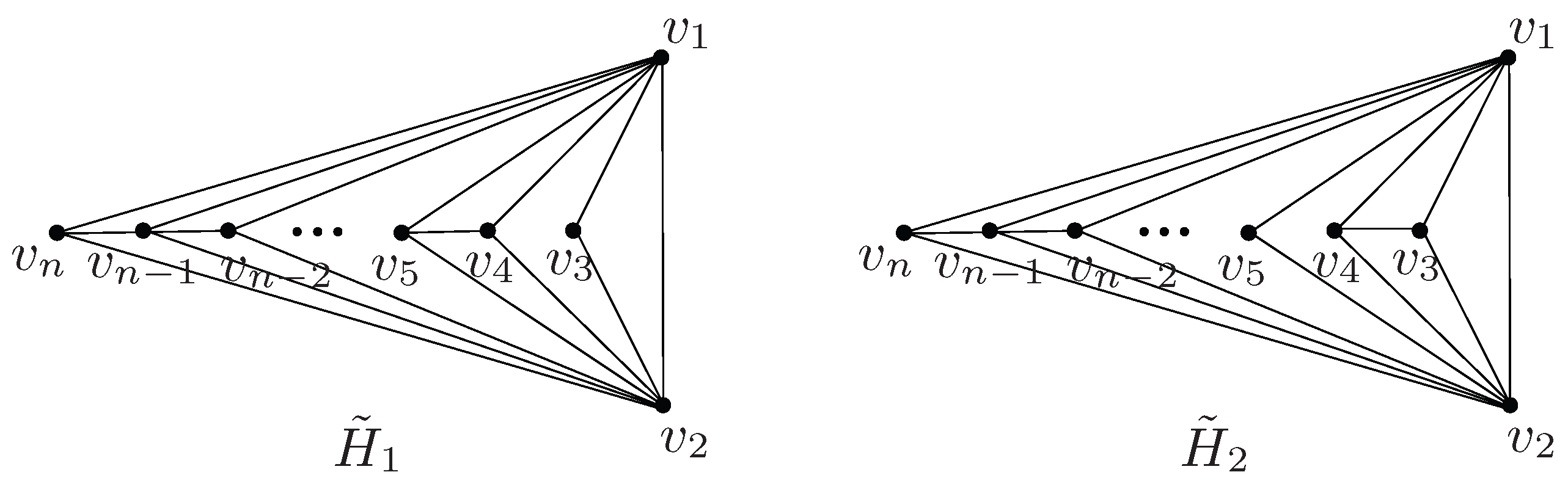
3. Ordering Planar Graphs by Q-Spectral Radius

This section characterizes all planar graphs with n vertices whose signless Laplacian spectral radius does not exceed $n+{\displaystyle \frac{9}{5}}$. Let ${\mathcal{P}}_n$ denote the set of all planar graphs on n vertices, and let ${\mathcal{H}}_i$ denote the set of all planar graphs with $\Delta \left(G\right)=n-1$ and ${\Delta }_2\left(G\right)=n-i$ $(i=1,2)$. Let ${\tilde{H}}_i$ denote the graph obtained from ${\mathcal{H}}_1$ by deleting an edge; without loss of generality, assume that ${\tilde{H}}_1$ denotes the graph obtained from ${\mathcal{H}}_1$ by deleting the edge $v_3{v}_4$ or $v_{n-1}{v}_n$ and ${\tilde{H}}_2$ denotes the graph obtained from ${\mathcal{H}}_1$ by deleting the edge $v_{k-1}{v}_k$ ($5\le k\le n-1$).

Lemma 10.

Let $n\ge 28$ and $G\in {\mathcal{P}}_n$ with $\Delta \left(G\right)\le n-3$. Then, we have $q_1\left(G\right)\le n+{\displaystyle \frac{3}{2}}$.

Proof. 

Suppose that $d\left(v_1\right)=\Delta \left(G\right)$, $d\left(v_2\right)={\Delta }_2\left(G\right)$ and $d\left(v_3\right)={\Delta }_3\left(G\right)$. Since G is a planar graph, we have $d\left(v_3\right)\le {\displaystyle \frac{n}{2}}+1$. Noting that ${\Delta }_2\left(G\right)+{\Delta }_3\left(G\right)\le n+2$. As a result, ${\sum }_{v\sim u}d\left(v\right)\le 3(n-3)+n+2=4n-7$. By Lemma 6, then we have

$$\begin{array}{ccc}\hfill d\left(u\right)+m\left(u\right)& =& d\left(u\right)+{\displaystyle \frac{{\sum }_{v\sim u}d\left(v\right)}{d\left(u\right)}}\hfill \\ & \le & max\{1+{\displaystyle \frac{n-4}{1}},2+{\displaystyle \frac{2(n-4)}{2}},n-3+{\displaystyle \frac{4n-7}{n-3}}\}\hfill \\ & \le & n+1+{\displaystyle \frac{12}{n-4}}\hfill \\ & \le & n+{\displaystyle \frac{3}{2}}.\hfill \end{array}$$

Proof completed. □

Lemma 11.

Assuming that G is a maximal planar graph with $n-2\le \Delta \left(G\right)\le n-1$, ${\Delta }_2\left(G\right)\le n-10$, we have $q_1\left(G\right)\le n+{\displaystyle \frac{9}{5}}$.

Proof. 

Let $d\left(u\right)=\Delta \left(G\right)$ and $d\left(v\right)={\Delta }_2\left(G\right)$. Supposing that $X={(x_1,x_2,\dots ,x_n)}^T\in R$ is a positive vector, then

$$x_i=\left\{\begin{array}{cc}1,\hfill & i=1;\hfill \\ {\displaystyle \frac{2}{3k}},\hfill & i=2;\hfill \\ {\displaystyle \frac{2}{(n-k-1)}},\hfill & 3\le i\le n.\hfill \end{array}\right.$$

For vertex u, if $d\left(u\right)=n-1$, we have

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d\left(u\right)x_1+{\sum }_{w\in N\left(u\right)}{x}_j}{x_1}}& \le & d\left(u\right)+{\displaystyle \frac{{\sum }_{w\in N\left(u\right)}{x}_j}{x_1}}\hfill \\ & \le & n-1+{\displaystyle \frac{2(k-1)}{3k}}+{\displaystyle \frac{2(n-k-2)}{(n-k-1)}}\hfill \\ & \le & n+{\displaystyle \frac{9}{5}}.\hfill \end{array}$$

If $d\left(u\right)=n-2$, then

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d\left(u\right)x_1+{\sum }_{w\in N\left(u\right)}{x}_j}{x_1}}& \le & d\left(u\right)+{\displaystyle \frac{{\sum }_{w\in N\left(u\right)}{x}_j}{x_1}}\hfill \\ & \le & n-2+{\displaystyle \frac{2(k-1)}{3k}}+{\displaystyle \frac{2(n-k-2)}{(n-k-1)}}\hfill \\ & \le & n+{\displaystyle \frac{9}{5}}.\hfill \end{array}$$

For vertex v,

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d\left(v\right)x_i+{\sum }_{w\in N\left(v\right)}{x}_j}{x_i}}& \le & d\left(v\right)-1+{\displaystyle \frac{x_1+{\sum }_{w\in N\left(v\right)}{x}_j}{x_2}}\hfill \\ & \le & d\left(v\right)-1+{\displaystyle \frac{{\sum }_{j=1}^{k+1}{x}_j+\frac{2d\left(v\right)-2k-2}{n-k-1}}{\frac{2}{3k}}}\hfill \\ & \le & d\left(v\right)-1+{\displaystyle \frac{5k}{2}}+{\displaystyle \frac{3kd\left(v\right)-3k^2-3k}{n-k-1}}.\hfill \end{array}$$

Let $f\left(k\right)=d\left(v\right)-1+{\displaystyle \frac{5k}{2}}+{\displaystyle \frac{5k(d\left(v_i\right)-k-1)}{2(n-k-1)}}.$ Differentiating $f\left(k\right)$ with based on k, we have

$$f^{\prime }\left(k\right)={\displaystyle \frac{5\left[n^2-2n+1+nd\left(v_i\right)-d\left(v_i\right)-n+1-4nk+4k+2k^2\right]}{2{(n-k-1)}^2}}.$$

Thus we have $f^{\prime }\left(k\right)>0$, and $f\left(k\right)$ is monotone increasing with k. Since $d\left(v_2\right)\le n-10$, we have

$$d\left(v\right)-1+{\displaystyle \frac{5k}{2}}+{\displaystyle \frac{5kd\left(v\right)-5k^2-5k}{2(n-k-1)}}\le n+{\displaystyle \frac{9}{5}}.$$

For $v_i$ ($3\le i\le n$). Thus we have

$${\displaystyle \frac{d\left(v_i\right)x_i+{\sum }_{v_j\sim v_i}{x}_j}{x_i}}\le \left\{\begin{array}{c}d\left(v_i\right)+{\displaystyle \frac{{\sum }_{j=1}^{k+1}{x}_j+\frac{2(d\left(v_i\right)-k-1)}{n-k-1}}{\frac{2}{n-k-1}}}\le n+{\displaystyle \frac{9}{5}},\hfill \\ d\left(v_i\right)+{\displaystyle \frac{1+\frac{2(d\left(v_i\right)-1)}{n-k-1}}{\frac{2}{n-k-1}}}\le n+{\displaystyle \frac{9}{5}}.\hfill \end{array}\right.$$

Based on the discussion, we have $Q\left(G\right)X\le (n+{\displaystyle \frac{9}{5}})X$. Thus, according to Lemma 2, we have $q_1\left(G\right)\le n+{\displaystyle \frac{9}{5}}$. Proof completed. □

Lemma 12.

Let $n\ge 314$ and $G\in {\mathcal{P}}_n$ with $\Delta \left(G\right)=n-2$ and $n-9\le {\Delta }_2\left(G\right)\le n-2$. Then we have $q_1\left(G\right)\le n+{\displaystyle \frac{9}{5}}$.

Proof. 

Suppose that $d\left(u\right)=\Delta \left(G\right)\le n-2$ and $d\left(v\right)={\Delta }_2\left(G\right)$. If $n-9\le {\Delta }_2\left(G\right)\le n-3$, then let $X={(x_1,x_2,\dots ,x_n)}^T\in R$ be a positive vector, where

$$x_i=\left\{\begin{array}{cc}1,\hfill & i=1;\hfill \\ {\displaystyle \frac{4}{5}},\hfill & i=2;\hfill \\ {\displaystyle \frac{10}{5(n-2)}},\hfill & 3\le k\le n.\hfill \end{array}\right.$$

For u, we have

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d\left(u\right)x_1+{\sum }_{w\in N\left(u\right)}{x}_j}{x_1}}& \le & {\displaystyle \frac{d\left(u\right)x_1+{\sum }_{w\in N\left(u\right)}{x}_j}{x_1}}\hfill \\ & \le & n-2+{\displaystyle \frac{4}{5}}+{\displaystyle \frac{10n-30}{5n-10}}\hfill \\ & \le & n+{\displaystyle \frac{4}{5}}.\hfill \end{array}$$

For v, we have

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d\left(v\right)x_2+{\sum }_{w\sim N\left(v\right)}{x}_j}{x_2}}& \le & {\displaystyle \frac{(n-3)x_2+{\sum }_{w\sim N\left(v\right)}{x}_j}{x_2}}\hfill \\ & \le & n-3+{\displaystyle \frac{1+\frac{10n-40}{5n-10}}{\frac{4}{5}}}\hfill \\ & \le & n+{\displaystyle \frac{4}{5}}.\hfill \end{array}$$

For $v_i$ ($3\le i\le n$), since $n-9\le {\Delta }_2\left(G\right)\le n-3$, we have $d\left(v_i\right)\le 18$. Thus,

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d\left(v_i\right)x_i+{\sum }_{v_j\sim v_i}{x}_j}{x_i}}& \le & d\left(v_i\right)+{\displaystyle \frac{\frac{9}{5}+\frac{10(d\left(v_i\right)-2)}{5(n-2)}}{\frac{10}{5(n-2)}}}\hfill \\ & \le & 2d\left(v_i\right)-2+{\displaystyle \frac{9(n-2)}{10}}\hfill \\ & \le & n+{\displaystyle \frac{4}{5}}.\hfill \end{array}$$

Based on the discussion, we obtain $Q\left(G\right)X\le (n+{\displaystyle \frac{4}{5}})X$. Thus, according to Lemma 2, we have $q_1\left(G\right)\le n+{\displaystyle \frac{4}{5}}$.

For ${\Delta }_2\left(G\right)=n-2$, let $X={(x_1,x_2,\dots ,x_n)}^T\in R$ be a positive vector, where

$$x_i=\left\{\begin{array}{cc}1,\hfill & i=1;\hfill \\ 1,\hfill & i=2;\hfill \\ {\displaystyle \frac{11}{4(n-2)}},\hfill & 3\le k\le n.\hfill \end{array}\right.$$

If $v_1\sim v_2$, similar to the above discussion, we have $q_1\left(G\right)\le n+{\displaystyle \frac{9}{5}}$. Otherwise, similar to the above discussion, we have $q_1\left(G\right)\le n+{\displaystyle \frac{4}{5}}$. Proof completed. □

Lemma 13.

Supposing that $G\in {\mathcal{P}}_n$ with $n\ge 380$, let $\Delta \left(G\right)=n-1$, $n-9\le {\Delta }_2\left(G\right)\le n-3$. We have $q_1\left(G\right)\le n+{\displaystyle \frac{7}{5}}$.

Proof. 

Assuming that $d\left(v_1\right)=\Delta \left(G\right)$ and $d\left(v_2\right)={\Delta }_2\left(G\right)$. Let $X={(x_1,x_2,\dots ,x_n)}^T\in R$ be a positive vector, where

$$x_i=\left\{\begin{array}{cc}1,\hfill & i=1;\hfill \\ {\displaystyle \frac{5}{8}},\hfill & i=2;\hfill \\ {\displaystyle \frac{14}{8(n-2)}},\hfill & 3\le k\le n.\hfill \end{array}\right.$$

For $v_1$, we have

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d\left(v_1\right)x_1+{\sum }_{w\in N\left(v_1\right)}{x}_j}{x_1}}& \le & {\displaystyle \frac{d\left(v_1\right)x_1+{\sum }_{w\in N\left(v_1\right)}{x}_j}{x_1}}\hfill \\ & \le & n-1+{\displaystyle \frac{5}{8}}+{\displaystyle \frac{14(n-2)}{8(n-2)}}\hfill \\ & \le & n+{\displaystyle \frac{7}{5}}.\hfill \end{array}$$

For $v_2$, we have

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d\left(v_2\right)x_2+{\sum }_{v_j\sim v_2}{x}_j}{x_2}}& \le & {\displaystyle \frac{(n-3)x_2+{\sum }_{v_j\sim v_1}{x}_j}{x_2}}\hfill \\ & \le & n-3+{\displaystyle \frac{1+\frac{14(n-4)}{8(n-2)}}{\frac{5}{8}}}\hfill \\ & \le & n+{\displaystyle \frac{7}{5}}.\hfill \end{array}$$

For $v_i$ ($3\le i\le n$), since $n-9\le {\Delta }_2\left(G\right)\le n-3$, we have $d\left(v_i\right)\le 18$. Thus,

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d\left(v_i\right)x_i+{\sum }_{v_j\sim v_i}{x}_j}{x_i}}& \le & d\left(v_i\right)+{\displaystyle \frac{\frac{13}{8}+\frac{14(d\left(v_i\right)-2)}{8(n-2)}}{\frac{14}{8(n-2)}}}\hfill \\ & \le & 2d\left(v_i\right)-2+{\displaystyle \frac{13(n-2)}{14}}\hfill \\ & \le & n+{\displaystyle \frac{7}{5}}.\hfill \end{array}$$

Based on the discussion above, we have $Q\left(G\right)X\le (n+{\displaystyle \frac{7}{5}})X$. Thus, according to Lemma 2, we have $q_1\left(G\right)\le n+{\displaystyle \frac{7}{5}}$. Proof completed. □

Lemma 14.

Let $n\ge 398$ and $G\in {\mathcal{P}}_n$ with $\Delta \left(G\right)=n-1$ and $n-2\le {\Delta }_2\left(G\right)\le n-1$. Then,

(i) 

$n+{\displaystyle \frac{7}{5}}<q_1\left(G\right)<n+{\displaystyle \frac{9}{5}}$ for $G\in {\mathcal{H}}_2$;

(ii) 

$n+{\displaystyle \frac{19}{10}}<q_1\left(G\right)<q_1\left({\tilde{H}}_2\right)<q_1\left({\tilde{H}}_1\right)<q_1\left(H_n\right)$ for $G\in {\mathcal{H}}_1\setminus \{{\tilde{H}}_1,{\tilde{H}}_2,H_n\}$.

Proof. 

For $G\in {\mathcal{H}}_2$, $G_1$ must be the planar graph with the minimum edges in ${\mathcal{H}}_2$. It is easy to see that

$$Q\left(G_1\right)=\left(\begin{array}{cccccc}n-1& 1& 1& 1& \cdots & 1\\ 1& n-2& 0& 1& \cdots & 1\\ 1& 0& 1& 0& \cdots & 0\\ 1& 1& 0& 2& \cdots & 0\\ ⋮& ⋮& ⋮& ⋮& \dots & ⋮\\ 1& 1& 0& 0& \cdots & 2\end{array}\right).$$

Let $d\left(v_1\right)=d\left(v_2\right)=n-1$ and $d\left(v_3\right)=1$; the graph $G_1$ has an obvious vertex partition $V\left(G_1\right)=\{v_1,v_2,v_3,V\left(G_1\right)\setminus \{v_1,v_2,v_3\}\}$. And the corresponding quotient matrix of $Q\left(G_1\right)$ is

$$B\left(G_1\right)=\left(\begin{array}{cccc}n-1& 1& 1& n-3\\ 1& n-2& 0& n-3\\ 1& 0& 1& 0\\ 1& 1& 0& 2\end{array}\right).$$

We know the characteristic polynomial of $B\left(G_1\right)$ is as follows:

$$f_1\left(x\right)=x^4-2n{x}^3+(n^2+n-1)x^2+(-n^2-3n+12)x+4n-12.$$

Since $f_1(n+{\displaystyle \frac{7}{5}})=-0.64n^2+16.448n+6.6816\le 0$ when $n\ge 27$ and $f_1(n+2)>0$, it follows that $n+{\displaystyle \frac{7}{5}}<q_1\left(B\left(G_1\right)\right)<n+2$. And by Lemma 8, it follows that $q_1\left(G\right)>n+{\displaystyle \frac{7}{5}}$ for $G\in {\mathcal{H}}_2$.

Next consider the maximum planar graph with $\Delta \left(G\right)=n-1$ and ${\Delta }_2\left(G\right)=n-2$. Let $X={(x_1,x_2,\dots ,x_n)}^T\in R$ be a positive vector, where

$$x_i=\left\{\begin{array}{cc}1,\hfill & i=1;\hfill \\ {\displaystyle \frac{4}{5}},\hfill & i=2;\hfill \\ {\displaystyle \frac{2}{(n-2)}},\hfill & 3\le k\le n.\hfill \end{array}\right.$$

Similarly to Lemma 13, we have $q_1\left(G\right)\le n+{\displaystyle \frac{9}{5}}$ by Lemma 2. Thus we have $n+{\displaystyle \frac{7}{5}}<q_1\left(G\right)\le n+{\displaystyle \frac{9}{5}}$ for any $G\in {\mathcal{H}}_2$.

For $G\in {\mathcal{H}}_1$, the planar graph $G_2$, as shown in Figure 2, must be the planar graph with the smallest edges in ${\mathcal{H}}_1$. It is easy to see that

$$Q\left(G_2\right)=\left(\begin{array}{ccccc}n-1& 1& 1& \cdots & 1\\ 1& n-1& 1& \cdots & 1\\ 1& 1& 2& \cdots & 0\\ ⋮& ⋮& ⋮& \dots & ⋮\\ 1& 1& 0& \cdots & 2\end{array}\right).$$

Let $d\left(v_1\right)=d\left(v_2\right)=n-1$; the graph $G_2$ has an obvious partition $V\left(G_2\right)=\{\{v_1,v_2\},$ $V\left(G_2\right)\setminus \{v_1,v_2\}\}$. And the corresponding quotient matrix of $Q\left(G_2\right)$ is

$$B\left(G_2\right)=\left(\begin{array}{cc}n& n-2\\ 2& 2\end{array}\right).$$

We have the characteristic polynomial of $B\left(G_2\right)$ is as follows:

$$f_2\left(x\right)=x^2+(-n-2)x+4.$$

Since $f(n+{\displaystyle \frac{19}{10}})<0$, and $f(n+2)>0$, it follows that $n+{\displaystyle \frac{19}{10}}<q_1\left(B\left(G_2\right)\right)<n+2$. By Lemma 9, we have $n+{\displaystyle \frac{19}{10}}<q_1\left(G_2\right)<n+2$. And by Lemma 8, it follows that $q_1\left(G\right)>n+{\displaystyle \frac{19}{10}}$ for any $G\in {\mathcal{H}}_1$.

Next consider the graph $H_n-e\subseteq {\mathcal{H}}_1$. If ${\Delta }_2(H_n-e)=n-2$, as shown in Figure 3, from the above discussion, we have $q_1(H_n-e)<n+{\displaystyle \frac{9}{5}}$. If $e\in E(G-\{v_1,v_2\})$ and $e=v_3{v}_4$ or $e=v_{n-1}{v}_n$, then we have $H_n-e\cong {\tilde{H}}_1$. If $e\in E(G-\{v_1,v_2\})$ and $e=v_{k-1}{v}_k$ ($5\le k\le n-1$), then we have $H_n-e\cong {\tilde{H}}_2$, as shown in Figure 4.

Let $X={(x_1,x_2,\dots ,x_n)}^T\in R^n$ be the Perron eigenvector of $Q({\tilde{H}}_1)$. For $e=v_3{v}_4$ and $k=5$. Note that

$$q({\tilde{H}}_1)x_{k-1}=3x_{k-1}+x_k+x_1+x_2.$$

(1)

$$q({\tilde{H}}_1)x_k=4x_k+x_{k-1}+x_{k+1}+x_1+x_2.$$

(2)

From Equations (1) and (2), we obtain

$$q({\tilde{H}}_1)(x_{k-1}+x_k)=5x_k+4x_{k-1}+2x_1+2x_2.$$

(3)

Note that

$$q({\tilde{H}}_1)x_4=3x_4+x_3+x_1+x_2.$$

(4)

$$q({\tilde{H}}_1)x_3=2x_3+x_1+x_2.$$

(5)

From Equations (4) and (5), we get

$$q({\tilde{H}}_1)(x_3+x_4)=3x_3+3x_4+2x_1+2x_2.$$

(6)

From Equations (3) and (6), we get

$$(q({\tilde{H}}_1)-3)[(x_k+x_{k-1})-(x_3+x_4)]=2x_k+x_{k-1}.$$

It follows that $x_k+x_{k-1}>x_3+x_4$.

For $e=v_3{v}_4$ and $6\le k\le n-1$, similar to the above discussion, we have

$$(q({\tilde{H}}_1)-3)[(x_k+x_{k-1})-(x_3+x_4)]=2x_k+2x_{k-1}+x_{k+1}+x_{k+2}.$$

It follows that $x_k+x_{k-1}>x_3+x_4$.

Let $H={\tilde{H}}_1-v_{k-1}{v}_k+v_3{v}_4$. Note that

$$X^{T}Q({\tilde{H}}_1)X-X^{T}Q\left(H\right)X={(x_k+x_{k-1})}^2-{(x_3+x_4)}^2.$$

It follows that $q({\tilde{H}}_1)=X^{T}Q({\tilde{H}}_1)X>X^{T}Q(H)X=q(H)$. Since $H\cong {\tilde{H}}_2$, we have $q({\tilde{H}}_1)>q({\tilde{H}}_2)$. For $e=v_{n-1}{v}_n$, by an argument similar to the above, we have $q_1({\tilde{H}}_1)>q_1({\tilde{H}}_2)$. By Lemmas 1 and 8, we have $n+{\displaystyle \frac{19}{10}}\le q_1\left(G\right)\le q_1({\tilde{H}}_2)\le q_1({\tilde{H}}_1)\le q_1(H_n)$ for $G\in {\mathcal{H}}_1\setminus \{{\tilde{H}}_1,{\tilde{H}}_2,H_n\}$. Proof completed. □

Theorem 1.

Let G be a planar graph of order $n\ge 398$. If $G\in {\mathcal{P}}_n\setminus \{{\tilde{H}}_1,{\tilde{H}}_2,H_n\}$, then we have

$$q_1\left(G\right)<q_1\left({\tilde{H}}_2\right)<q_1\left({\tilde{H}}_1\right)<q_1\left(H_n\right),$$

where $H_n=K_2\vee P_{n-2}$.

Proof. 

The result follows immediately from Lemmas 10–14. □

Corollary 1.

Let $n\ge 398$ and $G\in {\mathcal{P}}_n\setminus \{{\tilde{H}}_1,{\tilde{H}}_2,H_n\}$. Then,

$$S_2\left(G\right)\le S_2({\tilde{H}}_2)<S_2({\tilde{H}}_1)<S_2\left(H_n\right)<2n+1,$$

where $H_n=K_2\vee P_{n-2}$.

Proof. 

Assuming that $d\left(v_1\right)=\Delta \left(G\right)$ and $d\left(v_2\right)={\Delta }_2\left(G\right)$, we consider the following two cases:

Case 1. $\Delta \left(G\right)\le n-2$.

If ${\Delta }_2\left(G\right)\le n-3$, by Lemma 3, then we have $q_2\left(G\right)\le n-2$. By Theorem 1, we have $q_1\left(G\right)\le n+{\displaystyle \frac{9}{5}}$. Thus we have $S_2\left(G\right)=q_1\left(G\right)+q_2\left(G\right)\le 2n-{\displaystyle \frac{6}{5}}$. If ${\Delta }_2\left(G\right)=n-2$ and $v_1\sim v_2$, by Lemma 4, then we have $q_2\left(G\right)=n-3$. By Lemma 12, we have $q_1\left(G\right)\le n+{\displaystyle \frac{9}{5}}$. Thus we have $S_2\left(G\right)=q_1\left(G\right)+q_2\left(G\right)\le 2n-{\displaystyle \frac{6}{5}}$. Otherwise, by Lemma 3, we have $q_2\left(G\right)\le n-2$. By Lemma 14, we have $q_1\left(G\right)\le n+{\displaystyle \frac{9}{5}}$. Thus we have $S_2\left(G\right)=q_1\left(G\right)+q_2\left(G\right)\le 2n-{\displaystyle \frac{1}{5}}$.

Case 2. $\Delta \left(G\right)=n-1$.

If $n-9\le {\Delta }_2\left(G\right)\le n-3$, consider the subgraph H of G where $H=G-v_1$. Let $X={(x_1,x_2,\dots ,x_n)}^T\in R$ be a positive vector, where

$$x_i=\left\{\begin{array}{cc}{\displaystyle \frac{5}{8}},\hfill & i=1;\hfill \\ {\displaystyle \frac{2}{3(n-2)}},\hfill & 2\le k\le n.\hfill \end{array}\right.$$

Similarly to the above discussion, we have $q_1\left(H\right)\le n-{\displaystyle \frac{37}{10}}$. By Lemma 7, we have $q_2\left(G\right)\le n-{\displaystyle \frac{27}{10}}$. By Lemma 13, we have $q_1\left(G\right)\le n+{\displaystyle \frac{7}{5}}$. Thus, we have $S_2\left(G\right)=q_1\left(G\right)+q_2\left(G\right)\le 2n-{\displaystyle \frac{13}{10}}$.

If ${\Delta }_2\left(G\right)=n-2$, by Lemmas 3 and 5, we have $n-{\displaystyle \frac{13}{5}}\le q_2\left(G\right)\le n-2$. By Lemma 14, we have $n+{\displaystyle \frac{7}{5}}<q_1\left(G\right)<n+{\displaystyle \frac{9}{5}}$. It follows that $2n-{\displaystyle \frac{6}{5}}<S_2\left(G\right)=q_1\left(G\right)+q_2\left(G\right)<2n-{\displaystyle \frac{1}{5}}$.

If ${\Delta }_2\left(G\right)=n-1$, by Lemma 3, we have $q_2\left(G\right)=n-2$ for any $G\in {\mathcal{H}}_1$. By Lemma 14, we have $n+{\displaystyle \frac{19}{10}}<q_1\left(G\right)<q_1({\tilde{H}}_2)<q_1({\tilde{H}}_1)<q_1\left(H_n\right)$ for any $G\in {\mathcal{H}}_1\setminus \{{\tilde{H}}_1,{\tilde{H}}_2,H_n\}$. It follows that $2n-{\displaystyle \frac{1}{10}}<S_2\left(G\right)<S_2({\tilde{H}}_2)<S_2({\tilde{H}}_1)<S_2\left(H_n\right)$ for any $G\in {\mathcal{H}}_1\setminus \{{\tilde{H}}_1,{\tilde{H}}_2,H_n\}$.

From Lemma 1, $S_2\left(G\right)<S_2({\tilde{H}}_2)<S_2({\tilde{H}}_1)<S_2\left(H_n\right)<2n+1$ where $G\in {\mathcal{H}}_i\setminus \{{\tilde{H}}_2,{\tilde{H}}_1,H_n\}$$(i=1,2)$. This completes the proof. □

4. Conclusions

In this paper, we establish a full ordering of planar graphs according to their signless Laplacian spectral radii with $n\ge 398$. The main results are as follows:

1.

The graph $H_n$ has the largest signless Laplacian eigenvalues. The graphs ${\widehat{H}}_1$ and ${\widehat{H}}_2$, which are derived by removing specific edges from $H_n$, achieve the second and third largest $q_1$, respectively.

2.

As for the application, we determine the planar graphs with the first three largest sums of the first and second largest signless Laplacian eigenvalues $S_2$. The order of $S_2$ matches with that of $q_1$, and we give explicit upper bounds that refine existing conjectures for planar graphs.

And these results help with the extreme spectral theory for planar graphs and strategize about how structural constraints affect spectral invariants. Future work might look at similar ordering issues for smaller n or different spectral matrices.