1. Introduction
Recently, the development of flexible lifetime distributions has become increasingly important for accurately modeling real-world phenomena, particularly in reliability and survival analysis. Among these, the Chris–Jerry (CJ(
)) distribution, introduced by Onyekwere and Obulezi [
1], has emerged as a valuable contribution to the statistical literature. Its density can take unimodal or decreasing shapes, while its hazard function can exhibit a bathtub shape. This model is notable for its ability to capture positively skewed data, enhancing its applicability across a wide range of practical scenarios. It also provides closed-form expressions for its probability density and cumulative distribution functions, which facilitate both theoretical derivations and computational implementation. This flexibility makes the CJ distribution particularly suitable for modeling failure times in engineering systems and biomedical studies. Furthermore, its structure supports effective parameter estimation using both classical and Bayesian methods, even under complex censoring schemes, as demonstrated by Alotaibi et al. [
2]. These properties underscore the CJ distribution’s potential as a robust and versatile tool in statistical inference and reliability analysis.
Let
Y be a non-negative continuous random variable representing a lifetime. If
Y∼
with
, then the probability density function (PDF) and cumulative distribution function (CDF) of
Y are given by
and
respectively.
The corresponding reliability function (RF) and hazard rate function (HRF), denoted by
and
, at a mission time
, are given, respectively, by
and
Progressive Type-II censoring (T2-PC) has been widely used in reliability and survival analysis because of its advantages over conventional Type-II censoring (T2-C). One key benefit is the flexibility to remove functioning experimental units during the study, which is particularly valuable in industrial reliability assessments and clinical trials. In a typical T2-PC setup, suppose
m failures are observed among
n identical test units, where
. A predetermined censoring scheme
is specified before the experiment. At the first failure time, denoted
, a randomly chosen
units are withdrawn from the remaining
units. After the second failure,
, another
units are removed from the remaining
units, and this process continues. After the
m-th failure, all remaining units corresponding to
are censored, thus completing the experiment; see Balakrishnan and Cramer [
3].
Within the hybrid censoring framework, Kundu and Joarder [
4] introduced the progressive Type-I hybrid censoring (T1-PHC) scheme. Under this design,
n units are observed according to a fixed progressive censoring plan
, and the experiment terminates at
, where
t is a pre-specified time threshold. However, a key limitation of the T1-PHC scheme is the potential for a reduced observed sample size, which can compromise the efficiency of inferential procedures. To address this issue, Ng et al. [
5] proposed the adaptive T2-PC (T2-APC) scheme, which improves estimation precision. In this design, the number of failures
m is predetermined, and although a censoring scheme
is initially specified, its elements can be adaptively modified during the course of the experiment. The sampling structure follows that of the T2-PC, but the stopping criterion is adjusted to enhance practical applicability.
Nonetheless, if the test units exhibit very long survival times, the overall experiment duration under the T2-APC design may become impractically long. To overcome this limitation, Yan et al. [
6] recently proposed the improved T2-APC (IT2-APC) scheme. This approach generalizes both the T1-PHC and T2-APC designs and introduces two time thresholds,
and
, where
, thereby imposing an upper bound on the total test duration. The IT2-APC retains the progressive unit-removal mechanism of the T2-PC, with
m planned failures from a total of
n test units under a censoring scheme
. After the first failure time,
, a random selection of
units is withdrawn from the remaining
units. Subsequent failures trigger the removal of
units based on the updated risk set. Let
denote the number of observed failures by time
, and similarly, let
represent the number of observed failures by time
. Depending on when the experiment terminates, the observed data will correspond to one of the next several censoring scenarios:
Case-1: As , stop the test at .
Case-2: As , reset as , stop the test at .
Case-3: As , reset as , stop the test at .
Let
be the observed sample of size
obtained under an IT2-APC scheme from a continuous population with PDF
and CDF
. The joint likelihood function (LF) of
for this sample can be written as
where
and
A is a term free of parameter(s). To distinguish,
Table 1 explains the binary operators of the IT2-APC scheme represented in the LF (
5).
It is important to note that several well-known censoring schemes can be obtained as special cases of the IT2-APC design, including the following:
The T1-PHC, proposed by Kundu and Joarder [
4], when
;
The T2-APC, proposed by Ng et al. [
5], when
;
The T2-PC, described by Balakrishnan and Cramer [
3], when
;
The T2-C, described by Bain and Engelhardt [
7], when
,
for
, and
.
Essentially, the threshold
serves as an early warning of the progress of the experiment, while the threshold
indicates the absolute maximum allowable duration of the study. If the threshold
is reached before a pre-specified number of failures
m occurs, the experiment is terminated at
. This modification addresses the limitation of the T2-APC design proposed by Ng et al. [
5], in which the total test duration was not guaranteed. By introducing the upper bound
, the IT2-APC strategy ensures that the total experiment time will not exceed this limit. In the literature, several works have dealt with this censoring plan, including the Weibull distribution (Nassar and Elshahhat [
8]), Burr Type-III (Asadi et al. [
9]), Nadarajah–Haghighi (El-Sherpieny et al. [
10]), and the power half-normal (Alqasem and Elshahhat [
11]).
The rapid advancement of technology and digital systems has increased the demand for censoring schemes that are both flexible and computationally efficient, particularly for analyzing modern reliability data characterized by bounded measures such as proportions or failure rates. Recent developments in lifetime data analysis highlight the importance of adaptable censoring strategies supported by computationally intensive Bayesian inference techniques. These insights reflect the growing need for robust methodologies that can effectively handle small sample data, high levels of oversight, and application-based reliability studies in engineering, biomedical sciences, and physical sciences. Although the CJ distribution is structurally simple, its key advantage is its ability to capture bathtub-shaped hazard behavior. Censored observations, particularly those arising from the IT2-APC design, are common due to cost and time constraints, underscoring the need for adaptive censoring strategies. Integrating the CJ model with this censoring mechanism enhances both the precision and reliability of lifetime data analysis. Under the IT2-APC framework, this study is conducted with the following key objectives:
To estimate the model parameter , as well as the RF and HRF , for the CJ distribution using both maximum likelihood and Bayesian approaches.
To construct confidence intervals for the parameters of interest based on the asymptotic properties of the maximum likelihood estimators (MLEs) and log-transformed MLEs (log-MLEs).
To derive the Bayesian estimates, highest posterior density (HPD) intervals, and Bayesian credible intervals (BCIs) for , , and via Markov chain Monte Carlo (MCMC) methods.
To implement the estimation procedures in the R programming environment (version 4.2.2) using the maxLik package (Henningsen and Toomet [
12]) for likelihood optimization and the coda package (Plummer et al. [
13]) for MCMC diagnostics.
To assess the accuracy and efficiency of the proposed estimators through comprehensive simulation studies and multiple performance metrics.
To demonstrate the practical applicability of the CJ distribution by analyzing two real-world datasets from physics and engineering sectors.
The remainder of this paper is organized as follows:
Section 2 and
Section 3 present the frequentist and Bayesian estimation methods, respectively. Simulation results are discussed in
Section 4, and two real-data applications are analyzed in
Section 5. Finally,
Section 6 summarizes the main findings and provides concluding remarks.
2. Likelihood Inference
This section focuses on the estimation of the MLEs for the CJ parameters
,
, and
. The
ACIs for
,
, and
are derived using the observed Fisher information (FI) matrix together with the delta method. Using (
1), (
2), and (
5), we can rewrite (
5) as follows:
where
,
, and
. The corresponding log-LF of (
6) becomes
Subsequently, the MLE of
, denoted by
, is obtained by maximizing (
7) and solving the following nonlinear normal equation:
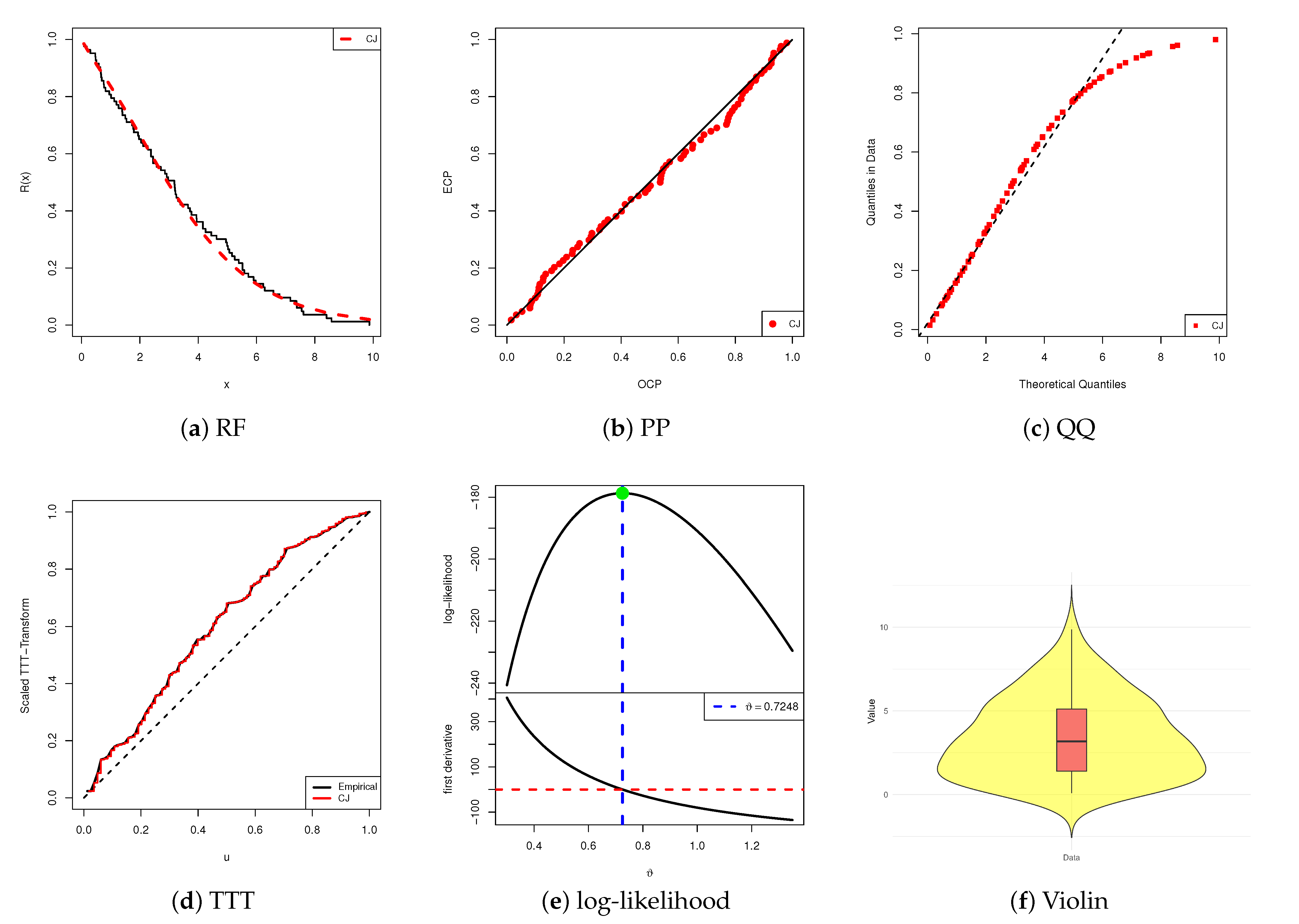
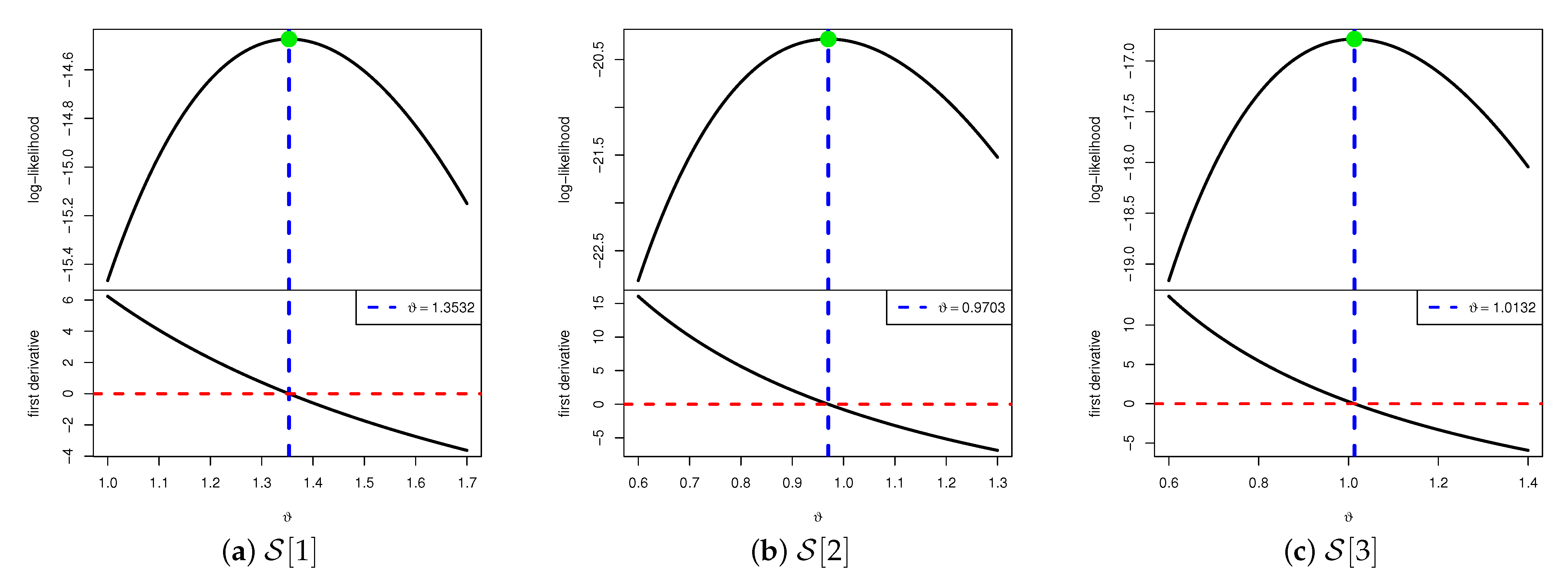
We now investigate the existence and uniqueness of
numerically by simulating an IT2-APC sample from the CJ distribution with parameters
, under the setup
,
,
, and a uniformly T2-PC scheme. The numerical results yield MLEs of
as 0.9947 and 1.3542 for
, respectively.
Figure 1 displays the log-LF defined in (
7) and the score function given in (
8), plotted as functions of
over a selected range. As shown, the vertical line representing the MLE of
intersects the log-LF curve at its maximum and intersects the score function at zero. These observations confirm that, for each value of
, the MLE exists and is unique.
The MLEs of RF and HRF, denoted
and
(for
), are obtained by substituting
into Equations (
2) and (
4), yielding
By applying the Newton–Raphson (NR) algorithm through the maxLik package in the R environment, the estimates , , and can be efficiently computed.
In addition to the point estimates, constructing the
ACIs for the parameters
,
, and
is of practical importance. Leveraging the asymptotic properties of the MLE
, these ACIs can be derived as follows. Specifically, the asymptotic distribution of
is approximately normal with mean
and variance-covariance (VC) matrix
, which is typically obtained from the FI matrix
. Due to the analytical complexity of the FI, it is often more practical to approximate
using the observed FI matrix evaluated at
, denoted by
. Consequently, the VC matrix is estimated as:
where
On the other hand, to construct the
ACIs for the RF
and HRF
, it is first necessary to estimate the variances of their respective estimators,
and
. A widely used approach for this purpose is the delta method, which approximates these variances—denoted by
and
, respectively. Following the treatment in Greene [
14], the delta method assumes that
is approximately normally distributed with mean
and variance
, and similarly,
is approximately normal with mean
and variance
.
Accordingly, the quantities of
and
are given, respectively, by:
where
Consequently, based on the normal approximation (NA) of
, the
ACI using the NA-based approach (ACI-NA) at significance level
is given by
where
is the upper
standard Gaussian percentile point. Similarly, the ACI-NA estimator of
or
can be obtained.
A key limitation of the traditional ACI-NA approach is that it may produce negative lower bounds for parameters that are inherently restricted to positive values. In such cases, it is common to truncate negative bounds at zero, although this adjustment is heuristic rather than statistically rigorous. To address this limitation and improve the reliability of interval estimation, following Meeker and Escobar [
15], the
ACI based on the log-transform normal approximation (ACI-NL) is developed. Thus, the
ACI-NL for
is given by
which is equivalent to
Similarly, the ACI-NL for or can be derived in the same manner.
3. Bayesian Inference
This section focuses on developing both point estimates and credible Bayesian intervals for
,
, and
. Within the Bayesian paradigm, prior distributions and loss functions play a crucial role. Selecting an appropriate prior for an unknown parameter can be challenging. As emphasized by Gelman et al. [
16], there is no universally accepted criterion for choosing a suitable prior in Bayesian analysis. Since the CJ parameter
lies in the interval
, the gamma distribution provides a natural and tractable choice as a prior for
. Assume
∼
where
a and
b are the hyperparameters. Then, the corresponding prior PDF, denoted by
, is given by
From (
6) and (
10), the posterior PDF (say
) of
can be expresses as follows:
where its normalized term (say,
) is given by
It is worth noting that we adopt the squared-error loss (SEL) function, primarily because it is the most widely used symmetric loss function in Bayesian analysis. Nevertheless, the proposed methodology can be readily extended to obtain Bayesian estimates under alternative loss functions. Based on the posterior distribution in (
11), and given the nonlinear structure of the likelihood function in (
6), the Bayesian estimates of
,
, and
under the SEL function are analytically intractable.
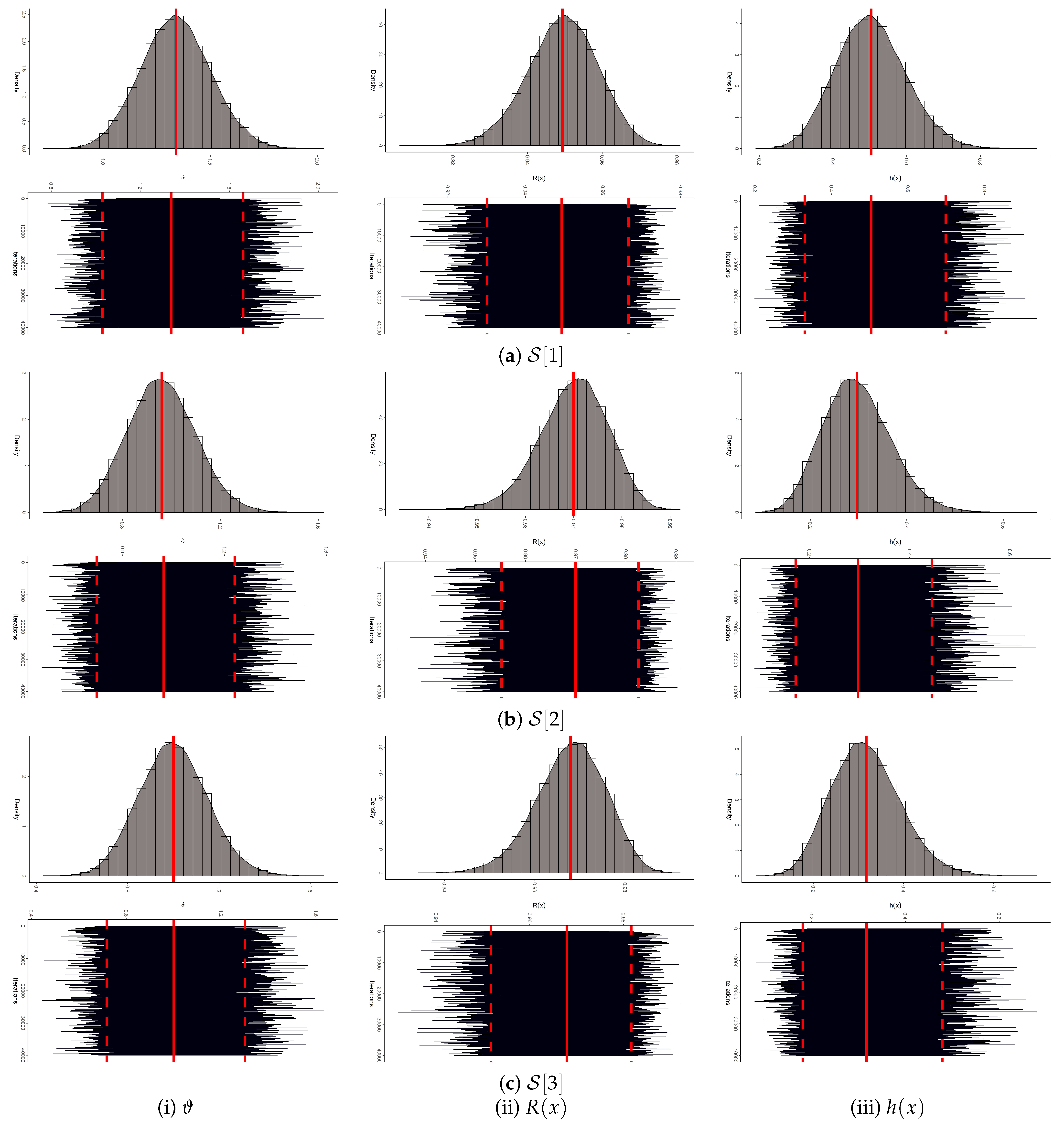
Consequently, by employing the MCMC technique, we generate Markovian samples from the posterior distribution in (
11). Examining (
11), it is evident that the PDF of
cannot be expressed using any standard continuous statistical model. However,
Figure 2 shows that the conditional PDF in (
11) is approximately normal. Accordingly, following Algorithm 1, the Metropolis–Hastings (M-H) algorithm is employed to update the posterior samples of
, after which the Bayesian estimates and the corresponding BCI/HPD interval estimates for
,
, and
are computed.
| Algorithm 1 The M-H Algorithm for , , and |
- 1:
Input: Initial estimate , estimated variance , total iterations , burn-in , confidence level - 2:
Output: Posterior mean , BCI and HPD intervals of - 3:
Set - 4:
Set - 5:
while
do - 6:
Generate - 7:
Compute acceptance ratio: - 8:
Generate - 9:
if then - 10:
Set - 11:
else - 12:
Set - 13:
end if - 14:
Update and using in ( 3) and ( 4) - 15:
Increment - 16:
end while - 17:
Discard the first samples as burn-in - 18:
Define - 19:
- 20:
Sort for in ascending order - 21:
Compute the BCI of as: - 22:
Compute the HPD interval of as:
where is the index that minimizes: - 23:
Redo Steps 19–22 for and
|
4. Monte Carlo Comparisons
To evaluate the precision and practical applicability of the estimated values of
,
, and
discussed in the preceding sections, a series of Monte Carlo simulations is conducted. Specifically, following Algorithm 2, the IT2-APC procedure is replicated 1000 times for each selected value of
(namely,
and
) to compute both point and interval estimates of the target parameters. For a fixed value of
, the corresponding estimates of the reliability and hazard functions,
, are obtained as (0.97797, 0.21747) for
, and (0.94002, 0.59745) for
. The simulation experiments are carried out under various configurations involving threshold parameters
, total sample sizes
n, effective sample sizes
m, and the progressive censoring scheme
. In particular, we consider
,
, and
.
Table 2 presents, for each value of
n, several choices of failure sizes
m along with their corresponding T2-PC schemes
. For illustrative purposes, a notation such as
indicates that five units are withdrawn from the experiment at each of the first two censoring stages.
| Algorithm 2 Simulate IT2-APC data. |
- 1:
Input: Assign values for n, m, , and - 2:
Set the true value of CJ() parameter. - 3:
Generate m independent uniform random variables - 4:
for to m do - 5:
Compute - 6:
end for - 7:
for to m do - 8:
Compute - 9:
end for - 10:
for to m do - 11:
Compute - 12:
end for - 13:
Observe failures at time - 14:
Discard observations for - 15:
Set truncated sample size: - 16:
Simulate order statistics from truncated distribution: PDF: where is the survival function - 17:
if
then - 18:
Case 1: Stop test at - 19:
else if t1 < ym < t2 then - 20:
Case 2: Stop test at - 21:
else if t1 < t2 < ym then - 22:
Case 3: Stop test at - 23:
end if
|
To further assess the sensitivity of the estimation procedures under the Bayesian framework, we consider two sets of hyperparameters for the CJ distribution under the two parameter settings. Following the prior elicitation strategy proposed by Kundu [
17], we specify the hyperparameter values
a and
b in the gamma prior PDF, as follows:
At : Prior-1:(4,5) and Prior-2:(8,10);
At : Prior-1:(7.5,5) and Prior-2:(15,10).
Once 1000 IT2-APC datasets are generated, the frequentist estimates and their corresponding 95% ACI-NA and ACI-NL intervals for , , and are computed using the maxLik package. For the Bayesian analysis, 12,000 MCMC samples are drawn, with the first 2000 iterations discarded as burn-in. The resulting Bayesian estimates, along with their 95% BCI and HPD intervals for , , and , are then computed using the coda package.
Now, to evaluate the offered estimators obtained for the CJ() parameter, we calculate the following metrics:
Mean Point Estimate:
Root Mean Squared Error:
Mean Relative Absolute Bias:
Average Interval Length:
Coverage Percentage:
where is the desired estimate of at ith sample, is indicator function, is two-sided of asymptotic (or credible) of . Similarly, the same precision metrics can be readily applied to or .
In
Table 3,
Table 4 and
Table 5, the point estimation results—including MPEs (1st Col.), RMSEs (2nd Col.), and MRABs (3rd Col.)—for
,
and
are reported. Meanwhile,
Table 6,
Table 7 and
Table 8 present the AILs (1st Col.) and CPs (2nd Col.) for the same parameters. Based on these tables, we derive the following observations, focusing on the lowest RMSEs, MRABs, and AILs, and the highest CPs:
All results for , , and exhibit consistently satisfactory performance across the simulated configurations. This demonstrates that both point and interval estimators remain stable under varying censoring levels, sample sizes, and prior specifications, highlighting the robustness of the proposed inference framework.
As n or m increase, the estimation accuracy of all model parameters improves. Larger sample sizes provide more information about the underlying failure-time distribution, reducing Monte Carlo variability and enhancing the coverage of interval estimates. A similar improvement is observed when the total number of removals, , decreases, as fewer removals preserve more observed failure times, thereby increasing the precision of parameter estimation.
Increasing the threshold values (for ) results in more precise parameter estimates. Specifically, the RMSEs, MRABs, and AILs for , , and decrease, while the corresponding CPs increase. This indicates that longer censoring times provide more information about the tail behavior of the distribution, thereby improving inference for both the reliability and hazard functions.
As the value of increases,
- –
The RMSEs of , , and increase, indicating that higher shape parameter values introduce heavier tails, which make estimation more challenging;
- –
The MRABs of and decrease, whereas that of increases, suggesting that bias behavior differs among the parameters, with being more sensitive to changes in than ;
- –
The AILs for all parameters increase, and the CPs tend to decrease, confirming that as grows, the variability in estimates increases, making it harder to achieve nominal coverage levels.
For the parameter values considered (), we observed that the RMSEs, MRABs, and AILs tend to increase as becomes larger, while the CPs decrease. These patterns are empirical for the chosen parameter values and may not necessarily generalize to all possible values of .
Bayesian estimates obtained via MCMC sampling, along with their corresponding credible intervals, exhibit superior robustness compared to their frequentist counterparts. The use of informative priors stabilizes inference, particularly under heavy censoring and small-sample scenarios, resulting in reduced RMSEs and narrower intervals without compromising coverage.
For each considered value of , the Bayesian estimator based on Prior-2 consistently produces more accurate results than other approaches. This improvement is attributable to the lower prior variance of Prior-2 relative to Prior-1, which enables the posterior distribution to concentrate more efficiently around the true parameter values. A similar trend is observed when comparing asymptotic intervals (ACI-NA and ACI-NL) with Bayesian intervals (BCI and HPD), as the latter adapt more effectively to model complexity.
A comparative evaluation of the T2-PC designs listed in
Table 2 reveals the following:
- –
The point and interval estimates of and under configurations C (for and ) outperform those obtained from alternative schemes, indicating that these designs optimally balance the trade-off between sample size, number of removals, and censoring thresholds;
- –
The estimates of achieve the highest accuracy under configurations A (for and ), suggesting that reliability estimation may require different censoring strategies than those optimal for hazard estimation.
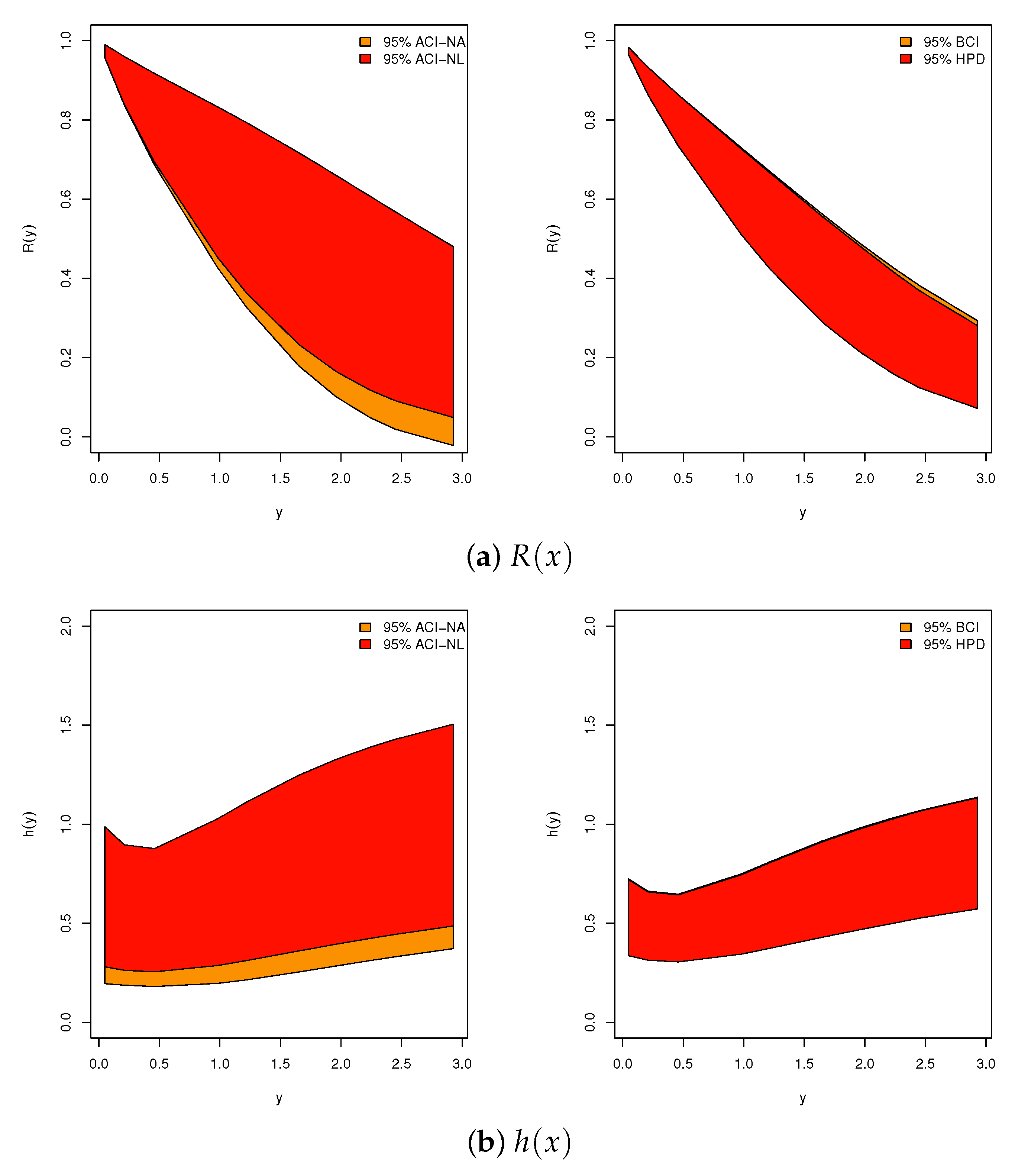
Comparing the proposed interval estimation techniques, we noted the following:
- –
The ACI-NA approach outperforms ACI-NL for estimating and , whereas the reverse holds for , indicating that linearization-based approximations are more effective for certain types of parameters;
- –
The HPD method yields superior interval estimates for all parameters compared to the BCI approach, highlighting the efficiency of HPD intervals in summarizing posterior distributions;
- –
Overall, Bayesian interval estimates (BCIs or HPD) consistently outperform asymptotic intervals (ACI-NA or ACI-NL), emphasizing the advantages of Bayesian inference in heavily censored experimental designs.
In conclusion, for practitioners involved in reliability analysis, the CJ lifetime population is best explored through a Bayesian framework using the MCMC methodology, particularly via the M-H sampling algorithm.
Table 3.
Point estimations of .
Table 3.
Point estimations of .
| | T2-PC | MLE | MCMC |
| Prior→ | | | | | | 1 | 2 |
| For |
|
(1,2) | (30,10) | A1[1] | 0.5502 | 0.3456 | 0.4151 | 0.8124 | 0.0878 | 0.0973 | 0.7688 | 0.0827 | 0.0808 |
| | | B1[2] | 0.5161 | 0.3551 | 0.4319 | 0.8233 | 0.0916 | 0.1019 | 0.7777 | 0.0906 | 0.0874 |
| | | C1[3] | 0.5502 | 0.2870 | 0.3291 | 0.8124 | 0.0860 | 0.0951 | 0.7688 | 0.0796 | 0.0808 |
| | (30,20) | A1[4] | 0.7572 | 0.1952 | 0.2176 | 0.8115 | 0.0841 | 0.0834 | 0.8568 | 0.0714 | 0.0792 |
| | | B1[5] | 0.7287 | 0.1855 | 0.2077 | 0.8066 | 0.0825 | 0.0814 | 0.8523 | 0.0698 | 0.0779 |
| | | C1[6] | 0.7321 | 0.1647 | 0.1879 | 0.8092 | 0.0771 | 0.0772 | 0.8561 | 0.0643 | 0.0727 |
| | (50,20) | A2[1] | 0.7114 | 0.1396 | 0.1521 | 0.8085 | 0.0700 | 0.0701 | 0.8524 | 0.0628 | 0.0664 |
| | | B2[2] | 0.7184 | 0.1472 | 0.1592 | 0.8027 | 0.0728 | 0.0737 | 0.8453 | 0.0638 | 0.0675 |
| | | C2[3] | 0.6948 | 0.1370 | 0.1493 | 0.8028 | 0.0673 | 0.0700 | 0.8453 | 0.0596 | 0.0651 |
| | (50,40) | A2[4] | 0.7613 | 0.1294 | 0.1397 | 0.7663 | 0.0615 | 0.0668 | 0.8367 | 0.0574 | 0.0581 |
| | | B2[5] | 0.7771 | 0.1340 | 0.1416 | 0.7675 | 0.0623 | 0.0695 | 0.8438 | 0.0592 | 0.0637 |
| | | C2[6] | 0.7642 | 0.1118 | 0.1152 | 0.7663 | 0.0590 | 0.0646 | 0.8367 | 0.0507 | 0.0545 |
| | (80,30) | A3[1] | 0.7107 | 0.0964 | 0.1064 | 0.7439 | 0.0585 | 0.0611 | 0.8421 | 0.0473 | 0.0502 |
| | | B3[2] | 0.7152 | 0.1004 | 0.1131 | 0.7461 | 0.0587 | 0.0634 | 0.8457 | 0.0498 | 0.0508 |
| | | C3[3] | 0.7024 | 0.0937 | 0.0966 | 0.7360 | 0.0566 | 0.0609 | 0.8357 | 0.0464 | 0.0484 |
| | (80,60) | A3[4] | 0.7595 | 0.0682 | 0.0661 | 0.7631 | 0.0532 | 0.0560 | 0.7930 | 0.0434 | 0.0450 |
| | | B3[5] | 0.7818 | 0.0860 | 0.0921 | 0.7598 | 0.0534 | 0.0585 | 0.7866 | 0.0451 | 0.0474 |
| | | C3[6] | 0.7663 | 0.0679 | 0.0656 | 0.7631 | 0.0500 | 0.0498 | 0.7930 | 0.0411 | 0.0445 |
|
(2,4) | (30,10) | A1[1] | 0.4977 | 0.2726 | 0.3291 | 0.7861 | 0.0849 | 0.0897 | 0.7477 | 0.0677 | 0.0730 |
| | | B1[2] | 0.4673 | 0.2956 | 0.3549 | 0.7928 | 0.0909 | 0.0911 | 0.7534 | 0.0682 | 0.0738 |
| | | C1[3] | 0.8685 | 0.2726 | 0.3209 | 0.8352 | 0.0828 | 0.0873 | 0.8002 | 0.0643 | 0.0685 |
| | (30,20) | A1[4] | 0.7668 | 0.1425 | 0.1455 | 0.8156 | 0.0766 | 0.0799 | 0.8610 | 0.0643 | 0.0684 |
| | | B1[5] | 0.7319 | 0.1314 | 0.1434 | 0.8063 | 0.0766 | 0.0791 | 0.8481 | 0.0629 | 0.0672 |
| | | C1[6] | 0.7907 | 0.1276 | 0.1325 | 0.8320 | 0.0738 | 0.0742 | 0.8795 | 0.0626 | 0.0668 |
| | (50,20) | A2[1] | 0.7141 | 0.1231 | 0.1289 | 0.8086 | 0.0629 | 0.0666 | 0.8525 | 0.0589 | 0.0610 |
| | | B2[2] | 0.7253 | 0.1258 | 0.1321 | 0.8004 | 0.0641 | 0.0686 | 0.8414 | 0.0622 | 0.0659 |
| | | C2[3] | 0.8431 | 0.1167 | 0.1245 | 0.8308 | 0.0626 | 0.0662 | 0.8734 | 0.0589 | 0.0610 |
| | (50,40) | A2[4] | 0.7340 | 0.1122 | 0.1181 | 0.7571 | 0.0592 | 0.0641 | 0.8201 | 0.0486 | 0.0515 |
| | | B2[5] | 0.7793 | 0.1131 | 0.1213 | 0.7701 | 0.0608 | 0.0644 | 0.8372 | 0.0511 | 0.0552 |
| | | C2[6] | 0.7312 | 0.1054 | 0.1056 | 0.7548 | 0.0583 | 0.0636 | 0.8162 | 0.0486 | 0.0515 |
| | (80,30) | A3[1] | 0.7011 | 0.0840 | 0.0821 | 0.7358 | 0.0551 | 0.0608 | 0.8356 | 0.0462 | 0.0481 |
| | | B3[2] | 0.7079 | 0.0998 | 0.0989 | 0.7427 | 0.0577 | 0.0626 | 0.8386 | 0.0462 | 0.0481 |
| | | C3[3] | 0.8045 | 0.0838 | 0.0799 | 0.7769 | 0.0547 | 0.0608 | 0.8777 | 0.0439 | 0.0454 |
| | (80,60) | A3[4] | 0.7306 | 0.0629 | 0.0626 | 0.7368 | 0.0522 | 0.0530 | 0.7670 | 0.0419 | 0.0446 |
| | | B3[5] | 0.7858 | 0.0831 | 0.0782 | 0.7598 | 0.0533 | 0.0561 | 0.7864 | 0.0419 | 0.0454 |
| | | C3[6] | 0.7147 | 0.0522 | 0.0530 | 0.7484 | 0.0450 | 0.0496 | 0.7751 | 0.0409 | 0.0443 |
|
For |
|
(1,2) | (30,10) | A1[1] | 1.4692 | 0.3722 | 0.1887 | 1.5360 | 0.0879 | 0.0515 | 1.4977 | 0.0822 | 0.0482 |
| | | B1[2] | 1.4442 | 0.5563 | 0.3117 | 1.5330 | 0.0977 | 0.0527 | 1.4948 | 0.0869 | 0.0484 |
| | | C1[3] | 1.7163 | 0.3401 | 0.1822 | 1.5360 | 0.0843 | 0.0484 | 1.4977 | 0.0769 | 0.0459 |
| | (30,20) | A1[4] | 1.4377 | 0.3302 | 0.1678 | 1.5159 | 0.0755 | 0.0450 | 1.5645 | 0.0746 | 0.0385 |
| | | B1[5] | 1.4231 | 0.3133 | 0.1641 | 1.5159 | 0.0755 | 0.0450 | 1.5644 | 0.0741 | 0.0383 |
| | | C1[6] | 1.8077 | 0.2626 | 0.1453 | 1.5272 | 0.0750 | 0.0446 | 1.5749 | 0.0707 | 0.0378 |
| | (50,20) | A2[1] | 1.4567 | 0.2380 | 0.1217 | 1.5175 | 0.0714 | 0.0429 | 1.5649 | 0.0594 | 0.0355 |
| | | B2[2] | 1.4452 | 0.2419 | 0.1432 | 1.5159 | 0.0748 | 0.0444 | 1.5642 | 0.0607 | 0.0366 |
| | | C2[3] | 1.7670 | 0.2177 | 0.1140 | 1.5228 | 0.0714 | 0.0429 | 1.5695 | 0.0594 | 0.0355 |
| | (50,40) | A2[4] | 1.4229 | 0.2030 | 0.1077 | 1.4549 | 0.0578 | 0.0347 | 1.5334 | 0.0511 | 0.0273 |
| | | B2[5] | 1.4609 | 0.2116 | 0.1133 | 1.4587 | 0.0609 | 0.0363 | 1.5401 | 0.0571 | 0.0344 |
| | | C2[6] | 1.4048 | 0.1910 | 0.1003 | 1.4469 | 0.0576 | 0.0346 | 1.5208 | 0.0494 | 0.0267 |
| | (80,30) | A3[1] | 1.4673 | 0.1723 | 0.0890 | 1.4524 | 0.0557 | 0.0330 | 1.5642 | 0.0467 | 0.0254 |
| | | B3[2] | 1.4678 | 0.1904 | 0.1002 | 1.4523 | 0.0570 | 0.0337 | 1.5642 | 0.0467 | 0.0254 |
| | | C3[3] | 1.7015 | 0.1553 | 0.0810 | 1.4671 | 0.0554 | 0.0326 | 1.5770 | 0.0447 | 0.0246 |
| | (80,60) | A3[4] | 1.4510 | 0.1341 | 0.0703 | 1.4498 | 0.0554 | 0.0318 | 1.4784 | 0.0423 | 0.0239 |
| | | B3[5] | 1.4746 | 0.1552 | 0.0768 | 1.4584 | 0.0554 | 0.0326 | 1.4888 | 0.0439 | 0.0241 |
| | | C3[6] | 1.4253 | 0.1093 | 0.0574 | 1.4485 | 0.0540 | 0.0310 | 1.4769 | 0.0406 | 0.0234 |
|
(2,4) | (30,10) | A1[1] | 1.5058 | 0.3567 | 0.1850 | 1.5339 | 0.0874 | 0.0484 | 1.4957 | 0.0774 | 0.0463 |
| | | B1[2] | 1.4770 | 0.3889 | 0.2324 | 1.5339 | 0.0879 | 0.0517 | 1.4957 | 0.0781 | 0.0467 |
| | | C1[3] | 1.5900 | 0.3359 | 0.1746 | 1.5360 | 0.0810 | 0.0467 | 1.4977 | 0.0743 | 0.0400 |
| | (30,20) | A1[4] | 1.4634 | 0.3089 | 0.1549 | 1.5175 | 0.0755 | 0.0450 | 1.5649 | 0.0741 | 0.0383 |
| | | B1[5] | 1.4727 | 0.2816 | 0.1472 | 1.5158 | 0.0751 | 0.0448 | 1.5644 | 0.0727 | 0.0383 |
| | | C1[6] | 1.6337 | 0.2455 | 0.1220 | 1.5189 | 0.0750 | 0.0446 | 1.5666 | 0.0618 | 0.0375 |
| | (50,20) | A2[1] | 1.4759 | 0.2207 | 0.1142 | 1.5176 | 0.0711 | 0.0427 | 1.5662 | 0.0576 | 0.0347 |
| | | B2[2] | 1.4663 | 0.2366 | 0.1205 | 1.5175 | 0.0714 | 0.0429 | 1.5649 | 0.0590 | 0.0353 |
| | | C2[3] | 1.5449 | 0.2157 | 0.1123 | 1.5189 | 0.0710 | 0.0425 | 1.5672 | 0.0576 | 0.0347 |
| | (50,40) | A2[4] | 1.4692 | 0.1915 | 0.1018 | 1.4546 | 0.0569 | 0.0343 | 1.5312 | 0.0494 | 0.0267 |
| | | B2[5] | 1.4706 | 0.1973 | 0.1115 | 1.4546 | 0.0594 | 0.0355 | 1.5325 | 0.0494 | 0.0272 |
| | | C2[6] | 1.8471 | 0.1796 | 0.0924 | 1.4700 | 0.0569 | 0.0343 | 1.5542 | 0.0483 | 0.0267 |
| | (80,30) | A3[1] | 1.4750 | 0.1637 | 0.0875 | 1.4524 | 0.0552 | 0.0327 | 1.5638 | 0.0448 | 0.0249 |
| | | B3[2] | 1.4671 | 0.1683 | 0.0891 | 1.4525 | 0.0554 | 0.0327 | 1.5636 | 0.0459 | 0.0251 |
| | | C3[3] | 1.5279 | 0.1411 | 0.0750 | 1.4535 | 0.0552 | 0.0326 | 1.5642 | 0.0445 | 0.0244 |
| | (80,60) | A3[4] | 1.4815 | 0.1118 | 0.0589 | 1.4595 | 0.0531 | 0.0297 | 1.4873 | 0.0407 | 0.0235 |
| | | B3[5] | 1.4820 | 0.1358 | 0.0727 | 1.4605 | 0.0536 | 0.0302 | 1.4912 | 0.0425 | 0.0241 |
| | | C3[6] | 1.7774 | 0.1064 | 0.0556 | 1.4706 | 0.0515 | 0.0282 | 1.5102 | 0.0401 | 0.0232 |
Table 4.
Point estimations of .
Table 4.
Point estimations of .
| | T2-PC | MLE | MCMC |
| Prior→ | | | | | | 1 | 2 |
| For |
|
(1,2) | (30,10) | A1[1] | 0.9882 | 0.1318 | 0.1207 | 0.9773 | 0.0394 | 0.0370 | 0.9794 | 0.0352 | 0.0298 |
| | | B1[2] | 0.9882 | 0.1376 | 0.1306 | 0.9773 | 0.0405 | 0.0378 | 0.9794 | 0.0365 | 0.0303 |
| | | C1[3] | 0.9895 | 0.1400 | 0.1399 | 0.9769 | 0.0438 | 0.0397 | 0.9790 | 0.0398 | 0.0317 |
| | (30,20) | A1[4] | 0.9809 | 0.0764 | 0.0709 | 0.9775 | 0.0343 | 0.0281 | 0.9753 | 0.0305 | 0.0269 |
| | | B1[5] | 0.9810 | 0.0877 | 0.0795 | 0.9776 | 0.0363 | 0.0296 | 0.9755 | 0.0313 | 0.0288 |
| | | C1[6] | 0.9796 | 0.0934 | 0.0829 | 0.9774 | 0.0371 | 0.0307 | 0.9753 | 0.0339 | 0.0291 |
| | (50,20) | A2[1] | 0.9825 | 0.0600 | 0.0541 | 0.9778 | 0.0305 | 0.0260 | 0.9758 | 0.0279 | 0.0246 |
| | | B2[2] | 0.9815 | 0.0648 | 0.0575 | 0.9778 | 0.0326 | 0.0271 | 0.9758 | 0.0294 | 0.0253 |
| | | C2[3] | 0.9818 | 0.0615 | 0.0548 | 0.9775 | 0.0316 | 0.0262 | 0.9755 | 0.0286 | 0.0249 |
| | (50,40) | A2[4] | 0.9795 | 0.0481 | 0.0422 | 0.9794 | 0.0271 | 0.0245 | 0.9763 | 0.0229 | 0.0202 |
| | | B2[5] | 0.9789 | 0.0585 | 0.0511 | 0.9794 | 0.0288 | 0.0257 | 0.9759 | 0.0273 | 0.0242 |
| | | C2[6] | 0.9797 | 0.0567 | 0.0505 | 0.9794 | 0.0277 | 0.0251 | 0.9763 | 0.0271 | 0.0224 |
| | (80,30) | A3[1] | 0.9823 | 0.0418 | 0.0355 | 0.9808 | 0.0263 | 0.0230 | 0.9763 | 0.0219 | 0.0186 |
| | | B3[2] | 0.9819 | 0.0432 | 0.0387 | 0.9805 | 0.0268 | 0.0234 | 0.9760 | 0.0221 | 0.0191 |
| | | C3[3] | 0.9817 | 0.0448 | 0.0412 | 0.9804 | 0.0270 | 0.0239 | 0.9758 | 0.0229 | 0.0192 |
| | (80,60) | A3[4] | 0.9795 | 0.0301 | 0.0241 | 0.9796 | 0.0227 | 0.0191 | 0.9783 | 0.0192 | 0.0167 |
| | | B3[5] | 0.9798 | 0.0313 | 0.0244 | 0.9796 | 0.0241 | 0.0207 | 0.9783 | 0.0197 | 0.0168 |
| | | C3[6] | 0.9787 | 0.0385 | 0.0339 | 0.9798 | 0.0251 | 0.0224 | 0.9786 | 0.0212 | 0.0181 |
|
(2,4) | (30,10) | A1[1] | 0.9735 | 0.1122 | 0.1114 | 0.9763 | 0.0383 | 0.0316 | 0.9779 | 0.0311 | 0.0276 |
| | | B1[2] | 0.9898 | 0.1217 | 0.1174 | 0.9785 | 0.0390 | 0.0329 | 0.9803 | 0.0322 | 0.0283 |
| | | C1[3] | 0.9910 | 0.1389 | 0.1218 | 0.9782 | 0.0399 | 0.0334 | 0.9801 | 0.0332 | 0.0296 |
| | (30,20) | A1[4] | 0.9778 | 0.0558 | 0.0477 | 0.9765 | 0.0332 | 0.0275 | 0.9742 | 0.0297 | 0.0258 |
| | | B1[5] | 0.9808 | 0.0570 | 0.0514 | 0.9776 | 0.0344 | 0.0291 | 0.9757 | 0.0298 | 0.0259 |
| | | C1[6] | 0.9794 | 0.0625 | 0.0530 | 0.9772 | 0.0344 | 0.0306 | 0.9751 | 0.0305 | 0.0265 |
| | (50,20) | A2[1] | 0.9755 | 0.0511 | 0.0450 | 0.9765 | 0.0289 | 0.0255 | 0.9745 | 0.0273 | 0.0236 |
| | | B2[2] | 0.9811 | 0.0548 | 0.0476 | 0.9779 | 0.0298 | 0.0265 | 0.9760 | 0.0292 | 0.0248 |
| | | C2[3] | 0.9816 | 0.0537 | 0.0465 | 0.9775 | 0.0296 | 0.0256 | 0.9755 | 0.0279 | 0.0241 |
| | (50,40) | A2[4] | 0.9810 | 0.0465 | 0.0379 | 0.9799 | 0.0268 | 0.0240 | 0.9772 | 0.0220 | 0.0195 |
| | | B2[5] | 0.9789 | 0.0495 | 0.0438 | 0.9793 | 0.0285 | 0.0246 | 0.9762 | 0.0241 | 0.0213 |
| | | C2[6] | 0.9808 | 0.0489 | 0.0426 | 0.9798 | 0.0273 | 0.0242 | 0.9770 | 0.0220 | 0.0209 |
| | (80,30) | A3[1] | 0.9774 | 0.0369 | 0.0293 | 0.9790 | 0.0257 | 0.0229 | 0.9743 | 0.0199 | 0.0175 |
| | | B3[2] | 0.9822 | 0.0377 | 0.0305 | 0.9808 | 0.0260 | 0.0231 | 0.9763 | 0.0218 | 0.0185 |
| | | C3[3] | 0.9820 | 0.0440 | 0.0366 | 0.9805 | 0.0267 | 0.0238 | 0.9761 | 0.0218 | 0.0188 |
| | (80,60) | A3[4] | 0.9818 | 0.0235 | 0.0196 | 0.9803 | 0.0204 | 0.0185 | 0.9791 | 0.0188 | 0.0161 |
| | | B3[5] | 0.9810 | 0.0284 | 0.0233 | 0.9808 | 0.0235 | 0.0196 | 0.9795 | 0.0190 | 0.0167 |
| | | C3[6] | 0.9786 | 0.0366 | 0.0286 | 0.9798 | 0.0240 | 0.0207 | 0.9786 | 0.0193 | 0.0171 |
|
For |
|
(1,2) | (30,10) | A1[1] | 0.9264 | 0.2092 | 0.1818 | 0.9378 | 0.0501 | 0.0468 | 0.9401 | 0.0466 | 0.0443 |
| | | B1[2] | 0.9413 | 0.2337 | 0.1862 | 0.9378 | 0.0523 | 0.0498 | 0.9401 | 0.0499 | 0.0458 |
| | | C1[3] | 0.9429 | 0.3503 | 0.3089 | 0.9380 | 0.0579 | 0.0501 | 0.9403 | 0.0523 | 0.0460 |
| | (30,20) | A1[4] | 0.9202 | 0.1622 | 0.1387 | 0.9384 | 0.0445 | 0.0431 | 0.9355 | 0.0422 | 0.0359 |
| | | B1[5] | 0.9443 | 0.1945 | 0.1571 | 0.9390 | 0.0451 | 0.0435 | 0.9361 | 0.0440 | 0.0364 |
| | | C1[6] | 0.9435 | 0.2020 | 0.1615 | 0.9390 | 0.0458 | 0.0449 | 0.9361 | 0.0443 | 0.0365 |
| | (50,20) | A2[1] | 0.9234 | 0.1304 | 0.1081 | 0.9386 | 0.0433 | 0.0410 | 0.9358 | 0.0352 | 0.0341 |
| | | B2[2] | 0.9431 | 0.1463 | 0.1356 | 0.9390 | 0.0435 | 0.0429 | 0.9361 | 0.0362 | 0.0349 |
| | | C2[3] | 0.9423 | 0.1384 | 0.1140 | 0.9389 | 0.0433 | 0.0415 | 0.9361 | 0.0357 | 0.0341 |
| | (50,40) | A2[4] | 0.9455 | 0.1120 | 0.0947 | 0.9431 | 0.0345 | 0.0329 | 0.9388 | 0.0297 | 0.0256 |
| | | B2[5] | 0.9423 | 0.1277 | 0.1076 | 0.9425 | 0.0368 | 0.0351 | 0.9376 | 0.0344 | 0.0330 |
| | | C2[6] | 0.9444 | 0.1223 | 0.1028 | 0.9427 | 0.0347 | 0.0333 | 0.9380 | 0.0309 | 0.0262 |
| | (80,30) | A3[1] | 0.9276 | 0.0925 | 0.0771 | 0.9420 | 0.0338 | 0.0314 | 0.9353 | 0.0270 | 0.0237 |
| | | B3[2] | 0.9418 | 0.1025 | 0.0846 | 0.9428 | 0.0341 | 0.0318 | 0.9361 | 0.0280 | 0.0243 |
| | | C3[3] | 0.9418 | 0.1119 | 0.0942 | 0.9428 | 0.0344 | 0.0324 | 0.9361 | 0.0290 | 0.0243 |
| | (80,60) | A3[4] | 0.9442 | 0.0655 | 0.0549 | 0.9431 | 0.0322 | 0.0296 | 0.9414 | 0.0243 | 0.0225 |
| | | B3[5] | 0.9428 | 0.0795 | 0.0668 | 0.9430 | 0.0330 | 0.0303 | 0.9413 | 0.0253 | 0.0228 |
| | | C3[6] | 0.9415 | 0.0910 | 0.0724 | 0.9425 | 0.0335 | 0.0310 | 0.9407 | 0.0266 | 0.0232 |
|
(2,4) | (30,10) | A1[1] | 0.9340 | 0.2090 | 0.1703 | 0.9378 | 0.0491 | 0.0444 | 0.9401 | 0.0441 | 0.0381 |
| | | B1[2] | 0.9391 | 0.2222 | 0.1825 | 0.9380 | 0.0520 | 0.0460 | 0.9403 | 0.0470 | 0.0447 |
| | | C1[3] | 0.9408 | 0.2426 | 0.2305 | 0.9380 | 0.0528 | 0.0500 | 0.9403 | 0.0474 | 0.0451 |
| | (30,20) | A1[4] | 0.9317 | 0.1525 | 0.1197 | 0.9389 | 0.0439 | 0.0428 | 0.9360 | 0.0369 | 0.0357 |
| | | B1[5] | 0.9414 | 0.1684 | 0.1445 | 0.9390 | 0.0442 | 0.0433 | 0.9361 | 0.0432 | 0.0360 |
| | | C1[6] | 0.9420 | 0.1852 | 0.1471 | 0.9389 | 0.0448 | 0.0440 | 0.9361 | 0.0440 | 0.0364 |
| | (50,20) | A2[1] | 0.9370 | 0.1291 | 0.1074 | 0.9389 | 0.0430 | 0.0408 | 0.9359 | 0.0342 | 0.0329 |
| | | B2[2] | 0.9418 | 0.1453 | 0.1166 | 0.9389 | 0.0433 | 0.0415 | 0.9361 | 0.0355 | 0.0339 |
| | | C2[3] | 0.9412 | 0.1335 | 0.1092 | 0.9389 | 0.0431 | 0.0412 | 0.9360 | 0.0347 | 0.0333 |
| | (50,40) | A2[4] | 0.9184 | 0.1095 | 0.0891 | 0.9418 | 0.0340 | 0.0330 | 0.9367 | 0.0292 | 0.0256 |
| | | B2[5] | 0.9417 | 0.1183 | 0.1065 | 0.9427 | 0.0357 | 0.0341 | 0.9380 | 0.0297 | 0.0263 |
| | | C2[6] | 0.9418 | 0.1128 | 0.0963 | 0.9427 | 0.0344 | 0.0330 | 0.9381 | 0.0295 | 0.0256 |
| | (80,30) | A3[1] | 0.9382 | 0.0846 | 0.0715 | 0.9428 | 0.0324 | 0.0314 | 0.9361 | 0.0269 | 0.0236 |
| | | B3[2] | 0.9414 | 0.0983 | 0.0836 | 0.9428 | 0.0333 | 0.0315 | 0.9362 | 0.0271 | 0.0238 |
| | | C3[3] | 0.9418 | 0.1012 | 0.0852 | 0.9428 | 0.0335 | 0.0315 | 0.9362 | 0.0275 | 0.0241 |
| | (80,60) | A3[4] | 0.9229 | 0.0634 | 0.0529 | 0.9418 | 0.0307 | 0.0269 | 0.9394 | 0.0241 | 0.0222 |
| | | B3[5] | 0.9411 | 0.0670 | 0.0562 | 0.9424 | 0.0317 | 0.0283 | 0.9408 | 0.0244 | 0.0225 |
| | | C3[6] | 0.9410 | 0.0815 | 0.0694 | 0.9424 | 0.0320 | 0.0288 | 0.9405 | 0.0254 | 0.0230 |
Table 5.
Point estimations of .
Table 5.
Point estimations of .
| | T2-PC | MLE | MCMC |
| Prior→ | | | | | | 1 | 2 |
| For |
|
(1,2) | (30,10) | A1[1] | 0.1166 | 0.1358 | 0.6020 | 0.2237 | 0.1107 | 0.4948 | 0.2036 | 0.0401 | 0.1683 |
| | | B1[2] | 0.1036 | 0.1381 | 0.6207 | 0.2286 | 0.1173 | 0.5235 | 0.2076 | 0.0434 | 0.1769 |
| | | C1[3] | 0.1166 | 0.1308 | 0.5379 | 0.2237 | 0.1107 | 0.4948 | 0.2036 | 0.0390 | 0.1647 |
| | (30,20) | A1[4] | 0.1875 | 0.0869 | 0.3541 | 0.2211 | 0.0563 | 0.2283 | 0.2420 | 0.0359 | 0.1314 |
| | | B1[5] | 0.2013 | 0.0927 | 0.3690 | 0.2233 | 0.0618 | 0.2358 | 0.2441 | 0.0366 | 0.1366 |
| | | C1[6] | 0.1886 | 0.0757 | 0.3153 | 0.2222 | 0.0551 | 0.2117 | 0.2438 | 0.0339 | 0.1251 |
| | (50,20) | A2[1] | 0.1797 | 0.0608 | 0.2433 | 0.2219 | 0.0530 | 0.2064 | 0.2420 | 0.0312 | 0.1165 |
| | | B2[2] | 0.1829 | 0.0640 | 0.2554 | 0.2194 | 0.0541 | 0.2115 | 0.2387 | 0.0323 | 0.1206 |
| | | C2[3] | 0.1723 | 0.0592 | 0.2404 | 0.2194 | 0.0504 | 0.2000 | 0.2387 | 0.0302 | 0.1154 |
| | (50,40) | A2[4] | 0.2009 | 0.0560 | 0.2243 | 0.2030 | 0.0483 | 0.1894 | 0.2346 | 0.0273 | 0.1117 |
| | | B2[5] | 0.2087 | 0.0578 | 0.2269 | 0.2035 | 0.0489 | 0.1945 | 0.2379 | 0.0284 | 0.1141 |
| | | C2[6] | 0.2023 | 0.0475 | 0.1873 | 0.2030 | 0.0460 | 0.1683 | 0.2346 | 0.0268 | 0.1089 |
| | (80,30) | A3[1] | 0.1788 | 0.0427 | 0.1721 | 0.1930 | 0.0373 | 0.1356 | 0.2373 | 0.0265 | 0.1042 |
| | | B3[2] | 0.1808 | 0.0443 | 0.1830 | 0.1939 | 0.0435 | 0.1626 | 0.2389 | 0.0267 | 0.1064 |
| | | C3[3] | 0.1752 | 0.0413 | 0.1575 | 0.1896 | 0.0365 | 0.1310 | 0.2344 | 0.0261 | 0.1034 |
| | (80,60) | A3[4] | 0.1998 | 0.0299 | 0.1108 | 0.2010 | 0.0280 | 0.1035 | 0.2145 | 0.0238 | 0.0921 |
| | | B3[5] | 0.2103 | 0.0381 | 0.1509 | 0.1996 | 0.0361 | 0.1272 | 0.2116 | 0.0248 | 0.0999 |
| | | C3[6] | 0.2028 | 0.0276 | 0.1071 | 0.2010 | 0.0232 | 0.0871 | 0.2145 | 0.0225 | 0.0825 |
|
(2,4) | (30,10) | A1[1] | 0.1012 | 0.0386 | 0.1462 | 0.2123 | 0.0360 | 0.1326 | 0.1944 | 0.0319 | 0.1258 |
| | | B1[2] | 0.0888 | 0.0394 | 0.1484 | 0.2152 | 0.0393 | 0.1407 | 0.1968 | 0.0321 | 0.1273 |
| | | C1[3] | 0.2619 | 0.0379 | 0.1406 | 0.2340 | 0.0348 | 0.1326 | 0.2179 | 0.0310 | 0.1179 |
| | (30,20) | A1[4] | 0.1894 | 0.0340 | 0.1295 | 0.2210 | 0.0310 | 0.1281 | 0.2400 | 0.0298 | 0.1153 |
| | | B1[5] | 0.2037 | 0.0340 | 0.1362 | 0.2251 | 0.0336 | 0.1292 | 0.2461 | 0.0302 | 0.1178 |
| | | C1[6] | 0.2190 | 0.0328 | 0.1222 | 0.2325 | 0.0302 | 0.1194 | 0.2550 | 0.0294 | 0.1149 |
| | (50,20) | A2[1] | 0.1819 | 0.0293 | 0.1142 | 0.2219 | 0.0283 | 0.1107 | 0.2421 | 0.0276 | 0.1079 |
| | | B2[2] | 0.1866 | 0.0295 | 0.1181 | 0.2184 | 0.0291 | 0.1127 | 0.2369 | 0.0288 | 0.1126 |
| | | C2[3] | 0.2424 | 0.0286 | 0.1134 | 0.2320 | 0.0276 | 0.1094 | 0.2521 | 0.0270 | 0.1049 |
| | (50,40) | A2[4] | 0.1892 | 0.0270 | 0.1076 | 0.1991 | 0.0262 | 0.0998 | 0.2270 | 0.0247 | 0.0851 |
| | | B2[5] | 0.2087 | 0.0282 | 0.1095 | 0.2046 | 0.0269 | 0.1078 | 0.2348 | 0.0239 | 0.0946 |
| | | C2[6] | 0.1872 | 0.0265 | 0.1067 | 0.1981 | 0.0253 | 0.0900 | 0.2252 | 0.0237 | 0.0865 |
| | (80,30) | A3[1] | 0.1754 | 0.0257 | 0.1042 | 0.1895 | 0.0219 | 0.0845 | 0.2343 | 0.0212 | 0.0822 |
| | | B3[2] | 0.1782 | 0.0264 | 0.1060 | 0.1925 | 0.0227 | 0.0852 | 0.2357 | 0.0222 | 0.0832 |
| | | C3[3] | 0.2238 | 0.0255 | 0.1020 | 0.2072 | 0.0217 | 0.0828 | 0.2540 | 0.0197 | 0.0762 |
| | (80,60) | A3[4] | 0.1874 | 0.0232 | 0.0871 | 0.1895 | 0.0195 | 0.0786 | 0.2028 | 0.0191 | 0.0744 |
| | | B3[5] | 0.2114 | 0.0237 | 0.0922 | 0.1996 | 0.0209 | 0.0806 | 0.2115 | 0.0195 | 0.0756 |
| | | C3[6] | 0.1800 | 0.0202 | 0.0824 | 0.1945 | 0.0186 | 0.0742 | 0.2064 | 0.0185 | 0.0733 |
|
For |
| | T2-PC | MLE | MCMC |
|
Prior → | | | | | | 1 | 2 |
|
(1,2) | (30,10) | A1[1] | 0.5858 | 0.2424 | 0.3006 | 0.6197 | 0.2302 | 0.2944 | 0.5962 | 0.0529 | 0.0797 |
| | | B1[2] | 0.5694 | 0.3646 | 0.5019 | 0.6178 | 0.2498 | 0.3727 | 0.5945 | 0.0586 | 0.0802 |
| | | C1[3] | 0.7382 | 0.2160 | 0.2918 | 0.6197 | 0.2151 | 0.2749 | 0.5962 | 0.0508 | 0.0749 |
| | (30,20) | A1[4] | 0.5552 | 0.1997 | 0.2522 | 0.6074 | 0.1722 | 0.2326 | 0.6371 | 0.0477 | 0.0697 |
| | | B1[5] | 0.5623 | 0.2083 | 0.2597 | 0.6074 | 0.1896 | 0.2354 | 0.6372 | 0.0486 | 0.0697 |
| | | C1[6] | 0.8043 | 0.1663 | 0.2218 | 0.6143 | 0.1569 | 0.1928 | 0.6437 | 0.0469 | 0.0690 |
| | (50,20) | A2[1] | 0.5747 | 0.1399 | 0.1816 | 0.6084 | 0.1364 | 0.1747 | 0.6375 | 0.0445 | 0.0676 |
| | | B2[2] | 0.5669 | 0.1493 | 0.2167 | 0.6074 | 0.1491 | 0.1872 | 0.6371 | 0.0462 | 0.0687 |
| | | C2[3] | 0.7679 | 0.1332 | 0.1725 | 0.6116 | 0.1310 | 0.1718 | 0.6403 | 0.0440 | 0.0671 |
| | (50,40) | A2[4] | 0.5534 | 0.1247 | 0.1643 | 0.5705 | 0.1144 | 0.1536 | 0.6180 | 0.0365 | 0.0532 |
| | | B2[5] | 0.5750 | 0.1303 | 0.1716 | 0.5728 | 0.1203 | 0.1703 | 0.6221 | 0.0375 | 0.0561 |
| | | C2[6] | 0.5423 | 0.1134 | 0.1509 | 0.5658 | 0.1119 | 0.1428 | 0.6103 | 0.0359 | 0.0528 |
| | (80,30) | A3[1] | 0.5798 | 0.1041 | 0.1351 | 0.5689 | 0.1000 | 0.1335 | 0.6370 | 0.0342 | 0.0513 |
| | | B3[2] | 0.5797 | 0.1131 | 0.1499 | 0.5688 | 0.1030 | 0.1361 | 0.6370 | 0.0353 | 0.0522 |
| | | C3[3] | 0.7251 | 0.0939 | 0.1231 | 0.5776 | 0.0860 | 0.1142 | 0.6449 | 0.0341 | 0.0510 |
| | (80,60) | A3[4] | 0.5695 | 0.0806 | 0.1065 | 0.5671 | 0.0681 | 0.0898 | 0.5844 | 0.0337 | 0.0483 |
| | | B3[5] | 0.5828 | 0.0920 | 0.1154 | 0.5723 | 0.0828 | 0.1109 | 0.5907 | 0.0340 | 0.0503 |
| | | C3[6] | 0.5561 | 0.0666 | 0.0876 | 0.5663 | 0.0643 | 0.0845 | 0.5835 | 0.0326 | 0.0471 |
|
(2,4) | (30,10) | A1[1] | 0.6089 | 0.0526 | 0.0734 | 0.6184 | 0.0508 | 0.0731 | 0.5950 | 0.0478 | 0.0716 |
| | | B1[2] | 0.5910 | 0.0538 | 0.0797 | 0.6184 | 0.0529 | 0.0734 | 0.5950 | 0.0482 | 0.0722 |
| | | C1[3] | 0.6607 | 0.0500 | 0.0710 | 0.6197 | 0.0475 | 0.0708 | 0.5962 | 0.0455 | 0.0609 |
| | (30,20) | A1[4] | 0.5842 | 0.0464 | 0.0693 | 0.6074 | 0.0441 | 0.0580 | 0.6371 | 0.0437 | 0.0575 |
| | | B1[5] | 0.5782 | 0.0466 | 0.0697 | 0.6084 | 0.0455 | 0.0582 | 0.6375 | 0.0446 | 0.0580 |
| | | C1[6] | 0.6831 | 0.0456 | 0.0690 | 0.6092 | 0.0428 | 0.0572 | 0.6385 | 0.0387 | 0.0569 |
| | (50,20) | A2[1] | 0.5863 | 0.0439 | 0.0660 | 0.6084 | 0.0363 | 0.0564 | 0.6383 | 0.0352 | 0.0532 |
| | | B2[2] | 0.5802 | 0.0444 | 0.0664 | 0.6084 | 0.0367 | 0.0556 | 0.6375 | 0.0360 | 0.0542 |
| | | C2[3] | 0.6288 | 0.0438 | 0.0658 | 0.6092 | 0.0363 | 0.0545 | 0.6389 | 0.0345 | 0.0521 |
| | (50,40) | A2[4] | 0.5801 | 0.0351 | 0.0527 | 0.5704 | 0.0314 | 0.0442 | 0.6167 | 0.0301 | 0.0409 |
| | | B2[5] | 0.5809 | 0.0363 | 0.0545 | 0.5704 | 0.0349 | 0.0527 | 0.6175 | 0.0310 | 0.0420 |
| | | C2[6] | 0.8192 | 0.0348 | 0.0521 | 0.5795 | 0.0301 | 0.0411 | 0.6308 | 0.0297 | 0.0401 |
| | (80,30) | A3[1] | 0.5843 | 0.0339 | 0.0507 | 0.5689 | 0.0284 | 0.0388 | 0.6367 | 0.0275 | 0.0380 |
| | | B3[2] | 0.5794 | 0.0340 | 0.0510 | 0.5689 | 0.0298 | 0.0399 | 0.6366 | 0.0279 | 0.0386 |
| | | C3[3] | 0.6168 | 0.0332 | 0.0500 | 0.5695 | 0.0275 | 0.0380 | 0.6370 | 0.0267 | 0.0377 |
| | (80,60) | A3[4] | 0.5871 | 0.0321 | 0.0445 | 0.5729 | 0.0257 | 0.0365 | 0.5898 | 0.0248 | 0.0359 |
| | | B3[5] | 0.5874 | 0.0324 | 0.0459 | 0.5735 | 0.0270 | 0.0372 | 0.5922 | 0.0258 | 0.0368 |
| | | C3[6] | 0.7733 | 0.0311 | 0.0430 | 0.5797 | 0.0247 | 0.0359 | 0.6038 | 0.0244 | 0.0345 |
Table 6.
Interval estimations of .
Table 6.
Interval estimations of .
| | T2-PC | ACI-NA | ACI-NL | BCI | HPD |
| Prior→ | | | | | | | 1 | 2 | 1 | 2 |
| For |
|
(1,2) | (30,10) | A1[1] | 0.238 | 0.976 | 0.224 | 0.977 | 0.148 | 0.981 | 0.144 | 0.981 | 0.141 | 0.981 | 0.136 | 0.982 |
| | | B1[2] | 0.357 | 0.970 | 0.288 | 0.973 | 0.153 | 0.981 | 0.145 | 0.981 | 0.142 | 0.981 | 0.138 | 0.982 |
| | | C1[3] | 0.231 | 0.976 | 0.218 | 0.977 | 0.146 | 0.981 | 0.138 | 0.982 | 0.135 | 0.982 | 0.132 | 0.982 |
| | (30,20) | A1[4] | 0.213 | 0.977 | 0.204 | 0.978 | 0.146 | 0.981 | 0.137 | 0.982 | 0.134 | 0.982 | 0.128 | 0.982 |
| | | B1[5] | 0.210 | 0.978 | 0.196 | 0.978 | 0.138 | 0.982 | 0.133 | 0.982 | 0.128 | 0.982 | 0.122 | 0.982 |
| | | C1[6] | 0.198 | 0.978 | 0.186 | 0.979 | 0.130 | 0.982 | 0.129 | 0.982 | 0.126 | 0.982 | 0.121 | 0.982 |
| | (50,20) | A2[1] | 0.186 | 0.979 | 0.169 | 0.980 | 0.126 | 0.982 | 0.122 | 0.982 | 0.119 | 0.983 | 0.117 | 0.983 |
| | | B2[2] | 0.196 | 0.978 | 0.177 | 0.979 | 0.126 | 0.982 | 0.124 | 0.982 | 0.119 | 0.983 | 0.118 | 0.983 |
| | | C2[3] | 0.186 | 0.979 | 0.159 | 0.980 | 0.119 | 0.983 | 0.118 | 0.983 | 0.117 | 0.983 | 0.116 | 0.983 |
| | (50,40) | A2[4] | 0.185 | 0.979 | 0.140 | 0.981 | 0.119 | 0.983 | 0.116 | 0.983 | 0.114 | 0.983 | 0.113 | 0.983 |
| | | B2[5] | 0.185 | 0.979 | 0.146 | 0.981 | 0.119 | 0.983 | 0.118 | 0.983 | 0.116 | 0.983 | 0.115 | 0.983 |
| | | C2[6] | 0.181 | 0.979 | 0.139 | 0.982 | 0.113 | 0.983 | 0.107 | 0.983 | 0.106 | 0.983 | 0.106 | 0.983 |
| | (80,30) | A3[1] | 0.161 | 0.980 | 0.133 | 0.982 | 0.108 | 0.983 | 0.103 | 0.983 | 0.100 | 0.984 | 0.097 | 0.984 |
| | | B3[2] | 0.171 | 0.980 | 0.136 | 0.982 | 0.111 | 0.983 | 0.107 | 0.983 | 0.106 | 0.983 | 0.105 | 0.983 |
| | | C3[3] | 0.155 | 0.981 | 0.130 | 0.982 | 0.108 | 0.983 | 0.100 | 0.984 | 0.098 | 0.984 | 0.095 | 0.984 |
| | (80,60) | A3[4] | 0.146 | 0.981 | 0.110 | 0.983 | 0.098 | 0.984 | 0.096 | 0.984 | 0.096 | 0.984 | 0.088 | 0.984 |
| | | B3[5] | 0.147 | 0.981 | 0.129 | 0.982 | 0.100 | 0.984 | 0.098 | 0.984 | 0.097 | 0.984 | 0.088 | 0.984 |
| | | C3[6] | 0.145 | 0.981 | 0.098 | 0.984 | 0.096 | 0.984 | 0.095 | 0.984 | 0.090 | 0.984 | 0.086 | 0.984 |
|
(2,4) | (30,10) | A1[1] | 0.226 | 0.977 | 0.218 | 0.977 | 0.146 | 0.981 | 0.141 | 0.981 | 0.139 | 0.982 | 0.134 | 0.982 |
| | | B1[2] | 0.334 | 0.971 | 0.267 | 0.975 | 0.150 | 0.981 | 0.143 | 0.981 | 0.140 | 0.981 | 0.136 | 0.982 |
| | | C1[3] | 0.222 | 0.977 | 0.212 | 0.977 | 0.145 | 0.981 | 0.136 | 0.982 | 0.134 | 0.982 | 0.132 | 0.982 |
| | (30,20) | A1[4] | 0.210 | 0.978 | 0.203 | 0.978 | 0.144 | 0.981 | 0.135 | 0.982 | 0.133 | 0.982 | 0.125 | 0.982 |
| | | B1[5] | 0.200 | 0.978 | 0.188 | 0.979 | 0.134 | 0.982 | 0.131 | 0.982 | 0.126 | 0.982 | 0.119 | 0.983 |
| | | C1[6] | 0.189 | 0.979 | 0.179 | 0.979 | 0.130 | 0.982 | 0.126 | 0.982 | 0.122 | 0.982 | 0.117 | 0.983 |
| | (50,20) | A2[1] | 0.180 | 0.979 | 0.165 | 0.980 | 0.124 | 0.982 | 0.121 | 0.982 | 0.117 | 0.983 | 0.115 | 0.983 |
| | | B2[2] | 0.180 | 0.979 | 0.170 | 0.980 | 0.124 | 0.982 | 0.122 | 0.982 | 0.118 | 0.983 | 0.116 | 0.983 |
| | | C2[3] | 0.174 | 0.980 | 0.155 | 0.981 | 0.118 | 0.983 | 0.118 | 0.983 | 0.116 | 0.983 | 0.115 | 0.983 |
| | (50,40) | A2[4] | 0.169 | 0.980 | 0.136 | 0.982 | 0.117 | 0.983 | 0.115 | 0.983 | 0.113 | 0.983 | 0.111 | 0.983 |
| | | B2[5] | 0.173 | 0.980 | 0.137 | 0.982 | 0.118 | 0.983 | 0.117 | 0.983 | 0.115 | 0.983 | 0.113 | 0.983 |
| | | C2[6] | 0.169 | 0.980 | 0.135 | 0.982 | 0.112 | 0.983 | 0.107 | 0.983 | 0.106 | 0.983 | 0.105 | 0.983 |
| | (80,30) | A3[1] | 0.156 | 0.981 | 0.128 | 0.982 | 0.108 | 0.983 | 0.103 | 0.983 | 0.099 | 0.984 | 0.097 | 0.984 |
| | | B3[2] | 0.167 | 0.980 | 0.133 | 0.982 | 0.110 | 0.983 | 0.106 | 0.983 | 0.105 | 0.983 | 0.104 | 0.983 |
| | | C3[3] | 0.151 | 0.981 | 0.127 | 0.982 | 0.107 | 0.983 | 0.099 | 0.984 | 0.098 | 0.984 | 0.095 | 0.984 |
| | (80,60) | A3[4] | 0.143 | 0.981 | 0.109 | 0.983 | 0.096 | 0.984 | 0.096 | 0.984 | 0.095 | 0.984 | 0.085 | 0.984 |
| | | B3[5] | 0.143 | 0.981 | 0.123 | 0.982 | 0.099 | 0.984 | 0.098 | 0.984 | 0.097 | 0.984 | 0.085 | 0.984 |
| | | C3[6] | 0.142 | 0.981 | 0.097 | 0.984 | 0.095 | 0.984 | 0.094 | 0.984 | 0.089 | 0.984 | 0.085 | 0.984 |
|
For |
|
(1,2) | (30,10) | A1[1] | 0.849 | 0.943 | 0.785 | 0.946 | 0.208 | 0.978 | 0.200 | 0.978 | 0.194 | 0.978 | 0.191 | 0.978 |
| | | B1[2] | 0.977 | 0.936 | 0.872 | 0.942 | 0.213 | 0.977 | 0.206 | 0.978 | 0.195 | 0.978 | 0.193 | 0.979 |
| | | C1[3] | 0.831 | 0.944 | 0.773 | 0.947 | 0.207 | 0.978 | 0.192 | 0.979 | 0.181 | 0.979 | 0.178 | 0.979 |
| | (30,20) | A1[4] | 0.739 | 0.949 | 0.614 | 0.956 | 0.198 | 0.978 | 0.186 | 0.979 | 0.174 | 0.980 | 0.171 | 0.980 |
| | | B1[5] | 0.696 | 0.951 | 0.567 | 0.958 | 0.186 | 0.979 | 0.181 | 0.979 | 0.173 | 0.980 | 0.170 | 0.980 |
| | | C1[6] | 0.595 | 0.957 | 0.544 | 0.960 | 0.185 | 0.979 | 0.176 | 0.979 | 0.173 | 0.980 | 0.170 | 0.980 |
| | (50,20) | A2[1] | 0.564 | 0.958 | 0.543 | 0.960 | 0.173 | 0.980 | 0.170 | 0.980 | 0.166 | 0.980 | 0.159 | 0.980 |
| | | B2[2] | 0.587 | 0.957 | 0.543 | 0.960 | 0.181 | 0.979 | 0.176 | 0.979 | 0.166 | 0.980 | 0.162 | 0.980 |
| | | C2[3] | 0.562 | 0.959 | 0.540 | 0.960 | 0.171 | 0.980 | 0.170 | 0.980 | 0.157 | 0.980 | 0.156 | 0.981 |
| | (50,40) | A2[4] | 0.481 | 0.963 | 0.450 | 0.965 | 0.171 | 0.980 | 0.167 | 0.980 | 0.157 | 0.981 | 0.153 | 0.981 |
| | | B2[5] | 0.531 | 0.960 | 0.518 | 0.961 | 0.171 | 0.980 | 0.170 | 0.980 | 0.157 | 0.980 | 0.156 | 0.981 |
| | | C2[6] | 0.458 | 0.964 | 0.438 | 0.965 | 0.156 | 0.981 | 0.154 | 0.981 | 0.145 | 0.981 | 0.143 | 0.981 |
| | (80,30) | A3[1] | 0.395 | 0.968 | 0.391 | 0.968 | 0.143 | 0.981 | 0.140 | 0.981 | 0.130 | 0.982 | 0.129 | 0.982 |
| | | B3[2] | 0.437 | 0.965 | 0.423 | 0.966 | 0.156 | 0.981 | 0.154 | 0.981 | 0.142 | 0.981 | 0.141 | 0.981 |
| | | C3[3] | 0.380 | 0.968 | 0.360 | 0.970 | 0.140 | 0.981 | 0.138 | 0.982 | 0.129 | 0.982 | 0.128 | 0.982 |
| | (80,60) | A3[4] | 0.327 | 0.971 | 0.311 | 0.972 | 0.128 | 0.982 | 0.125 | 0.982 | 0.120 | 0.982 | 0.118 | 0.983 |
| | | B3[5] | 0.377 | 0.969 | 0.347 | 0.970 | 0.131 | 0.982 | 0.128 | 0.982 | 0.124 | 0.982 | 0.119 | 0.983 |
| | | C3[6] | 0.309 | 0.972 | 0.293 | 0.973 | 0.126 | 0.982 | 0.122 | 0.982 | 0.119 | 0.983 | 0.117 | 0.983 |
|
(2,4) | (30,10) | A1[1] | 0.820 | 0.944 | 0.768 | 0.947 | 0.201 | 0.978 | 0.194 | 0.978 | 0.194 | 0.979 | 0.189 | 0.979 |
| | | B1[2] | 0.917 | 0.939 | 0.819 | 0.945 | 0.211 | 0.978 | 0.199 | 0.978 | 0.194 | 0.978 | 0.193 | 0.979 |
| | | C1[3] | 0.804 | 0.945 | 0.752 | 0.948 | 0.201 | 0.978 | 0.189 | 0.979 | 0.178 | 0.979 | 0.175 | 0.979 |
| | (30,20) | A1[4] | 0.716 | 0.950 | 0.595 | 0.957 | 0.196 | 0.978 | 0.184 | 0.979 | 0.172 | 0.980 | 0.170 | 0.980 |
| | | B1[5] | 0.674 | 0.952 | 0.550 | 0.959 | 0.183 | 0.979 | 0.179 | 0.979 | 0.172 | 0.980 | 0.169 | 0.980 |
| | | C1[6] | 0.570 | 0.958 | 0.526 | 0.960 | 0.180 | 0.979 | 0.174 | 0.980 | 0.171 | 0.980 | 0.168 | 0.980 |
| | (50,20) | A2[1] | 0.544 | 0.960 | 0.525 | 0.961 | 0.171 | 0.980 | 0.169 | 0.980 | 0.163 | 0.980 | 0.156 | 0.981 |
| | | B2[2] | 0.563 | 0.958 | 0.525 | 0.960 | 0.178 | 0.979 | 0.171 | 0.980 | 0.166 | 0.980 | 0.162 | 0.980 |
| | | C2[3] | 0.542 | 0.960 | 0.524 | 0.961 | 0.170 | 0.980 | 0.169 | 0.980 | 0.157 | 0.981 | 0.155 | 0.981 |
| | (50,40) | A2[4] | 0.468 | 0.964 | 0.441 | 0.965 | 0.168 | 0.980 | 0.165 | 0.980 | 0.157 | 0.981 | 0.153 | 0.981 |
| | | B2[5] | 0.520 | 0.961 | 0.510 | 0.961 | 0.170 | 0.980 | 0.168 | 0.980 | 0.157 | 0.981 | 0.155 | 0.981 |
| | | C2[6] | 0.447 | 0.965 | 0.428 | 0.966 | 0.155 | 0.981 | 0.153 | 0.981 | 0.144 | 0.981 | 0.141 | 0.981 |
| | (80,30) | A3[1] | 0.395 | 0.968 | 0.387 | 0.968 | 0.142 | 0.981 | 0.139 | 0.982 | 0.129 | 0.982 | 0.128 | 0.982 |
| | | B3[2] | 0.427 | 0.966 | 0.414 | 0.967 | 0.155 | 0.981 | 0.152 | 0.981 | 0.141 | 0.981 | 0.141 | 0.981 |
| | | C3[3] | 0.373 | 0.969 | 0.354 | 0.970 | 0.138 | 0.982 | 0.137 | 0.982 | 0.128 | 0.982 | 0.128 | 0.982 |
| | (80,60) | A3[4] | 0.323 | 0.972 | 0.308 | 0.972 | 0.127 | 0.982 | 0.122 | 0.982 | 0.119 | 0.983 | 0.117 | 0.983 |
| | | B3[5] | 0.371 | 0.969 | 0.342 | 0.970 | 0.130 | 0.982 | 0.127 | 0.982 | 0.120 | 0.982 | 0.118 | 0.983 |
| | | C3[6] | 0.306 | 0.972 | 0.289 | 0.973 | 0.127 | 0.982 | 0.122 | 0.982 | 0.119 | 0.983 | 0.117 | 0.983 |
Table 7.
Interval estimations of .
Table 7.
Interval estimations of .
| | T2-PC | ACI-NA | ACI-NL | BCI | HPD |
| Prior→ | | | | | | | 1 | 2 | 1 | 2 |
| For |
|
(1,2) | (30,10) | A1[1] | 0.684 | 0.937 | 0.693 | 0.937 | 0.647 | 0.940 | 0.622 | 0.940 | 0.221 | 0.968 | 0.215 | 0.969 |
| | | B1[2] | 0.721 | 0.935 | 0.803 | 0.929 | 0.710 | 0.936 | 0.633 | 0.941 | 0.227 | 0.968 | 0.220 | 0.968 |
| | | C1[3] | 0.744 | 0.933 | 0.817 | 0.928 | 0.721 | 0.935 | 0.633 | 0.941 | 0.336 | 0.961 | 0.270 | 0.965 |
| | (30,20) | A1[4] | 0.601 | 0.943 | 0.606 | 0.943 | 0.597 | 0.943 | 0.596 | 0.943 | 0.191 | 0.970 | 0.181 | 0.971 |
| | | B1[5] | 0.606 | 0.941 | 0.621 | 0.942 | 0.604 | 0.943 | 0.601 | 0.943 | 0.202 | 0.970 | 0.191 | 0.970 |
| | | C1[6] | 0.622 | 0.940 | 0.631 | 0.941 | 0.614 | 0.942 | 0.611 | 0.942 | 0.206 | 0.969 | 0.204 | 0.969 |
| | (50,20) | A2[1] | 0.594 | 0.943 | 0.599 | 0.943 | 0.585 | 0.944 | 0.582 | 0.944 | 0.177 | 0.971 | 0.157 | 0.973 |
| | | B2[2] | 0.600 | 0.943 | 0.605 | 0.943 | 0.595 | 0.943 | 0.589 | 0.944 | 0.182 | 0.971 | 0.172 | 0.972 |
| | | C2[3] | 0.596 | 0.943 | 0.599 | 0.943 | 0.593 | 0.943 | 0.587 | 0.944 | 0.182 | 0.971 | 0.166 | 0.972 |
| | (50,40) | A2[4] | 0.578 | 0.945 | 0.586 | 0.944 | 0.565 | 0.945 | 0.548 | 0.946 | 0.172 | 0.972 | 0.137 | 0.974 |
| | | B2[5] | 0.586 | 0.944 | 0.591 | 0.944 | 0.573 | 0.945 | 0.560 | 0.946 | 0.176 | 0.971 | 0.139 | 0.974 |
| | | C2[6] | 0.580 | 0.944 | 0.589 | 0.944 | 0.568 | 0.945 | 0.550 | 0.946 | 0.172 | 0.972 | 0.138 | 0.974 |
| | (80,30) | A3[1] | 0.526 | 0.948 | 0.544 | 0.947 | 0.514 | 0.949 | 0.509 | 0.949 | 0.153 | 0.973 | 0.128 | 0.974 |
| | | B3[2] | 0.529 | 0.948 | 0.544 | 0.947 | 0.519 | 0.948 | 0.515 | 0.949 | 0.158 | 0.972 | 0.129 | 0.974 |
| | | C3[3] | 0.558 | 0.946 | 0.568 | 0.945 | 0.535 | 0.947 | 0.526 | 0.948 | 0.169 | 0.972 | 0.134 | 0.974 |
| | (80,60) | A3[4] | 0.468 | 0.952 | 0.516 | 0.949 | 0.453 | 0.953 | 0.448 | 0.953 | 0.144 | 0.973 | 0.098 | 0.976 |
| | | B3[5] | 0.488 | 0.950 | 0.524 | 0.948 | 0.479 | 0.951 | 0.452 | 0.953 | 0.144 | 0.973 | 0.110 | 0.976 |
| | | C3[6] | 0.509 | 0.949 | 0.526 | 0.948 | 0.489 | 0.950 | 0.462 | 0.952 | 0.145 | 0.973 | 0.124 | 0.975 |
|
(2,4) | (30,10) | A1[1] | 0.679 | 0.938 | 0.685 | 0.937 | 0.642 | 0.940 | 0.611 | 0.942 | 0.221 | 0.968 | 0.215 | 0.969 |
| | | B1[2] | 0.715 | 0.935 | 0.792 | 0.930 | 0.706 | 0.936 | 0.612 | 0.942 | 0.227 | 0.968 | 0.220 | 0.968 |
| | | C1[3] | 0.740 | 0.934 | 0.807 | 0.929 | 0.715 | 0.935 | 0.614 | 0.942 | 0.336 | 0.961 | 0.270 | 0.965 |
| | (30,20) | A1[4] | 0.600 | 0.943 | 0.604 | 0.943 | 0.597 | 0.942 | 0.593 | 0.943 | 0.191 | 0.970 | 0.181 | 0.971 |
| | | B1[5] | 0.606 | 0.943 | 0.608 | 0.942 | 0.601 | 0.943 | 0.598 | 0.943 | 0.202 | 0.970 | 0.191 | 0.970 |
| | | C1[6] | 0.621 | 0.942 | 0.624 | 0.941 | 0.614 | 0.942 | 0.611 | 0.942 | 0.206 | 0.969 | 0.204 | 0.969 |
| | (50,20) | A2[1] | 0.592 | 0.943 | 0.596 | 0.943 | 0.583 | 0.944 | 0.569 | 0.945 | 0.177 | 0.971 | 0.157 | 0.973 |
| | | B2[2] | 0.597 | 0.943 | 0.602 | 0.943 | 0.592 | 0.944 | 0.586 | 0.944 | 0.182 | 0.971 | 0.172 | 0.972 |
| | | C2[3] | 0.594 | 0.943 | 0.597 | 0.943 | 0.589 | 0.944 | 0.584 | 0.944 | 0.182 | 0.971 | 0.166 | 0.972 |
| | (50,40) | A2[4] | 0.565 | 0.945 | 0.584 | 0.944 | 0.549 | 0.946 | 0.527 | 0.948 | 0.172 | 0.972 | 0.137 | 0.974 |
| | | B2[5] | 0.577 | 0.944 | 0.590 | 0.944 | 0.564 | 0.945 | 0.550 | 0.946 | 0.176 | 0.971 | 0.139 | 0.974 |
| | | C2[6] | 0.571 | 0.945 | 0.587 | 0.944 | 0.560 | 0.946 | 0.540 | 0.947 | 0.172 | 0.972 | 0.138 | 0.974 |
| | (80,30) | A3[1] | 0.522 | 0.948 | 0.535 | 0.947 | 0.510 | 0.949 | 0.500 | 0.950 | 0.153 | 0.973 | 0.128 | 0.974 |
| | | B3[2] | 0.527 | 0.948 | 0.535 | 0.947 | 0.518 | 0.948 | 0.506 | 0.949 | 0.158 | 0.972 | 0.129 | 0.974 |
| | | C3[3] | 0.547 | 0.946 | 0.559 | 0.946 | 0.527 | 0.948 | 0.519 | 0.948 | 0.169 | 0.972 | 0.134 | 0.974 |
| | (80,60) | A3[4] | 0.460 | 0.952 | 0.506 | 0.949 | 0.452 | 0.953 | 0.445 | 0.953 | 0.144 | 0.973 | 0.098 | 0.976 |
| | | B3[5] | 0.480 | 0.951 | 0.510 | 0.949 | 0.472 | 0.952 | 0.445 | 0.953 | 0.144 | 0.973 | 0.110 | 0.976 |
| | | C3[6] | 0.498 | 0.950 | 0.510 | 0.949 | 0.480 | 0.951 | 0.455 | 0.953 | 0.145 | 0.973 | 0.124 | 0.975 |
|
For |
|
(1,2) | (30,10) | A1[1] | 0.861 | 0.926 | 0.898 | 0.923 | 0.833 | 0.927 | 0.825 | 0.928 | 0.758 | 0.932 | 0.736 | 0.934 |
| | | B1[2] | 0.875 | 0.925 | 0.898 | 0.923 | 0.844 | 0.927 | 0.831 | 0.928 | 0.772 | 0.932 | 0.751 | 0.933 |
| | | C1[3] | 0.898 | 0.923 | 0.915 | 0.922 | 0.888 | 0.924 | 0.846 | 0.927 | 0.833 | 0.927 | 0.797 | 0.930 |
| | (30,20) | A1[4] | 0.841 | 0.927 | 0.853 | 0.926 | 0.793 | 0.930 | 0.786 | 0.931 | 0.563 | 0.945 | 0.517 | 0.949 |
| | | B1[5] | 0.847 | 0.926 | 0.859 | 0.926 | 0.798 | 0.930 | 0.790 | 0.930 | 0.653 | 0.939 | 0.538 | 0.947 |
| | | C1[6] | 0.861 | 0.926 | 0.879 | 0.924 | 0.802 | 0.930 | 0.793 | 0.930 | 0.685 | 0.937 | 0.581 | 0.944 |
| | (50,20) | A2[1] | 0.834 | 0.927 | 0.841 | 0.927 | 0.774 | 0.931 | 0.772 | 0.932 | 0.532 | 0.947 | 0.516 | 0.949 |
| | | B2[2] | 0.838 | 0.927 | 0.851 | 0.926 | 0.774 | 0.931 | 0.772 | 0.932 | 0.555 | 0.946 | 0.516 | 0.949 |
| | | C2[3] | 0.834 | 0.927 | 0.841 | 0.927 | 0.774 | 0.931 | 0.772 | 0.932 | 0.535 | 0.947 | 0.516 | 0.949 |
| | (50,40) | A2[4] | 0.773 | 0.931 | 0.813 | 0.929 | 0.755 | 0.933 | 0.748 | 0.933 | 0.440 | 0.954 | 0.421 | 0.955 |
| | | B2[5] | 0.810 | 0.929 | 0.836 | 0.927 | 0.768 | 0.932 | 0.761 | 0.932 | 0.506 | 0.949 | 0.492 | 0.950 |
| | | C2[6] | 0.788 | 0.930 | 0.817 | 0.928 | 0.764 | 0.932 | 0.753 | 0.933 | 0.461 | 0.952 | 0.433 | 0.954 |
| | (80,30) | A3[1] | 0.740 | 0.934 | 0.758 | 0.932 | 0.694 | 0.937 | 0.677 | 0.938 | 0.368 | 0.959 | 0.349 | 0.960 |
| | | B3[2] | 0.743 | 0.933 | 0.758 | 0.932 | 0.694 | 0.937 | 0.677 | 0.938 | 0.382 | 0.958 | 0.379 | 0.958 |
| | | C3[3] | 0.743 | 0.933 | 0.758 | 0.932 | 0.725 | 0.935 | 0.695 | 0.937 | 0.421 | 0.955 | 0.408 | 0.956 |
| | (80,60) | A3[4] | 0.632 | 0.941 | 0.685 | 0.937 | 0.594 | 0.943 | 0.584 | 0.944 | 0.301 | 0.963 | 0.285 | 0.964 |
| | | B3[5] | 0.644 | 0.940 | 0.686 | 0.937 | 0.596 | 0.943 | 0.587 | 0.944 | 0.318 | 0.962 | 0.303 | 0.963 |
| | | C3[6] | 0.674 | 0.938 | 0.690 | 0.937 | 0.645 | 0.940 | 0.632 | 0.941 | 0.365 | 0.959 | 0.337 | 0.961 |
|
(2,4) | (30,10) | A1[1] | 0.856 | 0.926 | 0.893 | 0.923 | 0.833 | 0.927 | 0.825 | 0.928 | 0.758 | 0.932 | 0.736 | 0.934 |
| | | B1[2] | 0.856 | 0.926 | 0.893 | 0.923 | 0.833 | 0.927 | 0.825 | 0.928 | 0.772 | 0.932 | 0.751 | 0.933 |
| | | C1[3] | 0.893 | 0.923 | 0.910 | 0.922 | 0.888 | 0.924 | 0.844 | 0.927 | 0.831 | 0.928 | 0.796 | 0.930 |
| | (30,20) | A1[4] | 0.834 | 0.927 | 0.847 | 0.927 | 0.789 | 0.930 | 0.773 | 0.931 | 0.563 | 0.945 | 0.517 | 0.949 |
| | | B1[5] | 0.845 | 0.927 | 0.850 | 0.926 | 0.792 | 0.930 | 0.790 | 0.930 | 0.652 | 0.939 | 0.538 | 0.947 |
| | | C1[6] | 0.853 | 0.926 | 0.873 | 0.925 | 0.796 | 0.930 | 0.790 | 0.930 | 0.685 | 0.937 | 0.581 | 0.944 |
| | (50,20) | A2[1] | 0.829 | 0.928 | 0.836 | 0.927 | 0.772 | 0.932 | 0.761 | 0.932 | 0.532 | 0.947 | 0.516 | 0.949 |
| | | B2[2] | 0.831 | 0.928 | 0.845 | 0.927 | 0.773 | 0.931 | 0.770 | 0.932 | 0.555 | 0.946 | 0.516 | 0.949 |
| | | C2[3] | 0.830 | 0.928 | 0.836 | 0.927 | 0.772 | 0.932 | 0.761 | 0.932 | 0.535 | 0.947 | 0.516 | 0.949 |
| | (50,40) | A2[4] | 0.762 | 0.932 | 0.788 | 0.930 | 0.753 | 0.933 | 0.743 | 0.933 | 0.440 | 0.954 | 0.421 | 0.955 |
| | | B2[5] | 0.785 | 0.931 | 0.830 | 0.928 | 0.764 | 0.932 | 0.759 | 0.932 | 0.506 | 0.949 | 0.492 | 0.950 |
| | | C2[6] | 0.764 | 0.932 | 0.793 | 0.930 | 0.764 | 0.932 | 0.745 | 0.933 | 0.461 | 0.952 | 0.433 | 0.954 |
| | (80,30) | A3[1] | 0.720 | 0.935 | 0.747 | 0.933 | 0.693 | 0.937 | 0.676 | 0.938 | 0.368 | 0.959 | 0.349 | 0.960 |
| | | B3[2] | 0.731 | 0.934 | 0.747 | 0.933 | 0.694 | 0.937 | 0.677 | 0.938 | 0.382 | 0.958 | 0.379 | 0.958 |
| | | C3[3] | 0.735 | 0.934 | 0.750 | 0.933 | 0.710 | 0.936 | 0.679 | 0.938 | 0.421 | 0.955 | 0.408 | 0.956 |
| | (80,60) | A3[4] | 0.625 | 0.941 | 0.663 | 0.939 | 0.586 | 0.944 | 0.576 | 0.945 | 0.301 | 0.963 | 0.285 | 0.964 |
| | | B3[5] | 0.636 | 0.941 | 0.677 | 0.938 | 0.594 | 0.943 | 0.587 | 0.944 | 0.318 | 0.962 | 0.303 | 0.963 |
| | | C3[6] | 0.665 | 0.939 | 0.682 | 0.938 | 0.634 | 0.941 | 0.621 | 0.942 | 0.365 | 0.959 | 0.337 | 0.961 |
Table 8.
Interval estimations of .
Table 8.
Interval estimations of .
| | T2-PC | ACI-NA | ACI-NL | BCI | HPD |
| Prior→ | | | | | | | 1 | 2 | 1 | 2 |
| For |
|
(1,2) | (30,10) | A1[1] | 0.793 | 0.928 | 0.713 | 0.933 | 0.703 | 0.933 | 0.626 | 0.938 | 0.238 | 0.961 | 0.224 | 0.962 |
| | | B1[2] | 0.808 | 0.927 | 0.737 | 0.931 | 0.713 | 0.933 | 0.626 | 0.938 | 0.357 | 0.954 | 0.288 | 0.958 |
| | | C1[3] | 0.686 | 0.934 | 0.677 | 0.935 | 0.640 | 0.937 | 0.615 | 0.938 | 0.231 | 0.961 | 0.218 | 0.962 |
| | (30,20) | A1[4] | 0.614 | 0.939 | 0.600 | 0.939 | 0.597 | 0.940 | 0.595 | 0.940 | 0.210 | 0.963 | 0.196 | 0.963 |
| | | B1[5] | 0.624 | 0.938 | 0.615 | 0.938 | 0.608 | 0.939 | 0.605 | 0.939 | 0.213 | 0.962 | 0.204 | 0.963 |
| | | C1[6] | 0.600 | 0.939 | 0.594 | 0.940 | 0.591 | 0.940 | 0.589 | 0.940 | 0.198 | 0.963 | 0.186 | 0.964 |
| | (50,20) | A2[1] | 0.593 | 0.940 | 0.590 | 0.940 | 0.587 | 0.940 | 0.580 | 0.941 | 0.186 | 0.964 | 0.169 | 0.965 |
| | | B2[2] | 0.599 | 0.939 | 0.594 | 0.940 | 0.589 | 0.940 | 0.582 | 0.940 | 0.196 | 0.963 | 0.177 | 0.965 |
| | | C2[3] | 0.593 | 0.940 | 0.588 | 0.940 | 0.579 | 0.941 | 0.576 | 0.941 | 0.186 | 0.964 | 0.159 | 0.966 |
| | (50,40) | A2[4] | 0.583 | 0.940 | 0.574 | 0.941 | 0.562 | 0.942 | 0.544 | 0.943 | 0.185 | 0.964 | 0.140 | 0.967 |
| | | B2[5] | 0.584 | 0.940 | 0.580 | 0.941 | 0.567 | 0.941 | 0.554 | 0.942 | 0.185 | 0.964 | 0.146 | 0.966 |
| | | C2[6] | 0.579 | 0.941 | 0.573 | 0.941 | 0.559 | 0.942 | 0.542 | 0.943 | 0.181 | 0.964 | 0.139 | 0.967 |
| | (80,30) | A3[1] | 0.537 | 0.943 | 0.523 | 0.944 | 0.513 | 0.945 | 0.509 | 0.945 | 0.161 | 0.965 | 0.133 | 0.967 |
| | | B3[2] | 0.562 | 0.942 | 0.552 | 0.942 | 0.529 | 0.944 | 0.520 | 0.944 | 0.171 | 0.965 | 0.136 | 0.967 |
| | | C3[3] | 0.537 | 0.943 | 0.520 | 0.944 | 0.508 | 0.945 | 0.503 | 0.945 | 0.155 | 0.966 | 0.130 | 0.967 |
| | (80,60) | A3[4] | 0.518 | 0.944 | 0.482 | 0.946 | 0.474 | 0.947 | 0.447 | 0.948 | 0.146 | 0.966 | 0.110 | 0.968 |
| | | B3[5] | 0.520 | 0.944 | 0.503 | 0.945 | 0.484 | 0.946 | 0.457 | 0.948 | 0.147 | 0.966 | 0.129 | 0.967 |
| | | C3[6] | 0.510 | 0.945 | 0.463 | 0.948 | 0.448 | 0.948 | 0.443 | 0.949 | 0.145 | 0.966 | 0.098 | 0.969 |
|
(2,4) | (30,10) | A1[1] | 0.783 | 0.929 | 0.708 | 0.933 | 0.699 | 0.933 | 0.606 | 0.939 | 0.226 | 0.962 | 0.218 | 0.962 |
| | | B1[2] | 0.797 | 0.928 | 0.733 | 0.932 | 0.708 | 0.933 | 0.608 | 0.939 | 0.334 | 0.955 | 0.267 | 0.959 |
| | | C1[3] | 0.677 | 0.935 | 0.672 | 0.935 | 0.635 | 0.937 | 0.605 | 0.939 | 0.222 | 0.962 | 0.212 | 0.962 |
| | (30,20) | A1[4] | 0.602 | 0.939 | 0.599 | 0.939 | 0.595 | 0.940 | 0.593 | 0.940 | 0.200 | 0.963 | 0.188 | 0.964 |
| | | B1[5] | 0.618 | 0.938 | 0.614 | 0.939 | 0.608 | 0.939 | 0.604 | 0.939 | 0.210 | 0.963 | 0.203 | 0.963 |
| | | C1[6] | 0.598 | 0.939 | 0.594 | 0.940 | 0.590 | 0.940 | 0.586 | 0.940 | 0.189 | 0.964 | 0.179 | 0.964 |
| | (50,20) | A2[1] | 0.591 | 0.940 | 0.588 | 0.940 | 0.582 | 0.940 | 0.577 | 0.941 | 0.180 | 0.964 | 0.165 | 0.965 |
| | | B2[2] | 0.596 | 0.940 | 0.591 | 0.940 | 0.586 | 0.940 | 0.579 | 0.941 | 0.180 | 0.964 | 0.170 | 0.965 |
| | | C2[3] | 0.589 | 0.940 | 0.586 | 0.940 | 0.577 | 0.941 | 0.563 | 0.942 | 0.174 | 0.965 | 0.155 | 0.966 |
| | (50,40) | A2[4] | 0.580 | 0.941 | 0.566 | 0.941 | 0.555 | 0.942 | 0.534 | 0.943 | 0.169 | 0.965 | 0.136 | 0.967 |
| | | B2[5] | 0.583 | 0.940 | 0.571 | 0.941 | 0.559 | 0.942 | 0.544 | 0.943 | 0.173 | 0.965 | 0.137 | 0.967 |
| | | C2[6] | 0.578 | 0.941 | 0.560 | 0.942 | 0.543 | 0.943 | 0.521 | 0.944 | 0.169 | 0.965 | 0.135 | 0.967 |
| | (80,30) | A3[1] | 0.529 | 0.944 | 0.521 | 0.944 | 0.512 | 0.945 | 0.500 | 0.945 | 0.156 | 0.966 | 0.128 | 0.967 |
| | | B3[2] | 0.552 | 0.942 | 0.541 | 0.943 | 0.521 | 0.944 | 0.513 | 0.945 | 0.167 | 0.965 | 0.133 | 0.967 |
| | | C3[3] | 0.529 | 0.944 | 0.515 | 0.944 | 0.504 | 0.945 | 0.494 | 0.946 | 0.151 | 0.966 | 0.127 | 0.968 |
| | (80,60) | A3[4] | 0.504 | 0.945 | 0.474 | 0.947 | 0.466 | 0.947 | 0.440 | 0.949 | 0.143 | 0.967 | 0.109 | 0.969 |
| | | B3[5] | 0.504 | 0.945 | 0.492 | 0.946 | 0.475 | 0.947 | 0.450 | 0.948 | 0.143 | 0.967 | 0.123 | 0.968 |
| | | C3[6] | 0.500 | 0.945 | 0.454 | 0.948 | 0.447 | 0.948 | 0.440 | 0.949 | 0.142 | 0.967 | 0.097 | 0.969 |
|
For |
|
(1,2) | (30,10) | A1[1] | 0.912 | 0.920 | 0.889 | 0.921 | 0.858 | 0.924 | 0.847 | 0.925 | 0.839 | 0.925 | 0.785 | 0.928 |
| | | B1[2] | 0.977 | 0.917 | 0.927 | 0.920 | 0.912 | 0.921 | 0.872 | 0.923 | 0.858 | 0.924 | 0.845 | 0.925 |
| | | C1[3] | 0.912 | 0.921 | 0.875 | 0.922 | 0.847 | 0.925 | 0.839 | 0.925 | 0.831 | 0.926 | 0.773 | 0.929 |
| | (30,20) | A1[4] | 0.874 | 0.923 | 0.863 | 0.924 | 0.809 | 0.927 | 0.801 | 0.927 | 0.696 | 0.934 | 0.567 | 0.941 |
| | | B1[5] | 0.895 | 0.922 | 0.874 | 0.923 | 0.812 | 0.927 | 0.803 | 0.927 | 0.739 | 0.931 | 0.614 | 0.939 |
| | | C1[6] | 0.869 | 0.923 | 0.856 | 0.924 | 0.803 | 0.927 | 0.797 | 0.928 | 0.595 | 0.940 | 0.544 | 0.943 |
| | (50,20) | A2[1] | 0.856 | 0.924 | 0.849 | 0.925 | 0.787 | 0.928 | 0.782 | 0.929 | 0.564 | 0.941 | 0.543 | 0.943 |
| | | B2[2] | 0.867 | 0.923 | 0.854 | 0.924 | 0.787 | 0.928 | 0.784 | 0.928 | 0.587 | 0.940 | 0.543 | 0.943 |
| | | C2[3] | 0.856 | 0.924 | 0.849 | 0.925 | 0.787 | 0.928 | 0.782 | 0.929 | 0.562 | 0.942 | 0.540 | 0.943 |
| | (50,40) | A2[4] | 0.830 | 0.926 | 0.800 | 0.927 | 0.776 | 0.929 | 0.765 | 0.930 | 0.481 | 0.946 | 0.450 | 0.948 |
| | | B2[5] | 0.852 | 0.925 | 0.822 | 0.926 | 0.778 | 0.929 | 0.773 | 0.929 | 0.531 | 0.943 | 0.518 | 0.944 |
| | | C2[6] | 0.825 | 0.926 | 0.784 | 0.928 | 0.768 | 0.929 | 0.759 | 0.930 | 0.458 | 0.948 | 0.438 | 0.949 |
| | (80,30) | A3[1] | 0.770 | 0.929 | 0.753 | 0.930 | 0.708 | 0.933 | 0.690 | 0.934 | 0.395 | 0.952 | 0.391 | 0.952 |
| | | B3[2] | 0.770 | 0.929 | 0.756 | 0.929 | 0.739 | 0.931 | 0.709 | 0.933 | 0.437 | 0.949 | 0.423 | 0.950 |
| | | C3[3] | 0.769 | 0.929 | 0.750 | 0.930 | 0.708 | 0.933 | 0.690 | 0.934 | 0.380 | 0.952 | 0.360 | 0.954 |
| | (80,60) | A3[4] | 0.695 | 0.934 | 0.652 | 0.936 | 0.606 | 0.939 | 0.597 | 0.940 | 0.327 | 0.956 | 0.311 | 0.957 |
| | | B3[5] | 0.700 | 0.933 | 0.683 | 0.934 | 0.655 | 0.936 | 0.643 | 0.937 | 0.377 | 0.953 | 0.347 | 0.954 |
| | | C3[6] | 0.694 | 0.934 | 0.641 | 0.937 | 0.605 | 0.939 | 0.594 | 0.940 | 0.309 | 0.957 | 0.293 | 0.958 |
|
(2,4) | (30,10) | A1[1] | 0.906 | 0.921 | 0.869 | 0.923 | 0.849 | 0.925 | 0.845 | 0.925 | 0.820 | 0.926 | 0.768 | 0.929 |
| | | B1[2] | 0.932 | 0.920 | 0.917 | 0.921 | 0.906 | 0.921 | 0.860 | 0.924 | 0.847 | 0.925 | 0.819 | 0.926 |
| | | C1[3] | 0.906 | 0.921 | 0.869 | 0.923 | 0.847 | 0.925 | 0.839 | 0.925 | 0.804 | 0.927 | 0.752 | 0.930 |
| | (30,20) | A1[4] | 0.863 | 0.924 | 0.858 | 0.924 | 0.803 | 0.927 | 0.800 | 0.927 | 0.674 | 0.935 | 0.550 | 0.942 |
| | | B1[5] | 0.890 | 0.922 | 0.869 | 0.923 | 0.807 | 0.927 | 0.801 | 0.927 | 0.716 | 0.933 | 0.595 | 0.940 |
| | | C1[6] | 0.861 | 0.924 | 0.849 | 0.925 | 0.800 | 0.928 | 0.784 | 0.928 | 0.570 | 0.941 | 0.526 | 0.944 |
| | (50,20) | A2[1] | 0.852 | 0.924 | 0.845 | 0.925 | 0.784 | 0.928 | 0.773 | 0.929 | 0.544 | 0.943 | 0.525 | 0.944 |
| | | B2[2] | 0.861 | 0.924 | 0.847 | 0.925 | 0.785 | 0.928 | 0.782 | 0.929 | 0.563 | 0.942 | 0.525 | 0.944 |
| | | C2[3] | 0.852 | 0.924 | 0.845 | 0.925 | 0.783 | 0.928 | 0.773 | 0.929 | 0.542 | 0.943 | 0.524 | 0.944 |
| | (50,40) | A2[4] | 0.805 | 0.927 | 0.776 | 0.929 | 0.775 | 0.929 | 0.758 | 0.930 | 0.468 | 0.947 | 0.441 | 0.949 |
| | | B2[5] | 0.845 | 0.925 | 0.797 | 0.928 | 0.776 | 0.929 | 0.771 | 0.929 | 0.520 | 0.944 | 0.510 | 0.945 |
| | | C2[6] | 0.800 | 0.927 | 0.774 | 0.929 | 0.765 | 0.930 | 0.753 | 0.930 | 0.447 | 0.948 | 0.428 | 0.950 |
| | (80,30) | A3[1] | 0.757 | 0.930 | 0.743 | 0.931 | 0.708 | 0.933 | 0.690 | 0.934 | 0.395 | 0.952 | 0.387 | 0.952 |
| | | B3[2] | 0.761 | 0.930 | 0.746 | 0.931 | 0.724 | 0.932 | 0.692 | 0.934 | 0.427 | 0.950 | 0.414 | 0.950 |
| | | C3[3] | 0.757 | 0.930 | 0.730 | 0.932 | 0.706 | 0.933 | 0.689 | 0.934 | 0.373 | 0.953 | 0.354 | 0.954 |
| | (80,60) | A3[4] | 0.686 | 0.934 | 0.645 | 0.937 | 0.605 | 0.939 | 0.597 | 0.940 | 0.323 | 0.956 | 0.308 | 0.957 |
| | | B3[5] | 0.691 | 0.934 | 0.674 | 0.935 | 0.644 | 0.937 | 0.633 | 0.937 | 0.371 | 0.953 | 0.342 | 0.955 |
| | | C3[6] | 0.673 | 0.935 | 0.633 | 0.937 | 0.596 | 0.940 | 0.586 | 0.940 | 0.306 | 0.957 | 0.289 | 0.958 |