On Corresponding Cauchy–Riemann Equations Applied to Laplace-Type Operators over Generalized Quaternions, with an Application
Abstract
1. Introduction
- Scope and goals (compact overview)
- Setting and viewpoint.
- Contributions
- CR systems and differentiability: Starting from left/right difference quotients, we derive complete CR systems and prove necessity and—on under regularity—sufficiency for left/right differentiability. This creates a precise bridge between one-dimensional calculus and a genuinely four-dimensional setting.
- Dirac factorization and harmonicity: We factor a constant coefficient second-order operatorwhich implies that each real component of a differentiable mapping is -harmonic. The principal symbol cleanly separates the elliptic (Hamiltonian) and split (coquaternionic) regimes.
- Model boundary value problem: In the elliptic case , we establish a Poisson-type representation that solves a model Dirichlet problem on the unit ball , recovering the mean value and maximum principles.
- Linearization and computation: Real matrix models for left/right multiplication linearize the CR systems and the associated second-order operator, yielding identities suitable for symbolic or numerical verification.
- Examples and contrasts: A portfolio of examples (polynomials, affine CR families, and split-signature contrasts) illustrates the theory and highlights the role of signature.
- Related background
- Recent literature (2022–2025)
- Organization
2. Preliminaries and Notation
2.1. The Generalized Quaternion Algebra
2.2. Bilinear Expansion of the Product
2.3. Conjugation, Reduced Norm, Modulus, Inverse, and the Null Cone
- Topology
2.4. Left/Right Multiplication as Real Matrices
2.5. Notation for Functions and Differentials
2.6. Dirac/Fueter Operators and a Constant Coefficient Factorization
3. Main Results
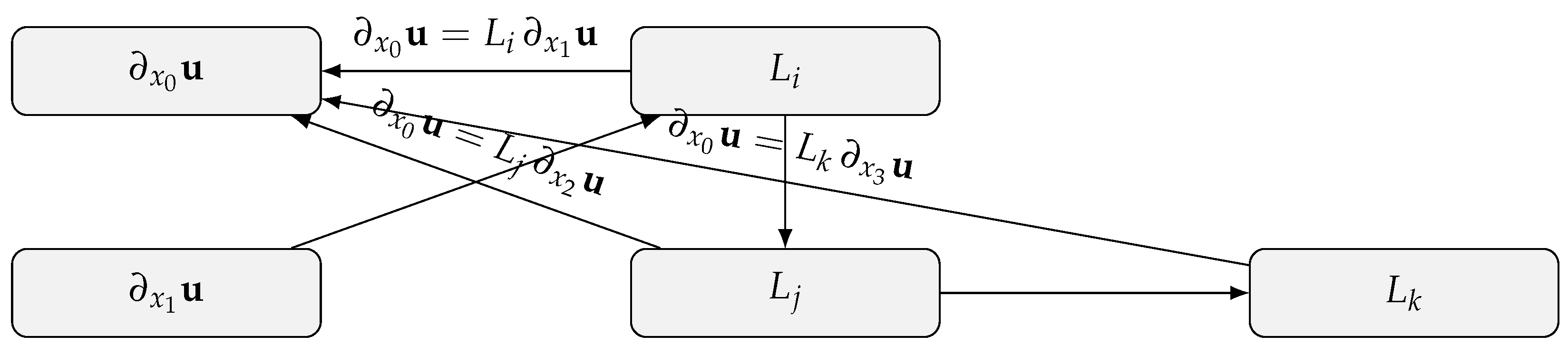
3.1. Left/Right Differentiability and CR–Type Systems
- 1.
- (Necessity) If f has a left (resp. right) derivative at , then the following left (resp. right) CR system holds at :
- 2.
- (Sufficiency) Conversely, if the left (resp. right) system (20) (resp. (21)) holds on a neighborhood of , then f is left (resp. right) differentiable at , and
3.2. CR → Dirac → Laplacian Pipeline and Harmonicity
- Two Laplace-type operators
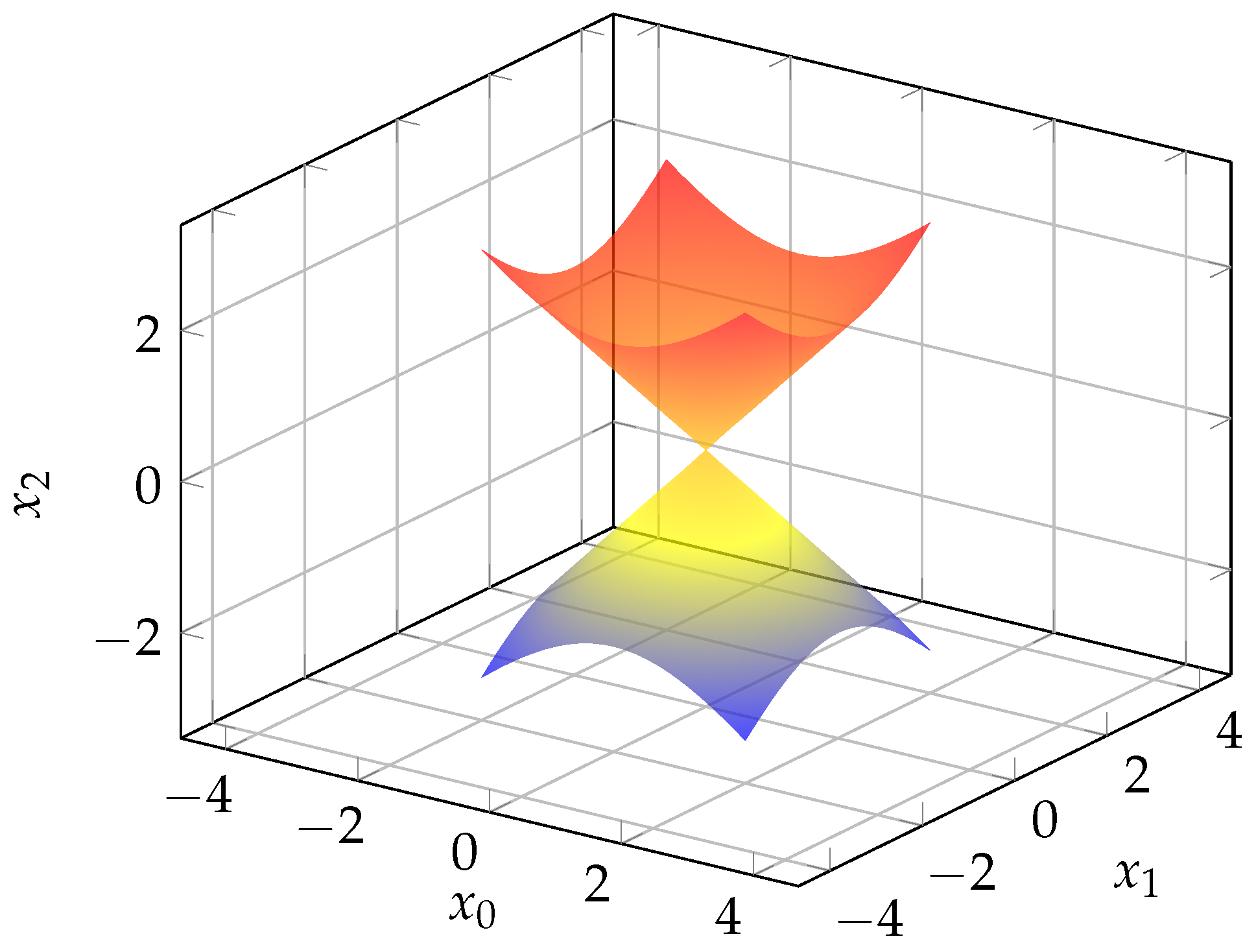
3.3. A Model Boundary Value Problem (Elliptic Case)
3.4. Right–Left Symmetries, Composition, and Computational Checks
- Symmetries and closures.
- Hamiltonian specialization
- Split quaternions
- Affine CR families
- Quadratic map
4. Extensions and Outlook
- Boundary integrals and Fueter-type formulas: Construct Cauchy-type integrals adapted to and derive Borel–Pompeiu representations that couple the CR systems to boundary data.
- Green kernels in split signature: Develop fundamental solutions for when and analyze radiation/causality conditions.
- Weak formulations: Pose the CR systems on Sobolev scales, establish trace/extension theorems, and study Fredholm properties under boundary conditions.
- Structure-preserving numerics: Design finite/boundary element schemes that encode the linearizations (22a) and (22b) and preserve symmetries.
- Links to Clifford/Fueter analysis: Connect with Fueter maps and iterated Dirac systems and compare growth/regularity classes.
5. Conclusions
- Summary of Contributions
- Differentiability via CR systems; Starting from difference quotients, we derived complete left/right CR systems and proved a sufficiency result: under regularity on , the CR identities imply the existence of the corresponding left/right derivative. This establishes a precise quaternionic analogue of the one-dimensional calculus paradigm.
- Second-order potential theory: Using Dirac/Fueter operators , we factored the constant coefficient operatorand showed that each real component is -harmonic. The principal symbol neatly separates the elliptic (Hamiltonian) and split (coquaternionic) regimes.
- Poisson representation (elliptic case): For , we gave a Poisson–type formula on the unit ball in , recovering mean-value and maximum principles for the components.
- Matrix linearization: Real models of left/right multiplication compress the CR systems into Jacobian matrix identities, enabling direct symbolic checks, stable discretizations, and fast prototyping.
- Examples and contrasts: Polynomial/affine families and split-signature examples illustrate the theory and the role of signature, including the behavior across the null cone.
- Boundary integral and Borel–Pompeiu formulas adapted to , linking CR data to boundary values.
- Green kernels and layer potentials for in split signature, with radiation/causality conditions.
- Weak formulations on Sobolev scales, trace/extension theory, and Fredholm properties under natural boundary conditions.
- Spectral and semigroup approaches for evolution problems driven by .
- Structure-preserving numerics (finite/boundary elements) exploiting the matrix linearizations and symmetries.
- Links to Clifford/Fueter analysis, including Fueter maps and iterated Dirac systems, where our linearization offers a practical bridge.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Notes on Sufficiency and Regularity
Appendix B. Proof Details for Theorem 1
Appendix C. Matrix Identities and Pseudo-Orthogonality
Appendix D. Proof Details for Theorem 3
Appendix E. Poisson Kernel on
References
- Chakrabarti, D.; Shaw, M.C. The Cauchy–Riemann equations on product domains. Math. Ann. 2011, 349, 977–998. [Google Scholar] [CrossRef]
- Hamilton, W.R. Ii. on quaternions; or on a new system of imaginaries in algebra. Lond. Edinb. Dublin Phil. Mag. J. Sci. 1844, 25, 10–13. [Google Scholar] [CrossRef]
- Cockle, J. LII. On systems of algebra involving more than one imaginary; and on equations of the fifth degree. Lond. Edinb. Dublin Phil. Mag. J. Sci. 1849, 35, 434–437. [Google Scholar] [CrossRef]
- Clifford, W.K. Preliminary sketch of biquaternions. Proc. Lond. Math. Soc. 1873, 4, 381–395. [Google Scholar] [CrossRef]
- Luna-Elizárraras, M.E.; Shapiro, M.; Struppa, D.C.; Vajiac, A. Complex Laplacian and derivatives of bicomplex functions. Complex Anal. Oper. Theory 2013, 7, 1675–1711. [Google Scholar] [CrossRef]
- Kajiwara, J.; Li, X.D.; Shon, K.H. Regeneration in complex, quaternion and Clifford analysis. In Finite or Infinite Dimensional Complex Analysis and Applications; Springer: Boston, MA, USA, 2004; pp. 287–298. [Google Scholar]
- Krantz, S.G. Partial Differential Equations and Complex Analysis; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Kim, J.E. Properties of regular functions of a quaternion variable modified with tricomplex quaternion. Adv. Math. Sci. J. 2021, 10, 2663–2673. [Google Scholar] [CrossRef]
- Kim, J.E.; Shon, K.H. Differentiability properties of functions of generalized quaternionic variables. Non-Linear Func. Anal. Appl. 2017, 22, 889–897. [Google Scholar]
- Marão, J.A.P.; Neto, M.F.B. A note on the hypercomplex Riemann-Cauchy like relations for quaternions and Laplace equations. arXiv 2013, arXiv:1304.3731. [Google Scholar] [CrossRef]
- Mandic, D.P.; Jahanchahi, C.; Took, C.C. Took, A quaternion gradient operator and its applications. IEEE Signal Proc. Lett. 2011, 18, 47–50. [Google Scholar] [CrossRef]
- Haydys, A. Nonlinear Dirac operator and quaternionic analysis. Comm. Math. Phys. 2008, 281, 251–261. [Google Scholar] [CrossRef]
- Sudbery, A. Quaternionic analysis. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1979. [Google Scholar]
- Gogberashvili, M. (2+1)-Maxwell equations in split quaternions. Physics 2022, 4, 329–363. [Google Scholar] [CrossRef]
- Jiang, T.; Wang, G.; Guo, Z.; Zhang, D. Algebraic algorithms for a class of Schrödinger equations in split quaternionic mechanics. Math. Methods Appl. Sci. 2024, 47, 6205–6215. [Google Scholar] [CrossRef]
- Guo, Z.; Jiang, T.; Vasil’ev, V.I.; Wang, G. A novel algebraic approach for the Schrödinger equation in split quaternionic mechanics. Appl. Math. Lett. 2023, 137, 108485. [Google Scholar] [CrossRef]
- González-Cervantes, J.O.; Bory-Reyes, J. A fractional Borel–Pompeiu type formula and a related fractional ψ-Fueter operator with respect to a vector-valued function. Math. Methods Appl. Sci. 2023, 46, 2012–2022. [Google Scholar] [CrossRef]
- González-Cervantes, J.O.; Bory-Reyes, J.; Sabadini, I. A Borel–Pompeiu formula in a (q,q′)-model of quaternionic analysis. J. Math. Phys. 2025, 66, 023507. [Google Scholar] [CrossRef]
- Avila, J.C.; Frías-Armenta, M.E.; López-González, E. Generalized Cauchy–Riemann equations in non-identity bases with application to the algebrizability of vector fields. In Forum Mathematicum; De Gruyter: Berlin, Germany, 2023; Volume 35, pp. 1471–1483. [Google Scholar]
- Faustino, N. On Discrete Conjugate Harmonic Functions in Hypercomplex Analysis: N. Faustino. Complex Anal. Oper. Theory 2025, 19, 94. [Google Scholar] [CrossRef]
- Baliarsingh, P.; Sahoo, S. On Generalized Quaternion Integral Transform and its Applications. Complex Anal. Oper. Theory 2025, 19, 161. [Google Scholar] [CrossRef]
- Dou, X.; Jin, M.; Ren, G.; Yang, T. Zeroes of weakly slice regular functions of several quaternionic variables on non-axially symmetric domains. arXiv 2024, arXiv:2401.04899. [Google Scholar] [CrossRef]
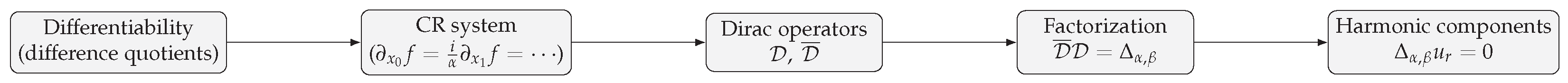
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.E. On Corresponding Cauchy–Riemann Equations Applied to Laplace-Type Operators over Generalized Quaternions, with an Application. Axioms 2025, 14, 700. https://doi.org/10.3390/axioms14090700
Kim JE. On Corresponding Cauchy–Riemann Equations Applied to Laplace-Type Operators over Generalized Quaternions, with an Application. Axioms. 2025; 14(9):700. https://doi.org/10.3390/axioms14090700
Chicago/Turabian StyleKim, Ji Eun. 2025. "On Corresponding Cauchy–Riemann Equations Applied to Laplace-Type Operators over Generalized Quaternions, with an Application" Axioms 14, no. 9: 700. https://doi.org/10.3390/axioms14090700
APA StyleKim, J. E. (2025). On Corresponding Cauchy–Riemann Equations Applied to Laplace-Type Operators over Generalized Quaternions, with an Application. Axioms, 14(9), 700. https://doi.org/10.3390/axioms14090700





