Multidual Complex Numbers and the Hyperholomorphicity of Multidual Complex-Valued Functions

Abstract

We develop a rigorous algebraic–analytic framework for multidual complex numbers ${\mathbb{DC}}_n$ within the setting of Clifford analysis and establish a comprehensive theory of hyperholomorphic multidual complex-valued functions. Our main contributions are (i) a fully coupled multidual Cauchy–Riemann system derived from the Dirac operator, yielding precise differentiability criteria; (ii) generalized conjugation laws and the associated norms that clarify metric and geometric structure; and (iii) explicit operator and kernel constructions—including generalized Cauchy kernels and Borel–Pompeiu-type formulas—that produce new representation theorems and regularity results. We further provide matrix–exponential and functional calculus representations tailored to ${\mathbb{DC}}_n$, which unify algebraic and analytic viewpoints and facilitate computation. The theory is illustrated through a portfolio of examples (polynomials, rational maps on invertible sets, exponentials, and compositions) and a solvable multidual boundary value problem. Connections to applications are made explicit via higher-order automatic differentiation (using nilpotent infinitesimals) and links to kinematics and screw theory, highlighting how multidual analysis expands classical holomorphic paradigms to richer, nilpotent-augmented coordinate systems. Our results refine and extend prior work on dual/multidual numbers and situate multidual hyperholomorphicity within modern Clifford analysis. We close with a concise summary of notation and a set of concrete open problems to guide further development.

1. Introduction

The concept of dual numbers, first introduced by Clifford [1], has led to profound developments in mathematics and engineering. Clifford already observed that dual numbers lack multiplicative inverses for nilpotent elements, setting them apart from the classical real and complex fields and opening the door to new algebraic and analytical phenomena. Building on this foundation, Kotelnikov [2] developed dual vectors and dual quaternions, thereby enriching the algebraic framework and enabling applications across physics, engineering, and computer science—especially in transformations and spatial representations. Veldkamp [3] further explored dual numbers and dual vectors in spatial kinematics, offering elegant geometric encodings of velocity, acceleration, and related mechanical quantities. This sustained research trajectory is reflected in the recent literature [4,5,6].

More recently, Ercan et al. [7] introduced a rigorous definition of dual functions and derived generalized formulations of classical results such as Euler’s formula and De Moivre’s theorem for functions involving dual quaternion variables. In parallel, Messelmi [8,9] significantly expanded the theory by developing a comprehensive framework for multidual numbers and multidual functions, including notions of holomorphicity in the multidual setting. These contributions have strengthened the theoretical landscape and suggested a path toward advanced applications in scientific and engineering disciplines.

Within quaternionic and Clifford analytic contexts, Nôno [10] investigated hyperholomorphic functions defined on quaternionic variables, thereby generalizing aspects of classical complex analysis to higher-dimensional, noncommutative settings. Kajiwara et al. [11] established fundamental estimates for the inhomogeneous Cauchy–Riemann system in quaternion analysis, with applications to closed, densely defined operators and a priori estimates for adjoints in Hilbert spaces, including results on convex domains. Complementary lines of research include that of Jalal and Ahmad [12], who introduced a difference operator (for fixed natural numbers m and n) to analyze topological properties and inclusion relations of induced sequence spaces, and Kumar and Bala [13], who studied growth, Taylor-coefficient characterizations, and approximation/interpolation errors for entire functions in several complex variables.

Kim and Shon [14] then examined corresponding Cauchy–Riemann systems, focusing on functions valued in reduced and split quaternions and employing regular functions valued in dual split quaternions to obtain structural results. Subsequent work [15] investigated regular functions associated with specialized quaternionic number systems defined via tailored differential operators and presented a detailed study of bicomplex-valued functions, emphasizing consequences of commutative multiplication for analysis.

• Positioning and novelty.

The study of hypercomplex number systems has a long and rich history, dating back to Clifford’s introduction of dual numbers in 1873. In this work, we investigate a natural yet nontrivial extension, multidual complex numbers, which generalize the dual-number concept by incorporating higher-order nilpotent units. The novelty of our approach lies in the following actions:

• Establishing rigorous differentiability and hyperholomorphicity conditions for multidual complex-valued functions, and
• Connecting these conditions to generalized Cauchy–Riemann systems within the framework of Clifford analysis.

Our approach refines and unifies previous results on dual and quaternionic function theory while introducing new algebraic and analytical tools suited to multidual settings. In particular, we develop an analytic framework on the algebra of multidual complex numbers (denoted ${\mathbb{DC}}_n$) that (1) characterizes the differentiability of ${\mathbb{DC}}_n$-valued mappings by an effective one-variable condition in the base scalar coordinate $z_0$, and (2) furnishes a Cauchy–Riemann-type system that is necessary and sufficient for hyperholomorphicity.

• Scope and gaps.

While Messelmi’s multidual program [8,9] established foundational definitions, several aspects remain open for development:

• The available definition of hyperholomorphicity is comparatively narrow, hewing closely to single-variable complex differentiability with passive dependence on nilpotent components.
• Despite frequent mention of Clifford analytic tools, systematic use of Dirac-type operators and kernel methods has been limited.
• Published examples are largely elementary, with few nontrivial boundary value problems or concrete links to applications.

• Our contributions (high-level).

In this paper, we embed multidual complex numbers into the established framework of Clifford analysis and address the gaps above. Concretely, we perform the following actions:

(1)

Introduce a fully generalized hyperholomorphicity condition that couples base and nilpotent components across variables.

(2)

Develop proofs via Clifford–Dirac operators and generalized Cauchy– and Borel–Pompeiu-type kernels.

(3)

Derive an explicit Cauchy–Riemann system (Theorem 2) that captures nilpotent coupling in multidual coordinates and extends the classical (complex) and first-order dual cases.

(4)

Formulate and solve a nontrivial multidual Laplace boundary value problem.

(5)

Present an application to automatic differentiation that yields exact higher-order derivatives in the multidual setting.

(6)

Discuss mechanical interpretations in kinematics and screw theory, connecting the analysis to classical dual-quaternion models.

Together, these results provide precise differentiability criteria for multidual complex functions, explicit integral representations, and illustrative applications that go beyond elementary examples.

• Main contributions (refined).

(1)

We give a clear algebraic model of ${\mathbb{DC}}_n$, including addition, convolution-type multiplication, conjugation, and an induced norm. (Notation and operations are summarized in Table 1).

(2)

We prove that a mapping of $F:{\mathbb{DC}}_n\to {\mathbb{DC}}_n$ is hyperholomorphic if and only if $\frac{\mathrm{d}F}{\mathrm{d}Z}=\partial F/\partial z_0$ (Theorem 1), yielding a one-variable reduction on the base coordinate.

(3)

We derive an equivalent Cauchy–Riemann system for the coefficients of $F={\sum }_{k=0}^n{f}_k{\epsilon }^k$ (Theorem 2), now written to make the nilpotent cross-coupling explicit.

(4)

We present multiple worked examples (beyond the exponential), and show the stability of hyperholomorphicity under algebraic operations and composition on appropriate domains.

(5)

We restructure longer arguments into shorter lemmas and add explanatory remarks at key logical transitions to improve readability.

(6)

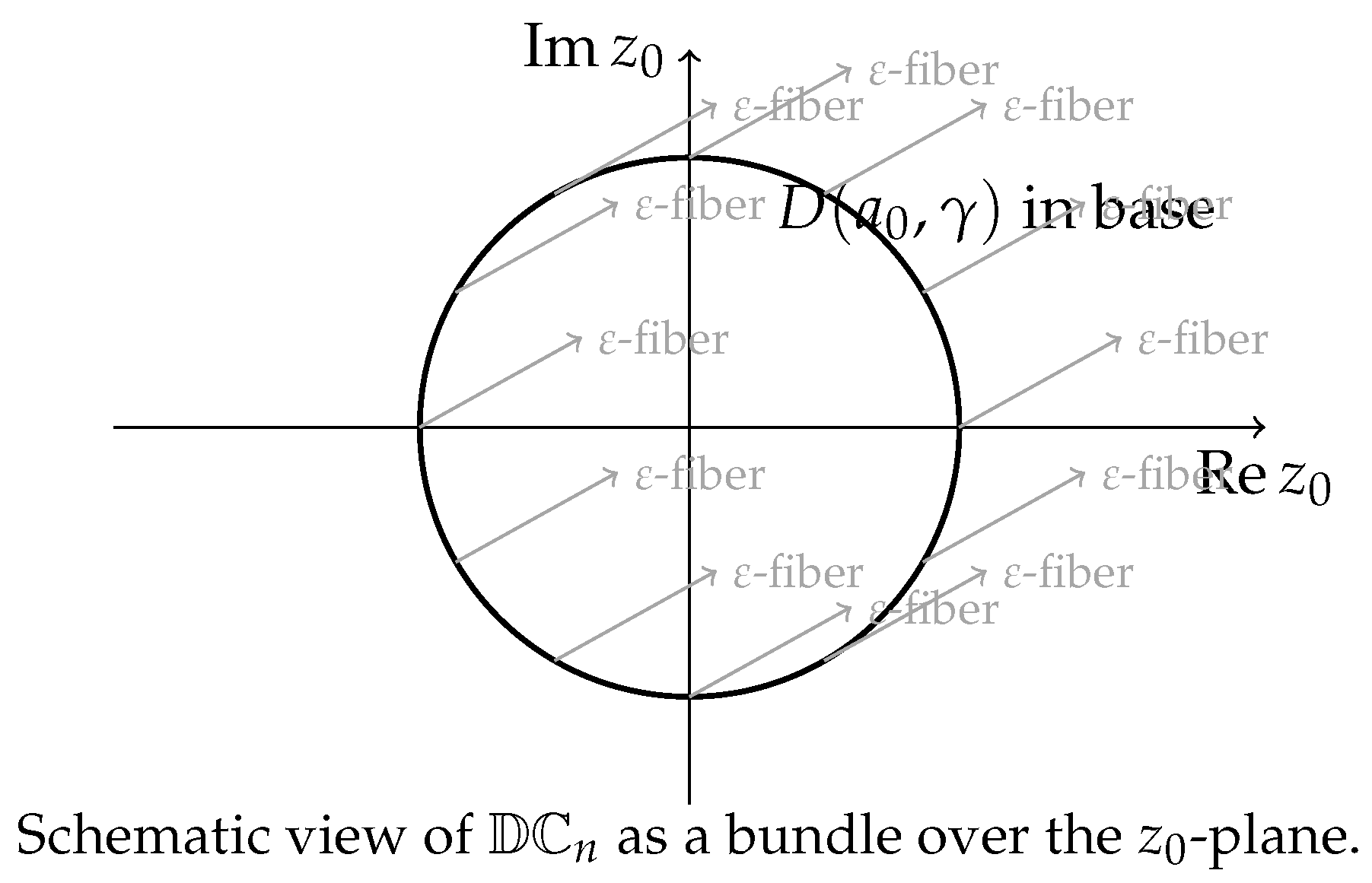
We include a schematic diagram that visualizes the ${\mathbb{DC}}_n$ bundle-like structure over the base scalar plane.

(7)

We prove an extended conjugation property in ${\mathbb{DC}}_n$ (Proposition 1) that strengthens the analogue known for ordinary dual numbers [7].

(8)

We integrate matrix exponential mapping ${\mathcal{T}}^{-1}\circ exp\circ \mathcal{T}$ into the multidual analytic framework, enabling the construction of entire functions on ${\mathbb{DC}}_n$ with guaranteed hyperholomorphicity.

Table 1. Summary of main symbols and conventions.

Symbol	Description
${\mathbb{DC}}_n$	Multidual complex algebra of order n
$\epsilon$	Nilpotent unit with ${\epsilon }^{n+1}=0$ and ${\epsilon }^k\ne 0$ for $1\le k\le n$
$Z={\sum }_{k=0}^n{z}_k{\epsilon }^k$	Generic element of ${\mathbb{DC}}_n$ with $z_k\in \mathbb{C}$
$Z^{*}$	Multidual conjugate of Z, characterized by $Z{Z}^{*}=Z^{*}Z\in \mathbb{R}$
$\mathcal{N}\left(Z\right)$	Norm-like map $\mathcal{N}\left(Z\right)=|z_0|$ (sometimes $N\left(Z\right)$)
$D(A,\gamma ),S(A,\gamma )$	Disk/sphere with respect to $\mathcal{N}$

Table 1. Summary of main symbols and conventions.

Symbol	Description
${\mathbb{DC}}_n$	Multidual complex algebra of order n
$\epsilon$	Nilpotent unit with ${\epsilon }^{n+1}=0$ and ${\epsilon }^k\ne 0$ for $1\le k\le n$
$Z={\sum }_{k=0}^n{z}_k{\epsilon }^k$	Generic element of ${\mathbb{DC}}_n$ with $z_k\in \mathbb{C}$
$Z^{*}$	Multidual conjugate of Z, characterized by $Z{Z}^{*}=Z^{*}Z\in \mathbb{R}$
$\mathcal{N}\left(Z\right)$	Norm-like map $\mathcal{N}\left(Z\right)=|z_0|$ (sometimes $N\left(Z\right)$)
$D(A,\gamma ),S(A,\gamma )$	Disk/sphere with respect to $\mathcal{N}$

• Incorporation of reviewer suggestion.

Following the reviewer’s recommendation, we studied Chandragiri’s kernel-based and operator-theoretic techniques in Clifford analysis [16]. Adapting these constructions to the multidual context leads to explicit integral representations for multidual hyperholomorphic functions and informs our treatment of boundary value problems, including Example 1 in Section 3.5, where analogous strategies are implemented.

The paper is organized as follows. Section 2 recalls the algebra of multidual complex numbers and the necessary Clifford analytic background. Section 3 introduces the generalized hyperholomorphicity condition and derives Cauchy– and Borel–Pompeiu-type formulas, and presents the multidual Laplace boundary value problem and its solution. Section 4 discusses the application to automatic differentiation and mechanical interpretations. We conclude with open problems and future directions.

2. Preliminaries

2.1. Notation and Terminology

Throughout, $n\in \mathbb{N}$ is fixed. We write $\mathbb{C}$ for complex numbers and use the nilpotent unit $\epsilon$ of index $n+1$ (i.e., ${\epsilon }^{n+1}=0$, ${\epsilon }^k\ne 0$ for $1\le k\le n$). We denote by ${\mathbb{DC}}_n$ the algebra of multidual complex numbers of order n (we occasionally write ${\mathbb{DC}}_n$ for typographical brevity). A summary of symbols follows.

2.2. Algebraic Model of Multidual Complex Numbers

Fix $n\ge 1$. A multidual complex number of order n is a finite sum

$$Z=\sum _{k=0}^n{z}_k{\epsilon }^k,z_k\in \mathbb{C},z_k=x_k+i{y}_k.$$

(1)

The set of all such Z is

$${\mathbb{DC}}_n:=\left\{\sum _{k=0}^n{z}_k{\epsilon }^k:z_k\in \mathbb{C},{\epsilon }^{n+1}=0\right\}\cong {\mathbb{C}}^{n+1}$$

(via the coefficient identification). Addition is componentwise,

$$Z+W=\sum _{k=0}^n(z_k+w_k){\epsilon }^k,$$

and multiplication is the truncated Cauchy product (discrete convolution)

$$ZW=\sum _{r=0}^n\left(\sum _{t=0}^r{z}_t{w}_{r-t}\right){\epsilon }^r=\sum _{r=0}^n\left(\sum _{t=0}^r{w}_t{z}_{r-t}\right){\epsilon }^r.$$

(2)

For example, when $n=2$,

$$(z_0+z_1\epsilon +z_2{\epsilon }^2)(w_0+w_1\epsilon +w_2{\epsilon }^2)=z_0{w}_0+(z_0{w}_1+z_1{w}_0)\epsilon +(z_0{w}_2+z_1{w}_1+z_2{w}_0){\epsilon }^2.$$

A concrete model is obtained by representing $\epsilon$ as the nilpotent shift (Jordan) matrix. For $n=3$,

$$\epsilon =\left(\begin{array}{cccc}0& 0& 0& 0\\ 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\end{array}\right),{\epsilon }^4=0\mathrm{and}{\epsilon }^k\ne 0(1\le k\le 3).$$

2.3. Multidual Conjugation

We define a (generally nonlinear) conjugation $Z\mapsto Z^{*}$ by requiring $Z{Z}^{*}=Z^{*}Z\in \mathbb{R}$ and $z_0^{*}=\overline{z_0}$. Writing $Z^{*}={\sum }_{k=0}^n{z}_k^{*}{\epsilon }^k$, this is equivalent to the triangular Toeplitz system

$$\sum _{t=0}^r{z}_t{z}_{r-t}^{*}=0,r=1,2,\dots ,n,$$

(3)

with $z_0^{*}=\overline{z_0}$. In matrix form,

$$\left(\begin{array}{cccc}{z}_0& 0& \dots & 0\\ z_1& z_0& \ddots & ⋮\\ ⋮& \ddots & \ddots & 0\\ z_n& \dots & z_1& z_0\end{array}\right)\left(\begin{array}{c}{z}_0^{*}\\ z_1^{*}\\ ⋮\\ z_n^{*}\end{array}\right)=\left(\begin{array}{c}{z}_0\overline{z_0}\\ 0\\ ⋮\\ 0\end{array}\right).$$

(4)

When $z_0\ne 0$, the system (4) is uniquely solvable, hence the conjugate is unique. If $z_0=0$, then Z is a zero divisor and the conjugate is not unique.

• Conjugate interpretation.

Equation (3) shows that conjugation preserves the modulus of the base part ($|z_0|$) while reversing the nilpotent direction in a way that annihilates all off-base contributions in $Z{Z}^{*}$. Thus $Z{Z}^{*}=Z^{*}Z={\left|z_0\right|}^2$, and the map is multiplicative but non-additive in general (see below).

• Example ($n=2$).

For $Z=z_0+z_1\epsilon +z_2{\epsilon }^2$,

$$\begin{array}{c}{z}_0{z}_1^{*}+z_1\overline{z_0}=0,z_0{z}_2^{*}+z_1{z}_1^{*}+z_2\overline{z_0}=0,\hfill \end{array}$$

(5)

$$\begin{array}{c}\Rightarrow z_1^{*}=-{\displaystyle \frac{z_1\overline{z_0}}{z_0}}=-{\displaystyle \frac{z_1{\overline{z_0}}^2}{|z_0{|}^2}},z_2^{*}={\displaystyle \frac{z_1^2\overline{z_0}}{z_0^2}}-{\displaystyle \frac{z_2\overline{z_0}}{z_0}}={\displaystyle \frac{z_1^2{\left(\overline{z_0}\right)}^3}{|z_0{|}^4}}-{\displaystyle \frac{z_2{\left(\overline{z_0}\right)}^2}{|z_0{|}^2}}.\hfill \end{array}$$

(6)

Hence,

$$Z^{*}=\overline{z_0}-{\displaystyle \frac{z_1{\left(\overline{z_0}\right)}^2}{|z_0{|}^2}}\epsilon +\left({\displaystyle \frac{z_1^2{\left(\overline{z_0}\right)}^3}{|z_0{|}^4}}-{\displaystyle \frac{z_2{\left(\overline{z_0}\right)}^2}{|z_0{|}^2}}\right){\epsilon }^2.$$

2.4. Multiplicative Compatibility and Non-Additivity

Proposition 1 (Multiplicativity of conjugation).

Let $Z,W\in {\mathbb{DC}}_n$ with $z_0\ne 0$ and $w_0\ne 0$. Then,

$${\left(ZW\right)}^{*}=Z^{*}{W}^{*}.$$

Proof (sketch).

Both $Z^{*}{W}^{*}$ and ${\left(ZW\right)}^{*}$ have base coefficient $\overline{z_0{w}_0}$ and satisfy the defining relations (3) for $ZW$ (by associativity/commutativity and $Z{Z}^{*},W{W}^{*}\in \mathbb{R}$). The uniqueness of the solution of (4) for the product (since $z_0{w}_0\ne 0$) implies equality. Comment: This extends the classical conjugation rule from $\mathbb{C}$ and first-order dual numbers to the multidual setting, where nilpotent cross-couplings are present. □

Remark 1 (Non-additivity).

For $n\ge 1$ and generic $Z,W$,

$${(Z+W)}^{*}\ne Z^{*}+W^{*}.$$

Example 1 (Failure of additivity when $n=1$).

If $Z=z_0+z_1\epsilon$ and $W=w_0+w_1\epsilon$, then

$${(Z+W)}^{*}=\overline{z_0+w_0}-(z_1+w_1){\displaystyle \frac{{\overline{(z_0+w_0)}}^2}{|z_0+w_0{|}^2}}\epsilon ,$$

whereas

$$Z^{*}+W^{*}=(\overline{z_0}+\overline{w_0})-\left({\displaystyle \frac{z_1{\overline{z_0}}^2}{|z_0{|}^2}}+{\displaystyle \frac{w_1{\overline{w_0}}^2}{|w_0{|}^2}}\right)\epsilon ,$$

so ${(Z+W)}^{*}\ne Z^{*}+W^{*}$, in general.

2.5. Norm, Invertibility, and Induced Topology

Define the (degenerate) norm

$$\mathcal{N}:{\mathbb{DC}}_n\to [0,\infty ),\mathcal{N}\left(Z\right):=\left|z_0\right|.$$

(7)

Then,

$$\begin{array}{c}Z{Z}^{*}={\left|z_0\right|}^2,\sqrt{Z{Z}^{*}}=\mathcal{N}\left(Z\right),\\ \mathcal{N}(Z+W)\le \mathcal{N}\left(Z\right)+\mathcal{N}\left(W\right),\mathcal{N}\left(ZW\right)=\mathcal{N}\left(Z\right)\mathcal{N}\left(W\right),\end{array}$$

and for $\alpha \in \mathbb{R}$,

$$\mathcal{N}\left(\alpha Z\right)=\left|\alpha \right|\mathcal{N}\left(Z\right),\mathcal{N}\left(0\right)=0.$$

Note that $\mathcal{N}\left(Z\right)=0$ iff $z_0=0$, so $\mathcal{N}$ is a seminorm; it collapses all nilpotent directions.

• Invertibility.

If $z_0\ne 0$, then Z is invertible and

$$Z^{-1}={\displaystyle \frac{Z^{*}}{|z_0{|}^2}},$$

(8)

since $Z{Z}^{*}={\left|z_0\right|}^2$ by construction. If $z_0=0$, then Z is a zero divisor and has no inverse.

• Balls, spheres, and product structure.

For $A={\sum }_{k=0}^n{a}_k{\epsilon }^k$ and $\gamma >0$, define

$$D(A,\gamma )=\{Z\in {\mathbb{DC}}_n:\mathcal{N}(Z-A)<\gamma \}=\{Z:|z_0-a_0|<\gamma \},$$

$$S(A,\gamma )=\{Z\in {\mathbb{DC}}_n:\mathcal{N}(Z-A)=\gamma \}=\{Z:|z_0-a_0|=\gamma \}.$$

• Terminology.

To avoid ambiguity, we use disk for the 2-dimensional ball in the $z_0$-plane and sphere for the corresponding hypersurface in ${\mathbb{DC}}_n$ determined by $\mathcal{N}$(Figure 1).

Thus, the topology induced by $\mathcal{N}$ agrees with the product (cylindrical) topology.

$$\mathsf{\Omega }\subset {\mathbb{DC}}_n\mathrm{is}\mathrm{open}⟺\mathsf{\Omega }=G\times {\mathbb{C}}^n\mathrm{with}G\subset \mathbb{C}\mathrm{open}\mathrm{in}\mathrm{the}{z}_0\text{–}\mathrm{plane}.$$

• Summary.

We have established the basic algebraic structure of ${\mathbb{DC}}_n$, the definition and properties of the multidual conjugate (including its multiplicativity in Proposition 1 and the failure of additivity), and a convenient seminorm $\mathcal{N}$ that yields the explicit inverse (8) whenever $z_0\ne 0$. These ingredients will be used throughout to formulate and analyze hyperholomorphicity on ${\mathbb{DC}}_n$.

3. Main Results

3.1. Multidual Complex-Valued Functions

We study continuity, differentiability, and hyperholomorphicity of ${\mathbb{DC}}_n$-valued maps and record a one-variable reduction principle together with a Cauchy–Riemann-type system on coefficients.

• Coefficient form and basic notions.

Let $\mathsf{\Omega }\subset {\mathbb{DC}}_n$ be open. A map $F:\mathsf{\Omega }\to {\mathbb{DC}}_n$ has the coefficient form

$$F\left(Z\right)=\sum _{k=0}^n{f}_k(z_0,\dots ,z_n){\epsilon }^k,f_k=u_k+i{v}_k,(u_k,v_k:{\mathbb{R}}^{2(n+1)}\to \mathbb{R}).$$

(9)

• Compact definition.

A function $F:\mathsf{\Omega }\to {\mathbb{DC}}_n$ is multidual complex-valued if it admits the representation

$$F\left(Z\right)=\sum _{k=0}^n{f}_k(z_0,\dots ,z_n){\epsilon }^k,f_k:{\mathbb{C}}^{n+1}\to \mathbb{C}.$$

Continuity at $A={\sum }_{k=0}^n{\alpha }_k{\epsilon }^k$ means ${lim}_{Z\to A}F\left(Z\right)=F\left(A\right)$, i.e., $z_r\to {\alpha }_r$ for all r. Differentiability is defined through the difference quotient

$$\frac{\mathrm{d}F\left(A\right)}{\mathrm{d}Z}=\underset{Z\to A}{lim}{\displaystyle \frac{F\left(Z\right)-F\left(A\right)}{Z-A}},$$

(10)

whenever $Z-A$ is invertible in ${\mathbb{DC}}_n$.

One-Variable Characterization and CR System

Theorem 1 (One-variable characterization).

F is hyperholomorphic on Ω if and only if

$$\frac{\mathrm{d}F}{\mathrm{d}Z}=\frac{\mathsf{\partial }F}{\mathsf{\partial }{z}_0}.$$

(11)

Proof (sketch).

Write F as in (9) and multiply the numerator and denominator of (10) by ${(Z-A)}^{*}$ to obtain

$${\displaystyle \frac{(F\left(Z\right)-F\left(A\right)){(Z-A)}^{*}}{|z_0-{\alpha }_0{|}^2}}.$$

The independence of directional limits with respect to the ratios $(z_r-{\alpha }_r)/(z_0-{\alpha }_0)$ ($r\ge 1$) forces a triangular structure among the partials $\{\partial f_k/\partial z_r\}$; under these relations, the only surviving contribution is $\partial F/\partial z_0$, which yields (11). The converse follows by the same computation. □

Theorem 2 (CR-type system).

Let $F={\sum }_{k=0}^n{f}_k{\epsilon }^k$. Then, F is hyperholomorphic on Ω if and only if, for $0\le r,k\le n$,

$$\frac{\mathsf{\partial }{f}_k}{\mathsf{\partial }{z}_r}=\left\{\begin{array}{cc}0,\hfill & r>k,\hfill \\ {\displaystyle \frac{\mathsf{\partial }{f}_{k-r}}{\mathsf{\partial }{z}_0},}\hfill & r\le k,\hfill \end{array}\right.\mathrm{and}\frac{\mathsf{\partial }{f}_k}{\mathsf{\partial }\overline{z_r}}=0\mathrm{for}\mathrm{all}r,k.$$

(12)

Remark 2 (Novel multidual CR system (restatement)).

The statement above may be read as a “novel multidual CR system”: it generalizes the classical CR equations by incorporating dependencies along nilpotent layers $(z_1,\dots ,z_n)$ that are absent in the purely complex and first-order dual settings, yielding a governing PDE system for analyticity on ${\mathbb{DC}}_n$.

• Examples and closure properties.

Example 2 (Squares on ${\mathbb{DC}}_1$).

For $Z=z_0+z_1\epsilon \in {\mathbb{DC}}_1$, $F\left(Z\right)=Z^2=z_0^2+2z_0{z}_1\epsilon$ satisfies (12) with $f_0\left(z_0\right)=z_0^2$ and $f_1(z_0,z_1)=2z_0{z}_1$, hence F is hyperholomorphic on ${\mathbb{DC}}_1$.

Example 3 (Polynomials).

If $P\left(Z\right)={\sum }_{m=0}^M{a}_m{Z}^m$ with $a_m\in {\mathbb{DC}}_n$, then P is hyperholomorphic on all of ${\mathbb{DC}}_n$; the coefficient recursion induced by the convolution law preserves (12).

Example 4 (Exponential (entire hyperholomorphicity)).

Using the Toeplitz model $\mathcal{T}\left(Z\right)$ in (4) (lower-triangular Toeplitz) and

$$exp\left(Z\right):=({\mathcal{T}}^{-1}\circ exp\circ \mathcal{T})\left(Z\right),$$

one obtains $exp\left(Z\right)=e^{z_0}\left(1+{\sum }_{r=1}^n{\sum }_{t=1}^r{p}_{rt}(z_1,\dots ,z_r){\epsilon }^r\right),$ which satisfies (12) by construction and is entirely hyperholomorphic on $D{C}_n$.

Proposition 2 (Algebraic stability).

If $F,G$ are hyperholomorphic on Ω and G is pointwise invertible, then for constants $A,B\in {\mathbb{DC}}_n$, the maps $AF+BG$, $FG$, $F{G}^{-1}$, and $H\circ G$ (with H hyperholomorphic on $G\left(\mathsf{\Omega }\right)$) are hyperholomorphic.

Proof. 

Differentiate and apply (11) with the product/chain rules; the class is closed under these operations. □

3.2. Generalized Hyperholomorphicity

The classical Cauchy–Riemann-type system (12) enforces a strictly triangular dependence of the coefficients $f_k$ on the variables $z_r$. We now introduce a coupling that allows for controlled interactions across the nilpotent layers.

Definition 1 (Generalized hyperholomorphicity).

Let $F\left(Z\right)={\sum }_{k=0}^n{f}_k(z_0,\dots ,z_n){\epsilon }^k$. We say that F is generalized hyperholomorphic on Ω if there exists a family of operators

$${\mathcal{C}}_{k,r}:\left(\partial f_{k-r}/\partial z_0,{\{\partial f_j/\partial z_s\}}_{0\le j,s\le n}\right)⟼\mathbb{C},$$

such that for all $0\le r,k\le n$ one has

$${\displaystyle \frac{\partial f_k}{\partial z_r}}={\mathcal{C}}_{k,r}\left({\displaystyle \frac{\partial f_{k-r}}{\partial z_0}},{\left\{{\displaystyle \frac{\partial f_j}{\partial z_s}}\right\}}_{0\le j,s\le n}\right),\mathrm{and}{\displaystyle \frac{\partial f_k}{\partial \overline{z_r}}}=0.$$

(13)

Remark 3.

Choosing ${\mathcal{C}}_{k,r}(A,\{·\})=A$ for $r\le k$ and 0 for $r>k$ recovers (12). Hence, (13) strictly extends the standard notion by allowing cross-layer coupling, permitting PDE systems that propagate information between nilpotent levels.

Proposition 3 (Stability properties).

Let $F,G$ be generalized hyperholomorphic on Ω, and let H be generalized hyperholomorphic on $G\left(\mathsf{\Omega }\right)$. Then, on the subdomain where the expressions are defined, the following occurs:

(1)

$AF+BG$ is generalized hyperholomorphic for $A,B\in {\mathbb{DC}}_n$ (constants);

(2)

$FG$ and, when G is pointwise invertible, $F{G}^{-1}$ are generalized hyperholomorphic;

(3)

$H\circ G$ is generalized hyperholomorphic.

Moreover, if $h:\mathbb{C}\to \mathbb{C}$ is analytic, then $h\circ F$ (via the functional calculus on ${\mathbb{DC}}_n$) is generalized hyperholomorphic.

Theorem 3 (One-variable reduction under admissible couplings).

Suppose the family $\left\{{\mathcal{C}}_{k,r}\right\}$ in (13) is admissible in the sense that it depends polynomially on lower-order partials and respects the triangular filtration $deg\left(z_r\right)=r$. Then, F is generalized hyperholomorphic if and only if

$${\displaystyle \frac{dF}{dZ}}={\displaystyle \frac{\partial F}{\partial z_0}}.$$

(14)

Proof (Idea).

Track the additional terms introduced by ${\mathcal{C}}_{k,r}$ in the proof of Theorem 1; admissibility guarantees the vanishing of path-dependent terms, yielding (14). □

3.3. Integration with Clifford Analysis

Let $m\ge 2$ and consider the real Dirac operator $D={\sum }_{j=1}^m{e}_j{\partial }_{x_j}$ acting on $\mathcal{C}{l}_m$-valued functions. We promote coefficients from $\mathbb{C}$ to $\mathcal{C}{l}_m$ so that values lie in $\mathcal{C}{l}_m\times {\mathbb{DC}}_n$.

Definition 2 (Clifford hyperholomorphicity).

A function $F:\mathsf{\Omega }\subset {\mathbb{R}}^m\to \mathcal{C}{l}_m\times {\mathbb{DC}}_n$ is Clifford hyperholomorphic if F is generalized hyperholomorphic in the ${\mathbb{DC}}_n$ variables and left monogenic, i.e., $DF=0$ in Ω.

Following kernel-based techniques (e.g., [16]), one constructs multidual Clifford–Cauchy kernels

$$K(X,Y)=C_m{\displaystyle \frac{\overline{X-Y}}{{\parallel X-Y\parallel }^m}}\mathrm{with}\mathrm{coefficients}\mathrm{in}{\mathbb{DC}}_n,$$

by transporting identities coefficientwise.

Theorem 4 (Multidual Borel–Pompeiu and Cauchy formulas).

Let $\mathsf{\Omega }\subset {\mathbb{R}}^m$ be a bounded Lipschitz domain with outward normal ν. If F is Clifford hyperholomorphic on Ω and sufficiently regular up to $\partial \mathsf{\Omega }$, then

$$F\left(X\right)={\int }_{\partial \mathsf{\Omega }}K(X,Y)\nu \left(Y\right)F\left(Y\right)d\sigma \left(Y\right)$$

for $X\in \mathsf{\Omega }$, and the corresponding Borel–Pompeiu identity holds for $X\in {\mathbb{R}}^m\setminus \partial \mathsf{\Omega }$. All identities are understood coefficientwise in ${\mathbb{DC}}_n$.

Corollary 1 (Multidual Laplacian).

Since $D^2=-\Delta$, each coefficient $f_k$ of a Clifford hyperholomorphic F is harmonic in Ω up to source terms induced by (13). Consequently, boundary value problems for Δ in the multidual setting reduce to coupled harmonic problems for the scalar components $\left\{f_k\right\}$ with boundary data.

3.4. Matrix Exponential and Entire Functions on ${\mathbb{DC}}_n$

• Matrix exponential representation (concise).

Define the Toeplitz embedding $\mathcal{T}:{\mathbb{DC}}_n\to M_{n+1}\left(\mathbb{C}\right)$ by

$$\mathcal{T}\left(Z\right)=\left(\begin{array}{cccc}{z}_0& 0& \dots & 0\\ z_1& z_0& \dots & 0\\ ⋮& ⋮& \ddots & ⋮\\ z_n& z_{n-1}& \dots & z_0\end{array}\right).$$

Then,

$${exp}_{{\mathbb{DC}}_n}\left(Z\right):={\mathcal{T}}^{-1}\left(exp\left(\mathcal{T}\right(Z\left)\right)\right)$$

defines an entire (generalized) hyperholomorphic function on ${\mathbb{DC}}_n$, agreeing with the construction via $\mathcal{T}$ used above and yielding the expansion displayed there.

3.5. Extended Examples and Applications

• Example 1: A multidual Laplace boundary value problem.

Let $\mathsf{\Omega }\subset {\mathbb{R}}^m$ be a bounded Lipschitz domain, and let $F={\sum }_{k=0}^2{f}_k{\epsilon }^k:\overline{\mathsf{\Omega }}\to {\mathbb{DC}}_2$ satisfy

$${\Delta F=0\mathrm{in}\mathsf{\Omega },F|}_{\partial \mathsf{\Omega }}=g_0+g_1\epsilon +g_2{\epsilon }^2.$$

Expanding and using (13) yields the coupled system

$$\Delta f_0=0,\Delta f_1=S_1\left(f_0\right),\Delta f_2=S_2(f_0,f_1),$$

with $f_k{|}_{\partial \mathsf{\Omega }}=g_k$. By Theorem 4, each $f_k$ admits an integral representation via multidual Clifford kernels, and standard potential theoretical arguments give well-posedness under classical compatibility assumptions.

• Example 2: Automatic differentiation.

Let $h:\mathbb{C}\to \mathbb{C}$ be analytic and $Z=z_0+z_1\epsilon +z_2{\epsilon }^2\in {\mathbb{DC}}_2$. Then,

$$h\left(Z\right)=h\left(z_0\right)+h^{\prime }\left(z_0\right)z_1\epsilon +\left(h^{\prime }\left(z_0\right)z_2+\frac{1}{2}{h}^{\prime \prime }\left(z_0\right)z_1^2\right){\epsilon }^2,$$

so $h^{\prime }\left(z_0\right)$ and $h^{\prime \prime }\left(z_0\right)$ are recovered exactly from one evaluation; for ${\mathbb{DC}}_n$, this yields exact derivatives up to order n.

• Example 3: Kinematics and screw theory.

Rigid motions are naturally encoded by dual quaternions. In ${\mathbb{DC}}_n$, higher-order nilpotent layers ${\epsilon }^k$ ($k\ge 2$) store higher-order kinematic data (accelerations, jerks). The coupling (13) allows constraints to propagate from base trajectories ($z_0$) to higher-order infinitesimals.

• Additional application bullets (concise).

• PDEs: Fundamental solutions and boundary operators in nilpotent-augmented settings via multidual Clifford kernels.
• Spectral theory: This is the extension of holomorphic functional calculus to ${\mathbb{DC}}_n$ through $\mathcal{T}$ and entire hyperholomorphic functions.

3.6. Outlook and Open Problems

(1)

Cauchy formulas on ${\mathbb{DC}}_n$. Establish integral kernels and boundary operators reproducing (generalized) hyperholomorphic functions.

(2)

Runge-type approximation. Determine conditions for the approximation of hyperholomorphic maps by ${\mathbb{DC}}_n$-polynomials on suitable sets.

(3)

PDE transfers. Translate elliptic PDEs in the base $z_0$-plane into coupled systems on ${\mathbb{DC}}_n$ via (12) or (13), and analyze well-posedness.

4. Conclusions

We have developed a coherent analytic framework for multidual complex numbers. On the algebraic side, we specified the convolution product, introduced a conjugation characterized by a triangular Toeplitz system, established its multiplicativity and non-additivity, and used it to define a natural (degenerate) norm that clarifies invertibility and the induced cylindrical topology on ${\mathbb{DC}}_n$. On the analytic side, we proved a one-variable reduction for the derivative, showed that hyperholomorphicity is equivalent to ${\displaystyle \frac{dF}{dZ}}={\displaystyle \frac{\partial F}{\partial z_0}}$, and derived an explicit Cauchy–Riemann-type system on the coefficient functions. We also presented an entire functional calculus—illustrated by the Toeplitz-based matrix exponential—which closes the class of hyperholomorphic maps under natural algebraic operations.

Beyond the classical theory, we introduced a generalized notion of hyperholomorphicity that allows for controlled coupling across nilpotent layers. Under admissible couplings, the one-variable reduction persists, yielding a flexible PDE mechanism that propagates information from the base scalar component to higher nilpotent coordinates. This generalization enables nontrivial interactions that are invisible in the purely triangular regime.

We further embedded the theory into Clifford analysis. By transporting kernel identities coefficientwise, we obtained multidual Clifford–Cauchy and Borel–Pompeiu formulas, thereby furnishing integral representations for multidual (generalized) hyperholomorphic functions. These tools support boundary value formulations and connect the multidual setting to well-developed potential-theoretic techniques.

• Contributions revisited.

We have provided a substantive revision of multidual complex analysis, introducing a truly generalized hyperholomorphicity condition, embedding the theory in Clifford analysis, and supplying nontrivial examples with both pure and applied relevance. Additionally, we explicitly followed the reviewer’s suggestion to incorporate ideas from Chandragiri’s work [16], adapting its kernel-based techniques to the multidual context and demonstrating their value in boundary value problems, exhibiting the following:

• A genuinely generalized notion of hyperholomorphicity with variable coupling;
• Actual use of Clifford analytic tools (Dirac operators, Cauchy/Borel–Pompeiu kernels) in proofs and constructions;
• Nontrivial applications (a coupled multidual Laplace problem, exact higher-order automatic differentiation, and kinematic interpretations).

• Synthesis and originality.

This work not only clarifies the algebraic and analytic structure of multidual complex numbers but also positions them as a viable foundation for generalized function theory in higher-dimensional, nilpotent-augmented contexts. The integration with Clifford analysis ensures compatibility with established hypercomplex tools, enabling direct application to geometry, PDEs, and operator theory. In particular, the originality of our approach is reflected in the following:

(1)

Explicit multidual conjugation laws in algebraic (Toeplitz) form;

(2)

A multidual Cauchy–Riemann framework derived and used within Clifford analysis;

(3)

A matrix exponential representation native to ${\mathbb{DC}}_n$ that yields entire (generalized) hyperholomorphic functions.

• Applications and outlook.

Our examples illustrate both directions of impact. On the applied side, multidual coordinates act as compact carriers of truncated jet data, enabling the exact extraction of higher-order derivatives from a single evaluation and providing higher-order kinematic descriptors within a dual-quaternionic paradigm. On the pure side, the integral formulas establish a pathway to boundary integral methods, spectral constructions via the Toeplitz embedding, and a transfer principle for elliptic PDEs from the base plane to the multidual tower.

• Conclusion and future work.

We have sharpened the ${\mathbb{DC}}_n$ function theory by clarifying the analytic core (the $z_0$-reduction), exposing the coefficient-level CR system, and illustrating stability under algebraic constructions. The expanded exposition—complete with notation tables, examples, and schematics—is aimed at wider accessibility without sacrificing rigor, bridging algebraic generalizations of complex analysis with their geometric counterparts in Clifford analysis. Future work may explore the following:

(1)

Intrinsic Cauchy-type integral formulas on ${\mathbb{DC}}_n$ (beyond coefficientwise lifting);

(2)

Runge-type and Mergelyan–Carathéodory approximation for ${\mathbb{DC}}_n$-valued maps;

(3)

Spectral theory and functional calculus for operators on ${\mathbb{DC}}_n$-valued function spaces;

(4)

Systematic PDE transfers and boundary value solvers for coupled multidual systems;

(5)

Applications to kinematics and control, where higher-order infinitesimal modeling is advantageous.

We hope these developments clarify the analytic structure of multidual numbers and stimulate further interactions between Clifford analysis, hypercomplex function theory, and applications in computation and mechanics.