The Classical Origin of Spin: Vectors Versus Bivectors
Abstract
1. Introduction
Outline
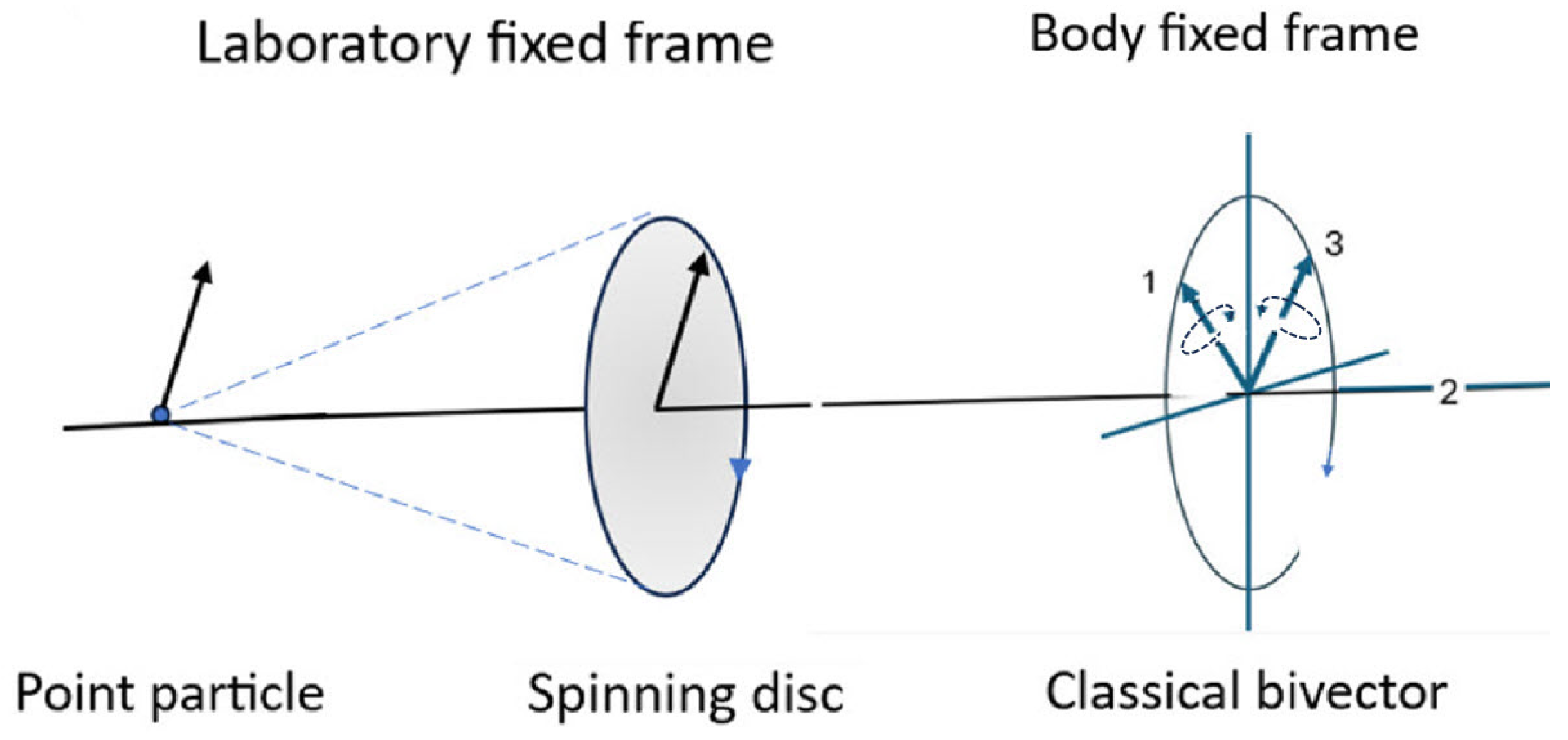
2. Classical Spin
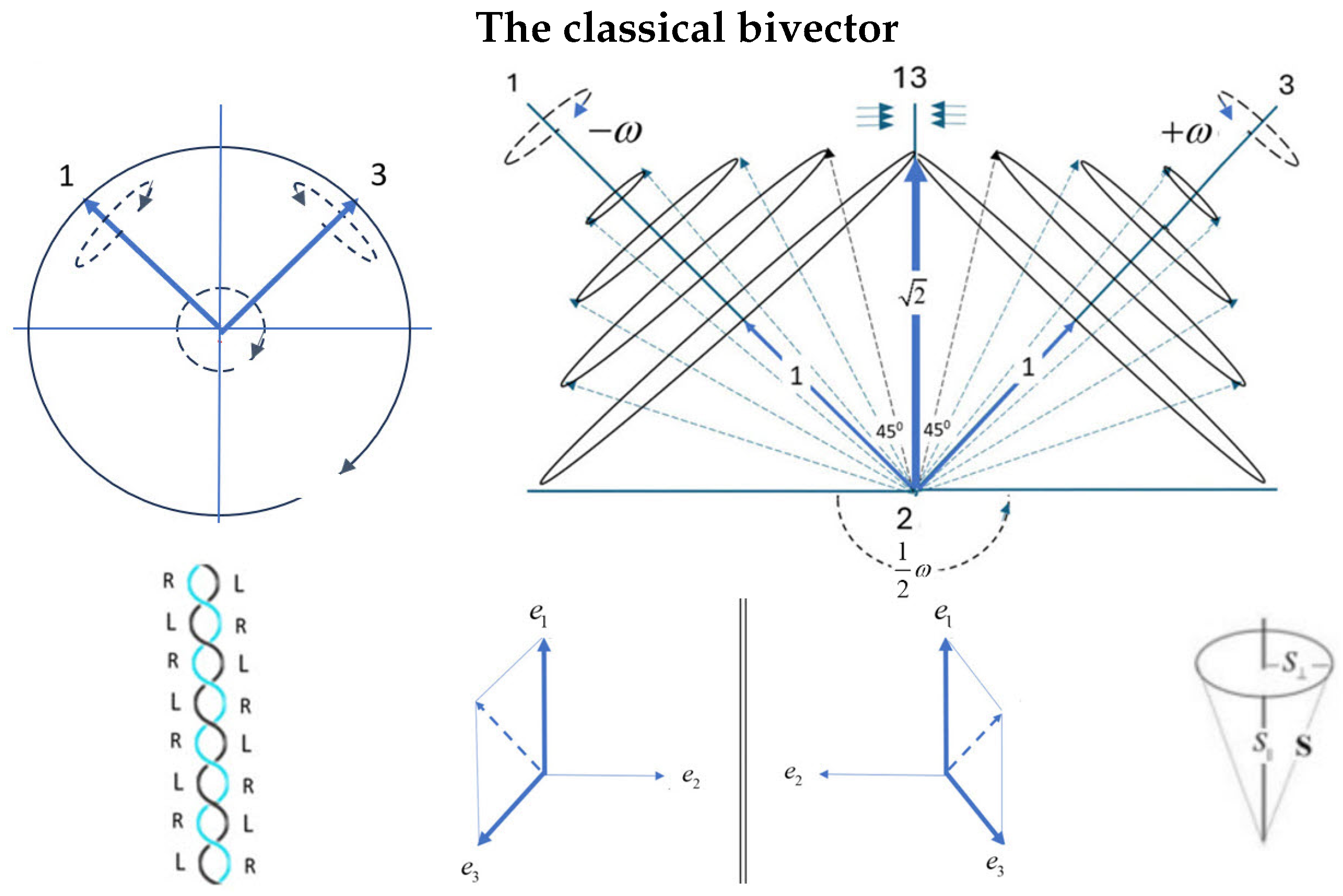
2.1. A Classical Bivector
2.2. Complementarity
2.3. Euler’s Equations
2.4. Resonance
2.5. Geometric Algebra: Bivector Dynamics
- Cold Dark Matter
- The Double Helix
2.6. A Classical Boson of Spin-1
2.7. Special Relativity
- The Quantum and Relativistic Limits
3. Correspondence and Parity
3.1. Parity from Reflection
3.2. Classical–Quantum Correspondence
3.3. Continuous Versus Discrete Symmetry
- Calculation of Planck’s Constant
- Quaternion Spin
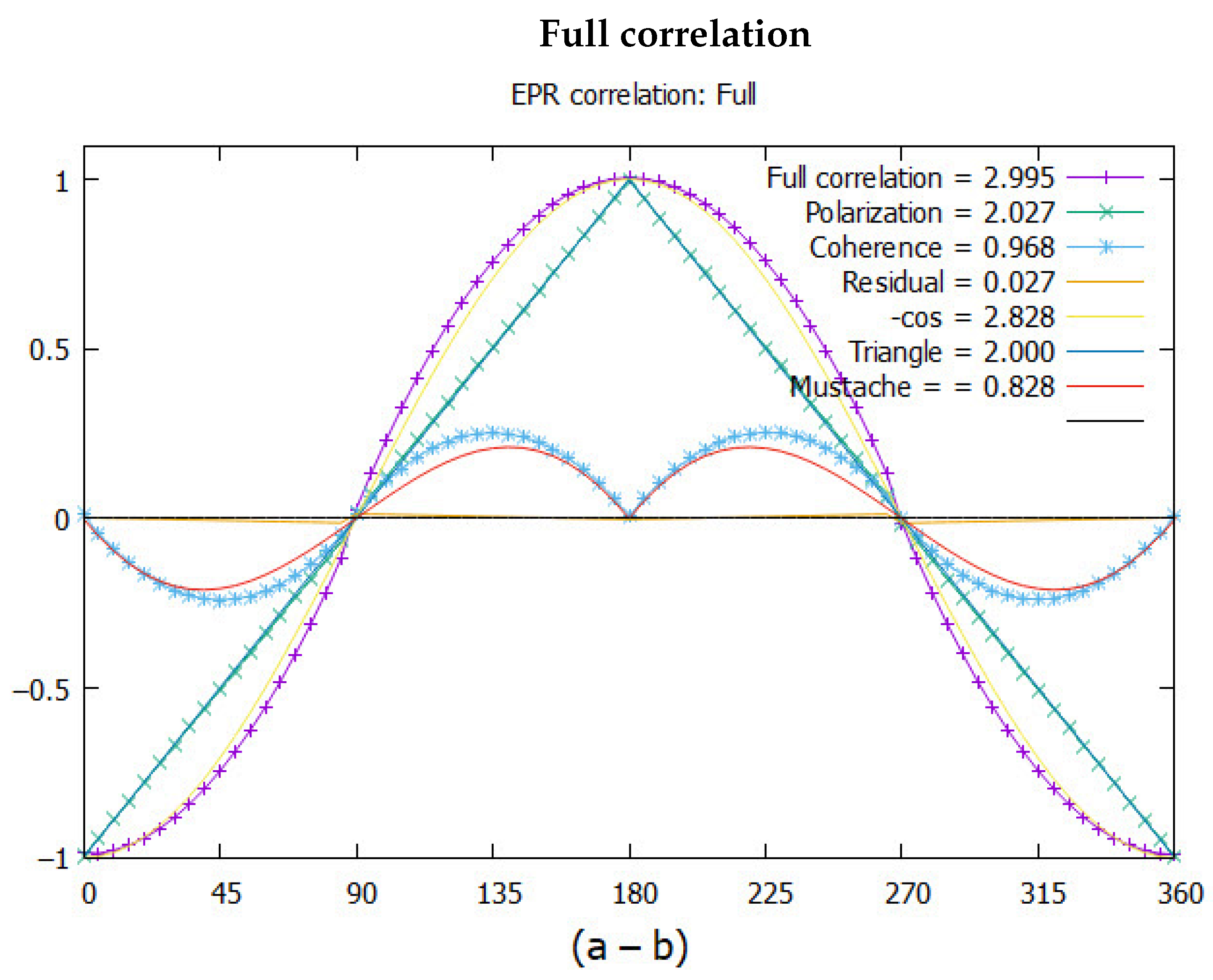
- The EPR Paradox
“If [a hidden-variable theory] is local it will not agree with quantum mechanics, and if it agrees with QM it will not be local.”
4. Interpretation
4.1. Hammers, Wrenches, and Matter
4.2. Determinism
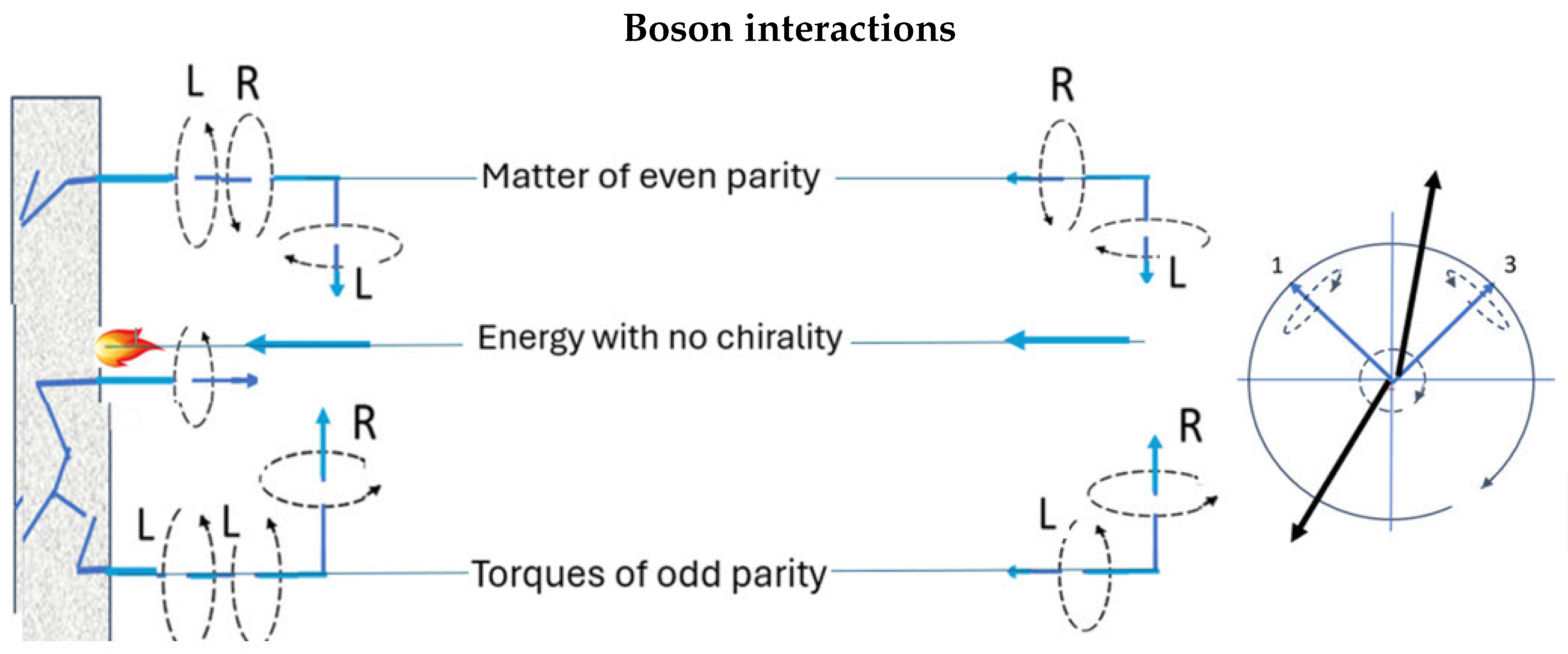
5. Unification of Bosons and Fermions
5.1. Internal Mass–Energy
5.2. Emergence of Spin
5.3. Emergence of Charge
5.4. Photons Are Massless Bivectors
6. Ontology
6.1. Particles
6.2. No Neutrinos
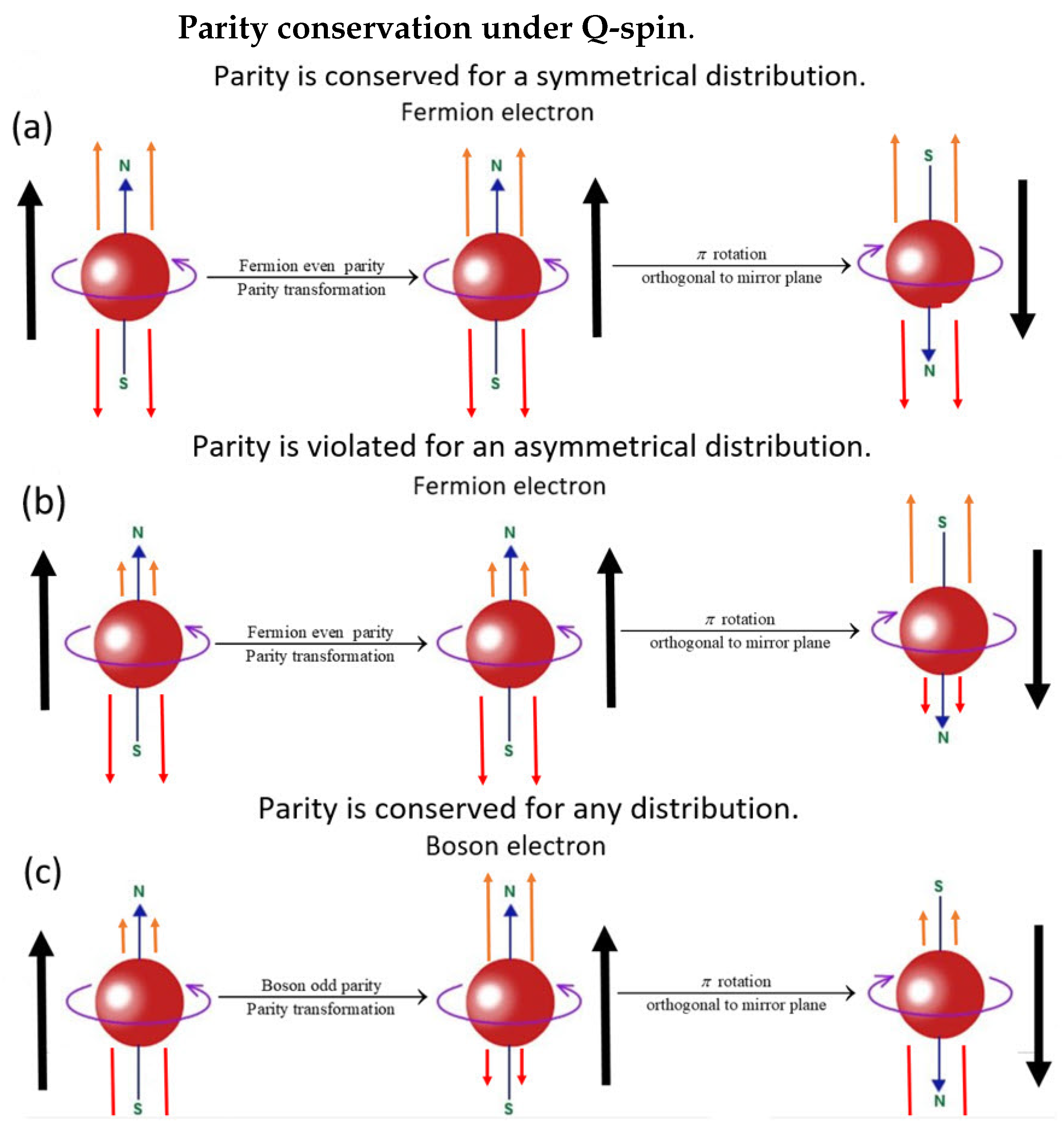
6.3. Parity Is Not Violated in the BiSM
“If an asymmetry in the distribution between and … is observed, it provides unequivocal proof that parity is not conserved in beta decay.”
6.4. Lie Versus Clifford Algebra
6.5. The Bivector Field
7. Quantization and Measurement
7.1. Lagrangians
7.2. Quantization
7.3. No Superposition; No Collapse
7.4. The Fermion Approximation
8. SM—BiSM and Experiment
8.1. The “Origin of Positrons in the Galaxy” Puzzle
8.2. Separating Vector and Bivector Motion
8.3. Low-Energy Studies
8.4. Classical Bivector
8.5. The Muon g-2 Anomaly
8.6. Electron Quadrupole Moment
8.7. Problems with Chirality
9. Summary
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Quantum Correspondence
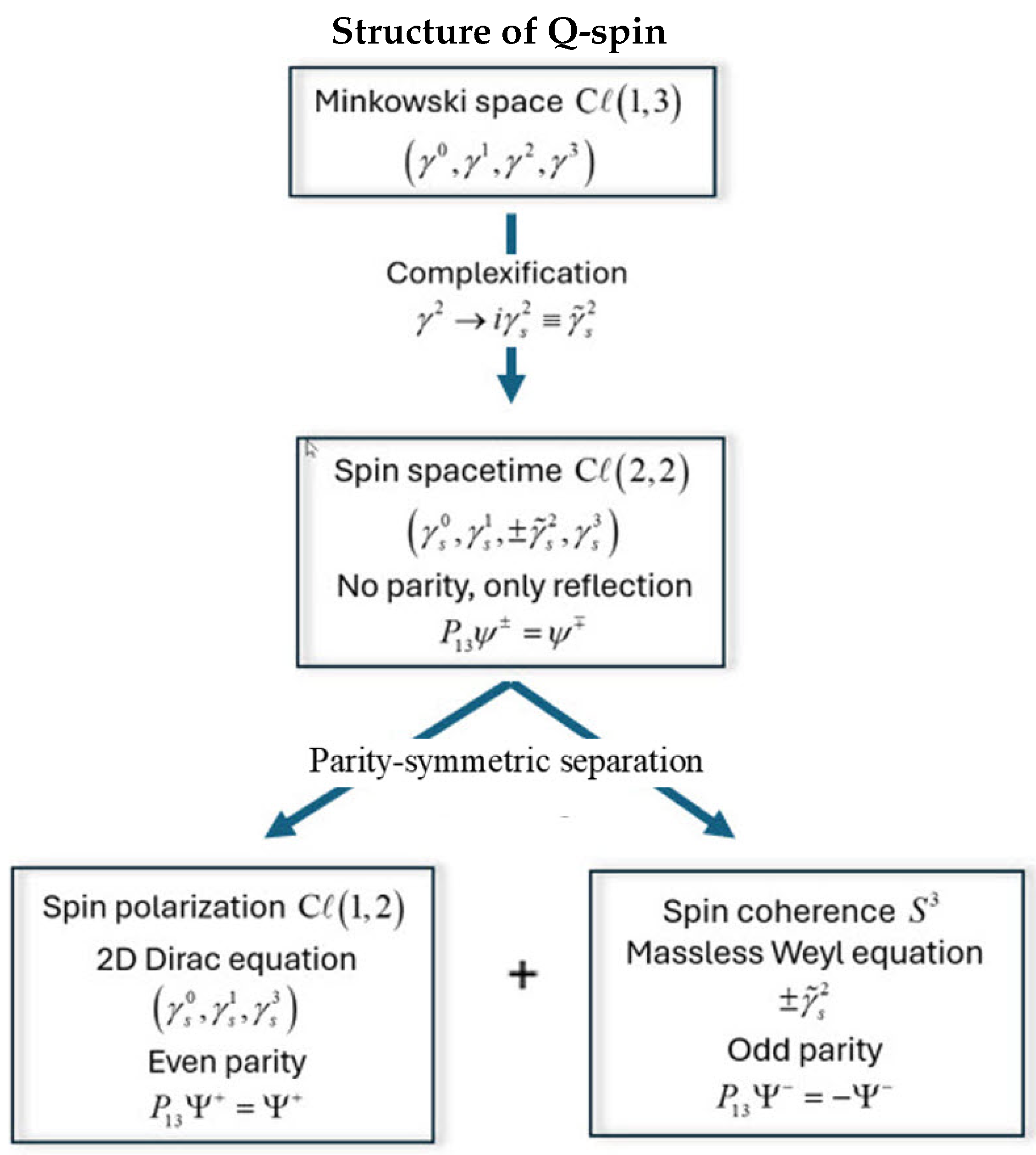
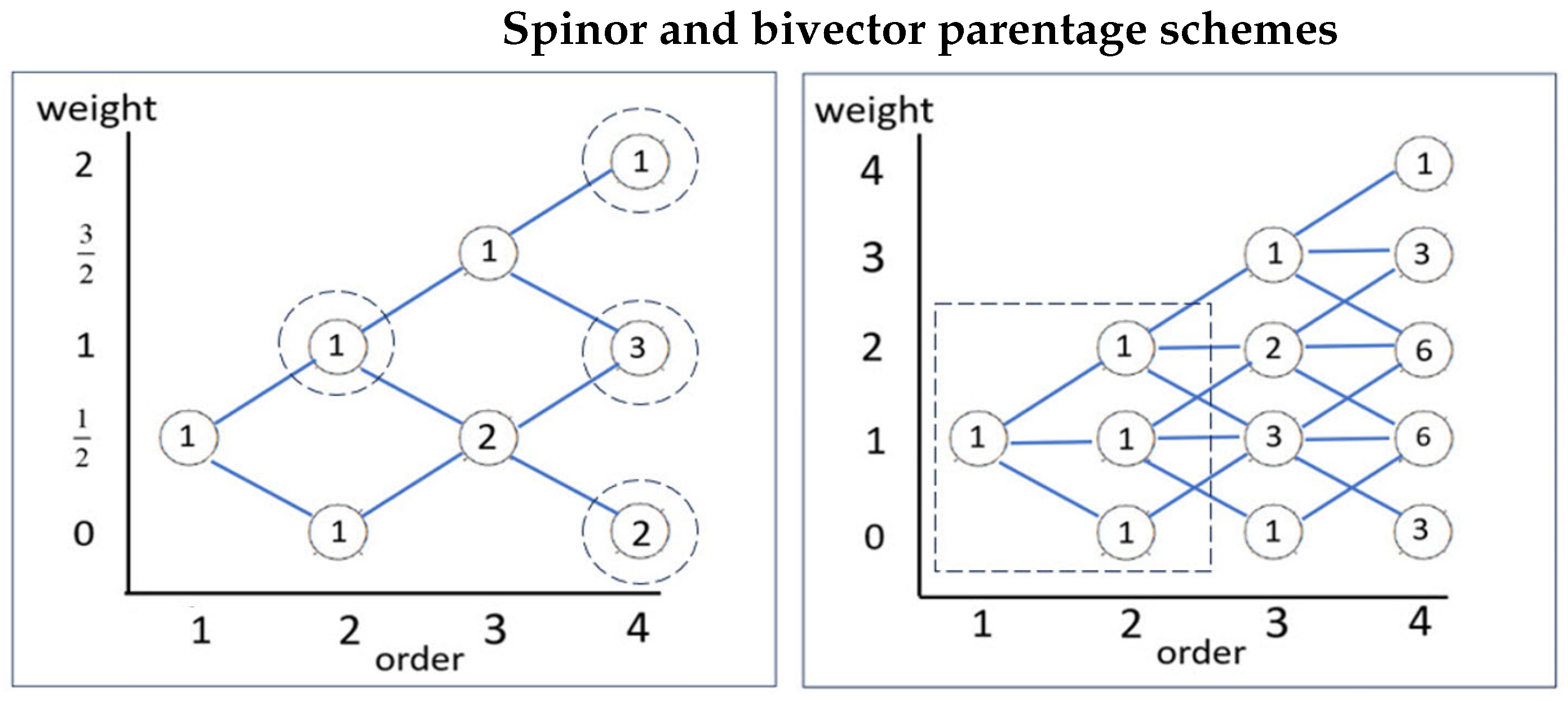
Appendix B. Parentage Schemes
Appendix C. Symmetry of Quaternion Spin
References
- Peskin, M.; Schroeder, D.V. An Introduction To Quantum Field Theory; Frontiers in Physics: Boulder, CO, USA, 1995. [Google Scholar]
- Dirac, P.A.M. The quantum theory of the electron. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1928, 117, 610–624. [Google Scholar]
- For a Pedagogical Survey. Available online: https://youtu.be/90W3aUl0gHU?si=uqtIU1mMNvdQJUzg (accessed on 21 August 2025).
- Sanctuary, B. Quaternion Spin. Mathematics 2024, 12, 1962. [Google Scholar] [CrossRef]
- Sanctuary, B. Spin Helicity and the Disproof of Bell’s Theorem. Quantum Rep. 2024, 6, 436–441. [Google Scholar] [CrossRef]
- Sanctuary, B. EPR Correlations Using Quaternion Spin. Quantum Rep. 2024, 6, 409–425. [Google Scholar] [CrossRef]
- Doran, C.; Lasenby, J. Geometric Algebra for Physicists; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Dirac, P.A.M. A Theory of Electrons and Protons. Proc. R. Soc. Lond. A 1930, 126, 360–365. [Google Scholar]
- Greiner, W. Relativistic QM-Wave Equations; Springer: Berlin/Heidelberg, Germany, 2000; pp. 310–360. [Google Scholar]
- Paganini, P. Fundamentals of Particle Physics: Understanding the Standard Model; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- Skyrme, T.H.R. A unified field theory of mesons and baryons. Nucl. Phys. 1962, 31, 556–569. [Google Scholar] [CrossRef]
- Pezzaglia, W.M. Physical applications of a generalized Clifford calculus (Papapetrou equations and metamorphic curvature). arXiv 1997, arXiv:gr-qc/9710027. [Google Scholar] [CrossRef]
- Hestenes, D. Spin and uncertainty in the interpretation of quantum mechanics. Am. J. Phys. 1979, 47, 399–415. [Google Scholar] [CrossRef]
- Hestenes, D.; Sobczyk, G. Clifford Algebra to Geometric Calculus: A Unified Language for Mathematics and Physics; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2012; Volume 5. [Google Scholar]
- Nash, C.; Sen, S. Topology and Geometry for Physicists; Elsevier: Amsterdam, The Netherlands, 1988. [Google Scholar]
- Schwarz, A.S. Quantum Field Theory and Topology; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2013; Volume 307. [Google Scholar]
- Hestenes, D. The zitterbewegung interpretation of quantum mechanics. Found. Phys. 1990, 20, 1213–1232. [Google Scholar] [CrossRef]
- Muralidhar, K. The spin bivector and zeropoint energy in geometric algebra. Adv. Studies Theor. Phys. 2012, 6, 675–686. [Google Scholar]
- Goldstein, H. Classical Mechanics; Pearson Education India: Noida, India, 2011. [Google Scholar]
- Nadler, E.O.; Benson, A.J. Semianalytic model for decaying dark matter halos. arXiv 2025, arXiv:2501.12636. [Google Scholar] [CrossRef]
- Carroll, S.M. Spacetime and Geometry; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Leonard, I.E.; Lewis, J.E. Geometry of Convex Sets; John Wiley and Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Hadwiger, H. Minkowskische addition und subtraktion beliebiger punktmengen und die theoreme von erhard schmidt. Math. Z. 1950, 53, 210–218. [Google Scholar] [CrossRef]
- Noether, E. Invariante Variations probleme. Gott. Nachr. 1918, 235–257. [Google Scholar]
- Etingof, P.; Golberg, O.; Hensel, S.; Liu, T.; Schwendner, A.; Vaintrob, D.; Yudovina, E. Introduction to representation theory. arXiv 2009, arXiv:0901.0827. [Google Scholar]
- Ballentine, L.E. The statistical interpretation of quantum mechanics. Rev. Mod. Phys. 1970, 42, 358. [Google Scholar] [CrossRef]
- Dirac, P.A.M. On the theory of quantum mechanics. Proc. R. Soc. London A 1926, 112, 661–677. [Google Scholar]
- Von Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1955. [Google Scholar]
- Aharonov, Y.; Susskind, L. Charge Superselection Rule. Phys. Rev. 1967, 155, 1428. [Google Scholar] [CrossRef]
- Giacomini, F.; Castro-Ruiz, E.; Brukner, Č. Quantum mechanics and the covariance of physical laws in quantum reference frames. Nat. Commun. 2019, 10, 494. [Google Scholar] [CrossRef]
- Bartlett, S.D.; Rudolph, T.; Spekkens, R.W. Reference frames, superselection rules, and quantum information. Rev. Mod. Phys. 2007, 79, 555. [Google Scholar] [CrossRef]
- Bell, J.S. On the Einstein Podolsky Rosen paradox. Phys. Phys. Fiz. 1964, 1, 195. [Google Scholar] [CrossRef]
- Clauser, J.F.; Horne, M.A.; Shimony, A.; Holt, R.A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 1969, 23, 880. [Google Scholar] [CrossRef]
- Aspect, A.; Dalibard, J.; Roger, G. Experimental test of Bell’s inequalities using time-varying analyzers. Phys. Rev. Lett. 1982, 49, 1804. [Google Scholar] [CrossRef]
- Weihs, G.; Jennewein, T.; Simon, C.; Weinfurter, H.; Zeilinger, A. Violation of Bell’s inequality under strict Einstein locality conditions. Phys. Rev. Lett. 1998, 81, 5039. [Google Scholar] [CrossRef]
- Bell, J.S. Speakable and Unspeakable in Quantum Mechanics; Cambridge University Press: New York, NY, USA, 1987; p. 65. [Google Scholar]
- Brunner, N.; Cavalcanti, D.; Pironio, S.; Scarani, V.; Wehner, S. Bell nonlocality. Rev. Mod. Phys. 2014, 86, 419–478. [Google Scholar] [CrossRef]
- Wiseman, H.M. The two Bell’s theorems of John Bell. J. Phys. A Math. Theor. 2014, 47, 424001. [Google Scholar] [CrossRef]
- Kupczynski, M. Quantum nonlocality: How does nature do it? Entropy 2024, 26, 191. [Google Scholar] [CrossRef] [PubMed]
- Kochen, S.; Specker, E.P. The problem of HV in quantum mechanics. In Ernst Specker Selecta; Birkhäuser: Basel, Switzerland, 1990; pp. 235–263. [Google Scholar]
- Schwinger, J. Quantum electrodynamics. I. A covariant formulation. Phys. Rev. 1948, 74, 1439. [Google Scholar] [CrossRef]
- Feynman, R.P. Space-time approach to quantum electrodynamics. In Quantum Electrodynamics; CRC Press: Boca Raton, FL, USA, 2018; pp. 178–198. [Google Scholar]
- Dyson, F.J. The Radiation Theories of Tomonaga, Schwinger, and Feynman. Phys. Rev. 1949, 75, 486. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Low, F.E. Quantum electrodynamics at small distances. Phys. Rev. 1954, 95, 1300. [Google Scholar] [CrossRef]
- Wilson, K.G. Renormalization group and critical phenomena. I. Renormalization group and the Kadanoff scaling picture. Phys. Rev. B 1971, 4, 3174. [Google Scholar] [CrossRef]
- Wilson, K.G.; Kogut, J. The renormalization group and the epsilon expansion. Phys. Rep. 1974, 12, 75–199. [Google Scholar] [CrossRef]
- Gross, D.J. Twenty five years of asymptotic freedom. Nucl. Phys. B-Proc. Suppl. 1999, 74, 426–446. [Google Scholar] [CrossRef]
- Sanyuk, V.I.; Sukhanov, A.D. Dirac in 20th century physics: A centenary assessment. Phys.-Uspekhi 2003, 46, 937. [Google Scholar] [CrossRef]
- Wilczek, F. Quantum mechanics of fractional-spin particles. Phys. Rev. Lett. 1982, 49, 957. [Google Scholar] [CrossRef]
- Kamada, S. Braid and Knot Theory in Dimension Four; American Mathematical Socient: Providence, RI, USA, 1964. [Google Scholar]
- Charvin, G.; Vologodskii, A.; Bensimon, D.; Croquette, V. Braiding DNA: Experiments, simulations, and models. Biophys. J. 2005, 88, 4124–4136. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Khrennikov, A. Contextual approach to quantum mechanics and the theory of the fundamental prespace. arXiv 2003, arXiv:quant-ph/0306003. [Google Scholar] [CrossRef]
- Khrennikov, A.Y. Contextual Approach to Quantum Formalism; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; Volume 160. [Google Scholar]
- Gell-Mann, M. The Interpretation of the New Particles as Displaced Charged Multiplets. Nuovo C. 1956, 4 (Suppl. S2), 848–866. [Google Scholar] [CrossRef]
- Nakano, T.; Nishijima, N. Charge Independence for V-particles. Prog. Theor. Phys. 1953, 10, 581. [Google Scholar] [CrossRef]
- Griffiths, D. Introduction to Elementary Particles; Wiley: Hoboken, NJ, USA, 2009; pp. 59–60. ISBN 978-3-527-40601-2. [Google Scholar]
- Laurikainen, K.V. Beyond the Atom: The Philosophical Thought of Wolfgang Pauli; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Pauli, W. Pauli Letter Collection: Letter to Lise Meitner (No. CERN-ARCH-PLC, pp. Letter-2412). 1930. Available online: https://cds.cern.ch/record/83292?ln=en (accessed on 21 August 2025).
- Fermi, E. Versuch einer Theorie der β-Strahlen. I. Z. FüR Phys. 1934, 88, 161–177. [Google Scholar] [CrossRef]
- Fukuda, S.; Fukuda, Y.; Hayakawa, T.; Ichihara, E.; Ishitsuka, M.; Itow, Y.; Kajita, T.; Kameda, J.; Kaneyuki, K.; Kasuga, S.; et al. The super-kamiokande detector. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectromet. Detect. Assoc. Equip. 2003, 501, 418–462. [Google Scholar] [CrossRef]
- Abbasi, R.; Ackermann, M.; Adams, J.; Ahlers, M.; Ahrens, J.; Andeen, K.; Auffenberg, J.; Bai, X.; Baker, M.; Barwick, S.; et al. The IceCube data acquisition system: Signal capture, digitization, and timestamping. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectromet. Detect. Assoc. Equip. 2009, 601, 294–316. [Google Scholar] [CrossRef]
- Bellerive, A.; Klein, J.R.; McDonald, A.B.; Noble, A.J.; Poon, A.W. The Sudbury Neutrino Observatory. Nucl. Phys. B 2016. [Google Scholar] [CrossRef]
- Waxman, E. Neutrino astrophysics: A new tool for exploring the universe. Science 2007, 315, 63–65. [Google Scholar] [CrossRef][Green Version]
- Mertens, S. Direct neutrino mass experiments. J. Phys. Conf. Ser. 2016, 718, 022013. [Google Scholar] [CrossRef]
- Abe, S.; Ebihara, T.; Enomoto, S.; Furuno, K.; Gando, Y.; Ichimura, K.; Ikeda, H.; Inoue, K.; Kibe, Y.; Kishimoto, Y.; et al. KamLAND Measurement of Reactor Antineutrino Disappearance in the First Phase of the KamLAND Experiment. Phys. Rev. Lett. 2008, 100, 221803. [Google Scholar] [CrossRef]
- An, F.P.; Bai, J.Z.; Balantekin, A.B.; Band, H.R.; Beavis, D.; Beriguete, W.; Bishai, M.; Blyth, S.; Boddy, K.; Brown, R.L.; et al. Observation of electron-antineutrino disappearance at Daya Bay. Phys. Rev. Lett. 2016, 108, 171803. [Google Scholar] [CrossRef]
- Bellini, G.; Benziger, J.; Bick, D.; Bonfini, G.; Bravo, D.; Avanzini, M.B.; Caccianiga, B.; Cadonati, L.; Calaprice, F.; Carraro, C.; et al. Cosmic-muon flux and annual modulation in Borexino at 3800 m water-equivalent depth. J. Cosmol. Astropart. Phys. 2012, 2012, 015. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Altmann, D.; Anderson, T.; Arguelles, C.; Arlen, T.C.; et al. Observation of high-ener gy astrophysical neutrinos in three years of IceCube data. Phys. Rev. Lett. 2014, 113, 101101. [Google Scholar] [CrossRef] [PubMed]
- Abe, K.; Hayato, Y.; Iida, T.; Iyogi, K.; Kameda, J.; Koshio, Y.; Kozuma, Y.; Marti, L.; Miura, M.; Moriyama, S.; et al. Evidence for the appearance of atmospheric tau neutrinos in Super-Kamiokande. Phys. Rev. Lett. 2013, 110, 181802. [Google Scholar] [CrossRef]
- Cowan, C.L., Jr.; Reines, F.; Harrison, F.B.; Kruse, H.W.; McGuire, A.D. Detection of the free neutrino: A confirmation. Science 1956, 124, 103–104. [Google Scholar] [CrossRef]
- Wiebusch, C.H.V. The Detection of Faint Light in Deep Underwater Neutrino Telescopes. Ph.D. Dissertation, Department of Physics | RWTH Aachen University, Aachen Germany, 1995. [Google Scholar]
- Adrián-Martínez, S.; Al Samarai, I.; Albert, A.; André, M.; Anghinolfi, M.; Anton, G.; Anvar, S.; Ardid, M.; Astraatmadja, T.; Aubert, J.-J.; et al. Search for cosmic neutrino point sources with four years of data from the ANTARES telescope. Astrophys. J. 2012, 760, 53. [Google Scholar] [CrossRef][Green Version]
- Gaisser, T.K. Cosmic rays and particle physics. Comments Nucl. Part. Phys. 1982, 11, 25–39. [Google Scholar][Green Version]
- Patrignani, C.; Agashe, K.; Aielli, G.; Amsler, C.; Antonelli, M.; Asner, D.M.; Baer, H.; Banerjee, S.W.; Barnett, R.M.; Basaglia, T. Review of Particle Physics. Chin. Phys. C 2016, 40, 100001. [Google Scholar] [CrossRef]
- Lee, T.D.; Yang, C.N. Question of parity conservation in weak interactions. Phys. Rev. 1956, 104, 254. [Google Scholar] [CrossRef]
- Wu, C.S.; Ambler, E.; Hayward, R.W.; Hoppes, D.D.; Hudson, R.P. Experimental test of parity conservation in beta decay. Phys. Rev. 1957, 105, 1413. [Google Scholar] [CrossRef]
- Coope, J.A.R.; Snider, R.F.; McCourt, F.R. Irreducible cartesian tensors. J. Chem. Phys. 1965, 43, 2269–2275. [Google Scholar] [CrossRef]
- Coope, J.A.R.; Snider, R.F. Irreducible cartesian tensors. II. General formulation. J. Math. Phys. 1970, 11, 1003–1017. [Google Scholar] [CrossRef]
- Coope, J.A.R. Irreducible Cartesian Tensors. III. Clebsch-Gordan Reduction. J. Math. Phys. 1970, 11, 1591–1612. [Google Scholar] [CrossRef]
- Snider, R.F. Irreducible Cartesian Tensors; Walter de Gruyter GmbH and Co KG: Berlin, Germany, 2017; Volume 43. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Available online: https://en.wikipedia.org/wiki/Pauli_matrices (accessed on 21 August 2025).
- Frankel, T. The Geometry of Physics: An Introduction; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Ryder, L.H. Quantum Field Theory; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Donoghue, J.F.; Golowich, E.; Holstein, B.R. Dynamics of the Standard Model; Cambridge University Press: Cambridge, UK, 2014; p. 573. [Google Scholar]
- Born, M.; Oppenheimer, R. On the quantum theory of molecules. In Quantum Chemistry: Classic Scientific Papers; World Scientific: New Jersey, NJ, USA, 2000; pp. 1–24. [Google Scholar]
- Mohapatra, R.N.; Pal, P.B. Massive Neutrinos in Physics and Astrophysics; World Scientific: New Jersey, NJ, USA, 2004; Volume 72. [Google Scholar]
- Altarelli, G. The mystery of neutrino mixings. arXiv 2011, arXiv:1111.6421. [Google Scholar] [CrossRef]
- Fano, U. Description of states in quantum mechanics by density matrix and operator techniques. Rev. Mod. Phys. 1957, 29, 74. [Google Scholar] [CrossRef]
- Wilde, M.M. Quantum Information Theory; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Fields, B.; Sarkar, S. Big-bang nucleosynthesis (particle data group mini-review). arXiv 2006, arXiv:astro-ph/0601514. [Google Scholar] [CrossRef]
- Peres, A. (Ed.) Quantum Theory: Concepts and Methods; Springer: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Hu, X.M.; Guo, Y.; Liu, B.H.; Li, C.F.; Guo, G.C. Progress in quantum teleportation. Nat. Rev. Phys. 2023, 5, 339–353. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895. [Google Scholar] [CrossRef] [PubMed]
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the IEEE 35th Annual Symposium on Foundations of Computer Science (FOCS), Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar]
- Levitt, M.H. Spin Dynamics: Basics of Nuclear Magnetic Resonance; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Edmonds, A.R. Angular Momentum in Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1996; Volume 4. [Google Scholar]
- Guessoum, N.; Jean, P.; Gillard, W. The lives and deaths of positrons in the interstellar medium. Astron. Astrophys. 2005, 436, 171–185. [Google Scholar] [CrossRef]
- Weidenspointner, G.; Skinner, G.; Jean, P.; Knödlseder, J.; Von Ballmoos, P.; Bignami, G.; Diehl, R.; Strong, A.W.; Cordier, B.; Schanne, S.; et al. An asymmetric distribution of positrons in the Galactic disk revealed by gamma-rays. Nature 2008, 451, 159–162. [Google Scholar] [CrossRef]
- Beacom, J.F.; Bell, N.F.; Bertone, G. Gamma-ray constraint on Galactic positron production by MeV dark matter. Phys. Rev. Lett. 2005, 94, 171301. [Google Scholar] [CrossRef]
- Steinberg, A.M. Quantum Measurements: A modern view for quantum optics experimentalists. arXiv 2014, arXiv:1406.5535. [Google Scholar] [CrossRef]
- Whitesides, G.M.; Grzybowski, B. Self-assembly at all scales. Science 2002, 295, 2418–2421. [Google Scholar] [CrossRef]
- Doherty, M.W.; Manson, N.B.; Delaney, P.; Jelezko, F.; Wrachtrup, J.; Hollenberg, L.C. The nitrogen-vacancy colour centre in diamond. Phys. Rep. 2013, 528, 1–45. [Google Scholar] [CrossRef]
- Taylor, J.M.; Cappellaro, P.; Childress, L.; Jiang, L.; Budker, D.; Hemmer, P.R.; Yacoby, A.; Walsworth, R.; Lukin, M.D. High-sensitivity diamond magnetometer with nanoscale resolution. Nat. Phys. 2008, 4, 810–816. [Google Scholar] [CrossRef]
- Abi, B.; Albahri, T.; Al-Kilani, S.; Allspach, D.; Alonzi, L.P.; Anastasi, A.; Anisenkov, A.; Azfar, F.; Badgley, K.; Baeßler, S.; et al. Measurement of the positive muon anomalous magnetic moment to 0.46 ppm. Phys. Rev. Lett. 2021, 126, 141801. [Google Scholar] [CrossRef]
- Aoyama, T.; Asmussen, N.; Benayoun, M.; Bijnens, J.; Blum, T.; Bruno, M.; Caprini, I.; Calame, C.C.; Cè, M.; Colangelo, G.; et al. The anomalous magnetic moment of the muon in the Standard Model. Phys. Rep. 2020, 887, 1–166. [Google Scholar] [CrossRef]
- Moroi, T. Muon anomalous magnetic dipole moment in the minimal supersymmetric standard model. Phys. Rev. D 1996, 53, 6565. [Google Scholar] [CrossRef]
- Gabrielse, G.; Hanneke, D.; Kinoshita, T.; Nio, M.; Odom, B. New Determination of the Fine Structure Constant from the Electron g Value and QED. Phys. Rev. Lett. 2006, 97, 030802. [Google Scholar] [CrossRef] [PubMed]
- Mohr, P.J.; Taylor, B.N.; Newell, D.B. CODATA Recommended Values of the Fundamental Physical Constants. Rev. Mod. Phys. 2012, 84, 1527. [Google Scholar] [CrossRef]
- Hestenes, D.; Lasenby, A. Space-Time Algebra; Springer International Publishing: Cham, Switzerland, 2015; p. 2015. [Google Scholar]
- Bargmann, V.; Michel, L.; Telegdi, V.L. Precession of the Polarization of Particles Moving in a Homogeneous Electromagnetic Field. Phys. Rev. Lett. 1959, 2, 435. [Google Scholar] [CrossRef]
- Chiou, D.-W.; Chen, T.-W. Exact Foldy–Wouthuysen transformation of the Dirac–Pauli Hamiltonian. arXiv 2014, arXiv:1405.4495. [Google Scholar]
- Duval, C.; Horváthy, P.A. On the Bargmann–Michel–Telegdi equations, and spin–orbit coupling. Nucl. Phys. B Proc. Suppl. 2016, 912, 450–462. [Google Scholar] [CrossRef]
- Foldy, L.L.; Wouthuysen, S.A. On the Dirac Theory of Spin 1/2 Particles and Its Non-Relativistic Limit. Phys. Rev. 1950, 78, 29. [Google Scholar] [CrossRef]
- Costella, J.P.; McKellar, B.H.J. The Foldy–Wouthuysen transformation. Am. J. Phys. 1995, 63, 1119. [Google Scholar] [CrossRef]
- Silenko, A.J. General properties of the Foldy–Wouthuysen transformation and applicability of the corrected original method. Phys. Rev. A 2016, 93, 022108. [Google Scholar] [CrossRef]
- KATRIN Collaboration; Aker, M.; Batzler, D.; Beglarian, A.; Behrens, J.; Beisenkötter, J.; Biassoni, M.; Bieringer, B.; Biondi, Y.; Block, F.; et al. Direct neutrino-mass measurement based on 259 days of KATRIN data. Science 2025, 388, 180–185. [Google Scholar] [CrossRef] [PubMed]
- Freitas, A. TASI 2020 lectures on precision tests of the standard model. arXiv 2020, arXiv:2012.11642. [Google Scholar] [CrossRef]
- Erler, J.; Schott, M. Electroweak precision tests of the Standard Model after the discovery of the Higgs boson. Prog. Part. Nucl. Phys. 2019, 106, 68–119. [Google Scholar] [CrossRef]
- Fan, X.; Myers, T.G.; Sukra, B.A.D.; Gabrielse, G. Measurement of the electron magnetic moment. Phys. Rev. Lett. 2023, 130, 071801. [Google Scholar] [CrossRef] [PubMed]
- Lamb, W.E.; Retherford, R.C. Fine Structure of the Hydrogen Atom by a Microwave Method. Phys. Rev. 1947, 72, 241. [Google Scholar] [CrossRef]
- Casimir, H.B.G. On the Attraction Between Two Perfectly Conducting Plates. Proc. K. Ned. Akad. Wet. 1948, 51, 793. [Google Scholar]
- Penrose, R. Twistor algebra. J. Math. Phys. 1967, 8, 345–366. [Google Scholar] [CrossRef]
- Penrose, R. Solutions of the Zero-Rest-Mass Equations. J. Math. Phys. 1969, 10, 38–39. [Google Scholar] [CrossRef]
- Wikipedia: Physics Beyond the Standard Model. Available online: https://en.wikipedia.org/w/index.php?title=Physics_beyond_the_Standard_Model&oldid=1308782205 (accessed on 21 August 2025).
- Wheeler, J.A.; Zurek, W.H. (Eds.) The Physical Content of Quantum Kinematics and Mechanics. In Quantum Theory and Measurement; Princeton University Press: Princeton, NJ, USA, 1983; pp. 62–68. (In English) [Google Scholar]
- Albert Einstein, Delivered in a 1933 Lecture at Oxford Titled “On the Method of Theoretical Physics”. Available online: https://eclass.uoa.gr/modules/document/file.php/PHS539/%CE%9A%CE%B5%CE%AF%CE%BC%CE%B5%CE%BD%CE%B1%20%CE%B3%CE%B9%CE%B1%20%CE%BC%CE%B5%CE%BB%CE%AD%CF%84%CE%B7/%CE%9A11%20Einstein_On_The_Method_of_Theoretical_Physics.pdf (accessed on 5 April 2025).
- Newton, I. The Principia: Mathematical Principles of Natural Philosophy; Cohen, I.B.; Whitman, A., Translators; University of California Press: Berkeley, CA, USA, 1999. [Google Scholar]
- “Interpretations of Quantum Mechanics,” Wikipedia. The Free Encyclopedia. Available online: https://en.wikipedia.org/wiki/Interpretationsofquantummechanics (accessed on 5 April 2025).
- Hall, B.C. Lie groups, Lie algebras, and representations. In Quantum Theory for Mathematicians; Springer: New York, NY, USA, 2013; pp. 333–366. [Google Scholar]
- Georgi, H. Lie Algebras in Particle Physics: From Isospin to Unified Theories; Taylor & Francis: Abingdon, UK, 2000; p. 340. [Google Scholar]
- Cornwell, J.F. Group Theory in Physics; Academic Press: Cambridge, MA, USA, 1984. [Google Scholar]


| Framework | Approach | Strengths | Weaknesses |
|---|---|---|---|
| Bivector SM | The bivector boson spin-1 is fundamental in , and fermions are its blades; classical mechanics and geometric algebra; defines the quantum state as parity +1. | Ontic; unifies bosons-fermions; classical-quantum correspondence; mass, charge, and spin emerge; clarifies parity; origin of the double helix; parity conserved in -decay; neutrinos not needed; no superposition and collapse; local; disproves Bell’s theorem. | Highly nonstandard; requires vast reinterpretation SM data; untested. |
| Standard Model [1] | Gauge-theoretic QFT with fermions as fundamental; bosons arise from gauge fields; uses SU(3)× SU(2)×U(1). | Matches much of the high-energy experimental data; predictive; deeply integrated into QFT and particle physics. | Relies on unexplained parameters; parity violation; no ontic spin; non-local; chirality issues; semantically confusing; mathematically dense. |
| Hestenes [13,14] | Uses GA; spinors as real even multivectors in ; keeps fermions as fundamental. | Geometric clarity; keeps full QM predictive power; clarifies zbw and spin. | Retains superposition and fermions; does not change SM ontology; rests within QM formalism. |
| Doran and Lasenby [7] | General spacetime algebra (STA) framework for fields; rotor formalism for spin; unifies GA treatment of relativity and QM. | General; powerful for both relativity and QM in unified formalism; widely cited. | Retains SM ontology and quantum postulates; retains superposition. |
| Twistor Theory [123,124] | Formulates spacetime and fields in complex projective space; spinors are fundamental; aims at unifying geometry with quantum theory. | Related to conformal geometry and spin; applied to scattering amplitudes. Simplifies Feynman diagrams. Developed the Penrose transform. | Abstract, highly mathematical; physical interpretation less direct; built on spinor ontology. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanctuary, B. The Classical Origin of Spin: Vectors Versus Bivectors. Axioms 2025, 14, 668. https://doi.org/10.3390/axioms14090668
Sanctuary B. The Classical Origin of Spin: Vectors Versus Bivectors. Axioms. 2025; 14(9):668. https://doi.org/10.3390/axioms14090668
Chicago/Turabian StyleSanctuary, Bryan. 2025. "The Classical Origin of Spin: Vectors Versus Bivectors" Axioms 14, no. 9: 668. https://doi.org/10.3390/axioms14090668
APA StyleSanctuary, B. (2025). The Classical Origin of Spin: Vectors Versus Bivectors. Axioms, 14(9), 668. https://doi.org/10.3390/axioms14090668






