Abstract
This paper focuses on the variable coefficients geophysical KdV (VCGKdV) equation, which involves time-dependent perturbation, nonlinearity and dispersion parameters. It is a more realistic model than its constant coefficient counterpart and can be useful to, for instance, investigate the Coriolis effect on oceanic flows. Firstly, we analyzed this model using three strong methods that allow the investigation of its integrability: the Lie symmetry approach, Painlevé property and Hirota formalism. The general constraints between the involved parameters under which the complete integrability in Lie, Painlevé or Hirota sense exists, as well as the largest class of this type of equations, which admits the same class of imposed symmetries are generated. Then, some new specific families of solutions for the model endowed with either Lie symmetry properties, Lie and Painlevé constraints or with Lie, Painlevé and Hirota constraints were generated and compared with solutions derived with other techniques. By numerical simulations, the dynamical behaviors of some Lie invariant solutions and nonautonomous multiple solitons are depicted.
Keywords:
VCGKdV model; Lie symmetry; Pailevé property; Hirota bilinearisation; compatibility conditions; invariant solutions; nonautonomous solitons MSC:
35Q51; 35Q58; 35C08
1. Introduction
Very often, the study of natural phenomena leads to problems that can be reduced to solving nonlinear partial differential equations. (NPDEs). These equations describe important models with physical and mathematical meanings, the investigation of which involves finding solutions, or at least deciding whether they are integrable or not. Investigating integrability and finding exact solutions to the NPDEs have extensive applications in many scientific fields such as engineering, plasma physics, fluid mechanics, ecology, optical fibers, biology, chemical kinematics, meteorology and so on. There are many investigation methods for NPDEs, based on various mathematical approaches, such as inverse scattering transformation [1], Darboux transformation [2], bilinearization and super-bilinearization [3,4,5], classical and nonclassical group invariance [6,7,8,9], Painlevé expansion [10,11,12], Lax representation [13], etc. There are also specific solving methods, such as the functional expansion method [14,15,16], the exponential rational function approach [17], the planar dynamical system scheme [18], and so forth. Each method has its own significant properties.
In this paper, we will investigate a generalized model of the so-called Geophysical KdV model (GKdV) [19], obtained by incorporating a perturbation term , into the standard KdV equation with constant coefficients. It is described as follows:
In the above equation, , denotes the n-order spatial derivative, a is a perturbation parameter related to the Coriolis effect, b represents the nonlinearity factor and c is the spatial dispersion parameter of a third-order degree. The GKdV appears in various applications of acoustics, aerodynamics and medical engineering. It can be useful in analyzing the influence of Earth’s rotation on the propagation of oceanic waves, the so-called Coriolis effect [20]. In [21], the finite element method was used to analyze the impact of the Coriolis parameter a on these waves. The conservation laws of GKdV were derived in [22] with the help of the Euler and homotopy operators. Various soliton profiles for Equation (1) are presented, for example, in [23] by making use of —expansion method and the sine–cosine method, as well as in [24] by implementing the tanh–coth approach. Investigation of the Coriolis effect on oceanic flows and its bifurcation via GKdV Equation (1) with , , were performed in [21,25]. Similar investigations have been conducted on other nonlinear dynamical systems in various space–time dimensions [26].
As we have already mentioned, we want to generalize Equation (1) to the Variable Coefficients Geophysical KdV (VCGKdV) model described by the following nonautonomous NPDE:
Here, the arbitrary functions , , are, respectively, the perturbation, the nonlinearity and the spatial dispersion parameters. By choosing different forms of these functions, we obtain the freedom of modeling various real situations, for various nonuniformities of the physical space–time. This generalized model can be useful for instance to model the propagation of tsunami waves. The Coriolis term explains exactly how the Earth’s rotation affects the spread of tsunami waves.
It has been well proven in many studies that NPDEs with time variable coefficients provide more realistic models than their constant coefficient counterparts. For example, VCGKdV Equations [27] are used to model shallow water waves and internal waves in the ocean, as well as atmospheric gravity waves. This is the reason why we have investigated the VCGKdV model (2). This equation represents an extension of the standard KdV, and is intended to account for more complex phenomena relevant to large-scale waves in the atmosphere and ocean.
The paper has the following structure: after these introductory notes, Section 2 describes the VCGKdV model, respectively, from the perspectives of four powerful techniques, the direct and the inverse Lie symmetry methods, the Painlevé approach and the Hirota procedure. The general contraints between involved parameters, under which the complete integrability in the Lie, Painlevé or Hirota senses exists, as well as the largest class of VCGKdV equations, which admits the same class of imposed symmetries, is generated. In Section 3, the focus is on deriving the specific families of solutions for the model endowed with either Lie symmetry properties, Lie and Painlevé constraints or with Lie, Painlevé and Hirota constraints. Through numerical simulations, the physical characteristics of some Lie-invariant solutions and nonautonomous solitons are visualized. The final section of the paper is dedicated to concluding remarks.
The results obtained in this paper are significant because we deal with the simultaneous use of different powerful techniques responsible for integrability of nonlinear dynamical models, namely the Lie symmetry, Painlevé and Hirota approaches. Typically, these techniques stop when the integrability conditions are obtained, without providing information about the solutions that each of them generates. We extend the integrability check exactly with a comparative study on the solutions. For the first time, we utilize the VCGKDV model to assess the connections between various integrability conditions, and also some new families of solutions for the concerned model endowed with either Lie symmetry properties, Lie and Painlevé constraints or with Lie, Painlevé and Hirota constraints are generated. It is important to outline that the applied procedure is important by itself, being applicable to all the nonlinear differential equations.
2. Symmetries and Integrabilities of the VCGKdV Model
2.1. Lie Symmetry Analysis for the VCGKdV Model
2.1.1. Generalities of the Approach
Useful information about the dynamics of different systems can be obtained by studying their symmetries. In some cases, we can apply sophisticated approaches such as BRST symmetry, which embeds the symmetries of the system in larger spaces [28]. Here, we will refer to the Lie symmetry approach, which is suitable for studying the integrability of different NPDEs.
We start our investigations by assuming that the geophysical model (2) admits the following Lie operator, written in the canonical form:
We choose the characteristic function in the following form:
where , , , are functions to be determined.
The master Equation (2) remains invariant under the action of the symmetry operator (3) if, and only if, the following condition is verified [6]:
where represents the third extension of the symmetry generator (3).
The previous invariant condition (5) can be expressed in the equivalent form as follows:
where satisfies Equation (2) and , , are the first- and third-order total derivative operators with respect to the corresponding independent variables.
Substituting in Equations (2), (4) and (6), as well as the appropriate derivatives of the later, we obtained a determining system with 17 NPDEs. The differential equations of this system are compatible if and only if
with , q arbitrary constants.
In conclusion, the VCGKdV model accepts Lie symmetries and invariant solutions if the constraints (7) are satisfied. With these constraints, Equation (2) takes the following form:
The Lie invariant condition (5) becomes
with the attached Lie characteristic function (4) of the form
These last equations define the problem that will be investigated from here on.
2.1.2. Direct and Inverse Symmetry Approaches
The following two paths are now possible in solving the determining system: a direct symmetry approach, which assumes that , and , in the master Equation (2) as known functions and finds the variable coefficient functions , from the characteristic symmetry function (10); and an inverse symmetry approach [29] that supposes to consider , from (10) as known functions, and determine all the equations of type (2) which are equivalent from the point of view of the symmetry group they admit.
In path (i), by solving the Lie determining system, we obtain
where , are arbitrary functions and , , are arbitrary constants. The prime denotes the derivative with respect to t variable. The characteristic function (10) of the Lie symmetry operator takes the general form
The invariant solutions of Equation (8) are generated if we impose and solve the condition where admits the previous expression (12). Therefore, the general family of Lie invariant solutions is obtained as follows:
Remark 1.
If in (13), we consider that , and where are arbitrary constants, we come back to the geophysical KdV model (1) with constant coefficients; the mentioned family of solutions takes the form
where the argument is a particular form of ζ from (13). Choosing in (14) and as the trigonometric functions , or as the hyperbolic functions , , we recover the family of solutions obtained in [24]. We note that even for the geophysical KdV model with a constant coefficient, the solutions in (14) are more general than those reported in [24].
Following path (), we can determine all equations of the form (8) that admit the Lie symmetry operator (3) with the characteristic function (10). With the aid of the Maple program, we obtained the variable coefficient functions from (8) under the forms
Thus, the most general equations of the form (8) with the imposed symmetry group generated by the characteristic function (10) admit the form
with arbitrary constants , ,
2.2. Painlevé Approach for the Complete Integrability of the VCGKdV Model
A VCKdV equation, rather similar with (2), was considered in [10]
It has been proved that the model (17) admits the Painlevé property if the following condition among the coefficients holds that
where prime denotes the derivative with respect to time, and and is an arbitrary function. The condition (18) is achieved by making use of the connection between the Lax pair and the Painlevé property.
It is easy to see that Equation (17) becomes (2) when , Therefore, we can adapt the condition (18) to (2), and we verify that the VCGKdV model passes the Painlevé test if the following conditions are verified:
Once the conditions in (19) are fulfilled, the analyzed KdV model (2) is expected to be completely integrable. The constraint conditions (19) are called Painlevé integrability conditions.
The previous system can be solved and gives the most general Equation (2) that satisfies the Painlevé conditions (19), the most general VCGKdV model completely integrable in the Painlevé sense. The solution highlights that the functions and are not arbitrary functions, being expressed in terms of and as follows:
where , arbitrary constants.
We note that under the particular choices and , we recover the constraint (7) found when the symmetry approach was applied to the model, while the Painlevé function becomes
2.3. Hirota Formalism for the VCGKdV Model
2.3.1. General Issues on Integrability in the Hirota Sense
Single-soliton solutions can be easily found by using the traveling wave ansatz . Integrability in the Hirota sense supposes that one can combine any number N of one-soliton solutions into a N-soliton solution (N-ss) [30].
For finding multi-soliton solutions for NPDEs, Hirota’s bilinear method is the best tool [3,31], although many other methods can also be used. The method often involves perturbation techniques and transformations, as Hirota noticed that the best dependent variables necessary for constructing soliton solutions are those in which the solution appears as a finite sum of exponentials.
Introducing a new dependent variable and using an appropriate transformation, the equation is written in a bilinear form. However, in order to be able to apply the Hirota method, it is essential that the derivatives only appear in combinations that can be expressed using Hirota’s D-operator, defined as:
The D-operator is antisymmetric:
The bilinearization process can be quite difficult as it is far from being algorithmic [31,32]. Some useful formulas and properties of the bilinear derivative can be found in [33].
We apply the above procedure of Hirota for our model given in (2).
Using the substitution in (2), which involves one tau function, namely , our equation can be written in the following form:
In order to apply the Hirota bilinear formalism, we first must check if the above form (22) can be written in terms of the Hirota operator D. We noticed that this is possible for any and , if and only if
It is important to note that this condition is completely equivalent with the constraint (7) we found when only the Lie integrability was required.
2.3.2. General Solutions of VCGKdV with Bilinear Form
We consider the non-autonomous one-soliton solution (1-ss) for (24) as follows:
and we determine the dispersion relation as time-dependent as follows:
which means that the soliton is deformable in time during motion.
The non-autonomous two-soliton solution (2-ss) for (24) is generated by
where the time-dependent dispersion relations take the following form:
and the interaction term between the two solitons takes the following expression:
The 3-ss is generated in a similar form as above, with the difference that :
We notice that the soliton expressions contain no additional freedom. Based on these forms, the non-autonomous N-soliton solution (N-ss) can be found using the induction method as in [3], as follows:
3. VCGKdV Solutions via Various Approaches and Their Compatibility
We will use several specific and powerful techniques on VCGKDV. The reason is threefold. The first objective is to determine the largest class of VCGKDV-type equations which admits the same class of imposed symmetries. The second aim is to point out the general constraints between involved parameters under which the complete integrability in Lie, Painlevé or Hirota sense exists. The third aim is to point out some new specific classes of solutions for the VCGKDV model observing either Lie symmetry properties, Lie and Painlevé constraints or Lie, Painlevé and Hirota constraints. Following these directions, we will perform significant results which are summarized in the Concluding Remarks section.
3.1. Specific Lie-Invariant Solutions of the Model
In this subsection we take advantage of the previous Lie symmetry analysis in order to find new dynamical behaviors of the VCGKdV model (8), associated with the large family of invariant solutions (13).
These wave solutions, which are very useful in modeling real dynamics, are expressed in terms of three arbitrary constants, , , , and of three coefficient functions, the perturbation function related to the Coriolis effect, the nonlinearity function , and the three-order dispersive function . The dependence on the space variable x of the solution (13) is expressed through the arbitrary composed function ,
We observe that the forms under which the waves described by these solutions propagate are strongly influenced by their speeds. They are given by the integral term in and depend on the choices of the variable coefficient functions and . Below, we provide some graphical representations of the solutions (13), corresponding to the specific choices of the parameters , , , , and .
Let us first consider . We obtain the following class of invariant solutions:
where G is an arbitrary function of its argument and , , , are arbitrary constants.
We see that by choosing the functional parameters and linearlywith respect to time variable, the wave profile is generated by the expression chosen for the arbitrary composed function G with fourth-order nonlinearity in time.
The shape and motion of the wave-invariant solution (33) are shown in Figure 1 for particular function and for the parametric choices Under these conditions and picking up , a novel wave profile is depicted, which combines single solitons with M- and W-shaped soliton waves.
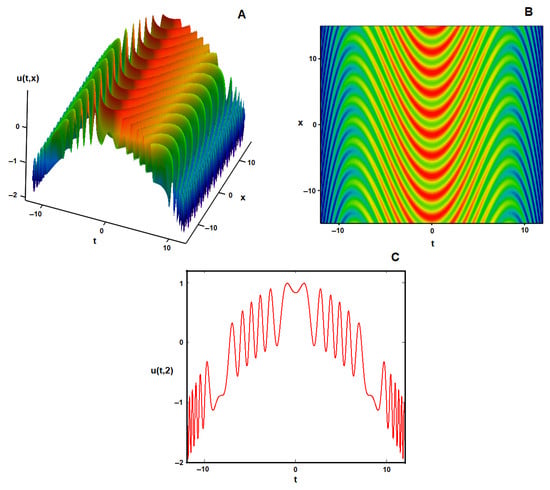
Figure 1.
and graphical representations, respectively, corresponding to the wave solution from (33) with the specific function and with the parametric relations : (A) the surface plot; (B) the contour plot of (A); (C) the shape of wave solution when .
Let us now choose , . We obtain another class of invariant solutions as follows:
We observe that, assuming the nonlinearity and perturbation functional parameters and as harmonic expressions, the wave dynamics are largely determined by the forms chosen for the arbitrary composite function V with harmonic-type argument.
Figure 2 shows the dynamic characteristics of the invariant wave solution (34) for the specific function and for the parametric choices We see that, assuming V as tanh function and by fixing , we obtain a periodic wave motion which combines single bright soliton with W-shaped soliton waves.
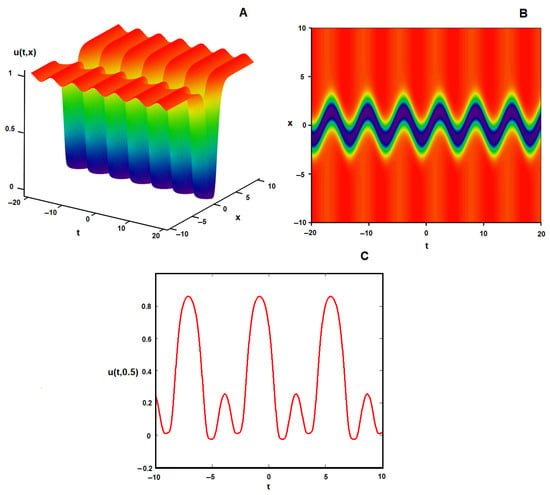
Figure 2.
and graphical representations, respectively, corresponding to the wave solution (34) with the particular function and with the parametric relations : (A) the surface plot; (B) the contour plot of (A); (C) the wave dynamics when .
3.2. Invariant Solutions Observing the Lie and Painlevé Constraints
We are now interested in looking for a connection between the Lie integrability conditions (15) and the Painlevé ones given by (19). We can do that by imposing the coefficient functions (15) as solutions of Painlevé conditions (19). Therefore, we are able to determine a constraint between the arbitrary functions , , , under which the Lie symmetry and Painlevé integrability requirements are simultaneously satisfied. We obtained this constraint under the form
with arbitrary constants. In this situation, we can say that the VCGKdV model (2) posseses the Painlevé integrability, as well as the Lie integrability.
Let us continue now by pointing out what is the effect on the geophysical KdV Equation (2) when we simultaneously ask for Lie and Painlevé integrabilities. We already saw in the previous section that the Lie invariance requirement reduces the class of Equations (2)–(16), which admits the invariant solutions (13). Now, we will continue by supplementarily imposing the constraint (35) induced by the Painlevé integrability condition, and we will investigate its effect at the level of both the equation and solutions mentioned above.
At the level of the VCGKdV, the sub-class of the Lie-invariant equation, which is simultaneously integrable in the Lie and Painlevé sense, are obtained by substituting (35) in (16). Its evolutionary form is
To now see the effect of the constraint (35) on the general class of Lie-invariant solutions (13), we return to the Lie characteristic function given by (10), now imposing that and are connected by (35). In these circumstances, solving the invariance condition , we obtain the following family of invariant solutions:
This special family of invariant solutions which also satisfies the Painlevé integrability conditions is expressed in terms of the arbitrary functions , , the composed functions and the arbitrary constants . This family of wave solutions (37) can be written in a more compact form by using the notations and with . It takes the form
Invoking freedom in choosing the forms of arbitrary functions , and , the family of solutions (38) of the VCGKdV model (2) describes a large type of dynamic behaviors attached to various nonlinear phenomena.
We will show here the profiles of some particular wave solutions which belong to the class (38), depicting them in the following Figure 3 and Figure 4.
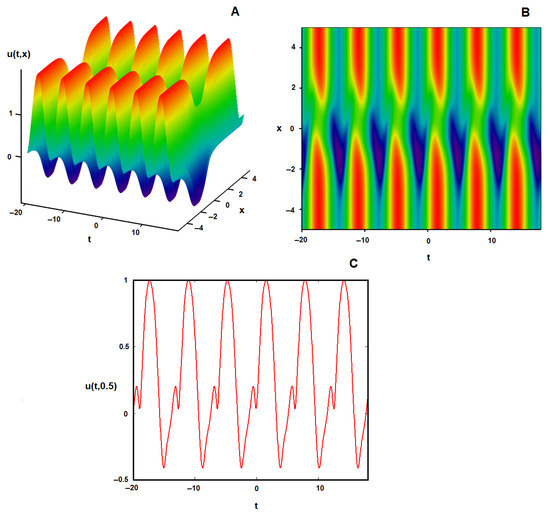
Figure 3.
and graphical representations, respectively, of the wave solution of type (38) corresponding to the hyperbolic composed function , , , with , and to the parametric relations : (A) the surface plot; (B) the contour plot of (A); (C) the wave dynamics when .
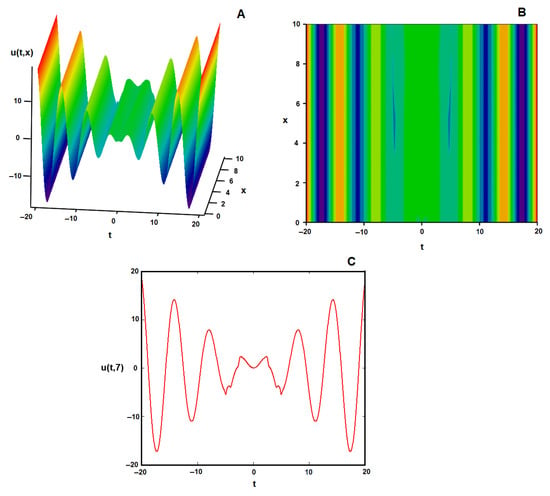
Figure 4.
and graphical representations, respectively, of the wave solution of the type (38), corresponding to the composed function , , , with , and the parametric relations . (A) the surface plot; (B) the contour plot of (A); (C) the wave dynamics when .
The graphical representations of the wave solution of type (38) are displayed in Figure 3 for the hyperbolic composed function , , with , and for the parametric choices . We note that by fixing into the previous N function, we obtain an interesting dynamics described by the propagation of two peaks–solitons, as Figure 3 illustrates.
Figure 4 shows the dynamic characteristics of another wave solution of type (38) by choosing the composed function , , , with , and the parametric choices . We see that by fixing into the previous new N function, the wave propagation is described by a lattice of nonautonomous solitons whose amplitude varies with time, as Figure 4 depicts.
3.3. Nonautonomous Soliton Solutions Observing the Lie, Painlevé and Hirota Constraints
Adding to Equation (16) and the constraint (35), we obtained Equation (36), endowed with Lie symmetry and Painlevé properties, as we proved in the previous section. Here, the aim is to additionally impose the Hirota bilinear requirements to the same model. Using the substitution in (36), it can be written in the Hirota bilinear form as
under the condition
The soliton solutions have the expressions given in the previous section in (26), (28), (31), (32) with the difference that the dispersion relation becomes
because
Using the software Mathematica 10.1, we plot in Figure 5, Figure 6 and Figure 7 the 1-ss, 2-ss and 3-ss , respectively, for the chosen parameters and functions.
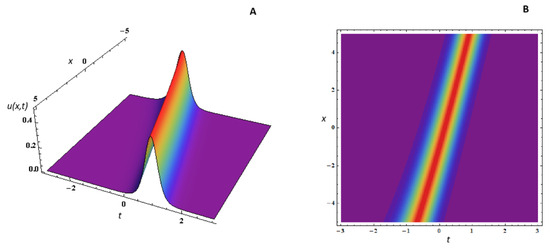
Figure 5.
Surface plot of given by Equation (26) for and the functions (A); contour plot for same parameters and functions (B).
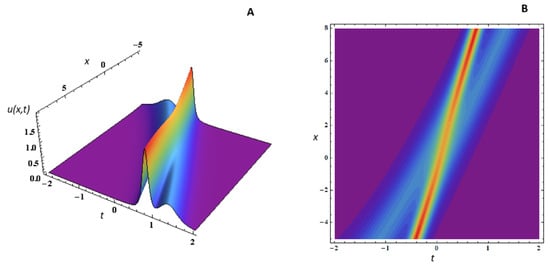
Figure 6.
Surface plot of given by Equation (28) for and the functions (A); contour plot for same parameters and functions (B).
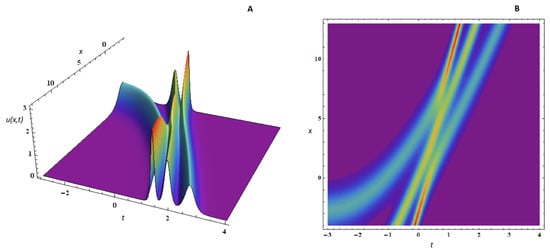
Figure 7.
Surface plot of given by Equation (31) for , and the functions (A); contour plot for same parameters and functions (B).
More precisely, Figure 5 describes the propagation in time of the one-soliton solution (1-ss) for , the chosen wave number, arbitrary phase and integration constant, , and . We considered particular choices for the functions and , that are responsible, respectively, for Lie and Painlevé integabilities of the model; namely, admits a trigonometric form, while is linear in time variable. Both surface and contour plots are presented.
Figure 6 describes the two-soliton solution propagation for and for , under the chosen wave numbers , phases and the arbitrary constant . The two-soliton interaction is also visible in the chosen intervals of time and space. As well known, when solitons interact, they typically experience a phase shift, meaning that their position or phase changes after the interaction, this being a key feature of soliton interactions. We also notice a change in amplitude, though only during the interaction.
The three-soliton solution is plotted in Figure 7, for and . We chose the wave numbers of close numeric values, , in order to obtain close values of amplitudes for the solitons. For the arbitrary phases, we used the values and keep the same integration constant. We kept the same expressions as in Figure 5 and Figure 6 for the functions involved. The interaction of the solitons, two by two, is visible both on surface and contour plot, showing the specific elastic scattering. More precisely, the solitons emerge from the collision unchanged in shape or amplitude, except for the phase shift.
Remark 2.
Now, we are interested to obtain nonautonomous lump soliton solutions for (36) by combining the Hirota bilinear method and the Cole–Hopf transformation The constraint conditions for and under which these solitons exist will be highlighted.
We can produce lump solutions if F is chosen to be a polynomial. More precisely, F admits the form
where , It involves three arbitrary constants, , , , and two arbitrary functions, , . To ensure that , we require .
By introducing the expression (41) into the bilinear form (39) and vanishing the coefficient functions of various powers of , we obtain a differential system with unknown functions , , and . We solved this using the Maple program. Therefore, the function (41) becomes
where
with C an arbitrary constant. Further, solving the previous mentioned differential system, we obtained the dependence of the unknown functions and of free function . Invoking the large relations, we omit them, but they will be displayed in the next particular situation.
So, in order to simplify the calculations, let us choose and Therefore, takes the reduced form:
Considering, for example, the upper sign in (43), and the Cole–Hopf transformation the following nonautonomous lump soliton solutions are generated:
4. Concluding Remarks
It is well known that in media with time-dependent perturbation, nonlinearity and dispersion, NPDEs with variable coefficients provide more realistic models than their constant coefficient counterparts. This is the reason that we investigated the VCGKdV model (2), which arises from different fields like mechanics, medical engineering and acoustics, and can describe sound transmission in fluids in various real situations and for various inhomogeneity features of the physical space.
The VCGKdV equations provide a powerful framework for understanding nonlinear wave dynamics in both oceanographic and atmospheric contexts. These equations offer insight into a wide range of phenomena, from coastal wave propagation to the behavior of atmospheric disturbances, making them crucial for understanding wave propagation in natural environments. To the VCGKdV Equation (2), we applied the Lie, Painlevé and Hirota approaches, methods of great significance in investigating nonlinear dynamical systems. They were applied individually or through their combinations. Our results can be synthesized as follows:
- This NPDE admits an infinite dimensional Lie algebra generated by the Lie operator with characteristic function (12) if and only if there is a linear dependence between the variable coefficient functions and of the model;
- The coefficients , and for which the VCGKdV model admits the Painlevé property have to verify the ODE system (19). Its solutions are (20), which express more general dependences between them as those obtained for the existence of the Lie symmetry. In the last case, and may be arbitrary functions, and has to be proportional with . The constraints (20) express the coefficient functions by more general relations, even using an arbitrary function . These Painlevé conditions reduce to the Lie symmetry conditions chosen parameter values and . For these value, the VCGKdV simultaneously admits Lie and Painlevé integrability and takes the form (36);
- When the Hirota approach was applied to Equation (36), we came to the conclusion that integrability in the Hirota sense is perfectly compatible with integrability in the sense of Lie and Painlevé. Thus, using the substitution in (2), we get that the equation admits the bilinear form (25) when . This condition (23) is identical to (7), which expresses the requirement for Lie and Painlevé integrability. The Hirota complete integrability of Equation (2) is proved by the existence of the nonautonomous N-soliton solution generated by the tau function (32).
- We extended the study of the compatibility between the three approaches, Lie, Painlevé and Hirota, at the level of the solutions of the VCGKdV (36). From this perspective, we obtained that:
- (a)
- Two families of Lie invariant solutions depending on three arbitrary constants and three arbitrary functions of time were pointed out as follows: (13), valid when Lie invariance has been required alone, and (37), valid when Lie and Painlevé integrabilities are required together. They take similar forms if and are related by
- (b)
- (c)
- Through numerical simulations, we visualized the physical characteristics of some of the obtained solutions, by selecting some significant parameters. In fact, for other choices of parameters and arbitrary functions, many other solutions, and thereby new features of the associated kinetics of VCGKdV Equation (2), can be illustrated. Some graphical representations are also shown for one-, two-, three-soliton solutions of (36).
As a final conclusion, the paper had two objectives: to show the effectiveness of some fundamental methods for the study of integrability of equations with variable coefficients, and to present new results on the dynamics of the geophysical KdV model. The methods used were the Lie symmetry, Painlevé and Hirota approaches, and their full efficiency was directly revealed by the novel numerical results on the VCGKdV model. New classes of solutions, combined with their graphical representations, were included. These methods have great potential in many other mathematical, physical and engineering applications.
Author Contributions
Conceptualization, R.C. (Rodica Cimpoiasu) and R.C. (Radu Constantinescu); methodology, R.C. (Rodica Cimpoiasu), R.C. (Radu Constantinescu) and C.N.B.; formal analysis, R.C. (Radu Constantinescu) and C.N.B.; writing—review and editing, R.C. (Rodica Cimpoiasu), R.C. (Radu Constantinescu) and C.N.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors acknowledge the support offered by the University of Craiova.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ma, W.X. The inverse scattering transform and soliton solutions of a combined modified Korteweg–de Vries equation. J. Math. Anal. Appl. 2019, 471, 796–811. [Google Scholar] [CrossRef]
- Matveev, V.B.; Salle, M.A. Darboux Transformations and Solitons. Springer Series in Nonlinear Dynamics; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Hirota, R. Exact Solutions of the Korteweg–De Vries Equation for Multiple Collisions of Solitons. Phys. Rev. Lett. 1971, 27, 1192–1194. [Google Scholar] [CrossRef]
- Babalic, C.N.; Carstea, A.S. Bilinear approach to supersymmetric Gardner equation. Theor. Math. Phys. 2016, 188, 1172–1180. [Google Scholar] [CrossRef]
- Babalic, C.N.; Carstea, A.S. On some new forms of lattice integrable equations. Cent. Eur. J. Phys. 2014, 12, 341–347. [Google Scholar] [CrossRef]
- Olver, P.J. Applications of Lie Groups to Differential Equations, GTM 107, 2nd ed.; Springer: New York, NY, USA, 1993. [Google Scholar]
- Clarkson, P.A.; Mansfield, E.L. Symmetry reductions and exact solutions of a class of nonlinear heat equations. Phys. D 1994, 70, 250–288. [Google Scholar] [CrossRef]
- Qu, C. Group classification and generalized conditional symmetry reduction of the nonlinear diffusion-convection equation with a nonlinear source. Stud. Appl. Math. 1997, 99, 107–136. [Google Scholar] [CrossRef]
- Cimpoiasu, R. Conservation Laws and associated Lie Symmetries for the 2D Ricci Flow Model. Rom. J. Phys. 2013, 58, 519–528. [Google Scholar]
- Brugarino, T. Painlevé property, auto-Bäcklund transformation, Lax pairs, and reduction to the standard form for the Korteweg–De Vries equation with nonuniformities. J. Math. Phys. 1989, 30, 1013–1015. [Google Scholar] [CrossRef]
- Baldwin, D.; Hereman, W. Symbolic Software for the Painlevé Test of Nonlinear Ordinary and Partial Differential Equations. J. Nonlinear Math. Phys. 2006, 13, 90–110. [Google Scholar] [CrossRef]
- Joshi, N. Painlevé Property of General Variable-Coefficient Versions of the Korteweg de Vries and Nonlinear Schrödinger Equations. Phys. Lett. A 1987, 125, 456–460. [Google Scholar] [CrossRef]
- Babalic, N.C.; Constantinescu, R.; Gerdjikov, V.S. On Tzitzeica equation and spectral properties of related Lax operators. Balk. J. Geom. Its Appl. 2014, 19, 11–22. [Google Scholar]
- Zayed, E.M.E.; Alurrfi, K.A.E. New extended auxiliary equation method and its applications to nonlinear Schrödinger-type equations. Optik 2016, 127, 9131–9151. [Google Scholar] [CrossRef]
- Ionescu, C.; Constantnescu, R.; Stoicescu, M. Functional expansions for finding traveling wave solutions. J. Appl. Anal. Comput. 2020, 10, 569–583. [Google Scholar] [CrossRef] [PubMed]
- Ionescu, C.; Babalic, C.N.; Constantinescu, R.; Efrem, R. The Functional Expansion Approach for Solving NPDEs as a Generalization of the Kudryashov and G′/G Methods. Symmetry 2022, 14, 827. [Google Scholar] [CrossRef]
- Fadhal, E.; Akbulut, A.; Kaplan, M.; Awadalla, M.; Abuasbeh, K. Extraction of exact solutions of higher order Sasa-Satsuma equation in the sense of beta derivative. Symmetry 2022, 14, 2390. [Google Scholar] [CrossRef]
- Zhang, H.; Jing, M.; Dong, S.; Dong, D.; Liu, Y.; Meng, Y. Stability and evolutionary trend of Hopf bifurcations in double-input SEPIC DC–DC converters. Int. J. Bifurc. Chaos 2019, 29, 1950192. [Google Scholar] [CrossRef]
- Karunakar, P.; Chakraverty, S. Effect of Coriolis constant on geophysical Korteweg-de Vries equation. J. Ocean Eng. Sci. 2019, 4, 113–121. [Google Scholar] [CrossRef]
- Geyer, A.; Quirchmayr, R. Shallow water equations for equatorial tsunami waves. Philos. Trans. R. Soc. A 2017, 376, 20170100. [Google Scholar] [CrossRef] [PubMed]
- Turgut, A.K.; Saha, A.; Dhawan, S.; Kara, A.H. Investigation of Coriolis effect on oceanic flows and its bifurcation via geophysical Korteweg-de Vries equation. Numer. Methods Partial. Differ. Equ. 2020, 36, 1234–1253. [Google Scholar]
- Rizvi, S.T.R.; Seadawy, A.R.; Younis, M.; Ali, I.; Althobaiti, S.; Mahmoud, S.F. Soliton solutions, Painleve analysis and conservation laws for a nonlinear evolution equation. Results Phys. 2021, 23, 103999. [Google Scholar] [CrossRef]
- Behera, S.; Aljahdaly, N.H. Soliton Solutions of Nonlinear Geophysical Kdv Equation Via Two Analytical Methods. Int. J. Theor. Phys. 2024, 63, 107. [Google Scholar] [CrossRef]
- Naowarat, S.; Saifullah, S.; Ahmad, S.; De la Sen, M. Periodic, singular and dark solitons of a generalized geophysical KdV equation by using the tanh-coth method. Symmetry 2023, 15, 135. [Google Scholar] [CrossRef]
- Rizvi, S.T.R.; Seadawy, A.R.; Ashraf, F.; Younis, M.; Iqbal, H.; Baleanu, D. Lump and interaction solutions of a geophysical Korteweg–de Vries equation. Results Phys. 2020, 19, 103661. [Google Scholar] [CrossRef]
- Cimpoiasu, R.; Cimpoiasu, V.; Constantinescu, R. Nonlinear dynamical systems in various space-time dimensions. Rom. J. Phys. 2010, 55, 25–35. [Google Scholar]
- Zahran, E.H.M.; Bekir, A. New unexpected behavior to the soliton arising from the geophysical Korteweg-de Vries equation. Mod. Phys. Lett. B 2022, 36, 2150623. [Google Scholar] [CrossRef]
- Ionescu, C. The sp(3) BRST Hamiltonian formalism for the Yang–Mills fields. Mod. Phys. Lett. A 2008, 23, 737–750. [Google Scholar]
- Cimpoiasu, R.; Constantinescu, R. Lie symmetries and invariants for a 2D nonlinear heat equation. Nonlinear Anal.-Theor. 2008, 68, 2261–2268. [Google Scholar] [CrossRef]
- Hietarinta, J. Hirota’s bilinear method and soliton solutions. Phys. AUC 2005, 15, 31–37. [Google Scholar]
- Hietarinta, J. Hirota’s Bilinear Method and Partial Integrability. In Partially Integrable Evolution Equations in Physics NATO ASI Series; Conte, R., Boccara, N., Eds.; Springer: Dordrecht, Germany, 1990; Volume 310. [Google Scholar]
- Hirota, R. Direct Methods in Soliton Theory. In Solitons. Topics in Current Physics; Bullough, R.K., Caudrey, P.J., Eds.; Springer: Berlin/Heidelberg, Germany, 1980; Volume 17. [Google Scholar]
- Hirota, R. A new form of Bäcklund transformations and its relation to the inverse scattering problem. Prog. Theor. Phys. 1974, 52, 1498. [Google Scholar] [CrossRef]
- Alquran, M.; Alhami, R. Analysis of lumps, single-stripe, breather-wave, and two-wave solutions to the generalized perturbed-KdV equation by means of Hirota’s bilinear method. Nonlinear Dynam. 2022, 109, 1985–1992. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).