A Cubic Spline Numerical Method for a Singularly Perturbed Two-Parameter Ordinary Differential Equation
Abstract
1. Introduction
2. Analytical Properties
3. The Fully Discrete Problem
4. Convergence Analysis
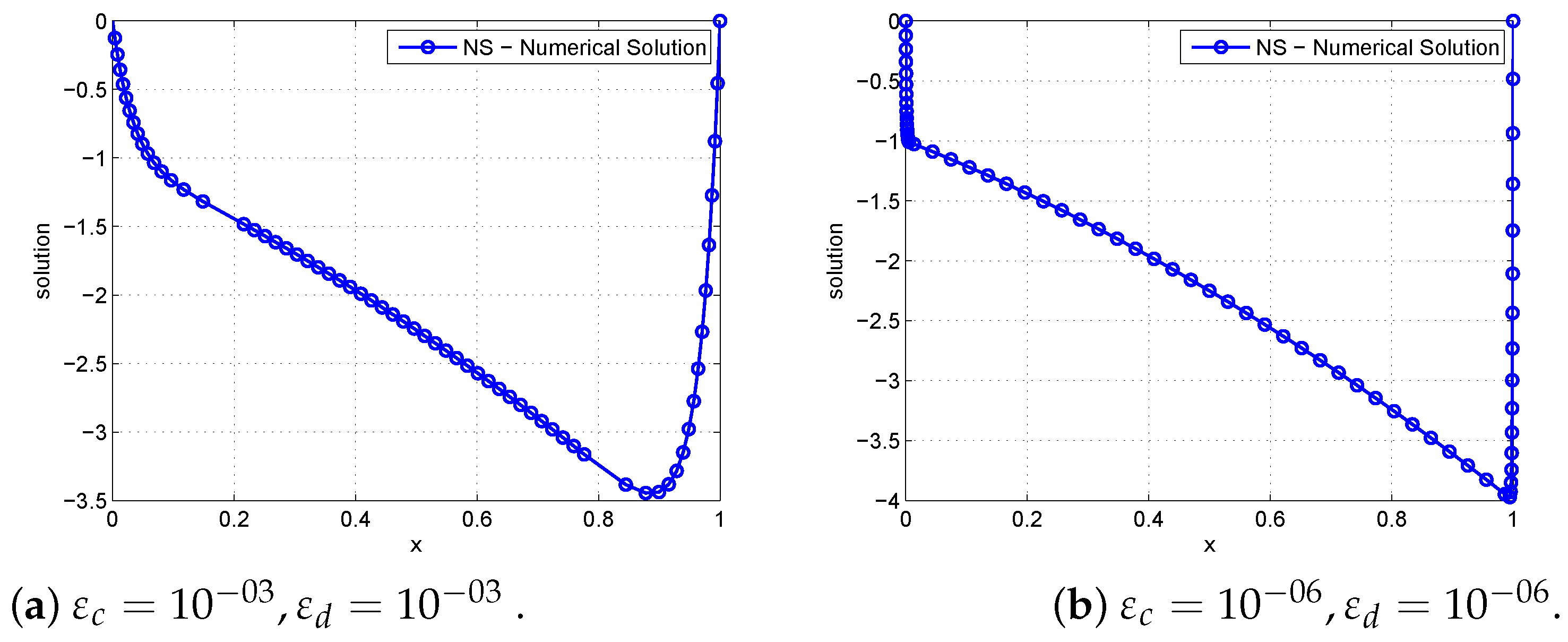
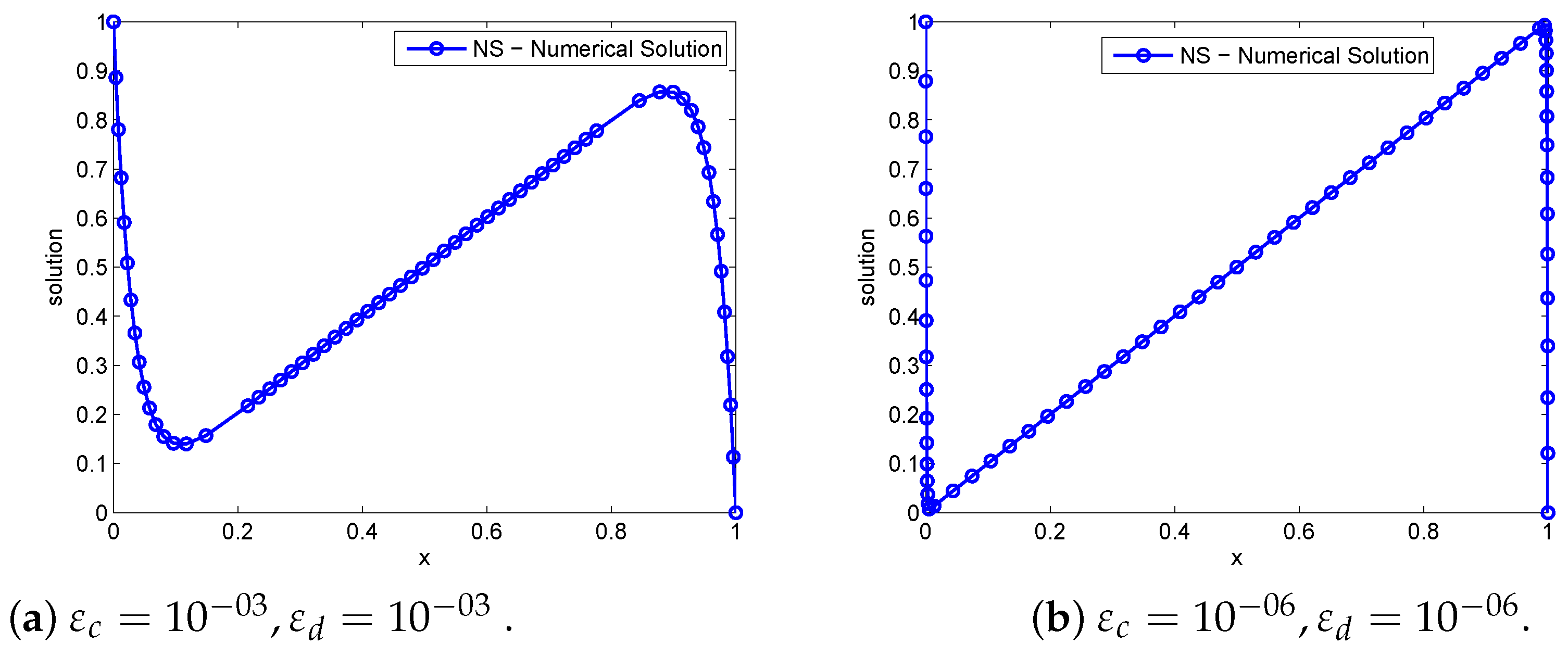
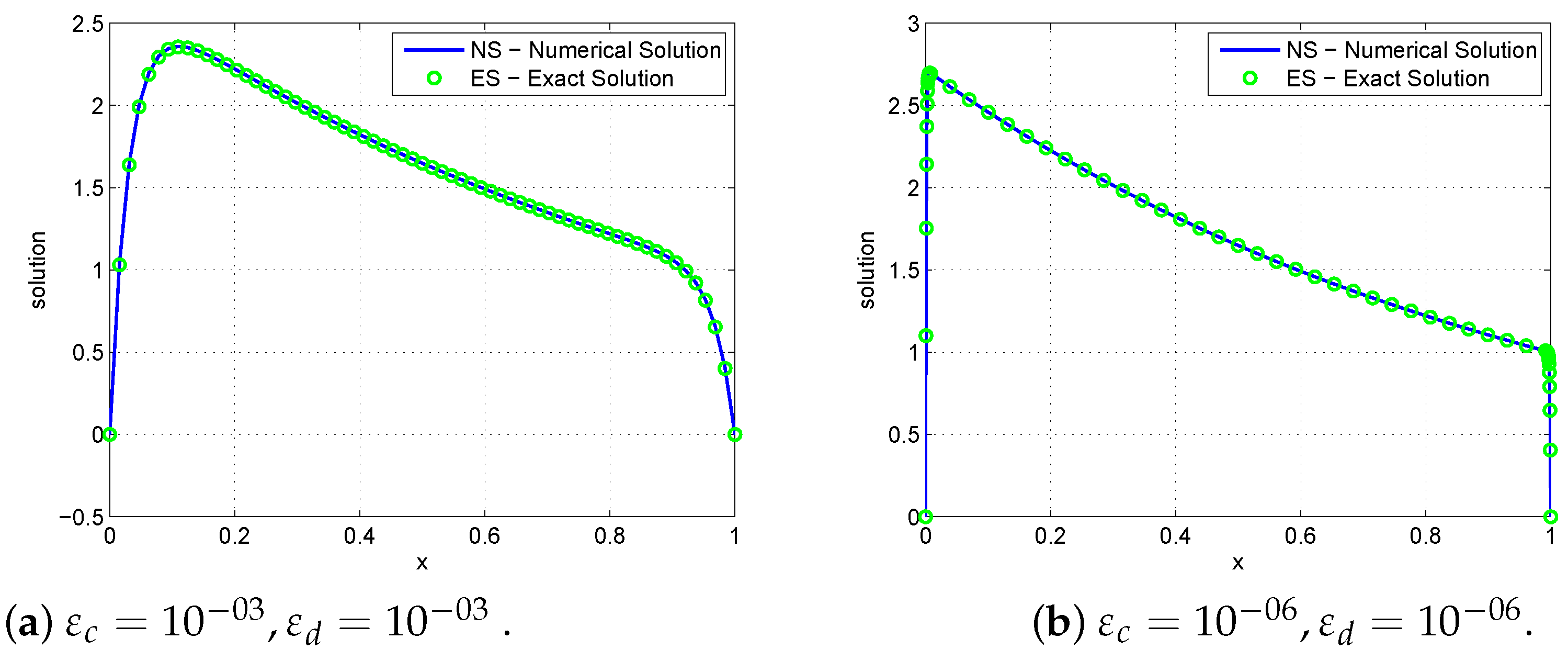
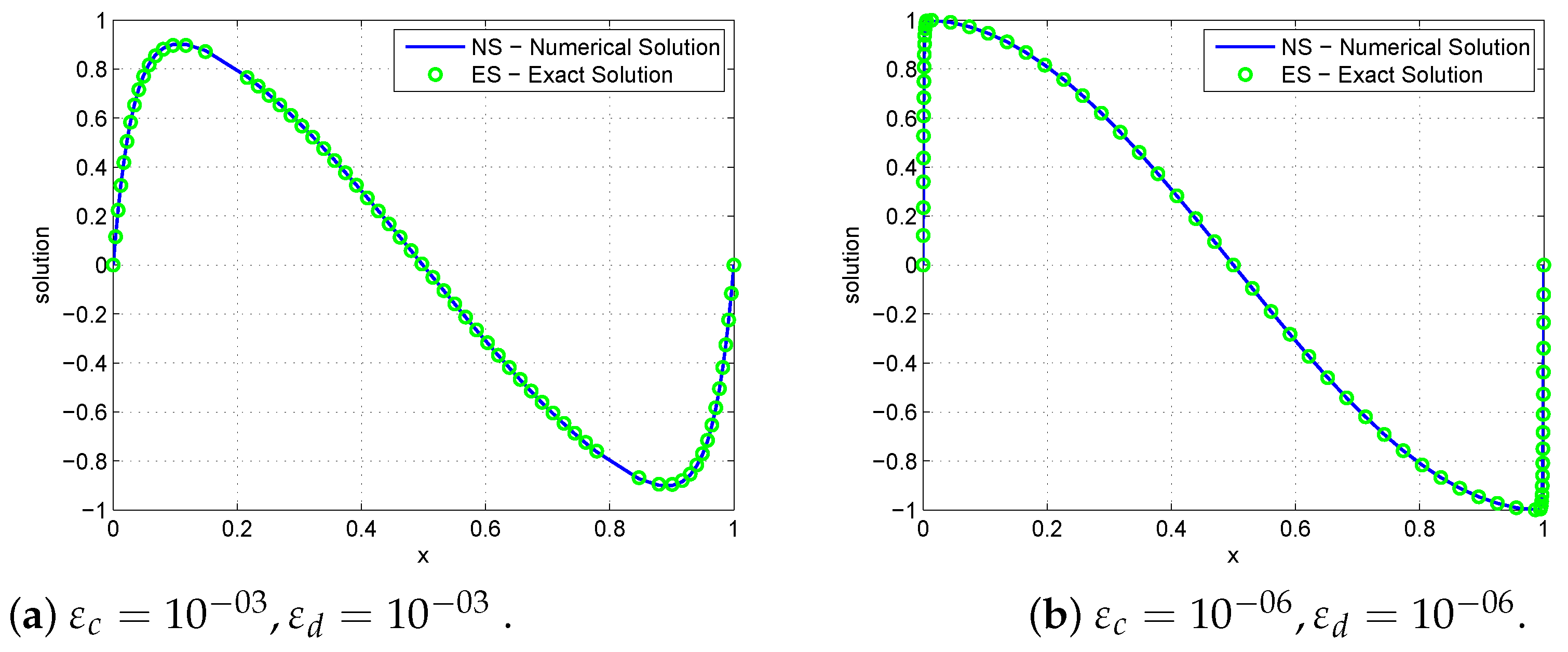
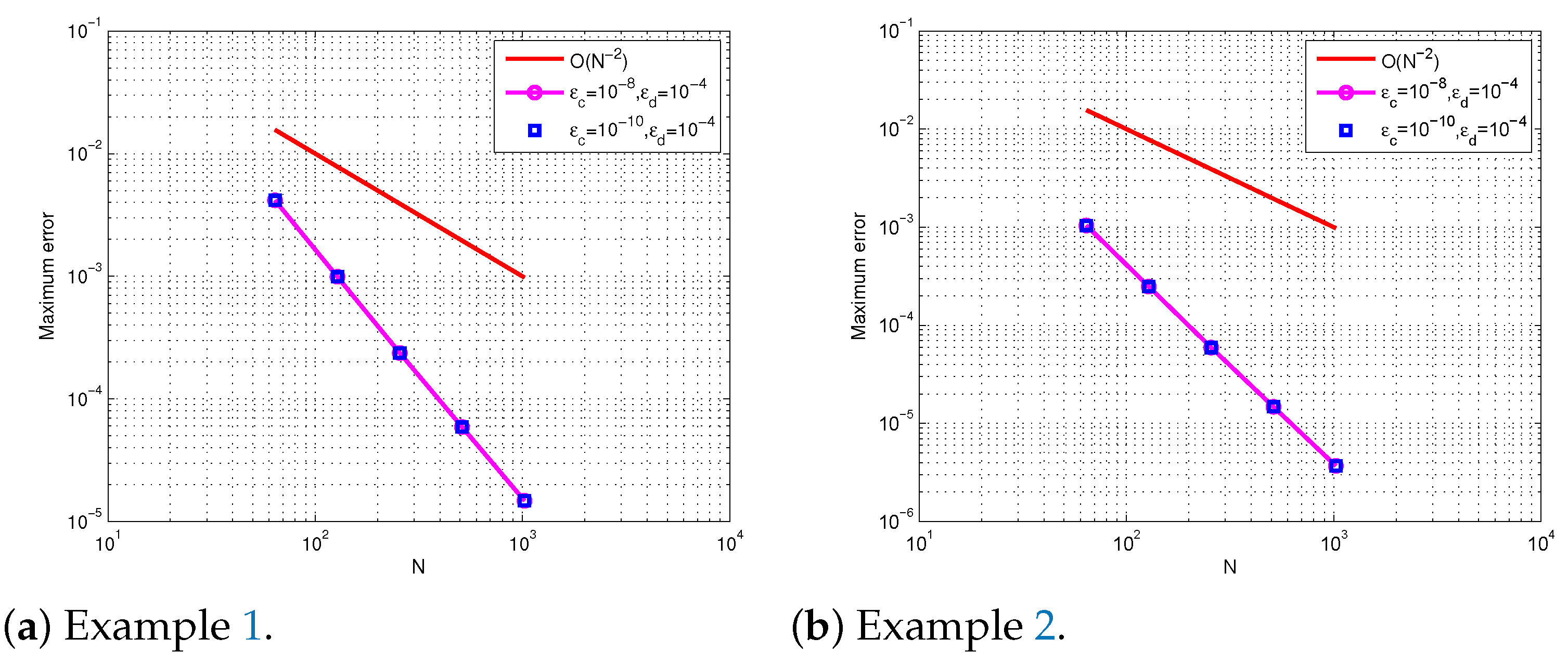
5. Counter Examples, Numerical Results, and Discussions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- O’Malley, R., Jr. Singular perturbations of boundary value problems for linear ordinary differential equations involving two parameters. J. Math. Anal. Appl. 1967, 19, 291–308. [Google Scholar] [CrossRef]
- O’Malley, R., Jr. Two-parameter singular perturbation problems for second-order equations. J. Math. Mech. 1967, 16, 1143–1164. [Google Scholar]
- Chen, J.; O’Malley, R., Jr. On the asymptotic solution of a two-parameter boundary value problem of chemical reactor theory. SIAM J. Appl. Math. 1974, 26, 717–729. [Google Scholar] [CrossRef]
- Vasil’Eva, A.B. Asymptotic methods in the theory of ordinary differential equations containing small parameters in front of the higher derivatives. USSR Comput. Math. Math. Phys. 1963, 3, 823–863. [Google Scholar] [CrossRef]
- DiPrima, R.C. Asymptotic methods for an infinitely long slider squeeze-film bearing. J. Lubr. Technol. 1968, 90, 173–183. [Google Scholar] [CrossRef]
- Bigge, J.; Bohl, E. Deformations of the bifurcation diagram due to discretization. Math. Comput. 1985, 45, 393–403. [Google Scholar] [CrossRef]
- Bhathawala, P.H.; Verma, A.P. A two-parameter singular perturbation solution of one dimension flow through unsaturated porous media. Appl. Math. 1975, 43, 380–384. [Google Scholar]
- Vulanovic, R.; Nhan, T.A. Robust hybrid schemes of higher order for singularly perturbed convection-diffusion problems. Appl. Math. Comput. 2020, 386, 125495. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, X. Optimal order of uniform convergence for finite element method on Bakhvalov-type meshes. J. Sci. Comput. 2020, 85, 2. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, J. Supercloseness of weak Galerkin method on Bakhvalov-type mesh for a singularly perturbed problem in 1D. Numer. Algorithms. 2023, 93, 367–395. [Google Scholar] [CrossRef]
- Zheng, Q.; Liu, Z. Uniform convergence analysis of a new adaptive upwind finite difference method for singularly perturbed convection-reaction-diffusion boundary value problems. J. Appl. Math. Comput. 2024, 70, 601–618. [Google Scholar] [CrossRef]
- Wondimu, F.; File, G.; Aga, T. Fourth order compact finite difference method for solving singularly perturbed 1D reaction diffusion equations with Dirichlet boundary conditions. Momona Ethiop. J. Sci. 2016, 8, 168–181. [Google Scholar] [CrossRef]
- Gelu, F.W.; Duressa, G.F.; Bullo, T.A. Tenth order compact finite difference method for solving singularly perturbed 1D reaction-diffusion equations. Int. J. Eng. Appl. Sci. 2016, 8, 15–24. [Google Scholar] [CrossRef]
- Gelu, F.W.; Duressa, G.F.; Bullo, T.A. Sixth-order compact finite difference method for singularly perturbed 1D reaction diffusion problems. J. Taibah Univ. Sci. 2017, 11, 302–308. [Google Scholar] [CrossRef]
- Ahmed, S.; Jahan, S.; Ansari, K.J.; Shah, K.; Abdeljawad, T. Wavelets collocation method for singularly perturbed differential-difference equations arising in control system. Results Appl. Math. 2024, 21, 100415. [Google Scholar] [CrossRef]
- Patidar, K.C. A robust fitted operator finite difference method for a two-parameter singular perturbation problem. J. Differ. Equ. Appl. 2008, 14, 1197–1214. [Google Scholar] [CrossRef]
- Shivhare, M.; Pramod Chakravarthy, P.; Kumar, D. Quadratic B-spline collocation method for two-parameter singularly perturbed problem on exponentially graded mesh. Int. J. Comput. Math. 2021, 98, 2461–2481. [Google Scholar] [CrossRef]
- Roos, H.-G.; Uzelac, Z. The SDFEM for a convection-diffusion problem with two small parameters. Comput. Methods Appl. Math. 2003, 3, 443–458. [Google Scholar] [CrossRef]
- Linss, T.; Roos, H.-G. Analysis of a finite-difference scheme for a singularly perturbed problem with two small parameters. J. Math. Anal. Appl. 2004, 289, 355–366. [Google Scholar] [CrossRef]
- Lodhi, R.K.; Jaiswal, B.R.; Nandan, D.; Ramesh, K. Numerical solution of two-parameter singularly perturbed convection-diffusion boundary value problems via fourth order compact finite difference method. Math. Model. Eng. Probl. 2021, 8, 819–825. [Google Scholar] [CrossRef]
- Kambampati, S.; Emineni, S.P.; Reddy, M.; Kolloju, P. Fourth order computational spline method for two-parameter singularly perturbed boundary value problem. Int. J. Appl. Mech. Eng. 2023, 28, 79–93. [Google Scholar] [CrossRef]
- Khandelwal, P.; Khan, A. Singularly perturbed convection-diffusion boundary value problems with two small parameters using nonpolynomial spline technique. Math. Sci. 2017, 11, 119–126. [Google Scholar] [CrossRef]
- O’Riordan, E.; Pickett, M.L. Numerical approximations to the scaled first derivatives of the solution to a two parameter singularly perturbed problem. J. Comput. Appl. Math. 2019, 347, 128–149. [Google Scholar] [CrossRef]
- Kadalbajoo, M.K.; Yadaw, A.S. B-spline collocation method for a two-parameter singularly perturbed convection-diffusion boundary value problems. Appl. Math. Comput. 2008, 201, 504–513. [Google Scholar] [CrossRef]
- Kadalbajoo, M.K.; Jha, A. Exponentially fitted cubic spline for two-parameter singularly perturbed boundary value problems. Int. J. Comput. Math. 2012, 89, 836–850. [Google Scholar] [CrossRef]
- Brdar, M.; Zarin, H. Convection-diffusion-reaction problems on a B-type mesh. PAMM Proc. Appl. Math. Mech. 2013, 13, 423–424. [Google Scholar] [CrossRef]
- Brdar, M.; Zarin, H. On graded meshes for a two-parameter singularly perturbed problem. Appl. Math. Comput. 2016, 282, 97–107. [Google Scholar] [CrossRef]
- Brdar, M.; Zarin, H. A singularly perturbed problem with two parameters on a Bakhvalov-type mesh. J. Comput. Appl. Math. 2016, 292, 307–319. [Google Scholar] [CrossRef]
- Andisso, F.S.; Duressa, G.F. Graded mesh B-spline collocation method for two parameters singularly perturbed boundary value problems. MethodsX 2023, 11, 102336. [Google Scholar] [CrossRef]
- Cheng, Y. On the local discontinuous Galerkin method for singularly perturbed problem with two parameters. J. Comput. Appl. Math. 2021, 392, 113485. [Google Scholar] [CrossRef]
- Agmas, A.F.; Gelu, F.W.; Fino, M.C. A robust, exponentially fitted higher-order numerical method for a two-parameter singularly perturbed boundary value problem. Frontiers Appl. Math. Stat. 2025, 10, 1501271. [Google Scholar] [CrossRef]
- Doolan, E.P.; Miller, J.J.; Schilders, W.H. Uniform Numerical Methods for Problems with Initial and Boundary Layers; Boole Press: Dublin, Ireland, 2000. [Google Scholar]
- Surla, K.; Uzelac, Z.; Teofanov, L. The discrete minimum principle for quadratic spline discretization of a singularly perturbed problem. Math. Comput. Simul. 2009, 79, 2490–2505. [Google Scholar] [CrossRef]
- Kumar, D. A uniformly convergent scheme for two-parameter problems having layer behaviour. Int. J. Comput. Math. 2022, 99, 553–574. [Google Scholar] [CrossRef]

| 32 | 64 | 128 | 256 | 512 | 1024 | ||
|---|---|---|---|---|---|---|---|
| Ours | |||||||
| 6.8747 | 1.6838 | 4.0666 | 9.7083 | 2.3231 | 5.7900 | 1.4465 | |
| 2.0296 | 2.0498 | 2.0665 | 2.0632 | 2.0044 | 2.0010 | ||
| 7.0732 | 1.7286 | 4.1640 | 9.9101 | 2.3688 | 5.9029 | 1.4747 | |
| 2.0328 | 2.0536 | 2.0710 | 2.0647 | 2.0047 | 2.0010 | ||
| 7.0752 | 1.7290 | 4.1650 | 9.9121 | 2.3693 | 5.9040 | 1.4750 | |
| 2.0328 | 2.0535 | 2.0711 | 2.0647 | 2.0047 | 2.0010 | ||
| 7.0752 | 1.7290 | 4.1650 | 9.9121 | 2.3693 | 5.9040 | 1.4750 | |
| 2.0328 | 2.0535 | 2.0711 | 2.0647 | 2.0047 | 2.0010 | ||
| 7.0752 | 1.7290 | 4.1650 | 9.9121 | 2.3693 | 5.9040 | 1.4750 | |
| 2.0328 | 2.0535 | 2.0711 | 2.0647 | 2.0047 | 2.0010 | ||
| In [33] | |||||||
| - | 8.534 | 2.907 | 8.742 | 2.807 | 8.777 | 2.698 | |
| - | 1.554 | 1.733 | 1.639 | 1.677 | 1.702 |
| 32 | 64 | 128 | 256 | 512 | 1024 | ||
|---|---|---|---|---|---|---|---|
| 1.7916 | 4.3753 | 1.0529 | 2.5021 | 5.9810 | 1.4903 | 3.7233 | |
| 2.0338 | 2.0550 | 2.0732 | 2.0647 | 2.0048 | 2.0009 | ||
| 1.7689 | 4.3228 | 1.0413 | 2.4782 | 5.9235 | 1.4761 | 3.6877 | |
| 2.0328 | 2.0536 | 2.0710 | 2.0648 | 2.0047 | 2.0010 | ||
| 1.7687 | 4.3223 | 1.0412 | 2.4779 | 5.9229 | 1.4759 | 3.6873 | |
| 2.0328 | 2.0536 | 2.0711 | 2.0647 | 2.0047 | 2.0010 | ||
| 1.7687 | 4.3223 | 1.0412 | 2.4779 | 5.9229 | 1.4759 | 3.6873 | |
| 2.0328 | 2.0536 | 2.0711 | 2.0647 | 2.0047 | 2.0010 | ||
| 1.7916 | 4.3753 | 1.0529 | 2.5021 | 5.9810 | 1.4903 | 3.7233 | |
| 2.0338 | 2.0550 | 2.0732 | 2.0647 | 2.0048 | 2.0009 |
| 32 | 64 | 128 | 256 | 512 | 1024 | ||
|---|---|---|---|---|---|---|---|
| Ours | |||||||
| 8.1690 | 1.8710 | 4.2318 | 9.5562 | 2.1847 | 5.4095 | 1.3500 | |
| 2.1263 | 2.1445 | 2.1468 | 2.1290 | 2.0139 | 2.0025 | ||
| 8.0733 | 1.8499 | 4.1868 | 9.4644 | 2.1638 | 5.3576 | 1.3371 | |
| 2.1257 | 2.1435 | 2.1453 | 2.1289 | 2.0139 | 2.0025 | ||
| 8.0724 | 1.8497 | 4.1863 | 9.4635 | 2.1636 | 5.3571 | 1.3370 | |
| 2.1257 | 2.1435 | 2.1452 | 2.1289 | 2.0139 | 2.0025 | ||
| 8.0724 | 1.8497 | 4.1863 | 9.4635 | 2.1636 | 5.3571 | 1.3370 | |
| 2.1257 | 2.1435 | 2.1452 | 2.1289 | 2.0139 | 2.0025 | ||
| 8.1690 | 1.8710 | 4.2318 | 9.5562 | 2.1847 | 5.4095 | 1.3500 | |
| 2.1263 | 2.1445 | 2.1468 | 2.1290 | 2.0139 | 2.0025 | ||
| In [34] | |||||||
| - | 4.4699 | 1.5184 | 7.8068 | 2.9511 | 8.6431 | 1.7362 |
| 32 | 64 | 128 | 256 | 512 | 1024 | ||
|---|---|---|---|---|---|---|---|
| 4.4492 | 9.4575 | 2.4671 | 5.6751 | 1.3067 | 3.1987 | 9.9258 | |
| 2.0729 | 2.0998 | 2.1201 | 2.1187 | 2.0304 | 1.6882 | ||
| 3.9665 | 9.4465 | 2.2047 | 5.0753 | 1.1731 | 2.9113 | 9.3317 | |
| 2.0700 | 2.0992 | 2.1190 | 2.1132 | 2.0106 | 1.6415 | ||
| 3.9620 | 9.4358 | 2.2022 | 5.0696 | 1.1719 | 2.9085 | 9.3259 | |
| 2.0700 | 2.0992 | 2.1190 | 2.1130 | 2.0105 | 1.6410 | ||
| 3.9619 | 9.4357 | 2.2022 | 5.0695 | 1.1719 | 2.9085 | 9.3259 | |
| 2.0700 | 2.0992 | 2.1190 | 2.1130 | 2.0105 | 1.6410 | ||
| 4.4492 | 9.4575 | 2.4671 | 5.6751 | 1.3067 | 3.1987 | 9.9258 | |
| 2.0729 | 2.0998 | 2.1201 | 2.1187 | 2.0304 | 1.6882 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Salman, H.J.; Gelu, F.W.; Al Ghafli, A.A. A Cubic Spline Numerical Method for a Singularly Perturbed Two-Parameter Ordinary Differential Equation. Axioms 2025, 14, 547. https://doi.org/10.3390/axioms14080547
Al Salman HJ, Gelu FW, Al Ghafli AA. A Cubic Spline Numerical Method for a Singularly Perturbed Two-Parameter Ordinary Differential Equation. Axioms. 2025; 14(8):547. https://doi.org/10.3390/axioms14080547
Chicago/Turabian StyleAl Salman, Hassan J., Fasika Wondimu Gelu, and Ahmed A. Al Ghafli. 2025. "A Cubic Spline Numerical Method for a Singularly Perturbed Two-Parameter Ordinary Differential Equation" Axioms 14, no. 8: 547. https://doi.org/10.3390/axioms14080547
APA StyleAl Salman, H. J., Gelu, F. W., & Al Ghafli, A. A. (2025). A Cubic Spline Numerical Method for a Singularly Perturbed Two-Parameter Ordinary Differential Equation. Axioms, 14(8), 547. https://doi.org/10.3390/axioms14080547






