Enhanced Fast Fractional Fourier Transform (FRFT) Scheme Based on Closed Newton-Cotes Rules

Abstract

The paper presents an enhanced numerical framework for computing the one-dimensional fast Fractional Fourier Transform (FRFT) by integrating closed-form Composite Newton-Cotes quadrature rules. We show that a FRFT of a $QN$-length weighted sequence can be decomposed analytically into two mathematically commutative compositions: one involving the composition of a FRFT of an N-length sequence and a FRFT of a Q-length weighted sequence, and the other in reverse order. The composite FRFT approach is applied to the inversion of Fourier and Laplace transforms, with a focus on estimating probability densities for distributions with complex-valued characteristic functions. Numerical experiments on the Variance-Gamma (VG) and Generalized Tempered Stable (GTS) models show that the proposed scheme significantly improves accuracy over standard (non-weighted) fast FRFT and classical Newton-Cotes quadrature, while preserving computational efficiency. The findings suggest that the composite FRFT framework offers a robust and mathematically sound tool for transform-based numerical approximations, particularly in applications involving oscillatory integrals and complex-valued characteristic functions.

1. Introduction

The Fractional Fourier Transform (FRFT) is a generalization of the classical Fourier Transform (FT), characterized by a fractional order parameter that allows for continuous interpolation between the time and frequency domains [1,2,3,4,5]. Since its introduction, the FRFT has proven to be a versatile tool in applied mathematics, with significant applications in signal processing, optics, quantum mechanics, and financial modeling [6,7,8]. The increasing relevance of the FRFT is primarily attributed to its ability to represent non-stationary signals and analyze problems where phase and frequency information evolve continuously.

In recent years, applications in high-resolution radar imaging [6], quantum information systems [9], and fractional signal processing [10] have underscored the demand for FRFT algorithms that are not only computationally efficient but also numerically stable. However, current fast FRFT algorithms often suffer from precision limitations due to step-function approximations or fail to provide robust numerical integration schemes when applied to oscillatory integrals and complex-valued characteristic functions [2,11,12].

Conversely, Newton-Cotes quadrature rules, especially in their composite form, have long been recognized as effective and robust numerical integration methods. These rules approximate definite integrals by interpolating the integrand with polynomials evaluated at equally spaced points [13,14,15,16,17]. In particular, closed Newton-Cotes formulas, such as Simpson’s rule and the 3/8 rule, have been extended to higher-order schemes that provide accurate results for smooth integrands [18,19].

The motivation for the present work stems from the structural similarity between FRFT algorithms and numerical quadrature techniques. Both rely on integral approximations based on polynomial interpolation and discretization of function samples. In particular, classical fast FRFT algorithms approximate oscillatory integrals in a manner reminiscent of step-wise Filon-type quadrature methods [20,21,22,23]. This similarity suggests that incorporating high-order Newton-Cotes quadrature rules into the FRFT could yield a more accurate and mathematically tractable framework for evaluating fractional transforms.

This paper presents a composite FRFT scheme that integrates closed Newton-Cotes quadrature rules of degree Q for improved numerical integration. The proposed framework offers both computational efficiency and theoretical rigor, surpassing conventional FRFT algorithms in terms of both accuracy and numerical stability. To demonstrate the efficacy of the proposed method, we empirically validate it using probability models [24,25,26,27,28,29] commonly employed in financial mathematics, including the Variance-Gamma (VG) and Generalized Tempered Stable (GTS) distributions. Our results reveal significant improvements in both accuracy and stability compared to standard FRFT and classical quadrature methods.

The remainder of the paper is organized as follows: Section 2 provides a detailed discussion on the construction and properties of closed Newton-Cotes rules. Section 3 introduces the composite FRFT framework and its two commutative decompositions. Section 4 presents numerical experiments and performance comparisons using the VG and GTS models to validate the proposed method.

2. Composite Newton-Cotes Quadrature Formulas

The Newton-Cotes rules value the integrand f at equally spaced points $x_i$ over the interval $[a,b]$, where $x_i=a+i{\displaystyle \frac{b-a}{M}}=a+ih$ with $h={\displaystyle \frac{b-a}{M}}$; $M=QN$ and $x_{Qp+Q}=x_{Q(p+1)}$, where Q is the number of h within the subinterval $[x_{Qp},x_{Qp+Q}]$ of interval $[a,b]$.

2.1. Composite Rules

To have greater accuracy, the idea of the composite rule is to subdivide the interval [a, b] into smaller intervals such as $[x_{Qp},x_{Qp+Q}]$, applying the quadrature formula in each of these smaller intervals and adding up the results to obtain more accurate approximations (1):

$${\int }_a^{b}f(x)dx=\sum _{p=0}^{N-1}{\int }_{x_{Qp}}^{x_{Qp+Q}}f(x)dx.$$

(1)

We define the Lagrange basis polynomials over the sub-interval $[x_{Qp},x_{Qp+Q}]$ (2):

$$l_{Qp+j}(x)=\prod _{\begin{array}{c}i\ne j\\ i=0\end{array}}^Q{\displaystyle \frac{x-x_{Qp+i}}{x_{Qp+j}-x_{Qp+i}}},l_j(x_i)={\delta }_{ij}=\left\{\begin{array}{cc}0\hfill & \hfill :i\ne j\\ 1\hfill & \hfill :i=j.\end{array}\right.$$

(2)

The Lagrange interpolating polynomial and the integration can be derived (3):

$$\tilde{f}(x)={\sum }_{j=0}^{Q}f(x_{Qp+j})l_{Qp+j}(x),{\int }_{x_{Qp}}^{x_{Qp+Q}}\tilde{f}(x)dx={\sum }_{j=0}^{Q}f(x_{Qp+j}){\int }_{x_{Qp}}^{x_{Qp+Q}}{l}_{Qp+j}(x)dx.$$

(3)

The integration of Lagrange basis polynomials (4):

$${\int }_{x_{Qp}}^{x_{Qp+Q}}{l}_{Qp+j}(x)dx={\displaystyle \frac{b-a}{M}}{\displaystyle \frac{{(-1)}^{(Q-j)}}{j!(Q-j)!}}{\int }_0^Q{\prod _{\begin{array}{c}i\ne j\\ i=0\end{array}}}^Q(y-i)dy.$$

(4)

We have the Lagrange Interpolating integration over $[x_{Qp},x_{Qp+Q}]$ (5)

$${\int }_{x_{Qp}}^{x_{Qp+Q}}\tilde{f}(x)dx={\displaystyle \frac{b-a}{M}}\sum _{j=0}^Q,W_{j}f(x_{Qp+j})W_j={\displaystyle \frac{{(-1)}^{(Q-j)}}{j!(Q-j)!}}{\int }_0^Q\prod _{\begin{array}{c}i\ne j\\ i=0\end{array}}^Q(y-i)dy.$$

(5)

For theoretical and applied perspectives on Composite Newton-Cotes quadrature methods, see  [30,31,32,33,34] and  [35,36,37,38], respectively.

Proposition 1.

For Q even, $M=QN$ integer, and  $f\in {\mathcal{C}}^{Q+2}([a,b])$, there exists $\eta \in ]a,b[$ such that

$${\int }_a^{b}f(x)dx={\displaystyle \frac{b-a}{M}}{\sum }_{p=0}^{{\displaystyle \frac{M}{Q}}-1}{\sum }_{j=0}^Q{W}_{j}f(x_{Qp+j})+h^{Q+3}{\displaystyle \frac{N{f}^{(Q+2)}(\eta )}{(Q+2)!}}{\int }_0^Q{\int }_0^y{\prod }_{i=0}^Q(a-i)dady,$$

(6)

with

$$W_j={\displaystyle \frac{{(-1)}^{(Q-j)}}{j!(Q-j)!}}{\int }_0^Q\prod _{\begin{array}{c}i\ne j\\ i=0\end{array}}^Q(y-i)dy.$$

For Proposition 1 proof, see [39,40]

The error analysis of the Newton-Cotes formulas of degree Q in [39,40,41,42] shows that the level of accuracy is greater when Q is even. In fact, we have $O(h^{Q+3})$ for Q even, against $O(h^{Q+2})$ for Q odd.

2.2. Weights Computation

Before using the formula in (6), the expression of ${\left\{W_j\right\}}_{0\le j\le Q}$ can be simplified as follows:

Proposition 2.

For Q even and $M=QN$ integer, $j\in \{0,1,2,\dots ,Q\}$

$$W_j=\sum _{i=0}^Q{C}_i^j{\displaystyle \frac{Q^{i+1}}{i+1}}{\displaystyle \frac{{(-1)}^{(Q-j)}}{j!(Q-j)!}}.$$

(7)

For Proposition 2 proof, see [39,40].

The coefficient values ${(C_i^j)}_{\begin{array}{c}0\le i\le Q\\ 0\le j\le Q\end{array}}$ of the polynomial function are obtained by solving the following Equation (8) with a Vandermonde matrix [43].

$$\prod _{\begin{array}{c}i\ne j\\ i=0\end{array}}^Q(y-i)=\sum _{i=0}^Q{C}_i^j{y}^i.$$

(8)

For $Q\le 12$,

Table 1. Weight values ${\left\{W_j\right\}}_{0\le j\le Q}$.

Q	W0	W1	W2	W3	W4	W5	W6	W7	W8	W9	W10	W11	W12
1	${\displaystyle \frac{1}{2}}$	${\displaystyle \frac{1}{2}}$	0	0	0	0	0	0	0	0	0	0	0
2	${\displaystyle \frac{1}{3}}$	${\displaystyle \frac{4}{3}}$	${\displaystyle \frac{1}{3}}$	0	0	0	0	0	0	0	0	0	0
3	${\displaystyle \frac{3}{8}}$	${\displaystyle \frac{9}{8}}$	${\displaystyle \frac{9}{8}}$	${\displaystyle \frac{3}{8}}$	0	0	0	0	0	0	0	0	0
4	${\displaystyle \frac{14}{45}}$	${\displaystyle \frac{64}{45}}$	${\displaystyle \frac{8}{15}}$	${\displaystyle \frac{64}{45}}$	${\displaystyle \frac{14}{45}}$	0	0	0	0	0	0	0	0
5	${\displaystyle \frac{95}{288}}$	${\displaystyle \frac{125}{96}}$	${\displaystyle \frac{125}{144}}$	${\displaystyle \frac{125}{144}}$	${\displaystyle \frac{125}{96}}$	${\displaystyle \frac{95}{288}}$	0	0	0	0	0	0	0
6	${\displaystyle \frac{41}{140}}$	${\displaystyle \frac{54}{35}}$	${\displaystyle \frac{27}{140}}$	${\displaystyle \frac{68}{35}}$	${\displaystyle \frac{27}{140}}$	${\displaystyle \frac{54}{35}}$	${\displaystyle \frac{41}{140}}$	0	0	0	0	0	0
7	${\displaystyle \frac{108}{355}}$	${\displaystyle \frac{810}{559}}$	${\displaystyle \frac{343}{640}}$	${\displaystyle \frac{649}{536}}$	${\displaystyle \frac{649}{536}}$	${\displaystyle \frac{343}{640}}$	${\displaystyle \frac{810}{559}}$	${\displaystyle \frac{108}{355}}$	0	0	0	0	0
8	${\displaystyle \frac{499}{1788}}$	${\displaystyle \frac{1183}{712}}$	${\displaystyle \frac{-182}{695}}$	${\displaystyle \frac{388}{131}}$	${\displaystyle \frac{-319}{249}}$	${\displaystyle \frac{388}{131}}$	${\displaystyle \frac{-182}{695}}$	${\displaystyle \frac{1183}{712}}$	${\displaystyle \frac{499}{1788}}$	0	0	0	0
9	${\displaystyle \frac{130}{453}}$	${\displaystyle \frac{419}{265}}$	${\displaystyle \frac{23}{212}}$	${\displaystyle \frac{307}{158}}$	${\displaystyle \frac{213}{367}}$	${\displaystyle \frac{213}{367}}$	${\displaystyle \frac{307}{158}}$	${\displaystyle \frac{23}{212}}$	${\displaystyle \frac{419}{265}}$	${\displaystyle \frac{130}{453}}$	0	0	0
10	${\displaystyle \frac{139}{518}}$	${\displaystyle \frac{245}{138}}$	${\displaystyle \frac{-171}{211}}$	${\displaystyle \frac{414}{91}}$	${\displaystyle \frac{-557}{128}}$	${\displaystyle \frac{1763}{247}}$	${\displaystyle \frac{-557}{128}}$	${\displaystyle \frac{414}{91}}$	${\displaystyle \frac{-171}{211}}$	${\displaystyle \frac{245}{138}}$	${\displaystyle \frac{139}{518}}$	0	0
11	${\displaystyle \frac{65}{237}}$	${\displaystyle \frac{850}{499}}$	${\displaystyle \frac{-83}{203}}$	${\displaystyle \frac{787}{247}}$	${\displaystyle \frac{-223}{184}}$	${\displaystyle \frac{227}{116}}$	${\displaystyle \frac{227}{116}}$	${\displaystyle \frac{-223}{184}}$	${\displaystyle \frac{787}{247}}$	${\displaystyle \frac{-83}{203}}$	${\displaystyle \frac{850}{499}}$	${\displaystyle \frac{65}{237}}$	0
12	${\displaystyle \frac{20}{77}}$	${\displaystyle \frac{375}{199}}$	${\displaystyle \frac{-270}{187}}$	${\displaystyle \frac{673}{99}}$	${\displaystyle \frac{-1019}{104}}$	${\displaystyle \frac{816}{49}}$	${\displaystyle \frac{-1537}{92}}$	${\displaystyle \frac{816}{49}}$	${\displaystyle \frac{-1019}{104}}$	${\displaystyle \frac{673}{99}}$	${\displaystyle \frac{-270}{187}}$	${\displaystyle \frac{375}{199}}$	${\displaystyle \frac{20}{77}}$

provides the values of weights ${\left\{W_j\right\}}_{0\le j\le Q}$ in (7)

Remark 1.

For $Q>12$, the weights ${\left\{W_j\right\}}_{0\le j\le Q}$ can be computed using the MATLAB R2023b scripts provided in Appendix A. Notably:

• The return distribution and risk profile analysis in [44] utilized the weights with parameter values $Q=12$ and $Q=13$.
• The methodology for modeling financial return data in [45] adopted $Q=15$.

Figure 1 compares the performance of the standard non-weighted fast FRFT and the Composite Newton-Cotes integration scheme defined in Equation (6), using the approximation error ($\check{f}-f$) and ($\overline{f}-f$) as evaluation metrics. The Variance-Gamma (VG*) distribution corresponds to the risk-neutral Probability Density Function (PDF) of the Variance-Gamma $(\mu ,\delta ,\alpha ,\theta ,\sigma )$ model, as detailed in [46,47] and further elaborated in Section 4. The resulting error profiles reveal distinct behaviors for the two methods. The Composite Newton-Cotes approach, depicted by the blue curve, yields consistently lower approximation errors and thus demonstrates enhanced numerical accuracy.

3. Fast Fractional Fourier Transform (FRFT) and Composite Newton-Cotes Quadrature Rules

3.1. Fast Fourier Transform and Fractional Fourier Transform

The conventional fast Fourier transform (FFT) algorithm is widely used to compute discrete convolutions, discrete Fourier transforms (DFT) of sparse sequences, and perform high-resolution trigonometric interpolation [2,48]. The discrete Fourier transforms (DFT) are based on $N^{th}$ roots of unity $e^{-{\displaystyle \frac{2\pi i}{N}}}$. The generalization of DFT is the FRFT, which is based on fractional roots of unity $e^{-2\pi i\alpha }$, where $\alpha$ is an arbitrary complex number.

The FRFT is defined on M-long sequence ($x_1$, $x_2$, …, $x_M$) as follows:  

$$G_{k+s}(x,\delta )=\sum _{j=0}^{M-1}{x}_j{e}^{-2\pi ij(k+s)\delta },0\le k<M,0\le s\le 1.$$

(9)

Let us have $2j(k+s)=j^2+{(k+s)}^2-{(k-j+s)}^2$; Equation (9) becomes (10)  

$$\begin{array}{cc}\hfill & G_{k+s}(x,\delta )=\sum _{j=0}^{M-1}{x}_j{e}^{-\pi i(j^2+{(k+s)}^2-{(k-j+s)}^2)\delta }\hfill \\ \hfill & =e^{-\pi i{(k+s)}^2\delta }\sum _{j=0}^{M-1}{x}_j{e}^{-\pi i{j}^2\delta }{e}^{\pi i{(k-j+s)}^2\delta }=e^{-\pi i{(k+s)}^2}\sum _{j=0}^{M-1}{y}_j{z}_{k-j}.\hfill \end{array}$$

(10)

The expression ${\sum }_{j=0}^{M-1}{y}_j{z}_{k-j}$ is a discrete convolution. Still, we need a circular convolution (i.e., $z_{k-j}=z_{k-j+M}$) to evaluate $G_{k+s}(x,\delta )$. The conversion from discrete convolution to discrete circular convolution is possible by extending the sequences y and z to length $2M$, as defined below:

$$\begin{array}{ccccc}\hfill y_j& =x_j{e}^{-\pi i{j}^2\delta },\hfill & \hfill z_j& =e^{\pi i{(j+s)}^2\delta },\hfill & \hfill 0\le j<M.\\ \hfill y_j& =0,\hfill & \hfill z_j& =e^{\pi i{(j+s-2M)}^2\delta },\hfill & \hfill M\le j<2M.\end{array}$$

Taking into account the $2M$-long sequence, the previous FRFT becomes  

$$G_{k+s}(x,\delta )=e^{-\pi i{(k+s)}^2\delta }\sum _{j=0}^{2M-1}{y}_j{z}_{k-j}=e^{-\pi i{(k+s)}^2\delta }{DFT}_k^{-1}\left[DFT(y)DFT(z)\right],$$

(11)

where $DFT$ is the Discrete Fourier Transform, and $DF{T}^{-1}$ is the inverse of $DFT$. For an M-long sequence z, we have  

$$DF{T}_k(z)=\sum _{j=0}^{M-1}{z}_j{e}^{-{\displaystyle \frac{2\pi }{M}}jk},DF{T}_k^{-1}(z)={\displaystyle \frac{1}{M-1}}\sum _{j=0}^{M-1}{z}_j{e}^{{\displaystyle \frac{2\pi }{M}}jk}.$$

(12)

This procedure is referred to in the literature as the fast FRFT Algorithm, with a total computational cost of $20Mlo{g}_{2}M+44M$ operations [48].

We assume that $\mathcal{F}\left[f\right](y)$ is zero outside the interval $[-{\displaystyle \frac{a}{2}},{\displaystyle \frac{a}{2}}]$; and $\beta ={\displaystyle \frac{a}{M}}$ is the step size of the M input values of $\mathcal{F}\left[f\right](y)$, defined by $y_j=(j-{\displaystyle \frac{M}{2}})\beta$ for $0\le j<M$. Similarly, $\gamma$ is the step size of the M output values of $f(x)$, defined by $x_k=(k-{\displaystyle \frac{M}{2}})\gamma$ for $0\le k<M$.

By choosing the step size $\beta$ on the input side and the step size $\gamma$ in the output side, we fix the FRFT parameter $\delta ={\displaystyle \frac{\beta \gamma }{2\pi }}$ and yield [49] the density function f at $x_{k+s}$ (13).

$$\begin{array}{cc}\hfill & f(x_{k+s})={\displaystyle \frac{1}{2\pi }}{\int }_{-\infty }^{+\infty }\mathcal{F}\left[f\right](y)e^{i{x}_{k+s}y}\mathrm{d}y\approx {\displaystyle \frac{1}{2\pi }}{\int }_{-a/2}^{a/2}\mathcal{F}\left[f\right](y)e^{i{x}_{k+s}y}\mathrm{d}y\hfill \\ \hfill & \approx {\displaystyle \frac{\gamma }{2\pi }}\sum _{j=0}^{M-1}\mathcal{F}\left[f\right](y_j)e^{2\pi i(k+s-{\displaystyle \frac{M}{2}})(j-{\displaystyle \frac{M}{2}})\delta }={\displaystyle \frac{\gamma }{2\pi }}{e}^{-\pi i(k+s-{\displaystyle \frac{M}{2}})M\delta }{G}_{k+s}(\mathcal{F}\left[f\right](y_j)e^{-\pi ijM\delta },-\delta ).\hfill \end{array}$$

We have:  

$$\begin{array}{c}\hfill \tilde{f}(x_{k+s})={\displaystyle \frac{\gamma }{2\pi }}{e}^{-\pi i(k+s-{\displaystyle \frac{M}{2}})M\delta }{G}_{k+s}(\mathcal{F}\left[f\right](y_j)e^{-\pi ijM\delta },-\delta ),0\le s<1.\end{array}$$

(13)

3.2. FRFT of QN-Long Weighted Sequence

The Q-point rule Composite Newton-Cotes Quadrature (6) is integrated into the Fractional Fourier (FRFT) algorithm (13) to produce a FRFT of QN-long weighted sequence.

We assume that $\mathcal{F}\left[f\right](x)$ is zero outside the interval $[-{\displaystyle \frac{a}{2}},{\displaystyle \frac{a}{2}}]$, $M=QN$, and $\beta ={\displaystyle \frac{a}{M}}$ is the step size of the M input values $\mathcal{F}\left[f\right](y)$, defined by $y_{j+Qp}=(Qp+j-{\displaystyle \frac{M}{2}})\beta$ for $0\le p<N$ and $0\le j<Q$. Similarly, the output values of $f(x)$ are defined by $x_{Ql+f+s}=(Ql+f+s-{\displaystyle \frac{M}{2}})\gamma$ for $0\le l<N$, $0\le f<Q$ and $0\le s\le 1$.

$$\begin{array}{cc}\hfill f(x_{Ql+f+s})& ={\displaystyle \frac{1}{2\pi }}{\int }_{\infty }^{+\infty }{e}^{iy{x}_{Ql+f+s}}F\left[f\right](y)dy={\displaystyle \frac{1}{2\pi }}{\int }_{-a/2}^{a/2}{e}^{iy{x}_{Ql+f+s}}F\left[f\right](y)dy\hfill \\ \hfill & ={\displaystyle \frac{1}{2\pi }}\sum _{p=0}^{N-1}{\int }_{y_{Qp}}^{y_{Qp+Q}}{e}^{iy{x}_{Ql+f+s}}F\left[f\right](y)dy(\mathrm{composite}\mathrm{rule}).\hfill \end{array}$$

(14)

Based on the Lagrange interpolating integration over [$y_{Qp}$, $y_{Qp+Q}$] [39,40], we have (15):

$${\int }_{y_{Qp}}^{y_{Qp+Q}}{e}^{iy{x}_{Ql+f+s}}F\left[f\right](y)dy\approx \beta \sum _{j=0}^Q{w}_j{e}^{i{y}_{j+Qp}{x}_{Ql+f+s}}F\left[f\right](y_{j+Qp}).$$

(15)

$\tilde{f}(x_{Ql+f+s})$ is the approximation of $f(x_{Ql+f+s})$, and (14) becomes (16):

$$\begin{array}{cc}\hfill & \tilde{f}(x_{Ql+f+s})={\displaystyle \frac{\beta }{2\pi }}\sum _{p=0}^{N-1}\sum _{j=0}^Q{w}_{j}F\left[f\right](y_{j+Qp})e^{i{x}_{Ql+f+s}{y}_{j+Qp}},0\le s<1;\hfill \\ \hfill & ={\displaystyle \frac{\beta }{2\pi }}\sum _{j=0}^Q\sum _{p=0}^{N-1}{w}_{j}F\left[f\right](y_{j+Qp})e^{2\pi i\delta (Ql+f+s-{\displaystyle \frac{M}{2}})(Qp+j-{\displaystyle \frac{M}{2}})},\beta \gamma =2\pi \delta ;\hfill \\ \hfill & ={\displaystyle \frac{\beta }{2\pi }}{e}^{-\pi i\delta M(Ql+f+s-{\displaystyle \frac{M}{2}})}{G}_{Ql+f+s}(w_j\mathcal{F}\left[f\right](y_{j+Qp})e^{-\pi i(j+Qp)M\delta },-\delta ).\hfill \end{array}$$

(16)

We have the following inverse Fourier transform function (17):  

$$\begin{array}{c}\hfill \tilde{f}(x_{Ql+f+s})={\displaystyle \frac{\beta }{2\pi }}{e}^{-\pi i\delta M(Ql+f+s-{\displaystyle \frac{M}{2}})}{G}_{Ql+f+s}(w_j\mathcal{F}\left[f\right](y_{j+Qp})e^{-\pi i(j+Qp)M\delta },-\delta ).\end{array}$$

(17)

FRFT is applied on the QN-long weighted sequence ${\left\{w_j\mathcal{F}\left[f\right](y_{j+Qp})e^{-\pi i(j+Qp)M\delta }\right\}}_{\begin{array}{c}0\le j<Q\\ 0\le p<N\end{array}}$.

3.3. Composite of FRFTs: FRFT of Q-Long Weighted Sequence and FRFT of N-Long Sequence

We consider ${\tilde{f}}_{QN}(x_{Ql+f+s})$ to be the approximation of $f(x_{Ql+f+s})$. We have the following development:

$$\begin{array}{cc}\hfill & {\tilde{f}}_{QN}(x_{Ql+f+s})={\displaystyle \frac{\beta }{2\pi }}\sum _{p=0}^{N-1}\sum _{j=0}^Q{w}_{j}F\left[f\right](y_{j+Qp})e^{i{x}_{Ql+f+s}{y}_{j+Qp}}\hfill \\ \hfill & ={\displaystyle \frac{\beta }{2\pi }}\sum _{j=0}^Q{w}_j\sum _{p=0}^{N-1}F\left[f\right](y_{j+Qp})e^{2\pi i\delta (Ql+f+s-{\displaystyle \frac{M}{2}})(Qp+j-{\displaystyle \frac{M}{2}})},\beta \gamma =2\pi \delta \hfill \\ \hfill & ={\displaystyle \frac{\beta }{2\pi }}{e}^{-\pi i\delta M(Ql+f+s-{\displaystyle \frac{M}{2}})}\sum _{j=0}^Q{w}_j{e}^{2\pi i\delta (Ql+f+s-{\displaystyle \frac{M}{2}})j}\sum _{p=0}^{N-1}F\left[f\right](y_{j+Qp})e^{2\pi i\delta (Ql+f+s-{\displaystyle \frac{M}{2}})Qp}\hfill \\ \hfill & ={\displaystyle \frac{\beta }{2\pi }}{e}^{-\pi i\delta M(Ql+f+s-{\displaystyle \frac{M}{2}})}\sum _{j=0}^Q{w}_j{G}_{l+{\displaystyle \frac{f+s}{Q}}}({\xi }_p,-\delta Q^2)e^{2\pi i\delta (Ql-{\displaystyle \frac{M}{2}})j}{e}^{2\pi i\delta (f+s)j},\hfill \end{array}$$

where $G_{l+{\displaystyle \frac{f+s}{Q}}}$ is a FRFT on N-long complex sequence ${\left\{{\xi }_p\right\}}_{0\le p<N}$. Let us have ${\alpha }_1=-\delta Q^2$; then,

$$\begin{array}{cc}\hfill G_{l+{\displaystyle \frac{f+s}{Q}}}({\xi }_p,{\alpha }_1)& =\sum _{p=0}^{N-1}{\xi }_p{e}^{-2\pi i(l+{\displaystyle \frac{f+s}{Q}})p{\alpha }_1},{\xi }_p=e^{-\pi iMpQ\delta }F\left[f\right](y_{j+Qp})\hfill \end{array}$$

(18)

and ${\tilde{f}}_{QN}(x_{Ql+f+s})$ becomes (19)

$$\begin{array}{c}\hfill {\tilde{f}}_{QN}(x_{Ql+f+s})={\displaystyle \frac{\beta }{2\pi }}{e}^{-\pi i\delta M(Ql+f+s-{\displaystyle \frac{M}{2}})}{G}_{f+s}(z_j,-\delta ),\end{array}$$

(19)

where $G_{f+s}$ is a FRFT on Q-long complex sequence ${\left\{z_j\right\}}_{0\le j\le Q}$. Let us have ${\alpha }_2=-\delta$; then,

$$\begin{array}{cc}\hfill G_{f+s}(z_j,{\alpha }_2)& =\sum _{j=0}^Q{z}_j{e}^{-2\pi i(f+s)j{\alpha }_2},z_j=w_j{G}_{l+{\displaystyle \frac{f+s}{Q}}}({\xi }_p,{\alpha }_1)e^{2\pi i\delta (Ql-{\displaystyle \frac{M}{2}})j}.\hfill \end{array}$$

To sum up, we have the following expression for ${\tilde{f}}_{QN}(x_{Ql+f+s})$:

$$\begin{array}{c}\hfill {\tilde{f}}_{QN}(x_{Ql+f+s})={\displaystyle \frac{\beta }{2\pi }}{e}^{-\pi i\delta M(Ql+f+s-{\displaystyle \frac{M}{2}})}{G}_{f+s}(G_{l+{\displaystyle \frac{f+s}{Q}}}({\xi }_p,{\alpha }_1)w_j{e}^{2\pi i\delta (Ql-{\displaystyle \frac{M}{2}})j},{\alpha }_2).\end{array}$$

(20)

It can be observed from (17) and (20) that the FRFT ($G_{Ql+f}$) is equivalent to the composition of $G_{f+s}$ and $G_{l+{\displaystyle \frac{f+s}{Q}}}$, which means that

$$\begin{array}{c}\hfill G_{Ql+f+s}(w_j\mathcal{F}\left[f\right](y_{j+Qp})e^{-\pi i(j+Qp)N\delta },{\alpha }_2)=G_{f+s}\left(G_{l+{\displaystyle \frac{f+s}{Q}}}({\xi }_p,{\alpha }_1)w_j{e}^{2\pi i\delta (Ql-{\displaystyle \frac{M}{2}})j},{\alpha }_2\right).\end{array}$$

(21)

Figure 2 displays the approximation errors, ($\overline{f}-f$) and ($\widehat{f}-f$), corresponding to the non-weighted fast FRFT (Equation (13)) and the composite FRFT method (Equation (20)), respectively. The observed error profiles are consistent with those in Figure 1, reinforcing the robustness of the results across different numerical schemes. The underlying Variance-Gamma (VG*) Probability Density Function (PDF) is derived from the risk-neutral distribution of the Variance-Gamma model, parameterized by $(\mu ,\delta ,\alpha ,\theta ,\sigma )$, as detailed in Section 4.

3.4. Composite of FRFTs: FRFT of N-Long Sequence and FRFT of Q-Long Weighted Sequence

The expression in (16) is recalled for further development:

$$\begin{array}{cc}\hfill & {\tilde{f}}_{NQ}(x_{Ql+f+s})={\displaystyle \frac{\beta }{2\pi }}\sum _{p=0}^{N-1}\sum _{j=0}^Q{w}_{j}F\left[f\right](y_{j+Qp})e^{i{x}_{Ql+f+s}{y}_{j+Qp}},\beta \gamma =2\pi \delta \hfill \\ \hfill & ={\displaystyle \frac{\beta }{2\pi }}{e}^{-\pi i\delta M(Ql+f+s-{\displaystyle \frac{M}{2}})}\sum _{p=0}^{N-1}{e}^{2\pi i\delta (Ql+f+s-{\displaystyle \frac{M}{2}})Qp}\sum _{j=0}^Q{w}_{j}F\left[f\right](y_{j+Qp})e^{2\pi i\delta (Ql-{\displaystyle \frac{M}{2}})j}{e}^{2\pi i\delta (f+s)j}\hfill \\ \hfill & ={\displaystyle \frac{\beta }{2\pi }}{e}^{-\pi i\delta M(Ql+f+s-{\displaystyle \frac{M}{2}})}\sum _{p=0}^{N-1}{G}_{f+s}(z_j,-\delta )e^{-\pi i\delta MQp}{e}^{2\pi i(l+{\displaystyle \frac{f+s}{Q}})\delta Q^{2}p},\hfill \end{array}$$

where $G_{f+s}$ is a FRFT on Q-long complex sequence ${\left\{z_j\right\}}_{0\le j<Q}$

$$\begin{array}{c}\hfill G_{f+s}(z_j,{\alpha }_2)=\sum _{j=0}^Q{z}_j{e}^{-2\pi i(f+s)j{\alpha }_2},z_j=w_{j}F\left[f\right](y_{j+Qp})e^{2\pi i\delta (Ql-{\displaystyle \frac{M}{2}})j},\end{array}$$

(22)

and ${\tilde{f}}_{NQ}((x_{Ql+f+s})$ becomes

$$\begin{array}{c}\hfill {\tilde{f}}_{NQ}(x_{Ql+f+s})={\displaystyle \frac{\beta }{2\pi }}{e}^{-\pi i\delta M(Ql+f+s-{\displaystyle \frac{M}{2}})}{G}_{l+{\displaystyle \frac{f+s}{Q}}}({\xi }_p,{\alpha }_1),\end{array}$$

(23)

where $G_{l+{\displaystyle \frac{f+s}{Q}}}$ is a FRFT on N-long complex sequence ${\left\{{\xi }_p\right\}}_{0\le p<N}$

$$\begin{array}{c}\hfill G_{l+{\displaystyle \frac{f+s}{Q}}}({\xi }_p,{\alpha }_1)=\sum _{p=0}^{N-1}{\xi }_p{e}^{-2\pi i(l+{\displaystyle \frac{f+s}{Q}})p{\alpha }_1},{\xi }_p=G_{f+s}(z_j,{\alpha }_2)e^{-\pi i\delta MQp}.\end{array}$$

(24)

As a result, we have the following expression for ${\tilde{f}}_{NQ}(x_{Ql+f+s})$:

$$\begin{array}{c}\hfill {\tilde{f}}_{NQ}(x_{Ql+f+s})={\displaystyle \frac{\beta }{2\pi }}{e}^{-\pi i\delta M(Ql+f+s-{\displaystyle \frac{M}{2}})}{G}_{l+{\displaystyle \frac{f+s}{Q}}}(G_{f+s}(z_j,-\delta )e^{-\pi i\delta MQp},-\delta Q^2).\end{array}$$

(25)

By comparing the inverse Fourier transform in (17) and (25), we deduce that the FRFT ($G_{Ql+f+s}$) is a composition of two FRFTs ($G_{l+{\displaystyle \frac{f+s}{Q}}}$ and $G_{f+s}$). The result (26) is similar to the result (21).

$$\begin{array}{c}\hfill G_{Ql+f+s}(w_j\mathcal{F}\left[f\right](y_{j+Qp})e^{-\pi i(j+Qp)N\delta },{\alpha }_2)=G_{l+{\displaystyle \frac{f+s}{Q}}}\left(G_{f+s}(z_j,{\alpha }_2)e^{-\pi i\delta MQp},{\alpha }_1\right).\end{array}$$

(26)

Based on the numerical results obtained from Equations (20) and (25), the estimated error is between $\tilde{f}NQ$ and $\tilde{f}QN$ is shown in Figure 3.

Figure 3 indicates that the composite FRFT formulations in Equations (21) and (26) are equivalent not only algebraically, but also numerically.

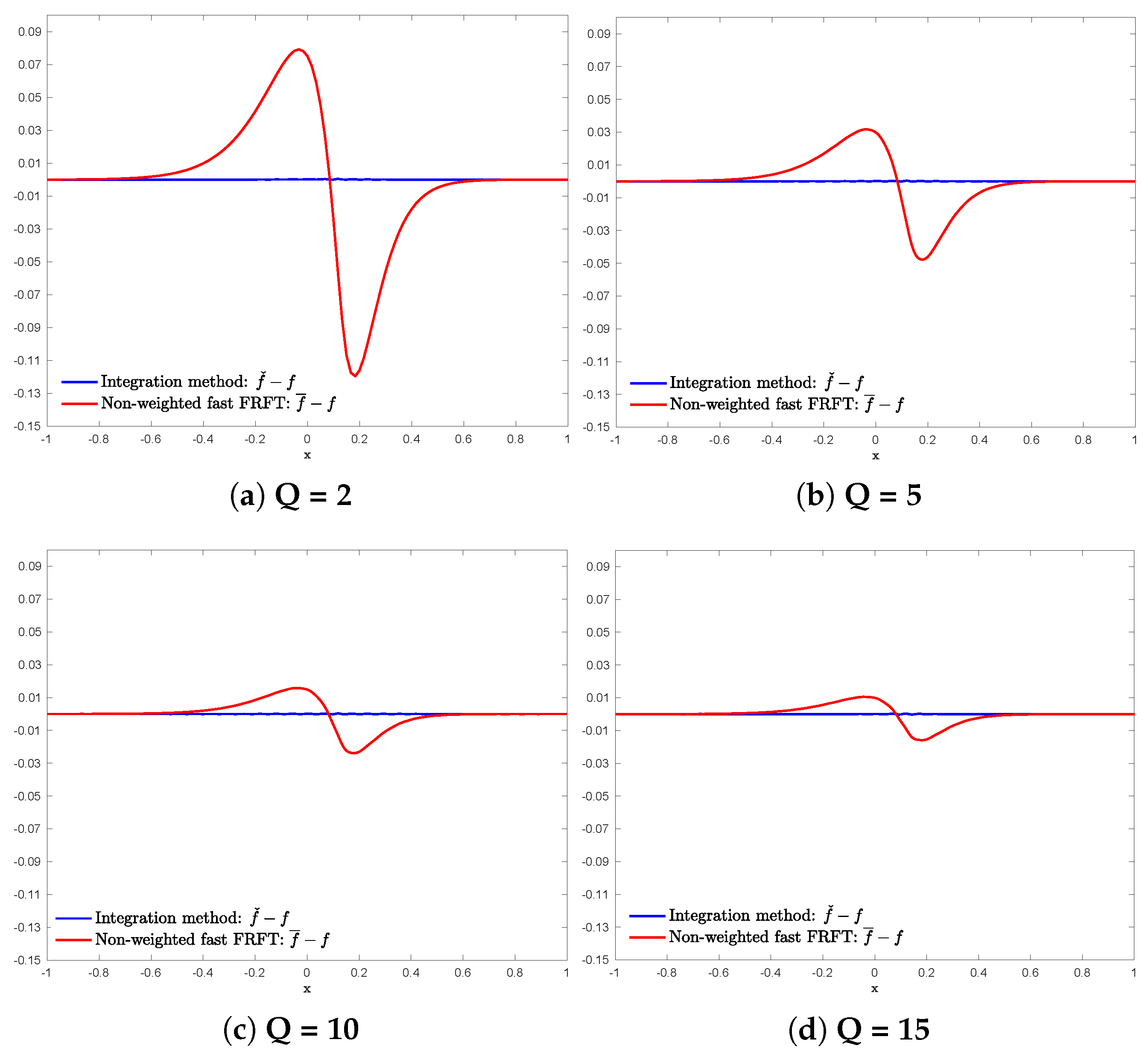
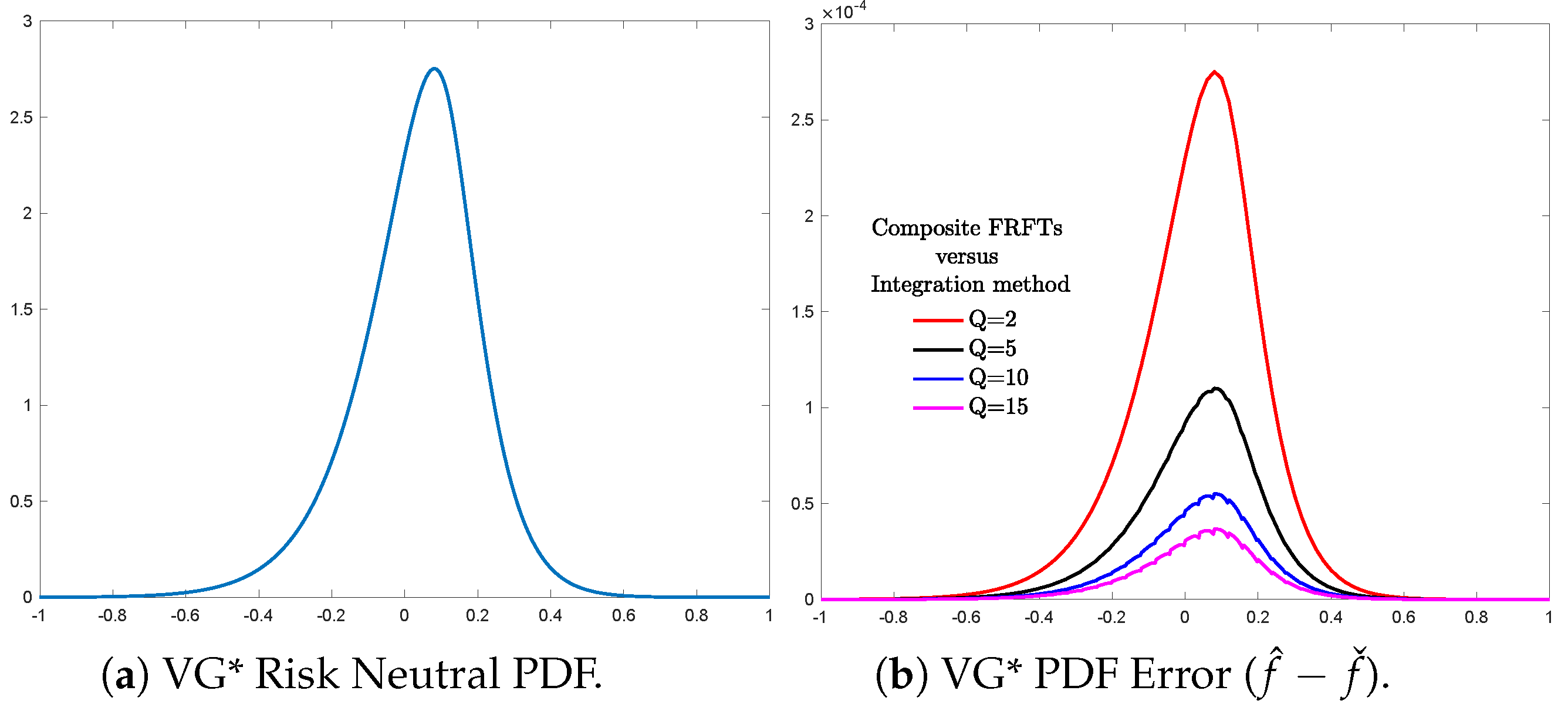
4. Illustration Examples

4.1. Variance-Gamma (VG) Distribution

In the study, the VG model has five parameters: parameters of location ($\mu$), symmetry ($\delta$), volatility ($\sigma$), and the Gamma parameters of shape ($\alpha$) and scale ($\theta$). The VG model density function can be proven to be (27):

$$\begin{array}{c}\hfill f(y)={\displaystyle \frac{1}{\sigma \Gamma (\alpha ){\theta }^{\alpha }}}{\int }_0^{+\infty }{\displaystyle \frac{1}{\sqrt{2\pi \nu }}}{e}^{-{\displaystyle \frac{{(y-\mu -\delta \nu )}^2}{2\nu {\sigma }^2}}}{\nu }^{\alpha -1}{e}^{-{\displaystyle \frac{\nu }{\theta }}}d\nu .\end{array}$$

(27)

The VG model density function (27) has an analytical expression with a modified Bessel function of the second kind. The expression can be obtained by making some transformations and changing variables as follows:

$$\begin{array}{c}\hfill -{\displaystyle \frac{{(y-\mu -\delta \nu )}^2}{2\nu {\sigma }^2}}-{\displaystyle \frac{\nu }{\theta }}=\delta ({\displaystyle \frac{y-\mu }{{\sigma }^2}})-{\displaystyle \frac{1}{2{\sigma }^2}}({\delta }^2+{\displaystyle \frac{2{\sigma }^2}{\theta }})\nu -{({\displaystyle \frac{y-\mu }{\sigma }})}^2{\displaystyle \frac{1}{2\nu }},\end{array}$$

(28)

and (27) becomes

$$\begin{array}{c}\hfill f(y)={\displaystyle \frac{e^{\delta (\frac{y-\mu }{{\sigma }^2})}}{\sqrt{2\pi }\sigma \Gamma (\alpha ){\theta }^{\alpha }}}{\int }_0^{+\infty }{e}^{-{\displaystyle \frac{1}{2{\sigma }^2}}({\delta }^2+{\displaystyle \frac{2{\sigma }^2}{\theta }})\nu -{({\displaystyle \frac{y-\mu }{\sigma }})}^2{\displaystyle \frac{1}{2\nu }}}{\nu }^{\alpha -{\displaystyle \frac{3}{2}}}d\nu .\end{array}$$

(29)

By considering the modified Bessel function of the second kind ($k_{\alpha }(z)$) [50], we have

$$\begin{array}{c}\hfill k_{\alpha }(z)={\displaystyle \frac{1}{2}}{({\displaystyle \frac{1}{2}}z)}^{\alpha }{\int }_0^{+\infty }{e}^{(-t-{\displaystyle \frac{z^2}{4t}})}{\displaystyle \frac{1}{t^{\alpha +1}}}dt,\left|arg(z)\right|\le {\displaystyle \frac{\pi }{4}},\end{array}$$

(30)

where $k_{\alpha }(z)$ is the second kind of solution for the modified Bessel’s equation:

$$\begin{array}{c}\hfill z^2{\displaystyle \frac{d^{2}w}{d{z}^2}}+z{\displaystyle \frac{dw}{dz}}-(z^2+{\alpha }^2)w=0.\end{array}$$

(31)

By changing variable, $u={\displaystyle \frac{1}{2{\sigma }^2}}({\delta }^2+{\displaystyle \frac{2{\sigma }^2}{\theta }})\nu$, (29) becomes

$$\begin{array}{c}\hfill f(y)={\displaystyle \frac{2e^{\delta (\frac{y-\mu }{{\sigma }^2})}}{\sqrt{2\pi }\sigma \Gamma (\alpha ){\theta }^{\alpha }}}{\left({\displaystyle \frac{|y-\mu |}{\sqrt{{\delta }^2+\frac{2{\sigma }^2}{\theta }}}}\right)}^{\alpha -{\displaystyle \frac{1}{2}}}{k}_{-\alpha +{\displaystyle \frac{1}{2}}}\left({\displaystyle \frac{\sqrt{{\delta }^2+\frac{2{\sigma }^2}{\theta }}|y-\mu |}{{\sigma }^2}}\right).\end{array}$$

(32)

By choosing $\theta =2$, one recovers the four-parameter Variance–Gamma (VG) distribution as highlighted in recent reviews and foundational work [51,52]. Equivalently, setting $\alpha ={\displaystyle \frac{1}{\theta }}$ yields a form often referred to as the generalized Laplace or Bessel-function distribution, which includes the symmetric Laplace distribution as a special case [53,54].

A special case $f(\mu )$ provides a simplified expression

$$\begin{array}{c}\hfill f(\mu )={\displaystyle \frac{1}{\sqrt{2\pi }\sigma \Gamma (\alpha ){\theta }^{\alpha }}}{\int }_0^{+\infty }{e}^{-{\displaystyle \frac{1}{2{\sigma }^2}}({\delta }^2+{\displaystyle \frac{2{\sigma }^2}{\theta }})\nu }{\nu }^{\alpha -{\displaystyle \frac{3}{2}}}d\nu ={\displaystyle \frac{\Gamma (\alpha -\frac{1}{2})}{\sqrt{2\pi \theta }\sigma \Gamma (\alpha ){(1+\frac{\theta }{2}\frac{{\delta }^2}{{\sigma }^2})}^{\alpha -\frac{1}{2}}}}.\end{array}$$

(33)

Table 2. Estimated parameters for the Variance-Gamma (VG) distribution.

Model	$\mathit{\mu }$	$\mathit{\delta }$	$\mathit{\sigma }$	$\mathit{\alpha }$	$\mathit{\theta }$
VG	$0.08476896$	$-0.0577418$	$1.02948292$	$0.88450029$	$0.93779517$
VG(*)	$0.11998901$	$-0.0343164$	$0.10294829$	$2.54736083$	$0.98780338$

provides estimation results of the five parameters $(\mu ,\delta ,\alpha ,\theta ,\sigma )$ of the Variance-Gamma variable. VG model estimation in the first row of Table 2 was obtained by the maximum likelihood method [46,55,56]. The VG(*) model estimation in the second row of Table 2 is the Equivalent Martingale Measure (EMM) [57] and generates a risk-neutral probability density function for a 0.8-year period.

Figure 4a provides a graphical representation of the risk-neutral probability associated with the Variance Gamma (VG*) model for a 0.8-year period. In this case, the probability density at u satisfies $f(\widehat{\mu })\approx 0.8552$ for the Variance-Gamma (VG) model and $f(\widehat{\mu })\approx 2.5949$ for the Variance-Gamma (VG*) model.

The Fourier transform function of the Variance Gamma distribution has an explicit closed form, and the inverse function is summarized as follows:

$$\begin{array}{cc}\hfill \mathcal{F}\left[f\right](x)& ={\displaystyle \frac{e^{-i\mu x}}{{\left(1+\frac{1}{2}\theta {\sigma }^2{x}^2+i\delta \theta x\right)}^{\alpha }}},f(y)={\displaystyle \frac{1}{2\pi }}{\int }_{-\infty }^{+\infty }{e}^{iyx+\mathsf{\Psi }(-x)}dx.\hfill \end{array}$$

(34)

Based on the integral method in Proposition 1 (6), the non-weighted fast FRFT, and the composite FRFTs developed in (13) and (20), respectively, we have the following numerical estimation methods of the inverse function (34).

$$\begin{array}{cc}\hfill \widehat{f}(x_{Ql+f})& ={\displaystyle \frac{\beta }{2\pi }}{e}^{-\pi i\delta M(Ql+f-{\displaystyle \frac{M}{2}})}{G}_f(G_{l+{\displaystyle \frac{f}{Q}}}(\xi ,{\alpha }_1)w_j{e}^{2\pi i\delta (Ql-{\displaystyle \frac{M}{2}})j},{\alpha }_2)(\mathrm{Composite}\mathrm{FRFT}).\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill \overline{f}(x_k)& ={\displaystyle \frac{\gamma }{2\pi }}{e}^{-\pi i(k-{\displaystyle \frac{N}{2}})N\delta }{G}_k(\mathcal{F}\left[f\right](y_j)e^{-\pi ijN\delta },-\delta )(\mathrm{Non}-\mathrm{weighted}\mathrm{fast}\mathrm{FRFT}).\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill \check{f}(x_k)& ={\displaystyle \frac{\beta }{2\pi }}\sum _{p=0}^{N-1}\sum _{j=0}^Q{W}_j{e}^{(i{y}_{j+Qp}{x}_k)}F\left[f\right](y_{j+Qp})(\mathrm{Integral}\mathrm{approximation}).\hfill \end{array}$$

(37)

The error in the VG* probability density ($\widehat{f}-\check{f}$), shown in Figure 4b, indicates that the composite FRFTs (35) perform better than the Newton-Cotes integration (37). However, as the values of Q increase, the improvement in accuracy becomes marginal.

4.2. Generalized Tempered Stable (GTS) Distribution

We consider a GTS variable $Y=\mu +X=\mu +X_{+}-X_{-}\sim GTS(\mu ,{\beta }_{+},{\beta }_{-},{\alpha }_{+},{\alpha }_{-},{\lambda }_{+},{\lambda }_{-})$ with $X_{+}\sim TS({\beta }_{+},{\alpha }_{+},{\lambda }_{+},{\lambda }_{-})$ and $X_{-}\sim TS({\beta }_{-},{\alpha }_{-},{\lambda }_{-},{\lambda }_{-})$. The characteristic exponent can be written [44]

$$\begin{array}{c}\hfill \mathsf{\Psi }(\xi )=\mu \xi i+{\alpha }_{+}\Gamma (-{\beta }_{+})\left({({\lambda }_{+}-i\xi )}^{{\beta }_{+}}-{{\lambda }_{+}}^{{\beta }_{+}}\right)+{\alpha }_{-}\Gamma (-{\beta }_{-})\left({({\lambda }_{-}+\xi )}^{{\beta }_{-}}-{{\lambda }_{-}}^{{\beta }_{-}}\right).\end{array}$$

(38)

Table 3. Estimated parameters for the Generalized Tempered Stable (GTS) distribution.

Model	$\mathit{\mu }$	${\mathit{\beta }}_{+}$	${\mathit{\beta }}_{-}$	${\mathit{\alpha }}_{+}$	${\mathit{\alpha }}_{-}$	${\mathit{\lambda }}_{+}$	${\mathit{\lambda }}_{-}$
GTS	−0.693477	0.682290	0.242579	0.458582	0.414443	0.822222	0.727607
GTS*	−0.208043	0.682290	0.242579	0.594234	4.068436	84.667097	70.31591

presents the estimation results of the seven-parameter $({\beta }_{+},{\beta }_{-},{\alpha }_{+},{\alpha }_{-},{\lambda }_{+},{\lambda }_{-})$ Generalized Tempered Stable (GTS) Distribution. The GTS model estimations presented in the first row of Table 3 were obtained using the Maximum Likelihood method, as described in [45,47].

The GTS(*) model estimations in the second row of Table 2 are the Equivalent Martingale Measure (EMM) [58] and generate a risk-neutral probability density function for a month period. Figure 5a provides a graphical representation of risk-neutral probability associated with the GTS Distribution for a month period. The characteristic function of the GTS variable, the Fourier Transform ($F(f)$), and the corresponding density function f are given by the following expressions:

$$\vartheta (\xi )=E\left[e^{iY\xi }\right]=e^{\mathsf{\Psi }(\xi )}F\left[f\right](\xi )=\vartheta (-\xi )f(y)={\displaystyle \frac{1}{2\pi }}{\int }_{-\infty }^{+\infty }{e}^{iyx+\mathsf{\Psi }(-x)}dx.$$

(39)

The GTS probability density function does not have a closed-form expression. Figure 5 provides an estimation of the GTS* risk neutral probability density error using three methods: the integration method ($\check{f}$) in Equation (37), the non-weighted fast FRFT ($\overline{f}$) in Equation (36), and the composite FRFTs ($\widehat{f}$) in Equation (35). As shown in Figure 5c,d, the composite FRFTs and the integration method outperform the non-weighted fast FRFT. Figure 5b produces the same results as Figure 4b.

Refer to Appendices A–D for the Matlab scripts supporting the empirical results.

To complement the graphical evaluation with a quantitative assessment, we introduce the following error metrics, which serve to measure the magnitude of discrepancy between the proposed and reference methods.

$$\begin{array}{cc}\hfill R(\widehat{f},\overline{f})& ={\int }_{-\infty }^{+\infty }\left|\widehat{f}(x)-\overline{f}(x)\right|dx\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill R(\widehat{f},\check{f})& ={\int }_{-\infty }^{+\infty }\left|\widehat{f}(x)-\check{f}(x)\right|dx\hfill \end{array}$$

(41)

$R(\widehat{f},\overline{f})$ quantifies the absolute error between the composite FRFT method (Equation (35)) and the standard non-weighted fast FRFT (Equation (36)), without considering the direction of the error. Similarly, $R(\widehat{f},\check{f})$ measures the absolute discrepancy between the composite FRFT method (Equation (35)) and the integral approximation approach (Equation (37)).

Table 4. Absolute Error Metrics between approximation methods for the VG and GTS distributions at various levels Q.

	$\mathit{R}(\widehat{\mathit{f}},\overline{\mathit{f}})$		$\mathit{R}(\widehat{\mathit{f}},\check{\mathit{f}})$
Q	VG	GTS	VG	GTS
2	0.0550	0.1350	9.975 × ${10}^{-05}$	9.975 × ${10}^{-05}$
5	0.0220	0.0538	3.983 × ${10}^{-05}$	3.983 × ${10}^{-05}$
10	0.0110	0.0270	1.947 × ${10}^{-05}$	1.947 × ${10}^{-05}$
15	0.0073	0.0181	1.307 × ${10}^{-05}$	1.307 × ${10}^{-05}$

reports the numerical estimates of $R(\check{f},\overline{f})$ and $R(\widehat{f},\check{f})$ for both the Variance-Gamma (VG) and the Generalized Tempered Stable (GTS) distributions.

Remark 2.

The risk-neutral Probability Density Function (PDF) and its estimation play a vital role in option pricing as they provide insight into market expectations about future asset prices [59,60,61,62]. However, their significance extends beyond pricing, with several important applications in other areas of finance including:

• Risk Management: Assesses the potential for losses or gains in derivative portfolios.
• Investment Strategy: Informs investment decisions by revealing market expectations about future asset prices.
• Financial Analysis: Aids in analyzing the prices of financial instruments and evaluating their relative value.

5. Conclusions

This study presents an enhanced computational framework for the fast Fractional Fourier Transform (FRFT) by integrating closed-form Composite Newton-Cotes quadrature rules. The key theoretical contribution is the demonstration that the FRFT of a QN-length weighted sequence can be decomposed into two commutative compositions: (1) a composition of an N-length FRFT and a Q-length weighted FRFT, and (2) the reverse composition.

The proposed composite FRFT scheme significantly improves numerical accuracy compared to standard fast FRFT and classical Newton-Cotes quadrature while preserving computational efficiency. Comprehensive error analysis and numerical experiments, particularly on Variance-Gamma (VG) and Generalized Tempered Stable (GTS) distributions, validate the scheme’s accuracy and stability.

The composite FRFT’s ability to handle oscillatory integrals and complex-valued characteristic functions makes it particularly valuable for applications in signal processing, financial mathematics, and scientific computing, where high-precision transform inversion is critical.

Future research directions include extending the framework to multidimensional cases, exploring adaptive quadrature rules for further optimization, and investigating potential applications in machine learning for spectral and frequency-domain analysis. The paper establishes a robust and efficient alternative to existing FRFT methods, offering both theoretical rigor and practical utility in numerical analysis and applied mathematics.