Stability Analysis of a Master–Slave Cournot Triopoly Model: The Effects of Cross-Diffusion

Abstract

A Cournot triopoly is a type of oligopoly market involving three firms that produce and sell homogeneous or similar products without cooperating with one another. In Cournot models, firms’ decisions about production levels play a crucial role in determining overall market output. Compared to duopoly models, oligopolies with more than two firms have received relatively less attention in the literature. Nevertheless, triopoly models are more reflective of real-world market conditions, even though analyzing their dynamics remains a complex challenge. A reaction–diffusion system of PDEs generalizing a nonlinear triopoly model describing a master–slave Cournot game is introduced. The effect of diffusion on the stability of Nash equilibrium is investigated. Self-diffusion alone cannot induce Turing pattern formation. In fact, linear stability analysis shows that cross-diffusion is the key mechanism for the formation of spatial patterns. The conditions for the onset of cross-diffusion-driven instability are obtained via linear stability analysis, and the formation of several Turing patterns is investigated through numerical simulations.

1. Introduction

The present paper is devoted to the reaction–diffusion system of PDEs given by

$$\left\{\begin{array}{c}{\partial }_t{q}_1={\alpha }_1{q}_1[a-2(b+c_1)q_1-b{q}_2]+{\gamma }_{11}\Delta q_1+{\gamma }_{12}\Delta q_2\hfill \\ {\partial }_t{q}_2={\alpha }_2{q}_2[a-2(b+c_2)q_2-b{q}_1]+{\gamma }_{21}\Delta q_1+{\gamma }_{22}\Delta q_2\hfill \\ {\partial }_t{q}_3={\alpha }_3{q}_3[a-b(q_1+q_2)-2c_3{q}_3]+{\gamma }_{33}\Delta q_3\hfill \end{array}\right.$$

(1)

with the coercivity condition; that is, there exists $k>0$, such that, $\forall {\xi }_i,{\xi }_j$

$${\displaystyle \sum _{i,j=1}^2{\gamma }_{ij}{\xi }_i{\xi }_j\ge k{\left|\xi \right|}^2,\xi =({\xi }_1,{\xi }_2)}$$

(2)

where $q_i:(\mathbf{x},t)\in \Omega \times {\mathbb{R}}^{+}\to q_i(\mathbf{x},t)\in \mathbb{R}$, $(i=1,2,3)$, $\Omega$ = bounded domain in ${\mathbb{R}}^2$ with smooth boundary $\partial \Omega$, ${\partial }_t$ = temporal derivative, $\Delta$ = Laplacian operator, $a,b,c_i,{\alpha }_i,(i=1,2,3)$ positive assigned constants, ${\gamma }_{ii}(i=1,2,3),$ positive self-diffusion coefficients, and ${\gamma }_{12},{\gamma }_{21}$ constant cross-diffusion coefficients. To (1), we append the initial conditions

$${\displaystyle q_1(\mathbf{x},0)=q_{10}\left(\mathbf{x}\right),q_2(\mathbf{x},0)=q_{20}\left(\mathbf{x}\right)q_3(\mathbf{x},0)=q_{30}\left(\mathbf{x}\right),\mathbf{x}\in \Omega ,}$$

(3)

and the homogeneous Neumann (no-flux) boundary conditions on $\partial \Omega \times {\mathbb{R}}^{+},$

$$\nabla q_1·\mathbf{n}=0,\nabla q_2·\mathbf{n}=0,\nabla q_3·\mathbf{n}=0,$$

(4)

where ∇ is the gradient operator, and n is the outward unit normal to $\partial \Omega$. The kinetic of (1)–(4) reduces to

$$\left\{\begin{array}{c}{\displaystyle \frac{d{q}_1}{dt}={\alpha }_1{q}_1[a-2(b+c_1)q_1-b{q}_2]}\hfill \\ {\displaystyle \frac{d{q}_2}{dt}={\alpha }_2{q}_2[a-2(b+c_2)q_2-b{q}_1]}\hfill \\ {\displaystyle \frac{d{q}_3}{dt}={\alpha }_3{q}_3[a-b(q_1+q_2)-2c_3{q}_3]}\hfill \end{array}\right.$$

(5)

with $\{q_i=q_i\left(t\right),(i=1,2,3)\}$, and this model is the continuous counterpart of the nonlinear discrete triopoly model already introduced in [1], describing a master–slave Cournot triopoly game with bounded rational rule. This model governs the behavior of the outputs $q_1$ and $q_2$ of two master firms, X and Y, and the output, $q_3$, of a slave firm, Z, respectively, where $a,b$ are positive assigned constants representing the intercept and slope of the inverse demand function, respectively, and $c_i,{\alpha }_i(i=1,2,3)$ are positive variable cost parameters and output speed adjustments, respectively. The three firms $X,Y,Z$ produce the homogeneous commodity, and there is no price competition between them. Unlike many models in the literature, in this model, a special price-determined mechanism has been considered in the triopoly market in which the price is decided by two master firms, and the slave firm just accepts it. Details on the derivation of (5) and the meaning of the parameters can be found in [1]. Research on the dynamic non-linear economic system is a very hot topic in the economic field. Many researchers have investigated this aspect and achieved many achievements. In recent years, many dynamic game models have been introduced. A comprehensive review of the history of Cournot-type models and some of their developments in the literature can be found in [2,3]. To make the theory more realistic, many authors have combined game theory with dynamic systems theory, giving rise to the field of bounded rational dynamic games (the general formula of a duopoly game with a form of bounded rationality has been given in [4]). Some authors have assumed a delay in the term of bounded rationality [5,6], while others have proposed many types of expectations (a player, in order to adjust their own output, can choose the strategy rule among many available ones). Naive or adaptive expectations and bounded rationality strategies are just a few examples, and consequently, many models have been constructed. A product differentiation Cournot–Bertrand duopoly model with linear demand and cost functions was studied in [7], and a Cournot–Bertrand duopoly game model with limited information was considered in [8], while in [9], a triopoly model was presented to reveal the complex dynamics and transitions between different dynamic behaviors. The study [10] is devoted to exploring the complex dynamics of a Cournot–Bertrand model, where one agent chooses quantity and the other chooses price; in [11], the dynamics of a nonlinear Cournot duopoly with managerial delegation are analyzed, while in [12], a Cournot model in electric power triopoly with nonlinear inverse demand function and cost functions is considered. Although there has been a large literature examining dynamic duopoly models, there is a relative lack of research on models in which three firms participate in competition. The motivation of this study is also to contribute to this strand. Since the reaction–diffusion systems of PDEs are often used to model spatial effects in many fields of applied mathematics, such as ecology [13,14,15,16,17,18], biology and medicine [19], epidemiology [20,21], and the social sciences [22,23,24,25], when the output is in the market, it is quite natural to generalize (5) via (1)–(4) by introducing self- and cross-diffusion terms. Although these various fields and systems may seem completely different, the mathematics describing pattern formation in them is surprisingly similar. Indeed, since Turing’s seminal work [26], reaction–diffusion models have been used to explain the formation of self-regulated patterns, initially in biochemical and biological systems [27] and then in many other fields of applied mathematics, as cited above. The study of these systems has been faced both theoretically, using analytical methods derived from the theory of partial differential equations and dynamical systems, and numerically, using computer simulations. Cross-diffusion, used to describe attraction/repulsion between species in population models, is another important aspect in the realistic modeling of diffusion and reaction. Its characteristic effect relates a gradient in the concentration of one variable to an induced flux of another. Recent experimental findings have demonstrated that the cross-diffusion is quite significant in generating a spatial structure for developmental biology. The theoretical research on the effect of cross-diffusion on population dynamics has been widely investigated by many mathematicians. Motivated by these arguments, in this paper, we introduce (1), which generalizes the ODE model (5) by considering the spatial dependence of its variables and introducing the diffusion terms. Such a generalization has already been considered in [28] for the Cournot–Kopel duopoly model, with adaptive expectations, and in [29] for a duopoly model with bounded rationality based on constant conjectural variation starting from the ODE model considered in [30].

In our model, the spatial diffusion of the outputs of firms is described by both the usual linear diffusion terms and the cross-diffusion ones. Self-diffusion terms model the random diffusion of the products of firms in the market. Of course, in coupled dynamics, this movement cannot be considered as just random. Instead, it is conditioned by the presence, abundance, or scarcity of the products of the other firms. The self-diffusion coefficients ${\gamma }_{ii},(i=1,2,3)$ are assumed to be positive, while the constant cross-diffusion coefficients ${\gamma }_{ij},i\ne j$ may be positive, negative, or zero. A positive cross-diffusion coefficient describes the spread of that product in the direction of a lower concentration of the other one. We show that the action of cross-diffusion can be very relevant. Precisely, a steady state that is stable according to the ODEs model, while remaining stable when considering self-diffusion terms, can become unstable for large sets of values of the cross-diffusion coefficients. This approach can be extended to other interacting models with different functional responses and also in other fields of applied mathematics where nonlinear mathematical models that have a similar structure are considered [30,31,32,33,34] and a comparative study of the pattern formation scenario can be explored.

The plan of the paper is the following: Section 2 considers the system equilibria, and it provides the basis for characterizing them; with a focus on the Nash internal equilibrium, the basic concepts for linear stability analysis are recalled, along with the expressions for the principal invariants, and the necessary and sufficient conditions for linear stability (Routh–Hurwitz conditions). Then, Section 3 shows how, in the absence of diffusion, the Nash equilibrium is always linearly stable, while the presence of diffusion can make it unstable; sufficient conditions for Turing instability are also found. Moreover, some properties of the solution to the ODE model are found: the first orthant is invariant, and an absorbing set of the phase space is characterized. Section 4 presents some numerical examples in which appropriate values of the diffusion coefficients result in spatially inhomogeneous equilibrium values due to Turing instabilities; it also presents details on the numerical methods. Finally, Section 5 concludes by recalling the main contributions of the work.

2. Preliminary to Stability/Instability Analysis

Constant steady states are the non-negative solutions of the system

$$\left\{\begin{array}{c}{\alpha }_1{q}_1\left(t\right)[a-2(b+c_1)q_1\left(t\right)-b{q}_2\left(t\right)]=0\hfill \\ {\alpha }_2{q}_2\left(t\right)[a-2(b+c_2)q_2\left(t\right)-b{q}_1\left(t\right)]=0\hfill \\ {\alpha }_3{q}_3\left(t\right)[a-b(q_1\left(t\right)+q_2\left(t\right))-2c_3{q}_3\left(t\right)]=0.\hfill \end{array}\right.$$

(6)

It is worth noting that, obviously, (1)–(4) and (5) have the same constant steady states. Apart from the solution $E_0=(0,0,0)$, system (6) admits the boundary equilibria

$$\begin{array}{c}{E}_1=\left({\displaystyle 0,0,\frac{a}{2c_3}}\right),E_2=\left({\displaystyle 0,\frac{a}{2(b+c_2)},0}\right),E_3=\left({\displaystyle \frac{a}{2(b+c_1)},0,0}\right),\hfill \\ E_4=\left({\displaystyle 0,\frac{a}{2(b+c_2)},\frac{a}{2c_3}-\frac{ab}{4(b+c_2)c_3}}\right),E_5=\left({\displaystyle \frac{a}{2(b+c_1)},0,\frac{a}{2c_3}-\frac{ab}{4(b+c_1)c_3}}\right),\hfill \\ E_6=\left({\displaystyle \frac{a}{2(b+c_1)},\frac{(2c_1+b)a}{2(b+c_1)(b+2c_2)},0}\right),\hfill \end{array}$$

(7)

and the Nash equilibrium point $E^{*}=(q_1^{*},q_2^{*},q_3^{*})$ where

$${\displaystyle q_1^{*}=\frac{(2c_2+b)a}{\overline{Q}},q_2^{*}=\frac{(2c_1+b)a}{\overline{Q}}{q}_3^{*}=\frac{a}{2c_3}\left({\displaystyle \frac{(b+2c_1)(b+2c_2)}{\overline{Q}}}\right)}$$

(8)

and $\overline{Q}=2(b+c_2)(b+2c_1)+b(b+2c_2).$

From this point on, we consider the interior equilibrium $E^{*}$. Introducing the perturbation fields $\{U=q_1-q_1^{*},V=q_2-q_2^{*},W=q_3-q_3^{*}\},$ system (1) becomes

$$\begin{array}{cc}{\displaystyle \frac{\partial }{\partial t}\left(\begin{array}{c}U\hfill \\ V\hfill \\ W\hfill \end{array}\right)}\hfill & =\left(\begin{array}{ccc}{a}_{11}& a_{12}& 0\\ a_{21}& a_{22}& 0\\ a_{31}& a_{32}& a_{33}\end{array}\right)\left(\begin{array}{c}U\hfill \\ V\hfill \\ W\hfill \end{array}\right)\hfill \\ \\ & +\left(\begin{array}{ccc}{\gamma }_{11}\Delta U& {\gamma }_{12}\Delta V& 0\\ {\gamma }_{21}\Delta U& {\gamma }_{22}\Delta V& 0\\ 0& 0& {\gamma }_{33}\Delta W\end{array}\right)+\left(\begin{array}{c}{F}_1\hfill \\ F_2\hfill \\ F_3\hfill \end{array}\right),\hfill \end{array}$$

(9)

with

$$\left\{\begin{array}{c}{a}_{11}=-2{\alpha }_1(b+c_1)q_1^{*},a_{12}=-{\alpha }_{1}b{q}_1^{*},a_{21}=-{\alpha }_{2}b{q}_2^{*},\hfill \\ a_{22}=-2{\alpha }_2(b+c_2)q_2^{*},a_{31}=-{\alpha }_{3}b{q}_3^{*},a_{32}=-{\alpha }_{3}b{q}_3^{*},\hfill \\ a_{33}=-2{\alpha }_3{c}_3{q}_3^{*},F_1=-2{\alpha }_1(b+c_1)U^2-{\alpha }_{1}bUV,\hfill \\ F_2=-2{\alpha }_2(b+c_2)V^2-{\alpha }_{2}bUV,F_3=-{\alpha }_{3}W(bU+bV+2c_{3}W).\hfill \end{array}\right.$$

(10)

To (9) and (10), we associate the initial-boundary conditions

$$\left\{\begin{array}{c}U(\mathbf{x},0)=U_0\left(\mathbf{x}\right),V(\mathbf{x},0)=V_0\left(\mathbf{x}\right),W(\mathbf{x},0)=W_0\left(\mathbf{x}\right),\mathbf{x}\in \Omega ,\hfill \\ \nabla U·\mathbf{n}=\nabla V·\mathbf{n}=\nabla W·\mathbf{n}=0,\mathrm{on} \partial \Omega \times {\mathbb{R}}^{+}.\hfill \end{array}\right.$$

(11)

Denoting as $W^{*}(\Omega )$ the functional space defined by

$$W^{*}(\Omega )=\left\{{\displaystyle \phi \in W^{1,2}(\Omega )\cap W^{1,2}(\partial \Omega ):\frac{d\phi }{d\mathbf{n}}=0 \mathrm{on} \partial \Omega \times {\mathbf{R}}^{+}}\right\},$$

with the Sobolev space $W^{1,2}(\Omega )=\{\phi \in L^2(\Omega ):\mathrm{there}\mathrm{exist}{\displaystyle \frac{\partial \phi }{\partial x_i}}\in L^2(\Omega )\mathrm{for}i=1,2\}$, where ${\displaystyle \frac{\partial \phi }{\partial x_i}}$ denotes the weak derivative of $\phi$ with respect to $x_i$, our aim is to find conditions ensuring the stability/instability of $E^{*}$ with respect to the perturbations $(U,V,W)\in {\left[W^{*}(\Omega )\right]}^3$. Let

$$0={\beta }_0<{\beta }_1<{\beta }_2<\cdots <{\beta }_n<\cdots$$

(12)

be the eigenvalues of the operator $-\Delta$ on $\Omega$ with homogeneous Neumann boundary conditions. The linearized version of (9) is

$${\displaystyle \frac{\partial \mathbf{X}}{\partial t}=\mathcal{L}\mathbf{X},}$$

(13)

where

$$\mathcal{L}=\left(\begin{array}{ccc}{a}_{11}+{\gamma }_{11}\Delta & a_{12}+{\gamma }_{12}\Delta & 0\\ a_{21}+{\gamma }_{21}\Delta & a_{22}+{\gamma }_{22}\Delta & 0\\ a_{31}& a_{32}& a_{33}+{\gamma }_{33}\Delta \end{array}\right),\mathbf{X}=\left(\begin{array}{c}U\hfill \\ V\hfill \\ W\hfill \end{array}\right).$$

(14)

For each $i=0,1,2,3,\dots$, ${\lambda }_i$ is an eigenvalue of $\mathcal{L}$ if and only if ${\lambda }_i$ is an eigenvalue of the matrix (see [18])

$${\tilde{\mathcal{L}}}_i=\left(\begin{array}{ccc}{a}_{11}-{\beta }_i{\gamma }_{11}& a_{12}-{\beta }_i{\gamma }_{12}& 0\\ a_{21}-{\beta }_i{\gamma }_{21}& a_{22}-{\beta }_i{\gamma }_{22}& 0\\ a_{31}& a_{32}& a_{33}-{\beta }_i{\gamma }_{33}\end{array}\right).$$

(15)

The characteristic equation of ${\tilde{\mathcal{L}}}_i$ is

$${\lambda }_i^3-{\mathtt{I}}_{1i}{\lambda }_i^2+{\mathtt{I}}_{2i}{\lambda }_i+I_{3i}=0,$$

(16)

where ${\mathtt{I}}_{ji},(j=1,2,3)$, are the principal ${\tilde{\mathcal{L}}}_i-$invariants given by

$$\left\{\begin{array}{cc}{\mathtt{I}}_{1i}=\hfill & tr{\tilde{\mathcal{L}}}_i={\mathtt{I}}_1^0-{\beta }_i({\gamma }_{11}+{\gamma }_{22}+{\gamma }_{33})\hfill \\ {\mathtt{I}}_{2i}=\hfill & (a_{11}-{\beta }_i{\gamma }_{11})(a_{22}-{\beta }_i{\gamma }_{22})-(a_{12}-{\beta }_i{\gamma }_{12})(a_{21}-{\beta }_i{\gamma }_{21})\hfill \\ & +(a_{11}-{\beta }_i{\gamma }_{11})(a_{33}-{\beta }_i{\gamma }_{33})+(a_{22}-{\beta }_i{\gamma }_{22})(a_{33}-{\beta }_i{\gamma }_{33})\hfill \\ {\mathtt{I}}_{3i}=\hfill & det{\tilde{\mathcal{L}}}_i=I_3^0-{\gamma }_{33}\Gamma {\beta }_i^3\hfill \\ & +[(a_{33}\Gamma +{\gamma }_{33}(a_{11}{\gamma }_{22}+a_{22}{\gamma }_{11}-a_{21}{\gamma }_{12}-a_{12}{\gamma }_{21})]{\beta }_i^2\hfill \\ & -[a_{33}(a_{11}{\gamma }_{22}+a_{22}{\gamma }_{11}-a_{21}{\gamma }_{12}-a_{12}{\gamma }_{21})+{\gamma }_{33}(a_{11}{a}_{22}-a_{12}{a}_{21})]{\beta }_i,\hfill \end{array}\right.$$

(17)

$\Gamma ={\gamma }_{11}{\gamma }_{22}-{\gamma }_{21}{\gamma }_{12}>0$ and ${\mathtt{I}}_j^0,(j=1,2,3)$, being the principal invariants in absence of diffusion, i.e.,

$$\left\{\begin{array}{c}{\mathtt{I}}_1^0=a_{11}+a_{22}+a_{33},\hfill \\ {\mathtt{I}}_2^0=a_{11}{a}_{22}-a_{12}{a}_{21}+a_{11}{a}_{33}+a_{22}{a}_{33},\hfill \\ {\mathtt{I}}_3^0=a_{33}(a_{11}{a}_{22}-a_{12}{a}_{21}).\hfill \end{array}\right.$$

(18)

As it is well known in the literature, the necessary and sufficient conditions guaranteeing that all the roots of (16) have a negative real part (and hence that the equilibria are linearly stable) are the Routh–Hurwitz conditions [35]:

$${\mathtt{I}}_{1i}<0,{\mathtt{I}}_{3i}<0,{\mathtt{I}}_{1i}{\mathtt{I}}_{2i}-{\mathtt{I}}_{3i}<0\forall i.$$

(19)

Let us remark that the instability of the economically meaningful equilibrium $E^{*}$ is guaranteed when at least one of (19) is reversed for at least one index, $\overline{i}.$

3. Linearized Analysis: Stability and Diffusion-Driven Turing Instability

3.1. The Model Without Diffusion

We remark that the first orthant is invariant. In fact, integrating (5), one obtains

$$\left\{\begin{array}{c}{\displaystyle q_1\left(t\right)=q_{10}exp{\int }_0^t{\alpha }_1[a-2(b+c_1)q_1-b{q}_2]d\tau ,}\hfill \\ {\displaystyle q_2\left(t\right)=q_{20}exp{\int }_0^t{\alpha }_2[a-2(b+c_2)q_2-b{q}_1]d\tau ,}\hfill \\ {\displaystyle q_3\left(t\right)=q_{30}exp{\int }_0^t{\alpha }_3[a-b(q_1\left(t\right)+q_2\left(t\right))-2c_3{q}_3\left(t\right)]d\tau }\hfill \end{array}\right.$$

(20)

and hence

$$\left\{q_{10}>0,q_{20}>0,q_{30}>0\right\}\Rightarrow \left\{q_1\left(t\right)>0,q_2\left(t\right)>0,q_3\left(t\right)>0\right\},\forall t>0,$$

(21)

i.e., the positive orthant is invariant.

Definition 1. 

A set, $\mathcal{A}$, of the phase space $(q_1,q_2,q_3)$ is an absorbing set if

(i) 

$\mathcal{A}$ is an attractor; i.e., there exists an open set, $\mathcal{B}\subset \mathcal{A}$, such that

$$\underset{t\to \infty }{lim}d[(q_{10},q_{20},q_{30}),\mathcal{A}]=0,$$

for any initial data $(q_{10},q_{20},q_{30})\in \mathcal{B}$, with

$$d\left(t\right)=\underset{\mathcal{A}}{inf}\left(\right|q_{10}-{\overline{Q}}_1{|}^2+|q_{20}-{\overline{Q}}_2{|}^2+|q_{30}-{\overline{Q}}_3{|}^2),({\overline{Q}}_1,{\overline{Q}}_2,\overline{Q_3})\in \mathcal{A}.$$

(ii) 

$\mathcal{A}$ is positively invariant, i.e.,

$$(q_{10},q_{20},q_{30})\in \mathcal{A}\Rightarrow (q_1\left(t\right),q_2\left(t\right),q_3\left(t\right))\in \mathcal{A},\forall t>0.$$

Theorem 1. 

For all $\overline{\epsilon }$, the set

$$S_{\overline{\epsilon }}=\left\{{\displaystyle (q_1,q_2,q_3)\in {\mathbb{R}}_{+}^3:q_1<\frac{a}{2(b+c_1)}+\overline{\epsilon },q_2<\frac{a}{2(b+c_2)}+\overline{\epsilon },q_3<\frac{a}{2c_3}+\overline{\epsilon }}\right\}$$

is an absorbing set of the phase space.

Proof. 

From (5)₁, it turns out that

$${\displaystyle \frac{d{q}_1}{dt}\le {\alpha }_1{q}_1[a-2(b+c_1)q_1],}$$

(22)

through which, dividing by $q_1^2$ and by setting ${\displaystyle w=\frac{1}{q_1}}$, we obtain

$${\displaystyle \frac{dw}{dt}\ge -a{\alpha }_{1}w+2(b+c_1){\alpha }_1.}$$

Via integration, it follows that

$${\displaystyle w\ge w_0{e}^{-a{\alpha }_{1}t}+\frac{2(b+c_1)}{a}(1-e^{-a{\alpha }_{1}t})}$$

and from

$${\displaystyle \underset{t\to \infty }{lim}w\ge \frac{2(b+c_1)}{a},}$$

one immediately obtains that, $\forall \overline{\epsilon }>0$, there exists $t_1\left(\overline{\epsilon }\right)>0$, such that

$${\displaystyle q_1\left(t\right)\le \frac{a}{2(b+c_1)}+\overline{\epsilon },\forall t\ge t_1.}$$

(23)

Analogously, from (5)₂ and (5)₃, it follows respectively that

$${\displaystyle q_2\left(t\right)\le \frac{a}{2(b+c_2)}+\overline{\epsilon },\forall t\ge t_2}$$

(24)

and

$${\displaystyle q_3\left(t\right)\le \frac{a}{2c_3}+\overline{\epsilon },\forall t\ge t_3.}$$

(25)

In view of (23)–(25), on taking $t\ge \tau =max\{t_1,t_2,t_3\}$, it follows that $S_{\overline{\epsilon }}$ is an attractor for all $\overline{\epsilon }>0$. Since, for all $\overline{\epsilon }>0,S_{\overline{\epsilon }}$ is also positively invariant, the thesis is proven. □

In the absence of diffusion, the necessary and sufficient condition guaranteeing the linear stability of $E^{*}$ is $\{{\mathtt{I}}_1^0<0,{\mathtt{I}}_3^0<0,{\mathtt{I}}_1^0{\mathtt{I}}_2^0-{\mathtt{I}}_3^0<0\}$ [35], where $I_j^0(j=1,2,3)$ are given by (18). A simple calculation shows that $E^{*}$ is always linearly stable in the absence of diffusion.

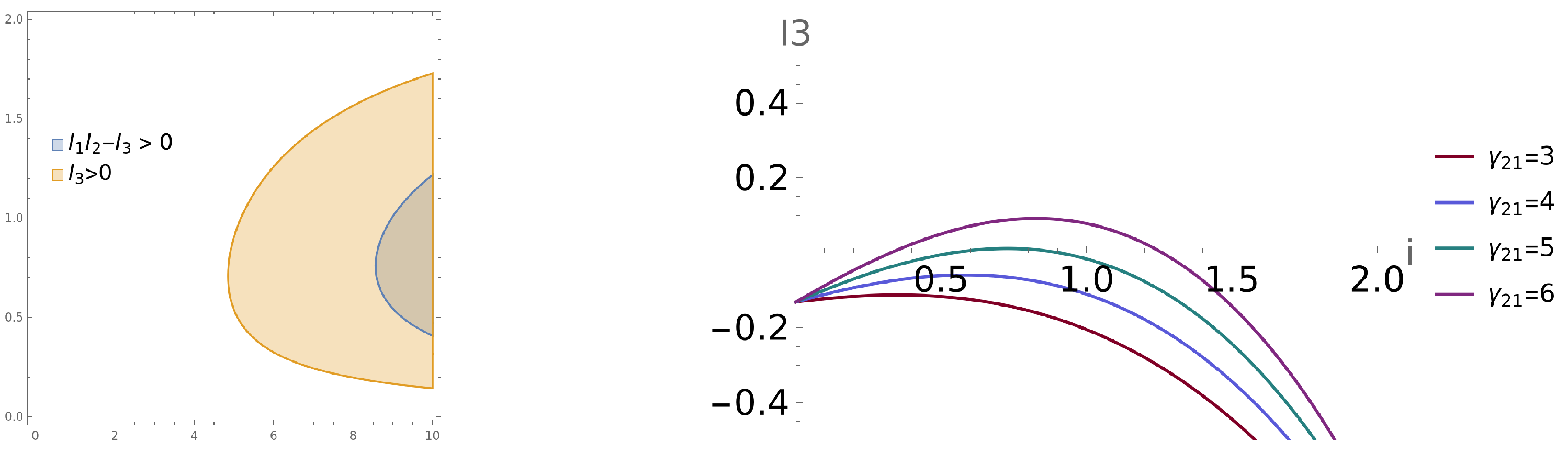
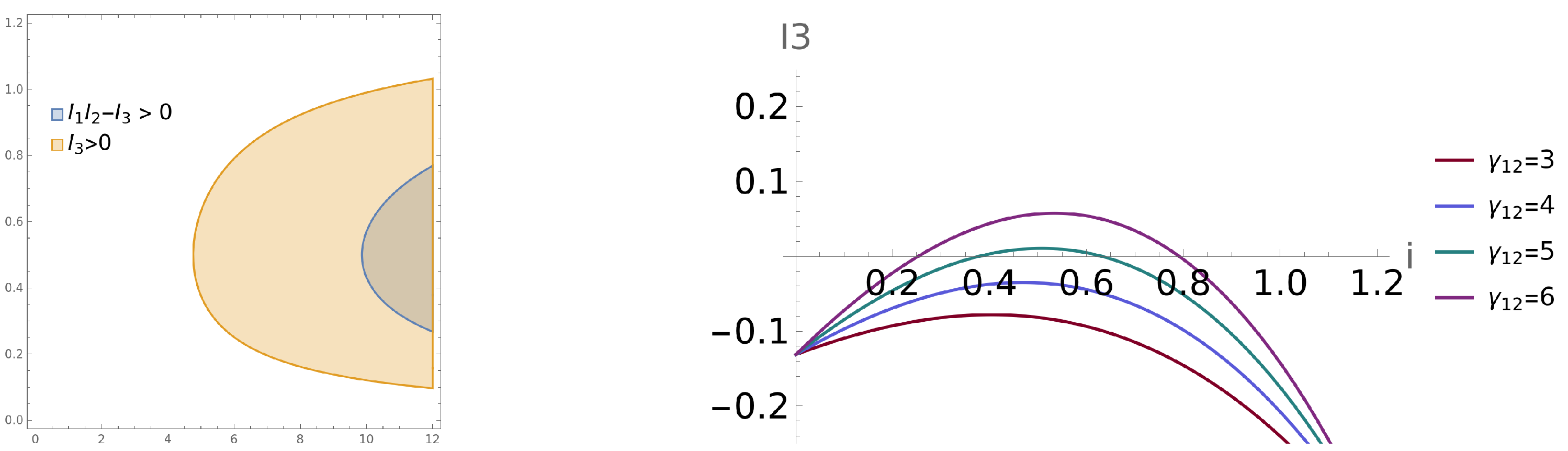
3.2. The Model with Diffusion: Cross Diffusion-Driven Turing Instability

In this subsection, we shall investigate the conditions of the system (1) for the onset of Turing instability. Precisely, we look for conditions guaranteeing that $E^{*}$, stable in the absence of diffusion, becomes unstable in the presence of diffusion (Turing instability). First, we notice that when, ${\gamma }_{12}={\gamma }_{21}=0$, there is no diffusion-driven Turing instability for (1).

Since ${\mathtt{I}}_1^0<0\Rightarrow {\mathtt{I}}_{1i}<0$, for all i, Turing instability may occur only if ${\mathtt{I}}_3^0<0,{\mathtt{I}}_1^0{\mathtt{I}}_2^0-{\mathtt{I}}_3^0<0$, together with ${\mathtt{I}}_{3\overline{i}}>0$ or ${\mathtt{I}}_{1\overline{i}}{\mathtt{I}}_{2\overline{i}}-{\mathtt{I}}_{3\overline{i}}>0$ for at least one index, $\overline{i}$. In the following Theorem 2, some sufficient conditions ensuring the onset of Turing instability are stated.

Theorem 2. 

If either

$$\left\{\begin{array}{c}{\displaystyle 0<{\gamma }_{12}<\frac{b{\gamma }_{11}}{2b+2c_1},{\gamma }_{21}>0}\hfill \\ {\displaystyle \frac{{\gamma }_{12}{\gamma }_{21}}{{\gamma }_{11}}<{\gamma }_{22}<\frac{b{\gamma }_{21}}{2b+2c_1}}\hfill \\ {\displaystyle a>\frac{{\beta }_1[4c_1(b+c_2)+b(3b+4c_2)]\Gamma }{(b+2c_2){\alpha }_1(b{\gamma }_{21}-2(b+c_1){\gamma }_{22})}}\hfill \\ {\displaystyle {\alpha }_2<-\frac{{\beta }_1(a(b+2c_2){\alpha }_1(b{\gamma }_{21}-2(b+c_1){\gamma }_{22})+{\beta }_1(4c_1(b+c_2)+b(3b+4c_2))\Gamma }{a(b+2c_1)(a(b+2c_1{\alpha }_2){\alpha }_1+2{\beta }_1(b+c_2){\gamma }_{11}-b{\beta }_1{\gamma }_{12}}}\hfill \end{array}\right.$$

(26)

or

$$\left\{\begin{array}{c}{\displaystyle {\gamma }_{12}>\frac{2b{\gamma }_{11}+2c_2{\gamma }_{11}}{b},{\gamma }_{21}>0}\hfill \\ {\displaystyle {\gamma }_{22}>\frac{{\gamma }_{12}{\gamma }_{21}}{{\gamma }_{11}},a<\frac{-2b{\beta }_1{\gamma }_{11}-2{\beta }_1{c}_2{\gamma }_{11}+b{\beta }_1{\gamma }_{12}}{b{\alpha }_1+2c_2{\alpha }_1}}\hfill \\ {\displaystyle {\alpha }_2>-\frac{{\beta }_1(a(b+2c_2){\alpha }_1(b{\gamma }_{21}-2(b+c_1){\gamma }_{22})+{\beta }_1(4c_1(b+c_2)+b(3b+4c_2))\Gamma }{a(b+2c_1)(a(b+2c_1{\alpha }_2){\alpha }_1+2{\beta }_1(b+c_2){\gamma }_{11}-b{\beta }_1{\gamma }_{12}}}\hfill \end{array}\right.$$

(27)

or

$$\left\{\begin{array}{c}{\displaystyle {\gamma }_{12}>\frac{ab{\alpha }_1+2a{c}_2{\alpha }_1+2b{\beta }_1{\gamma }_{11}+2c_2{\beta }_1{\gamma }_{11}}{b{\beta }_1},}\hfill \\ \\ {\displaystyle {\gamma }_{22}<\frac{-a(b+2c_2){\alpha }_1(a(b+2c_1){\alpha }_2-b{\beta }_1{\gamma }_{21})}{{\beta }_1(2a(b+c_1)(b+2c_2){\alpha }_1+{\beta }_1(4c_1(b+c_2)+b(3b+4c_2)){\gamma }_{11}}}\hfill \\ \\ {\displaystyle +\frac{{\beta }_1(-a(b+2c_1){\alpha }_2(2(b+c_2){\gamma }_{11}-b{\gamma }_{12})+{\beta }_1(b(3b+4c_1)+4(b+c_1)c_2){\gamma }_{12}{\gamma }_{21}}{{\beta }_1(2a(b+c_1)(b+2c_2){\alpha }_1+{\beta }_1(4c_1(b+c_2)+b(3b+4c_2)){\gamma }_{11}},}\hfill \\ \\ {\displaystyle \frac{a(b+2c_1){\alpha }_2(a(b+2c_2){\alpha }_1+2{\beta }_1(b+c_2){\gamma }_{11}-b{\beta }_1{\gamma }_{12})}{{\beta }_1(ab(b+2c_2){\alpha }_1+{\beta }_1(4c_1(b+c_2)+b(3b+4c_2)){\gamma }_{12})}<{\gamma }_{21}<0}\hfill \end{array}\right.$$

(28)

holds, then Turing instability occurs.

Proof. 

Since $E^{*}$ is stable in the absence of diffusion, in view of (17)₃, it turns out that either (26) or (27) or (28) guarantees that ${\mathtt{I}}_{3i}>0.$ □

4. Numerical Examples

In the following, we illustrate the effect of cross-diffusion on the dynamics of the considered model. Turing instability, observed in models from different application fields, is determined by interactions between populations and their rates of diffusion. A Turing pattern is a kind of nonlinear wave that is maintained through the dynamic equilibrium of the system. The tuning of parameters and boundary conditions can lead to a variety of spatial patterns: spots, stripes, and a labyrinthine structure… (see [16,36] for examples of pattern characterization using multiple scale analysis of the amplitude equations).

Table 1. Parameters of model (5) and their values in the numerical simulations.

Name	Description	Value (Ex 1)	Value (Ex 2)
a	inverse demand function intercept	10	10
b	inverse demand function slope	1	1
${\alpha }_1$	output adjustment speed for X	0.2	0.05
${\alpha }_2$	output adjustment speed for Y	0.05	0.2
${\alpha }_3$	output adjustment speed for Z	0.05	0.05
$c_1$	variable cost parameter for X	0.6	0.6
$c_2$	variable cost parameter for Y	0.5	0.5
$c_3$	variable cost parameter for Z	0.7	0.7

reports the values chosen for the parameters, which are very close to the ones considered in [1]. Specifically, the positive parameters a and b represent the intercept and slope of the inverse demand function, respectively, so we chose a = 10 and b = 1. The variable cost parameters for each one of the firms, $c_1$, $c_2$, and $c_3$, reduce the firms’ profit; a simple choice for their value is a fraction of b, and we chose $c_1$ = 0.6, $c_2$ = 0.5, $c_3$ = 0.7 in both examples. Finally, the output adjustment speeds ${\alpha }_1$, ${\alpha }_2$, and ${\alpha }_3$ are part of the bounded rational rule: each firm makes the next-period output decision based on its current output and marginal profit. Even if tuning these parameters do not modify the value of the Nash equilibrium point, they are very relevant in the evolution of the spatial instability. In particular, a larger value of this speed adjustment in only one of the firms, coupled with unbalanced (i.e., unequal) cross-diffusion, can induce instability patterns. This is the reason why we explored, in the two examples, the scenarios ${\alpha }_1>{\alpha }_2$ and ${\alpha }_2>{\alpha }_1$, respectively. As proven through the theoretical analysis in Section 3.2, self-diffusion alone cannot induce Turing pattern formation; on the other hand, there are admissible choices for the cross-diffusion coefficients ${\gamma }_{12}$ and ${\gamma }_{21}$ that lead to a diffusion-driven instability and the related appearance of different persistent spatial structures in the solution. The reported simulations are intended to explore this specific scenario and confirm the impact of cross-diffusion on the equilibrium solution of the system (1).

4.1. Details on the Implementation of the 2D Finite-Difference Method to Solve the Spatial Triopoly System

Concerning the numerical implementation, we considered the 2D problem and adopted a mixed discretization strategy in order to temper accuracy with efficiency: the self-diffusion terms are treated implicitly (i.e., collocated at time $t_{n+1}$), while the cross diffusion ones are discretized explicitly in time, along with the nonlinear terms. With this choice, at each time step, the numerical approximation of the three equations in (1) reduces to a linear system of equations collocated on a 2D numerical grid. This system can be decoupled as three smaller linear systems to be solved separately.

Once defined, a space grid on the plane domain $[x_A,x_B]\times [y_A,y_B]$ with nodes $(x_i,y_j)$, where $x_i=x_A+i\Delta h$ and $y_j=y_A+j\Delta h$, for $i=1,\dots ,N$, $j=1,\dots ,M$, the semi-implicit finite difference approximation of system (1) at each time step $t_n=n\Delta t$ can be written in compact form as follows:

$$\left\{\begin{array}{c}\left[1+\mu {\gamma }_{11}L\right]{\mathbf{q}}_1^{(n+1)}={\alpha }_1{\mathbf{q}}_1^{\left(n\right)}[a-2(b+c_1){\mathbf{q}}_1^{\left(n\right)}-b{\mathbf{q}}_2^{\left(n\right)}]+\mu {\gamma }_{12}L{\mathbf{q}}_2^{\left(n\right)}\equiv {\mathbf{w}}_{\mathbf{1}}^{\left(n\right)};\hfill \\ \left[1+\mu {\gamma }_{22}L\right]{\mathbf{q}}_2^{(n+1)}={\alpha }_2{\mathbf{q}}_2^{\left(n\right)}[a-2(b+c_2){\mathbf{q}}_2^{\left(n\right)}-b{\mathbf{q}}_1^{\left(n\right)}]+\mu {\gamma }_{21}L{\mathbf{q}}_1^{\left(n\right)}\equiv {\mathbf{w}}_{\mathbf{2}}^{\left(n\right)};\hfill \\ \left[1+\mu {\gamma }_{33}L\right]q_3^{(n+1)}={\alpha }_3{q}_3^{\left(n\right)}[a-b(q_1^{\left(n\right)}+q_2^{\left(n\right)})-2c_3{q}_3^{\left(n\right)}]\equiv {\mathbf{w}}_{\mathbf{3}}^{\left(n\right)}\hfill \end{array}\right.$$

(29)

where ${\mathbf{q}}_1^{\left(n\right)}$, ${\mathbf{q}}_2^{\left(n\right)}$, ${\mathbf{q}}_3^{\left(n\right)}$ are the vectors of the approximate solution at time $n\Delta t$ in each of the grid point $(x_i,y_j)$, L is the discrete Laplacian matrix, and the scale parameter is $\mu =\Delta t/\Delta h^2$. We implemented two different numerical algorithms in Matlab for the problem at hand and compared their performance. Specifically, along with the very classical lower–upper decomposition (LU) algorithm [37], we also considered the faster generalized minimal residual method (GMRES) [38]. When the LU algorithm is used, the numerical implementation of this scheme follows these steps:

• Input user-provided parameters (a, b, $c_1$,$c_2$, $c_3$, ${\alpha }_1$, ${\alpha }_2$, ${\alpha }_3$);
• Input diffusion coefficients (${\gamma }_{11}$, ${\gamma }_{22}$, ${\gamma }_{33}$, ${\gamma }_{12}$, ${\gamma }_{21}$);
• Input space and time discretization parameters (the time and space steps $\Delta t$ and $\Delta h$ and the extremes of the space interval $x_A$, $x_B$, $y_A$, $y_B$);
• Evaluate the Nash equilibrium $E^{*}=(q_1^{*},q_2^{*},q_3^{*})$, given by (8);
• Set the initial data as a random perturbation around the Nash equilibrium;
• Construct the discrete Laplacian matrix to approximate the space derivatives;
• Construct the matrices $B_1=I+\mu {\gamma }_{11}L$, $B_2=I+\mu {\gamma }_{22}L$, and $B_3=I+\mu {\gamma }_{33}L$;
• Perform the LU factorization of $B_1$, $B_2$, and $B_3$, obtaining $B_i=L_i{U}_i$, for $i=1,2,3$;
• Time stepping procedure (repeat for each timestep):

  -

  Update the right-hand-side ${\mathbf{w}}_{\mathbf{i}}$, for $i=1,2,3$, of system (29);

  -

  Forward substitution to solve $L_i{\mathbf{z}}_{\mathbf{i}}={\mathbf{w}}_{\mathbf{i}}$ for ${\mathbf{z}}_{\mathbf{i}}$ and for $i=1,2,3$;

  -

  Back-substitution to solve $U_i{\mathbf{q}}_{\mathbf{i}}={\mathbf{z}}_{\mathbf{i}}$ for ${\mathbf{q}}_{\mathbf{i}}$, for $i=1,2,3$.

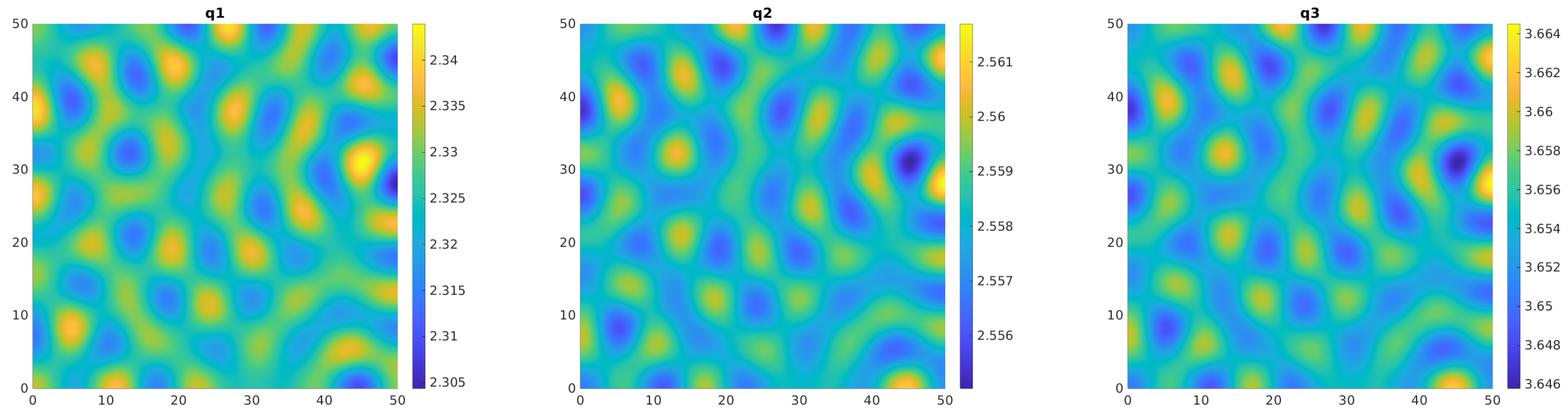
4.2. Simulation Results

Our findings (confirmed through the results of a commercial solver on the same problem) show a sensible attenuation of the numerical solution when using the GMRES algorithm, while the LU algorithm preserves a correct shape of the solution on the entire space domain. However, in the 2D case, the GMRES algorithm is notably faster. Then, we decided first to determine via a theoretical analysis a suitable range for the model’s parameters and then to realize some preliminary simulations using GMRES to qualitatively explore the system behavior in correlation with the chosen parameter values; finally, the results were refined by running the simulations with the more accurate LU algorithm. A third algorithm, in which all terms are discretized explicitly in time, along with the adoption of a very small time step, was also considered. Its results are fully consistent with those provided through the simulations performed using the LU algorithm.

Specifically, we chose two different parameters’ settings, as reported in Table 1. Moreover, we chose the self-diffusion coefficients as ${\gamma }_{11}$ = 0.1, ${\gamma }_{22}$ = 0.5, and ${\gamma }_{33}$ = 0.1. The Nash equilibrium point $E^{*}$, as shown in (8), does not depend on the output adjustment speed, so its approximate value is $E^{*}\approx (2.326,2.558,3.654)$. In the absence of diffusion, this equilibrium point is stable (${\mathtt{I}}_3^0<0,{\mathtt{I}}_1^0{\mathtt{I}}_2^0-{\mathtt{I}}_3^0<0$). We recall that spatial instability of the Turing type occurs when at least one of the inequalities in (19) is reversed for at least one index, i. Now, as stated in Section 3.2, the necessary and sufficient conditions are ${\mathtt{I}}_{3i}>0$ or ${\mathtt{I}}_{1i}{\mathtt{I}}_{2i}-{\mathtt{I}}_{3i}>0$ for at least one index, i. In both the proposed examples, the cross-diffusion parameters we chose lead to spatial instability and the occurrence of patterns. This can be clearly seen in Figure 1, which refers to Example 1. The figure describes the instability regions in the plane $(i,{\gamma }_{21})$ once we fixed ${\gamma }_{12}$ = −0.2 and how increasing values of this cross-diffusion coefficient can lead to the situation discussed in Section 3.2, where first ${\mathtt{I}}_{3i}$, and then ${\mathtt{I}}_{1i}{\mathtt{I}}_{2i}-{\mathtt{I}}_{3i}$ become positive for some index, i. Similarly, Figure 2, which refers to Example 2, with ${\gamma }_{21}$ = −0.04, describes the instability regions in the plane $(i,{\gamma }_{12})$ and how increasing the values of this cross-diffusion coefficient can lead to positive values of ${\mathtt{I}}_{3i}$ and ${\mathtt{I}}_{1i}{\mathtt{I}}_{2i}-{\mathtt{I}}_{3i}$.

In all experiments, the initial conditions for the three variables $q_1,q_2,q_3$ are set as small random perturbations around the equilibrium point $E^{*}$. Then, the presence of cross-diffusion leads to the insurgence of spatial patterns that evolve until they stabilize in the labyrinthine structures shown in Figure 3 and Figure 4. Specifically, the spatial distribution of the three populations around the Nash equilibrium $E^{*}$ shows peaks (the yellow zones) and valleys (the blue zones), whose height and depth are reported in the color bars on the right of each subfigure. It should be noted that, in the first example, the dynamics of the slave variable $q_3$ follows that of $q_1$ (in the resulting spatial distribution, the peaks of both variables correspond, with a similar correspondence for the valleys) (see Figure 3). In contrast, in the second example, where we simply switched the output adjustment speed values for $q_1$ and $q_2$, we find that the dynamics of the slave variable $q_3$ follows that of $q_2$ (as shown in Figure 4). All simulations were performed on the square $[0,50]\times [0,50]$ with the space step $\Delta x$ = 0.2 and the time step $\Delta t$ = 2.0 × 10⁻⁴. The final time, T, of the simulations, along with the chosen diffusion coefficients, is reported in the Figure captions.

5. Conclusions

In this paper, a reaction–diffusion system of PDEs generalizing a nonlinear triopoly model describing a Cournot game has been introduced. The spatial diffusion of the outputs of firms was described using both the usual linear diffusion terms and the cross-diffusion ones. We have found that self-diffusion alone is unable to induce Turing instability; on the other hand, cross-diffusion is the key to the occurrence of spatial patterns. Turing instability, also known as diffusion-driven instability, occurs when a steady state stable in the absence of diffusion becomes unstable due to differences in how quickly different economic factors (like capital, special products, or innovation) spread or diffuse across space (in other words, in the presence of diffusion, that is when the spatial heterogeneity is considered). Turing instability can indeed lead to uneven spatial development within an economic system, and spatial patterns form. In an economic scenario, various dynamics could arise. From the purely economic point of view of the production of goods to be placed on the market by the firms involved in the triopoly, it is important to know the conditions on model parameters that lead to the Turing instability of the Nash equilibrium. From the point of view of the social–economic implications, if some products, for instance, innovation or new technologies, spread faster in some areas than others, this can create an uneven landscape of economic development. Areas with faster access to new knowledge and new products might experience rapid growth, attracting resources and further accelerating development, while others lag behind. Turing instability and Turing patterns can lead to the amplification of existing inequalities and, in extreme cases, create areas of poverty or welfare with a consequent impact on society. In this paper, a linear instability analysis of the Nash equilibrium has been performed; in particular, conditions that guarantee the onset of cross-diffusion-induced instability have been determined. These results have also been confirmed through numerical simulations: our experiments have shown how, when the values of the diffusion coefficients are varied, Turing patterns emerge, representing a spatial redistribution of the products in the market. Moreover, even though the Nash equilibrium point for the non-spatial system does not depend on the adjustment speed values of the three variables, the observed Turing patterns are strongly conditioned by these values. Specifically, the patterns shown by the slave variable qualitatively correspond to the patterns of the first or the second master variable, according to the chosen values for their adjustment speed. This study shows the importance of considering the spatial spread (now well known and recognized in many fields) of products in the market in the analysis of the interactions between different firms. In some cases, indeed, the explicit introduction of spatial diffusion can modify the forecasts of the non-spatial counterpart model. For the sake of completeness, it is worth mentioning a few other examples in the recent literature where Turing instability has been studied, e.g., in ecological [39], chemical [40], and neuronal [41] models, and the crucial role of cross-diffusion has been highlighted. We are quite confident that this study can contribute new perspectives not only in the field of economics but also in other areas where mathematical models with a similar structure are considered.