A Comprehensive Study on the Applications of NTIM and OAFM in Analyzing Fractional Navier–Stokes Equations

Abstract

This article introduces two enhanced techniques: the Natural Transform Iterative Method (NTIM) and the Optimal Auxiliary Function Method (OAFM). These approaches provide a close approximation for solving fractional-order Navier–Stokes equations, which are widely employed in domains such as biology, ecology, and applied sciences. By comparing the solutions derived from these methods to exact solutions, it is clear that they provide accurate and efficient outcomes. These findings highlight the straightforward yet effective use of these methodologies in modeling engineering systems. Navier–Stokes equations have numerous practical uses, including analyzing fluid flow in pipelines and channels, predicting weather patterns, and constructing aircraft and vehicles.

1. Introduction

Solving methods of fractional differential equations are lucrative, as numerous studies have generated novel solutions that meet the requirements of various disciplines. To model diverse natural processes that necessitate non-integer derivatives, Caputo and Riemann–Liouville (RL) derivatives have traditionally been considered the most suitable. However, the limitations inherent in these approaches have prompted the search for alternative derivative definitions. Both Caputo and RL fractional derivatives possess singular kernels, and notably, the RL derivative of a constant does not yield zero. To address the singular kernel issue, Caputo and Fabrizio [1] introduced a fractional derivative operator without a singular kernel. The Caputo–Fabrizio operator has demonstrated effectiveness across a range of applications [2,3,4,5]. Furthermore, a new fractional derivative based on the Mittag-Leffler function was introduced in [6]. This led to the development of the Atangana–Baleanu (AB) fractional derivatives: one in the RL sense and the other in the Caputo sense. A prominent limitation of fractional derivatives such as the AB Caputo and AB Riemann types is the absence of the semigroup property—a key characteristic of classical derivatives. Despite their shared features of non-singular and nonlocal kernels, the lack of this property carries significant implications for the theoretical behavior and interpretation of these derivatives in various mathematical and scientific contexts. These novel fractional operators have only recently been identified within a newly proposed classification framework for fractional operators [7,8,9,10].

Fractional-order partial differential equations (FPDEs) are widely employed in fluid mechanics, mathematical biology, viscoelasticity, electrochemistry, life sciences, and physics to model a variety of nonlinear and complex systems [11,12,13,14]. For instance, fractional derivatives are effective in describing nonlinear seismic oscillations [15] and enhance the foundational assumptions in fluid dynamic traffic models [16]. Furthermore, studies such as [17,18] have formulated FPDEs to represent seepage flow in porous media and shallow-water wave propagation, grounded in empirical observations. Accurately characterizing the behavior of fractional differential equations remains a significant challenge. Developing robust methods to approximate the behavior of such equations has proven to be a complex and demanding task. Notably, fractional modeling presents one of the most promising approaches in nano hydrodynamics, particularly where the continuum assumption no longer holds. In recent years, several computational methods have been proposed to address FPDEs, including the variational iteration method [19], the fractional reduced differential transform method [20,21], the homotopy perturbation Sumudu transform method [22], the homotopy perturbation method [23], the Adomian decomposition method [24], and the homotopy analysis method [25].

Navier formulated the Navier–Stokes equation in 1822 [26] to describe the motion of viscous fluid flow. This equation has since been used to model a wide range of physical phenomena, including airflow over aircraft wings, liquid flow through pipelines, blood circulation, and ocean currents. Due to its inherent nonlinearity, the Navier–Stokes equation can be solved exactly only under certain simplified conditions, which typically require assumptions regarding the fluid state and basic flow configurations. As the foundational equation governing viscous fluid motion, the Navier–Stokes model has undergone extensive investigation and adaptation. The literature documents several techniques developed to address fractional-order Navier–Stokes equations. The fractional form of the Navier–Stokes equation was first introduced in 2005 by El-Shahed and Salem [27]. Subsequently, Kumar et al. [28] derived an analytical solution to a nonlinear fractional Navier–Stokes problem by integrating the homotopy perturbation method with the Laplace transform. The homotopy analysis method has also been employed by Ragab et al. [29] and Ganji et al. [30] to solve similar fractional formulations. Furthermore, Birajdar [31] and Maitama [32] applied the Adomian decomposition method to these equations. Kumar et al. [33] advanced this work by using a combination of the Adomian decomposition technique and Laplace transform to obtain analytical solutions. In contrast, Jena et al. [34] addressed the same equation using the finite Hankel transform alongside the Laplace transform. In the present study, the fractional Navier–Stokes problem is addressed using the homotopy perturbation transform method to achieve an accurate or approximate solution.

The homotopy analysis method (HAM) was initially introduced by Hashim et al. [35,36]. The HAM constructs a continuous mapping from an initial approximation to approach the accurate solution of a given equation. To establish this mapping, an auxiliary linear operator is chosen, and an additional convergence control parameter ensures the convergence of the resulting series solution. The time-fractional Korteweg–De Vries (KdV) equations are particularly useful for analyzing the effects of higher-order wave dispersion. Meanwhile, the Korteweg–De Vries–Burger’s equation is employed to model surface waves in shallow water. The strength of the fractional KdV equation lies in its inherent nonlocal characteristics, which enhance its applicability to real-world physical phenomena [37,38].

Although notable advancements have been made in tackling fractional Navier–Stokes equations, many current approaches face challenges in achieving both high accuracy and computational efficiency. The Natural Transform Iterative Method (NTIM) and the Optimal Auxiliary Function Method (OAFM) have shown promising results when applied to other classes of fractional differential equations. However, their application—either in combination or in direct comparison—remains largely unexplored for fractional Navier–Stokes systems. This study addresses this gap by employing both techniques on such systems, assessing their effectiveness, and offering fresh perspectives on their comparative strengths.

This paper begins with an overview of fractional calculus, outlining the fundamental concepts relevant to this study in Section 2. Section 3 introduces the Natural Transform Iterative Method (NTIM) and the Optimal Auxiliary Function Method (OAFM), the two techniques employed to address the Navier–Stokes equation. Section 4 details the application of these methods to the problem. Finally, Section 5 presents the numerical results obtained using the NTIM and OAFM, supported by clearly illustrated graphs and tables.

2. Basic Definitions

In this section, we discuss some crucial ideas that are essential to the current framework: natural transform [39] and the fundamentals of fractional calculus.

Definition 1.

The Riemann–Liouville (R-L) fractional integral is defined as

$${\mathbf{J}}_{\tau }^{\gamma }\varsigma (\tau )={\displaystyle \frac{1}{\mathrm{\Gamma }(\gamma )}}{\int }_0^{\tau }{(\tau -t)}^{\gamma -1}\varsigma (t)dt,(\gamma >0,\tau >0),$$

(1)

$${\mathbf{J}}_{\tau }^0\varsigma (\tau )=\varsigma (\tau ),$$

where $\mathrm{\Gamma }(.)$ is the gamma function:

$$\mathrm{\Gamma }(\rho )={\int }_0^{\infty }{e}^{-\eta }{\eta }^{\rho -1}d\eta ,\rho ϵ\mathbb{C}.$$

The Riemann–Liouville model has limitations when applied to practical problems through fractional calculus. In his work on viscoelasticity theory, Caputo presented a modified fractional differential operator ($D_{\breve{a}}^{\gamma }$).

Definition 2.

Caputo’s time-fractional derivative operator of order $\gamma >0$ is defined as

$$\begin{array}{cc}\hfill D_{\breve{a}}^{\gamma }& \varsigma (\tau )={\displaystyle \frac{1}{\mathrm{\Gamma }(\nu -\breve{a})}}{\int }_{\breve{a}}^{\tau }{(\tau -\eta )}^{m-\gamma -1}{\varsigma }^m(\eta )d\eta .\hfill \\ & m-1<\gamma \le m,mϵN,andfϵ{\mathbb{C}}_{-1}^m.\hfill \end{array}$$

(2)

Definition 3.

The natural transform of $\ddot{\vartheta }(\widehat{t})$ is defined as

$${\aleph }^{+}\left\{\ddot{\vartheta }(\widehat{t})\right\}=\mathbb{R}(\overline{\delta },\kappa )={\displaystyle \frac{1}{\kappa }}{\int }_0^{\infty }{e}^{{\displaystyle \frac{-\overline{\delta }\widehat{t}}{\kappa }}}(\ddot{\vartheta }(\widehat{t}))d\widehat{t}.$$

(3)

where $\overline{\delta },\kappa >0$ are the transform variables.

Definition 4.

The inverse natural transform is described as follows:

$${\aleph }^{-}\{\mathbb{R}(\overline{\delta },\kappa )\}=\ddot{\vartheta }(\widehat{t})={\displaystyle \frac{1}{2\pi \iota }}{\int }_{c-\iota \infty }^{c+\iota \infty }{e}^{{\displaystyle \frac{\overline{\delta }\widehat{t}}{\kappa }}}(\mathbb{R}(\overline{\delta },\kappa ))d\overline{\delta }.$$

(4)

The integral is represented as $\overline{\delta }=a+b\iota$ in the complex plane along $\overline{\delta }=c$, where $cϵR$.

Definition 5.

If the $nth$ derivative of $\ddot{\vartheta }(\widehat{t})$ is ${\ddot{\vartheta }}^n(\widehat{t})$, then its natural transform is given as

$${\aleph }^{+}\left\{{\ddot{\vartheta }}^n(\widehat{t})\right\}={\mathbb{R}}_n(\overline{\delta },\kappa )={\displaystyle \frac{{\overline{\delta }}^n}{{\kappa }^n}}\mathbb{R}(\overline{\delta },\kappa )-{\Sigma }_{\xi =0}^{n-1}{\displaystyle \frac{{\overline{\delta }}^{n-\xi -1}}{{\kappa }^{n-\xi }}}\left\{{\ddot{\vartheta }}^n(0)\right\},n\ge 1.$$

(5)

3. Basic Procedure of Methods

This study presents an original application of the Natural Transform Iterative Method (NTIM) and a refined version of the Optimal Auxiliary Function Method (OAFM) to fractional Navier–Stokes equations, highlighting both methodological advancements and practical gains in terms of accuracy and computational efficiency. The implementation of these techniques was performed using Wolfram Mathematica 14.0, which provides robust capabilities for symbolic computation, particularly in handling fractional derivatives.

3.1. Natural Transform Iterative Method

Consider the FDE of the following form [40]:

$$D_{\sigma }^{\dot{\eta }}\left(\tilde{\varrho }(\tilde{\lambda },\sigma )\right)=\tilde{\rho }(\tilde{\lambda },\sigma )+\overrightarrow{\chi }(\tilde{\varrho }(\tilde{\lambda },\sigma ))+\ddot{\zeta }(\tilde{\varrho }(\tilde{\lambda },\sigma )),\tilde{\lambda },\sigma \ge 0,m-1\le \dot{\eta }\le m.$$

(6)

where $D_{\sigma }^{\dot{\eta }}$ represents the Caputo fractional derivative. The linear and nonlinear functions are represented by $\overrightarrow{\chi }$ and $\ddot{\zeta }$, respectively. The known function is represented by $\tilde{\rho }(\tilde{\lambda },\sigma )$. The initial conditions are given as

$$\tilde{\varrho }(\tilde{\lambda },0)=\tilde{\theta }(\tilde{\varrho }).$$

(7)

Equation (6) has been transformed naturally using the natural transform:

$${\aleph }^{+}\left[D_{\sigma }^{\dot{\eta }}\right(\tilde{\varrho }(\tilde{\lambda },\sigma )\left)\right]={\aleph }^{+}\left[\tilde{\rho }(\tilde{\lambda },\sigma )\right]+{\aleph }^{+}\left[\overrightarrow{\chi }\right(\tilde{\varrho }(\tilde{\lambda },\sigma ))+\ddot{\zeta }(\tilde{\varrho }(\tilde{\lambda },\sigma )\left)\right].$$

(8)

One way to represent Equation (8), which makes use of the natural transform differentiation feature, is

$${\displaystyle \frac{s^{\dot{\eta }}}{{\tilde{\varrho }}^{\dot{\eta }}}}{\aleph }^{+}\left[\tilde{\varrho }(\tilde{\lambda },\sigma )\right]-{\displaystyle \frac{s^{\dot{\eta }-1}}{{\tilde{\varrho }}^{\dot{\eta }}}}\tilde{\varrho }(\tilde{\lambda },0)={\aleph }^{+}\left[\tilde{\rho }(\tilde{\lambda },\sigma )\right]+{\aleph }^{+}\left[\overrightarrow{\chi }\right(\tilde{\varrho }(\tilde{\lambda },\sigma ))+\ddot{\zeta }(\tilde{\varrho }(\tilde{\lambda },\sigma )\left)\right].$$

(9)

By arranging Equation (9), we have

$${\aleph }^{+}\left[\tilde{\varrho }(\tilde{\lambda },\sigma )\right]={\displaystyle \frac{\tilde{\theta }(\tilde{\varrho })}{s}}+{\displaystyle \frac{{\tilde{\varrho }}^{\dot{\eta }}}{s^{\dot{\eta }}}}\left({\aleph }^{+}\right[\tilde{\rho }(\tilde{\lambda },\sigma )\left]\right)+{\displaystyle \frac{{\tilde{\varrho }}^{\dot{\eta }}}{s^{\dot{\eta }}}}\left({\aleph }^{+}\right[\overrightarrow{\chi }\left(\tilde{\varrho }(\tilde{\lambda },\sigma )\right)+\ddot{\zeta }\left(\tilde{\varrho }(\tilde{\lambda },\sigma )\right)\left]\right).$$

(10)

When calculating the NTIM solution, $\tilde{\varrho }(\tilde{\lambda },\sigma )$ is extended as

$$\tilde{\varrho }(\tilde{\lambda },\sigma )=\sum _{j=0}^{\infty }{\tilde{\varrho }}_j(\tilde{\lambda },\sigma ),$$

(11)

and the nonlinear term $\ddot{\zeta }(\tilde{\varrho }(\tilde{\lambda },\sigma ))$ is defined as

$$\ddot{\zeta }\left(\sum _{k=0}^{\infty }{\tilde{\varrho }}_k(\tilde{\lambda },\sigma )\right)=\ddot{\zeta }\left({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )\right)+\sum _{m=1}^{\infty }\left\{\ddot{\zeta }\right(\sum _{i=0}^j{\tilde{\varrho }}_i(\tilde{\lambda },\sigma ))-\ddot{\zeta }(\sum _{i=0}^{m-1}{\tilde{\varrho }}_i(\tilde{\lambda },\sigma )\left)\right\}.$$

(12)

Plugging Equations (11) and (12) in Equation (10), we obtain

$${\aleph }^{+}\left[\sum _{j=1}^{\infty }{\tilde{\varrho }}_j\right]={\displaystyle \frac{\tilde{\theta }(\tilde{\varrho })}{s}}+{\displaystyle \frac{{\tilde{\varrho }}^{\dot{\eta }}}{s^{\dot{\eta }}}}\left({\aleph }^{+}\right[\tilde{\rho }(\tilde{\lambda },\sigma )\left]\right)+{\displaystyle \frac{{\tilde{\varrho }}^{\dot{\eta }}}{s^{\dot{\eta }}}}\left({\aleph }^{+}\right[\sum _{m=0}^{\infty }\overrightarrow{\chi }\left({\tilde{\varrho }}_m\right)+\ddot{\zeta }\left({\tilde{\varrho }}_0\right)+\sum _{m=1}^{\infty }\left\{\ddot{\zeta }\sum _{i=0}^m\right({\tilde{\varrho }}_i)-\ddot{\zeta }\sum _{i=0}^{m-1}({\tilde{\varrho }}_i\left)\right\}\left]\right).$$

(13)

making use of the recursive relation

$${\aleph }^{+}\left[{\tilde{\varrho }}_0(\tilde{\lambda },\sigma )\right]={\displaystyle \frac{\tilde{\theta }(\tilde{\varrho })}{s}}+{\displaystyle \frac{{\tilde{\varrho }}^{\dot{\eta }}}{s^{\dot{\eta }}}}\left({\aleph }^{+}\right[\tilde{\rho }(\tilde{\lambda },\sigma )\left]\right),$$

$${\aleph }^{+}\left[{\tilde{\varrho }}_1(\tilde{\lambda },\sigma )\right]={\displaystyle \frac{{\tilde{\varrho }}^{\dot{\eta }}}{s^{\dot{\eta }}}}\left[\overrightarrow{\chi }\right({\tilde{\varrho }}_0(\tilde{\lambda },\sigma ))+\ddot{\zeta }({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )\left)\right],$$

$${\aleph }^{+}\left[{\tilde{\varrho }}_2(\tilde{\lambda },\sigma )\right]={\displaystyle \frac{{\tilde{\varrho }}^{\dot{\eta }}}{s^{\dot{\eta }}}}\left[\overrightarrow{\chi }\right({\tilde{\varrho }}_1(\tilde{\lambda },\sigma ))+\ddot{\zeta }({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )+{\tilde{\varrho }}_1(\tilde{\lambda },\sigma ))-\ddot{\zeta }({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )\left)\right],$$

$$⋮$$

$$\begin{array}{cc}\hfill {\aleph }^{+}\left[{\tilde{\varrho }}_{i+1}(\tilde{\lambda },\sigma )\right]=& {\displaystyle \frac{{\tilde{\varrho }}^{\dot{\eta }}}{s^{\dot{\eta }}}}\left[\overrightarrow{\chi }\right({\tilde{\varrho }}_i(\tilde{\lambda },\sigma ))+\ddot{\zeta }({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )+{\tilde{\varrho }}_1(\tilde{\lambda },\sigma )+{\tilde{\varrho }}_2(\tilde{\lambda },\sigma )+\cdots +{\tilde{\varrho }}_i(\tilde{\lambda },\sigma ))\hfill \\ & -\ddot{\zeta }({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )+{\tilde{\varrho }}_1(\tilde{\lambda },\sigma )+\cdots +{\tilde{\varrho }}_{i-1}(\tilde{\lambda },\sigma ))],i\ge 0.\hfill \end{array}$$

(14)

The inverse natural transform of Equation (14), which gives us

$${\tilde{\varrho }}_0(\tilde{\lambda },\sigma )={\aleph }^{-}[{\displaystyle \frac{\tilde{\theta }(\tilde{\varrho })}{s}}+{\displaystyle \frac{{\tilde{\varrho }}^{\dot{\eta }}}{s^{\dot{\eta }}}}({\aleph }^{+}\left[\tilde{\rho }(\tilde{\lambda },\sigma )\right]\left)\right],$$

$${\tilde{\varrho }}_1(\tilde{\lambda },\sigma )={\aleph }^{-}\left[{\displaystyle \frac{{\tilde{\varrho }}^{\dot{\eta }}}{s^{\dot{\eta }}}}\right[\overrightarrow{\chi }\left({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )\right)+\ddot{\zeta }\left({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )\right)\left]\right],$$

$${\tilde{\varrho }}_2(\tilde{\lambda },\sigma )={\aleph }^{-}\left[{\displaystyle \frac{{\tilde{\varrho }}^{\dot{\eta }}}{s^{\dot{\eta }}}}\right[\overrightarrow{\chi }\left({\tilde{\varrho }}_1(\tilde{\lambda },\sigma )\right)+\ddot{\zeta }({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )+{\tilde{\varrho }}_1(\tilde{\lambda },\sigma ))-\ddot{\zeta }\left({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )\right)\left]\right],$$

$$⋮$$

$$\begin{array}{cc}\hfill {\tilde{\varrho }}_{i+1}(\tilde{\lambda },\sigma )=& {\aleph }^{-}\left[{\displaystyle \frac{{\tilde{\varrho }}^{\dot{\eta }}}{s^{\dot{\eta }}}}\right[\overrightarrow{\chi }\left({\tilde{\varrho }}_i(\tilde{\lambda },\sigma )\right)+\ddot{\zeta }({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )+{\tilde{\varrho }}_1(\tilde{\lambda },\sigma )+{\tilde{\varrho }}_2(\tilde{\lambda },\sigma )+\cdots +{\tilde{\varrho }}_i(\tilde{\lambda },\sigma ))\hfill \\ & -\ddot{\zeta }({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )+{\tilde{\varrho }}_1(\tilde{\lambda },\sigma )+\cdots +{\tilde{\varrho }}_{i-1}(\tilde{\lambda },\sigma ))\left]\right],i\ge 0.\hfill \end{array}$$

(15)

By adding all the components, we can get the approximate solution of Equation (6):

$$\tilde{\varrho }(\tilde{\lambda },\sigma )={\tilde{\varrho }}_0(\tilde{\lambda },\sigma )+{\tilde{\varrho }}_1(\tilde{\lambda },\sigma )+\cdots +{\tilde{\varrho }}_{m-1}(\tilde{\lambda },\sigma ),mϵN.$$

(16)

According to Bhalekar and Daftardar-Gejji [41], the convergence of the NTIM is equivalent to the convergence of NIM.

3.2. Optimal Auxiliary Function Method

Let us consider the general nonlinear equation of the form to demonstrate the basic idea of the OAFM [42]:

$$\overrightarrow{\chi }\left(\tilde{\varrho }(\tilde{\lambda },\sigma )\right)+\ddot{\zeta }\left(\tilde{\varrho }(\tilde{\lambda },\sigma )\right)+\tilde{\rho }(\tilde{\lambda },\sigma )=0.$$

(17)

With corresponding given initial/boundary conditions:

$$\tilde{B}(\tilde{\varrho },{\displaystyle \frac{\partial \tilde{\varrho }}{\partial \sigma }})=0.$$

(18)

$\ddot{\zeta }$ stands for the nonlinear term, $\tilde{\rho }$ is the provided function, and $\overrightarrow{\chi }$ is the linear term. It is possible to express the approximate answer to Equation (17) as

$${\tilde{\varrho }}^{\ast }(\tilde{\lambda },\sigma )={\tilde{\varrho }}_0(\tilde{\lambda },\sigma )+{\tilde{\varrho }}_1(\tilde{\lambda },\sigma ,C_n),n=1,2,3,4\dots s.$$

(19)

We insert Equation (19) into (17) to obtain the initial and first approximate solution of Equation (17).

Use the linear term to get the first approximation, ${\tilde{\varrho }}_0(\tilde{\lambda },\sigma )$:

$$\overrightarrow{\chi }\left({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )\right)+\tilde{\rho }(\tilde{\lambda },\sigma )=0,\tilde{B}({\tilde{\varrho }}_0,{\displaystyle \frac{\partial {\tilde{\varrho }}_0}{\partial \sigma }})=0.$$

(20)

The specified initial/boundary condition determines the behavior of the linear operator $\overrightarrow{\chi }$, and the function $\tilde{\rho }(\tilde{\lambda },\sigma )$ is not fixed. Finding the value of the first approximation, ${\tilde{\varrho }}_1(\tilde{\lambda },\sigma )$, requires taking into account the nonlinear differential equation and the specified initial and boundary conditions:

$$\overrightarrow{\chi }\left({\tilde{\varrho }}_1(\tilde{\lambda },\sigma ,C_n)\right)+\ddot{\zeta }({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )+{\tilde{\varrho }}_1(\tilde{\lambda },\sigma ,C_n))=0,$$

(21)

with the corresponding initial/boundary condition:

$$\tilde{B}({\tilde{\varrho }}_1,{\displaystyle \frac{\partial {\tilde{\varrho }}_1}{\partial \sigma }})=0.$$

(22)

The nonlinear component in the final equation can be expressed as follows:

$$\ddot{\zeta }({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )+{\tilde{\varrho }}_1(\tilde{\lambda },\sigma ))=\ddot{\zeta }\left({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )\right)+\sum _{k=1}^{\infty }{\displaystyle \frac{{\tilde{\varrho }}_1^{(k)}}{k!}}{N}^{(k)}\left({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )\right).$$

(23)

The limit solution of Equation (23) can be obtained by stating it in an algorithmic sequence. To manage every obstacle encountered when resolving the nonlinear differential of Equation (21) and to quicken the initial approximation’s convergence, ${\tilde{\varrho }}_1(\tilde{\lambda },\sigma )$, we choose a different term to symbolize Equation (21):

$$\overrightarrow{\chi }\left({\tilde{\varrho }}_1(\tilde{\lambda },\sigma ,C_n)\right)+{\tilde{S}}_1\left({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )\right)\ddot{\zeta }\left({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )\right)+{\tilde{S}}_2({\tilde{\varrho }}_0(\tilde{\lambda },\sigma ),C_m)=0,$$

(24)

$$\tilde{B}({\tilde{\varrho }}_1,{\displaystyle \frac{\partial {\tilde{\varrho }}_1}{\partial \sigma }})=0.$$

(25)

Remark 1.

The auxiliary functions ${\tilde{S}}_1$ and ${\tilde{S}}_2$ are based on the ${\tilde{\varrho }}_0(\tilde{\lambda },\sigma )$ and unknown parameters $C_n$ and $C_m$, where $n=1,2,3,\dots s$ and $m=s+1,s+2,s+3\dots q$.

Remark 2.

Where ${\tilde{S}}_1$ and ${\tilde{S}}_2$ are not unique. It might be ${\tilde{\varrho }}_0(\tilde{\lambda },\sigma )$ or $\ddot{\zeta }\left({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )\right)$ or perhaps a mixture of both ${\tilde{\varrho }}_0(\tilde{\lambda },\sigma )$ and $\ddot{\zeta }\left({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )\right)$.

Remark 3.

${\tilde{S}}_1\left({\tilde{\varrho }}_0(\tilde{\lambda },\sigma ,C_n)\right)$ and ${\tilde{S}}_2\left({\tilde{\varrho }}_0(\tilde{\lambda },\sigma ,C_m)\right)$ are the sum polynomial functions if ${\tilde{\varrho }}_0(\tilde{\lambda },\sigma )$ or $\ddot{\zeta }\left({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )\right)$ are polynomial functions. Similar to how ${\tilde{S}}_1\left({\tilde{\varrho }}_0(\tilde{\lambda },\sigma ,C_n)\right)$ and ${\tilde{S}}_2\left({\tilde{\varrho }}_0(\tilde{\lambda },\sigma ,C_m)\right)$ are the sum trigonometric functions when ${\tilde{\varrho }}_0(\tilde{\lambda },\sigma )$ or $\ddot{\zeta }\left({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )\right)$ are the exponential functions, these two functions are the sum exponential functions when ${\tilde{\varrho }}_0(\tilde{\lambda },\sigma )$ or $\ddot{\zeta }\left({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )\right)$ are the trigonometric functions. The exact answer is ${\tilde{\varrho }}_0(\tilde{\lambda },\sigma )$ if $\ddot{\zeta }\left({\tilde{\varrho }}_0(\tilde{\lambda },\sigma )\right)=0$, which is the specific case.

Remark 4.

To find the values of the unknown parameters $C_n$ and $C_m$, we use a number of methods, such as the Ritz approach, the Collocation method, the Least Squares method, and Galerkin’s method.

Remark 5.

The suggested method is simple and powerful, with auxiliary functions ${\tilde{S}}_1$ and ${\tilde{S}}_2$ controlling convergence and providing accurate results after only one iteration. It is not dependent on small or big parameters.

4. Solving Fractional Order Navier–Stokes Equations

Example 1.

Consider the two-dimensional fractional-order Navier–Stokes equation:

$$D_{\xi }^{\beta }(\psi )+\psi {\partial }_{\delta }(\psi )+\psi {\partial }_{\pi }(\psi )=\sigma [{\partial }_{\delta ,\delta }(\psi )+{\partial }_{\pi ,\pi }(\psi )]+\rho .$$

(26)

$$D_{\xi }^{\beta }(\varpi )+\psi {\partial }_{\delta }(\varpi )+\varpi {\partial }_{\pi }(\varpi )=\sigma [{\partial }_{\delta ,\delta }(\varpi )+{\partial }_{\pi ,\pi }(\varpi )]-\rho .$$

(27)

along with the boundary conditions:

$$\psi (\delta ,\pi ,0)=-sin(\delta +\pi ).$$

(28)

$$\varpi (\delta ,\pi ,0)=sin(\delta +\pi ).$$

(29)

The exact solutions of Equations (26) and (27) are

$$\psi (\delta ,\pi ,\xi )=-e^{-2\sigma \xi }sin(\delta +\pi ).$$

$$\varpi (\delta ,\pi ,\xi )=e^{-2\sigma \xi }sin(\delta +\pi ).$$

4.1. NTIM Solution

Applying natural transform on Equations (26) and (27), we get

$$\aleph \left\{D_{\xi }^{\beta }(\psi )\right\}=\aleph \{-\psi {\partial }_{\delta }(\psi )-\psi {\partial }_{\pi }(\psi )+\sigma [{\partial }_{\delta ,\delta }(\psi )+{\partial }_{\pi ,\pi }(\psi )]+\rho \}.$$

(30)

$$\aleph \left\{D_{\xi }^{\beta }(\varpi )\right\}=\aleph \{-\psi {\partial }_{\delta }(\varpi )-\varpi {\partial }_{\pi }(\varpi )+\sigma [{\partial }_{\delta ,\delta }(\varpi )+{\partial }_{\pi ,\pi }(\varpi )]+\rho \}.$$

(31)

Applying the natural transform differentiation property to Equations (30) and (31), we get

$${\displaystyle \frac{s^{\beta }}{{\nu }^{\beta }}}\psi (\delta ,\pi ,\xi )-{\displaystyle \frac{{\nu }^{\beta -1}}{s^{\beta }}}\psi (\delta ,\pi ,0)=\aleph \{-\psi {\partial }_{\delta }(\psi )-\psi {\partial }_{\pi }(\psi )+\sigma [{\partial }_{\delta ,\delta }(\psi )+{\partial }_{\pi ,\pi }(\psi )]+\rho \}.$$

(32)

$${\displaystyle \frac{s^{\beta }}{{\nu }^{\beta }}}\varpi (\delta ,\pi ,\xi )-{\displaystyle \frac{{\nu }^{\beta -1}}{s^{\beta }}}\varpi (\delta ,\pi ,0)=\aleph \{-\psi {\partial }_{\delta }(\varpi )-\varpi {\partial }_{\pi }(\varpi )+\sigma [{\partial }_{\delta ,\delta }(\varpi )+{\partial }_{\pi ,\pi }(\varpi )]+\rho \}.$$

(33)

Taking the inverse natural transform of Equations (32) and (33), we have

$$\psi (\delta ,\pi ,\xi )={\displaystyle \frac{\psi (\delta ,\pi ,0)}{s}}+{\aleph }^{-}\{{\displaystyle \frac{{\nu }^{\beta }}{s^{\beta }}}\aleph \{-\psi {\partial }_{\delta }(\psi )-\psi {\partial }_{\pi }(\psi )+\sigma [{\partial }_{\delta ,\delta }(\psi )+{\partial }_{\pi ,\pi }(\psi )]+\rho \left\}\right\}.$$

(34)

$$\varpi (\delta ,\pi ,\xi )={\displaystyle \frac{\varpi (\delta ,\pi ,0)}{s}}+{\aleph }^{-}\{{\displaystyle \frac{{\nu }^{\beta }}{s^{\beta }}}\aleph \{-\psi {\partial }_{\delta }(\varpi )-\varpi {\partial }_{\pi }(\varpi )+\sigma [{\partial }_{\delta ,\delta }(\varpi )+{\partial }_{\pi ,\pi }(\varpi )]+\rho \left\}\right\}.$$

(35)

Using the idea of the NTIM and the recursive relation of Equation (14), we obtained the solution components as

$${\psi }_0(\delta ,\pi ,\xi )={\aleph }^{-}\left\{{\displaystyle \frac{\psi (\delta ,\pi ,0)}{s}}\right\}.$$

$${\varpi }_0(\delta ,\pi ,\xi )={\aleph }^{-}\left\{{\displaystyle \frac{\varpi (\delta ,\pi ,0)}{s}}\right\}.$$

$${\psi }_1(\delta ,\pi ,\xi )={\aleph }^{-}\{{\displaystyle \frac{{\nu }^{\beta }}{s^{\beta }}}\aleph \{-{\psi }_0{\partial }_{\delta }({\psi }_0)-{\psi }_0{\partial }_{\pi }({\psi }_0)+\sigma [{\partial }_{\delta ,\delta }({\psi }_0)+{\partial }_{\pi ,\pi }({\psi }_0)]+\rho \left\}\right\}.$$

$${\varpi }_1(\delta ,\pi ,\xi )={\aleph }^{-}\{{\displaystyle \frac{{\nu }^{\beta }}{s^{\beta }}}\aleph \{-{\psi }_0{\partial }_{\delta }({\varpi }_0)-{\varpi }_0{\partial }_{\pi }({\varpi }_0)+\sigma [{\partial }_{\delta ,\delta }({\varpi }_0)+{\partial }_{\pi ,\pi }({\varpi }_0)]+\rho \left\}\right\}.$$

$$\begin{array}{cc}\hfill {\psi }_2(\delta ,\pi ,\xi )=& {\aleph }^{-}\{{\displaystyle \frac{{\nu }^{\beta }}{s^{\beta }}}\aleph \{-({\psi }_0+{\psi }_1){\partial }_{\delta }({\psi }_0+{\psi }_1)-({\psi }_0+{\psi }_1){\partial }_{\pi }({\psi }_0+{\psi }_1)+\sigma [{\partial }_{\delta ,\delta }({\psi }_1)+{\partial }_{\pi ,\pi }({\psi }_1)]+\rho \}\hfill \\ & -\{{\psi }_0{\partial }_{\delta }({\psi }_0)-{\psi }_0{\partial }_{\pi }({\psi }_0)\}\}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\varpi }_2(\delta ,\pi ,\xi )=& {\aleph }^{-}\{{\displaystyle \frac{{\nu }^{\beta }}{s^{\beta }}}\aleph \{-({\psi }_0+{\psi }_1){\partial }_{\delta }({\varpi }_0+{\varpi }_1)-({\varpi }_0+{\varpi }_1){\partial }_{\pi }({\varpi }_0+{\varpi }_1)+\sigma [{\partial }_{\delta ,\delta }({\varpi }_1)+{\partial }_{\pi ,\pi }({\varpi }_1)]+\rho \}\hfill \\ & -\{{\psi }_0{\partial }_{\delta }({\varpi }_0)-{\varpi }_0{\partial }_{\pi }({\varpi }_0)\}\}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\psi }_3(\delta ,\pi ,\xi )=& {\aleph }^{-}\{{\displaystyle \frac{{\nu }^{\beta }}{s^{\beta }}}\aleph \{-({\psi }_0+{\psi }_1+{\psi }_2){\partial }_{\delta }({\psi }_0+{\psi }_1+{\psi }_2)-({\psi }_0+{\psi }_1+{\psi }_2){\partial }_{\pi }({\psi }_0+{\psi }_1+{\psi }_2)\hfill \\ & +\sigma [{\partial }_{\delta ,\delta }({\psi }_2)+{\partial }_{\pi ,\pi }({\psi }_2)]+\rho \}-\{({\psi }_0+{\psi }_1){\partial }_{\delta }({\psi }_0+{\psi }_1)-({\psi }_0+{\psi }_1){\partial }_{\pi }({\psi }_0+{\psi }_1)\left\}\right\}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\varpi }_3(\delta ,\pi ,\xi )=& {\aleph }^{-}\{{\displaystyle \frac{{\nu }^{\beta }}{s^{\beta }}}\aleph \{-({\psi }_0+{\psi }_1+{\psi }_2){\partial }_{\delta }({\varpi }_0+{\varpi }_1+{\varpi }_2)-({\varpi }_0+{\varpi }_1+{\varpi }_2){\partial }_{\pi }({\varpi }_0+{\varpi }_1+{\varpi }_2)\hfill \\ & +\sigma [{\partial }_{\delta ,\delta }({\varpi }_2)+{\partial }_{\pi ,\pi }({\varpi }_2)]+\rho \}-\{({\psi }_0+{\psi }_1){\partial }_{\delta }({\varpi }_0+{\varpi }_1)-({\varpi }_0+{\varpi }_1){\partial }_{\pi }({\varpi }_0+{\varpi }_1)\left\}\right\}.\hfill \end{array}$$

(36)

By using the software Wolfram Mathematica 14.0, the solution components are obtained as

$${\psi }_0(\delta ,\pi ,\xi )=-sin(\delta +\pi ).$$

(37)

$${\varpi }_0(\delta ,\pi ,\xi )=sin(\delta +\pi ).$$

(38)

$${\psi }_1(\delta ,\pi ,\xi )={\displaystyle \frac{{\xi }^{\beta }(\rho -sin(2(\delta +\pi )))}{\mathrm{\Gamma }(\beta +1)}}.$$

(39)

$${\varpi }_1(\delta ,\pi ,\xi )=-{\displaystyle \frac{\rho {\xi }^{\beta }}{\mathrm{\Gamma }(\beta +1)}}.$$

(40)

$${\psi }_2(\delta ,\pi ,\xi )={\displaystyle \frac{{\xi }^{2\beta }(\frac{2\mathrm{\Gamma }{(2\beta +1)}^2{\xi }^{\beta }(2pcos(2(\delta +\pi ))-sin(4(\delta +\pi )))}{\mathrm{\Gamma }{(\beta +1)}^2\mathrm{\Gamma }(3\beta +1)}+2pcos(\delta +\pi )+sin(\delta +\pi )-3sin(3(\delta +\pi )))}{\mathrm{\Gamma }(2\beta +1)}}.$$

(41)

$${\varpi }_2(\delta ,\pi ,\xi )={\displaystyle \frac{{\xi }^{2\beta }sin(2(\delta +\pi ))cos(\delta +\xi )}{\mathrm{\Gamma }(2\beta +1)}}.$$

(42)

$$\begin{array}{cc}\hfill {\psi }_3(\delta ,\pi ,\xi )=& {\displaystyle \frac{1}{\sqrt{\pi }\mathrm{\Gamma }{(\beta +1)}^4\mathrm{\Gamma }(4\beta +1)}}\left({\xi }^{3\beta }\right({\displaystyle \frac{1}{\mathrm{\Gamma }{(\beta +\frac{1}{2})}^2\mathrm{\Gamma }(5\beta +1)}}\left({\pi }^{3/2}{4}^{-2\beta }\mathrm{\Gamma }{(\beta +1)}^2\mathrm{\Gamma }{(4\beta +1)}^2{\xi }^{2\beta }\right((4p^2\hfill \\ & -7)sin(2(\delta +\pi ))+8pcos(2(\delta +\pi ))+24pcos(4(\delta +\pi ))+3(4sin(4(\delta +\pi ))\hfill \\ & -9sin(6(\delta +\pi )))))+{\displaystyle \frac{1}{\mathrm{\Gamma }(\beta +\frac{1}{2})}}\left(\pi 4^{-\beta }\mathrm{\Gamma }{(\beta +1)}^2\mathrm{\Gamma }(3\beta +1){\xi }^{\beta }\right((4p^2+2)sin(\delta +\pi )\hfill \\ & +24\rho cos(3(\delta +\pi ))+3(sin(3(\delta +\pi ))-5sin(5(\delta +\pi )))\left)\right)+{\displaystyle \frac{1}{\mathrm{\Gamma }(3\beta +1)}}\left(2\right(\sqrt{\pi }\mathrm{\Gamma }(\beta +1)\mathrm{\Gamma }(2\beta \hfill \\ & +1){\xi }^{\beta }({\displaystyle \frac{2\mathrm{\Gamma }{(4\beta +1)}^2{\xi }^{\beta }\left(\right(4{\rho }^2+1)sin(2(\delta +\pi ))+8pcos(4(\delta +\pi ))-3sin(6(\delta +\pi )))}{\mathrm{\Gamma }(5\beta +1)}}\hfill \\ & +\mathrm{\Gamma }(\beta +1)\mathrm{\Gamma }(3\beta +1)(-2\rho cos(\delta +\pi )+6\rho cos(3(\delta +\pi ))+3sin(3(\delta +\pi ))-5sin(5(\delta +\pi ))))\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +{\displaystyle \frac{1}{\mathrm{\Gamma }(7\beta +1)}}\left(8^{2\beta +1}\mathrm{\Gamma }{(2\beta +1)}^2\mathrm{\Gamma }\right(3\beta +{\displaystyle \frac{1}{2}})\mathrm{\Gamma }(4\beta +1)t^{4\beta }(\rho (2\rho sin(4(\delta +\pi ))+cos(2(\delta +\pi ))\hfill \\ & +3cos(6(\delta +\pi )))-sin(8(\delta +\pi ))))+\sqrt{\pi }\mathrm{\Gamma }{(\beta +1)}^2\mathrm{\Gamma }(4\beta +1)({\displaystyle \frac{1}{\mathrm{\Gamma }(6\beta +1)}}(\mathrm{\Gamma }(5\beta \hfill \\ & +1){\xi }^{3\beta }(4\rho (\rho sin(\delta +\pi )+3\rho sin(3(\delta +\pi ))+2cos(\delta +\pi )+10cos(5(\delta +\pi )))+3sin(\delta +\pi )\hfill \\ & {-3sin(3(\delta +\pi ))+5sin(5(\delta +\pi ))-21sin(7(\delta +\pi ))))+2\mathrm{\Gamma }(\beta +1)}^2(\rho cos(2(\delta +\pi ))\hfill \\ & +2sin(2(\delta +\pi ))-3sin(4(\delta +\pi ))))\left)\right)\left)\right).\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill {\varpi }_3(\delta ,\pi ,\xi )=& {\displaystyle \frac{1}{2}}{\xi }^{3\beta }cos(\delta +\pi )(-{\displaystyle \frac{\mathrm{\Gamma }(4\beta +1){\xi }^{2\beta }(3cos(2(\delta +\pi ))-1)(4\rho cos(\delta +\pi )+3sin(\delta +\pi )-5sin(3(\delta +\pi )))}{\mathrm{\Gamma }{(2\beta +1)}^2\mathrm{\Gamma }(5\beta +1)}}\hfill \\ & +{\displaystyle \frac{\frac{4\mathrm{\Gamma }(5\beta +1){\xi }^{3\beta }(2cos(2(\delta +\pi ))-3cos(4(\delta +\pi ))-3)(\rho -sin(2(\delta +\pi )))}{\mathrm{\Gamma }{(\beta +1)}^2\mathrm{\Gamma }(6\beta +1)}-4\rho cos(\delta +\pi )-3sin(\delta +\pi )+5sin(3(\delta +\pi ))}{\mathrm{\Gamma }(3\beta +1)}}\hfill \\ & +{\displaystyle \frac{4\mathrm{\Gamma }(2\beta +1){\xi }^{\beta }(sin(4(\delta +\pi ))-2\rho cos(2(\delta +\pi )))}{\mathrm{\Gamma }{(\beta +1)}^2\mathrm{\Gamma }(4\beta +1)}}-{\displaystyle \frac{\mathrm{\Gamma }(3\beta +1){\xi }^{\beta }(2sin(2(\delta +\pi ))-3sin(4(\delta +\pi )))}{\mathrm{\Gamma }(\beta +1)\mathrm{\Gamma }(2\beta +1)\mathrm{\Gamma }(4\beta +1)}}).\hfill \end{array}$$

(44)

Combining the components, the third-order approximate solution is given as

$${\psi }_{NTIM}(\delta ,\pi ,\xi )={\psi }_0(\delta ,\pi ,\xi )+{\psi }_1(\delta ,\pi ,\xi )+{\psi }_2(\delta ,\pi ,\xi )+{\psi }_3(\delta ,\pi ,\xi ),$$

(45)

and

$${\varpi }_{NTIM}(\delta ,\pi ,\xi )={\varpi }_0(\delta ,\pi ,\xi )+{\varpi }_1(\delta ,\pi ,\xi )+{\varpi }_2(\delta ,\pi ,\xi )+{\varpi }_3(\delta ,\pi ,\xi ).$$

(46)

4.2. OAFM Solution

We consider linear and nonlinear terms in Equations (26) and (27) as

$$\overrightarrow{\chi }(\psi (\delta ,\pi ,\xi ))=D_{\xi }^{\beta }(\psi (\delta ,\pi ,\xi ))$$

$$\overrightarrow{\chi }(\varpi (\delta ,\pi ,\xi ))=D_{\xi }^{\beta }(\varpi (\delta ,\pi ,\xi ))$$

$$\ddot{\zeta }(\psi (\delta ,\pi ,\xi ))=-\psi (\delta ,\pi ,\xi ){\partial }_{\delta }(\psi (\delta ,\pi ,\xi ))-\psi (\delta ,\pi ,\xi ){\partial }_{\pi }(\psi (\delta ,\pi ,\xi ))+\sigma \left[{\partial }_{\delta ,\delta }\right(\psi (\delta ,\pi ,\xi ))+{\partial }_{\pi ,\pi }(\psi (\delta ,\pi ,\xi )\left)\right]+\rho .$$

(47)

$$\ddot{\zeta }(\varpi (\delta ,\pi ,\xi ))=-\psi (\delta ,\pi ,\xi ){\partial }_{\delta }(\varpi (\delta ,\pi ,\xi ))-\varpi (\delta ,\pi ,\xi ){\partial }_{\pi }(\varpi (\delta ,\pi ,\xi ))+\sigma \left[{\partial }_{\delta ,\delta }\right(\varpi (\delta ,\pi ,\xi ))+{\partial }_{\pi ,\pi }(\varpi (\delta ,\pi ,\xi )\left)\right]-\rho .$$

(48)

The initial approximate is obtained from Equation (9):

$$D_{\xi }^{\beta }\left({\psi }_0(\delta ,\pi ,\xi )\right)=0.$$

(49)

$$D_{\xi }^{\beta }\left({\varpi }_0(\delta ,\pi ,\xi )\right)=0.$$

(50)

Apply the inverse operator on Equations (49) and (50), we have the following solutions:

$${\psi }_0(\delta ,\pi ,\xi )=-sin(\delta +\pi ).$$

(51)

$${\varpi }_0(\delta ,\pi ,\xi )=sin(\delta +\pi ).$$

(52)

By plugging Equations (51) and (52) in Equations (47) and (48), we get the following equations:

$$\ddot{\zeta }\left({\psi }_0(\delta ,\pi ,\xi )\right)=\rho -sin(2(\delta +\pi )).$$

(53)

$$\ddot{\zeta }\left({\varpi }_0(\delta ,\pi ,\xi )\right)=-\rho .$$

(54)

The first approximation ${\psi }_1(\delta ,\pi ,\xi )$ and ${\varpi }_1(\delta ,\pi ,\xi )$ are as follows:

$$D_{\xi }^{\beta }\left({\psi }_1(\delta ,\pi ,\xi )\right)+{\mathrm{\Pi }}_1\{{\psi }_0(\delta ,\pi ,\xi ),{\overline{\omega }}_i\}N\left\{{\psi }_0(\delta ,\pi ,\xi )\right\}+{\mathrm{\Pi }}_2\{{\psi }_0(\delta ,\pi ,\xi ),{\overline{\omega }}_i\}.$$

(55)

$$D_{\xi }^{\beta }\left({\varpi }_1(\delta ,\pi ,\xi )\right)+{\mathrm{\Pi }}_3\{{\varpi }_0(\delta ,\pi ,\xi ),{\overline{\omega }}_i\}N\left\{{\varpi }_0(\delta ,\pi ,\xi )\right\}+{\mathrm{\Pi }}_4\{{\varpi }_0(\delta ,\pi ,\xi ),{\overline{\omega }}_i\}.$$

(56)

According to the nonlinear operator, we choose ${\mathrm{\Pi }}_1$, ${\mathrm{\Pi }}_2$, ${\mathrm{\Pi }}_3$, and ${\mathrm{\Pi }}_4$ as

$$\begin{array}{ccc}\hfill {\mathrm{\Pi }}_1& =& {\overline{\omega }}_4{sin}^4(\delta +\pi )+{\overline{\omega }}_3{(-sin(\delta +\pi ))}^3\hfill \\ \hfill {\mathrm{\Pi }}_2& =& {\overline{\omega }}_2{sin}^2(\delta +\pi )-{\overline{\omega }}_{1}sin(\delta +\pi )\hfill \\ \hfill {\mathrm{\Pi }}_3& =& {\overline{\omega }}_8{sin}^4(\delta +\pi )+{\overline{\omega }}_7{(-sin(\delta +\pi ))}^3\hfill \\ \hfill {\mathrm{\Pi }}_4& =& {\overline{\omega }}_6{sin}^2(\delta +\pi )-{\overline{\omega }}_{5}sin(\delta +\pi )\hfill \end{array}$$

Putting ${\mathrm{\Pi }}_1$, ${\mathrm{\Pi }}_2$, and Equation (53) into Equation (55), we get the first approximation of $\psi (\delta ,\pi ,\xi )$ as

$${\psi }_1(\delta ,\pi ,\xi )={\displaystyle \frac{{\xi }^{\beta }sin(\delta +\pi )(sin(\delta +\pi )(sin(\delta +\pi )({\overline{\omega }}_{4}sin(\delta +\pi )-{\overline{\omega }}_3)(\rho -sin(2(\delta +\pi )))+{\overline{\omega }}_2)-{\overline{\omega }}_1)}{\beta \mathrm{\Gamma }(\beta )}}.$$

(57)

Putting ${\mathrm{\Pi }}_3$, ${\mathrm{\Pi }}_4$, and Equation (54) into Equation (56), we get the first approximation of $\varpi (\delta ,\pi ,\xi )$ as

$${\varpi }_1(\delta ,\pi ,\xi )=-{\displaystyle \frac{{\xi }^{\beta }sin(\delta +\pi )({\overline{\omega }}_8\rho {sin}^3(\delta +\pi )-sin(\delta +\pi )({\overline{\omega }}_7\rho sin(\delta +\pi )+{\overline{\omega }}_6)+{\overline{\omega }}_5)}{\beta \mathrm{\Gamma }(\beta )}}.$$

(58)

We get the first-order approximate solution of $\psi (\delta ,\pi ,\xi )$ and $\varpi (\delta ,\pi ,\xi )$ as follows:

$${\psi }_{OAFM}(\delta ,\pi ,\xi )={\psi }_0(\delta ,\pi ,\xi )+{\psi }_1(\delta ,\pi ,\xi ).$$

(59)

$${\psi }_{OAFM}(\delta ,\pi ,\xi )=sin(\delta +\pi )({\displaystyle \frac{{\xi }^{\beta }(sin(\delta +\pi )(sin(\delta +\pi )({\overline{\omega }}_{4}sin(\delta +\pi )-{\overline{\omega }}_3)(\rho -sin(2(\delta +\pi )))+{\overline{\omega }}_2)-{\overline{\omega }}_1)}{\beta \mathrm{\Gamma }(\beta )}}-1).$$

(60)

$${\varpi }_{OAFM}(\delta ,\pi ,\xi )={\varpi }_0(\delta ,\pi ,\xi )+{\varpi }_1(\delta ,\pi ,\xi ).$$

(61)

$${\varpi }_{OAFM}(\delta ,\pi ,\xi )=sin(\delta +\pi )(1-{\displaystyle \frac{{\xi }^{\beta }({\overline{\omega }}_8\rho {sin}^3(\delta +\pi )-sin(\delta +\pi )({\overline{\omega }}_7\rho sin(\delta +\pi )+{\overline{\omega }}_6)+{\overline{\omega }}_5)}{\beta \mathrm{\Gamma }(\beta )}}).$$

(62)

To find the values of unknown parameters ${\overline{\omega }}_1$, ${\overline{\omega }}_2$, ${\overline{\omega }}_3$, and ${\overline{\omega }}_4$ for $\psi (\delta ,\pi ,\xi )$, and ${\overline{\omega }}_5$, ${\overline{\omega }}_6$, ${\overline{\omega }}_7$, and ${\overline{\omega }}_8$ for $\varpi (\delta ,\pi ,\xi )$, we used the collection method:

$$\begin{array}{ccc}\hfill {\overline{\omega }}_1& =& 3.7198667937151964\hfill \\ \hfill {\overline{\omega }}_2& =& 5.228149298569213\hfill \\ \hfill {\overline{\omega }}_3& =& -85.90373651612913\hfill \\ \hfill {\overline{\omega }}_4& =& -90.90413043651026\hfill \\ \hfill {\overline{\omega }}_5& =& -1.0476531705366368\hfill \\ \hfill {\overline{\omega }}_6& =& -0.0670374384329326\hfill \\ \hfill {\overline{\omega }}_7& =& -1.1739887449941295\hfill \\ \hfill {\overline{\omega }}_8& =& 1.0353507715432089\hfill \end{array}$$

Example 2.

Consider the two-dimensional fractional-order Navier–Stokes equation:

$$D_{\xi }^{\beta }(\psi )+\psi {\partial }_{\delta }(\psi )+\psi {\partial }_{\pi }(\psi )=\sigma [{\partial }_{\delta ,\delta }(\psi )+{\partial }_{\pi ,\pi }(\psi )]+\rho .$$

(63)

$$D_{\xi }^{\beta }(\varpi )+\psi {\partial }_{\delta }(\varpi )+\varpi {\partial }_{\pi }(\varpi )=\sigma [{\partial }_{\delta ,\delta }(\varpi )+{\partial }_{\pi ,\pi }(\varpi )]+\rho .$$

(64)

Subject to the boundary conditions:

$$\psi (\delta ,\pi ,0)=-e^{\delta +\pi }.$$

(65)

$$\varpi (\delta ,\pi ,0)=e^{\delta +\pi }.$$

(66)

The exact solutions of Equations (63) and (64) are

$$\psi (\delta ,\pi ,\xi )=-e^{\delta +\pi +2\sigma \xi }.$$

(67)

$$\varpi (\delta ,\pi ,\xi )=e^{\delta +\pi +2\sigma \xi }.$$

(68)

4.3. NTIM Solution

Applying a natural transform on Equations (63) and (64), we get

$$\aleph \left\{D_{\xi }^{\beta }(\psi )\right\}=\aleph \{-\psi {\partial }_{\delta }(\psi )-\psi {\partial }_{\pi }(\psi )+\sigma [{\partial }_{\delta ,\delta }(\psi )+{\partial }_{\pi ,\pi }(\psi )]+\rho \}.$$

(69)

$$\aleph \left\{D_{\xi }^{\beta }(\varpi )\right\}=\aleph \{-\psi {\partial }_{\delta }(\varpi )-\varpi {\partial }_{\pi }(\varpi )+\sigma [{\partial }_{\delta ,\delta }(\varpi )+{\partial }_{\pi ,\pi }(\varpi )]+\rho \}.$$

(70)

Applying the natural transform differentiation property to Equations (69) and (70), we get

$${\displaystyle \frac{s^{\beta }}{{\nu }^{\beta }}}\psi (\delta ,\pi ,\xi )-{\displaystyle \frac{{\nu }^{\beta -1}}{s^{\beta }}}\psi (\delta ,\pi ,0)=\aleph \{-\psi {\partial }_{\delta }(\psi )-\psi {\partial }_{\pi }(\psi )+\sigma [{\partial }_{\delta ,\delta }(\psi )+{\partial }_{\pi ,\pi }(\psi )]+\rho \}.$$

(71)

$${\displaystyle \frac{s^{\beta }}{{\nu }^{\beta }}}\varpi (\delta ,\pi ,\xi )-{\displaystyle \frac{{\nu }^{\beta -1}}{s^{\beta }}}\varpi (\delta ,\pi ,0)=\aleph \{-\psi {\partial }_{\delta }(\varpi )-\varpi {\partial }_{\pi }(\varpi )+\sigma [{\partial }_{\delta ,\delta }(\varpi )+{\partial }_{\pi ,\pi }(\varpi )]+\rho \}.$$

(72)

Taking the inverse natural transform of Equations (71) and (72), we have

$$\psi (\delta ,\pi ,\xi )={\displaystyle \frac{\psi (\delta ,\pi ,0)}{s}}+{\aleph }^{-}\{{\displaystyle \frac{{\nu }^{\beta }}{s^{\beta }}}\aleph \{-\psi {\partial }_{\delta }(\psi )-\psi {\partial }_{\pi }(\psi )+\sigma [{\partial }_{\delta ,\delta }(\psi )+{\partial }_{\pi ,\pi }(\psi )]+\rho \left\}\right\}.$$

(73)

$$\varpi (\delta ,\pi ,\xi )={\displaystyle \frac{\varpi (\delta ,\pi ,0)}{s}}+{\aleph }^{-}\{{\displaystyle \frac{{\nu }^{\beta }}{s^{\beta }}}\aleph \{-\psi {\partial }_{\delta }(\varpi )-\varpi {\partial }_{\pi }(\varpi )+\sigma [{\partial }_{\delta ,\delta }(\varpi )+{\partial }_{\pi ,\pi }(\varpi )]+\rho \left\}\right\}.$$

(74)

Using the idea of the NTIM and the recursive relation of Equation (14), we obtained the solution components as

$${\psi }_0(\delta ,\pi ,\xi )={\aleph }^{-}\left\{{\displaystyle \frac{\psi (\delta ,\pi ,0)}{s}}\right\}.$$

$${\varpi }_0(\delta ,\pi ,\xi )={\aleph }^{-}\left\{{\displaystyle \frac{\varpi (\delta ,\pi ,0)}{s}}\right\}.$$

$${\psi }_1(\delta ,\pi ,\xi )={\aleph }^{-}\{{\displaystyle \frac{{\nu }^{\beta }}{s^{\beta }}}\aleph \{-{\psi }_0{\partial }_{\delta }({\psi }_0)-{\psi }_0{\partial }_{\pi }({\psi }_0)+\sigma [{\partial }_{\delta ,\delta }({\psi }_0)+{\partial }_{\pi ,\pi }({\psi }_0)]+\rho \left\}\right\}.$$

$${\varpi }_1(\delta ,\pi ,\xi )={\aleph }^{-}\{{\displaystyle \frac{{\nu }^{\beta }}{s^{\beta }}}\aleph \{-{\psi }_0{\partial }_{\delta }({\varpi }_0)-{\varpi }_0{\partial }_{\pi }({\varpi }_0)+\sigma [{\partial }_{\delta ,\delta }({\varpi }_0)+{\partial }_{\pi ,\pi }({\varpi }_0)]+\rho \left\}\right\}.$$

$$\begin{array}{cc}\hfill {\psi }_2(\delta ,\pi ,\xi )=& {\aleph }^{-}\{{\displaystyle \frac{{\nu }^{\beta }}{s^{\beta }}}\aleph \{-({\psi }_0+{\psi }_1){\partial }_{\delta }({\psi }_0+{\psi }_1)-({\psi }_0+{\psi }_1){\partial }_{\pi }({\psi }_0+{\psi }_1)+\sigma [{\partial }_{\delta ,\delta }({\psi }_1)+{\partial }_{\pi ,\pi }({\psi }_1)]+\rho \}\hfill \\ & -\{{\psi }_0{\partial }_{\delta }({\psi }_0)-{\psi }_0{\partial }_{\pi }({\psi }_0)\}\}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\varpi }_2(\delta ,\pi ,\xi )=& {\aleph }^{-}\{{\displaystyle \frac{{\nu }^{\beta }}{s^{\beta }}}\aleph \{-({\psi }_0+{\psi }_1){\partial }_{\delta }({\varpi }_0+{\varpi }_1)-({\varpi }_0+{\varpi }_1){\partial }_{\pi }({\varpi }_0+{\varpi }_1)+\sigma [{\partial }_{\delta ,\delta }({\varpi }_1)+{\partial }_{\pi ,\pi }({\varpi }_1)]+\rho \}\hfill \\ & -\{{\psi }_0{\partial }_{\delta }({\varpi }_0)-{\varpi }_0{\partial }_{\pi }({\varpi }_0)\}\}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\psi }_3(\delta ,\pi ,\xi )=& {\aleph }^{-}\{{\displaystyle \frac{{\nu }^{\beta }}{s^{\beta }}}\aleph \{-({\psi }_0+{\psi }_1+{\psi }_2){\partial }_{\delta }({\psi }_0+{\psi }_1+{\psi }_2)-({\psi }_0+{\psi }_1+{\psi }_2){\partial }_{\pi }({\psi }_0+{\psi }_1+{\psi }_2)\hfill \\ & +\sigma [{\partial }_{\delta ,\delta }({\psi }_2)+{\partial }_{\pi ,\pi }({\psi }_2)]+\rho \}-\{({\psi }_0+{\psi }_1){\partial }_{\delta }({\psi }_0+{\psi }_1)-({\psi }_0+{\psi }_1){\partial }_{\pi }({\psi }_0+{\psi }_1)\left\}\right\}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\varpi }_3(\delta ,\pi ,\xi )=& {\aleph }^{-}\{{\displaystyle \frac{{\nu }^{\beta }}{s^{\beta }}}\aleph \{-({\psi }_0+{\psi }_1+{\psi }_2){\partial }_{\delta }({\varpi }_0+{\varpi }_1+{\varpi }_2)-({\varpi }_0+{\varpi }_1+{\varpi }_2){\partial }_{\pi }({\varpi }_0+{\varpi }_1+{\varpi }_2)\hfill \\ & +\sigma [{\partial }_{\delta ,\delta }({\varpi }_2)+{\partial }_{\pi ,\pi }({\varpi }_2)]+\rho \}-\{({\psi }_0+{\psi }_1){\partial }_{\delta }({\varpi }_0+{\varpi }_1)-({\varpi }_0+{\varpi }_1){\partial }_{\pi }({\varpi }_0+{\varpi }_1)\left\}\right\}.\hfill \end{array}$$

(75)

By using the software Wolfram Mathematica 14.0, the solution components are obtained as

$${\psi }_0(\delta ,\pi ,\xi )=-e^{\delta +\pi }.$$

$${\varpi }_0(\delta ,\pi ,\xi )=e^{\delta +\pi }.$$

$${\psi }_1(\delta ,\pi ,\xi )={\displaystyle \frac{{\xi }^{\beta }(\rho -2e^{2(\delta +\pi )})}{\mathrm{\Gamma }(\beta +1)}}.$$

$${\varpi }_1(\delta ,\pi ,\xi )=-{\displaystyle \frac{\rho {\xi }^{\beta }}{\mathrm{\Gamma }(\beta +1)}}.$$

$${\psi }_2(\delta ,\pi ,\xi )={\displaystyle \frac{2{\xi }^{2\beta }{e}^{\delta +\pi }(-\frac{4\mathrm{\Gamma }{(2\beta +1)}^2{\xi }^{\beta }{e}^{\delta +\pi }(2e^{2(\delta +\pi )}-\rho )}{\mathrm{\Gamma }{(\beta +1)}^2\mathrm{\Gamma }(3\beta +1)}+\rho -6e^{2(\delta +\pi )})}{\mathrm{\Gamma }(2\beta +1)}}.$$

$${\varpi }_2(\delta ,\pi ,\xi )={\displaystyle \frac{2{\xi }^{2\beta }{e}^{3(\delta +\pi )}}{\mathrm{\Gamma }(2\beta +1)}}.$$

$$\begin{array}{cc}\hfill {\psi }_3(\delta ,\pi ,\xi )=& {\displaystyle \frac{1}{\mathrm{\Gamma }(3\beta +1)}}\left(8e^{-5(\delta +\pi )}\right(-{\displaystyle \frac{1}{\mathrm{\Gamma }{(\beta +1)}^2\mathrm{\Gamma }(6\beta +1)}}\left(4\mathrm{\Gamma }(5\beta +1)\right({\xi }^{6\beta }\left(e^{4(\delta +\pi )}\right(3({\rho }^2+7)e^{4(\delta +\pi )}\hfill \\ & -40\rho e^{6(\delta +\pi )}+63e^{8(\delta +\pi )}+21)-21)+21\mathrm{\Gamma }(6\beta +1){\xi }^{6\beta }{(e^{4(\delta +\pi )}-1)}^2(e^{4(\delta +\pi )}+1)\left)\right)\hfill \\ & -{\displaystyle \frac{4^{\beta +1}\mathrm{\Gamma }(\beta +\frac{1}{2})\mathrm{\Gamma }(4\beta +1){\xi }^{5\beta }{e}^{7(\delta +\pi )}({\rho }^2-8\rho e^{2(\delta +\pi )}+12e^{4(\delta +\pi )})}{\sqrt{\pi }\mathrm{\Gamma }{(\beta +1)}^2\mathrm{\Gamma }(5\beta +1)}}+{\xi }^{3\beta }{e}^{7(\delta +\pi )}(\rho -12e^{2(\delta +\pi )})\left)\right)\hfill \\ & -{\displaystyle \frac{4\mathrm{\Gamma }(3\beta +1){\xi }^{4\beta }{e}^{\delta +\pi }({\rho }^2-24\rho e^{2(\delta +\pi )}+60e^{4(\delta +\pi )})}{\mathrm{\Gamma }(\beta +1)\mathrm{\Gamma }(2\beta +1)\mathrm{\Gamma }(4\beta +1)}}-{\displaystyle \frac{1}{\mathrm{\Gamma }{(2\beta +1)}^2\mathrm{\Gamma }(5\beta +1)}}\left(8\mathrm{\Gamma }(4\beta +1){\xi }^{5\beta }{e}^{2(\delta +\pi )}\right({\rho }^2\hfill \\ & -24\rho e^{2(\delta +\pi )}+108e^{4(\delta +\pi )}\left)\right)-{\displaystyle \frac{256\mathrm{\Gamma }{(2\beta +1)}^2\mathrm{\Gamma }(6\beta +1){\xi }^{7\beta }{e}^{4(\delta +\pi )}({\rho }^2-6p{e}^{2(\delta +\pi )}+8e^{4(\delta +\pi )})}{\mathrm{\Gamma }{(\beta +1)}^4\mathrm{\Gamma }{(3\beta +1)}^2\mathrm{\Gamma }(7\beta +1)}}\hfill \\ & -{\displaystyle \frac{16\mathrm{\Gamma }(2\beta +1){\xi }^{4\beta }{e}^{3(\delta +\pi )}(10e^{2(\delta +\pi )}-3\rho )}{\mathrm{\Gamma }{(\beta +1)}^2\mathrm{\Gamma }(4\beta +1)}}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\varpi }_3(\delta ,\pi ,\xi )=& 2{\xi }^{3\beta }{e}^{2(\delta +\pi )}\left(\right(5e^{2(\delta +\pi )}-p\left)\right({\displaystyle \frac{1}{\mathrm{\Gamma }(3\beta +1)}}+{\displaystyle \frac{32^{4\beta +1}\mathrm{\Gamma }(2\beta +\frac{1}{2}){\xi }^{2\beta }{e}^{2(\delta +\pi )}}{\sqrt{\pi }\mathrm{\Gamma }(2\beta +1)\mathrm{\Gamma }(5\beta +1)}})\hfill \\ & +{\displaystyle \frac{4{\xi }^{\beta }{e}^{\delta +\pi }(2e^{2(\delta +\pi )}-\rho )(\frac{\sqrt{\pi }{4}^{-2\beta }}{\mathrm{\Gamma }(2\beta +\frac{1}{2})}+\frac{6\mathrm{\Gamma }(5\beta +1){\xi }^{2\beta }{e}^{2(\delta +\pi )}}{\mathrm{\Gamma }(3\beta +1)\mathrm{\Gamma }(6\beta +1)})}{\mathrm{\Gamma }{(\beta +1)}^2}}+{\displaystyle \frac{6\mathrm{\Gamma }(3\beta +1){\xi }^{\beta }{e}^{3(\delta +\pi )}}{\mathrm{\Gamma }(\beta +1)\mathrm{\Gamma }(2\beta +1)\mathrm{\Gamma }(4\beta +1)}}).\hfill \end{array}$$

Combining the components, the third-order approximate solution is given as

$${\psi }_{NTIM}(\delta ,\pi ,\xi )={\psi }_0(\delta ,\pi ,\xi )+{\psi }_1(\delta ,\pi ,\xi )+{\psi }_2(\delta ,\pi ,\xi )+{\psi }_3(\delta ,\pi ,\xi ),$$

(76)

and

$${\varpi }_{NTIM}(\delta ,\pi ,\xi )={\varpi }_0(\delta ,\pi ,\xi )+{\varpi }_1(\delta ,\pi ,\xi )+{\varpi }_2(\delta ,\pi ,\xi )+{\varpi }_3(\delta ,\pi ,\xi ).$$

(77)

4.4. OAFM Solution

We consider linear and nonlinear terms in Equations (26) and (27) as

$$\overrightarrow{\chi }(\psi (\delta ,\pi ,\xi ))=D_{\xi }^{\beta }(\psi (\delta ,\pi ,\xi ))$$

$$\overrightarrow{\chi }(\varpi (\delta ,\pi ,\xi ))=D_{\xi }^{\beta }(\varpi (\delta ,\pi ,\xi ))$$

$$\ddot{\zeta }(\psi (\delta ,\pi ,\xi ))=-\psi (\delta ,\pi ,\xi ){\partial }_{\delta }(\psi (\delta ,\pi ,\xi ))-\psi (\delta ,\pi ,\xi ){\partial }_{\pi }(\psi (\delta ,\pi ,\xi ))+\sigma \left[{\partial }_{\delta ,\delta }\right(\psi (\delta ,\pi ,\xi ))+{\partial }_{\pi ,\pi }(\psi (\delta ,\pi ,\xi )\left)\right]+\rho .$$

(78)

$$\ddot{\zeta }(\varpi (\delta ,\pi ,\xi ))=-\psi (\delta ,\pi ,\xi ){\partial }_{\delta }(\varpi (\delta ,\pi ,\xi ))-\varpi (\delta ,\pi ,\xi ){\partial }_{\pi }(\varpi (\delta ,\pi ,\xi ))+\sigma \left[{\partial }_{\delta ,\delta }\right(\varpi (\delta ,\pi ,\xi ))+{\partial }_{\pi ,\pi }(\varpi (\delta ,\pi ,\xi )\left)\right]-\rho .$$

(79)

The initial approximate is obtained from Equation (9):

$$D_{\xi }^{\beta }\left({\psi }_0(\delta ,\pi ,\xi )\right)=0.$$

(80)

$$D_{\xi }^{\beta }\left({\varpi }_0(\delta ,\pi ,\xi )\right)=0.$$

(81)

Apply the inverse operator on Equations (80) and (81) and we have the following solutions:

$${\psi }_0(\delta ,\pi ,\xi )=-e^{(\delta +\pi )}.$$

(82)

$${\varpi }_0(\delta ,\pi ,\xi )=e^{(\delta +\pi )}.$$

(83)

By putting Equations (82) and (83) in Equations (78) and (79), respectively, we get

$$\ddot{\zeta }\left({\psi }_0(\delta ,\pi ,\xi )\right)=\rho -2e^{2(\delta +\pi )}.$$

(84)

$$\ddot{\zeta }\left({\varpi }_0(\delta ,\pi ,\xi )\right)=-\rho .$$

(85)

The first approximation ${\psi }_1(\delta ,\pi ,\xi )$ and ${\varpi }_1(\delta ,\pi ,\xi )$ are as follows:

$$D_{\xi }^{\beta }\left({\psi }_1(\delta ,\pi ,\xi )\right)+{\mathrm{\Pi }}_1\{{\psi }_0(\delta ,\pi ,\xi ),{\overline{\omega }}_i\}N\left\{{\psi }_0(\delta ,\pi ,\xi )\right\}+{\mathrm{\Pi }}_2\{{\psi }_0(\delta ,\pi ,\xi ),{\overline{\omega }}_i\}.$$

(86)

$$D_{\xi }^{\beta }\left({\varpi }_1(\delta ,\pi ,\xi )\right)+{\mathrm{\Pi }}_3\{{\varpi }_0(\delta ,\pi ,\xi ),{\overline{\omega }}_i\}N\left\{{\varpi }_0(\delta ,\pi ,\xi )\right\}+{\mathrm{\Pi }}_4\{{\varpi }_0(\delta ,\pi ,\xi ),{\overline{\omega }}_i\}.$$

(87)

According to the nonlinear operator, we choose ${\mathrm{\Pi }}_1$, ${\mathrm{\Pi }}_2$, ${\mathrm{\Pi }}_3$, and ${\mathrm{\Pi }}_4$ as

$$\begin{array}{ccc}\hfill {\mathrm{\Pi }}_1& =& {\overline{\omega }}_4{\left(e^{\delta +\pi }\right)}^4+{\overline{\omega }}_3{(-e^{\delta +\pi })}^3\hfill \\ \hfill {\mathrm{\Pi }}_2& =& {\overline{\omega }}_2{\left(e^{\delta +\pi }\right)}^2-{\overline{\omega }}_1{e}^{\delta +\pi }\hfill \\ \hfill {\mathrm{\Pi }}_3& =& {\overline{\omega }}_8{\left(e^{\delta +\pi }\right)}^4+{\overline{\omega }}_7{(-e^{\delta +\pi })}^3\hfill \\ \hfill {\mathrm{\Pi }}_4& =& {\overline{\omega }}_6{\left(e^{\delta +\pi }\right)}^2-{\overline{\omega }}_5{e}^{\delta +\pi }\hfill \end{array}$$

Putting ${\mathrm{\Pi }}_1$, ${\mathrm{\Pi }}_2$, and Equation (84) into Equation (86), we get the first approximation of $\psi (\delta ,\pi ,\xi )$ as

$${\psi }_1(\delta ,\pi ,\xi )={\displaystyle \frac{{\xi }^{\beta }\left(e^{3(\delta +\pi )}\right({\overline{\omega }}_4{e}^{\delta +\pi }-{\overline{\omega }}_3\left)\right(\rho -2e^{2(\delta +\pi )})+{\overline{\omega }}_1(-e^{\delta +\pi })+{\overline{\omega }}_2{e}^{2(\delta +\pi )})}{\beta \mathrm{\Gamma }(\beta )}}.$$

(88)

Putting ${\mathrm{\Pi }}_3$, ${\mathrm{\Pi }}_4$, and Equation (85) into Equation (87), we get the first approximation of $\varpi (\delta ,\pi ,\xi )$ as

$${\varpi }_1(\delta ,\pi ,\xi )={\displaystyle \frac{t^{\beta }{e}^{\delta +\pi }\left(e^{\delta +\pi }\right({\overline{\omega }}_7\rho e^{\delta +\pi }-{\overline{\omega }}_8\rho e^{2(\delta +\pi )}+{\overline{\omega }}_6)-{\overline{\omega }}_5)}{\beta \mathrm{\Gamma }(\beta )}}.$$

(89)

We get the first-order approximate solution of $\psi (\delta ,\pi ,\xi )$ and $\varpi (\delta ,\pi ,\xi )$ as follows:

$${\psi }_{OAFM}(\delta ,\pi ,\xi )={\psi }_0(\delta ,\pi ,\xi )+{\psi }_1(\delta ,\pi ,\xi ).$$

(90)

$${\psi }_{OAFM}(\delta ,\pi ,\xi )={\displaystyle \frac{{\xi }^{\beta }\left(e^{3(\delta +\pi )}\right({\overline{\omega }}_4{e}^{\delta +\pi }-{\overline{\omega }}_3\left)\right(\rho -2e^{2(\delta +\pi )})+{\overline{\omega }}_1(-e^{\delta +\pi })+{\overline{\omega }}_2{e}^{2(\delta +\pi )})}{\beta \mathrm{\Gamma }(\beta )}}-e^{\delta +\pi }.$$

(91)

$${\varpi }_{OAFM}(\delta ,\pi ,\xi )={\varpi }_0(\delta ,\pi ,\xi )+{\varpi }_1(\delta ,\pi ,\xi ).$$

(92)

$${\varpi }_{OAFM}(\delta ,\pi ,\xi )=e^{\delta +\pi }(1-{\displaystyle \frac{{\xi }^{\beta }\left(e^{\delta +\pi }\right(\rho e^{\delta +\pi }({\overline{\omega }}_8{e}^{\delta +\pi }-{\overline{\omega }}_7)-{\overline{\omega }}_6)+{\overline{\omega }}_5)}{\beta \mathrm{\Gamma }(\beta )}}).$$

(93)

To find the values of unknown parameters ${\overline{\omega }}_1$, ${\overline{\omega }}_2$, ${\overline{\omega }}_3$, and ${\overline{\omega }}_4$ for $\psi (\delta ,\pi ,\xi )$, and ${\overline{\omega }}_5$, ${\overline{\omega }}_6$, ${\overline{\omega }}_7$, and ${\overline{\omega }}_8$ for $\varpi (\delta ,\pi ,\xi )$, we used the Least Squares method:

$$\begin{array}{ccc}\hfill {\overline{\omega }}_1& =& -0.405482\hfill \\ \hfill {\overline{\omega }}_2& =& 0.00537914\hfill \\ \hfill {\overline{\omega }}_3& =& 6.217630561289015\times {10}^{-11}\hfill \\ \hfill {\overline{\omega }}_4& =& 0\hfill \\ \hfill {\overline{\omega }}_5& =& 0.0391033\hfill \\ \hfill {\overline{\omega }}_6& =& 0.000171358\hfill \\ \hfill {\overline{\omega }}_7& =& 2.07522567006846\times {10}^{-7}\hfill \\ \hfill {\overline{\omega }}_8& =& 1.0686888996281255\times {10}^{-9}\hfill \end{array}$$

5. Results and Discussions

Unlike earlier approaches such as the homotopy analysis method or Adomian decomposition method, our use of the NTIM and OAFM exhibits faster convergence and improved accuracy, particularly evident in

Table 1. The absolute error of NTIM and OAFM solution of $\psi (\delta ,\pi ,\xi )$ for $\beta =1$, $\xi =0.001$, $\rho =0$, and $\pi =0.1$.

$\mathit{\delta }$	$\mathit{\xi }$	${\mathit{\psi }}_{\mathit{NTIM}}(\mathit{\delta },\mathit{\pi },\mathit{\xi })$	${\mathit{\psi }}_{\mathit{OAFM}}(\mathit{\delta },\mathit{\pi },\mathit{\xi })$	${\mathit{\psi }}_{\mathit{Exact}}(\mathit{\delta },\mathit{\pi },\mathit{\xi })$	$\mathit{NTIM}\mathit{Error}$	$\mathit{OAFM}\mathit{Error}$
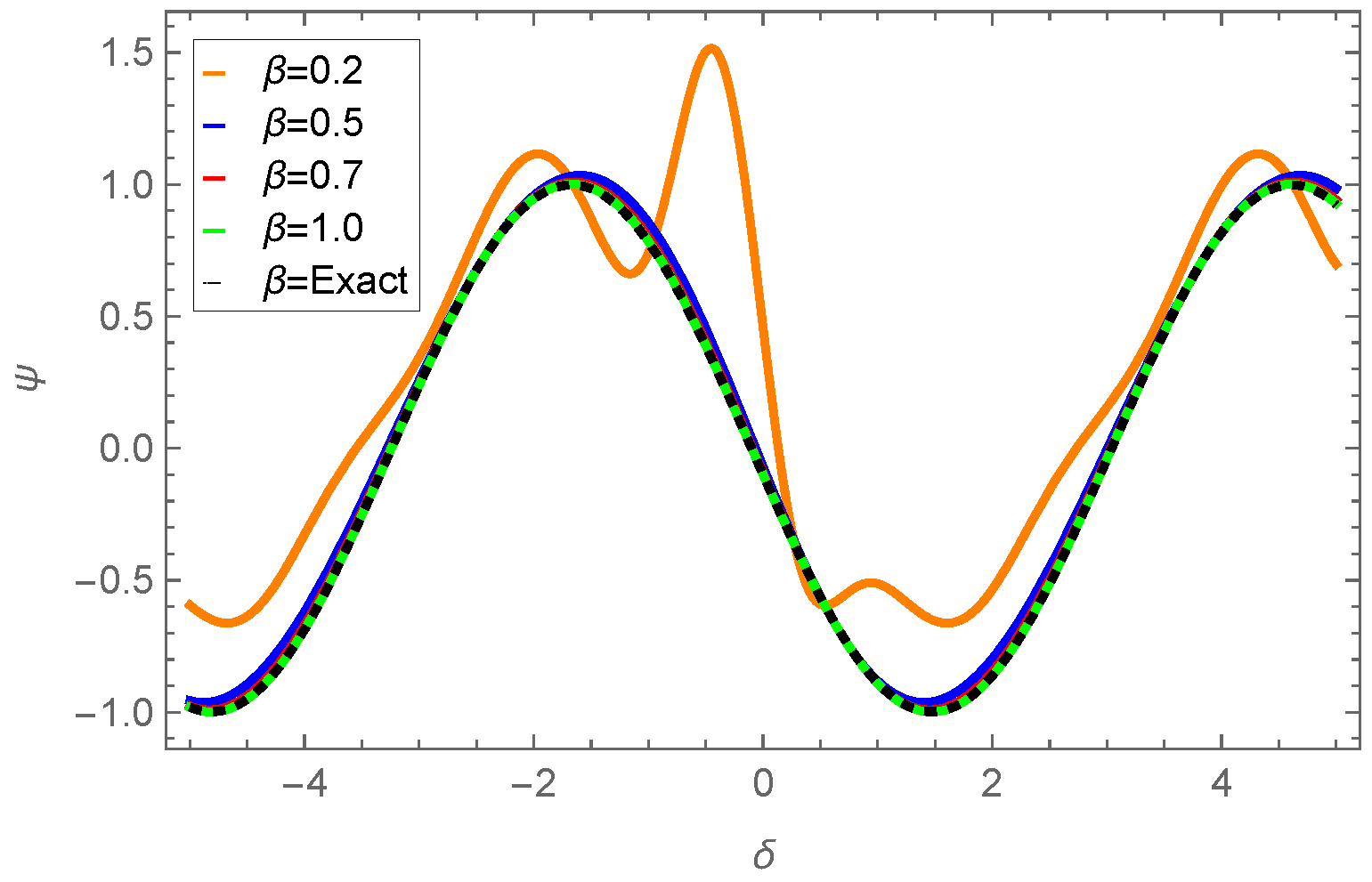
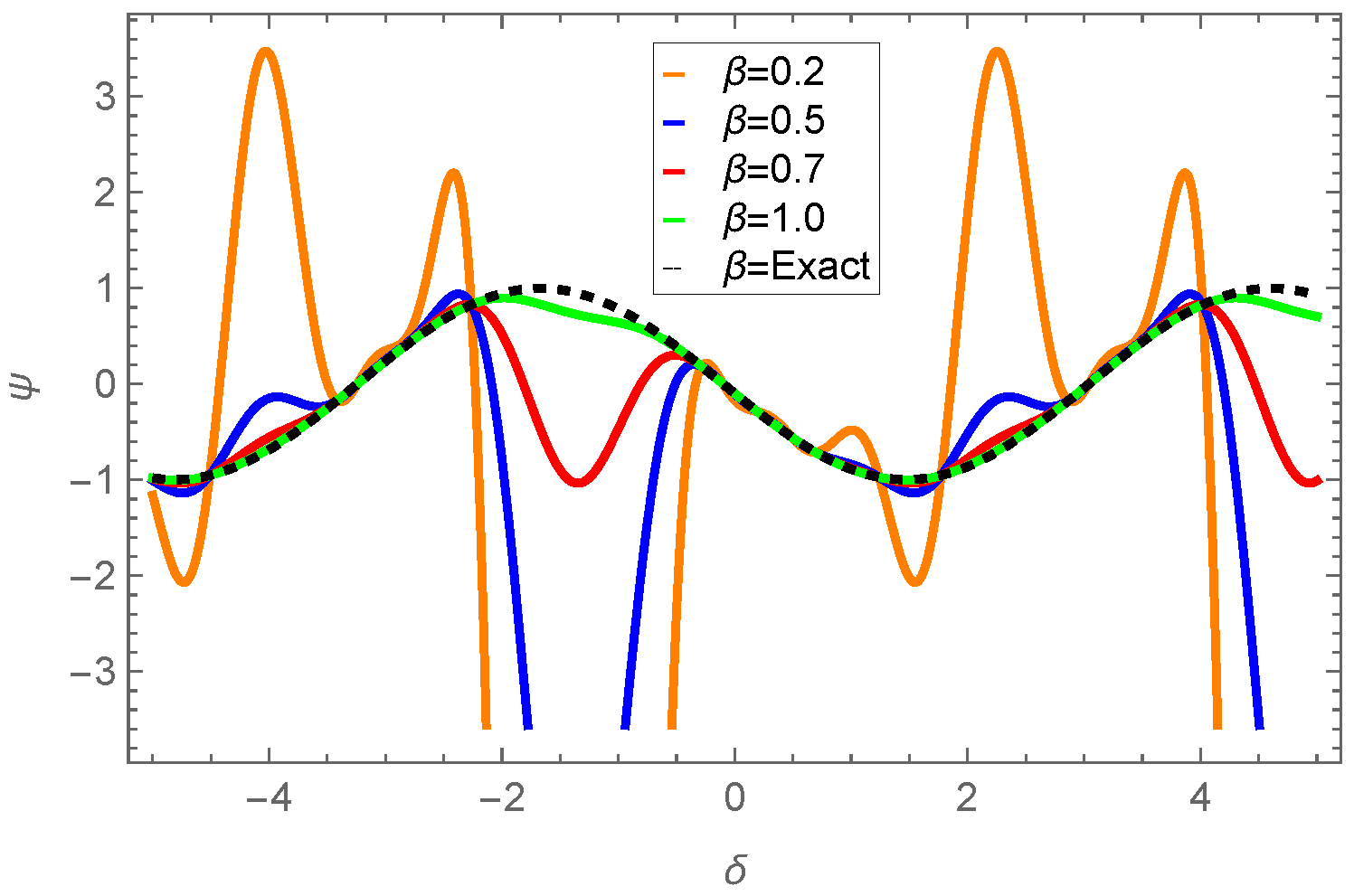
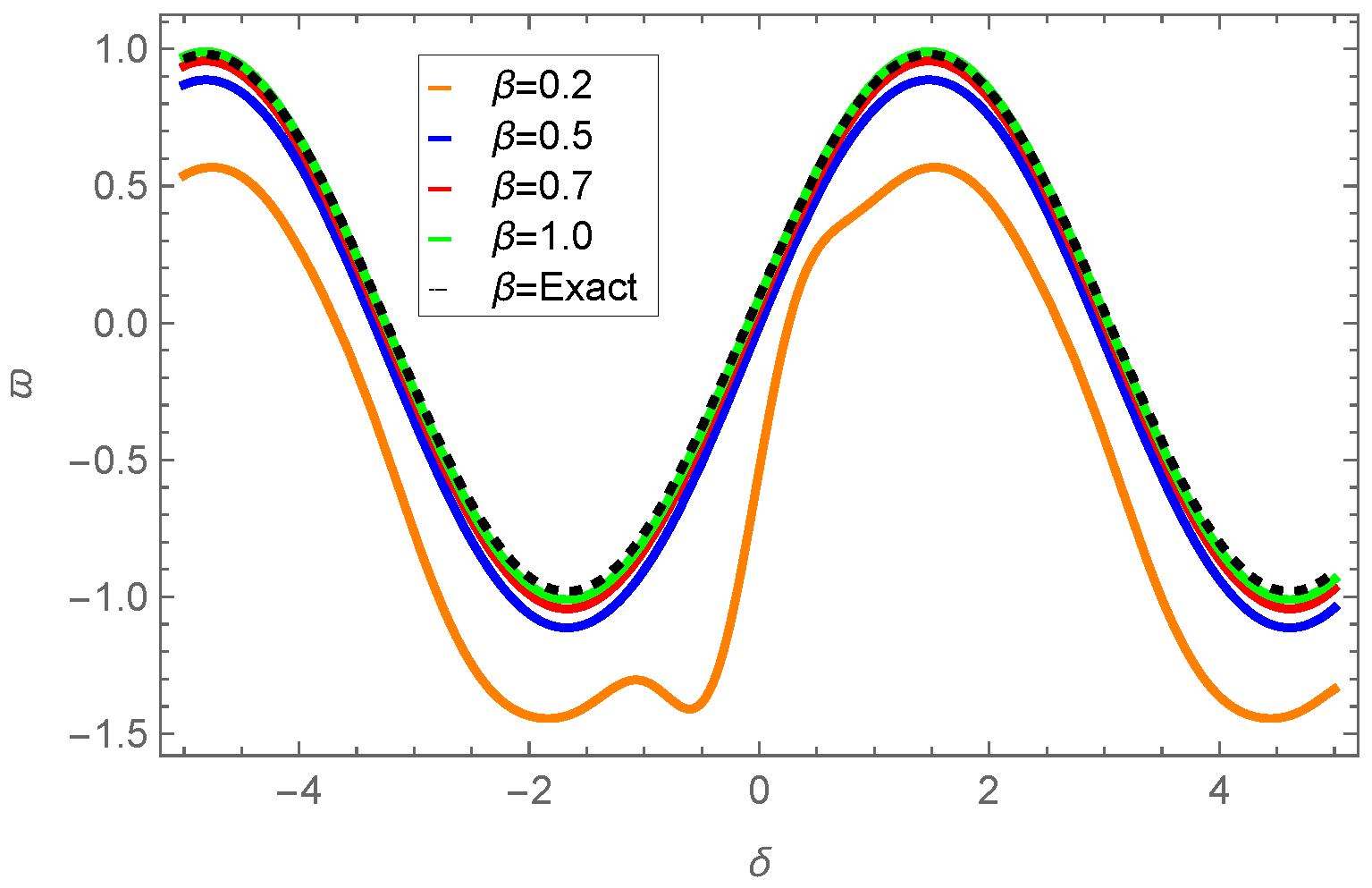
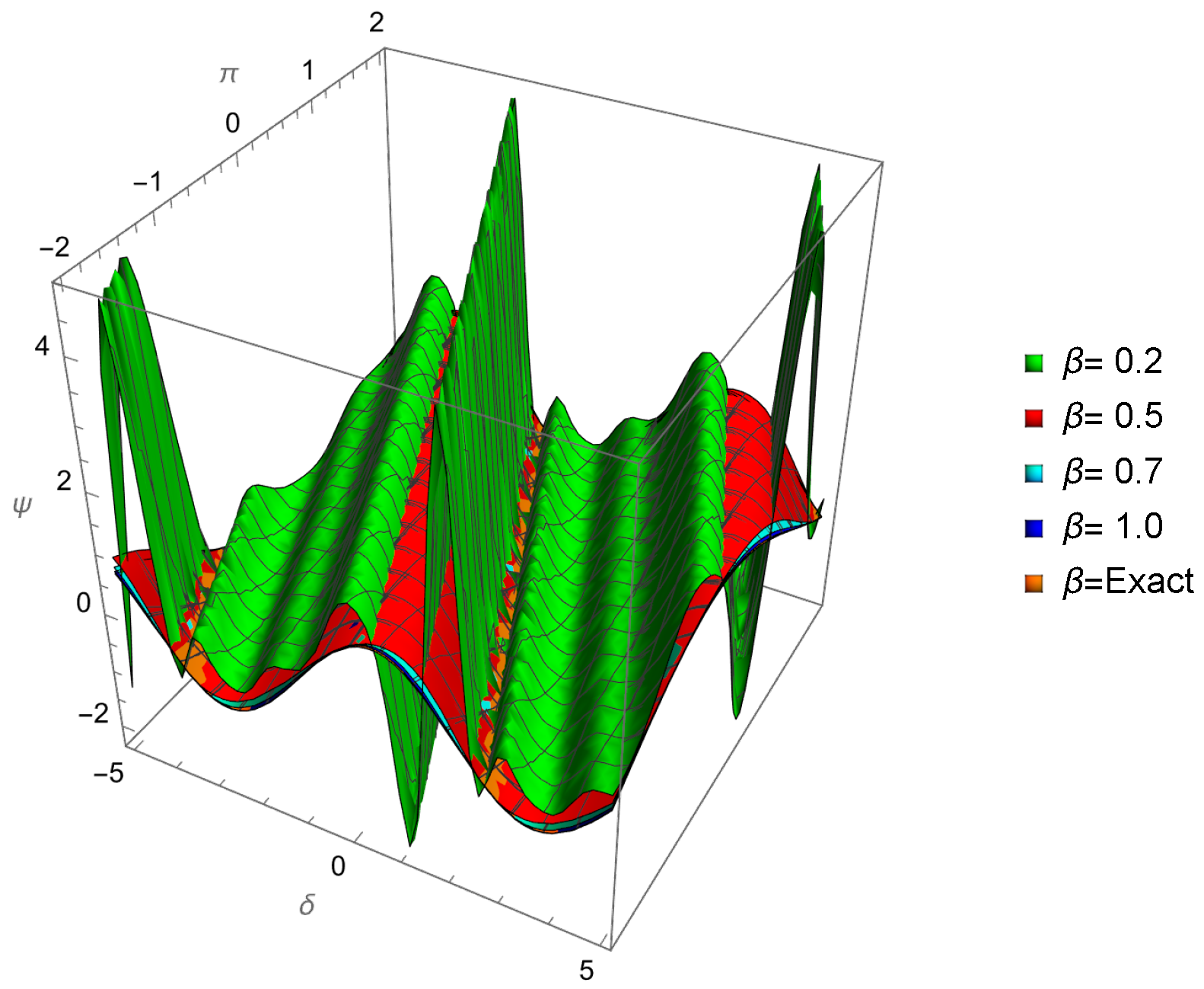
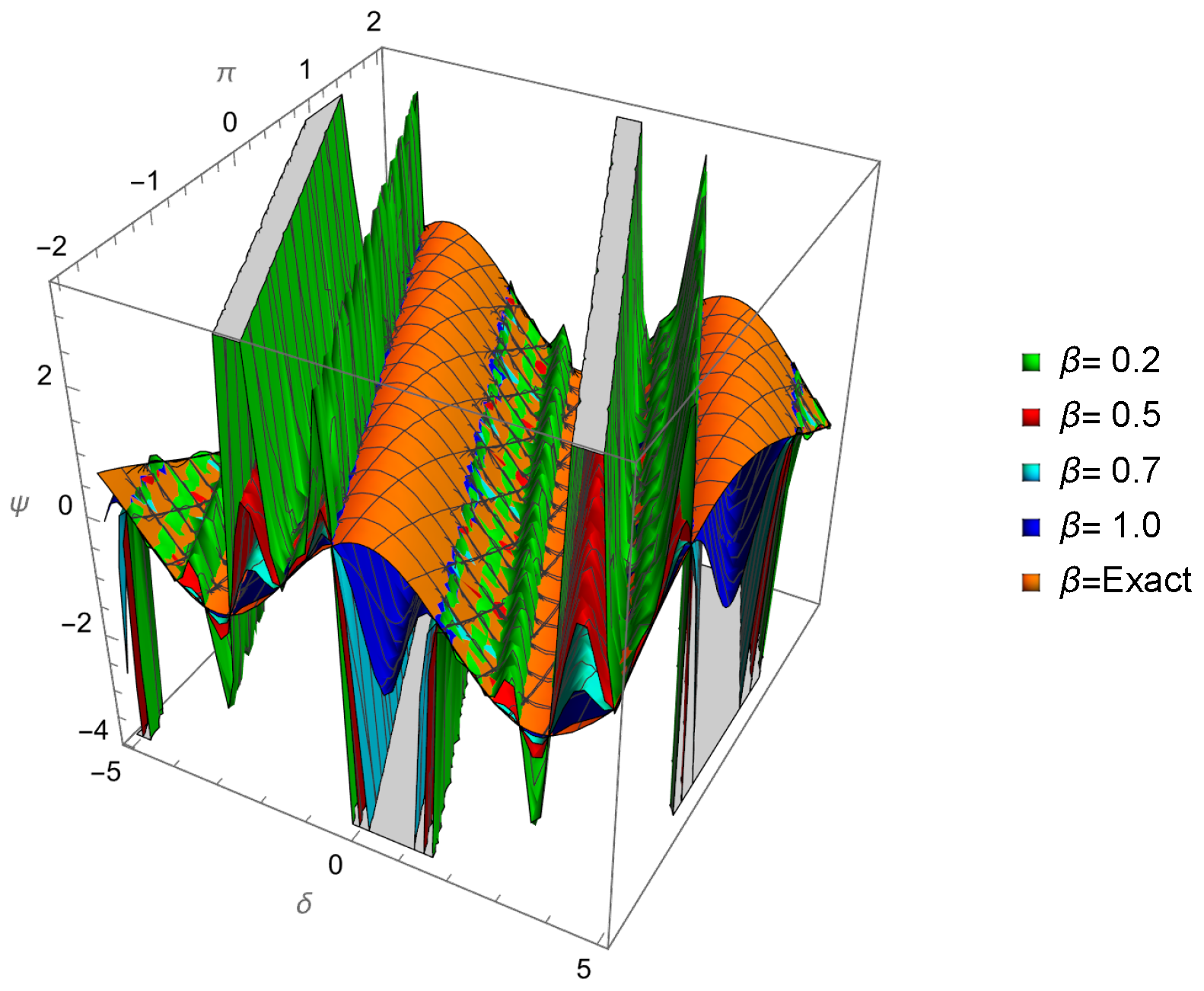
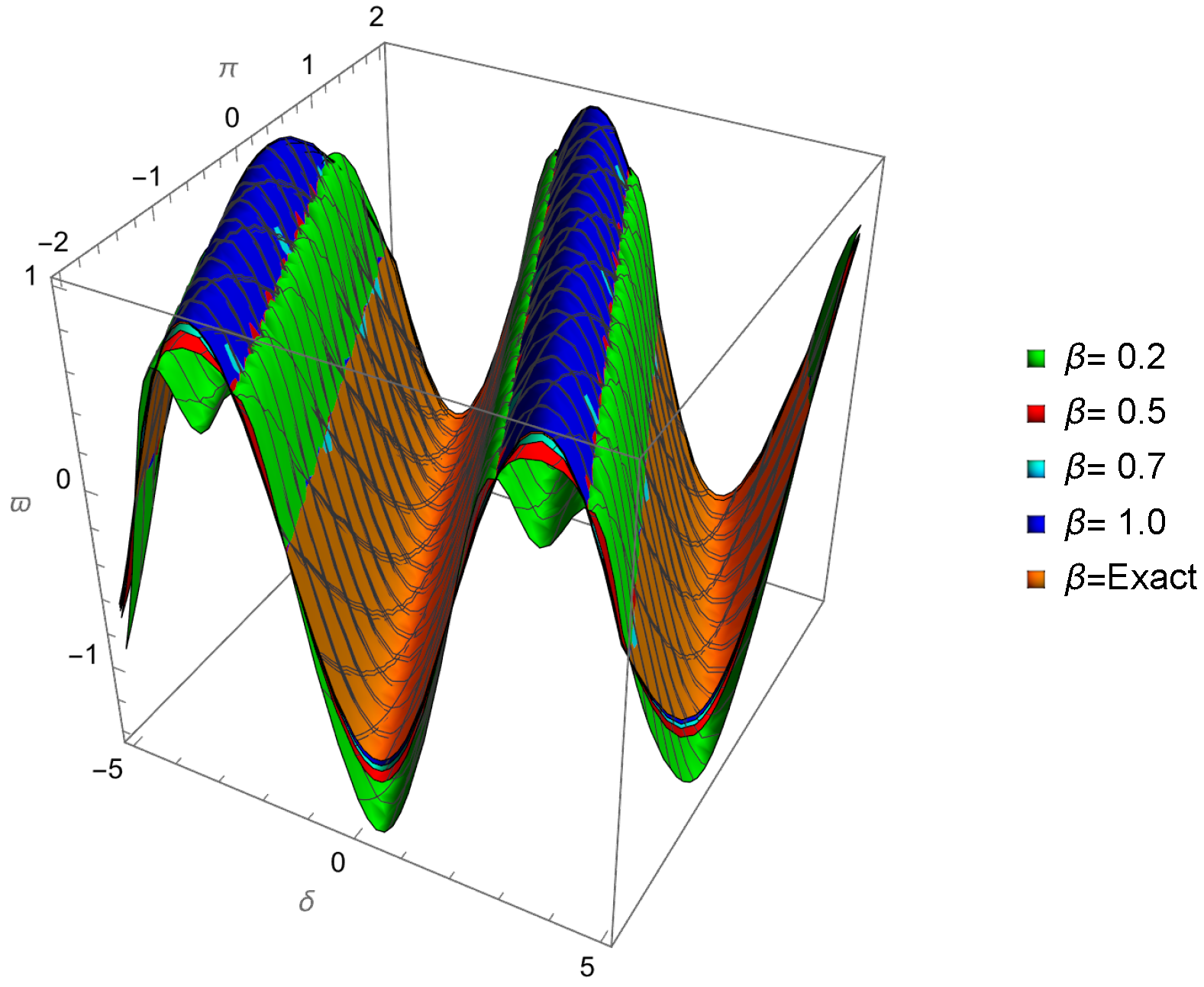
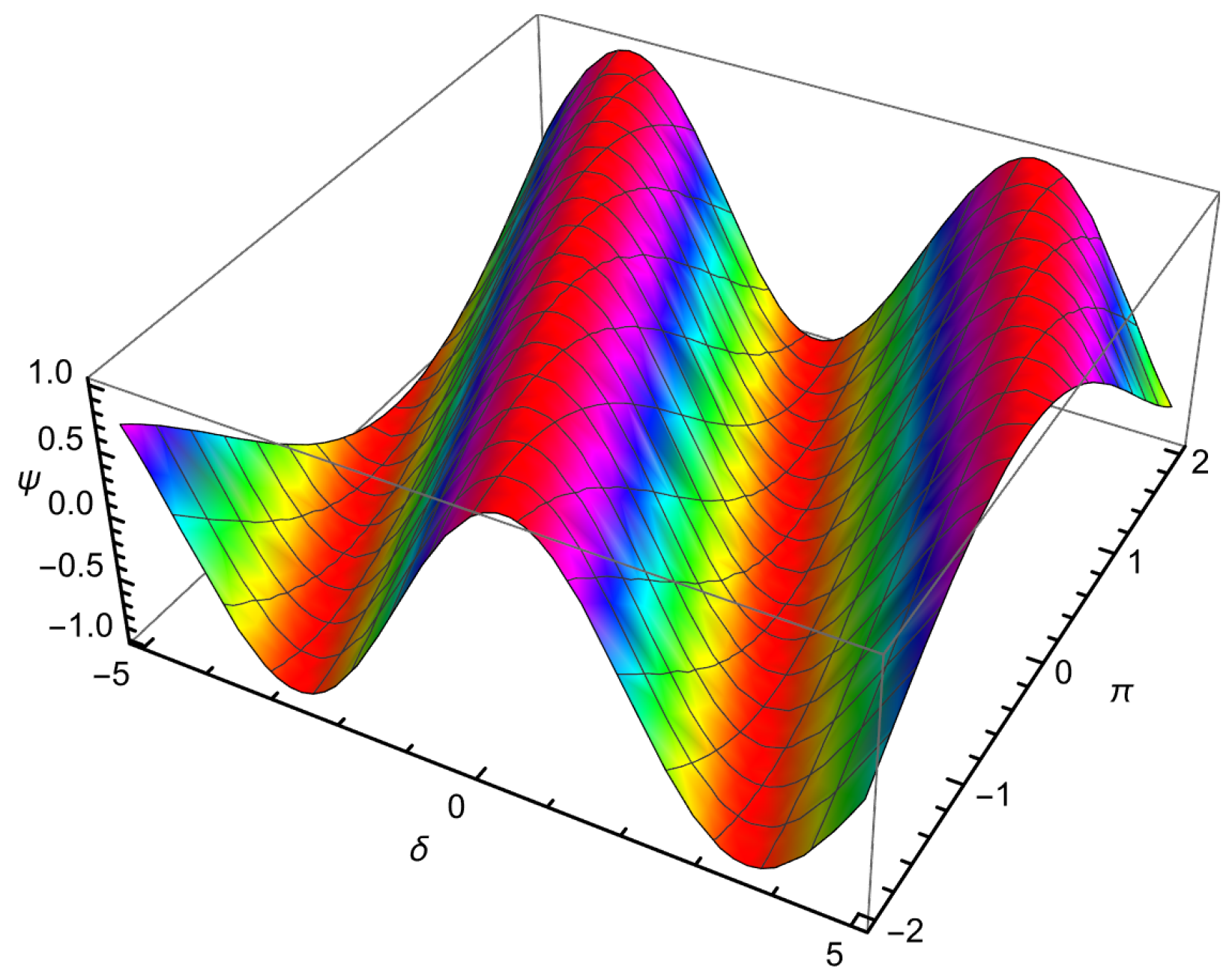
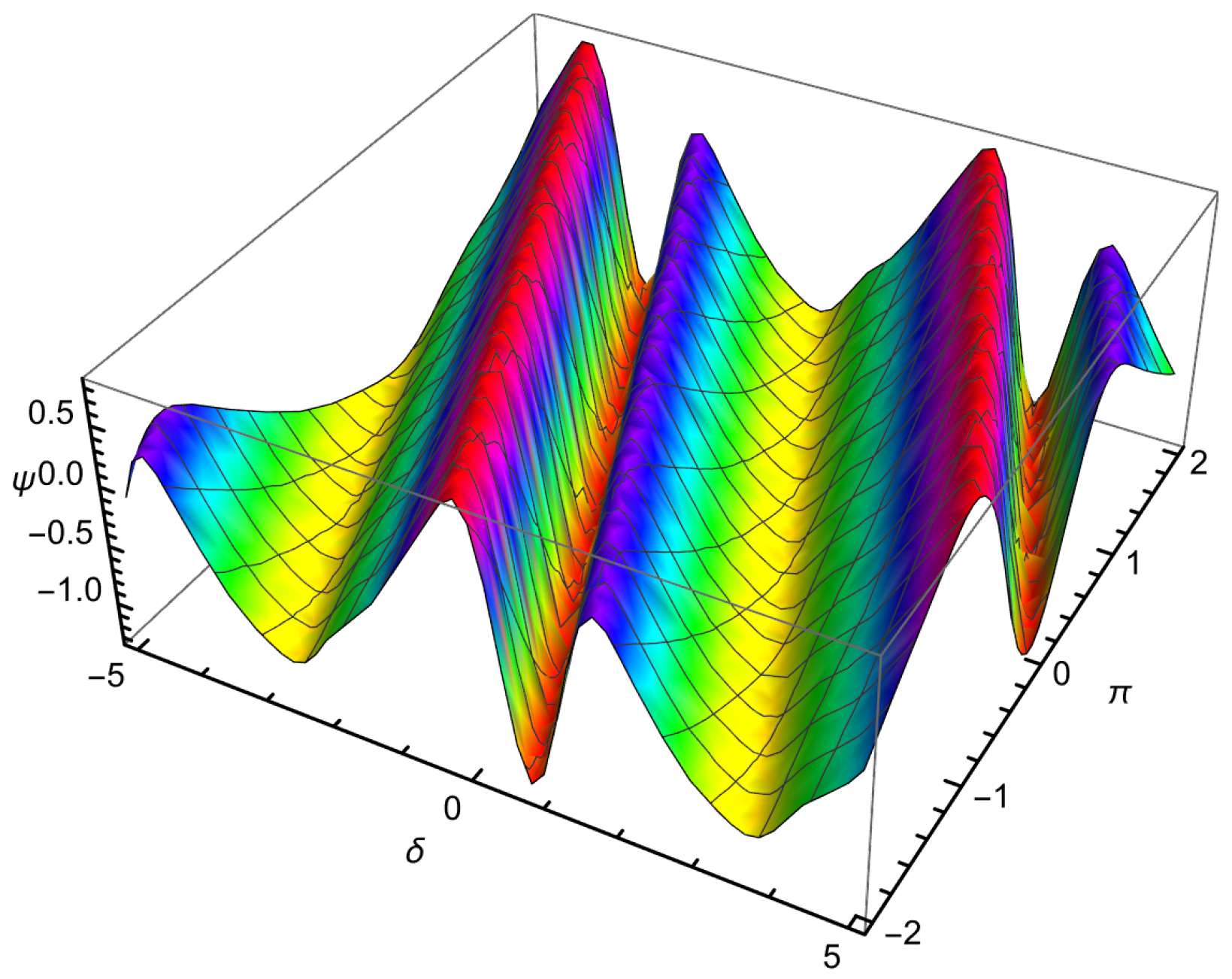
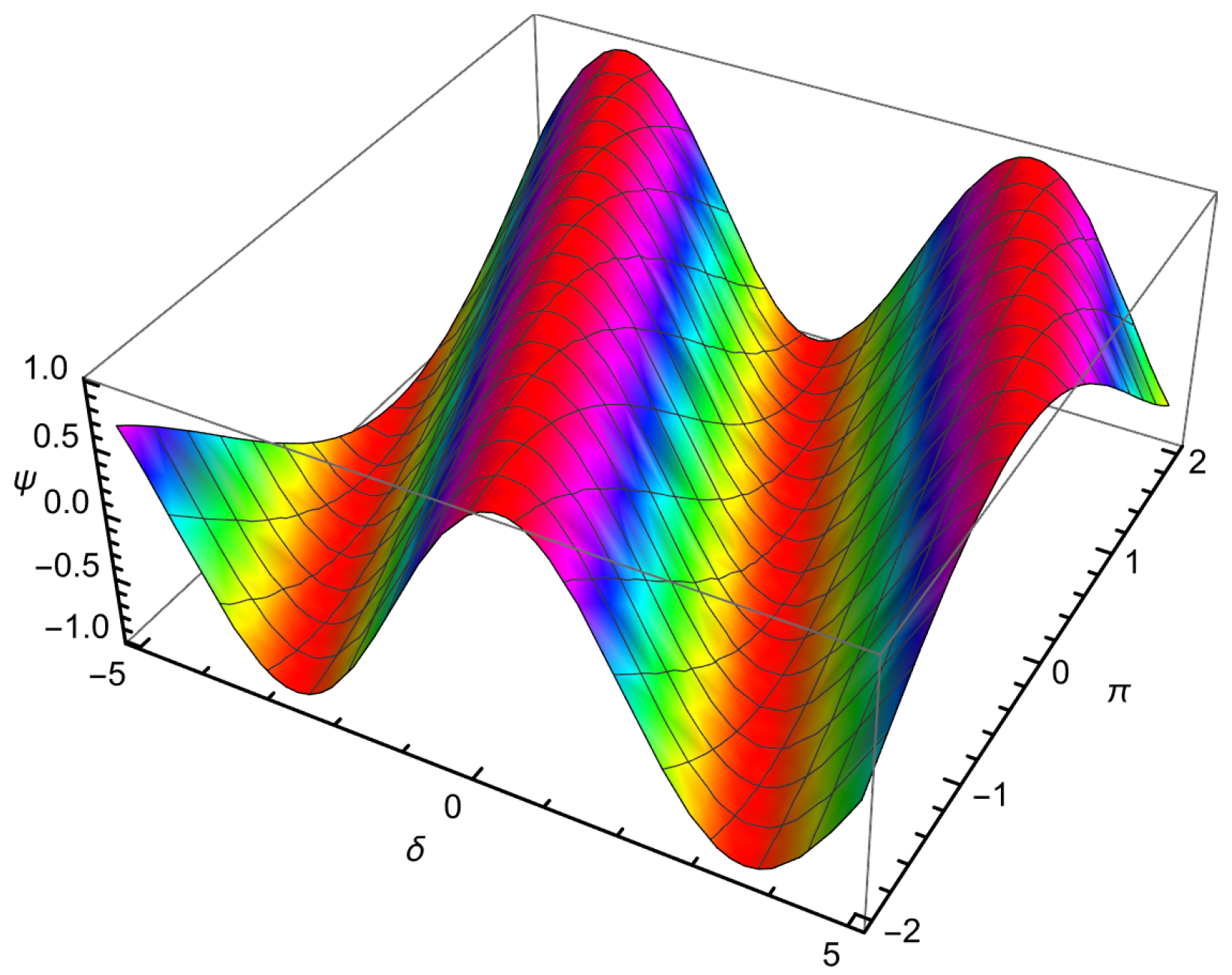
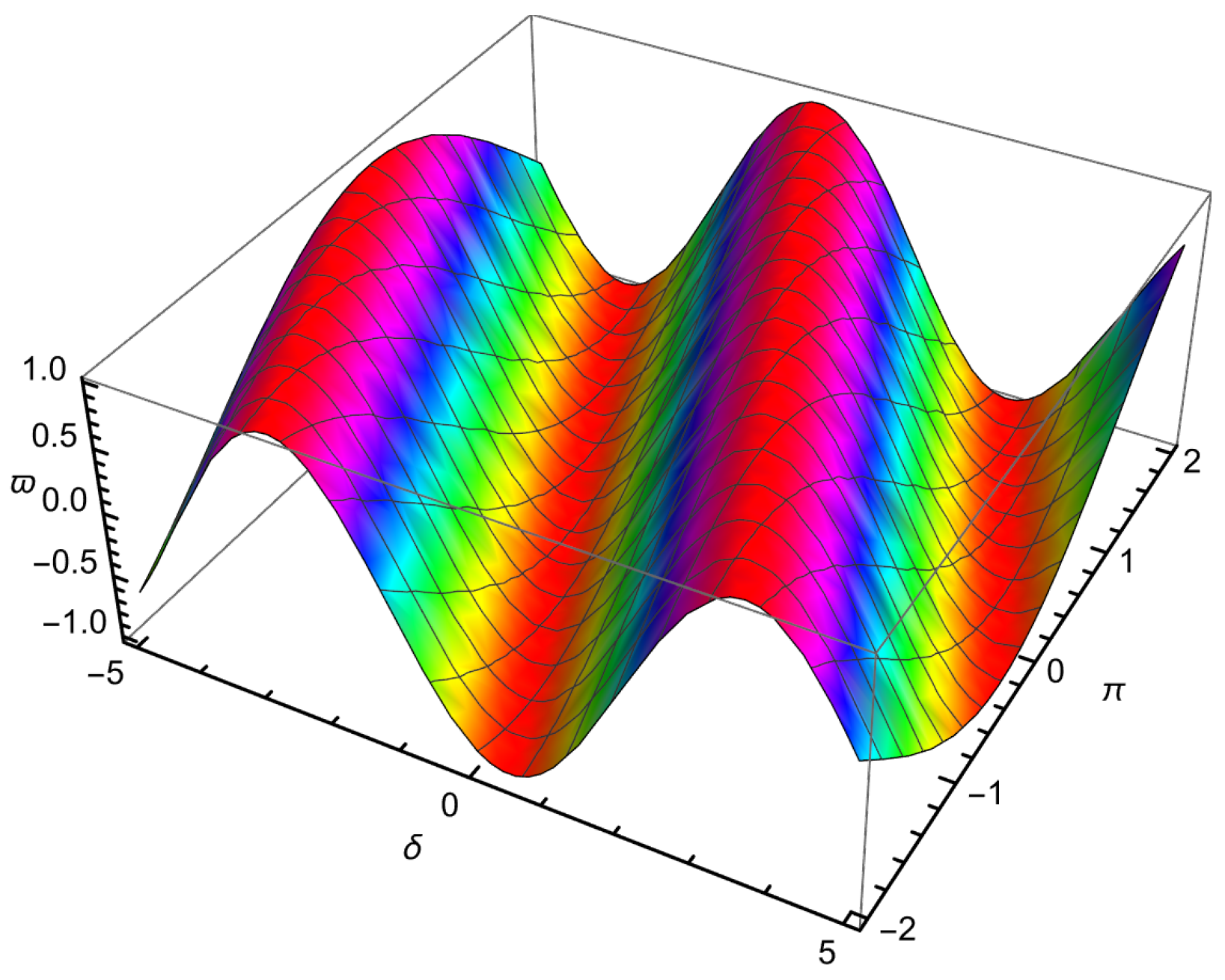
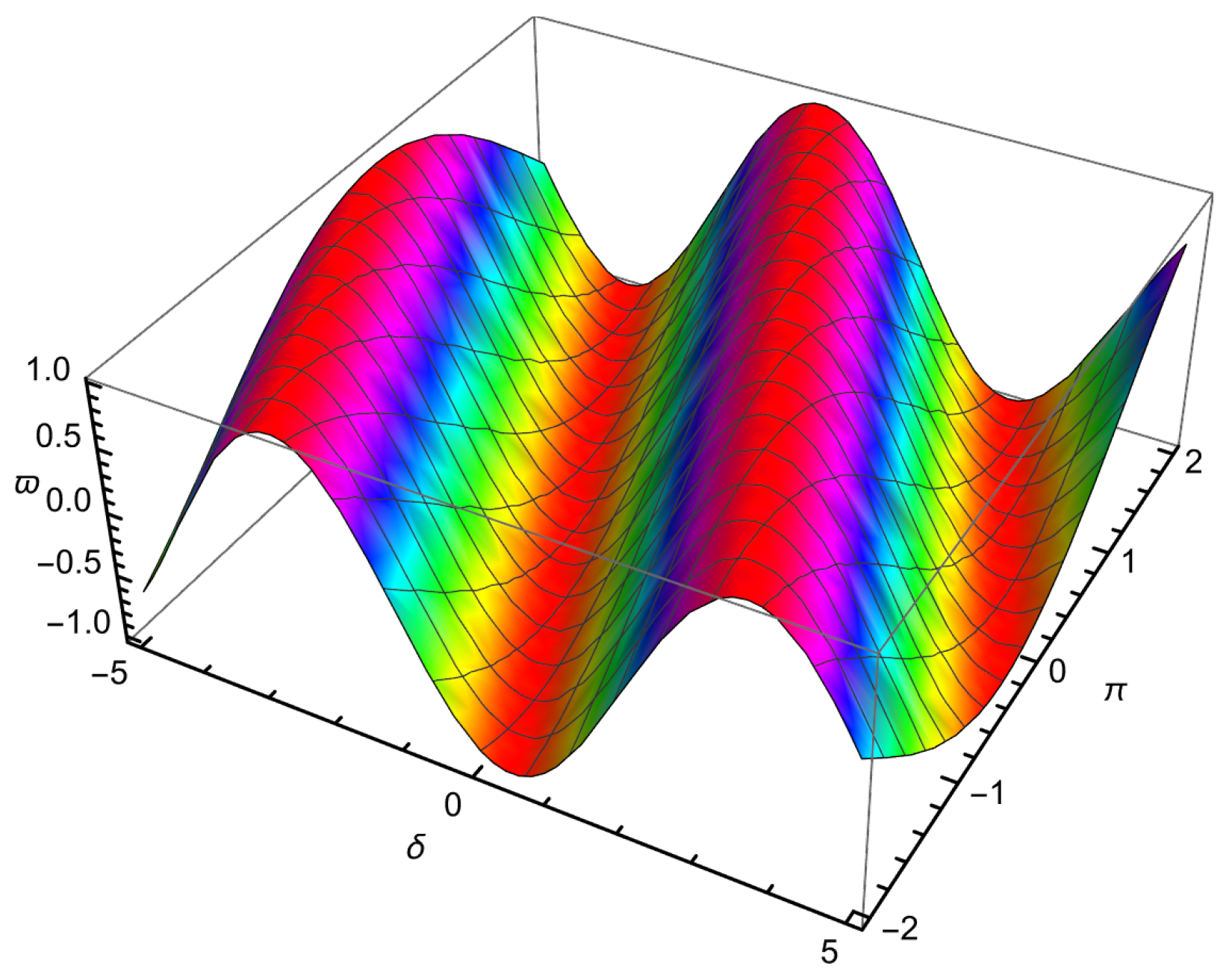
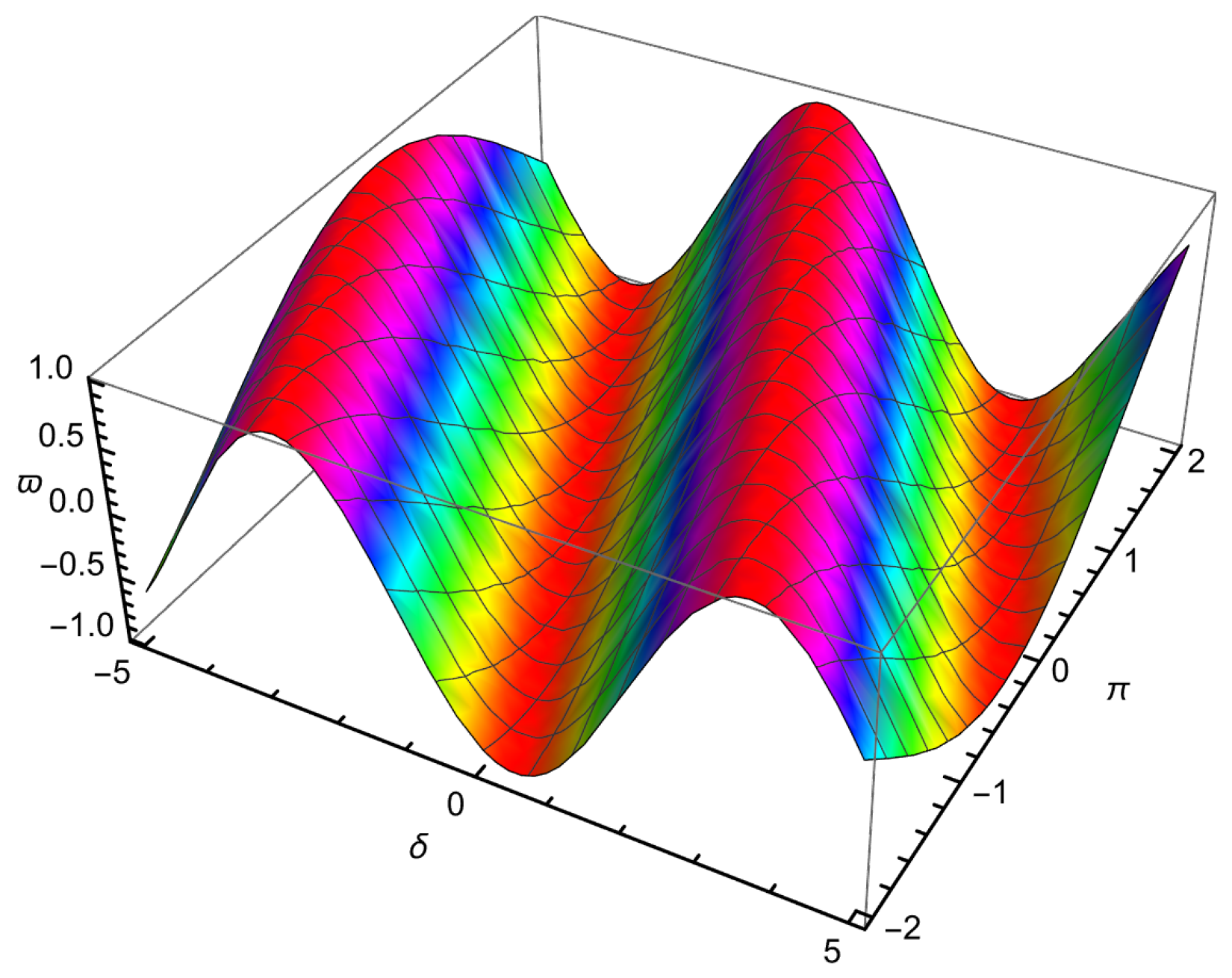
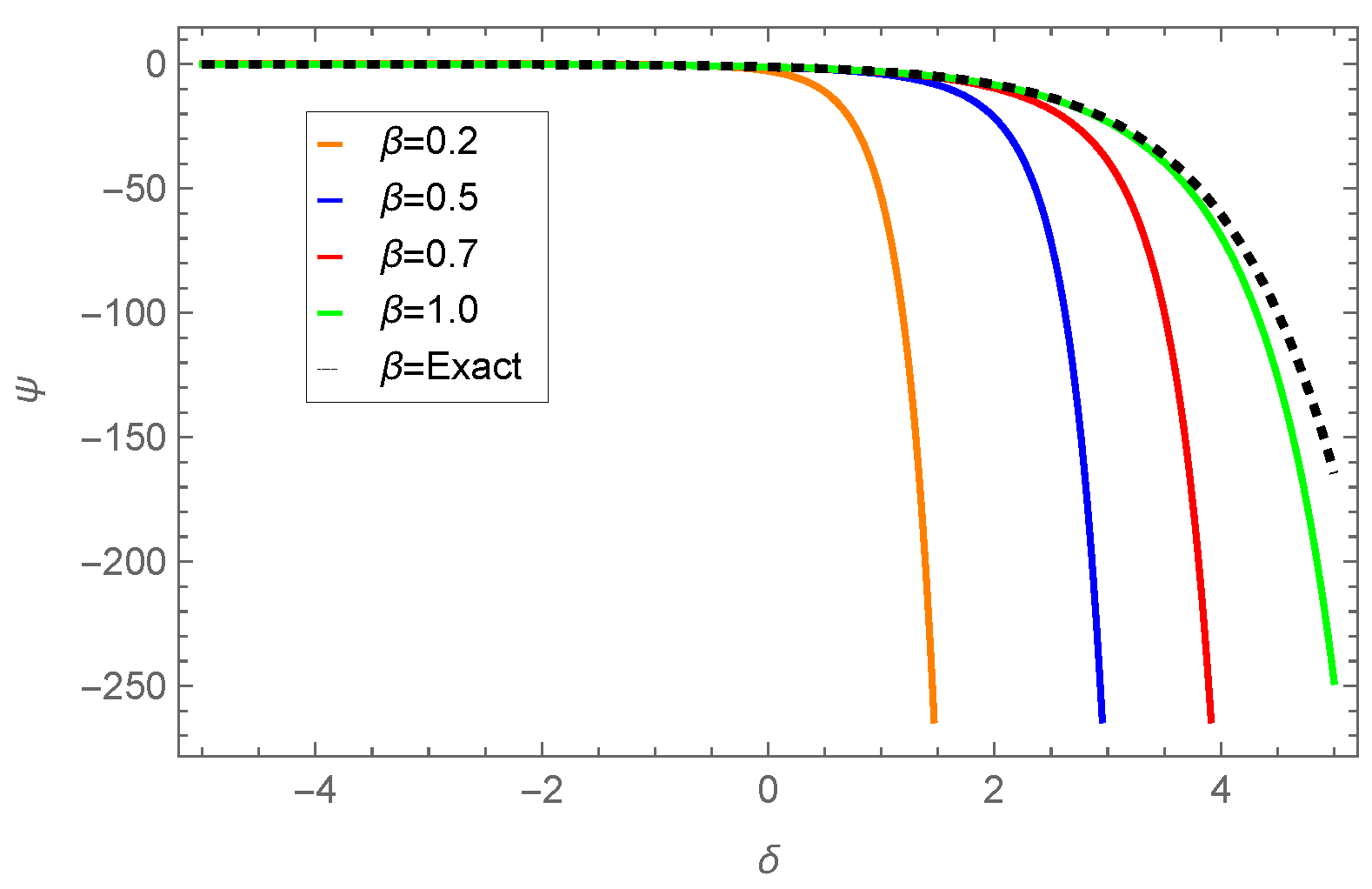
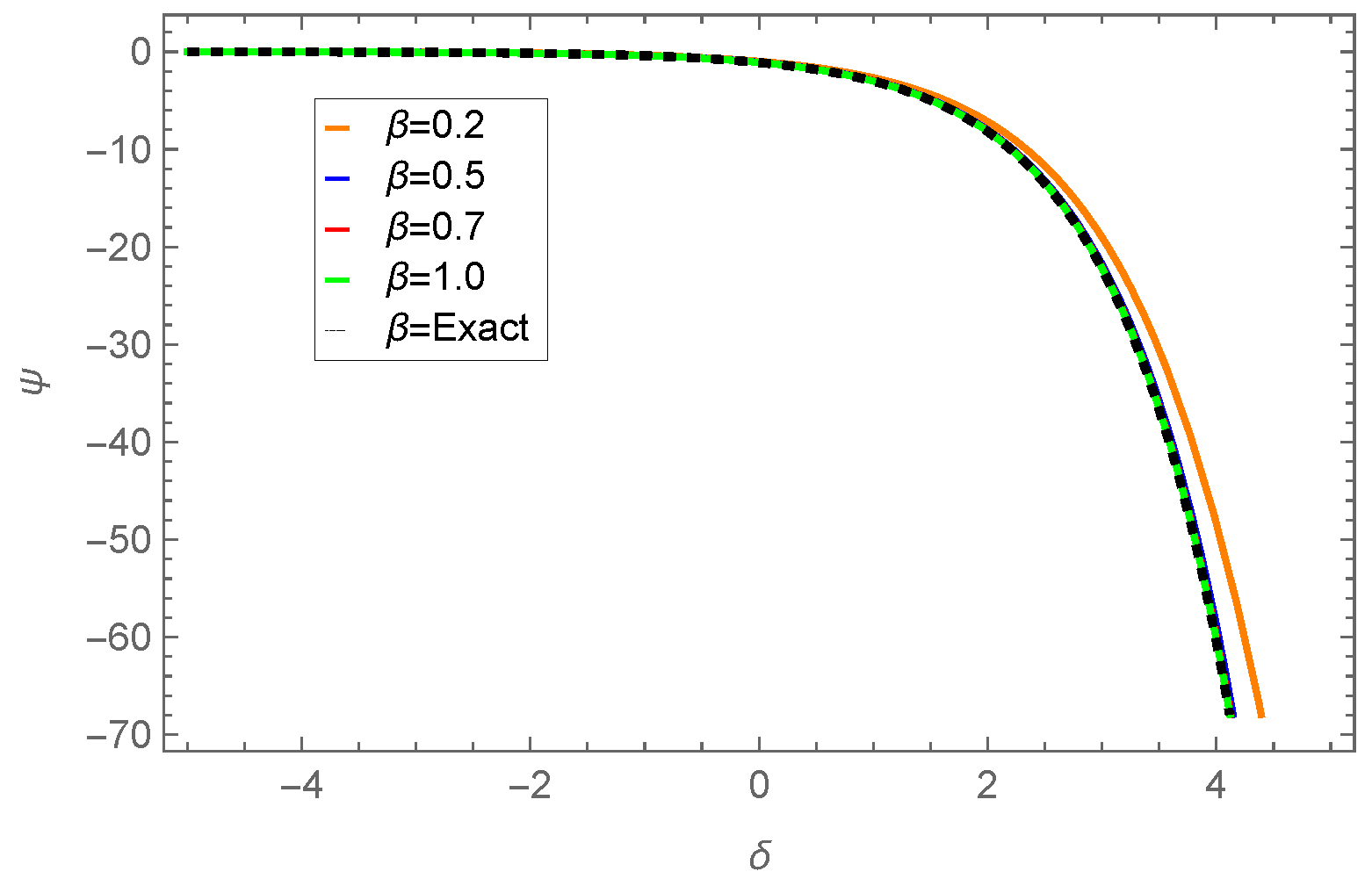
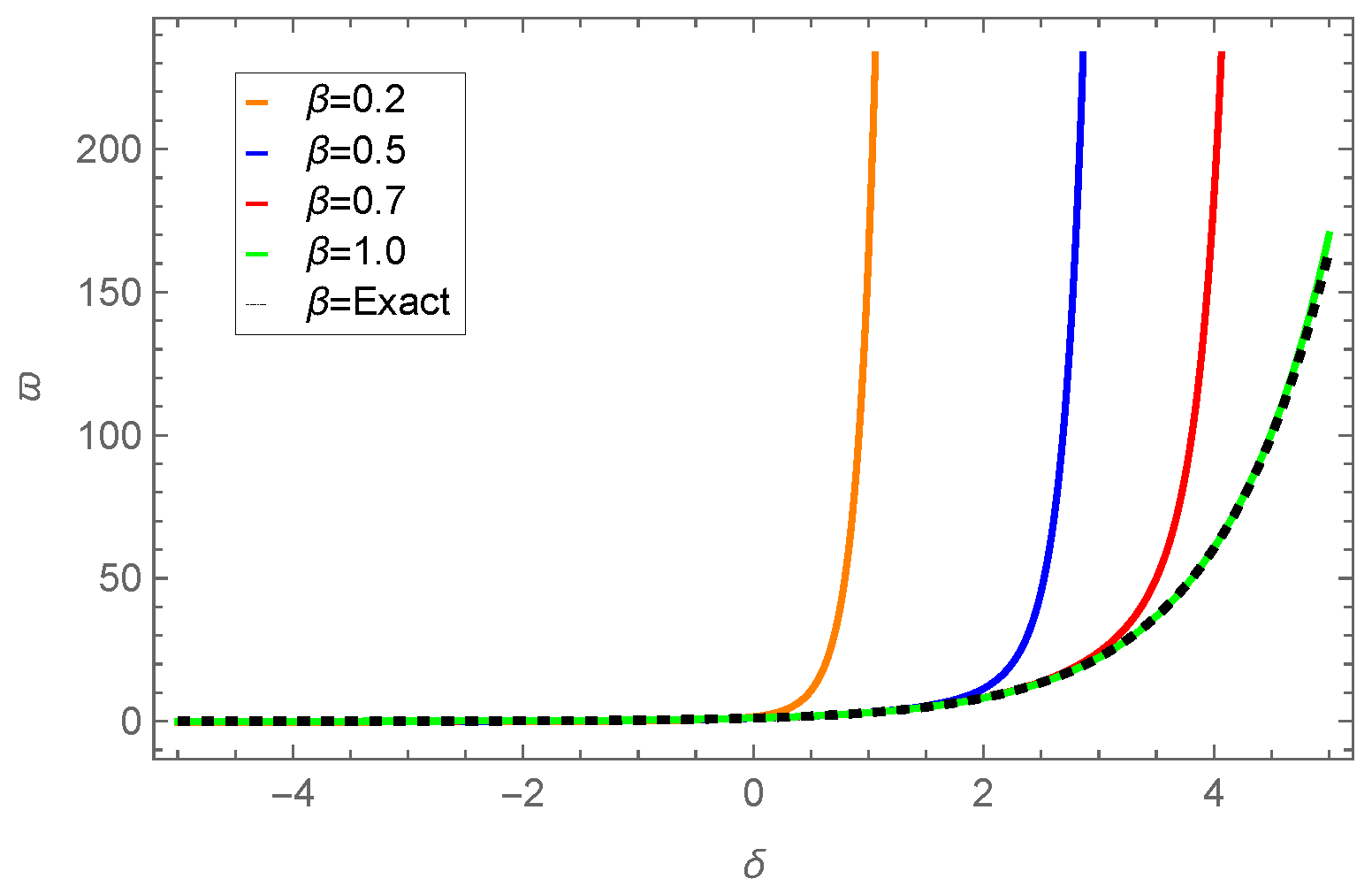
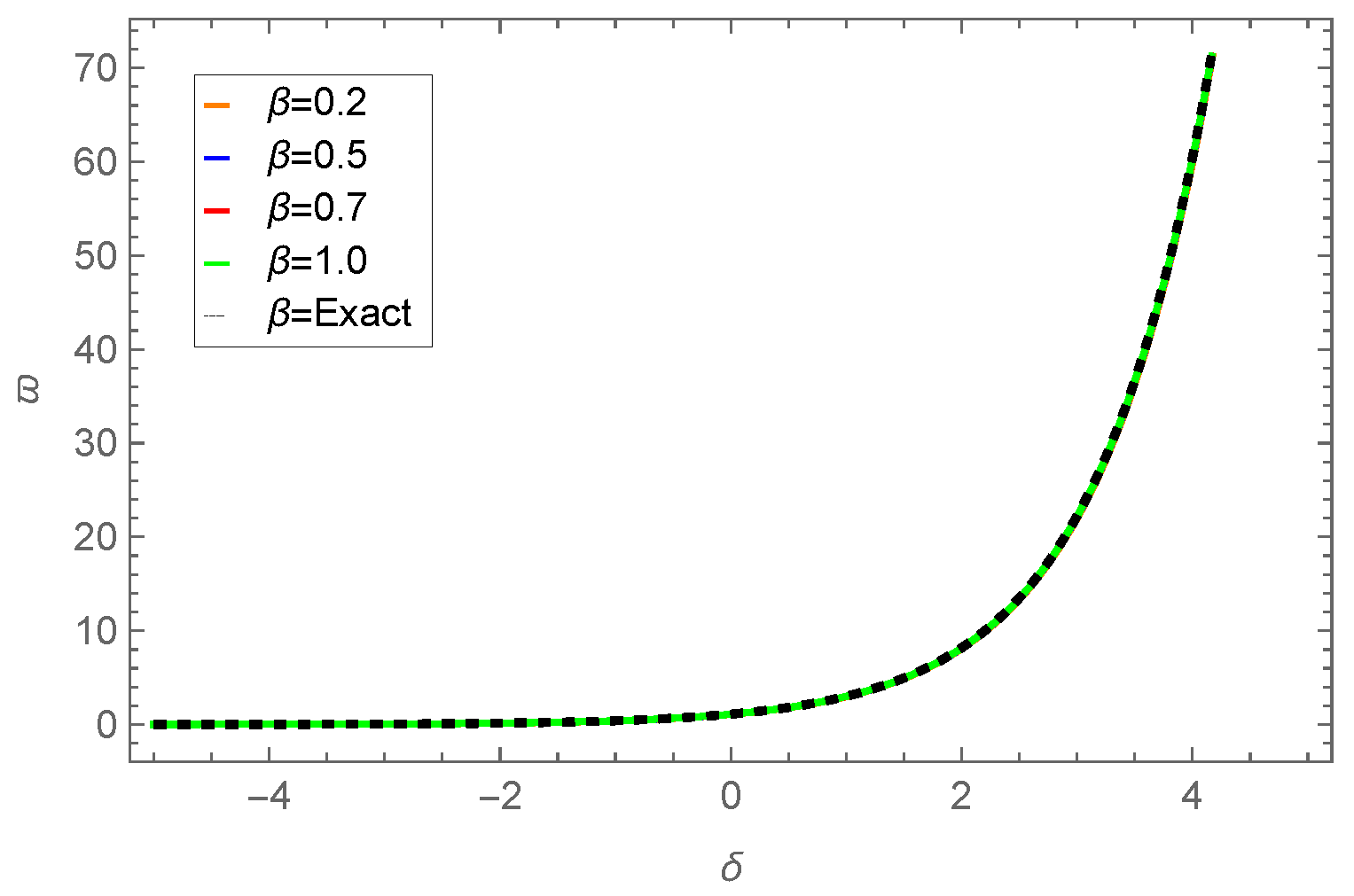
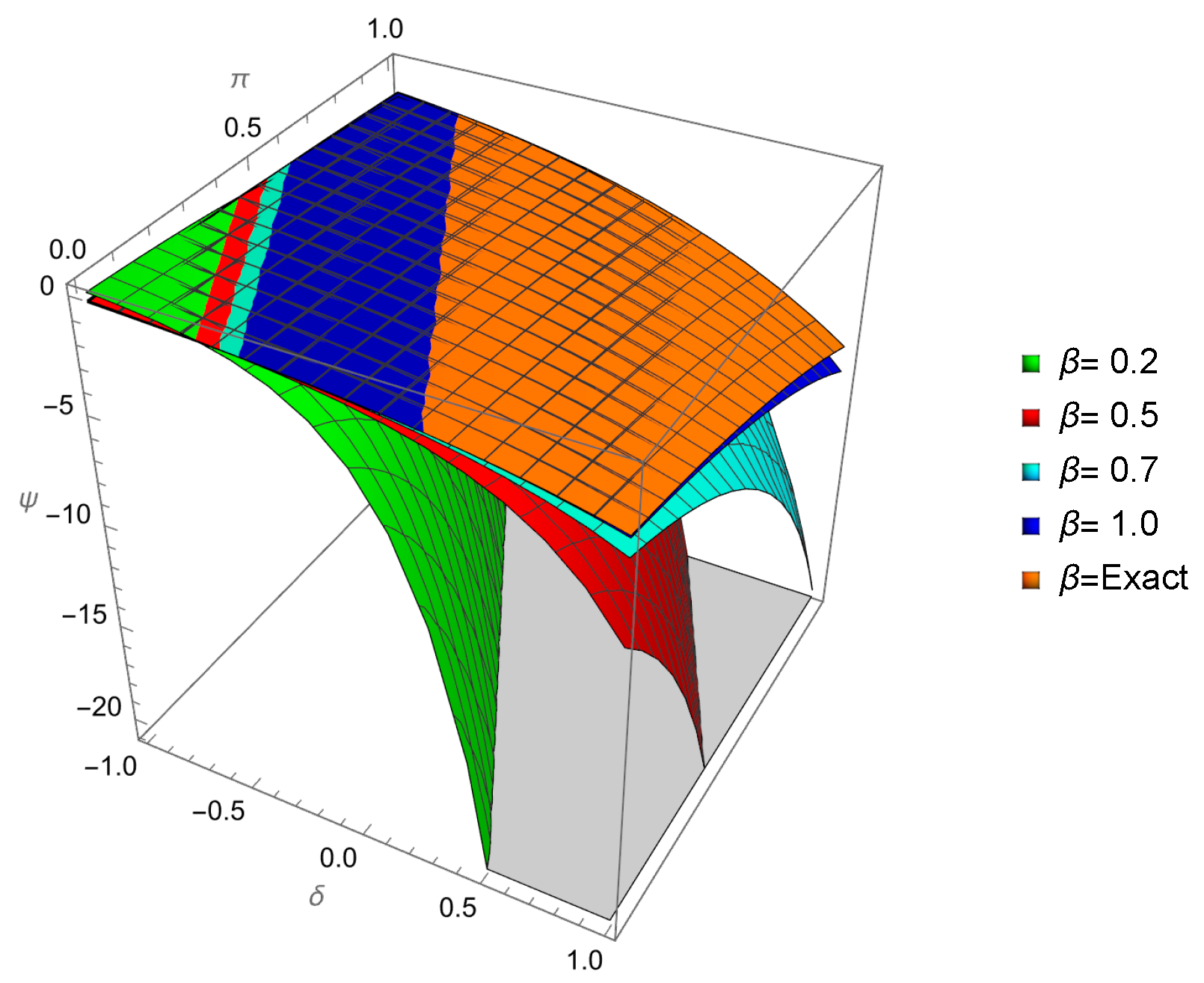
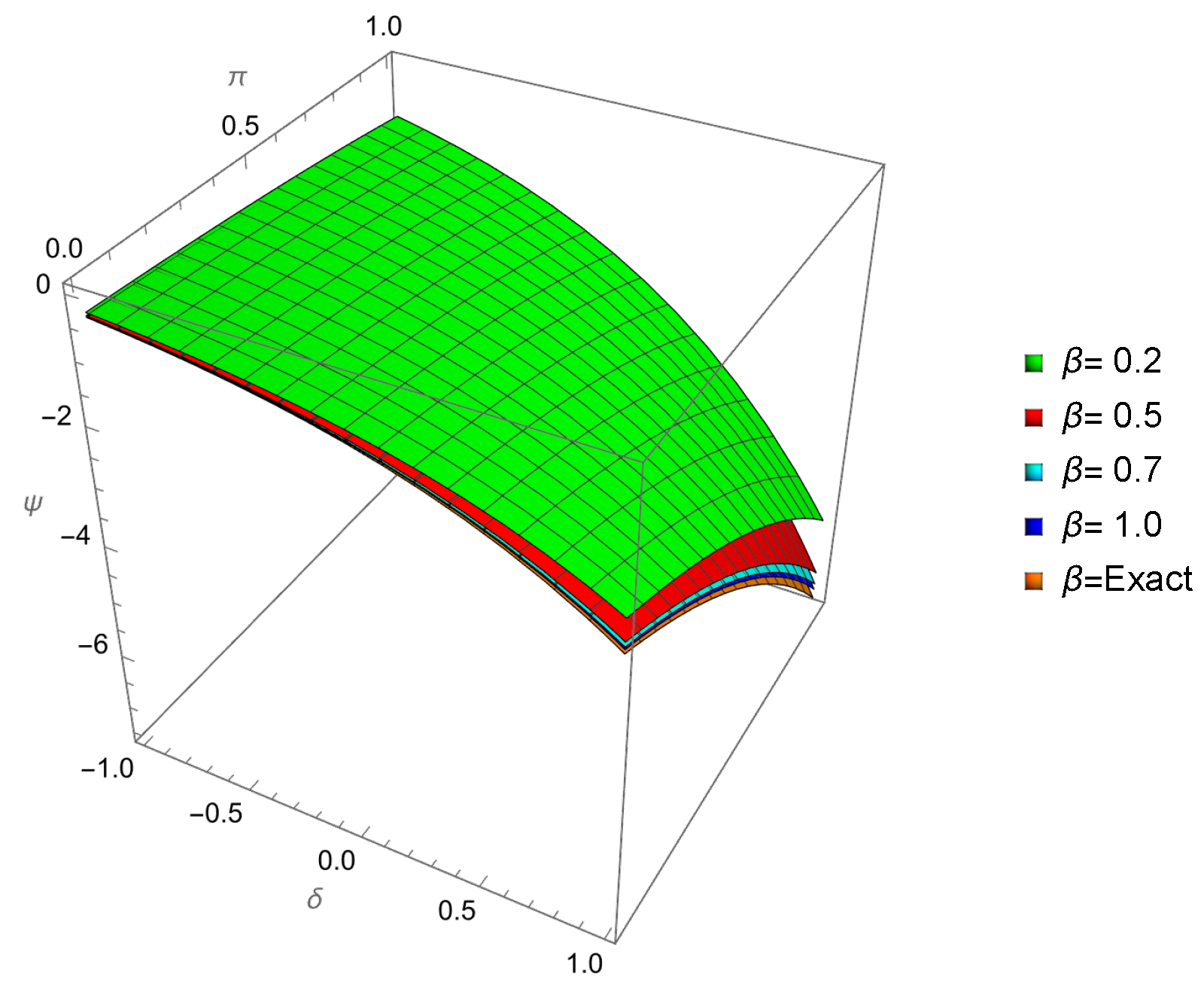
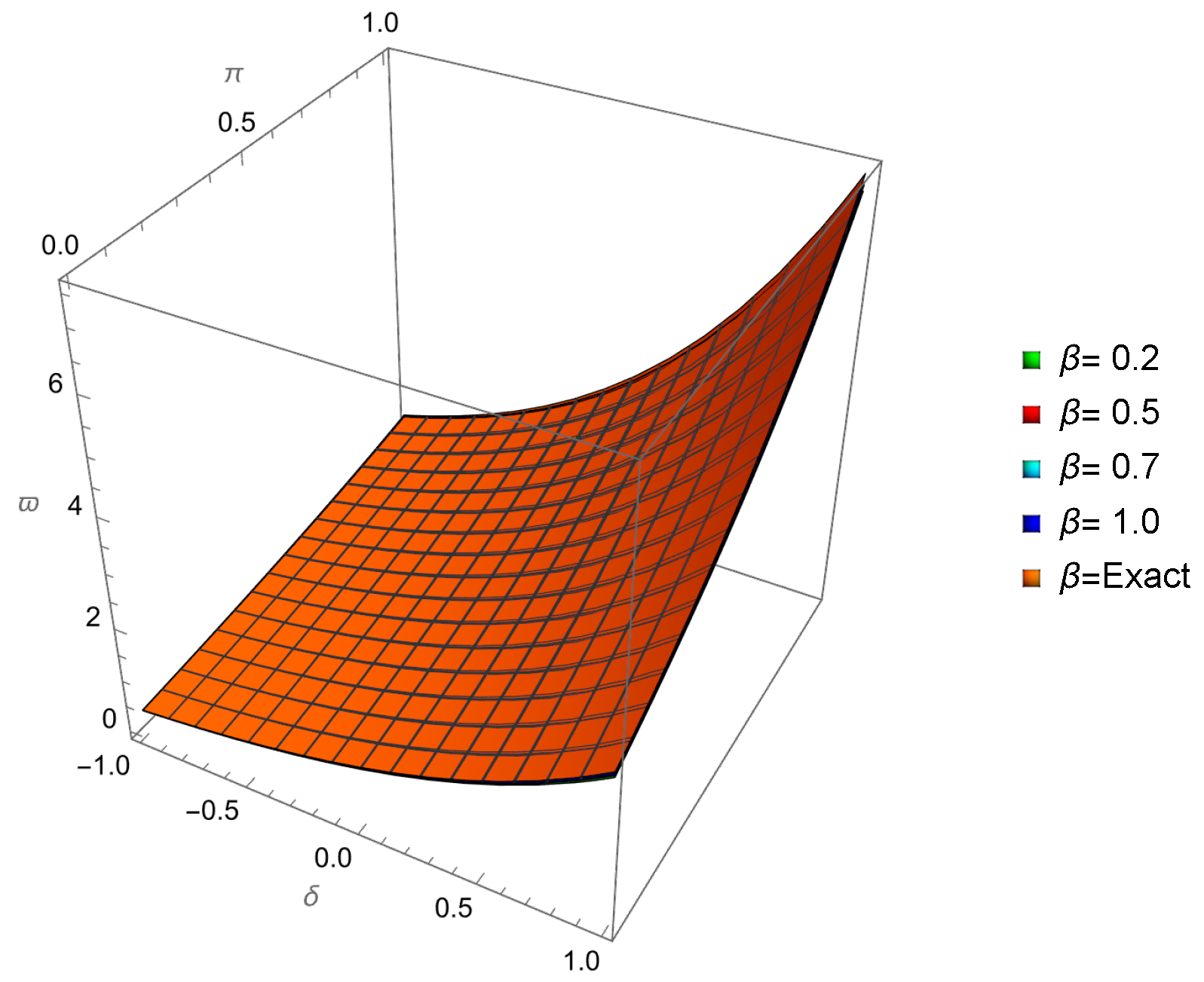
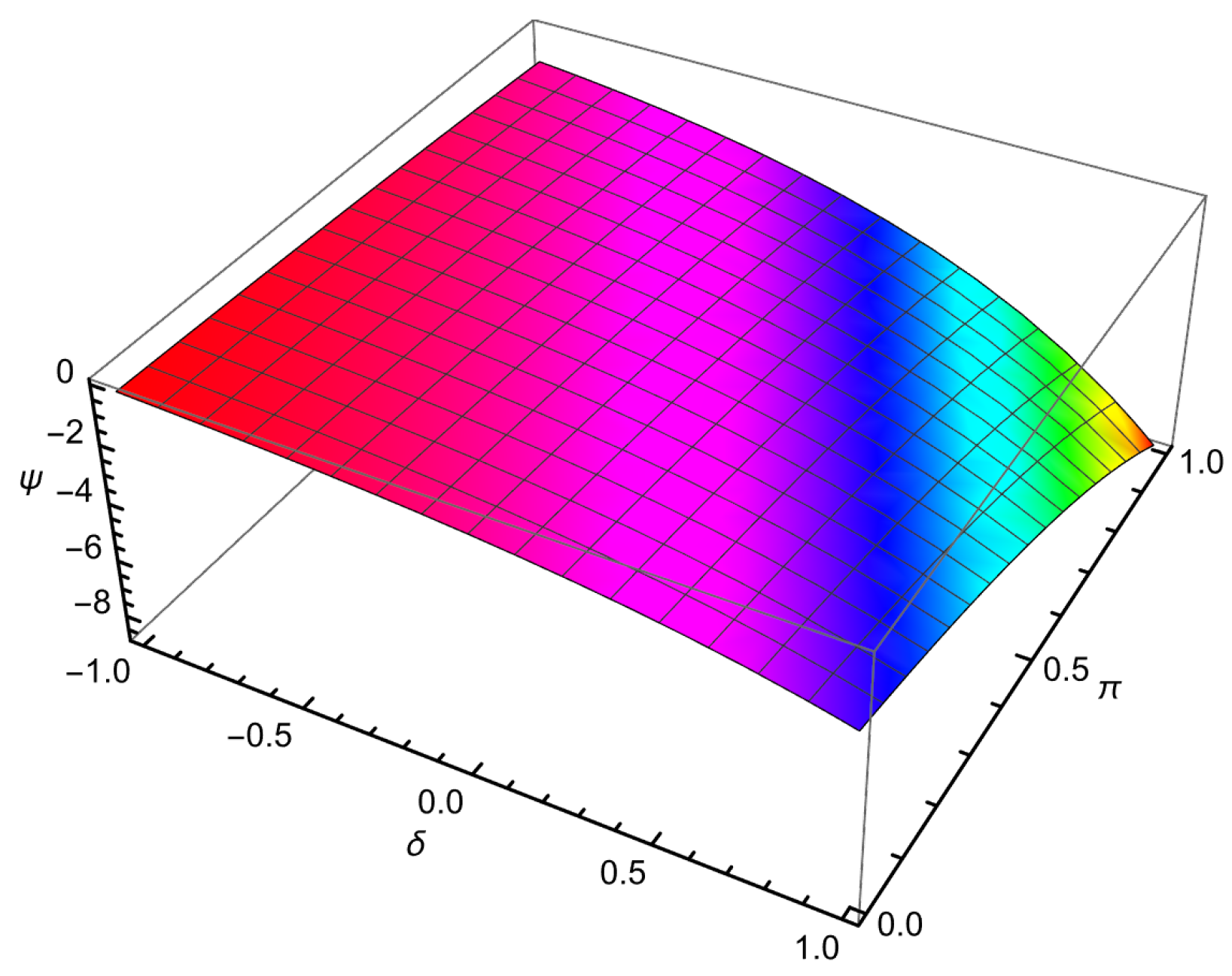
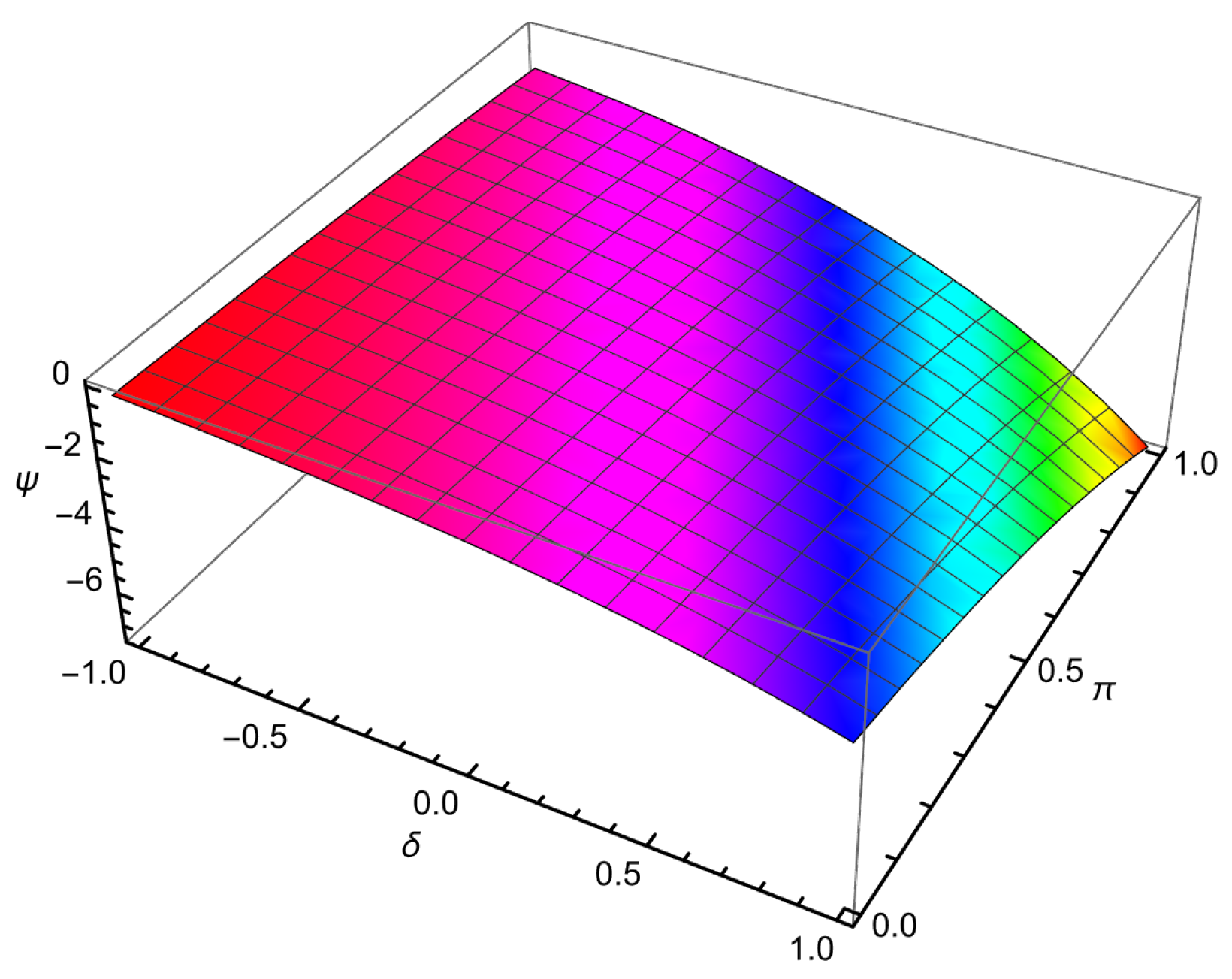
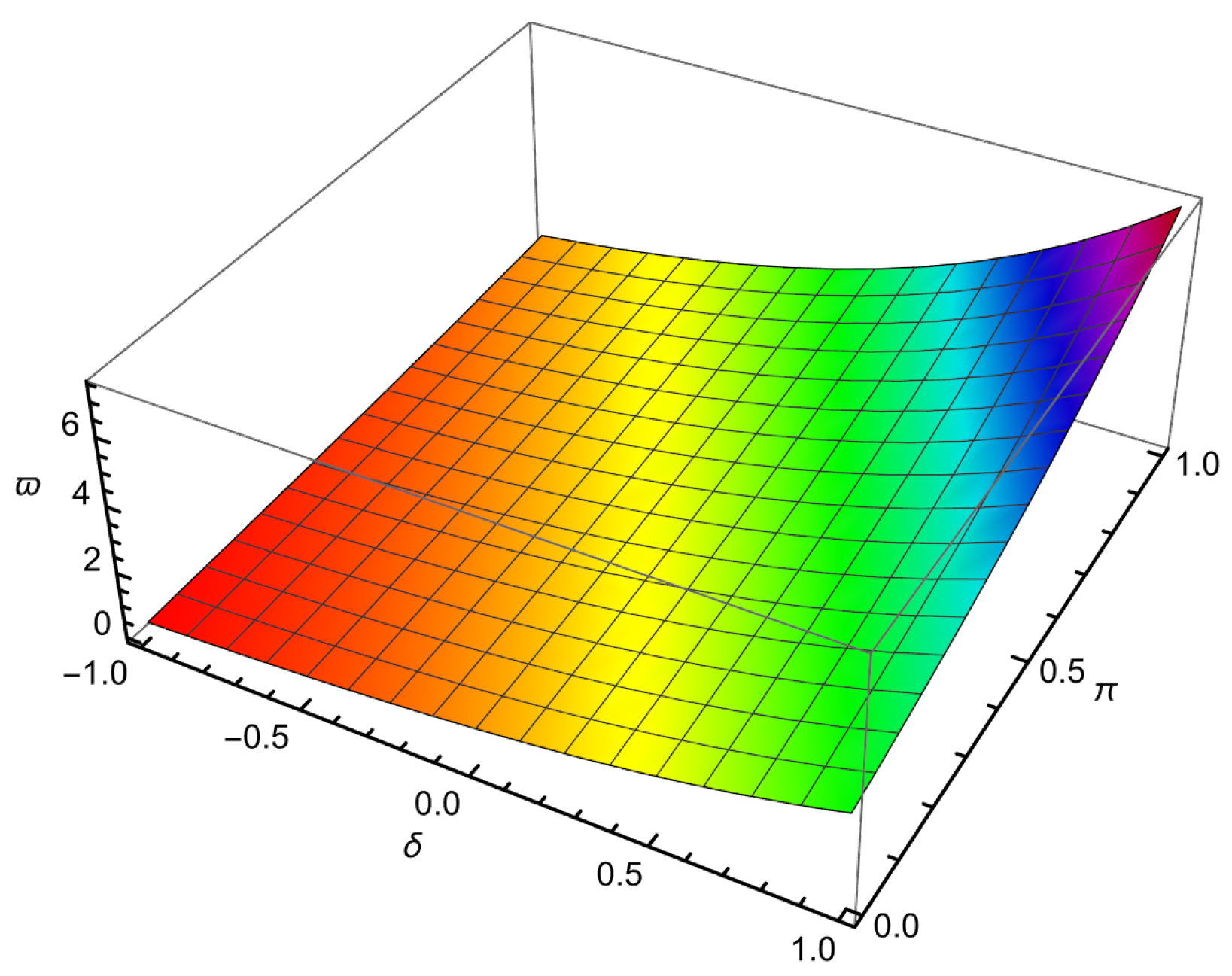
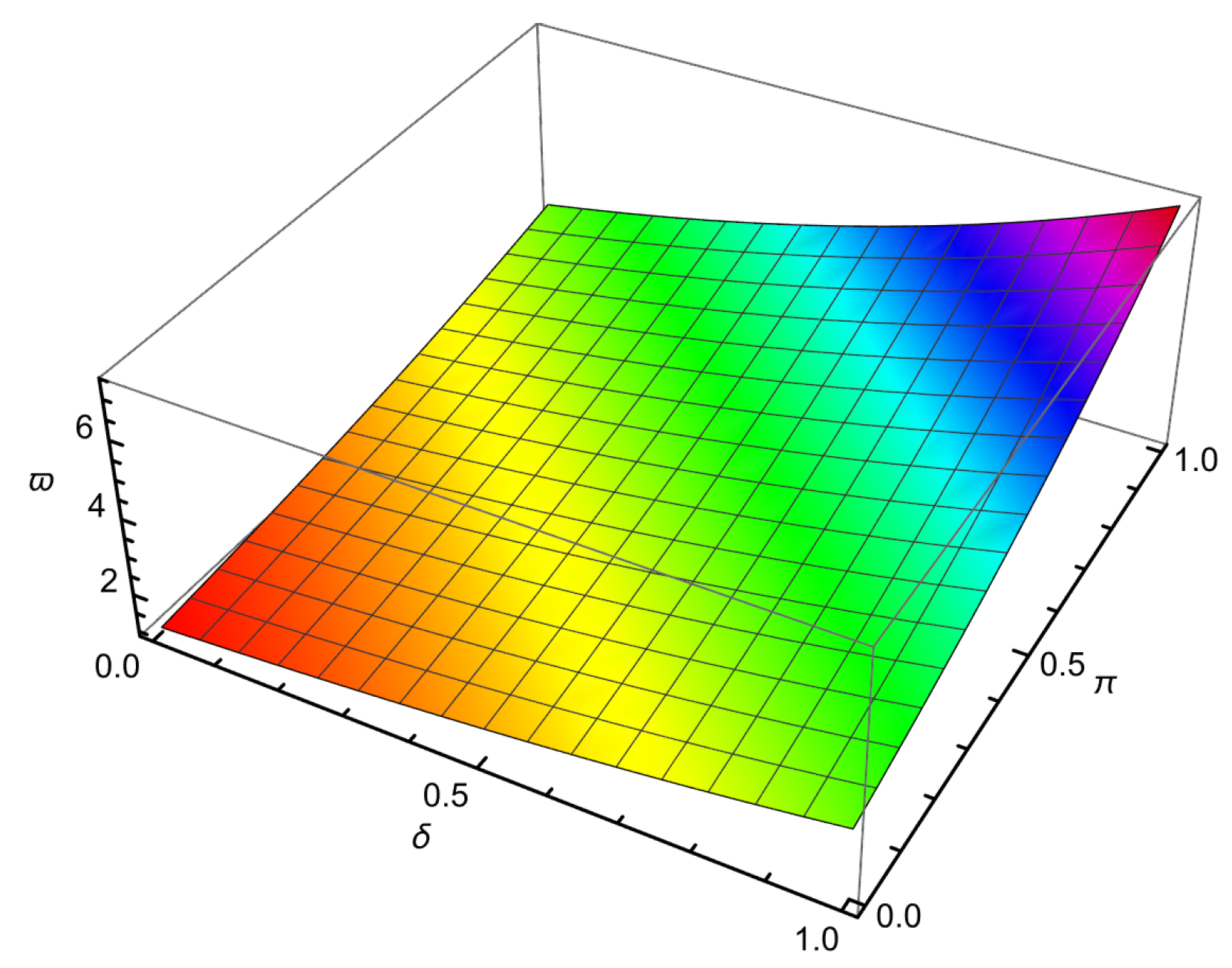
0.01	0.001	−0.109997	−0.110146	−0.109778	2.18662 × ${10}^{-4}$	3.67275 × ${10}^{-4}$
0.035	0.001	−0.134858	−0.135044	−0.13459	2.67256 × ${10}^{-4}$	4.5386 × ${10}^{-4}$
0.06	0.001	−0.159633	−0.159869	−0.159318	3.15181 × ${10}^{-4}$	5.50792 × ${10}^{-4}$
0.085	0.001	−0.184309	−0.18461	−0.183947	3.62315 × ${10}^{-4}$	6.63065 × ${10}^{-4}$
0.01	0.003	−0.110437	−0.11088	−0.109778	6.58592 × ${10}^{-4}$	1.10183 × ${10}^{-3}$
0.035	0.003	−0.135395	−0.135952	−0.13459	8.04935 × ${10}^{-4}$	1.36158 × ${10}^{-3}$
0.06	0.003	−0.160267	−0.160971	−0.159318	9.49249 × ${10}^{-4}$	1.65238 × ${10}^{-3}$
0.085	0.003	−0.185038	−0.185936	−0.183947	1.09117 × ${10}^{-3}$	1.9892 × ${10}^{-3}$
0.01	0.005	−0.11088	−0.111615	−0.109778	1.10203 × ${10}^{-3}$	1.83638 × ${10}^{-3}$
0.035	0.005	−0.135937	−0.13686	−0.13459	1.34688 × ${10}^{-3}$	2.2693 × ${10}^{-3}$
0.06	0.005	−0.160907	−0.162072	−0.159318	1.58831 × ${10}^{-3}$	2.75396 × ${10}^{-3}$
0.085	0.005	−0.185772	−0.187262	−0.183947	1.8257 × ${10}^{-3}$	3.31533 × ${10}^{-3}$

,

Table 2. The absolute error of NTIM and OAFM solution of $\varpi (\delta ,\pi ,\xi )$ for $\beta =1$, $\xi =0.001$, $\rho =0$, and $\pi =0.1$.

$\mathit{\delta }$	$\mathit{\xi }$	${\mathit{\varpi }}_{\mathit{NTIM}}(\mathit{\delta },\mathit{\pi },\mathit{\xi })$	${\mathit{\varpi }}_{\mathit{OAFM}}(\mathit{\delta },\mathit{\pi },\mathit{\xi })$	${\mathit{\varpi }}_{\mathit{Exact}}(\mathit{\delta },\mathit{\pi },\mathit{\xi })$	$\mathit{NTIM}\mathit{Error}$	$\mathit{OAFM}\mathit{Error}$
0.01	0.001	0.109778	0.109893	0.109778	1.08562 × ${10}^{-7}$	1.14202 × ${10}^{-4}$
0.035	0.001	0.13459	0.13473	0.13459	1.32282 × ${10}^{-7}$	1.3979 × ${10}^{-4}$
0.06	0.001	0.159318	0.159483	0.159318	1.55425 × ${10}^{-7}$	1.65209 × ${10}^{-4}$
0.085	0.001	0.183947	0.184137	0.183947	1.77893 × ${10}^{-7}$	1.90444 × ${10}^{-4}$
0.01	0.003	0.109779	0.110121	0.109778	9.78995 × ${10}^{-7}$	3.42605 × ${10}^{-4}$
0.035	0.003	0.134592	0.13501	0.13459	1.19287 × ${10}^{-6}$	4.19369 × ${10}^{-4}$
0.06	0.003	0.15932	0.159814	0.159318	1.40155 × ${10}^{-6}$	4.95626 × ${10}^{-4}$
0.085	0.003	0.183948	0.184518	0.183947	1.60412 × ${10}^{-6}$	5.71332 × ${10}^{-4}$
0.01	0.005	0.109781	0.110349	0.109778	2.72483 × ${10}^{-6}$	5.71008 × ${10}^{-4}$
0.035	0.005	0.134594	0.135289	0.13459	3.32007 × ${10}^{-6}$	6.98948 × ${10}^{-4}$
0.06	0.005	0.159322	0.160144	0.159318	3.90079 × ${10}^{-6}$	8.26043 × ${10}^{-4}$
0.085	0.005	0.183951	0.184899	0.183947	4.46451 × ${10}^{-6}$	9.52219 × ${10}^{-4}$

,

Table 3. The absolute error of NTIM and OAFM solution of $\psi (\delta ,\pi ,\xi )$ for $\beta =1$, $\rho =0$, and $\pi =0.1$.

$\mathit{\delta }$	$\mathit{\xi }$	${\mathit{\psi }}_{\mathit{NTIM}}(\mathit{\delta },\mathit{\pi },\mathit{\xi })$	${\mathit{\psi }}_{\mathit{OAFM}}(\mathit{\delta },\mathit{\pi },\mathit{\xi })$	${\mathit{\psi }}_{\mathit{Exact}}(\mathit{\delta },\mathit{\pi },\mathit{\xi })$	$\mathit{NTIM}\mathit{Error}$	$\mathit{OAFM}\mathit{Error}$
0.01	0.001	−1.11878	−1.11582	−1.11628	2.50051 × ${10}^{-3}$	4.59333 × ${10}^{-4}$
0.035	0.001	−1.14717	−1.14407	−1.14454	2.62893 × ${10}^{-3}$	4.71136 × ${10}^{-4}$
0.06	0.001	−1.17627	−1.17303	−1.17351	2.76396 × ${10}^{-3}$	4.83245 × ${10}^{-4}$
0.085	0.001	−1.20612	−1.20272	−1.20322	2.90593 × ${10}^{-3}$	4.95671 × ${10}^{-4}$
0.01	0.003	−1.12383	−1.1149	−1.11628	7.5518 × ${10}^{-3}$	1.378 × ${10}^{-3}$
0.035	0.003	−1.15248	−1.14312	−1.14454	7.941 × ${10}^{-3}$	1.41341 × ${10}^{-3}$
0.06	0.003	−1.18186	−1.17206	−1.17351	8.35031 × ${10}^{-3}$	1.44974 × ${10}^{-3}$
0.085	0.003	−1.212	−1.20173	−1.20322	8.78077 × ${10}^{-3}$	1.48701 × ${10}^{-3}$
0.01	0.005	−1.12895	−1.11398	−1.11628	1.26704 × ${10}^{-2}$	2.29667 × ${10}^{-3}$
0.035	0.005	−1.15786	−1.14218	−1.14454	1.33257 × ${10}^{-2}$	2.35568 × ${10}^{-3}$
0.06	0.005	−1.18753	−1.17109	−1.17351	1.4015 × ${10}^{-2}$	2.41623 × ${10}^{-3}$
0.085	0.005	−1.21796	−1.20074	−1.20322	1.474 × ${10}^{-2}$	2.47835 × ${10}^{-3}$

and

Table 4. The absolute error of NTIM and OAFM solution of $\varpi (\delta ,\pi ,\xi )$ for $\beta =1$, $\rho =0$, and $\pi =0.1$.

$\mathit{\delta }$	$\mathit{\xi }$	${\mathit{\varpi }}_{\mathit{NTIM}}(\mathit{\delta },\mathit{\pi },\mathit{\xi })$	${\mathit{\varpi }}_{\mathit{OAFM}}(\mathit{\delta },\mathit{\pi },\mathit{\xi })$	${\mathit{\varpi }}_{\mathit{Exact}}(\mathit{\delta },\mathit{\pi },\mathit{\xi })$	$\mathit{NTIM}\mathit{Error}$	$\mathit{OAFM}\mathit{Error}$
0.01	0.001	1.11628	1.11623	1.11628	1.39356 × ${10}^{-6}$	4.34366 × ${10}^{-5}$
0.035	0.001	1.14454	1.14449	1.14454	1.50217 × ${10}^{-6}$	4.45306 × ${10}^{-5}$
0.06	0.001	1.17351	1.17347	1.17351	1.61924 × ${10}^{-6}$	4.56521 × ${10}^{-5}$
0.085	0.001	1.20322	1.20317	1.20322	1.74544 × ${10}^{-6}$	4.68017 × ${10}^{-5}$
0.01	0.003	1.11629	1.11615	1.11628	1.2589 × ${10}^{-5}$	1.3031 × ${10}^{-4}$
0.035	0.003	1.14455	1.1444	1.14454	1.35714 × ${10}^{-5}$	1.33592 × ${10}^{-4}$
0.06	0.003	1.17353	1.17337	1.17351	1.46305 × ${10}^{-5}$	1.36956 × ${10}^{-4}$
0.085	0.003	1.20323	1.20308	1.20322	1.57724 × ${10}^{-5}$	1.40405 × ${10}^{-4}$
0.01	0.005	1.11631	1.11606	1.11628	3.51008 × ${10}^{-5}$	2.17183 × ${10}^{-4}$
0.035	0.005	1.14457	1.14431	1.14454	3.78436 × ${10}^{-5}$	2.22653 × ${10}^{-4}$
0.06	0.005	1.17355	1.17328	1.17351	4.08009 × ${10}^{-5}$	2.28261 × ${10}^{-4}$
0.085	0.005	1.20326	1.20298	1.20322	4.39897 × ${10}^{-5}$	2.34008 × ${10}^{-4}$

. Figure 1, Figure 2, Figure 3 and Figure 4 present a comparative analysis of the effects of varying fractional orders $\beta$ on the functions $\psi (\delta ,\pi ,\xi )$ and $\varpi (\delta ,\pi ,\xi )$, as obtained through the application of the Natural Transform Iterative Method (NTIM) and the Optimal Auxiliary Function Method (OAFM) in solving Problem 1. The three-dimensional solution profiles of $\psi (\delta ,\pi ,\xi )$ and $\varpi (\delta ,\pi ,\xi )$ for discrete $\beta$ values unfold in Figure 5, Figure 6, Figure 7 and Figure 8. It is discernible from these graphical depictions that, as $\beta$ approaches unity, both profiles converge admirably toward the exact solution.

Moving on to Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14, we witness the expression of three-dimensional profiles of $\psi (\delta ,\pi ,\xi )$ and $\varpi (\delta ,\pi ,\xi )$ brought forth by the proposed methods. Further exploration is facilitated in Figure 15, Figure 16, Figure 17 and Figure 18, where the distinct fractional values of $\beta$ for $\psi (\delta ,\pi ,\xi )$ and $\varpi (\delta ,\pi ,\xi )$ are delineated using the NTIM and OAFM to tackle Problem 2. Figure 19, Figure 20, Figure 21 and Figure 22 present captivating three-dimensional graphs of $\psi (\delta ,\pi ,\xi )$ and $\varpi (\delta ,\pi ,\xi )$ for an array of $\beta$ values. The methodologies put forth have yielded three-dimensional profiles, vividly depicted in Figure 23, Figure 24, Figure 25, Figure 26, Figure 27 and Figure 28. Notably, these figures provide compelling evidence of the convergence phenomenon of fractional solutions toward integer solutions. The precision achieved with the current methods underscores their efficacy in elucidating the mathematical intricacies inherent in the given problems.

6. Conclusions

This paper introduces a novel numerical framework for solving the fractional Navier–Stokes equations by integrating the Natural Transform Iterative Method (NTIM) with an improved version of the Optimal Auxiliary Function Method (OAFM). The solution is constructed in the form of a rapidly converging series, demonstrating both efficiency and accuracy. The strength of this combined approach is illustrated through several test problems, underscoring its reliability and effectiveness. A key advantage of the proposed methods lies in their ability to handle nonlinear fractional partial differential equations without resorting to discretization, linearization, or small perturbation techniques—significantly lowering computational demands. Compared to existing strategies, this hybrid methodology stands out as a powerful and flexible tool for tackling complex fractional systems, offering a fresh perspective and extending the frontiers of current analytical techniques.