A Geometric Variational Problem for Pseudo-Galilean Particles

Abstract

This study explores the dynamics of particle motion in pseudo-Galilean $3-$space $G_3^1$ by considering actions that incorporate both curvature and torsion of trajectories. We consider a general energy functional and formulate Euler–Lagrange equations corresponding to this functional under some boundary conditions in $G_3^1$. By adapting the geometric tools of the Frenet frame to this setting, we analyze the resulting variational equations and provide illustrative solutions that highlight their structural properties. In particular, we examine examples derived from natural Hamiltonian trajectories in $G_3^1$ and extend them to reflect the distinctive geometric features of pseudo-Galilean spaces, offering insight into their foundational behavior and theoretical implications.

1. Introduction

The investigation of particle dynamics through intrinsic geometric quantities such as curvature and torsion plays an important role in understanding both the physical behavior of trajectories and the mathematical structures underlying variational systems. In particular, the dependence of particle motion on these invariants has been widely studied in classical settings, where the extremal curves of a given functional often correspond to physically meaningful paths (see [1,2,3], etc.). Extending these concepts to non-Euclidean geometries, such as Galilean or pseudo-Galilean spaces, allows for a deeper exploration of generalized kinematic behavior and the adaptation of variational principles to degenerate metric structures. This framework not only broadens the scope of differential geometric analysis but also enhances the modeling of constrained systems in theoretical physics by incorporating the effects of geometric deformation and non-standard frame dynamics (see [4,5,6,7], etc.).

Building upon this geometric foundation, variational formulations provide a fundamental framework for analyzing particle dynamics and related physical systems. Rooted in the principles of the calculus of variations, these problems aim to determine the extremal behavior of functionals—mappings from function spaces to real numbers—under given constraints. A typical variational problem seeks a trajectory that optimizes a quantity, often expressed as an integral functional. For instance, the Hamiltonian of a space curve may be represented as $H=\int f(\kappa ,\tau ,{\kappa }^{\prime },{\tau }^{\prime },\dots )ds,$ where f is a real-valued function depending on geometric invariants such as curvature $\kappa$, torsion $\tau$, and their derivatives [2,3,8]. A reduced form $\int f\left(\kappa \right)ds,$ offers a more tractable model for special cases where curvature alone governs the dynamics (see [9,10,11], etc.). Such simplified formulations are valuable in studying the equilibrium and geometric structure of particle paths, especially in contexts where torsion effects are negligible. These models appear in diverse applications, including the mechanics of elastic rods, the geometry of filaments, and the theory of geodesics. Extending this approach, a more comprehensive formulation $\int f(\kappa ,\tau )ds$, incorporates both curvature and torsion, allowing the analysis of more intricate spatial behaviors. The inclusion of torsion accounts for the twisting nature of curves in a three-dimensional space, enabling the description of systems where both bending and twisting contribute significantly to the dynamics. This generalized Hamiltonian framework is especially relevant in modeling helical structures, non-linear dynamical systems, and energy-minimizing configurations in elasticity and material science (see [4,5,8,11,12,13], etc.).

In the context of Galilean or pseudo-Galilean geometry, time evolves uniformly, independent of spatial motion, across a fixed three-dimensional continuum. This classical framework offers a suitable ground for studying geometric variational principles involving curvature and torsion without invoking relativistic effects. Within this framework, Bilir et al. [10] addressed the classical elastic curve problem in the Galilean plane by deriving Euler–Lagrange equations and explicitly constructing solutions based on curvature-driven formulations. Expanding into three dimensions, Tükel and Turhan [14] formulated and solved the bending energy functional for elastic curves in the Galilean 3-space, obtaining analytical characterizations under specified boundary conditions. They further explored natural Hamiltonian structures derived from Frenet frame dynamics—particularly by employing the derivatives of the normal and binormal vector fields—and examined the variational behavior of the total squared torsion functional [15,16]. In a more recent contribution, Turhan [17] extended this approach to hyperelastic curves by investigating a class of curvature energy functionals in Galilean space, offering both analytical solutions and geometric interpretations under the natural Hamiltonian framework. Building upon these results, Tükel and Turhan’s latest work [18] broadens the variational framework to include functionals of the form $H\left(\gamma \right)=\underset{\gamma }{\int }f(\kappa ,\tau )ds$ in Galilean 3-space. By deriving the associated Euler–Lagrange equations, they present a unified treatment that includes special cases such as straight lines, helices, Salkowski-type curves, and generalized torsion-dominated models. This approach provides a solid foundation for investigating similar structures in pseudo-Galilean geometry without being limited to curves in Galilean space.

Galilean geometry, rooted in the foundational perspectives of Galileo Galilei, is a non-Euclidean spatial model primarily employed in the analysis of classical mechanical systems. Unlike Euclidean geometry, which assumes fixed distances and angles, Galilean geometry redefines the interaction between space and time, offering a structurally distinct reinterpretation of the space–time continuum. This framework serves as a conceptual bridge to more advanced geometric and physical theories. As a particular case within the family of real Cayley–Klein geometries, Galilean space exhibits intrinsic geometric characteristics that diverge from those of traditional Euclidean structures. Consequently, when classical geometric principles are adapted from Euclidean space to a Galilean setting, they often yield non-trivial and insightful results. In contrast, pseudo-Galilean space $G_3^1$ presents a distinct non-Euclidean structure characterized by its application in modern theoretical physics, particularly in the context of special relativity. The metric properties of pseudo-Galilean space define the relationship between spatial and temporal coordinates in a fundamentally different manner than in Galilean space. While both models fall under the broader category of non-Euclidean geometries, they differ significantly in terms of mathematical structure, physical interpretation, and domain of application. Regarding the results presented in this study—specifically those concerning variational equations and curvature-induced trajectories—when translated into the Galilean framework, they would take on a structurally simplified form, though one less aligned with relativistic consistency. In pseudo-Galilean space, certain metric-dependent terms play a significant role in shaping the Euler–Lagrange equations. However, due to the degenerate nature of the Galilean metric tensor, many of these terms either vanish or become negligible in Galilean space. This leads to a modification in the fundamental components of the variational approach. Notably, features such as space–time anisotropy and geometric constraints, which are more prominent in the pseudo-Galilean context, are significantly diminished in Galilean geometry. Therefore, applying the results of this study within a Galilean setting would yield a formulation that is mathematically reduced but physically distinct.

The foundational works on affine connections in [19,20], Schouten’s contributions to tensor analysis [21], and Arnold’s symplectic formulation of classical mechanics [22] reveal that the present study significantly departs from traditional frameworks based on tensors and manifolds. These classical sources typically rely on non-degenerate metric structures and are formulated within the context of general field theories or symplectic manifolds. In contrast, our study investigates a variational problem in pseudo-Galilean 3-space, focusing on the minimization of a general functional that depends on curvature and torsion. Within this scope, we construct a geometric framework based on curvature and torsion, derive the corresponding Euler–Lagrange equations adapted to the pseudo-Galilean metric, and analyze the physical and geometric implications of the resulting critical curves. Therefore, although inspired by classical geometric theories, this work offers a distinct and original contribution tailored to an unconventional and specialized geometric setting.

In this study, we formulate the variational analysis of pseudo-Galilean particles with curvature and torsion $H\left(\gamma \right)=\underset{\gamma }{\int }f(\kappa ,\tau )ds$, providing a foundation for further geometric exploration under degenerate metrics. Through the application of variational calculus, we have derived the corresponding Euler–Lagrange equations that determine the critical trajectories of this functional, subject to well-posed boundary constraints. The resulting system captures the complex interplay between bending and twisting deformations under the pseudo-Galilean metric. We present illustrative examples to clarify the qualitative behavior of the obtained solutions and to highlight the potential roles of such curves in both theoretical and physical applications. In the examples provided, we specifically examine the natural Hamiltonian system derived from the dynamics of the Frenet frame, particularly from the derivative of the binormal vector of the curve, and analyze the geometric character these structures exhibit in pseudo-Galilean space. The presented examples not only demonstrate the validity of the mathematical solutions but also offer valuable insights into how they can be applied in areas such as anisotropic space–time models, dislocation dynamics in solid-state physics, and certain quantum field theory scenarios. Therefore, we believe that extending Hamiltonian structures based on the Frenet frame will provide a rich and flexible theoretical foundation for future research, especially in systems where symmetry-breaking or direction-dependent interactions are prominent.

2. Preliminaries

The pseudo-Galilean space $G_3^1$ refers to a class of non-Euclidean spaces that provide a mathematical foundation for certain formulations in special relativity and related physical theories. A vector $x=(x_1,x_2,x_3)$ in pseudo-Galilean 3-space $G_3^1$ is called isotropic (non-isotropic) if $x_1=0$ ($x_1\ne 0$). Any unit non-isotropic vector has the form $x=(1,x_2,x_3)$. The isotropic vectors in $G_3^1$ can be classified into four distinct categories: spacelike vectors that satisfy $x_2^2-x_3^2>0$, timelike vectors for which $x_2^2-x_3^2<0$, and two types of light-like vectors characterized by the condition $x_2^2=\pm x_3^2$. A non-light-like isotropic vector qualifies as a unit vector provided that the relation $x_2^2-x_3^2=\pm 1$ holds.

We consider $x=(x_1,x_2,x_3)$ and $y=(y_1,y_2,y_3)$ to be vectors in $G_3^1$. The pseudo-Galilean scalar product of these vectors is defined by

$$<x,y{>}_{G_3^1}=\left\{\begin{array}{c}{x}_1{y}_1,\mathrm{if}{x}_1\ne 0\mathrm{or}{y}_1\ne 0,\hfill \\ x_2{y}_2-x_3{y}_3,\mathrm{if}{x}_1=0\mathrm{and}{y}_1=0.\hfill \end{array}\right.$$

The norm of the vector x is calculated as follows [23]:

$${∥x∥}_{G_3^1}=\left\{\begin{array}{c}\left|x_1\right|,\mathrm{if}{x}_1\ne 0,\hfill \\ \sqrt{\left|x_2^2-x_3^2\right|},\mathrm{if}{x}_1=0.\hfill \end{array}\right.$$

A curve $\alpha :I\subset R\to G_3^1$ defined by the parameterization $\alpha \left(t\right)=({\alpha }_1\left(t\right),{\alpha }_2\left(t\right),{\alpha }_3\left(t\right))$ is considered admissible provided that it contains no inflection points and lacks any isotropic tangents or such tangents and normals whose projections onto the absolute plane result in light-like vectors [24]. If $\alpha \left(x\right)=(x,{\alpha }_2\left(x\right),{\alpha }_3\left(x\right))$, with the condition ${\alpha }_2^{″}\left(x\right)-{\alpha }_3^{″}\left(x\right)\ne 0$, the arc-length parameter s is denoted via the expression $ds=∥{\dot{x}}_1\left(t\right)dt∥=dx$[25]. For simplicity, we assume $ds=dx$ and $s=x$ as the arc-length of $\alpha$ with curvature $\kappa \left(s\right)$ and torsion $\tau \left(s\right)$

$$\kappa \left(s\right)=\sqrt{\left|{\alpha }_2^{″}\left(s\right)-{\alpha }_3^{″}\left(s\right)\right|}$$

and

$$\tau \left(s\right)={\displaystyle \frac{det({\alpha }^{\prime }\left(s\right),{\alpha }^{″}\left(s\right),{\alpha }^{‴}\left(s\right))}{{\kappa }^2\left(s\right)}}.$$

The Frenet frame associated with the curve $\alpha \left(s\right)$ in $G_3^1$ is expressed as follows:

$$\begin{array}{ccc}\hfill T\left(s\right)& =& {\alpha }^{\prime }\left(s\right),\hfill \\ \hfill N\left(s\right)& =& {\displaystyle \frac{1}{\kappa \left(s\right)}}{\alpha }^{″}\left(s\right),\hfill \\ \hfill B\left(s\right)& =& {\displaystyle \frac{\epsilon }{\kappa \left(s\right)}}(0,{\alpha }_3^{″}\left(s\right),{\alpha }_2^{″}\left(s\right)),\hfill \end{array}$$

where $T\left(s\right)$, $N\left(s\right)$, and $B\left(s\right)$ are respectively called the tangent, principal normal, and binormal vector fields of the curve $\alpha$. Here $\epsilon =1$ or $-1$ is chosen by the criterion $det(T,N,B)=1$. If N is a spacelike or timelike vector, then the curve $\alpha \left(s\right)=(s,{\alpha }_2\left(s\right),{\alpha }_3\left(s\right))$ is timelike or spacelike, respectively. The Frenet formulas of $\alpha \left(s\right)$ are given by [26,27]

$$\left(\begin{array}{c}{T}^{\prime }\left(s\right)\\ N^{\prime }\left(s\right)\\ B^{\prime }\left(s\right)\end{array}\right)=\left(\begin{array}{ccc}0& \kappa \left(s\right)& 0\\ 0& 0& \tau \left(s\right)\\ 0& \tau \left(s\right)& 0\end{array}\right)\left(\begin{array}{c}T\left(s\right)\\ N\left(s\right)\\ B\left(s\right)\end{array}\right),$$

(1)

3. Particles with Pseudo-Galilean Curvature and Torsion

Let $G_3^1$ be the pseudo-Galilean 3-space and $\gamma$ be an admissible curve with speed $\nu =∥{\gamma }^{\prime }\left(t\right)∥,$ curvature $\kappa$, torsion $\tau$, and Frenet frame $\{T,N,B\}$. In this section, we concern ourselves with the mathematical model of a curvature and torsion action given by the functional $H\left(\gamma \right)={\int }_{\gamma }f(\kappa ,\tau )ds$in $G_3^1.$ Let $\mathsf{\Gamma }=\mathsf{\Gamma }(t,r)$ be a variation of $\gamma :[0,\ell ]\to G_3^1$ with $\mathsf{\Gamma }(t,0)=\gamma \left(t\right).$ Associated with $\mathsf{\Gamma },$ we consider the variation vector field W along $\gamma \left(t\right).$ The vector fields $V(t,r),$ $W(t,r)$ can be defined, where $V(0,t)={\gamma }^{\prime }\left(t\right)$ and $W\left(t\right)=W(0,t)$ is a variational vector field along $\gamma \left(t\right)$ (see, [4,9,17]). If s denotes the arclength parameter, then $\gamma (s,r),$ ${\kappa }^2(s,r)$, $V(s,r)$, etc., can be written for the corresponding reparameterizations, where $s\in$ [0,ℓ] and ℓ is the arc length of $\gamma$.

We arrive at the following lemma from the Frenet equations in (1).

Lemma 1 

([14]). Let $\gamma (t,r)$ be a variation of curve $\gamma \in$ $G_3^1.$ Then the following formulas are satified:

(i) $W\left(\nu \right)=<W^{\prime },T>\nu$

(ii) $W\left(\kappa \right)=\epsilon <W^{″},N>-2\kappa <W^{\prime },T>$

(iii) $W\left(\tau \right)=-\epsilon {\left({\displaystyle \frac{1}{\kappa }}(<W^{″},B>)\right)}^{\prime }.$

Now we suppose that $\gamma$ is a stationary point of the functional $H\left(\gamma \right).$ Thus, we have

$$\partial H\left(W\right)={\left.{\displaystyle \frac{\partial H(\gamma +\epsilon W)}{\partial \epsilon }}\right|}_{\epsilon =0}=0,$$

and we arrive at

$${\left.{\displaystyle \frac{\partial H}{\partial \epsilon }}\right|}_{\epsilon =0}=\underset{0}{\overset{\ell }{\int }}\left(f_{\kappa }W\left(\kappa \right)+f_{\tau }W\left(\tau \right)+<W^{\prime },T>\right)ds.$$

Taking into consideration Lemma 1, we find

$${\left.{\displaystyle \frac{\partial H}{\partial \epsilon }}\right|}_{\epsilon =0}=\underset{0}{\overset{\ell }{\int }}\left(\begin{array}{c}<W^{″},f_{\kappa }N>+<W^{\prime },-2\kappa f_{\kappa }T>+f_{\tau }<W^{‴},{\displaystyle \frac{1}{\kappa }}B>\\ +<W^{″},f_{\tau }{\left({\displaystyle \frac{1}{\kappa }}B\right)}^{\prime }>+<W^{\prime },-f_{\tau }\tau T>+<W^{\prime },fT>\end{array}\right)ds.$$

Utilizing conventional techniques, including the previously stated formulas and the method of integration by parts, the first variation of $H\left(\gamma \right)$ in the direction of W along the curve $\gamma$ can be expressed as follows:

$${\left.{\displaystyle \frac{\partial H}{\partial \epsilon }}\right|}_{\epsilon =0}=\underset{0}{\overset{\ell }{\int }}<E,W>ds+{\left.S[W,\gamma ]\right|}_0^{\ell },$$

where

$$E={\left(\epsilon f_{\kappa }N\right)}^{″}+{\left(f_{\tau }^{\prime }{\displaystyle \frac{\epsilon }{\kappa }}B\right)}^{″}+{\left(2\kappa f_{\kappa }T\right)}^{\prime }-{\left(fT\right)}^{\prime }$$

and

$$\begin{array}{ccc}\hfill {\left.S[W,\gamma ]\right|}_0^{\ell }& =& {\left.<W^{″},-f_{\tau }{\displaystyle \frac{\epsilon }{\kappa }}B>\right|}_0^{\ell }+{\left.<W^{\prime },\epsilon f_{\kappa }N+\epsilon {\displaystyle \frac{f_{\tau }^{\prime }}{\kappa }}B>\right|}_0^{\ell }\hfill \\ & & +{\left.<W,\left(f-2\kappa f_{\kappa }\right)T-{\left(f_{\kappa }N\right)}^{\prime }+{\left(f_{\tau }^{\prime }{\displaystyle \frac{\epsilon }{\kappa }}B\right)}^{\prime }>\right|}_0^{\ell }.\hfill \end{array}$$

It is noted that the symbols $f_{\kappa }$ and $f_{\tau }$ are used to represent the partial derivatives of f with respect to $\kappa$ and $\tau$, respectively. Furthermore, the analysis is restricted to variations whose endpoints are fixed and possess identical Frenet frames. Under these conditions, the boundary term ${\left.S[W,\gamma ]\right|}_0^l$, vanishes, implying that critical curves satisfy the condition $E^{\prime }=0,$ i.e., the Euler–Lagrange operator must vanish. If the necessary calculations are made and the Frenet equations are used, we have the following.

$$f^{\prime }={\left(2\kappa f_{\kappa }\right)}^{\prime },$$

(2)

$$-f\kappa +2{\kappa }^2{f}_{\kappa }+\epsilon f_{\kappa }^{″}+\epsilon {\tau }^2{f}_{\kappa }+{\left(\epsilon {\displaystyle \frac{f_{\tau }^{\prime }}{\kappa }}\right)}^{\prime }\tau +\left(\epsilon {\displaystyle \frac{f_{\tau }^{\prime }\tau }{\kappa }}\right)=0$$

(3)

and

$$\epsilon f_{\kappa }^{\prime }\tau +{\left(\epsilon f_{\kappa }\tau \right)}^{\prime }+{\left(\epsilon {\displaystyle \frac{f_{\tau }^{\prime }}{\kappa }}\right)}^{″}+\epsilon {\displaystyle \frac{f_{\tau }^{\prime }}{\kappa }}{\tau }^2=0.$$

(4)

From (2), we obtain the following.

$$f=2\kappa f_{\kappa }+C,$$

(5)

where C is an integration constant. Then, substituting (5) into (3), we obtain

$$-\kappa C+\epsilon f_{\kappa }^{″}+\epsilon {\tau }^2{f}_{\kappa }+{\left(\epsilon {\displaystyle \frac{f_{\tau }^{\prime }}{\kappa }}\right)}^{\prime }\tau +{\left(\epsilon {\displaystyle \frac{f_{\tau }^{\prime }\tau }{\kappa }}\right)}^{\prime }=0$$

(6)

Main Results

In this subsection, we present the main theorem that characterizes the Euler–Lagrange equations for the functional $H\left(\gamma \right)$ and provide supporting examples. Our proof utilizes the variational framework from Section 3, modified to accommodate the unique properties of the pseudo-Galilean metric.

Theorem 1. 

The motion equations of the particles with curvature and torsion action in $G_3^1$, defined by the functional $H\left(\gamma \right)={\int }_{\gamma }f(\kappa ,\tau )ds,$are characterized by the Euler–Lagrange Equations (4) and (6).

Proof. 

Let $\gamma \in G_i$ be an admissible curve that represents a critical point of the functional $H\left(\gamma \right)={\int }_{\gamma }f(\kappa ,\tau )ds$. Consider variations W of $\gamma$ that are compactly supported, which means that they vanish at the endpoints ($W\left(0\right)=W(\ell )=0$) and preserve the admissibility conditions. For such variations, the first variation of H becomes

$${\left.{\displaystyle \frac{d}{d\epsilon }}H(\gamma +\epsilon W)\right|}_{\epsilon =0}={\int }_0^{\ell }\langle E,W\rangle ds+S[W,\gamma ]{|}_0^{\ell }=0$$

where E is the Euler–Lagrange operator and $S[W,\gamma ]$ represents the boundary terms arising from integration by parts. Thus, the fundamental lemma of calculus of variations applies to the remaining integral term, yielding $E=0$, which generates the Euler–Lagrange Equations (4) and (6) characterizing the particle motion in $G_3^1$. □

To enhance the understanding of this theoretical framework, we present illustrative examples that showcase the implementation of the Euler–Lagrange equations and emphasize the geometric and physical interpretations resulting from the solutions.

In $G_3^1$, curves can be classified similarly according to their curvature and torsion characteristics, as adapted from standard classifications. This framework encompasses particular instances such as straight lines, planar curves, circular helices, generalized helices, as well as pseudo-Galilean analogues of Salkowski and anti-Salkowski curves, each identified by their distinctive geometric behavior under the pseudo-Galilean metric (see [27,28,29], etc.). In the following examples, we rely on this classification to examine and interpret the structure of critical curves.

Example 1. 

Let γ be an admissible curve in $G_3^1.$ We examine whether γ is critical for H based on its curvature and torsion values, as outlined in the following cases to illustrate its geometric properties.

$\left(i\right)$ Straight line. A straight line γ in $G_3^1$ is a critical point of the functional H.

$\left(ii\right)$ Planar curve. Let γ be a planar curve in $G_3^1$. If γ is a critical point of the functional H, then γ satisfies the equation $-\kappa C+\epsilon f_{\kappa }^{\prime \prime }=0.$

$\left(iii\right)$ Salkowski and anti-Salkowski curves. The Salkowski curves, characterized by constant curvature and arbitrary torsion, cannot satisfy the Euler–Lagrange Equations (4) and (6) for the functional H in $G_3^1$. Anti-Salkowski curves are space curves characterized by constant torsion and arbitrary curvature. Unlike classical helices, these curves preserve a fixed torsion while allowing curvature to vary along their arc length. When Euler–Lagrange Equations (4) and (6) are analyzed and a curve with constant torsion is substituted into the expressions, assuming the torsion term is constant, it follows that the previously free curvature function $\kappa \left(s\right)$ must also be constant in order for the equations to be satisfied. In other words, these Euler–Lagrange equations are only fulfilled under the condition $\kappa =const$. This implies that although anti-Salkowski curves are defined with variable curvature, only the special subclass with both constant curvature and constant torsion can be critical curves for the functional H. Therefore, not all anti-Salkowski curves solve this variational problem; only those satisfying both geometric constraints belong to the solution space of the Euler–Lagrange system.

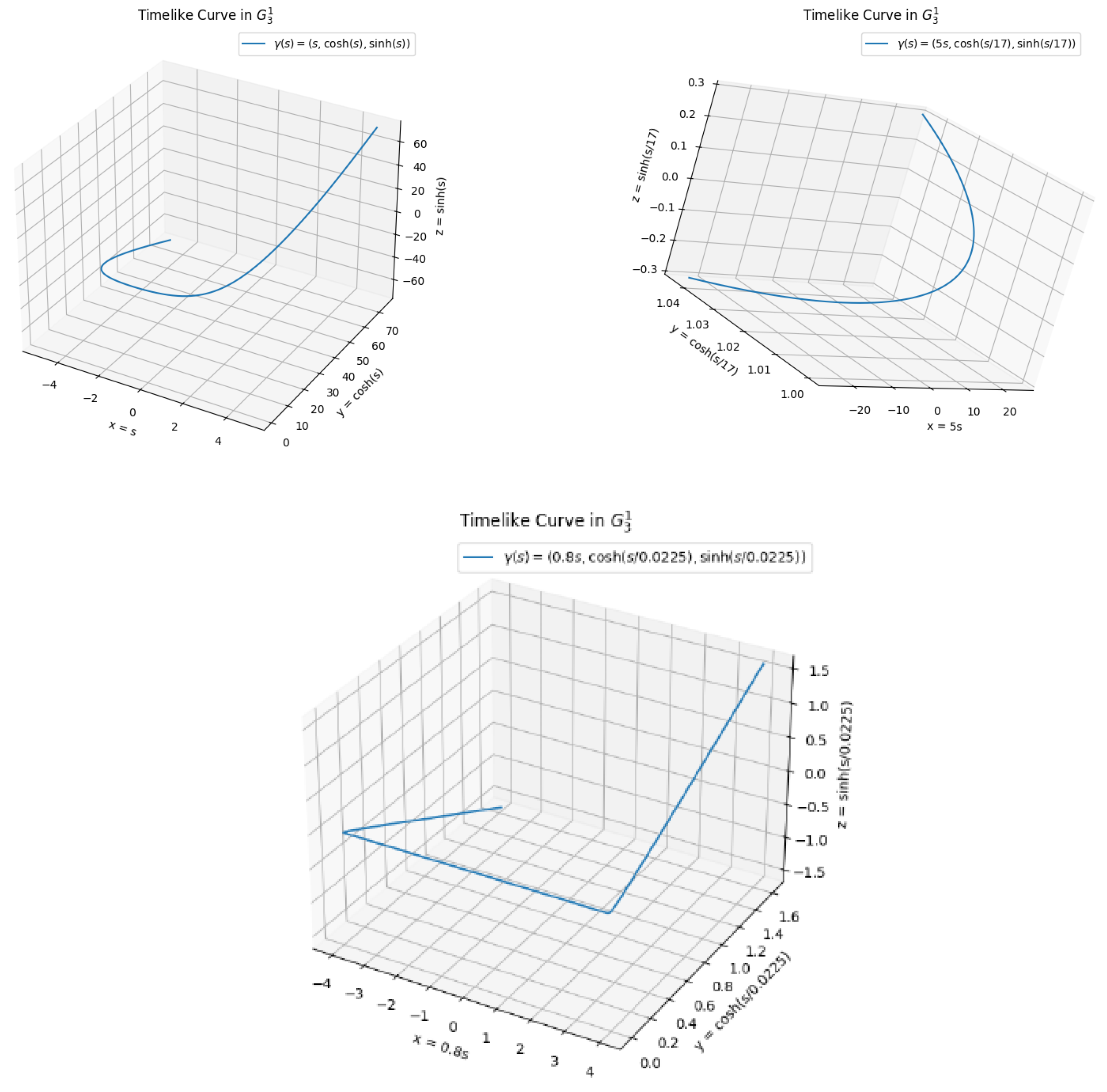
Example 2. 

We consider timelike curve $\gamma \left(s\right)=(as,cosh{\displaystyle \frac{s}{b}},sinh{\displaystyle \frac{s}{b}})$ in $G_3^1$ with $\kappa \left(s\right)={\displaystyle \frac{a}{b^2}}$ and $\tau \left(s\right)=\sqrt{{\displaystyle \frac{a^3}{b^5}}}$[30,31]. If the values of curvature and torsion are incorporated into the Euler–Lagrange Equations (4) and (6)), it can be observed that the curve γ serves as an example for the critical point for $C=0$ of the functional H (see, Figure 1).

The most fundamental example of natural Hamiltonian functionals is one defined in terms of curvature and constructed through the derivative of the tangent vector of the curve. This function is expressed as follows:

$$H_T\left(\gamma \right)=\int {\kappa }^{2}ds=\int \langle T^{\prime },T^{\prime }\rangle ds,$$

and is known as bending energy functional. Under appropriate boundary conditions, the critical points of this functional are referred to as elastic curves in the literature [2,11].

This approach is not limited to the tangent vector alone. Similarly, variational models can be constructed based on other elements of the Frenet frame, namely the normal and binormal vector fields. Consequently, the following two natural Hamiltonian functionals are defined:

$$H_N\left(\gamma \right)=\int \langle N^{\prime },N^{\prime }\rangle ds,H_B\left(\gamma \right)=\int \langle B^{\prime },B^{\prime }\rangle ,ds.$$

Here, $H_N$ characterizes the rate of change in the orientation of the curve, while $H_B$ measures the dynamics of variations in the binormal vector field and particularly represents equilibrium structures associated with torsional components in space. A specific application of these functionals, which can be regarded as particular cases of the general curvature and torsion functionals, is presented in the example below within the context of pseudo-Galilean geometry.

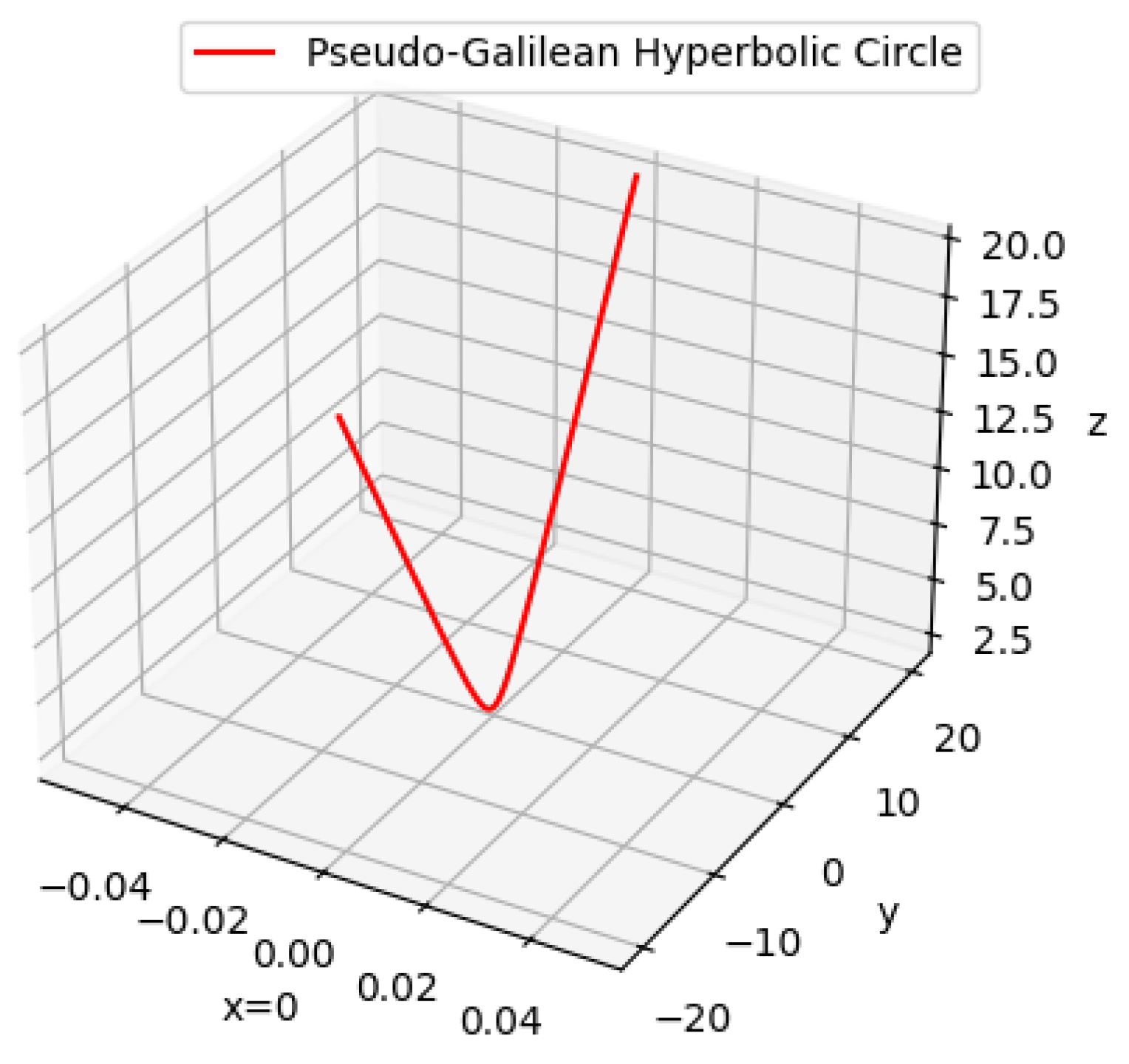
Example 3. 

We consider an admissible curve γ with pseudo-Galilean Frenet frame $\left\{T,N,B\right\}$ and curvature κ and torsion τ in $G_3^1.$ One of the generalizations of natural Hamiltonians is considered as the functional $\int <B^{\prime },B^{\prime }{>}^{n/2}ds.$ This functional is a generalized torsion energy action given by $\int \epsilon {\tau }^{n}ds$ (see [16]). In this specific case, since the integrand of the functional H does not involve the curvature κ, a direct analysis of the Euler–Lagrange equations (Equations (4) and (5)) reveals that the extremals of the functional are characterized by curves with constant torsion. Moreover, it is observed that if the torsion vanishes, the curvature function remains unconstrained; whereas, if the torsion is constant but nonzero, then the curvature must also be constant. These types of curves correspond to certain special classes depending on specific constancy conditions. For example, when the torsion is zero and the curvature is constant, the solutions are circular curves: Let $\beta \left(s\right)$ be a spacelike curve in the pseudo-Galilean space $G_3^1$ defined by the parametrization

$$\beta \left(s\right)=\left(0,a\mathrm{asinh}\left({\displaystyle \frac{s}{b}}\right),a\mathrm{acosh}\left({\displaystyle \frac{s}{b}}\right)\right),a,b\in \mathbb{R}.$$

Using the standard formulas for curvature and torsion in $G_3^1$, we obtain

$${\kappa }_{\beta }={\displaystyle \frac{a}{b^2}},{\tau }_{\beta }=0.$$

This curve is referred to as a hyperbolic circle (or “h-circle”) in pseudo-Galilean space. It can be visualized as a hyperbolic spiral in the z–y plane (Figure 2).

4. Conclusions

This study investigates the dynamics of particle models involving curvature and torsion under a degenerate metric structure within the framework of pseudo-Galilean geometry. It particularly explores how classical variational methods behave in this special type of space. The general variational problem formulated for energy functionals based on the geometric properties of curves is reinterpreted to suit the degenerate metric structure of pseudo-Galilean space, and Euler–Lagrange equations compatible with this structure are derived. The resulting mathematical model is analyzed in comparison with solutions from classical curve theory, and under selected parametric conditions, the characteristic features of critical curves are examined in detail. Notably, the way these curves are shaped in their pseudo-Galilean counterparts is illustrated with examples, allowing for both geometric and physical interpretations.

One of the most significant contributions of the study is that it explains how variational problems involving curvature and torsion, such as natural Hamiltonian systems, behave in degenerate metric spaces, thereby providing a theoretical foundation for potential applications in fields like quantum gravity, cosmology, or anisotropic physical systems. Moreover, the analytical approach developed here is extendable to other space–time models defined by similar degenerate metrics, offering an important perspective for future interdisciplinary research. In this context, the findings of the study are not only a mathematical extension but also shed light on new modeling approaches in physical geometry and theoretical physics. Especially in scenarios involving symmetry breaking or directionally preferred space–times, the framework offered by pseudo-Galilean geometry is anticipated to guide both experimental and theoretical investigations.