Fault-Tolerant Edge Metric Dimension of Zero-Divisor Graphs of Commutative Rings

Abstract

In recent years, the intersection of algebraic structures and graph-theoretic concepts has developed significant interest, particularly through the study of zero-divisor graphs derived from commutative rings. Let Z*(S) be the set of non-zero zero divisors of a finite commutative ring S with unity. Consider a graph Γ(S) with vertex set V(Γ) = Z*(S), and two vertices in Γ(S) are adjacent if and only if their product is zero. This graph Γ(S) is known as zero-divisor graph of S. Zero-divisor graphs provide a powerful bridge between abstract algebra and graph theory. The zero-divisor graphs for finite commutative rings and their minimum fault-tolerant edge-resolving sets are studied in this article. Through analytical and constructive techniques, we highlight how the algebraic properties of the ring influence the edge metric structure of its associated graph. In addition to this, the existence of a connected graph G having a resolving set of cardinality of 2n + 2 from a star graph $K_{\mathrm{1,2}n}$, is studied.

1. Introduction

Graph theory and algebra are two fundamental branches of mathematics that have exhibited substantial interaction in recent decades. This synergy is especially pronounced in the investigation of algebraic structures through graph-theoretic frameworks, wherein various types of graphs are systematically constructed to encapsulate the structural characteristics of rings, modules, groups, and other algebraic systems. Such graphical representations not only offer a combinatorial and visual perspective on abstract algebraic entities but also facilitate the application of graph-theoretic methods to address and resolve problems within algebra. A particularly compelling link between these areas is established through the study of zero-divisor graphs (ZDGs) associated with commutative rings. This concept, introduced by Beck in 1988, has generated substantial interest and research, leading to various extensions and modifications. Beck [1] defined an undirected graph Γ(S) with vertex set S for a commutative ring S. In this graph, two vertices u and v are connected through an edge if their product uv equals zero. This graphical representation helps in visualizing and understanding the interplay between the elements of the ring that annihilate each other. The concept of the zero-divisor graph (ZDG) was first introduced by Beck in 1988 and has since seen extensive development and application in various algebraic contexts. It is quite interesting to note that Γ(S) is a simple graph, having no loops, excluding the consideration of nilpotent elements in the ring. Furthermore, every vertex in Γ(S) is connected to the zero vertex, ensuring its connectivity with a diameter of at most 2. Anderson and Livingston [2] modified this definition of the ZDG introduced by Beck. Instead of considering each element of the ring S as the vertex set, they specifically focused on the zero-divisors of S.

Let us consider a simple connected graph β. The distance between the vertices l and m is represented by d(l,m) and is defined as the length of the smallest path in β between l and m if it exists, otherwise d(l,m) = ∞. The metric dimension (MD) of a graph, a concept introduced by Slater [3] in 1975, is a fundamental notion in graph theory. It is defined as the minimum cardinality of a set of vertices such that the distances from these vertices uniquely determine every other vertex in the graph. Harary and Melter [4] separately developed the same idea in 1976, but this time they referred to a particular set as a “resolving set” (RS). This concept has significant applications in various fields, including network theory and robotics. This notation is used to identify the minimum number of vertices needed to uniquely distinguish all other vertices within the graph.

For a simple, non-trivial, undirected, and connected graph β, two vertices x₁ and x₂ are said to be resolved by a vertex x if d(x,x₁) ≠ d(x,x₂). Let M_v = {t₁,t₂,…,t_k} be an ordered subset of vertices in β. Then, the metric representation of a vertex t in β with respect to the set M_v is the k-tuple ζ(t|M_v) = (d(t,t₁),d(t,t₂),…,d(t,t_k)). The set M_v is said to be an RS in β, if every vertex of β has unique metric representation with respect to the set M_v. A resolving set with the smallest number of elements in it is termed as metric basis, and the number of vertices in a metric basis is known as MD of β, denoted by dim(β).

Similarly, one can extend this concept, for the identification of all the edges in β. The concept of resolving all the edges of a graph, rather than its vertices, was introduced by Kelenc et al. [5], who termed it the edge metric dimension (EMD). They investigated the EMDs for several fundamental classes of graphs, including path graphs, cycle graphs, complete graphs, and others. They also provided several closed-form expressions and bounds for the edge metric dimension of various notable graph families. Since the introduction of these graph-theoretic parameters, numerous studies, including those exploring their applications, have been published over time. Singh and Bhat [6] examined graph invariants like MD, independence number, minimum vertex degree, domination number, Zagreb indices, and Laplacian energy for line graph of zero-divisor graphs of some rings. Pirzada and Raja [7] studied the MD of ZDGs. Sharma and Bhat [8] applied the concept of fault-tolerant metric dimension for the zero-divisor graphs. Bhat and Singh [9] deduced a general formula for number of zero-divisor graphs in matrix ring M_n(${\mathbb{Z}}_p$). They also studied the diameter of the ZDG of the matrix ring. The adjacency matrix, Wiener index, Zagreb indices, and Laplacian energy for zero-divisor graphs of Z_n has been examined by Singh and Bhat [10].

Since its introduction, considerable research has been devoted to exploring the theoretical foundations and a wide array of the practical applications of the MD. Melter and Tomescu [11] were the first to investigate these concepts, establishing that the cardinality of the metric basis is 3 for a digital plane under the Euclidean distance, while it is infinite for the digital plane using chessboard and city-block distances. Chartrand et al. [12] investigated all the graphs on r−vertices with MD r, r − 1, and 1. Sebő and Tannier [13] investigated the MD from the perspective of combinatorial optimization, and Khuller et al. [14] examined various properties of metric basis sets of cardinality 2 and provided an approximation, demonstrating that the MD of an n vertex graph can be computed in polynomial time within a factor of O(log n). In recent years, numerous variants of the MD have been developed to address diverse challenges across various disciplines. These include the local MD [15], the EMD [5], mixed MD [16], fault-tolerant MD [17], strong MD [13], and fault-tolerant EMD (FTEMD) [18]. In an application presented in [19], the elements of a minimum RS were referred to as sensors. The failure of any such sensor could result in insufficient data to effectively detect potential threats such as theft or fire. To address this limitation, Hernando et al. [17] introduced the concept of fault-tolerant resolving sets. These sets ensure that reliable information can still be retrieved even in the event of a sensor failure. Consequently, the fault-tolerant metric dimension extends the applicability of the traditional MD to contexts where robustness against failures is essential.

The fault-tolerant MD is directly linked to reliability theory, particularly in the evaluation and design of resilient networks with uncertainty and possible failures. Reliability theory deals with the ability to detect, locate, and respond to faults effectively. In this context, fault-tolerant MD is directly applicable to reliability theory. Fault-tolerant MD complements probabilistic failure models by guaranteeing structural diagnosability under worst-case scenarios. For instance, if failures occur randomly with a certain probability, the fault-tolerant resolving set ensures that the identification of nodes remains possible with high probability. Raza et al. [20] explored the role of fault-tolerant resolvability in specific direct interconnection network architectures. The fault-tolerant MDs of oxide connectivity networks were studied by Somasundari and Raj [21], while Sharma and Bhat [22] investigated the minimum fault-tolerant RS for the two-fold heptagonal-nonagonal circular ladder. Furthermore, Raza et al. [23] examined the applications of the FTEMD in polytopes. Liu et al. [24] analyzed the minimum fault-tolerant RS in wheel-related graphs, and Raza et al. [25] studied the extremal structure of graphs in relation to the FTEMD. Shahriyari et al. [26] examined MD as well as strong metric dimension in annihilator-ideal graphs of commutative rings. In this manuscript, the ZDGs for some finite commutative rings has been examined, and FTEMDs have been computed for them.

2. Preliminaries

In this section, we present several fundamental definitions that are crucial for understanding this paper. The following definitions provide the necessary groundwork for the ensuing analysis and discussion.

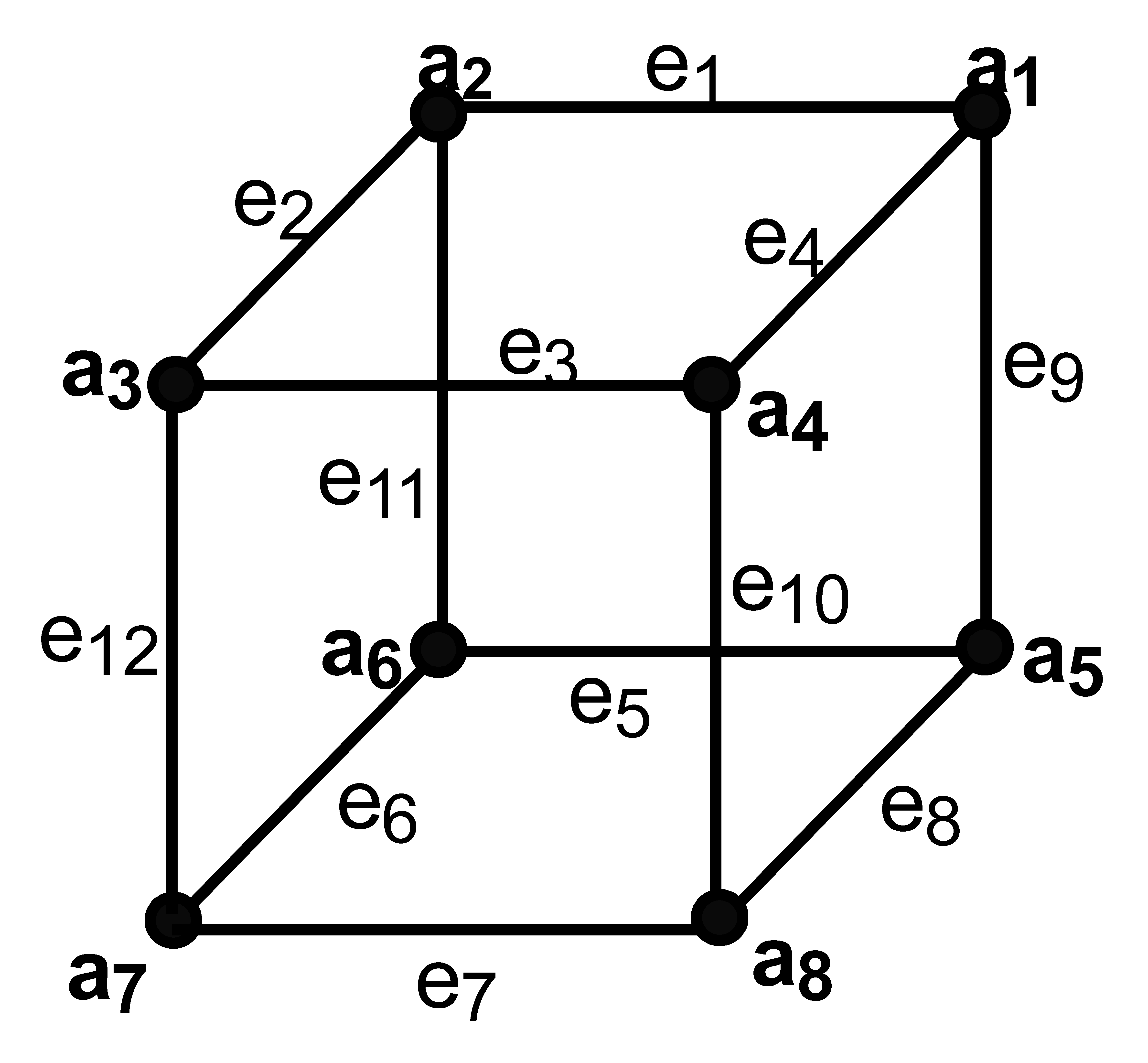
Definition 1.

Zero divisor graph: [2] Let S be a commutative ring with unity and Z*(S) be the set of the non-zero zero divisors of S. Then, the ZDG Γ(S) is a graph having a vertex set Z*(S) such that the distinct vertices m and n are adjacent in Γ(S) if mn = 0.

Definition 2.

Edge Metric Dimension: [5] Let β = β(V,E) be a simple connected graph, and T = {t₁,t₂,t₃,…,t_l}⊂V(β). The edge metric coordinate representation of the edge pq of β with respect to T is the l-vector (d(pq,t₁),d(pq,t₂),…,d(pq,t_l)) = ζ(pq|T). If every edge of β has unique edge metric coordinate representation, then the set T is termed as the edge-resolving set (ERS) for β. The cardinality of a minimal ERS, denoted by edim(β), is the EMD of the graph β.

Definition 3.

Fault-Tolerant Edge Metric Dimension: [18] Let C = {k₁,k₂,k₃,…,k_l}⊂V(β) be such that C − {x} serves as ERS for all x∈C. Then, C is termed as a fault-tolerant edge-resolving set (FTERS), and such a set with minimum cardinality is called a fault-tolerant edge metric basis (FTEMB). The cardinality of such basis is known as the FTEMD of β and is denoted by FTEMD(β) or edim_f(β)

Example: 

The FTEMD of the graph β is 4 i.e., FTEMD(β) = 4. The graph of β is presented in Figure 1.

Let $W=\{{\mathrm{a}}_1,{\mathrm{a}}_3,{\mathrm{a}}_6,{\mathrm{a}}_8\}\subset V\left(\beta \right)$. We claim that W is the minimum FTERS for β.

The following are the edge metric coordinates for the different edges of β:

$$\mathsf{\zeta }({\mathrm{e}}_1\left|W\right)=(0,1,1,2), \mathsf{\zeta }\left({\mathrm{e}}_7\right|W) = (2,1,1,0),$$

$$\mathsf{\zeta }({\mathrm{e}}_2\left|W\right)=(1,0,1,2), \mathsf{\zeta }\left({\mathrm{e}}_8\right|W) = (1,2,1,0),$$

$$\mathsf{\zeta }({\mathrm{e}}_3\left|W\right)=(1,0,2,1), \mathsf{\zeta }\left({\mathrm{e}}_9\right|W) = (0,2,1,1),$$

$$\mathsf{\zeta }({\mathrm{e}}_4\left|W\right)=(0,1,2,1), \mathsf{\zeta }\left({\mathrm{e}}_{10}\right|W) = (1,1,2,0),$$

$$\mathsf{\zeta }({\mathrm{e}}_5\left|W\right)=(1,2,0,1), \mathsf{\zeta }\left({\mathrm{e}}_{11}\right|W) = (1,1,0,2),$$

$$\mathsf{\zeta }({\mathrm{e}}_6\left|W\right)=(2,1,0,1), \mathsf{\zeta }\left({\mathrm{e}}_{12}\right|W) = (2,0,1,1),$$

It can be easily seen that each edge of β has unique representation with respect to set W, and so W serves as an ERS. Now, we claim that W − {x}, where $x\in W$, is also an ERS.

Because four elements are present in W and x∈W, we have four cases:

Case I.

If $x=a_1$, then $W-\left\{a_1\right\}=\{a_3, a_6, a_8\}$ $=$ M₁ (say), and we have

$$\mathsf{\zeta }(e_1\left|M_1\right)=(1,1,2), \mathsf{\zeta }\left(e_7\right|M_1)=(1,1,0),$$

$$\mathsf{\zeta }(e_2\left|M_1\right)=(0,1,2), \mathsf{\zeta }\left(e_8\right|M_1)=(2,1,0),$$

$$\mathsf{\zeta }(e_3\left|M_1\right)=(0,2,1), \mathsf{\zeta }\left(e_9\right|M_1)=(2,1,1),$$

$$\mathsf{\zeta }(e_4\left|M_1\right)=(1,2,1), \mathsf{\zeta }\left(e_{10}\right|M_1)=(1,2,0),$$

$$\mathsf{\zeta }(e_5\left|M_1\right)=(2,0,1), \mathsf{\zeta }\left(e_{11}\right|M_1)=(1,0,2),$$

$$\mathsf{\zeta }(e_6\left|M_1\right)=(1,0,1), \mathsf{\zeta }\left(e_{12}\right|M_1)=(0,1,1),$$

Thus, M₁ is an ERS for β.

Case II.

If $x=a_3$, then $W-\left\{a_3\right\}=\{a_1, a_6, a_8\}$$=$ M₂ (say), and we have

$$\mathsf{\zeta }(e_1\left|M_2\right)=(0,1,2), \mathsf{\zeta }\left(e_7\right|M_2)=(2,1,0),$$

$$\mathsf{\zeta }(e_2\left|M_2\right)=(1,1,2), \mathsf{\zeta }\left(e_8\right|M_2)=(1,1,0),$$

$$\mathsf{\zeta }(e_3\left|M_2\right)=(1,2,1), \mathsf{\zeta }\left(e_9\right|M_2)=(0,1,1),$$

$$\mathsf{\zeta }(e_4\left|M_2\right)=(0,2,1), \mathsf{\zeta }\left(e_{10}\right|M_2)=(1,2,0),$$

$$\mathsf{\zeta }(e_5\left|M_2\right)=(1,0,1), \mathsf{\zeta }\left(e_{11}\right|M_2)=(1,0,2),$$

$$\mathsf{\zeta }(e_6\left|M_2\right)=(2,0,1), \mathsf{\zeta }\left(e_{12}\right|M_2)=(2,1,1),$$

Thus, M₂ is an ERS for β.

Case III.

If $x=a_6$, then $W-\left\{a_6\right\}=\{a_1, a_3, a_8\}$$=$ M₃ (say), and we have

$$\mathsf{\zeta }(e_1\left|M_3\right)=(0,1,2), \mathsf{\zeta }\left(e_7\right|M_3)=(2,1,0),$$

$$\mathsf{\zeta }(e_2\left|M_3\right)=(1,0,2), \mathsf{\zeta }\left(e_8\right|M_3)=(1,2,0),$$

$$\mathsf{\zeta }(e_3\left|M_3\right)=(1,0,1), \mathsf{\zeta }\left(e_9\right|M_3)=(0,2,1),$$

$$\mathsf{\zeta }(e_4\left|M_3\right)=(0,1,1), \mathsf{\zeta }\left(e_{10}\right|M_3)=(1,1,0),$$

$$\mathsf{\zeta }(e_5\left|M_3\right)=(1,2,1), \mathsf{\zeta }\left(e_{11}\right|M_3)=(1,1,2),$$

$$\mathsf{\zeta }(e_6\left|M_3\right)=(2,1,1), \mathsf{\zeta }\left(e_{12}\right|M_3)=(2,0,1),$$

Thus, M₃ is an ERS for β.

Case IV.

If $x=a_8$, then $W-\left\{a_8\right\}=\{a_1, a_3, a_6\}=$ M₄ (say), and we have

$$\mathsf{\zeta }(e_1\left|M_4\right)=(0,1,1), \mathsf{\zeta }\left(e_7\right|M_4)=(2,1,1),$$

$$\mathsf{\zeta }(e_2\left|M_4\right)=(1,0,1), \mathsf{\zeta }\left(e_8\right|M_4)=(1,2,1),$$

$$\mathsf{\zeta }(e_3\left|M_4\right)=(1,0,2), \mathsf{\zeta }\left(e_9\right|M_4)=(0,2,1),$$

$$\mathsf{\zeta }(e_4\left|M_4\right)=(0,1,2), \mathsf{\zeta }\left(e_{10}\right|M_4)=(1,1,2),$$

$$\mathsf{\zeta }(e_5\left|M_4\right)=(1,2,0), \mathsf{\zeta }\left(e_{11}\right|M_4)=(1,1,0),$$

$$\mathsf{\zeta }(e_6\left|M_4\right)=(2,1,0), \mathsf{\zeta }\left(e_{12}\right|M_4)=(2,0,1),$$

Thus, M₄ is an ERS for δ.

Thus, W is an FTERS, and it follows that FTEMD(β) ≤ 4. The EMD of β is 3, as calculated in [27], and it is clear that the FTEMD of a graph is strictly greater than the EMD of the graph. Thus, FTEMD(β) > edim(β) and this shows that FTEMD(β) = 4.

3. Main Results

Theorem 1.

Let H be the star graph $K_{\mathrm{1,2}m }$, m ≥ 2. Then, there exists a connected graph G, such that G has a resolving set R with 2m + 2 number of elements. Further, for any x∈ R, there exists a connected graph G for which R − {x} is a resolving set.

Proof. 

Suppose the star graph $K_{\mathrm{1,2}m}$ with the x₀ vertex adjacent to vertices $x_1$, $x_2,\dots ,x_{2m}$, and take another graph P on 2m vertices $x_1^{*},x_2^{*},\dots ,x_{2m}^{*}$ with $x_0$ adjacent to $x_l^{*}$, for all $1 \le l \le 2m$, and no vertex $x_k$ is adjacent to $x_r^{*}$, for all $1 \le k,r \le 2m$. Now, add two more vertices y and y* and edges $x_{r}y$ and $x_r^{*}{y}^{*}$. The construction of graph up to here is similar to the graph in [7]. Additionally, add two new sets of vertices $Z=\{z_1,z_2,\dots ,z_m,z_{m+1}\}$ and $Z^{*}=\{z_1^{*},z_2^{*},\dots ,z_m^{*},z_{m+1}^{*}\}$ together with edges $z_{r}y$ and $z_r^{*}{y}^{*}$ for $1 \le r \le m+1$.

The resulting graph is denoted by M and is presented in Figure 2.

Let $W=Z-\left\{z_{m+1}\right\}$ and $W^{*}=Z^{*}-\left\{z_{m+1}^{*}\right\}$.

Furthermore, add the edges between $W$ and $x_1,x_2,\dots ,x_{2m}$, such that all of the possible 2m vectors (where each co-ordinate of the vector belongs to the set {1,2} appear exactly once as ζ($x_r$|W)) for 1 ≤ r ≤ 2m.

Similarly, add the edges between W* and $x_1^{*},x_2^{*},\dots ,x_m^{*}$ such that the metric representation ζ($x_r^{*}$|$W^{*}$)) is different for all r, 1 ≤ r ≤ 2m. Let the resulting graph be denoted by G. We claim that S = W ∪ W* is an RS for the graph G.

It can be easily seen that

$$\mathsf{\zeta }\left(x_0\right|W\cup W*) = (2,2,\dots ,2,2,\dots ,2),$$

$$\mathsf{\zeta }\left(x_i\right|W\cup W*) = (-,-,\dots ,-,3,3,\dots ,3),$$

$$\mathsf{\zeta }\left(x_i^{*}\right|W\cup W*) = (3,3,\dots ,3,-,-,\dots ,-),$$

ζ(y|W∪W*) = (1,1,…,1,4,…,4),

ζ(y*|W∪W*) = (4,4,…,4,1,…,1),

$$\mathsf{\zeta }\left(z_{n+1}\right|W\cup W*) = (2,2,\dots ,2,5,\dots ,5),$$

$$\mathsf{\zeta }\left(z_{n+1}^{*}\right|W\cup W*) = (2,2,\dots ,2,5,\dots ,5),$$

Therefore, each vertex in $V\left(G\right)-S$ has a unique metric representation with respect to the set S.

Thus, W∪W* is an RS with a cardinality of 2m. Let $S^{*}=S\cup \{z_{m+1},z_{m+1}^{*}\}$. Then, if S* is the superset of a resolving set, it is also a resolving set for G.

• Therefore, there exists the resolving set R = S* with 2m + 2 number of vertices.

One possible graph G for m = 2 is presented in Figure 3.

• Now, consider $R-\left\{x\right\}$, where $x\in R$.
• Because $R=W\cup W^{*}\cup \{z_{m+1},z_{m+1}^{*}\}$, without any loss to generality, assume that $x\in Z$ i.e., $x=z_i$ for some $1\le i\le m+1$.
• Then $R-\left\{x\right\}=\{z_1,z_2,\dots ,z_{i-1},z_{i+1},\dots ,z_m,z_{m+1},z_1^{\mathrm{*}},z_2^{\mathrm{*}},\dots ,z_m^{\mathrm{*}},z_{m+1}^{\mathrm{*}}\}$.

Now, consider a graph G′ obtained from G by removing all edges between z_i and x_i and add edges between $z_1,z_2,\dots ,z_{i-1},z_{i+1},\dots ,z_m,z_{m+1}$ and $x_i$’s where $1 \le i\le 2m$, such that each vertex $x_i$ receives a unique metric code of m-vector with respect to the set $U^{*}=\{z_1,z_2,\dots ,z_{i-1},z_{i+1},\dots ,z_m,z_{m+1}\}$.

i.e., ζ($x_k$|$U^{*}$) is unique for each $k=\mathrm{1,2},\dots ,i-1,i+1,\dots ,m$. Additionally, ζ($x_i$|Z*) is unique for each i, $1 \le i\le m$.

Consider $R^{\prime }=U^{*}\cup Z^{*}\cup \left\{z_{m+1}^{*}\right\}$. Then $\left|R^{\prime }\right|=2m+1$.

Additionally, observe that

$$\mathsf{\zeta }\left(x_0\right|R^{\prime }) = (2,2,\dots ,2,2,\dots ,2,2),$$

$$\mathsf{\zeta }\left(x_i\right|R^{\prime }) = (-,-,\dots ,-,3,3,\dots ,3,4),$$

$$\mathsf{\zeta }\left(x_i^{*}\right|R^{\prime }) = (3,3,\dots ,3,-,-,\dots ,-,4),$$

$$\mathsf{\zeta }\left(y\right|R^{\prime }) = (1,1,\dots ,1,4,\dots ,4,5),$$

$$\mathsf{\zeta }(y*|R^{\prime }) = (4,4,\dots ,4,1,\dots ,1,1),$$

Clearly, each vertex in the graph G′ − R′ has unique metric representation with respect to the set R′, and so R′ serves as a resolving set for the graph G′.

Similarly, $x\in \{z_1^{*},z_2^{*},\dots ,z_m^{*},z_{m+1}^{*}\}$, then a connected graph G″ exists such that R − {x} is an RS for G″. This proves the theorem. □

Theorem 2.

If S is a commutative ring with unity such that S is not an integral domain, then the FTEMD of the ZDG of S is finite if S is finite.

Proof. 

First, suppose that S is a finite commutative ring with unity. Then, it is clear that the vertex set of the ZDG of R is finite. It follows that the FTEMD(Γ(S)) has a finite value.

Conversely, let us suppose that the FTEMD(Γ(S) is finite. Let W = {$z_1,z_2,\dots ,z_k$} be a fault-tolerant edge metric basis for the zero-divisor graph Γ(S), and |W| = k, k ≥ 0. Then (by [2] theorem 3), the diameter of Γ(S) ≤ 3 i.e., diam(Γ(S)) ≤ 3, and thus the distance between any two vertices of Γ(S) is an element of the set {0,1,2,3}. The fault-tolerant edge metric representation of an edge e with respect to the set W is ζ_F(e|W) = (d(e,$z_1$),d(e,$z_2$),…,d(e,$z_k$)) and is a k-vector, in which each coordinate is an element of the set {0,1,2,3}. Therefore, there are (3 + 1)^k= 4^k possibilities for ζ_F(e|W). Additionally, since ζ_F(e|W) is unique for each e ∈ E(Γ), so the cardinality of edge set E(Γ) ≤ 4^m. Since the zero-divisor graph is always connected, it follows that the vertex set V (Γ) is finite. Hence, R is finite. □

Theorem 3.

The FTEMD(Γ(S)) is undefined if and only if S is an integral domain.

Proof. 

First, let us suppose that S is an integral domain. It follows that S cannot have non-zero–zero divisors. Thus, the vertex set of Γ(S) is empty, and so the FTEMD(Γ) is undefined.

Conversely, suppose that the FTEMD(Γ(S)) is undefined. It follows that the vertex set of Γ(S) either contains one element only or it is empty because 2 ≤ FTEMD(Γ(S)) ≤ m. Using [14], there does not exist a ring that has exactly one zero divisor and it implies that the vertex set V (Γ(S)) = ϕ. This completes the proof. □

Corollary 1.

The FTEMD of Γ(S) is undefined if and only if S is a field.

Proposition 1.

If S is a finite commutative ring having unity, then FTEMD(Γ(S)) = 2 if S is isomorphic to one of the following rings: ${\mathbb{Z}}_6, {\mathbb{Z}}_8, {\mathbb{Z}}_9, {\mathbb{Z}}_2\times {\mathbb{Z}}_2, {\displaystyle \frac{{\mathbb{Z}}_3\left(r\right)}{\left(r^2\right)}}, {\displaystyle \frac{{\mathbb{Z}}_2\left(r\right)}{\left(r^3\right)}}, or {\displaystyle \frac{{\mathbb{Z}}_4\left[r\right]}{(2r,r^2-2)}}.$

Proof. 

First, let the FTEMD(Γ(S)) = 2. Then, it is clear that dim_e(Γ(S)) = 1, which implies that Γ(S) is a path graph [5], i.e., Γ(S) ≅ P_m. From [28], |Z*(S)| is not more than 3 whenever Γ(S) is a path graph; Γ(S) is either P₂ or P₃.

Case I.

If Γ(S) ≅ P₂, then $Z\left(S\right)=\{u,v\}$ such that $uv=0$, and the rings that satisfy such a condition are ${{\mathbb{Z}}_9,\mathbb{Z}}_2\times {\mathbb{Z}}_2$ and ${\displaystyle \frac{{\mathbb{Z}}_3\left(r\right)}{\left(r^2\right)}}$.

Case II.

If Γ(S) ≅ P₃, then $Z\left(\mathit{S}\right)=\{u,v,w\}$ such that $uv=0$ and $vw=0$, and the rings that satisfy this condition are ${\mathbb{Z}}_6, {\mathbb{Z}}_8, {\displaystyle \frac{{\mathbb{Z}}_2\left(r\right)}{\left(r^3\right)}},$ and ${\displaystyle \frac{{\mathbb{Z}}_4\left[r\right]}{(2r,r^2-2)}}$.

Conversely, the ZDGs of the rings are as follows: ${\mathbb{Z}}_6,{\mathbb{Z}}_8,{\mathbb{Z}}_9,{\mathbb{Z}}_2\times {\mathbb{Z}}_2,{\displaystyle \frac{{\mathbb{Z}}_3\left(\mathrm{r}\right)}{\left({\mathrm{r}}^2\right)}},{\displaystyle \frac{{\mathbb{Z}}_2\left(\mathrm{r}\right)}{\left({\mathrm{r}}^3\right)}},\mathrm{o}\mathrm{r}{\displaystyle \frac{{\mathbb{Z}}_4\left[\mathrm{r}\right]}{(2\mathrm{r},{\mathrm{r}}^2-2)}}$ is either P₂ or P₃ [29]. Additionally, the relation of the zero divisor is not a transitive relation, the dim_e(Γ(S)) = 1, and so FTEMD(Γ(S)) = 2. □

Proposition 2.

If S is a finite commutative having unity, then FTEMD(Γ(S)) = 3 if S is isomorphic to one of the following rings: ${\mathbb{Z}}_3\times {\mathbb{Z}}_3, {\displaystyle \frac{{\mathbb{K}}_4\left[r\right]}{\left[r^2\right]}}, {\displaystyle \frac{{\mathbb{Z}}_4\left[r\right]}{(r^2+r+1)}}, {\displaystyle \frac{{\mathbb{Z}}_4\left[r\right]}{(2,{r)}^2}}, or {\displaystyle \frac{{\mathbb{Z}}_2[r,s]}{(r,{s)}^2}}$.

Proof. 

Given that S is isomorphic to one of the following rings, ${\mathbb{Z}}_3\times {\mathbb{Z}}_3,{\displaystyle \frac{{\mathbb{K}}_4\left[\mathrm{r}\right]}{\left[{\mathrm{r}}^2\right]}},{\displaystyle \frac{{\mathbb{Z}}_4\left[\mathrm{r}\right]}{({\mathrm{r}}^2+\mathrm{r}+1)}},{\displaystyle \frac{{\mathbb{Z}}_4\left[\mathrm{r}\right]}{(2,{\mathrm{r})}^2}},\mathrm{o}\mathrm{r}{\displaystyle \frac{{\mathbb{Z}}_2[\mathrm{r},\mathrm{s}]}{(\mathrm{r},{\mathrm{s})}^2}}$. From [2], it can be seen that the length of the cycle graph for the finite commutative rings cannot be more than 4. Figure 4 represents the ZDGs of the above rings, i.e., the ZDGs of the above rings are cycles, and so by [18], the FTEMD(Γ(S)) = 3. □

Theorem 4.

If R is a finite commutative ring having unity with |Z*(S)|≥ 3 such that there is a cut vertex in Γ(S) but no degree-1 vertex, then FTEMD(Γ(S)) = 6.

Proof. 

Consider a finite commutative ring S with unity such that |Z*(S)| ≥ 3, and there is a cut vertex in Γ(S) but no vertex having a degree of 1. Then (by [30]), S is isomorphic to one of the rings mentioned below:

$${\displaystyle \frac{{\mathbb{Z}}_2[r,\mathrm{s}]}{(r^2,{\mathrm{s}}^2-\mathrm{r}\mathrm{s})}}, {\displaystyle \frac{{\mathbb{Z}}_4\left[r\right]}{(r^2+2\mathrm{r})}}, {\displaystyle \frac{{\mathbb{Z}}_4[r,\mathrm{s}]}{(r^2,{\mathrm{s}}^2-\mathrm{r}\mathrm{s},\mathrm{r}\mathrm{s}-\mathrm{2,2}\mathrm{r},2\mathrm{s})}}, {\displaystyle \frac{{\mathbb{Z}}_8[r,\mathrm{s}]}{({2\mathrm{r},r}^2+4)}} ,$$

(1)

$${\displaystyle \frac{{\mathbb{Z}}_2[r,\mathrm{s}]}{(r^2,{\mathrm{s}}^2)}}, {\displaystyle \frac{{\mathbb{Z}}_4\left[r\right]}{\left(r^2\right)}}, {\displaystyle \frac{{\mathbb{Z}}_4[\mathrm{r},\mathrm{s}]}{({\mathrm{r}}^2,{\mathrm{s}}^2,\mathrm{r}\mathrm{s}-\mathrm{2,2}\mathrm{r},2\mathrm{s})}}.$$

(2)

The ZDGs of the rings given in Equation (1) are presented in Figure 5.

The ZDGs of the rings given in Equation (2) are presented in Figure 6.

For the graph presented in Figure 5 corresponding to the rings presented in Equation (1), the set $W=\{v_1,v_2,v_3,v_4,v_6,v_7\}$ serves as the FTERS. Because the EMD of Γ(S) is 5, the FTEMD(Γ(S)) ≥ 6. It follows that W is the minimum FTERS for Γ(S), and it implies that the FTEMD(Γ(S)) = 6.

For the graph presented in Figure 6 corresponding to the rings presented in Equation (2), the set $W\prime =\{x_1,x_2,x_3,x_4,x_5,x_6\}$ serves as the FTERS. Because the EMD of Γ(S) is 5, the FTEMD(Γ(S)) ≥ 6. It follows that W′ is the minimum FTERS for Γ(S), and it implies that the FTEMD(Γ(S)) = 6. □

4. Conclusions

The fault-tolerant edge-resolving sets for the zero-divisor graphs of finite commutative rings have been examined in this manuscript. Some results related to the existence of a connected graph from a star graph has been also studied. These results can be applied to the study of nanodevices and the structural characteristics of rings. In the future, we are going to study FTEMDs and other recently developed graph parameters for ideal-based zero-divisor graphs and annihilator ideal graphs. One can study the metric dimension and its variants for various rings like Artinian rings and local rings. This can be done by analyzing the graph of the annihilator ideals, Artinian rings, etc. and then taking subsets of their vertices so as to obtain the different resolving sets and then finding bounds for the metric dimension and its variants. One may also characterize classes of rings whose annihilator or zero-divisor graphs have fixed metric dimensions.