Reconstruction of Piecewise Smooth Functions Based on Fourier Extension
Abstract
1. Introduction
- Initial Extension: Compute boundary extensions for the global interval using data near the two endpoints.
- Singularity Identification: Detect intrinsic function discontinuities via Fourier-coefficient-based edge detection.
- Domain Partitioning: Subdivide the interval at identified non-smooth points, yielding sub-intervals with at least first-order differentiability.
- Recursive Refinement: For each sub-interval, repeat boundary-driven extensions and employ Fourier-transform differentiation properties to detect first-order derivative edges. Iteratively apply this process to resolve second-order derivative edges.
- Decoupling of boundary and interior singularities: By restricting initial extensions to the domain boundaries, the method prevents interior discontinuities from contaminating the Fourier coefficients, thereby cleanly separating boundary-induced artifacts from true edges.
- Hierarchical recovery of derivative discontinuities: Leveraging the analytic differentiation properties of the Fourier transform, the method systematically detects discontinuities in successive derivatives, enabling a structured and complete characterization of non-smooth behavior.
- Simultaneous stability and accuracy: By limiting the region of Fourier extension and employing local reconstruction, the method significantly reduces the amplification of singularities in the spectral coefficients, ensuring numerical stability and high approximation accuracy.
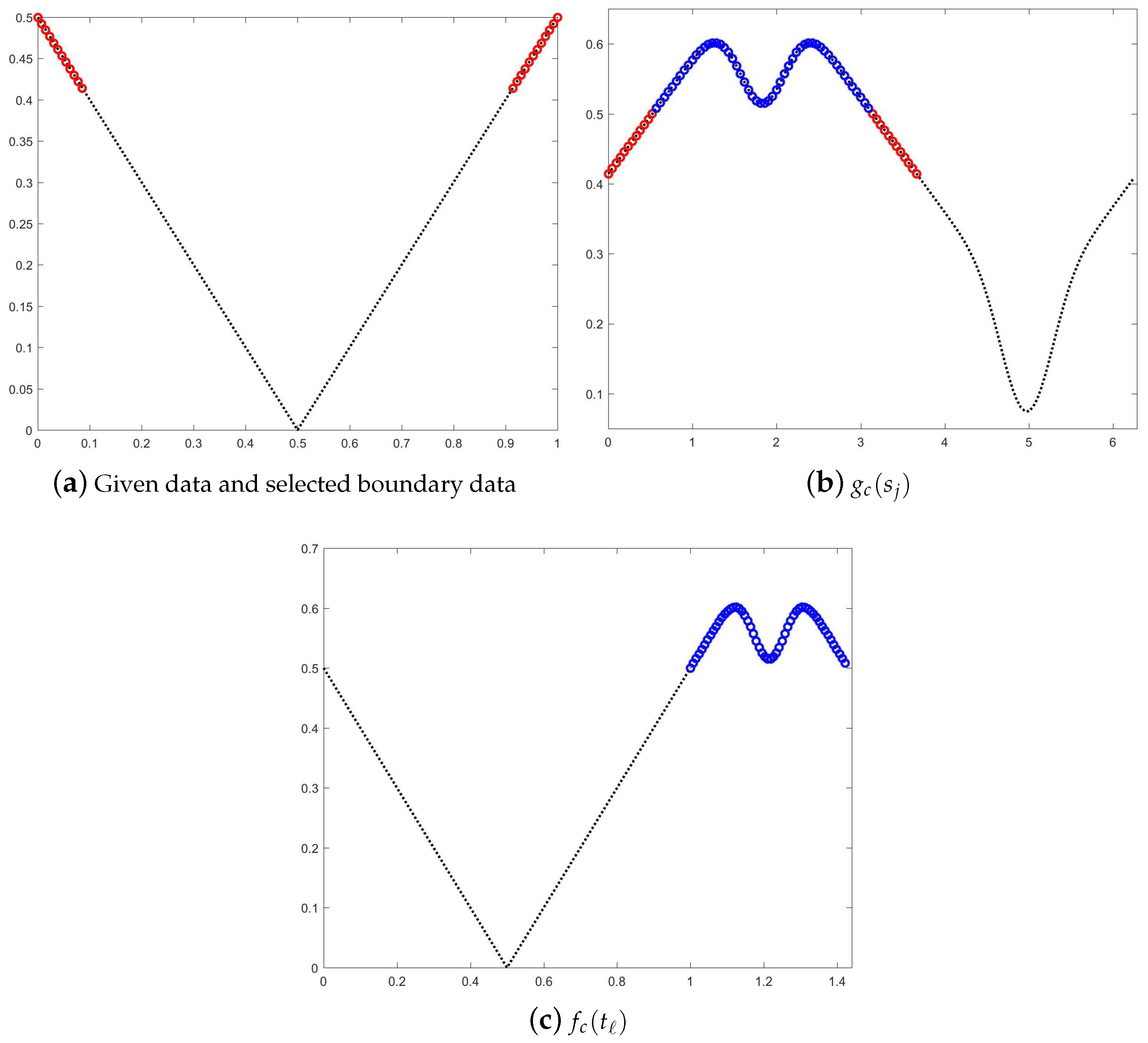
2. Fourier Extension Method Based on Boundary Interval Data
- Weight Simplification: Given the intentionally limited spectral resolution () employed in our extension framework, the weighting coefficients can be unified through the standard form (2). This represents a significant simplification compared to the multi-stage weighting mechanism proposed in [17], while maintaining equivalent regularization effectiveness for small-scale systems.
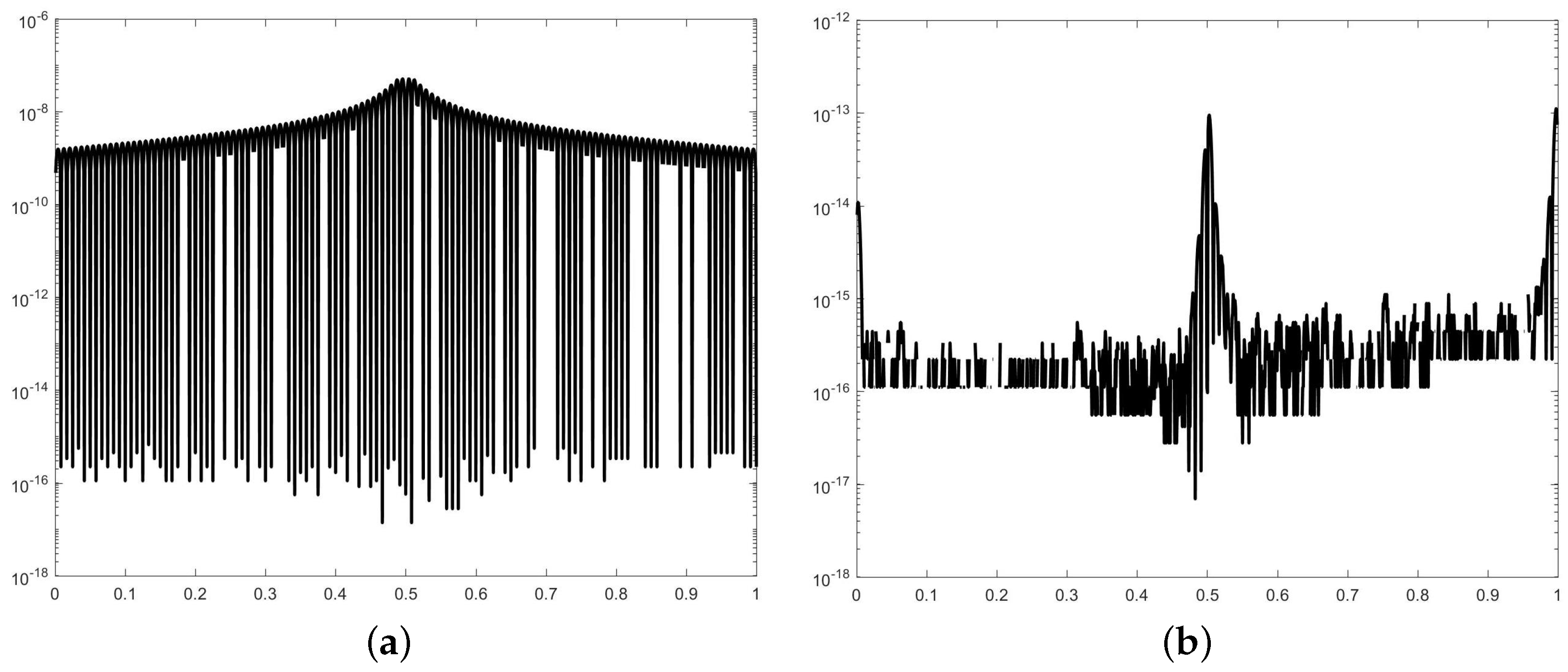
3. Edge Detection of Functions and Their Derivatives
- Fourier Extension: Construct a smooth periodic extension of the original function h using the method described in Section 2, thereby mitigating artificial endpoint effects.
- Spectral Differentiation: Compute the k-th derivative in the frequency domain via the Fourier differentiation property: .
- Edge Detection: Apply the mollified edge detection operator in Equation (7) to the differentiated function, optionally combined with a coordinate transformation for better localization.
4. Reconstruction of Piecewise Smooth Functions with k-Order Discontinuities
- Initialization: Set the initial edge set as .
- For each derivative order , perform the following:
- Local Approximation: On each subinterval defined by the current partition D, compute a Fourier extension of F using the method described in Section 2, incorporating coordinate transformations to handle non-periodic domains.
- Edge Detection: Compute the k-th derivative of the extended function and apply the edge detection Formula (7) (with appropriate coordinate adjustments) to identify potential jump discontinuities in the k-th derivative.
- Update: Incorporate the newly detected edges into D, ensuring that the list remains sorted.
5. Numerical Tests
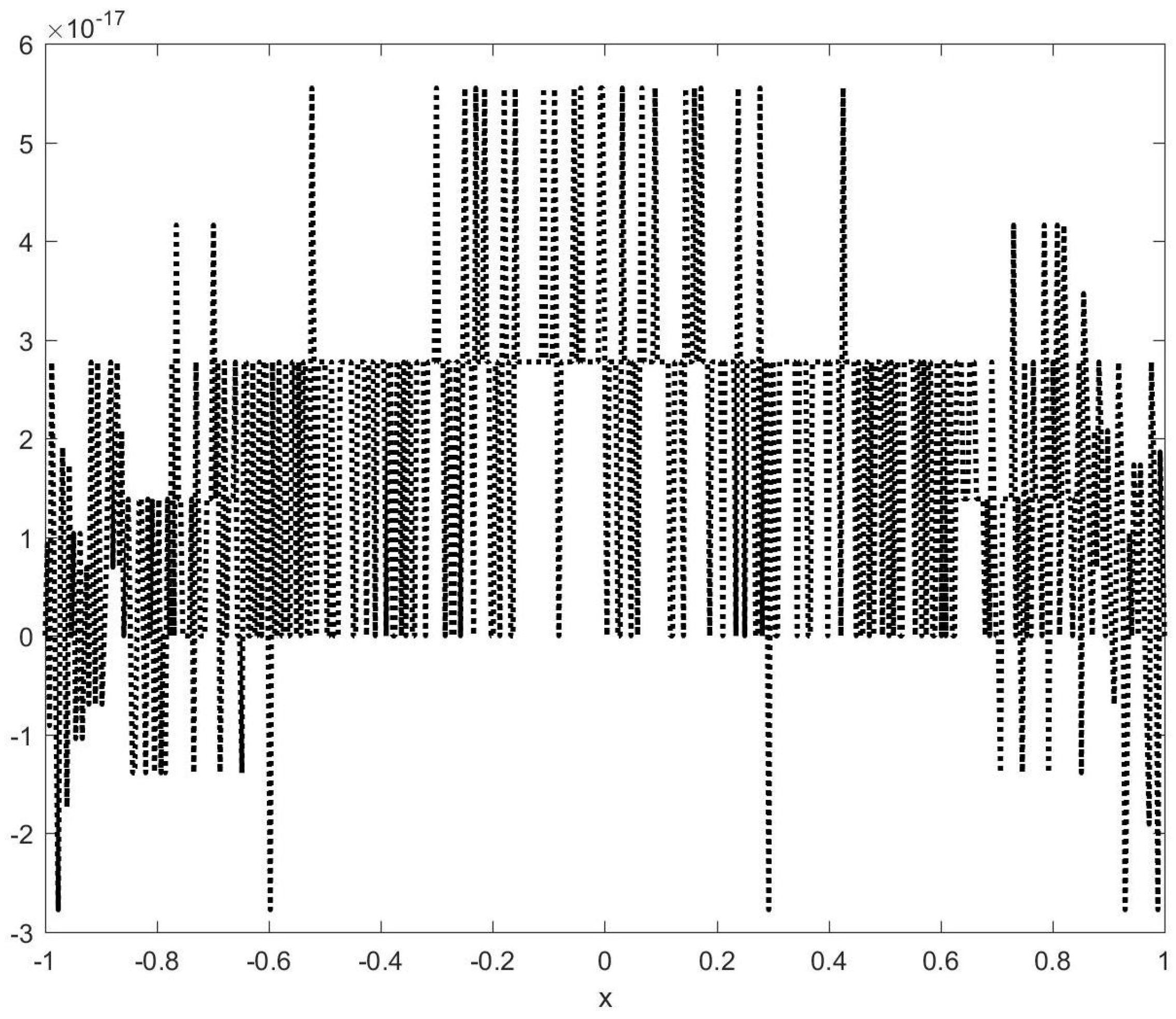
- Error metric: The approximation error is measured as the maximum pointwise difference on a refined evaluation grid, which is 10 times denser than the construction grid.
- Parameters: Regularization parameter ; domain ; initial sampling grid with points.
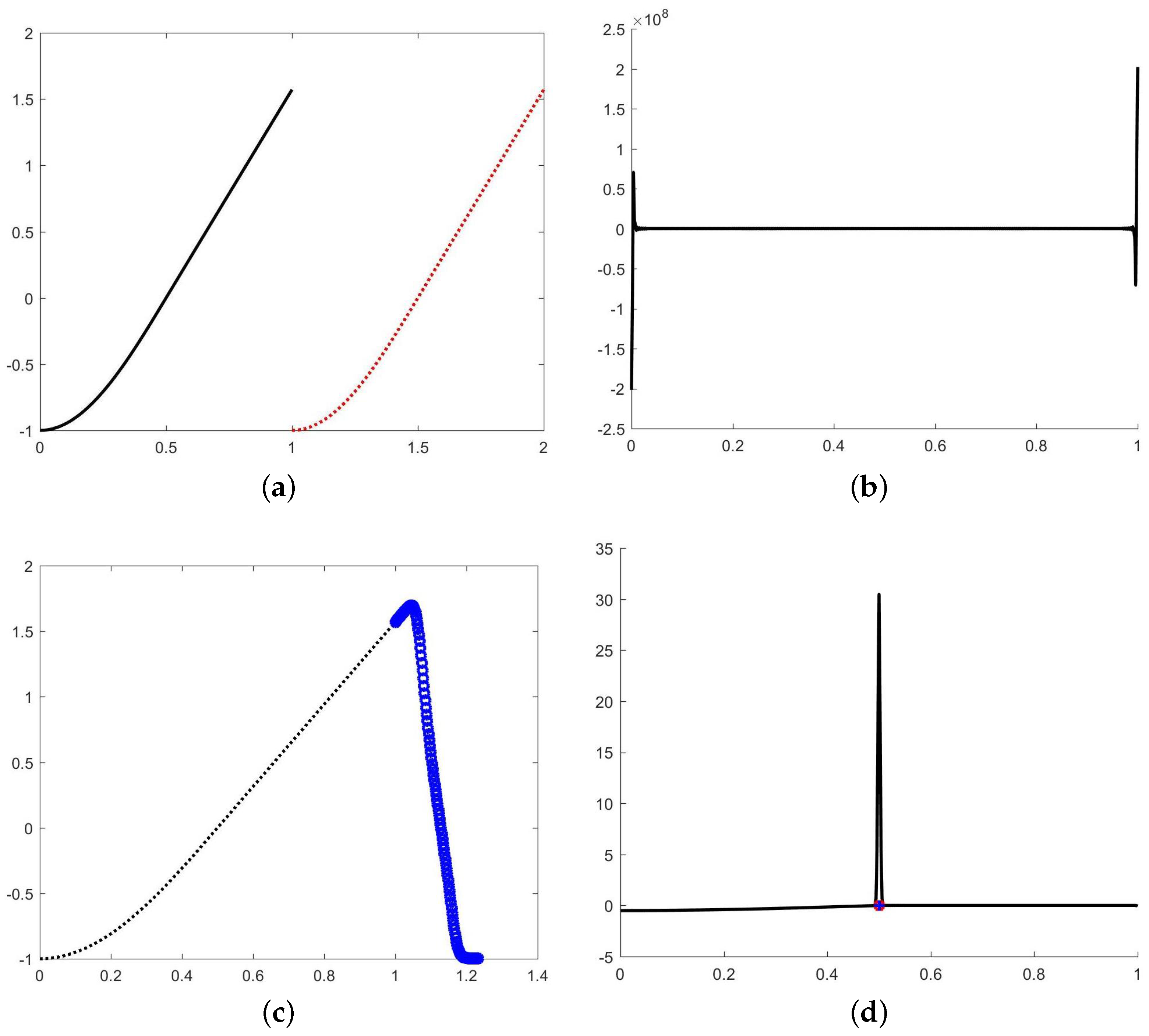
5.1. Example 1: First-Order Derivative Discontinuities
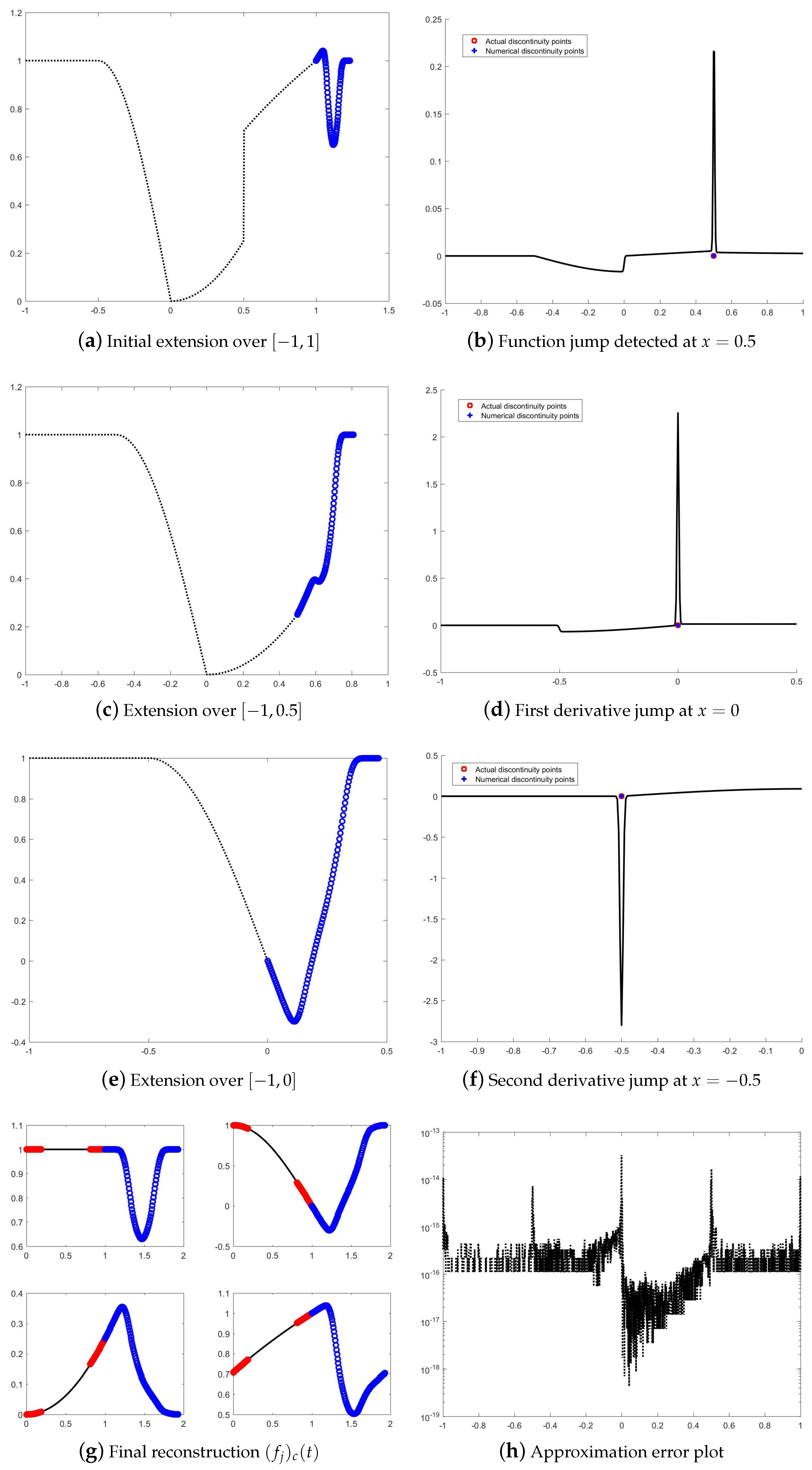
- Figure 4a displays the Fourier extension of F over the entire domain.
- Figure 4b shows the successful detection of all first-order derivative jumps.
- Figure 4c illustrates the reconstructed function on subintervals using localized Fourier extensions.
- Figure 4d confirms that the maximum error is close to machine precision (∼10−14).
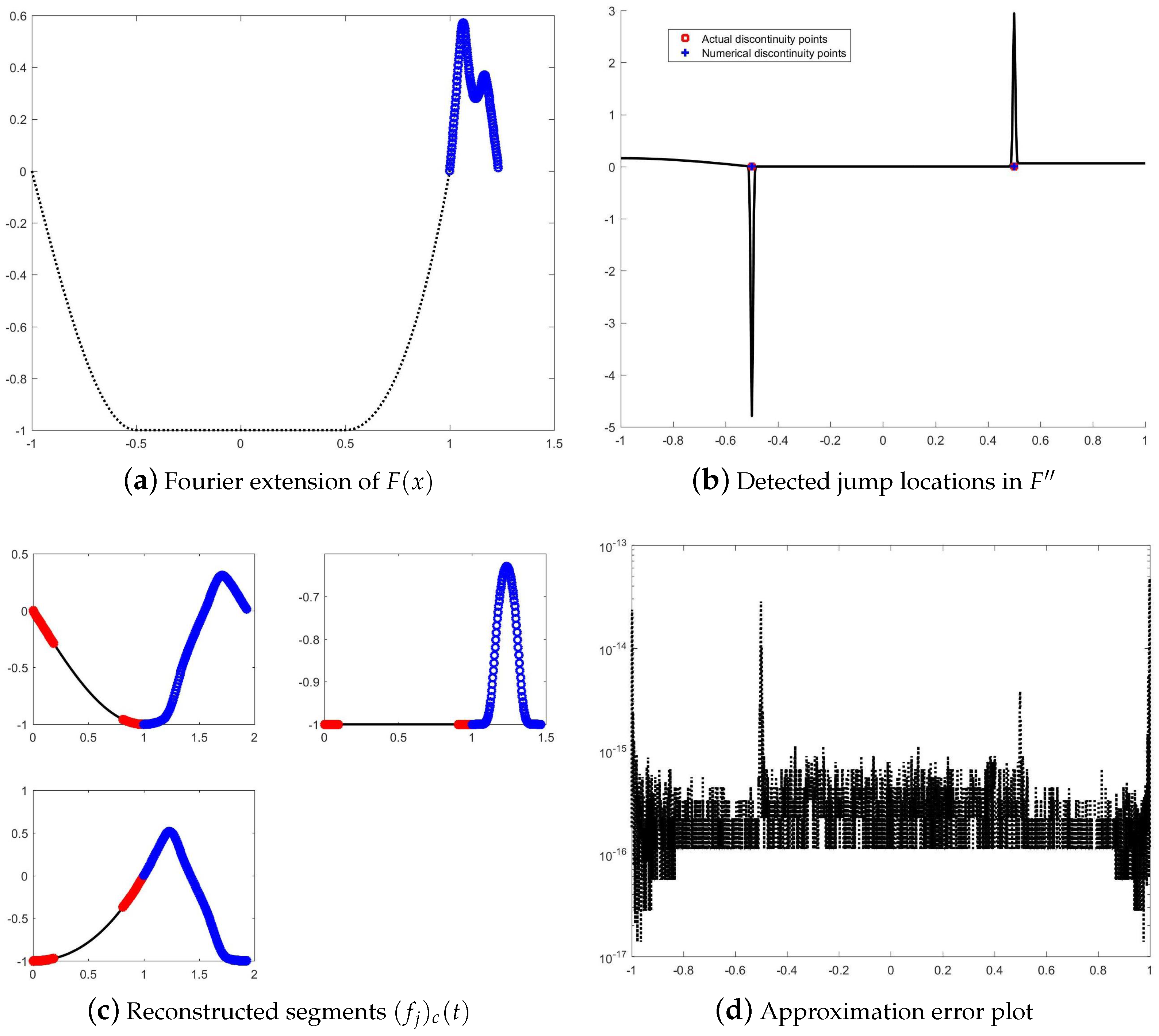
5.2. Example 2: Second-Order Derivative Discontinuities
5.3. Example 3: Mixed-Type Singularities
- A function jump at ;
- A first-order derivative discontinuity at ;
- A second-order derivative discontinuity at .
5.4. Summary of Results
- Accurate and automatic detection of edge locations at various smoothness levels;
- Efficient reconstruction using localized Fourier extensions with error bounded by ;
- Robust performance for both isolated and compound singularity structures.
5.5. Example 4: Apply the Method to Solve Differential Equation
6. Computational Complexity and Comparison with Gegenbauer Reconstruction
6.1. Computational Complexity of the Proposed Method
- Initial Fourier extension over the full domain.
- Iterative edge detection to identify discontinuity points and classify their orders.
- Segment-wise reconstruction via local Fourier extensions on smooth subintervals.
- Fourier extension (global and local): For smooth intervals of size , computing a Fourier extension using FFT-based methods costs . Summing over all intervals yields .
- Edge detection: Assuming d iterative detection stages (e.g., for jumps in F, , and ), the detection cost is , leveraging FFT-based derivative filters.
- Interval assembly: The segmentation and global reconstruction require operations.
6.2. Comparison with Gegenbauer Reconstruction
- Edge detection (using Fourier-based indicators or concentration kernels);
- Gegenbauer polynomial expansion on smooth subintervals;
- Coefficient computation via projection or least-squares.
6.2.1. Complexity Comparison
- Edge detection: Similar to our method, typically .
- Expansion cost: Each interval requires computing M Gegenbauer coefficients, costing . With K subintervals, the total cost is .
- Since M often grows with N to maintain accuracy, the overall complexity can approach in practice.
6.2.2. Qualitative Comparison
- It is highly adaptive, requiring minimal parameter tuning.
- The FFT-based implementation leads to quasi-linear computational complexity.
- It performs well even for functions with multiple and mixed-order singularities.
7. Conclusions
- Boundary Singularity Resolution. By constructing tailored Fourier extensions that span the domain boundaries, we effectively eliminate artificial discontinuities (i.e., “natural breakpoints”) at the endpoints. This preprocessing step is essential for the accurate spectral detection of internal derivative jumps.
- Stable Edge Detection. The extension process uses only data near the domain boundaries, isolating the edge treatment from internal irregularities. This localization ensures that edge information in the derivative spectra is accurately retained without interference, leading to numerically stable and reliable detection of singularities.
- Adaptive Segmentation and Local Reconstruction. After edge detection, the domain is adaptively partitioned into smooth subintervals. On each segment, high-fidelity Fourier extensions are computed independently. This strategy integrates precise singularity localization with the exponential convergence properties of spectral methods on smooth domains.
- Simultaneous handling of multiple, heterogeneous discontinuities;
- High local resolution near singular points;
- Uniform accuracy across discontinuity scales and types.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cockburn, B.; Shu, C.W.; Johnson, C.; Tadmor, E.; Shu, C.W. Essentially Non-Oscillatory and Weighted Essentially Non-Oscillatory Schemes for Hyperbolic Conservation Laws; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Simpson, D.J.W. Bifurcations in Piecewise-Smooth Continuous Systems; World Scientific: Singapore, 2010; Volume 70. [Google Scholar]
- Zhang, D.; Liang, J. Graph-based transform for 2D piecewise smooth signals with random discontinuity locations. IEEE Trans. Image Process. 2017, 26, 1679–1693. [Google Scholar] [CrossRef] [PubMed]
- Nürnberger, G. Approximation by Spline Functions; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Adcock, B.; Hansen, A.C. Stable reconstructions in Hilbert spaces and the resolution of the Gibbs phenomenon. Appl. Comput. Harmon. Anal. 2012, 32, 357–388. [Google Scholar] [CrossRef][Green Version]
- Gelb, A.; Gottlieb, D. The resolution of the Gibbs phenomenon for “spliced” functions in one and two dimensions. Comput. Math. Appl. 1997, 33, 35–58. [Google Scholar] [CrossRef]
- Geer, J.; Banerjee, N.S. Exponentially accurate approximations to piece-wise smooth periodic functions. J. Sci. Comput. 1997, 12, 253–287. [Google Scholar] [CrossRef]
- Boyd, J.P. Chebyshev and Fourier Spectral Methods, 2nd ed.; Dover Publications: New York, NY, USA, 2001. [Google Scholar]
- Eckhoff, K.S. Accurate and efficient reconstruction of discontinuous functions from truncated series expansions. Math. Comput. 1993, 61, 745–763. [Google Scholar] [CrossRef]
- Akansha, S. Piecewise nonlinear approximation for non-smooth functions. Results Appl. Math. 2024, 23, 100491. [Google Scholar] [CrossRef]
- Huybrechs, D. On the Fourier extension of nonperiodic functions. SIAM J. Numer. Anal. 2010, 47, 4326–4355. [Google Scholar] [CrossRef]
- Adcock, B.; Huybrechs, D.; Martín-Vaquero, J. On the numerical stability of Fourier extensions. Found. Comput. Math. 2014, 14, 635–687. [Google Scholar] [CrossRef][Green Version]
- Boyd, J.P. A comparison of numerical algorithms for Fourier extension of the first, second, and third kinds. J. Comput. Phys. 2002, 178, 118–160. [Google Scholar] [CrossRef]
- Matthysen, R.; Huybrechs, D. Function approximation on arbitrary domains using Fourier extension frames. SIAM J. Numer. Anal. 2018, 56, 1360–1385. [Google Scholar] [CrossRef]
- Adcock, B.; Huybrechs, D. On the resolution power of Fourier extensions for oscillatory functions. J. Comput. Appl. Math. 2014, 260, 312–336. [Google Scholar] [CrossRef][Green Version]
- Levin, D. Reconstruction of piecewise smooth multivariate functions from Fourier data. Axioms 2020, 9, 88. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, Y.; Yagola, A.G.; Li, X. A New Approach for Fourier Extension Based on Weighted Generalized Inverse. arXiv 2025, arXiv:2501.16096. [Google Scholar]
- Gelb, A.; Tadmor, E. Detection of edges in spectral data. Appl. Comput. Harmon. Anal. 1999, 7, 101–135. [Google Scholar] [CrossRef]
- Martinez, A.; Gelb, A.; Gutierrez, A. Edge detection from non-uniform Fourier data using the convolutional gridding algorithm. J. Sci. Comput. 2014, 61, 490–512. [Google Scholar] [CrossRef]
- Adcock, B.; Seifi, M. Frame approximation with bounded coefficients. Adv. Comput. Math. 2021, 47, 4. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, Y.; Yagola, A.G. Fast Algorithms for Fourier extension based on boundary interval data. arXiv 2024, arXiv:2409.04265. [Google Scholar]
- Cochran, D.; Gelb, A.; Wang, Y. Edge detection from truncated Fourier data using spectral mollifiers. Adv. Comput. Math. 2013, 38, 737–762. [Google Scholar] [CrossRef]

| Aspect | Proposed Fourier Extension Method | Gegenbauer Reconstruction |
|---|---|---|
| Edge detection | Iterative Fourier-based filters (multi-order) | Typically single-stage, Fourier-based |
| Basis for reconstruction | Local Fourier extensions on smooth subintervals | Gegenbauer polynomials |
| Computational complexity | ||
| Parameter tuning | Fully adaptive | Requires choice of M, |
| Handling mixed singularities | Robust via recursive detection | Limited; may require manual case handling |
| Accuracy | Spectral (∼10−14 observed) | Spectral if parameters are optimal |
| Ease of implementation | Moderate (FFT, segmentation) | More complex (special functions, tuning) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhao, Z.; Jia, X. Reconstruction of Piecewise Smooth Functions Based on Fourier Extension. Axioms 2025, 14, 489. https://doi.org/10.3390/axioms14070489
Li X, Zhao Z, Jia X. Reconstruction of Piecewise Smooth Functions Based on Fourier Extension. Axioms. 2025; 14(7):489. https://doi.org/10.3390/axioms14070489
Chicago/Turabian StyleLi, Xusheng, Zhenyu Zhao, and Xianzheng Jia. 2025. "Reconstruction of Piecewise Smooth Functions Based on Fourier Extension" Axioms 14, no. 7: 489. https://doi.org/10.3390/axioms14070489
APA StyleLi, X., Zhao, Z., & Jia, X. (2025). Reconstruction of Piecewise Smooth Functions Based on Fourier Extension. Axioms, 14(7), 489. https://doi.org/10.3390/axioms14070489





