The Generalized Multistate Complex Network Contagion Dynamics Model and Its Stability
Abstract
1. Introduction
- Our Contributions.
- A new framework for complex network contagion dynamics models is proposed, which can accommodate any number of good states and bad states. Moreover, the specific mathematical form of node interactions in the network is not restricted, meaning that various forms of contagion processes can be discussed within this model. The dynamics of the model are characterized as follows: sufficient conditions for the extinction of bad states under any infection state are provided; the epidemic threshold of the model is derived using the method of lateral stability; and sufficient conditions for the persistence of bad states are also given. The model and its corresponding theory in this chapter are universal and can encompass four existing multi-state complex network epidemic dynamics frameworks and their corresponding theories.
- Three operations on the state transition diagram are proposed to help eliminate the bad states in the system and help the model achieve stability conditions. The effectiveness of these three operations is demonstrated using perturbation theory when the magnitude of the operations is small.
- The theoretical results were validated through numerical simulations on real network data.
- Paper Outline.
- Related Work.
2. Preliminaries
2.1. Concepts and Properties About (Algebraic) Graph Theory and Real Matrices
2.2. Concepts and Properties About Dynamical Systems
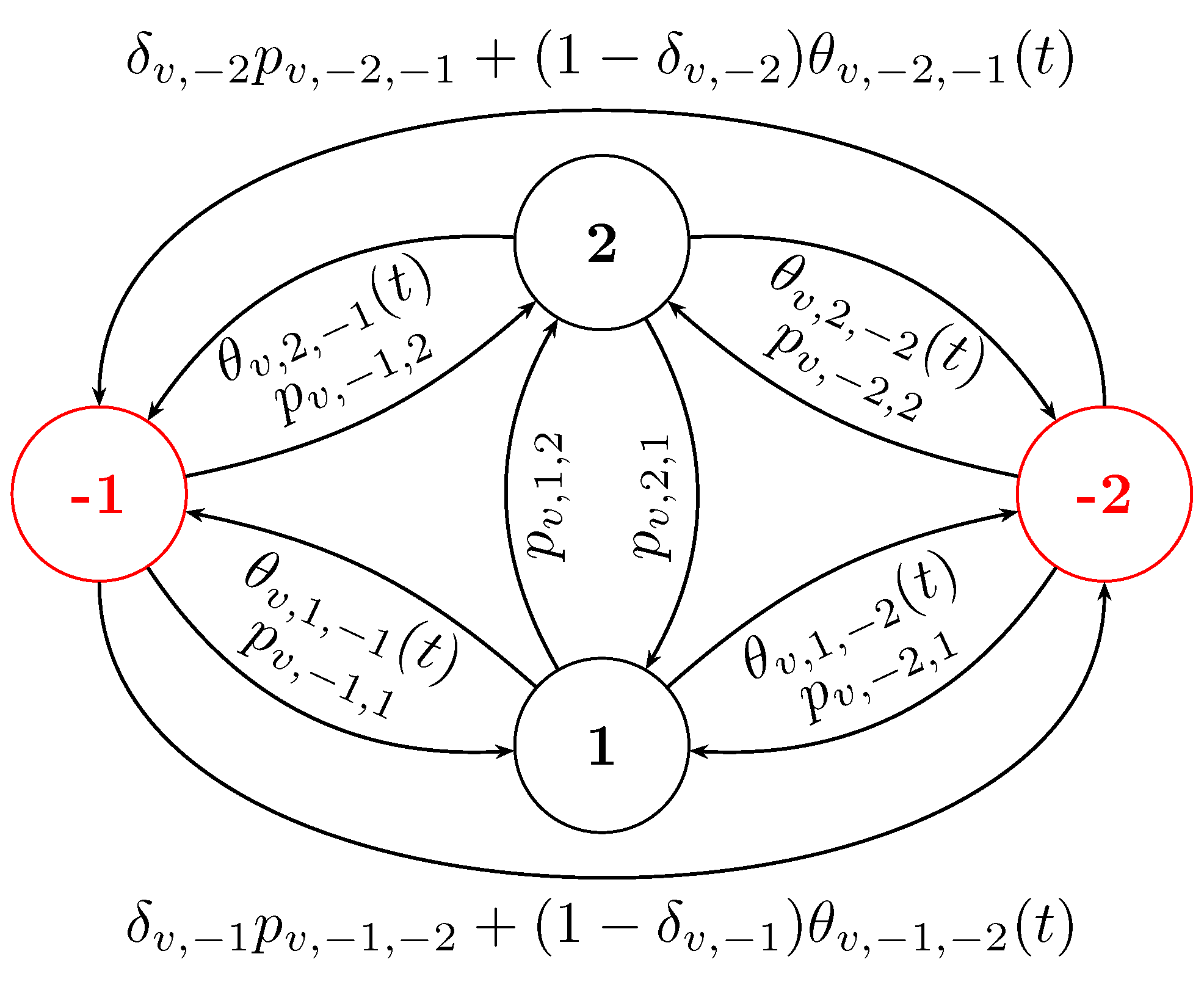
3. Model
3.1. Neighbor-Independent Transitions
3.2. Neighbor-Dependent Transitions
3.3. Master Equation
3.4. Instantiating to Accommodate Existing Models
- is a continuously differentiable function with respect to .
- always hold andwhen , where denotes the symbol for infinitesimals of the same order.
4. Analysis
4.1. Sufficient Conditions for Global Stability
4.2. Sufficient Conditions for the Local Asymptotic Stability of
4.3. Sufficient Conditions for the Persistence of Bad States
4.4. Defense Guidance: The Operations That Reduce and
- Operation 1: Increasing the bad-to-good transition rate where and and , that is, to enhance the recovery speed after being infected by a bad state.
- Operation 2: Decreasing the good-to-bad transition rate where and and , which means reducing the spread rate of the bad states.
- Operation 3: Adding a new special bad state; this new bad state will not infect nodes in a good state, but will infect nodes in other bad states. It can be understood as an active defense strategy in the field of cybersecurity, where a virus patch spreads throughout the network to eliminate the virus [36].
4.5. On the Generality of Our Model and Theoretical Results
5. Numerical Simulation
5.1. Simulation Setup
5.1.1. Instantiating the Network G
- Gnutella05 peer-to-peer network: This is a directed graph, representing a peer-to-peer (P2P) network. It has 8846 nodes, 31,839 arcs, and its adjacency matrix has the largest eigenvalue of . It is not strongly connected.
- Wiki-vote network: The directed network contains all the Wikipedia voting data from the inception of Wikipedia till January 2008. It has 7115 nodes, 103,689 arcs, and its adjacency matrix has the largest eigenvalue of . It is not strongly connected.
- AS-CAIDA (Cooperative Association for Internet Data Analysis) 2004 network: It is a directed network derived from a set of RouteViews BGP table snapshots. It has 16,301 nodes, 65,910 arcs, and its adjacency matrix has the largest eigenvalue of . It is strongly connected.
5.1.2. Setting Model Parameters
5.1.3. Simulation Method
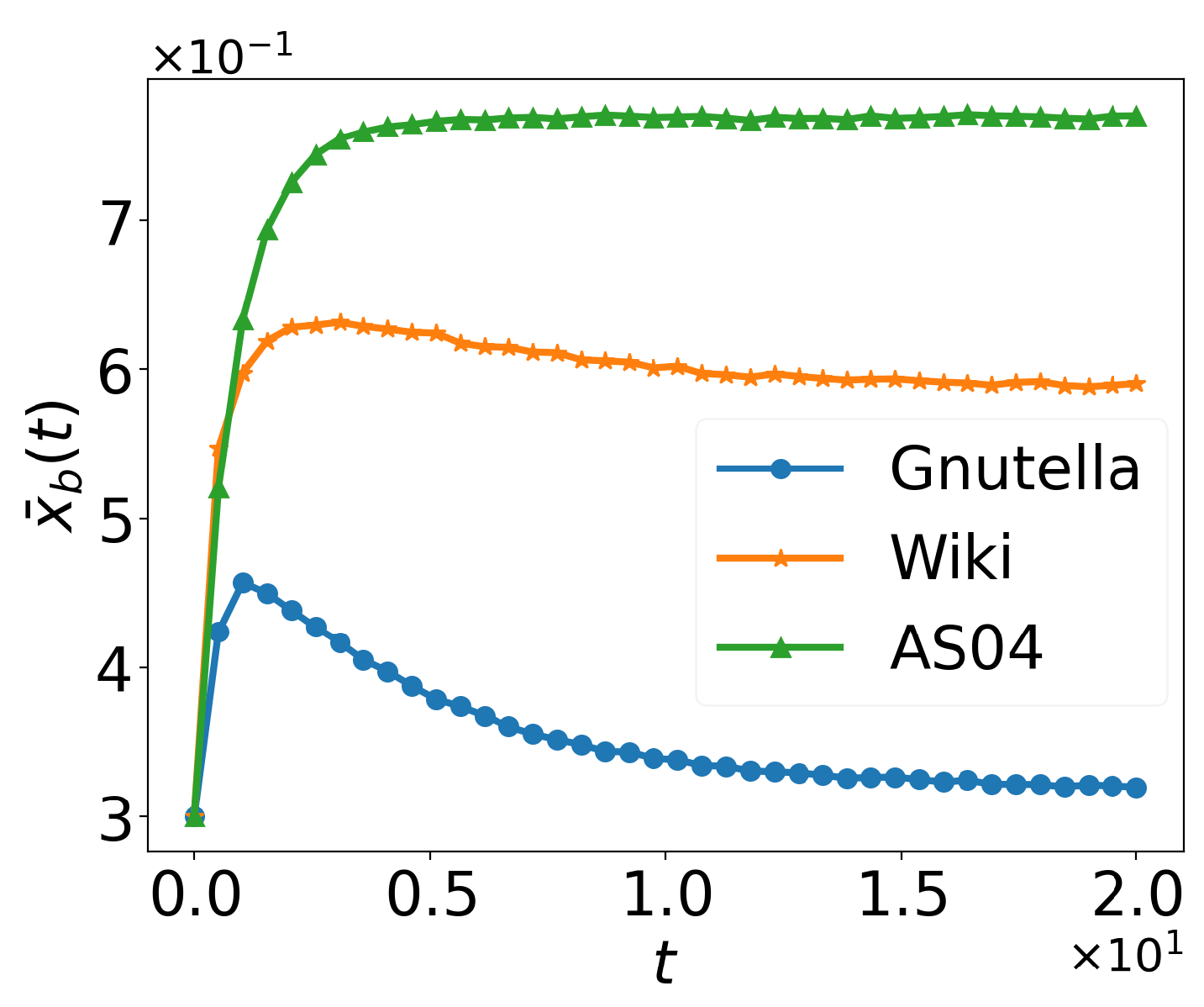
5.2. Confirming ’s Global Asymptotic Stability (Theorem 1)
5.3. Confirming ’s Locally Asymptotic Stability (Theorem 2)
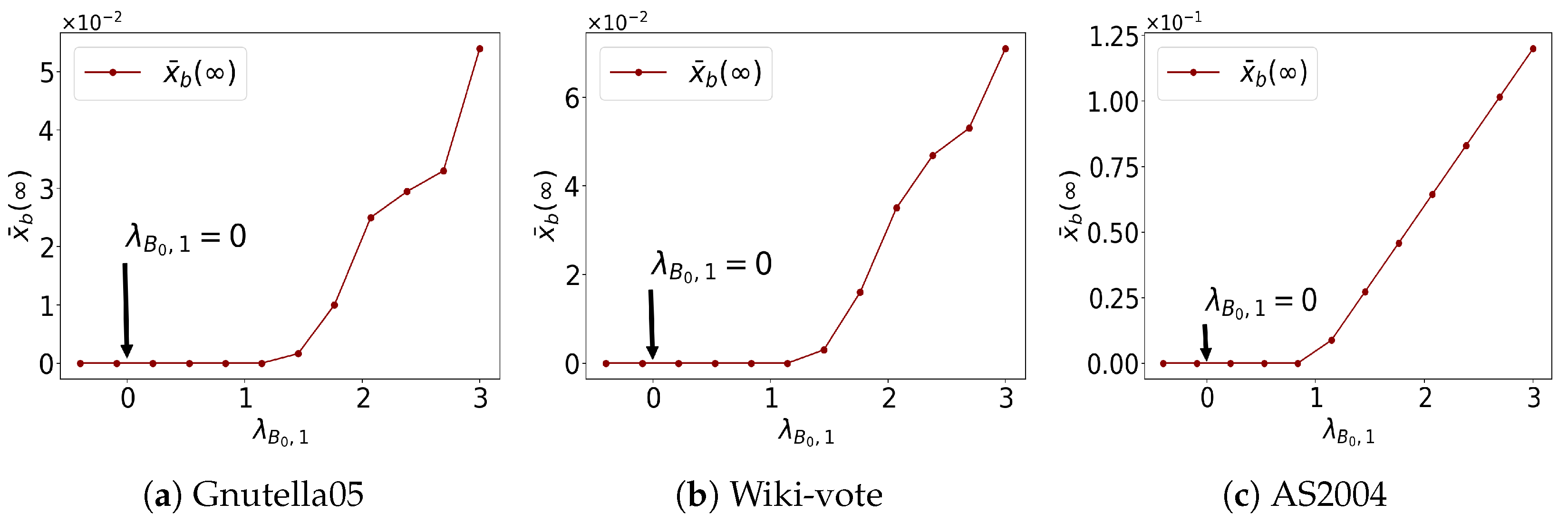
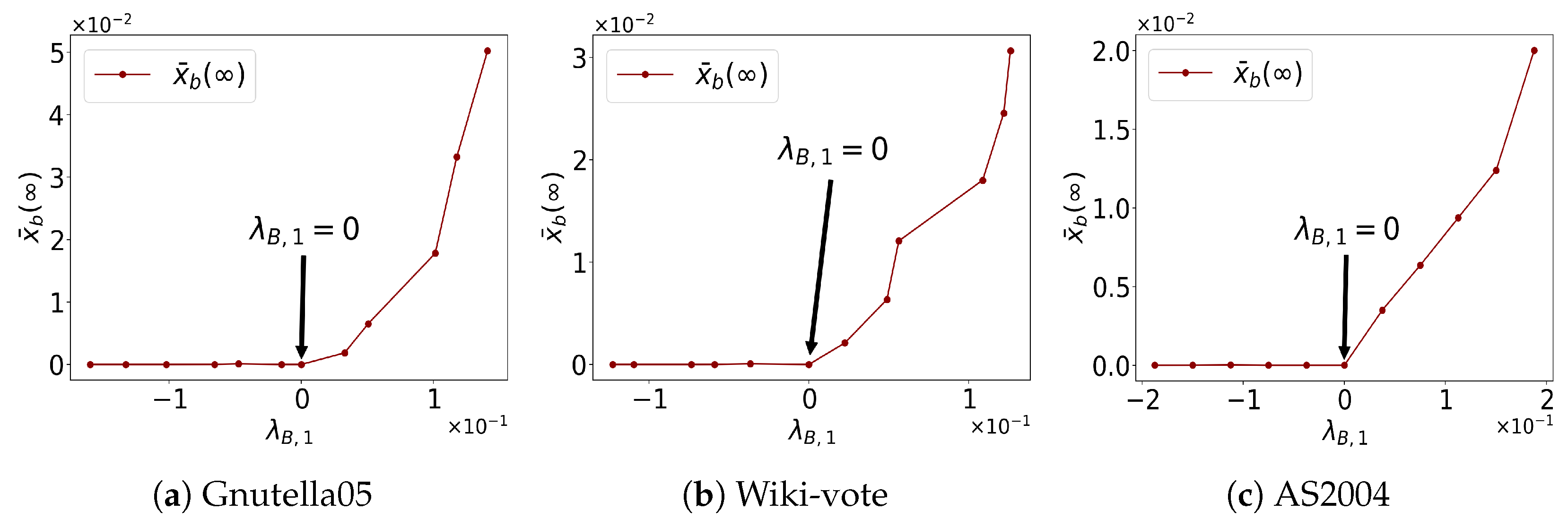
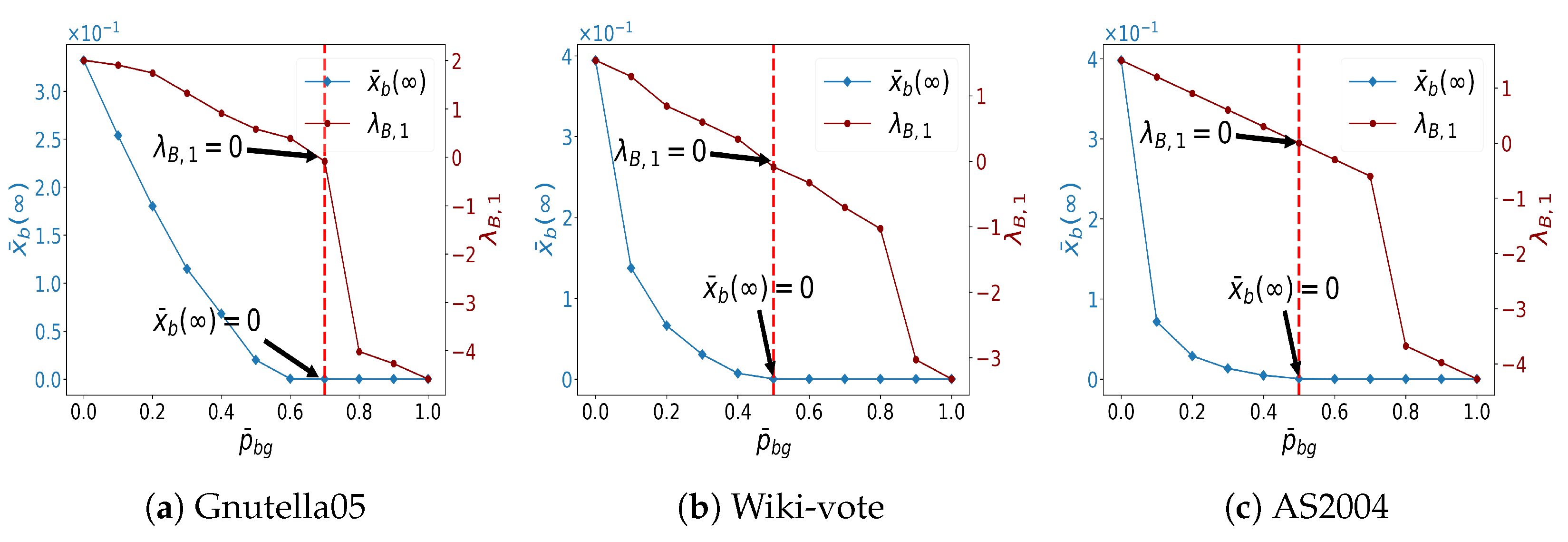
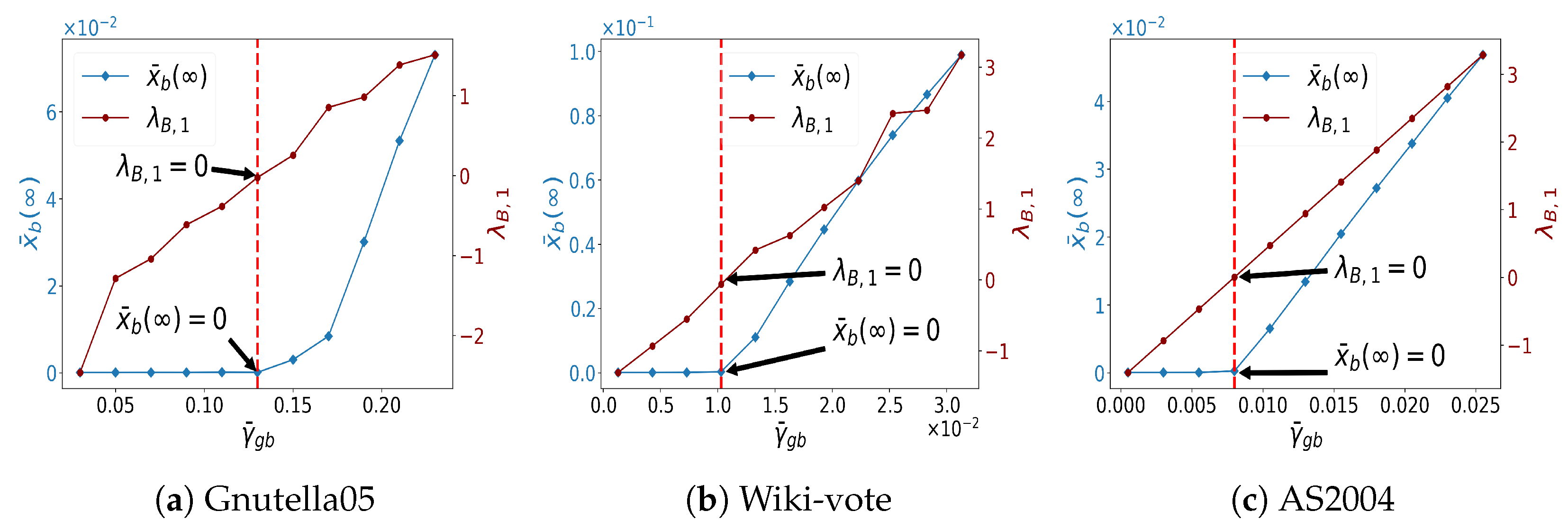
5.4. Sensitivity Analysis Regarding and
5.5. Confirming Persistence of Bad States (Theorems 3)
5.6. Confirming Practical Guidance (Theorems 4)
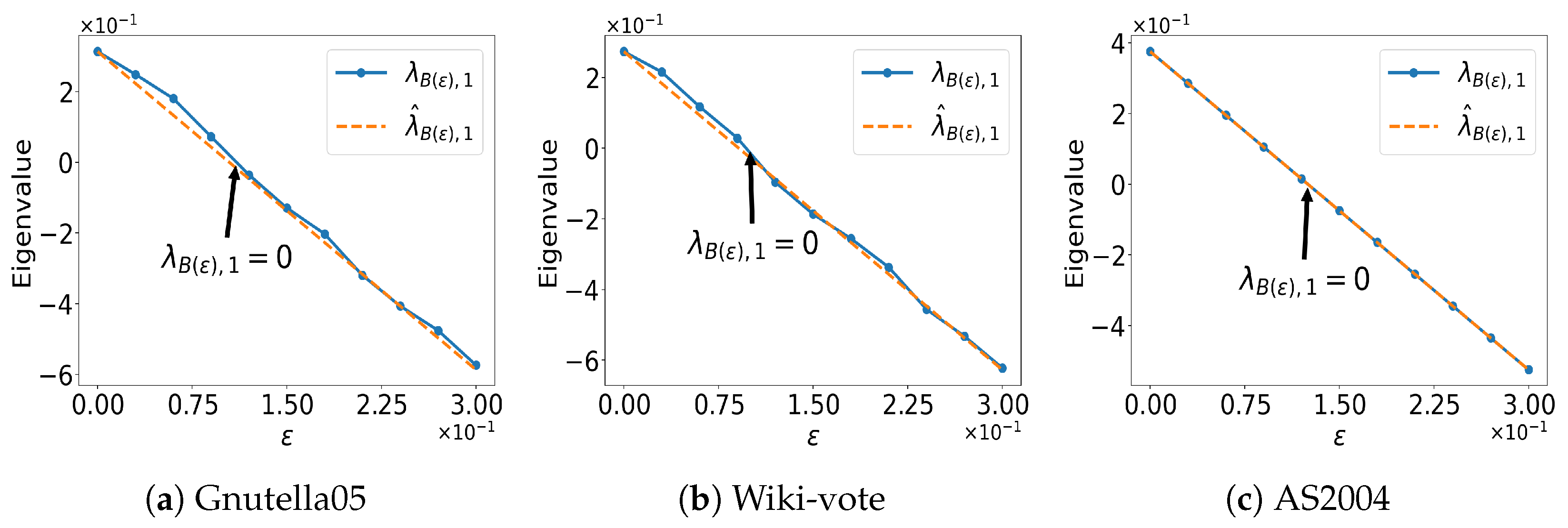
5.6.1. Confirming Operation 1
5.6.2. Confirming Operation 2
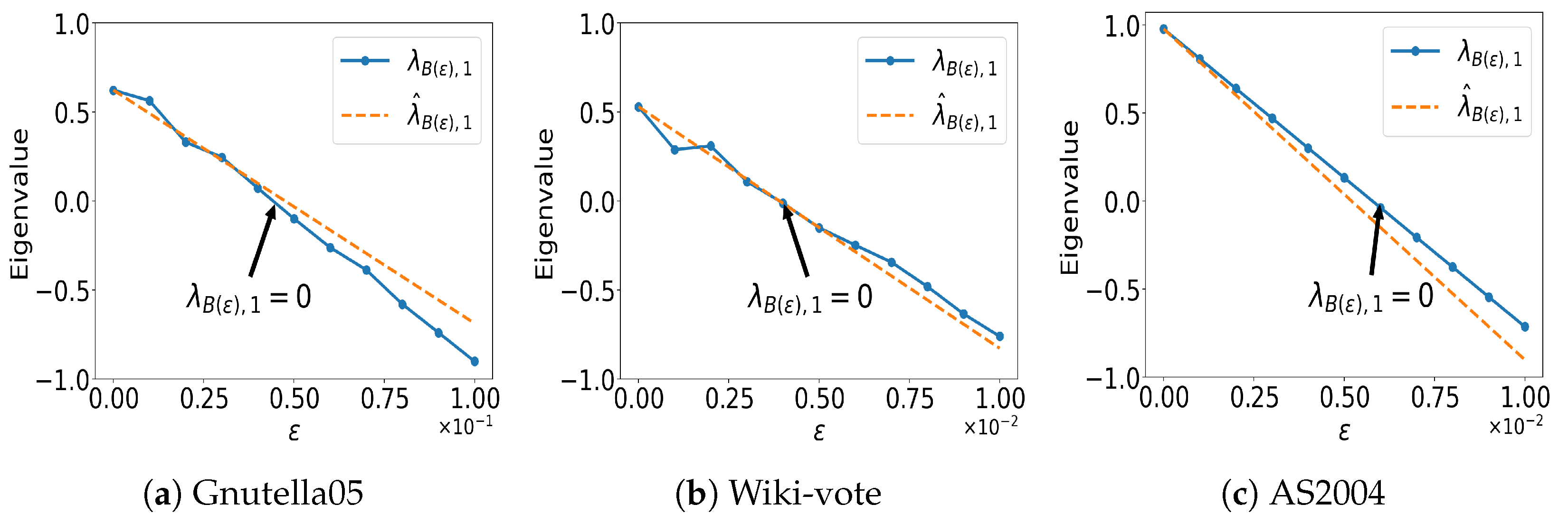
5.6.3. Confirming Operation 3
6. Conclusions and Discussion
6.1. Our Contibutions
6.2. Limitations and Future Work
- Construction of real (simulated) datasets for complex network contagion dynamics: We aim to collect real datasets that contain both dynamic information and underlying network structure, or to construct similar datasets through simulation experiments, such as using virtual machines to simulate the process of computer virus attacks on computer clusters to obtain relevant data. By building these datasets, we can closely integrate the theory of complex network epidemic dynamics with real scenarios, making the corresponding theories more convincing.
- Seeking more efficient modeling methods: To study the impact of network structure on dynamics, the current approach is to explicitly incorporate network structure into the model, which is a common method used in academia. However, this modeling approach results in high model dimensions and significantly increased computational complexity, making it difficult to predict future dynamic behaviors and other practical scenarios. Therefore, it is necessary to find a modeling method that can reflect the influence of network structure while also being solvable quickly.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Lemma A1 and Lemma A2
Appendix B. Proof of the Lemma 5
Appendix C. Proof of the Lemma 4
Appendix D. Proof of Theorem 1, Corollary 1, and Corollary 2
Appendix D.1. Proof of Theorem 1
Appendix D.2. Proof of Corollary 1
Appendix D.3. Proof Corollary 2
Appendix E. Proofs of Lemma 6 and Corollaries 3
Appendix E.1. Proof of Lemma 6
Appendix E.2. Proof of Corollary 3
Appendix F. Proof of Theorem 3 and Corollary 4
Appendix F.1. Proof of Theorem 3
Appendix F.2. Proof of Lemma 3
Appendix G. Proof of the Theorem 4
References
- Epstein, J.M.; Parker, J.; Cummings, D.; Hammond, R.A. Coupled contagion dynamics of fear and disease: Mathematical and computational explorations. PLoS ONE 2008, 3, e3955. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Chakrabarti, D.; Wang, C.; Faloutsos, C. Epidemic spreading in real networks: An eigenvalue viewpoint. In Proceedings of the 22nd International Symposium on Reliable Distributed Systems, Florence, Italy, 6–8 October 2003; pp. 25–34. [Google Scholar] [CrossRef]
- Lin, Z.; Lu, W.; Xu, S. Unified Preventive and Reactive Cyber Defense Dynamics Is Still Globally Convergent. IEEE/ACM ToN 2019, 27, 1098–1111. [Google Scholar] [CrossRef]
- Han, Y.; Lu, W.; Xu, S. Preventive and Reactive Cyber Defense Dynamics with Ergodic Time-dependent Parameters Is Globally Attractive. IEEE TNSE 2021, 8, 2517–2532. [Google Scholar] [CrossRef]
- Zheng, R.; Lu, W.; Xu, S. Active Cyber Defense Dynamics Exhibiting Rich Phenomena. In Proceedings of the 2015 Symposium and Bootcamp on the Science of Security, Urbana, IL, USA, 21–22 April 2015. [Google Scholar]
- Xu, S.; Lu, W.; Li, H. A Stochastic Model of Active Cyber Defense Dynamics. Internet Math. 2015, 11, 23–61. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. Infectious Diseases of Humans: Dynamics and Control; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Zhang, J.; Moura, J.M. Diffusion in social networks as SIS epidemics: Beyond full mixing and complete graphs. IEEE J. Sel. Top. Signal Process. 2014, 8, 537–551. [Google Scholar] [CrossRef]
- She, B.; Liu, J.; Sundaram, S.; Paré, P.E. On a networked SIS epidemic model with cooperative and antagonistic opinion dynamics. IEEE Trans. Control. Netw. Syst. 2022, 9, 1154–1165. [Google Scholar] [CrossRef]
- Huang, J.; Ma, X.; Wu, H.; Awuxi, H.; Zhang, X.; Chen, Y.; Alitengsaier, N.; Li, Q. Retrospective study on the epidemiological characteristics of multi-pathogen infections of hospitalized severe acute respiratory tract infection and influenza-like illness in Xinjiang from January to May 2024. BMC Infect. Dis. 2025, 25, 252. [Google Scholar] [CrossRef]
- Akhtar, Z.B. Securing operating systems (OS): A comprehensive approach to security with best practices and techniques. Int. J. Adv. Network, Monit. Control. 2024, 9, 100–111. [Google Scholar] [CrossRef]
- Bontchev, V. Possible macro virus attacks and how to prevent them. Comput. Secur. 1996, 15, 595–626. [Google Scholar] [CrossRef]
- Pawar, M.V.; Anuradha, J. Network security and types of attacks in network. Procedia Comput. Sci. 2015, 48, 503–506. [Google Scholar] [CrossRef]
- Cremer, F.; Sheehan, B.; Fortmann, M.; Kia, A.N.; Mullins, M.; Murphy, F.; Materne, S. Cyber risk and cybersecurity: A systematic review of data availability. Geneva Pap. Risk Insur. Issues Pract. 2022, 47, 698. [Google Scholar] [CrossRef]
- Li, M.Y.; Muldowney, J.S. Global stability for the SEIR model in epidemiology. Math. Biosci. 1995, 125, 155–164. [Google Scholar] [CrossRef] [PubMed]
- Paré, P.E.; Vrabac, D.; Sandberg, H.; Johansson, K.H. Analysis, Online Estimation, and Validation of a Competing Virus Model. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 2556–2561. [Google Scholar] [CrossRef]
- Basnarkov, L. SEAIR Epidemic spreading model of COVID-19. Chaos Solitons Fractals 2021, 142, 110394. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; Lu, W.; Zhan, Z. A Stochastic Model of Multivirus Dynamics. IEEE Trans. Dependable Secur. Comput. 2012, 9, 30–45. [Google Scholar] [CrossRef]
- Prakash, B.A.; Chakrabarti, D.; Faloutsos, M.; Valler, N.; Faloutsos, C. Threshold Conditions for Arbitrary Cascade Models on Arbitrary Networks. In Proceedings of the 2011 IEEE 11th International Conference on Data Mining, Vancouver, BC, Canada, 11–14 December 2011; pp. 537–546. [Google Scholar] [CrossRef]
- Sahneh, F.D.; Scoglio, C.; Van Mieghem, P. Generalized epidemic mean-field model for spreading processes over multilayer complex networks. IEEE/ACM Trans. Netw. 2013, 21, 1609–1620. [Google Scholar] [CrossRef]
- Brandon, J. Introduction to applied nonlinear dynamical systems and chaos, by S Wiggins. Pp 672. DM98.00. 1990. ISBN 3-540-9703-7 (Springer). Math. Gaz. 1991, 75, 255. [Google Scholar] [CrossRef]
- Green, S.L. Ordinary Differential Equations. By Jack K. Hale. Pp. xvi, 332. 1969. (Wiley-Interscience). Math. Gaz. 1971, 55, 485–486. [Google Scholar] [CrossRef]
- Gray, A.; Greenhalgh, D.; Hu, L.; Mao, X.; Pan, J. A stochastic differential equation SIS epidemic model. SIAM J. Appl. Math. 2011, 71, 876–902. [Google Scholar] [CrossRef]
- Zheng, R.; Lu, W.; Xu, S. Preventive and Reactive Cyber Defense Dynamics Is Globally Stable. IEEE TNSE 2018, 5, 156–170. [Google Scholar] [CrossRef]
- Persoons, R.; Van Mieghem, P. Finding patient zero in susceptible-infectious-susceptible epidemic processes. Phys. Rev. E 2024, 110, 044308. [Google Scholar] [CrossRef]
- Chakrabarti, D.; Wang, Y.; Wang, C.; Leskovec, J.; Faloutsos, C. Epidemic thresholds in real networks. ACM Trans. Inf. Syst. Secur. 2008, 10, 1–26. [Google Scholar] [CrossRef]
- Van Mieghem, P.; Omic, J.; Kooij, R. Virus Spread in Networks. IEEE/ACM Trans. Netw. 2009, 17, 1–14. [Google Scholar] [CrossRef]
- Mieghem, P.V. The N-intertwined SIS epidemic network model. Computing 2011, 93, 147–169. [Google Scholar] [CrossRef]
- Xu, S.; Lu, W.; Xu, L. Push- and pull-based epidemic spreading in networks: Thresholds and deeper insights. ACM TAAS 2012, 7, 1–26. [Google Scholar] [CrossRef]
- Xu, S. The Cybersecurity Dynamics Way of Thinking and Landscape (invited paper). In Proceedings of the ACM Workshop on Moving Target Defense, Los Angeles, CA, USA, 7 November 2022. [Google Scholar]
- Paré, P.E.; Liu, J.; Beck, C.L.; Nedić, A.; Başar, T. Multi-competitive viruses over time-varying networks with mutations and human awareness. Automatica 2021, 123, 109330. [Google Scholar] [CrossRef]
- Chakrabarti, D.; Leskovec, J.; Faloutsos, C.; Madden, S.; Guestrin, C.; Faloutsos, M. Information Survival Threshold in Sensor and P2P Networks. In Proceedings of the IEEE INFOCOM 2007—26th IEEE International Conference on Computer Communications, Anchorage, AK, USA, 6–12 May 2007; pp. 1316–1324. [Google Scholar] [CrossRef]
- Ashwin, P.; Buescu, J.; Stewart, I.N. From attractor to chaotic saddle: A tale of transverse instability. Nonlinearity 1996, 9, 703–737. [Google Scholar] [CrossRef]
- Strom, B.E.; Applebaum, A.; Miller, D.P.; Nickels, K.C.; Pennington, A.G.; Thomas, C.B. Mitre Att&CK: Design and Philosophy; Technical Report; The MITRE Corporation: McLean, VA, USA, 2018. [Google Scholar]
- Carlton, M.; Levy, Y. Cybersecurity skills: Foundational theory and the cornerstone of advanced persistent threats (APTs) mitigation. Online J. Appl. Knowl. Manag. (OJAKM) 2017, 5, 16–28. [Google Scholar] [CrossRef]
- Eshghi, S.; Khouzani, M.; Sarkar, S.; Venkatesh, S.S. Optimal patching in clustered epidemics of malware. IEEE Trans. Netw. 2015, 24, 283–298. [Google Scholar] [CrossRef]
- Liu, Z.; Zheng, R.; Lu, W.; Xu, S. Using event-based method to estimate cybersecurity equilibrium. IEEE/CAA J. Autom. Sin. 2020, 8, 455–467. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Milanese, A.; Sun, J.; Nishikawa, T. Approximating spectral impact of structural perturbations in large networks. Phys. Rev. E 2010, 81, 046112. [Google Scholar] [CrossRef]
- Mitchell, A.R. J. H. Wilkinson, The Algebraic Eigenvalue Problem (Clarendon Press, Oxford, 1965), 662pp., 110s. Proc. Edinb. Math. Soc. 1967, 15, 328. [Google Scholar] [CrossRef]
- Shilnikov, L.P.; Shilnikov, A.L.; Turaev, D.V.; Chua, L.O. Methods of Qualitative Theory in Nonlinear Dynamics: (Part II); World Scientific: Singapore, 2001. [Google Scholar]
- Kellogg, R.B.; Li, T.Y.; Yorke, J. A Constructive Proof of the Brouwer Fixed-Point Theorem and Computational Results. SIAM J. Numer. Anal. 1976, 13, 473–483. [Google Scholar] [CrossRef]

| Notation | Description |
|---|---|
| #, , | # the size of a set; the real part of a complex number; the modulus of a complex number or the absolute value of a real number |
| is a diagonal matrix with diagonal elements | |
| the set of non-negative real numbers | |
| the ℓ-th eigenvalue of matrix H in the descending order of their real parts, | |
| G, A | directed graph and its adjacency matrix |
| , , , n, m | is the set of n good states; is the set of m bad states; |
| , | is the d-dimension identity matrix; is the zero matrix |
| ⊙ | the Hadamard product (element-wise product between matrices) |
| infinitesimals of the same order | |
| the set of eigenvalues of a matrix, the spectral radius of a matrix | |
| state of node u at time t | |
| , | the neighbor-independent transition rate of node v where and , and |
| , | the probability that Type 1 bad-to-bad transition occurs on node v where and |
| , | the transition rate that node u in state attacks node v in state to cause v’s state changes from i to , |
| the transition rate that the state of node v is at time t and becomes at time as . | |
| manifold { for } | |
| manifold for } | |
| the fixed point on | |
| , | is the probability that node is in state at time t, is the i-th entry of the fixed point of System (2), and |
| the Jacobian matrix of System (2) | |
| Indicator function |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Lu, W.; Xu, S. The Generalized Multistate Complex Network Contagion Dynamics Model and Its Stability. Axioms 2025, 14, 487. https://doi.org/10.3390/axioms14070487
Wang Y, Lu W, Xu S. The Generalized Multistate Complex Network Contagion Dynamics Model and Its Stability. Axioms. 2025; 14(7):487. https://doi.org/10.3390/axioms14070487
Chicago/Turabian StyleWang, Yinchong, Wenlian Lu, and Shouhuai Xu. 2025. "The Generalized Multistate Complex Network Contagion Dynamics Model and Its Stability" Axioms 14, no. 7: 487. https://doi.org/10.3390/axioms14070487
APA StyleWang, Y., Lu, W., & Xu, S. (2025). The Generalized Multistate Complex Network Contagion Dynamics Model and Its Stability. Axioms, 14(7), 487. https://doi.org/10.3390/axioms14070487





