Bayesian Quantile Regression for Partial Functional Linear Spatial Autoregressive Model
Abstract
:1. Introduction
2. Model and Likelihood
2.1. Model
2.2. Likelihood
3. Bayesian Quantile Regression
3.1. Priors
3.2. Posterior Inference
- Step 1
- Select the initial values of . Set ;
- Step 2
- A posterior sample is extracted from the posterior distribution of each parameter.
- Step 3
- Set and go to Step 2 until J, where J is the number of iteration times.
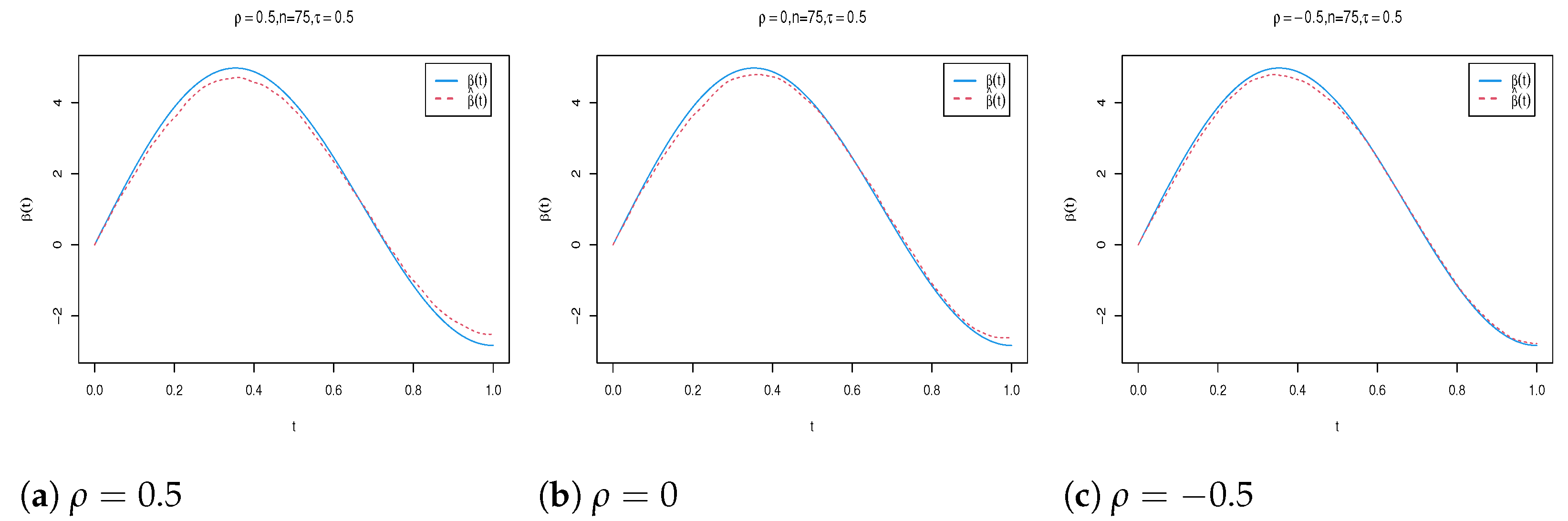
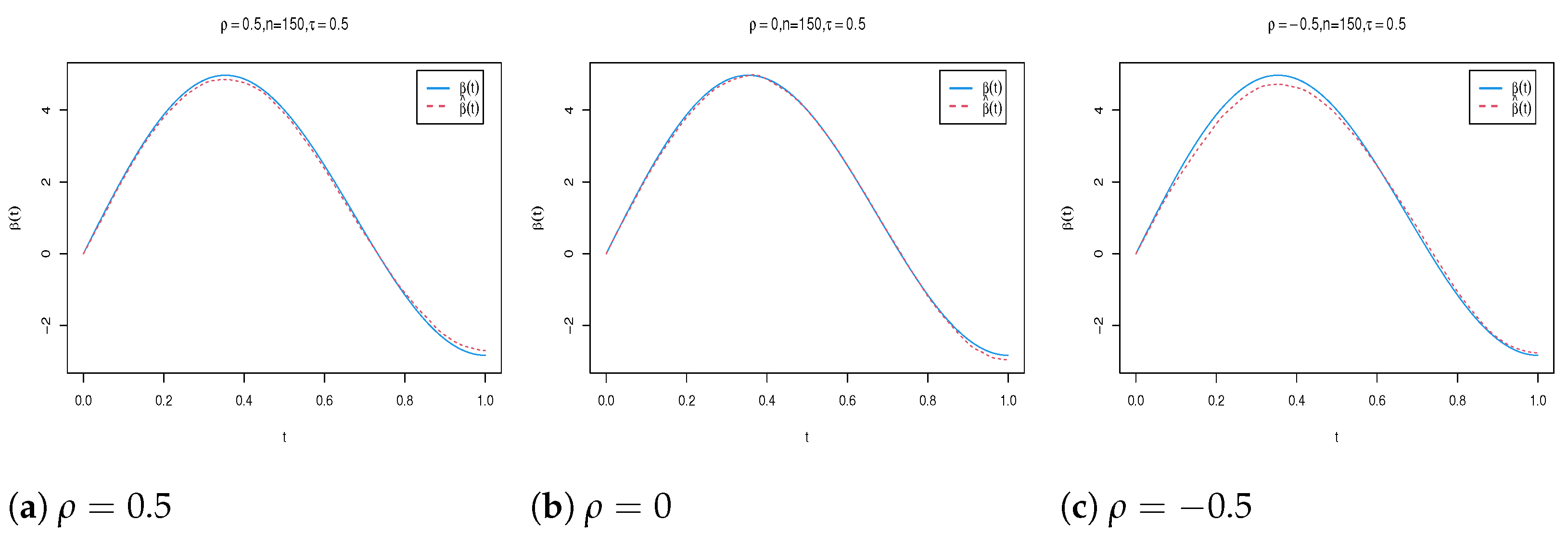
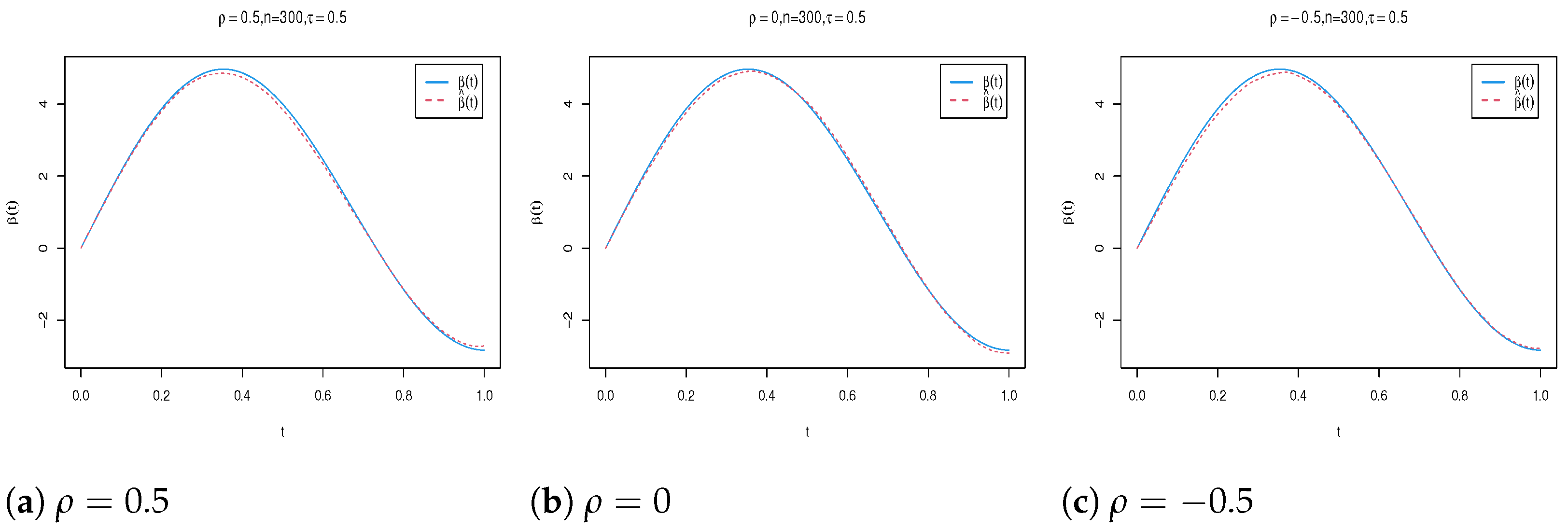
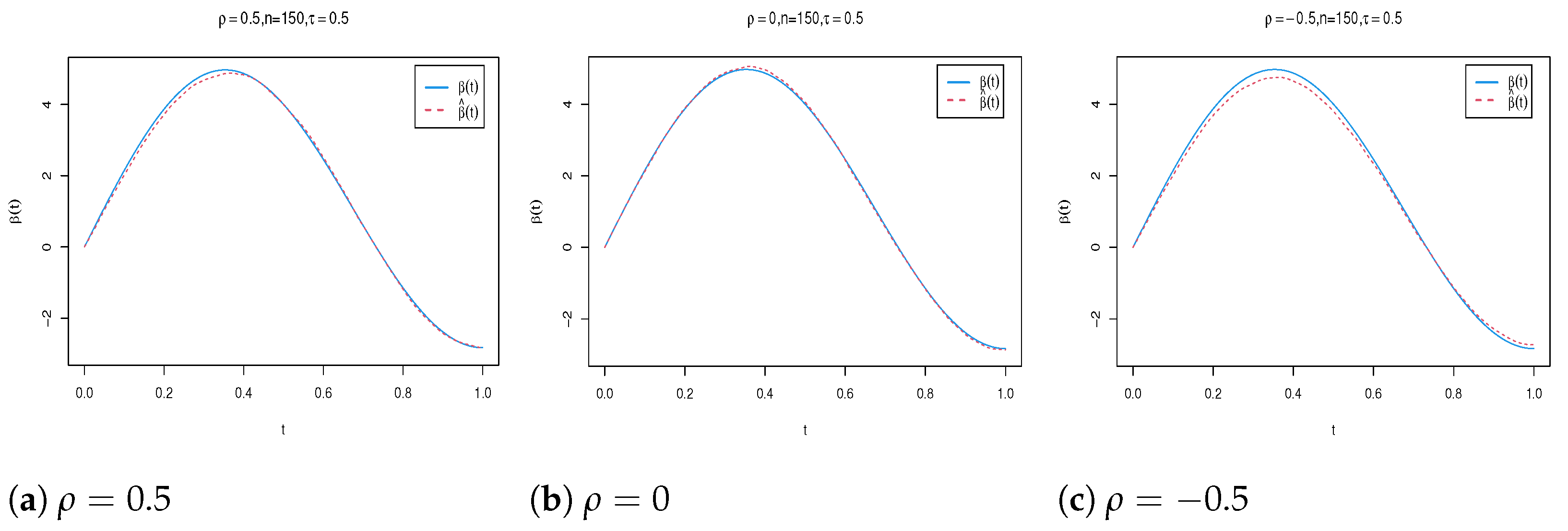
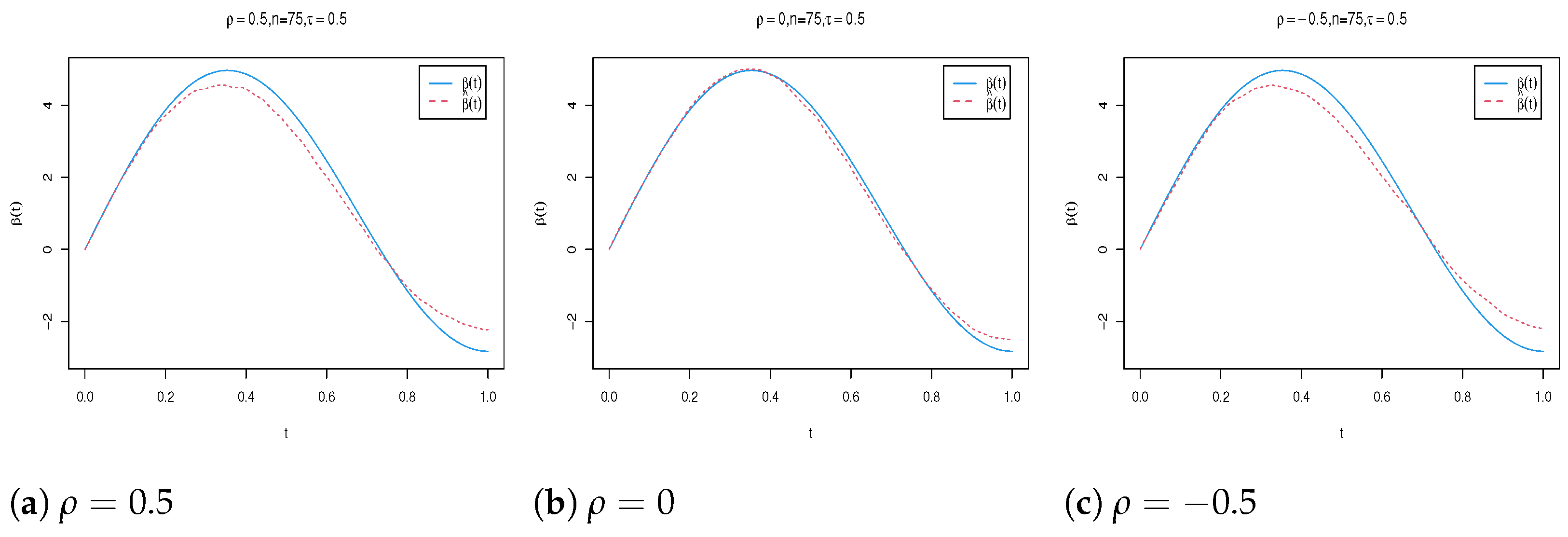
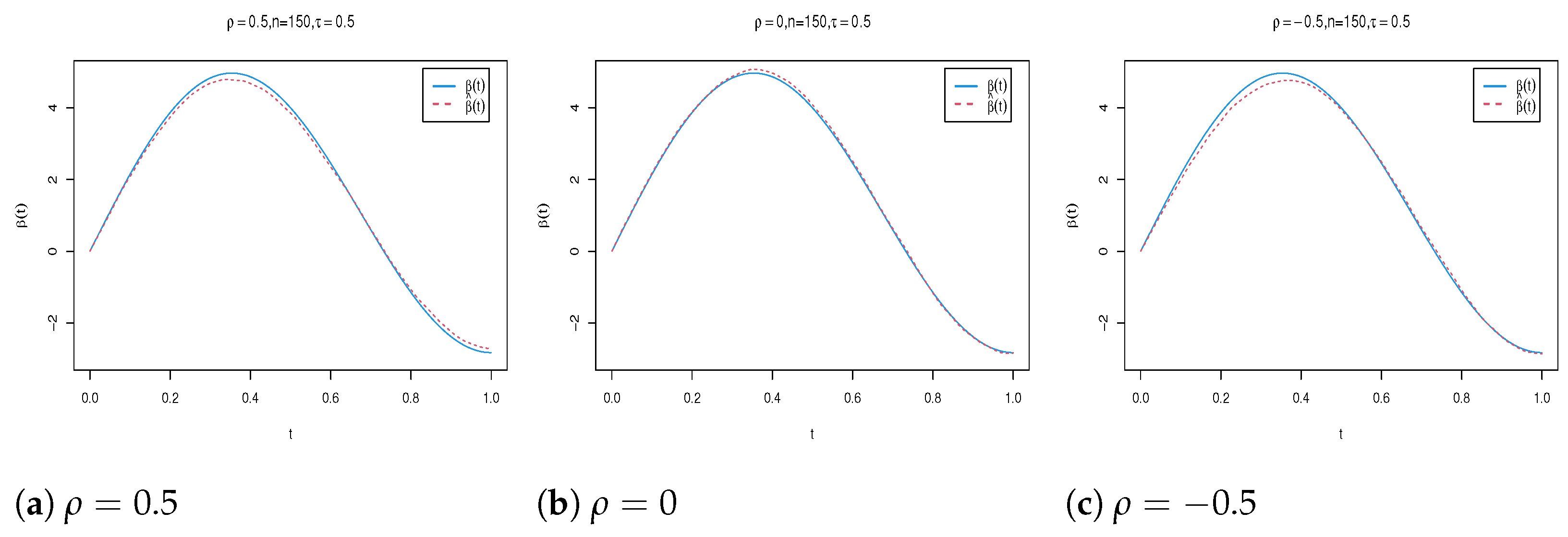
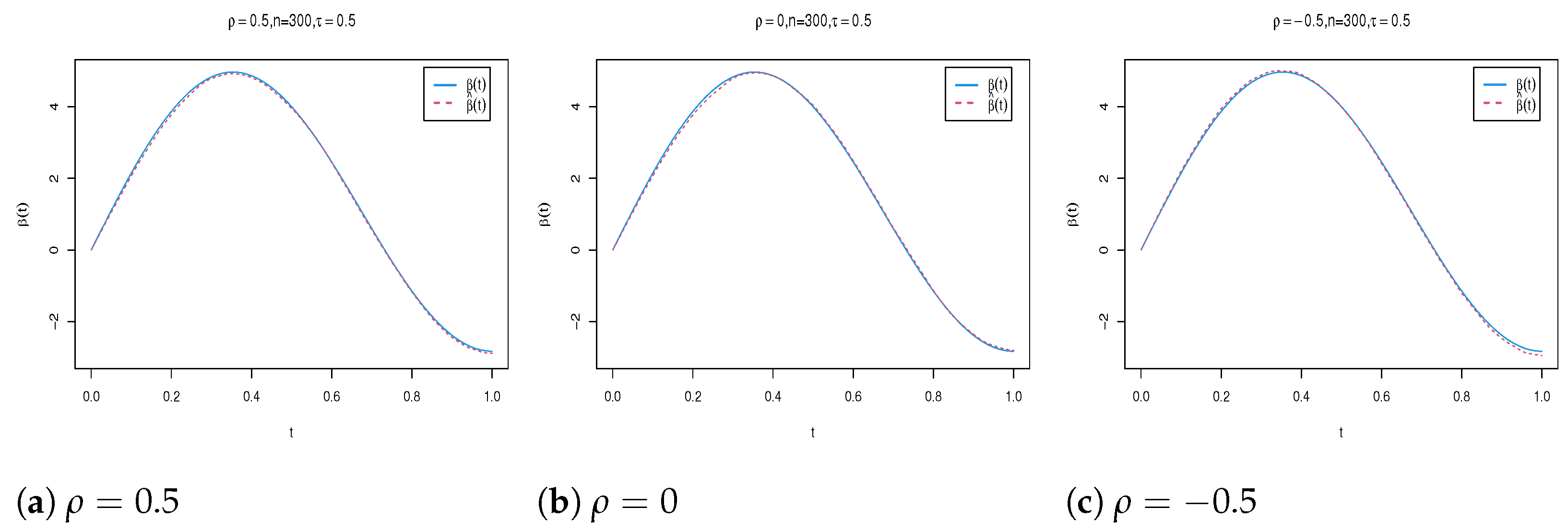
4. Simulation Study
- Case I: , with such that th quantile of is 0;
- Case II: , with such that th quantile of is 0;
- Case III: , with such that th quantile of is 0.
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yao, F.; Müller, H.; Wang, J. Functional linear regression analysis for longitudinal data. Ann. Stat. 2005, 33, 2873–2903. [Google Scholar] [CrossRef]
- Tang, Q.; Kong, L.; Ruppert, D.; Karunamuni, R.J. Partial functional partially linear single-index models. Stat. Sin. 2021, 31, 107–133. [Google Scholar] [CrossRef]
- Zhang, X.; Fang, K.; Zhang, Q. Multivariate functional generalized additive models. J. Stat. Comput. Simul. 2022, 92, 875–893. [Google Scholar] [CrossRef]
- Rao, A.R.; Reimherr, M. Modern non-linear function-on-function regression. Stat. Comput. 2023, 33, 130. [Google Scholar] [CrossRef]
- Shin, H. Partial functional linear regression. J. Stat. Plan. Inference 2009, 139, 3405–3418. [Google Scholar] [CrossRef]
- Cui, X.; Lin, H.; Lian, H. Partially functional linear regression in reproducing kernel Hilbert spaces. Comput. Stat. Data Anal. 2020, 150, 106978. [Google Scholar] [CrossRef]
- Xiao, P.; Wang, G. Partial functional linear regression with autoregressive errors. Commun. Stat.-Theory Methods 2022, 51, 4515–4536. [Google Scholar] [CrossRef]
- Li, T.; Yu, Y.; Marron, J.; Zhu, H. A partially functional linear regression framework for integrating genetic, imaging, and clinical data. Ann. Appl. Stat. 2024, 18, 704–728. [Google Scholar] [CrossRef]
- Koenker, R.; Bassett, G., Jr. Regression quantiles. Econom. J. Econom. Soc. 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Yang, G.; Liu, X.; Lian, H. Optimal prediction for high-dimensional functional quantile regression in reproducing kernel Hilbert spaces. J. Complex. 2021, 66, 101568. [Google Scholar] [CrossRef]
- Zhu, H.; Li, Y.; Liu, B.; Yao, W.; Zhang, R. Extreme quantile estimation for partial functional linear regression models with heavy-tailed distributions. Can. J. Stat. 2022, 50, 267–286. [Google Scholar] [CrossRef] [PubMed]
- Xia, L.; Du, J.; Zhang, Z. A Nonparametric Model Checking Test for Functional Linear Composite Quantile Regression Models. J. Syst. Sci. Complex. 2024, 37, 1714–1737. [Google Scholar] [CrossRef]
- Ling, N.; Yang, J.; Yu, T.; Ding, H.; Jia, Z. Semi-Functional Partial Linear Quantile Regression Model with Randomly Censored Responses. Commun. Math. Stat. 2024. [Google Scholar] [CrossRef]
- Liu, G.; Bai, Y. Functional Quantile Spatial Autoregressive Model and Its Application. J. Syst. Sci. Math. Sci. 2023, 43, 3361–3376. [Google Scholar]
- Lee, L.F. Asymptotic distributions of quasi-maximum likelihood estimators for spatial autoregressive models. Econometrica 2004, 72, 1899–1925. [Google Scholar] [CrossRef]
- Cheng, S.; Chen, J. Estimation of partially linear single-index spatial autoregressive model. Stat. Pap. 2021, 62, 495–531. [Google Scholar] [CrossRef]
- Wang, X.; Shao, J.; Wu, J.; Zhao, Q. Robust variable selection with exponential squared loss for partially linear spatial autoregressive models. Ann. Inst. Stat. Math. 2023, 75, 949–977. [Google Scholar] [CrossRef]
- Li, T.; Cheng, Y. Statistical Inference of Partially Linear Spatial Autoregressive Model Under Constraint Conditions. J. Syst. Sci. Complex. 2023, 36, 2624–2660. [Google Scholar] [CrossRef]
- Tang, Y.; Du, J.; Zhang, Z. A parametric specification test for linear spatial autoregressive models. Spat. Stat. 2023, 57, 100767. [Google Scholar] [CrossRef]
- Xu, D.; Tian, R.; Lu, Y. Bayesian Adaptive Lasso for the Partial Functional Linear Spatial Autoregressive Model. J. Math. 2022, 2022, 1616068. [Google Scholar] [CrossRef]
- Liu, G.; Bai, Y. Statistical inference in functional semiparametric spatial autoregressive model. AIMS Math. 2021, 6, 10890–10906. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, Y.; Zhang, L.; Xue, L. Statistical inference of varying-coefficient partial functional spatial autoregressive model. Commun. Stat.-Theory Methods 2023, 52, 4960–4980. [Google Scholar] [CrossRef]
- Dai, X.; Jin, L. Minimum distance quantile regression for spatial autoregressive panel data models with fixed effects. PLoS ONE 2021, 16, e0261144. [Google Scholar] [CrossRef] [PubMed]
- Gu, Y.; You, X.Y. A spatial quantile regression model for driving mechanism of urban heat island by considering the spatial dependence and heterogeneity: An example of Beijing, China. Sustain. Cities Soc. 2022, 79, 103692. [Google Scholar] [CrossRef]
- Dai, X.; Li, S.; Jin, L.; Tian, M. Quantile regression for partially linear varying coefficient spatial autoregressive models. Commun. Stat.-Simul. Comput. 2024, 53, 4396–4411. [Google Scholar] [CrossRef]
- Han, M. E-Bayesian estimation of the reliability derived from Binomial distribution. Appl. Math. Model. 2011, 35, 2419–2424. [Google Scholar] [CrossRef]
- Giordano, M.; Ray, K. Nonparametric Bayesian inference for reversible multidimensional diffusions. Ann. Stat. 2022, 50, 2872–2898. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, J. Bayesian analysis of partially linear, single-index, spatial autoregressive models. Comput. Stat. 2022, 37, 327–353. [Google Scholar] [CrossRef]
- Yu, C.H.; Prado, R.; Ombao, H.; Rowe, D. Bayesian spatiotemporal modeling on complex-valued fMRI signals via kernel convolutions. Biometrics 2023, 79, 616–628. [Google Scholar] [CrossRef]
- Yu, K.; Moyeed, R.A. Bayesian quantile regression. Stat. Probab. Lett. 2001, 54, 437–447. [Google Scholar] [CrossRef]
- Yu, Y. Bayesian quantile regression for hierarchical linear models. J. Stat. Comput. Simul. 2015, 85, 3451–3467. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Tang, N.S. Bayesian Quantile Regression with Mixed Discrete and Nonignorable Missing Covariates. Bayesian Anal. 2020, 15, 579–604. [Google Scholar] [CrossRef]
- Zhang, D.; Wu, L.; Ye, K.; Wang, M. Bayesian quantile semiparametric mixed-effects double regression models. Stat. Theory Relat. Fields 2021, 5, 303–315. [Google Scholar] [CrossRef]
- Yu, H.; Yu, L. Flexible Bayesian quantile regression for nonlinear mixed effects models based on the generalized asymmetric Laplace distribution. J. Stat. Comput. Simul. 2023, 93, 2725–2750. [Google Scholar] [CrossRef]
- Chu, Y.; Yin, Z.; Yu, K. Bayesian scale mixtures of normals linear regression and Bayesian quantile regression with big data and variable selection. J. Comput. Appl. Math. 2023, 428, 115192. [Google Scholar] [CrossRef]
- Yang, K.; Zhao, L.; Hu, Q.; Wang, W. Bayesian quantile regression analysis for bivariate vector autoregressive models with an application to financial time series. Comput. Econ. 2024, 64, 1939–1963. [Google Scholar] [CrossRef]
- Xie, T.; Cao, R.; Du, J. Variable selection for spatial autoregressive models with a diverging number of parameters. Stat. Pap. 2020, 61, 1125–1145. [Google Scholar] [CrossRef]
- Gelman, A. Inference and monitoring convergence. In Markov Chain Monte Carlo in Practice; CRC Press: Boca Raton, FL, USA, 1996; pp. 131–144. [Google Scholar]


| n | Para. | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bias | SD | Bias | SD | Bias | SD | |||||
| 0.5 | 75 | −0.031 | 0.196 | −0.025 | 0.155 | −0.017 | 0.192 | |||
| 0.038 | 0.216 | 0.033 | 0.186 | 0.006 | 0.188 | |||||
| −0.059 | 0.241 | −0.056 | 0.213 | −0.048 | 0.236 | |||||
| 0.031 | 0.223 | 0.010 | 0.184 | 0.040 | 0.194 | |||||
| 0.053 | 0.074 | 0.059 | 0.086 | 0.047 | 0.074 | |||||
| 150 | −0.036 | 0.125 | −0.019 | 0.128 | −0.036 | 0.123 | ||||
| 0.049 | 0.146 | −0.009 | 0.131 | 0.042 | 0.153 | |||||
| −0.066 | 0.171 | −0.061 | 0.143 | −0.064 | 0.154 | |||||
| 0.047 | 0.128 | 0.039 | 0.131 | 0.027 | 0.125 | |||||
| 0.057 | 0.067 | 0.057 | 0.067 | 0.055 | 0.067 | |||||
| 300 | −0.032 | 0.089 | −0.024 | 0.089 | −0.040 | 0.100 | ||||
| 0.033 | 0.115 | 0.013 | 0.092 | 0.024 | 0.099 | |||||
| −0.061 | 0.117 | −0.041 | 0.106 | −0.043 | 0.108 | |||||
| 0.036 | 0.094 | 0.020 | 0.076 | 0.018 | 0.085 | |||||
| 0.061 | 0.066 | 0.058 | 0.064 | 0.062 | 0.066 | |||||
| 0 | 75 | −0.009 | 0.182 | 0.012 | 0.184 | −0.054 | 0.186 | |||
| 0.016 | 0.241 | 0.010 | 0.184 | 0.057 | 0.194 | |||||
| −0.005 | 0.218 | 0.011 | 0.204 | −0.024 | 0.205 | |||||
| −0.001 | 0.181 | 0.000 | 0.156 | 0.021 | 0.198 | |||||
| −0.021 | 0.083 | −0.007 | 0.104 | −0.007 | 0.104 | |||||
| 150 | 0.028 | 0.131 | −0.018 | 0.111 | 0.028 | 0.135 | ||||
| 0.018 | 0.151 | 0.006 | 0.122 | 0.015 | 0.154 | |||||
| −0.031 | 0.139 | 0.005 | 0.119 | −0.005 | 0.141 | |||||
| 0.009 | 0.134 | 0.001 | 0.124 | −0.012 | 0.123 | |||||
| 0.017 | 0.061 | −0.003 | 0.065 | 0.000 | 0.062 | |||||
| 300 | −0.007 | 0.096 | −0.002 | 0.079 | 0.014 | 0.093 | ||||
| 0.012 | 0.099 | 0.003 | 0.093 | −0.007 | 0.091 | |||||
| 0.001 | 0.106 | 0.007 | 0.104 | −0.004 | 0.080 | |||||
| −0.014 | 0.088 | −0.014 | 0.094 | 0.003 | 0.085 | |||||
| 0.028 | 0.047 | −0.005 | 0.046 | 0.033 | 0.052 | |||||
| −0.5 | 75 | −0.048 | 0.202 | −0.031 | 0.179 | −0.050 | 0.211 | |||
| 0.034 | 0.220 | 0.065 | 0.184 | 0.023 | 0.206 | |||||
| −0.061 | 0.209 | −0.080 | 0.215 | −0.019 | 0.216 | |||||
| 0.036 | 0.209 | 0.016 | 0.183 | −0.004 | 0.181 | |||||
| −0.110 | 0.155 | −0.104 | 0.156 | −0.100 | 0.148 | |||||
| 150 | −0.027 | 0.131 | −0.020 | 0.114 | −0.038 | 0.147 | ||||
| 0.012 | 0.151 | 0.020 | 0.142 | 0.025 | 0.145 | |||||
| −0.029 | 0.153 | −0.037 | 0.148 | −0.050 | 0.149 | |||||
| 0.018 | 0.115 | 0.038 | 0.140 | 0.029 | 0.133 | |||||
| −0.085 | 0.119 | −0.107 | 0.131 | −0.098 | 0.120 | |||||
| 300 | −0.013 | 0.087 | −0.015 | 0.089 | −0.021 | 0.090 | ||||
| 0.021 | 0.104 | 0.036 | 0.110 | 0.014 | 0.101 | |||||
| −0.028 | 0.121 | −0.061 | 0.114 | −0.023 | 0.108 | |||||
| 0.015 | 0.106 | 0.022 | 0.088 | 0.016 | 0.089 | |||||
| −0.068 | 0.083 | −0.107 | 0.119 | −0.066 | 0.080 | |||||
| n | Para. | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bias | SD | Bias | SD | Bias | SD | |||||
| 0.5 | 75 | −0.036 | 0.229 | −0.031 | 0.205 | −0.047 | 0.242 | |||
| 0.040 | 0.233 | 0.041 | 0.202 | 0.051 | 0.304 | |||||
| −0.092 | 0.296 | −0.051 | 0.210 | −0.031 | 0.260 | |||||
| 0.050 | 0.238 | 0.029 | 0.196 | 0.009 | 0.250 | |||||
| 0.068 | 0.091 | 0.070 | 0.089 | 0.066 | 0.088 | |||||
| 150 | −0.028 | 0.158 | −0.048 | 0.134 | −0.038 | 0.162 | ||||
| 0.046 | 0.200 | 0.024 | 0.143 | 0.028 | 0.177 | |||||
| −0.095 | 0.228 | −0.053 | 0.154 | −0.059 | 0.176 | |||||
| 0.039 | 0.169 | 0.029 | 0.147 | 0.055 | 0.166 | |||||
| 0.079 | 0.086 | 0.070 | 0.085 | 0.076 | 0.084 | |||||
| 300 | −0.028 | 0.118 | −0.024 | 0.088 | −0.026 | 0.100 | ||||
| 0.023 | 0.115 | 0.018 | 0.097 | 0.014 | 0.120 | |||||
| −0.056 | 0.134 | −0.055 | 0.111 | −0.070 | 0.143 | |||||
| 0.021 | 0.112 | 0.031 | 0.097 | 0.051 | 0.128 | |||||
| 0.080 | 0.084 | 0.079 | 0.084 | 0.076 | 0.081 | |||||
| 0 | 75 | 0.010 | 0.247 | −0.036 | 0.203 | −0.041 | 0.204 | |||
| −0.018 | 0.302 | 0.034 | 0.270 | 0.046 | 0.252 | |||||
| 0.001 | 0.245 | −0.022 | 0.211 | 0.026 | 0.293 | |||||
| 0.026 | 0.211 | −0.004 | 0.242 | −0.026 | 0.253 | |||||
| −0.006 | 0.103 | −0.016 | 0.115 | −0.012 | 0.108 | |||||
| 150 | −0.001 | 0.156 | −0.004 | 0.145 | −0.002 | 0.161 | ||||
| −0.007 | 0.194 | 0.000 | 0.151 | −0.015 | 0.191 | |||||
| 0.006 | 0.166 | −0.008 | 0.149 | 0.007 | 0.175 | |||||
| −0.008 | 0.169 | −0.003 | 0.134 | −0.008 | 0.148 | |||||
| 0.000 | 0.062 | 0.001 | 0.063 | 0.009 | 0.063 | |||||
| 300 | −0.004 | 0.105 | −0.020 | 0.095 | 0.001 | 0.106 | ||||
| −0.012 | 0.120 | 0.011 | 0.107 | −0.013 | 0.120 | |||||
| −0.013 | 0.121 | 0.010 | 0.106 | −0.006 | 0.141 | |||||
| 0.008 | 0.097 | 0.000 | 0.088 | 0.005 | 0.114 | |||||
| 0.026 | 0.056 | −0.006 | 0.053 | 0.022 | 0.059 | |||||
| −0.5 | 75 | −0.041 | 0.240 | −0.039 | 0.175 | −0.020 | 0.247 | |||
| 0.058 | 0.272 | 0.023 | 0.204 | 0.075 | 0.260 | |||||
| −0.103 | 0.324 | −0.050 | 0.254 | −0.127 | 0.313 | |||||
| 0.038 | 0.252 | 0.044 | 0.202 | 0.075 | 0.258 | |||||
| −0.160 | 0.205 | −0.150 | 0.185 | −0.144 | 0.201 | |||||
| 150 | −0.031 | 0.147 | −0.042 | 0.146 | −0.029 | 0.186 | ||||
| 0.043 | 0.177 | 0.043 | 0.179 | 0.057 | 0.193 | |||||
| −0.055 | 0.194 | −0.081 | 0.177 | −0.093 | 0.214 | |||||
| 0.026 | 0.181 | 0.039 | 0.148 | 0.046 | 0.175 | |||||
| −0.130 | 0.162 | −0.149 | 0.174 | −0.131 | 0.156 | |||||
| 300 | −0.045 | 0.124 | −0.037 | 0.105 | −0.024 | 0.128 | ||||
| 0.044 | 0.151 | 0.028 | 0.109 | 0.047 | 0.121 | |||||
| −0.061 | 0.153 | −0.059 | 0.127 | −0.059 | 0.131 | |||||
| 0.026 | 0.112 | 0.040 | 0.103 | 0.014 | 0.109 | |||||
| −0.134 | 0.148 | −0.159 | 0.171 | −0.109 | 0.127 | |||||
| n | Para. | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bias | SD | Bias | SD | Bias | SD | |||||
| 0.5 | 75 | −0.018 | 0.364 | −0.078 | 0.340 | −0.054 | 0.321 | |||
| −0.029 | 0.448 | 0.026 | 0.339 | 0.051 | 0.487 | |||||
| −0.054 | 0.466 | −0.024 | 0.356 | −0.072 | 0.457 | |||||
| 0.048 | 0.377 | 0.022 | 0.300 | 0.065 | 0.474 | |||||
| 0.087 | 0.098 | 0.079 | 0.094 | 0.084 | 0.101 | |||||
| 150 | −0.018 | 0.237 | −0.057 | 0.186 | −0.038 | 0.301 | ||||
| −0.005 | 0.268 | 0.030 | 0.203 | −0.003 | 0.298 | |||||
| −0.032 | 0.319 | −0.041 | 0.197 | −0.035 | 0.288 | |||||
| 0.026 | 0.255 | 0.013 | 0.167 | 0.001 | 0.210 | |||||
| 0.062 | 0.077 | 0.066 | 0.076 | 0.087 | 0.096 | |||||
| 300 | −0.041 | 0.184 | −0.006 | 0.121 | −0.040 | 0.181 | ||||
| 0.009 | 0.189 | 0.006 | 0.111 | 0.014 | 0.180 | |||||
| −0.049 | 0.184 | −0.032 | 0.124 | −0.026 | 0.197 | |||||
| 0.039 | 0.180 | 0.029 | 0.107 | 0.014 | 0.168 | |||||
| 0.056 | 0.065 | 0.035 | 0.048 | 0.052 | 0.066 | |||||
| 0 | 75 | −0.020 | 0.382 | 0.030 | 0.295 | 0.010 | 0.326 | |||
| −0.041 | 0.457 | −0.047 | 0.286 | 0.037 | 0.386 | |||||
| 0.007 | 0.541 | 0.066 | 0.331 | −0.008 | 0.395 | |||||
| −0.037 | 0.409 | −0.034 | 0.253 | 0.032 | 0.340 | |||||
| −0.028 | 0.190 | −0.005 | 0.140 | 0.023 | 0.120 | |||||
| 150 | 0.025 | 0.245 | −0.026 | 0.160 | 0.026 | 0.294 | ||||
| −0.025 | 0.304 | 0.026 | 0.202 | −0.020 | 0.340 | |||||
| −0.043 | 0.296 | −0.031 | 0.190 | −0.039 | 0.332 | |||||
| 0.022 | 0.242 | 0.006 | 0.156 | 0.012 | 0.248 | |||||
| −0.002 | 0.101 | −0.006 | 0.098 | 0.030 | 0.109 | |||||
| 300 | −0.026 | 0.212 | −0.008 | 0.120 | −0.012 | 0.174 | ||||
| −0.006 | 0.209 | −0.015 | 0.135 | 0.029 | 0.201 | |||||
| 0.041 | 0.193 | 0.029 | 0.137 | −0.010 | 0.204 | |||||
| 0.008 | 0.172 | −0.019 | 0.112 | −0.023 | 0.188 | |||||
| 0.007 | 0.096 | 0.000 | 0.066 | 0.011 | 0.060 | |||||
| −0.5 | 75 | −0.034 | 0.515 | −0.048 | 0.304 | −0.078 | 0.472 | |||
| 0.002 | 0.548 | 0.045 | 0.336 | 0.130 | 0.479 | |||||
| −0.051 | 0.549 | −0.068 | 0.359 | −0.079 | 0.465 | |||||
| 0.080 | 0.471 | 0.003 | 0.312 | −0.027 | 0.397 | |||||
| −0.162 | 0.212 | −0.139 | 0.191 | −0.139 | 0.180 | |||||
| 150 | −0.001 | 0.286 | −0.024 | 0.168 | −0.044 | 0.276 | ||||
| 0.027 | 0.358 | 0.056 | 0.188 | 0.075 | 0.333 | |||||
| −0.052 | 0.301 | −0.070 | 0.217 | −0.022 | 0.352 | |||||
| 0.000 | 0.264 | 0.020 | 0.181 | 0.004 | 0.313 | |||||
| −0.129 | 0.166 | −0.108 | 0.143 | −0.137 | 0.178 | |||||
| 300 | −0.015 | 0.206 | −0.005 | 0.111 | −0.013 | 0.192 | ||||
| 0.039 | 0.209 | 0.016 | 0.125 | −0.003 | 0.231 | |||||
| −0.075 | 0.203 | −0.044 | 0.136 | −0.060 | 0.228 | |||||
| 0.077 | 0.179 | 0.027 | 0.129 | 0.041 | 0.196 | |||||
| −0.121 | 0.143 | −0.083 | 0.098 | −0.125 | 0.146 | |||||
| n | Case I | Case II | Case III | ||
|---|---|---|---|---|---|
| 0.5 | 75 | 1.055 | 1.234 | 1.751 | |
| 0.944 | 1.036 | 1.490 | |||
| 0.934 | 1.101 | 1.686 | |||
| 150 | 0.677 | 0.877 | 1.262 | ||
| 0.638 | 0.693 | 0.849 | |||
| 0.688 | 0.770 | 1.189 | |||
| 300 | 0.438 | 0.547 | 0.785 | ||
| 0.419 | 0.508 | 0.561 | |||
| 0.487 | 0.514 | 0.790 | |||
| 0 | 75 | 1.043 | 1.263 | 1.897 | |
| 0.884 | 1.018 | 1.310 | |||
| 1.021 | 1.080 | 1.944 | |||
| 150 | 0.702 | 0.771 | 1.156 | ||
| 0.619 | 0.657 | 1.007 | |||
| 0.621 | 0.796 | 1.233 | |||
| 300 | 0.505 | 0.543 | 0.806 | ||
| 0.455 | 0.484 | 0.568 | |||
| 0.481 | 0.569 | 0.815 | |||
| −0.5 | 75 | 1.099 | 1.164 | 1.816 | |
| 0.872 | 0.997 | 1.397 | |||
| 1.066 | 1.156 | 1.817 | |||
| 150 | 0.685 | 0.850 | 1.275 | ||
| 0.639 | 0.709 | 0.842 | |||
| 0.748 | 0.765 | 1.359 | |||
| 300 | 0.451 | 0.588 | 0.848 | ||
| 0.477 | 0.514 | 0.542 | |||
| 0.484 | 0.533 | 0.933 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, D.; Ke, S.; Dong, J.; Tian, R. Bayesian Quantile Regression for Partial Functional Linear Spatial Autoregressive Model. Axioms 2025, 14, 467. https://doi.org/10.3390/axioms14060467
Xu D, Ke S, Dong J, Tian R. Bayesian Quantile Regression for Partial Functional Linear Spatial Autoregressive Model. Axioms. 2025; 14(6):467. https://doi.org/10.3390/axioms14060467
Chicago/Turabian StyleXu, Dengke, Shiqi Ke, Jun Dong, and Ruiqin Tian. 2025. "Bayesian Quantile Regression for Partial Functional Linear Spatial Autoregressive Model" Axioms 14, no. 6: 467. https://doi.org/10.3390/axioms14060467
APA StyleXu, D., Ke, S., Dong, J., & Tian, R. (2025). Bayesian Quantile Regression for Partial Functional Linear Spatial Autoregressive Model. Axioms, 14(6), 467. https://doi.org/10.3390/axioms14060467






