About Some Unsolved Problems in the Stability Theory of Stochastic Differential and Difference Equations

Abstract

This paper continues a series of papers by the author devoted to unsolved problems in the theory of stability and optimal control for stochastic systems. A delay differential equation with stochastic perturbations of the white noise and Poisson’s jump types is considered. In contrast with the known stability condition, in which it is assumed that stochastic perturbations fade on the infinity quickly enough, a new situation is studied, in which stochastic perturbations can either fade on the infinity slowly or not fade at all. Some unsolved problem in this connection is brought to readers’ attention. Additionally, some unsolved problems of stabilization for one stochastic delay differential equation and one stochastic difference equation are also proposed.

1. Introduction

The unsolved problems proposed here continue a series of unsolved problems in stability and optimal control theory for stochastic differential and stochastic difference equations that have been presented during the recent years at some international conferences and papers (see [1,2,3,4,5,6,7,8,9,10]). All these problems still need to be solved.

Let $\{\mathrm{\Omega },\mathfrak{F},\mathbf{P}\}$ be a complete probability space; ${\left\{{\mathfrak{F}}_t\right\}}_{t\ge 0}$ be a nondecreasing family of sub-$\sigma$-algebras of $\mathfrak{F}$, i.e., ${\mathfrak{F}}_s\subset {\mathfrak{F}}_t$ for $s<t$; $\mathbf{E}$ be the expectation with respect to the measure $\mathbf{P}$; and $H_2$ be the space of ${\mathfrak{F}}_0$-adapted stochastic processes $\phi \left(s\right)$, $s\le 0$, ${\parallel \phi \parallel }^2=\underset{s\le 0}{sup}\mathbf{E}{\left|\phi \left(s\right)\right|}^2$.

Following Gikhman and Skorokhod [11,12], let us consider the stochastic delay differential equation

$$\begin{gathered} dx\left(t\right)=\left(Ax\left(t\right)+\sum _{i=1}^k{B}_{i}x(t-h_i)\right)dt+\sum _{i=1}^m{C}_i\left(t\right)x\left(t\right)d{w}_i\left(t\right) \\ +\int G(t,u)x\left(t\right)\tilde{\nu }(dt,du),t\ge 0, \\ x\left(s\right)=\varphi \left(s\right)\in H_2,s\in [-h,0],h=\underset{i=1,\dots ,k}{max}{h}_i, \end{gathered}$$

(1)

where $x\left(t\right)\in {\mathbf{R}}^n$, $A,B_i,C_i\left(t\right),G(t,u)$ are $n\times n$-matrices and $h_i>0$, $w_1\left(t\right),\dots ,w_m\left(t\right)$ are mutually independent standard Wiener processes, which are also independent of the Poisson measure $\nu (dt,du)$,

$$\mathbf{E}\nu (dt,du)=dt\mathrm{\Pi }\left(du\right),\tilde{\nu }(dt,du)=\nu (dt,du)-dt\mathrm{\Pi }\left(du\right).$$

Auxiliary Definitions and Statements

Let $x\left(t\right)$ be a solution to Equation (1) in the time moment t, and $x_t=x(t+s)$, $s<0$, be a trajectory of the Equation (1) solution until the time moment t. Consider a functional $V(t,\phi ):[0,\infty )\times H_2\to {\mathbf{R}}_{+}$ that can be presented in the form $V(t,\phi )=V(t,\phi (0),\phi (s\left)\right)$, $s<0$, and for $\phi =x_t$, put

$$\begin{gathered} V_{\phi }(t,x)=V(t,\phi )=V(t,x_t)=V(t,x,x(t+s)), \\ x=\phi \left(0\right)=x\left(t\right),s<0. \end{gathered}$$

(2)

Let D be a set of functionals $V(t,\phi )$, for which the function $V_{\phi }(t,x)$ defined in (2) has a continuous derivative with respect to t and two continuous derivatives with respect to x. Let ′ be the sign of transpose and $\nabla V_{\phi }(t,x)$ and ${\nabla }^2{V}_{\phi }(t,x)$ be respectively the first and the second derivatives of the function $V_{\phi }(t,x)$ with respect to x. For the functionals from D, the generator L of Equation (1) has the form [11,12,13]

$$\begin{array}{cc}LV(t,x_t)=\hfill & {\displaystyle \frac{\partial }{\partial t}}{V}_{\phi }(t,x\left(t\right))+\nabla V_{\phi }^{\prime }(t,x\left(t\right))(Ax\left(t\right)+{\displaystyle \sum _{i=1}^k}{B}_{i}x(t-h_i))\\ \hfill & +{\displaystyle \frac{1}{2}}{\displaystyle \sum _{i=1}^m}{x}^{\prime }\left(t\right)C_i^{\prime }\left(t\right){\nabla }^2{V}_{\phi }(t,x\left(t\right))C_i\left(t\right)x\left(t\right)\\ \hfill & +\int [V_{\phi }(t,x\left(t\right)+G(t,u)x\left(t\right))-V_{\phi }(t,x\left(t\right))\\ & -\nabla V_{\phi }^{\prime }(t,x\left(t\right))G(t,u)x\left(t\right)]\mathrm{\Pi }\left(du\right).\end{array}$$

(3)

Definition 1

([13]). The zero solution to Equation (1) is called:

-

mean square stable if, for each $\epsilon >0$, there exists $\delta >0$ such that ${\mathbf{E}\left|x\left(t\right)\right|}^2<\epsilon$, $t\ge 0$, provided that ${\parallel \varphi \parallel }^2<\delta$;

-

asymptotically mean square stable if it is mean square stable, and for each initial function $\varphi \left(s\right)$, the solution $x\left(t\right)$ to Equation (1) satisfies the condition $\underset{t\to \infty }{lim}\mathbf{E}{\left|x\left(t\right)\right|}^2=0$.

Theorem 1

([13]). Let there exist a functional $V(t,\phi )\in D$ and positive constants $c_1$, $c_2$ and $c_3$ such that the following conditions hold:

$$\begin{gathered} \mathbf{E}V(t,x_t)\ge c_1{\mathbf{E}\left|x\right(t\left)\right|}^2,\mathbf{E}V(0,\varphi )\le c_2{\parallel \varphi \parallel }^2, \\ \mathbf{E}LV(t,x_t)\le -c_3\mathbf{E}{\left|x\left(t\right)\right|}^2. \end{gathered}$$

Then the zero solution to Equation (1) is asymptotically mean square stable.

Some special cases of Equation (1) are considered in [14,15]. In particular, it is shown that if the zero solution of a deterministic system is asymptotically stable, then it remains asymptotically mean square stable under stochastic perturbations that fade quickly enough on the infinity.

In particular, in [15], the asymptotic mean square stability of the zero solution to Equation (1) with $k=m=1$ is proven by virtue of the general method of Lyapunov functional construction [13,16] and the method of Linear Matrix Inequalities (LMIs) [17,18,19]. By that it is supposed that, for some positive definite matrix P, the following conditions hold:

$$C^{\prime }\left(t\right)PC\left(t\right)\le {\sigma }^2\left(t\right)P,G^{\prime }(t,u)PG(t,u)\le {\gamma }^2(t,u)P,$$

$$\rho \left(t\right)={\sigma }^2\left(t\right)+\int {\gamma }^2(t,u)\mathrm{\Pi }\left(du\right),{\int }_0^{\infty }\rho \left(t\right)dt<\infty .$$

(4)

Using (4), the Lyapunov functional $V(t,x_t)$ is constructed in the form $V(t,x_t)=V_1(t,x\left(t\right))+V_2(t,x_t)$, where

$$\begin{gathered} V_1(t,x\left(t\right))=e^{-{\int }_0^t\rho \left(s\right)ds}{x}^{\prime }\left(t\right)Px\left(t\right),P>0, \\ {V}_2(t,x_t)={\int }_{t-h}^t{e}^{-{\int }_0^{s+h}\rho \left(\tau \right)d\tau }{x}^{\prime }\left(s\right)Rx\left(s\right)ds,R>0. \end{gathered}$$

(5)

Remark 1.

Note that, in order for the constructed Lyapunov functional $V(t,x_t)$ (5) to satisfy the conditions of Theorem 1, the integrability condition (4) of the function $\rho \left(t\right)$ must be satisfied. This condition means that stochastic perturbations fade on the infinity quickly enough. Below, another situation is studied. It is supposed that stochastic perturbations can either fade on the infinity slowly or not fade at all. By that, some unsolved problem is also proposed.

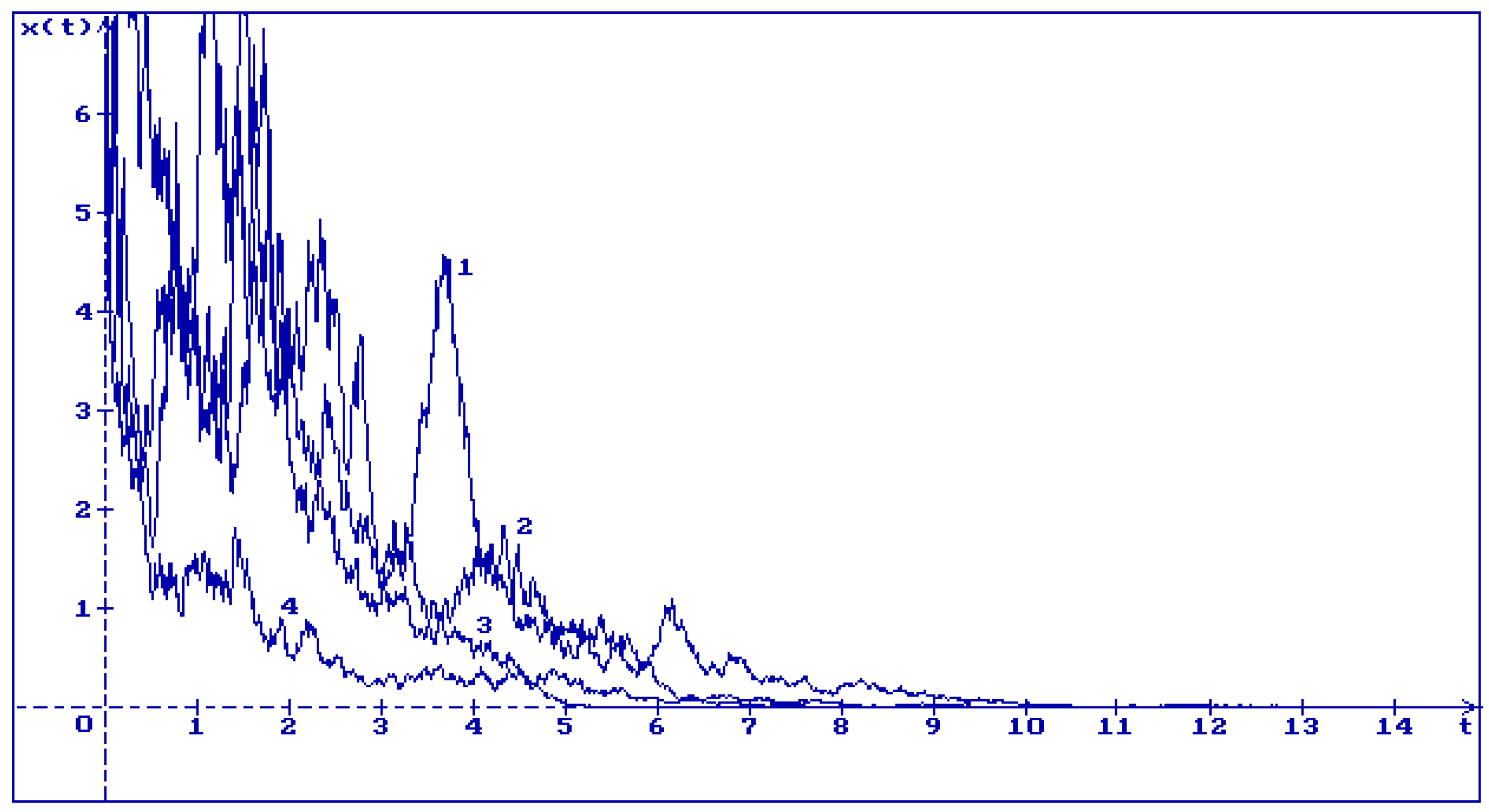
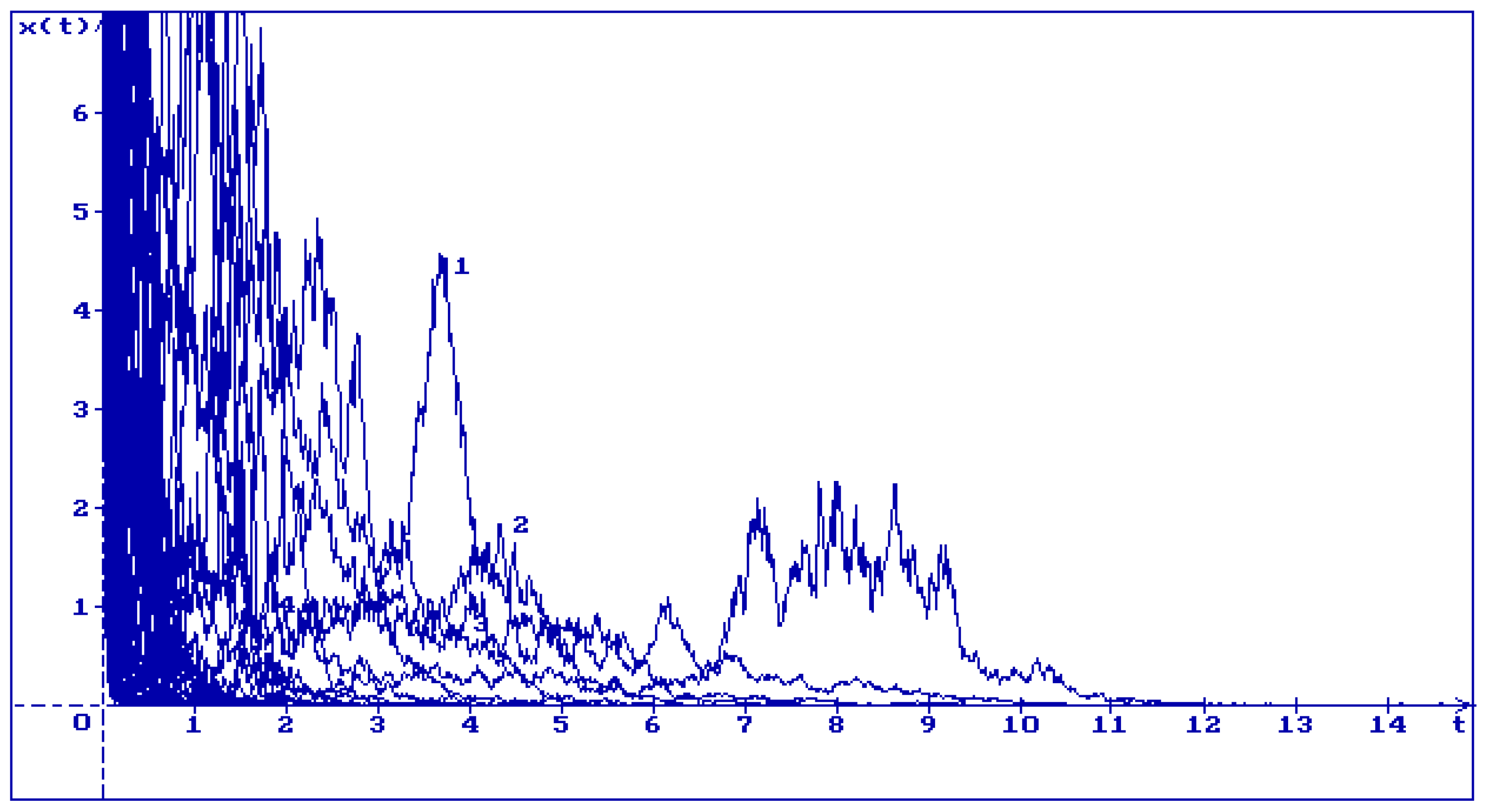
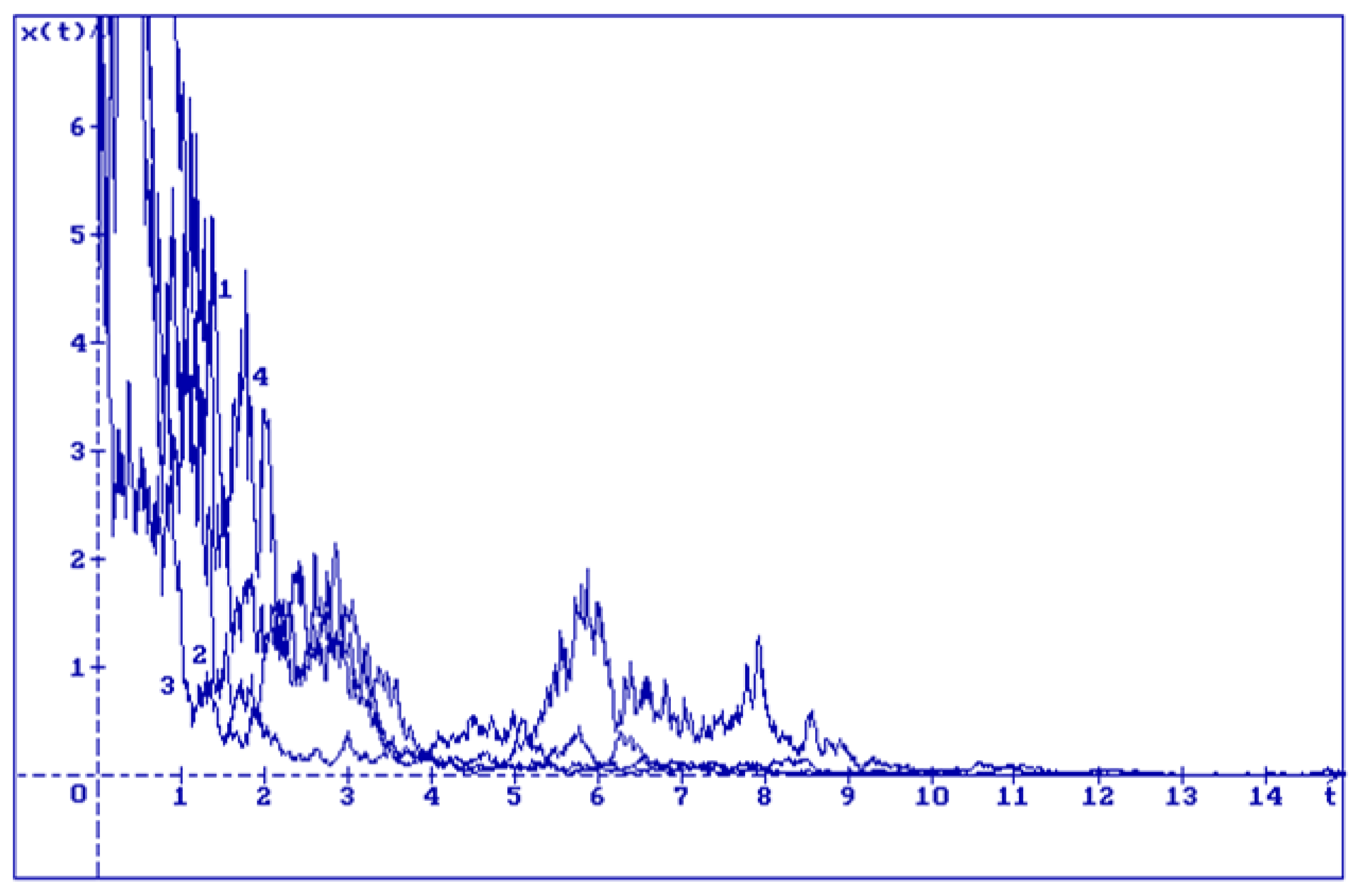
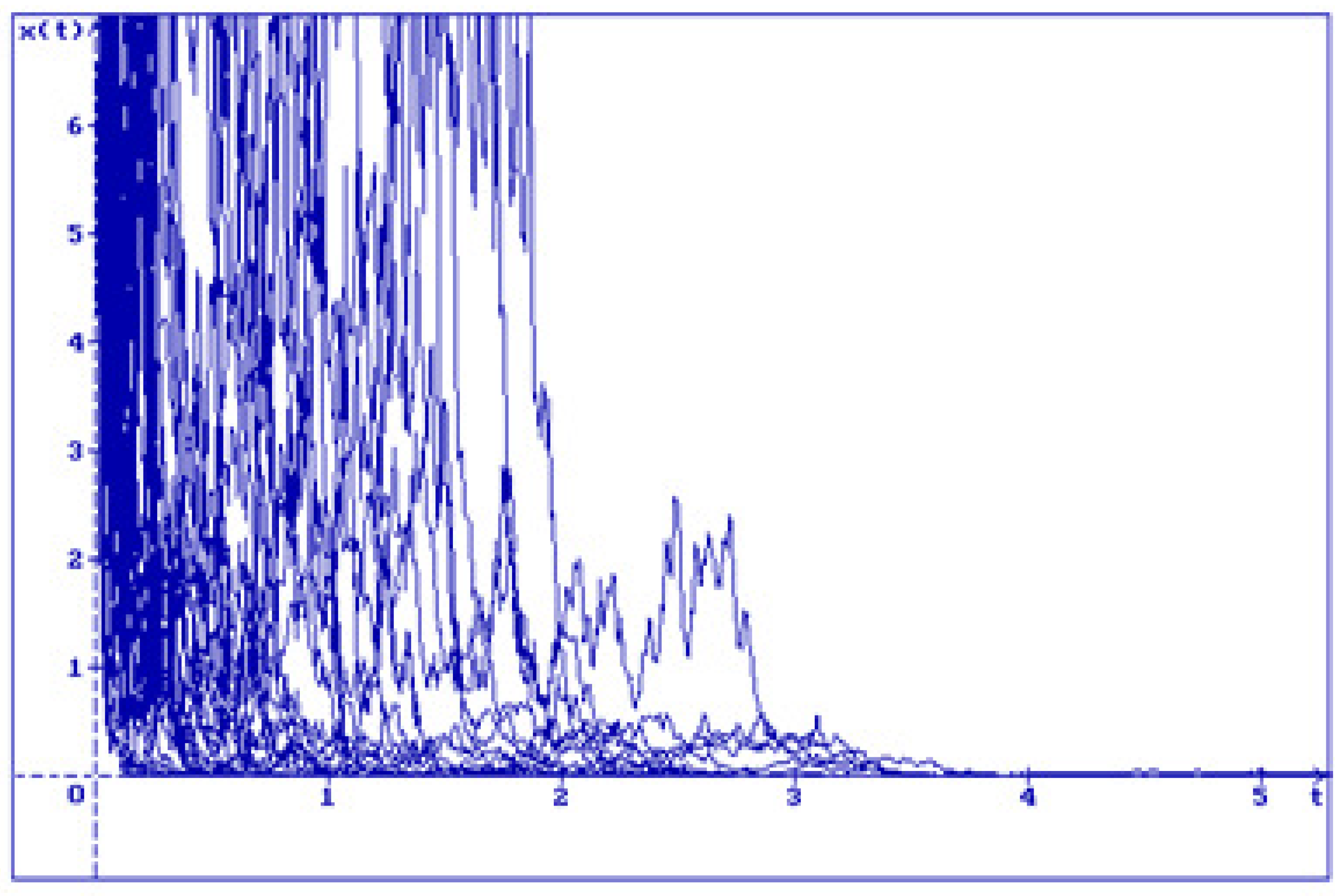
2. Equation Without Delays

Consider at first Equation (1) without delays, i.e., by the condition

$$B_i=0,i=1,\dots ,k.$$

(6)

Let L be the generator of Equation (1), (6). Then, via (3) for the function $V\left(x\left(t\right)\right)={\left|x\left(t\right)\right|}^2$ we have

$$\begin{gathered} LV\left(x\left(t\right)\right)=2x^{\prime }\left(t\right)Ax\left(t\right)+\sum _{i=1}^m{x}^{\prime }\left(t\right)C_i^{\prime }\left(t\right)C_i\left(t\right)x\left(t\right) \\ +\int x^{\prime }\left(t\right)G^{\prime }(t,u)G(t,u)x\left(t\right)\mathrm{\Pi }\left(du\right) \\ =x^{\prime }\left(t\right)[A+A^{\prime }+Q\left(t\right)]x\left(t\right), \end{gathered}$$

(7)

where

$$Q\left(t\right)=\sum _{i=1}^m{C}_i^{\prime }\left(t\right)C_i\left(t\right)+\int G^{\prime }(t,u)G(t,u)\mathrm{\Pi }\left(du\right).$$

Let $\rho \left(t\right)=\parallel Q\left(t\right)\parallel$ be the norm of the matrix $Q\left(t\right)$, i.e.,

$$x^{\prime }Q\left(t\right)x\le \rho \left(t\right){\left|x\right|}^2.$$

(8)

Assume that the symmetric matrix $A+A^{\prime }$ is a negative definite matrix, i.e.,

$$x^{\prime }(A+A^{\prime })x\le -\alpha {\left|x\right|}^2,\alpha >0,$$

(9)

and additionally, suppose that

$$\underset{t\ge 0}{sup}\rho \left(t\right)<\alpha \mathrm{or}{\int }_0^{\infty }\rho \left(t\right)dt<\infty .$$

(10)

Put also

$$\mu \left(t\right)={\displaystyle \frac{1}{t}}{\int }_0^t\rho \left(s\right)ds,\mu =\underset{t\to \infty }{lim\; sup}\mu \left(t\right).$$

(11)

Remark 2.

Note that if the first or the second condition (10) holds, then, respectively, $\mu <\alpha$ or $\mu =0<\alpha$. However, the condition $\mu <\alpha$ can be held even by the condition

$${\int }_0^{\infty }\rho \left(t\right)dt=\infty .$$

(12)

For example, for the function $\rho \left(t\right)={\displaystyle \frac{2\alpha }{t+1}}$ none of the conditions (10) are satisfied, but both conditions $\mu =0<\alpha$ and (12) are obviously satisfied.

Theorem 2.

Let α and μ, defined in (9) and (11), satisfy the condition $\mu <\alpha$. Then the zero solution to Equation (1), (6) is asymptotically mean square stable.

Proof. 

Using the generator (7) and the definitions (8) and (9) for $\rho \left(t\right)$ and $\alpha$, we have

$$LV\left(x\left(t\right)\right)\le {(-\alpha +\rho \left(t\right))\left|x\left(t\right)\right|}^2.$$

From this and Dynkin’s formula [11]

$$\mathbf{E}V\left(x\left(t\right)\right)=\mathbf{E}V\left(x\left(0\right)\right)+{\int }_0^t\mathbf{E}LV\left(x\left(s\right)\right)ds$$

for the function $V\left(x\left(t\right)\right)={\left|x\left(t\right)\right|}^2$ it follows that

$${\displaystyle \frac{d}{dt}}{\mathbf{E}\left|x\left(t\right)\right|}^2=\mathbf{E}LV\left(x\left(t\right)\right)\le (-\alpha +\rho \left(t\right))\mathbf{E}{\left|x\left(t\right)\right|}^2$$

or

$${\displaystyle \frac{{d\mathbf{E}\left|x\left(t\right)\right|}^2}{{\mathbf{E}\left|x\left(t\right)\right|}^2}}\le (-\alpha +\rho \left(t\right))dt.$$

Integrating this inequality and using (11), we obtain

$$\begin{array}{cc}\hfill {\mathbf{E}\left|x\left(t\right)\right|}^2& \le {\mathbf{E}\left|x\left(0\right)\right|}^{2}exp\left\{-\alpha t+{\int }_0^t\rho \left(s\right)ds\right\}\hfill \\ \hfill & =\mathbf{E}{\left|x\left(0\right)\right|}^{2}exp\left\{(-\alpha +\mu \left(t\right))t\right\}.\hfill \end{array}$$

From this and $\mu <\alpha$ it follows that ${\mathbf{E}\left|x\left(t\right)\right|}^2\le \mathbf{E}{\left|x\left(0\right)\right|}^2$ and $\underset{t\to \infty }{lim}\mathbf{E}{\left|x\left(t\right)\right|}^2=0$; i.e., the zero solution to Equation (1), (6) is asymptotically mean square stable. The proof is completed. □

Remark 3.

Note that the condition (4) of integrability of the function $\rho \left(t\right)$ is not a necessary condition for the asymptotic mean square stability of the zero solution to the stochastic differential Equation (1). For instance, for a simple scalar equation of the type of (1) with constant coefficients

$$dx\left(t\right)=-ax\left(t\right)dt+\sigma x\left(t\right)dw\left(t\right)+\int \gamma \left(u\right)x\left(t\right)\tilde{\nu }(dt,du),$$

(13)

where $a>0$ and $\rho \left(t\right)$ is the constant, i.e.,

$$\rho ={\sigma }^2+\int {\gamma }^2\left(u\right)\mathrm{\Pi }\left(du\right),$$

the condition (12) holds, but the zero solution to Equation (13) is asymptotically mean square stable if $\rho <2a$.

Unsolved problem. The proof of the asymptotic mean square stability of the zero solution to the stochastic delay differential Equation (1) under the condition (12) is currently an unsolved problem, which is brought to the attention of potential readers.

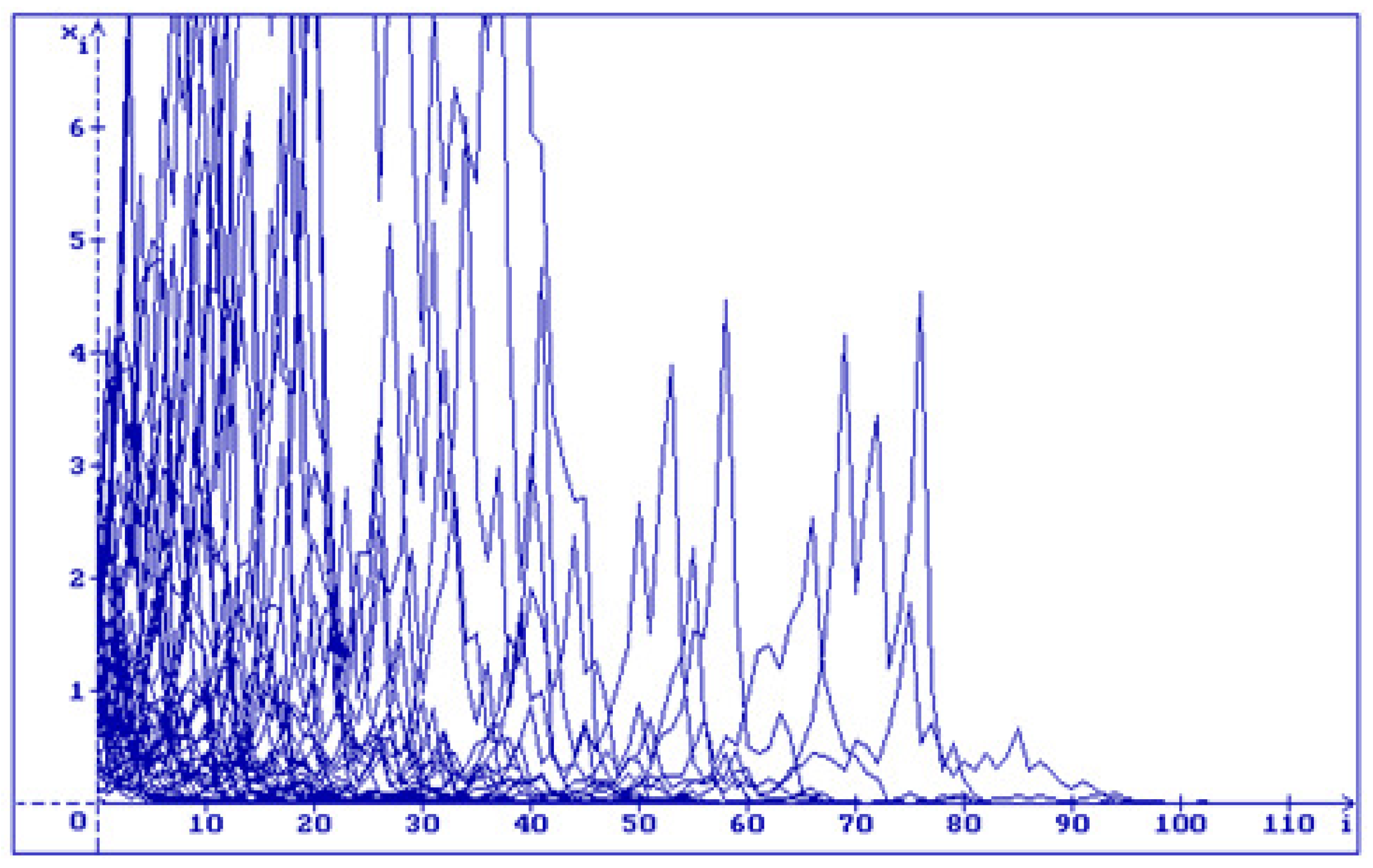
3. About the Problem of Stabilization by Noise

Note that the problem of stabilization has a long history; in particular, a very popular problem of stabilization of the inverted pendulum is considered in a lot of works, for example, the well-known work of Kapitsa [20] and many others [21,22,23,24,25,26,27,28,29,30,31,32]. Below, another problem of stabilization by noise is discussed.

Consider the scalar linear Ito’s stochastic differential equation [11]

$$\begin{gathered} dx\left(t\right)=\left(ax\right(t)+bx(t-h\left)\right)dt+\sigma x\left(t\right)dw\left(t\right), \\ x\left(s\right)=\varphi \left(s\right),s\in [-h,0], \end{gathered}$$

(14)

where a, b, and $\sigma$ are constants and $w\left(t\right)$ is the standard Wiener process.

Definition 2

([13,33]). The zero solution to Equation (14) is called stable in probability if, for any ${\epsilon }_1>0$ and ${\epsilon }_2>0$, there exists $\delta >0$ such that the solution $x(t,\varphi )$ to Equation (14) satisfies the condition $\mathbf{P}\left\{{sup}_{t\ge 0}\left|x(t,\varphi )\right|>{\epsilon }_1\right\}<{\epsilon }_2$ for any initial function $\varphi \left(s\right)$ such that $\mathbf{P}\left\{{sup}_{s\in [-h,0]}\left|\varphi \left(s\right)\right|<\delta \right\}=1$.

3.1. Equation Without Delay

Consider now Equation (14) by the condition $b=0$, i.e., without delay, as follows:

$$\begin{gathered} dx\left(t\right)=ax\left(t\right)dt+\sigma x\left(t\right)dw\left(t\right), \\ x\left(s\right)=\varphi \left(s\right),s\in [-h,0]. \end{gathered}$$

(15)

Khasminskii shows [33] that unstable by the conditions $a>0$ and $\sigma =0$, the zero solution to Equation (15) becomes stable by the presence of a big-enough level of noise. More exactly, by the condition

$$0<2a<{\sigma }^2$$

(16)

so-called “stabilization by noise” occurs and the zero solution to Equation (15) becomes stable in probability.

Really, let L be the generator [11,12,13,33] of Equation (15). Then for the Lyapunov function

$$v\left(x\right)={\left|x\right|}^{\nu },\nu =1-{\displaystyle \frac{2a}{{\sigma }^2}}\in (0,1),$$

we have

$$\begin{array}{c}Lv\left(x\right)={\displaystyle \frac{dv\left(x\right)}{dx}}ax+{\displaystyle \frac{1}{2}}{\displaystyle \frac{d^{2}v\left(x\right)}{d{x}^2}}{\sigma }^2{x}^2\hfill \\ \hspace{1em}\hspace{1em} ={\nu \left|x\right|}^{\nu -1}ax+{\displaystyle \frac{1}{2}}{\nu (\nu -1)\left|x\right|}^{\nu -2}{\sigma }^2{x}^2\hfill \\ \hspace{1em}\hspace{1em} \le a\nu {\left|x\right|}^{\nu }\left(1-(1-\nu ){\displaystyle \frac{{\sigma }^2}{2a}}\right)=0.\hfill \end{array}$$

It is known [13,33] that if there exist a Lyapunov function $v\left(x\right)$ with the condition $Lv\left(x\right)\le 0$, then the zero solution to Equation (15) is stable in probability.

3.2. Purely Stochastic Equation

From the condition (16), it follows, in particular, that the zero solution to the “purely stochastic” differential equation

$$dx\left(t\right)=\sigma x\left(t\right)dw\left(t\right)$$

(17)

is stable in probability for arbitrary $\sigma$. Moreover, the larger $\left|\sigma \right|$, the faster the trajectories of the solution to Equation (17) converge to zero.

Note that the solution to Equation (17) has the form [11]

$$x\left(t\right)=x\left(0\right)exp\left\{-{\displaystyle \frac{1}{2}}{\sigma }^{2}t+\sigma w\left(t\right)\right\}.$$

(18)

In Figure 1, one can see 4 trajectories of the solution (18) to Equation (17) for $x\left(0\right)=6$ and different values of $\sigma$, as follows:

$$\left(1\right)\sigma =0.8,\left(2\right)\sigma =0.9,\left(3\right)\sigma =1.0,\left(4\right)\sigma =1.1.$$

In Figure 2, one can see 50 trajectories of the solution (18) to Equation (17) for $x\left(0\right)=6$ and different values of $\sigma$, as follows:

$$\left(1\right)\sigma =0.8,\left(2\right)\sigma =0.9,\dots ,\left(49\right)\sigma =5.6,\left(50\right)\sigma =5.7.$$

A similar situation is demonstrated by 50 trajectories with negative $\sigma$: in Figure 3, for

$$\left(1\right)\sigma =-1.2,\left(2\right)\sigma =-1.3,\left(3\right)\sigma =-1.4,\left(4\right)\sigma =-1.5,$$

and in Figure 4, for

$$\left(5\right)\sigma =-1.6,\left(6\right)\sigma =-1.7,\dots ,\left(49\right)\sigma =-6.0,\left(50\right)\sigma =-6.1.$$

Remark 4.

From Figure 1, Figure 2, Figure 3 and Figure 4, one can see that if $\left|\sigma \right|$ increases, then the trajectories of the solution (18) converge to the zero faster.

Remark 5.

Note that, by the numerical simulation of the solution (18) for the simulation of trajectories of the Wiener process $w\left(t\right)$, the special algorithm was used, described in [13].

Unsolved problem. A generalization of Khasminskii’s statement (16) about stabilization by noise for the delay differential Equation (14) is currently the unsolved problem.

3.3. Stochastic Difference Equation

Consider now the scalar linear stochastic difference equation

$$x_{i+1}=a_1{x}_i+{\sigma }_1{x}_i{\xi }_{i+1},i=0,1,\dots ,$$

(19)

where $a_1$ and ${\sigma }_1$ are constants and ${\xi }_i$, $i=1,2,\dots$, is a sequence of mutually independent random values with the conditions

$$\mathbf{E}{\xi }_i=0,\mathbf{E}{\xi }_i^2=1.$$

(20)

It is known [16] that by the condition

$$a_1^2+{\sigma }_1^2<1$$

(21)

the zero solution to Equation (19) is asymptotic mean square stable.

Let us consider an analogue of the condition (16) for the linear stochastic difference Equation (19) by the condition $a_1>1$. For this aim, let us represent the difference analogue of Equation (15) in the form (19).

Put $t_i=i\mathrm{\Delta }$, $i=0,1,\dots$, $\mathrm{\Delta }>0$, $x_i=x\left(t_i\right)$, $w_i=w\left(t_i\right)$. Then the difference analogue of Equation (15) takes the form

$$x_{i+1}-x_i=a{x}_i\mathrm{\Delta }+\sigma x_i(w_{i+1}-w_i).$$

(22)

Note that

$${\xi }_{i+1}={\displaystyle \frac{1}{\sqrt{\mathrm{\Delta }}}}(w_{i+1}-w_i)$$

(23)

satisfies the conditions (20). Using (23), rewrite Equation (22) as follows:

$$x_{i+1}=(1+a\mathrm{\Delta })x_i+\sigma \sqrt{\mathrm{\Delta }}{x}_i{\xi }_{i+1},$$

i.e., in the form (19) with the coefficients

$$a_1=1+a\mathrm{\Delta },{\sigma }_1=\sigma \sqrt{\mathrm{\Delta }}.$$

(24)

From (24) we have

$$a={\displaystyle \frac{a_1-1}{\mathrm{\Delta }}},\sigma ={\displaystyle \frac{{\sigma }_1}{\sqrt{\mathrm{\Delta }}}},$$

and via (16) we obtain

$$0<2{\displaystyle \frac{a_1-1}{\mathrm{\Delta }}}<{\displaystyle \frac{{\sigma }_1^2}{\mathrm{\Delta }}},$$

i.e., the condition

$$0<2(a_1-1)<{\sigma }_1^2.$$

(25)

In Figure 5, 50 trajectories of Equation (19) are shown for $a_1=1.05$, ${\sigma }_1=0.5$, and different initial conditions, as follows:

$$\left(1\right)x_0=0.05,\left(2\right)x_0=0.10,\dots ,\left(49\right)x_0=2.45,\left(50\right)x_0=2.50.$$

By the fact that the condition (25) holds, all trajectories converge to zero.

Therefore, we obtain the following:

Hypothesis 1.

If the condition (25) holds, then the zero solution to Equation (19) is stable in probability.

Unsolved problem. Can the above reasoning be considered as a proof of Hypothesis 1 or not? Why?

4. Conclusions

Some unsolved problems in the field of stability of differential and difference equations under stochastic perturbations are brought to the attention of potential readers. In particular, the difference in the influence of quickly or slowly fading stochastic perturbations on the stability of stochastic differential equations is discussed, as well as the possibility of stabilizing solutions of stochastic differential equations using stochastic perturbations.

The proposed paper cannot be considered a classical research paper, in which new important results are obtained. There is hope that the solution to the unsolved problems, proposed both here and in similar previously published papers of the author, will contribute to the emergence of new ideas and the further development and improvement of the theory of stability of stochastic systems.

There is also hope that some potential readers of this paper, after some time, will submit to this journal interesting solutions to the unsolved problems proposed here.