Abstract
In this research, we investigate the phenomenon of multistability and complex dynamic behaviors in plasma waves by utilizing advanced mathematical techniques. We examine how fractional-order derivatives influence plasma wave stability by applying the fractional diffusion–reaction model, the framework of nonlinear dynamical systems, and the method. The principal direction of our work is associated with different forms of oscillations in the plasma wave: non-linear periodic, solitons, and kink waves. This leads to the study of small amplitude pulses and solitary waves, which are significant in plasma activities. Using bifurcation analysis, we discuss how these waves appear and develop under different conditions, as well as determine which conditions generate the chaotic behavior or highly complex patterns of waves. We study the details of transitions between waves and their chaotic behavior to characterize the laws that govern their plasma environment. Moreover, we have used non-linear modeling and numerical simulations to understand in detail the complex patterns and the factors of stability underlying the phenomena of plasma waves. In addition, our study also investigates the correspondence between non-linearity, multi-stability, and the birth of complex structures such as solitons and kink waves. The solutions of the dynamical system produced by the proposed nonlinear model generate different patterns of response based on system parameter variation. These patterns include oscillations and decay behaviors. Research results about system stability and solution convergence under various parameter settings provide an extended performance evaluation of the proposed method through a better understanding of system dynamics. They increase our understanding of chaotic behavior in plasma systems and pave the way for applications in plasma physics and energy systems, as well as advanced technologies.
Keywords:
fractional diffusion–reaction models; nonlinear dynamical systems; fractional order derivatives; linear and nonlinear periodic wave; multi-stability; mathematical techniques MSC:
78-XX
1. Introduction
There are plasma waves [1], which are an important characteristic of plasma physics [2], contributing to the analysis of the motion of charged particles in plasma objects. These waves may be of the nonlinear periodic types, solitons, kinks, pulses, and solitary ones [3,4,5]. In plasma system stabilization, each type of wave has associated characteristic parameters that determine the stability of the system. An exciting feature of plasma systems is their sustenance in different stable conditions under almost similar circumstances, which is called multi-stability. Moreover, the time development of plasma waves may be rather complex; that is, even small variations in some parameters can lead to highly unpredictable dynamics. An essential aspect of the future development of plasma-based technologies like energy systems, fusion devices, and communication systems relies on understanding these nonlinear behaviors.
In nonlinear plasma waves [6], solitons are particularly important. These are specific waves that preserve waveform and wave velocity over a large distance despite having quite high nonlinearity and dispersion [7]. Other waves, for instance, will simply decay out over time, and so solitons retain specific restored shapes and are excellent for transmitting energy and information within plasmas. Here we pay attention to questions related to the formation of solitons [8], their stability depending on the parameters of the medium, and their behavior with kink and pulse waves. Most of these interactions lead to the emergence of some subtle processes like energy transport, wave interference, or even shifting from one mode to a chaotic state. From the soliton analysis, we hope to improve the understanding of energy transfer and the overall stability of a plasma medium. Chaos [9] is another interesting characteristic of the dynamics of nonlinear plasma systems and forms an important part of the plasma systems [10]. When non-linearities are the main constraint, it is possible to jump from the well-defined response space to chaotic states, which differ significantly depending on the initial conditions or other parameters. This is a sensitivity to initial conditions that disturbs the usual behavior associated with waves, such as solitons, and leads to instability of the system. They also described how chaos affects turbulence, which is another ever-present problem in plasma systems in the real world. Thus, learning when and how chaos appears [11], we reveal the processes that facilitate such transitions, and thus it is possible to find methods for controlling or even preventing such patterns. Managing chaos is a key element when looking at the optimization and enhancement of plasma-based systems, where areas such as fusion energy and plasma transmission exist [12].
Introducing the fractional derivatives [13] to describe the memory effects and long-range interactions, we employ fractional calculus as a theoretical tool to model the behavior of the plasma waves [14]. While the traditional derivatives select a single point with which other points are compared, fractional derivatives give the possibility to describe non-local interactions and historical behavior that is frequently registered in plasma systems. These properties are important for further representation of the temporal dynamics of plasma waves [15], which are important in systems with nonlinear interactions and coupling between the wave components. Integrating fractional calculus into the mathematical models will enable us to capture better how plasma waves change and act under various conditions than the classical approach. For the description of non-linear plasma wave phenomena, we use the Caputo Time-Fractional Lakshmanan–Porsezian–Daniel (LPD) model as an extended nonlinear Schrödinger-type equation that includes higher-order dispersion together with non-linear effects [16]. The Caputo Time-Fractional LPD model is given as:
where represent the wave function. : is a Caputo fractional derivative of y with respect to t, order . The coefficient stands for the chromatic dispersion (CD). Nonzero constant stands for the self-phase modulation stemming from the Kerr law for a nonlinear refractive index. The coefficient denotes the fourth-order dispersion (4OD) [17] and operates at the level of microwave photon energy, and a nonzero constant s is associated with quintic nonlinearity. Nonzero constants (i = 1, ..., 4) represent the nonlinear dispersion and the related physical phenomena. Thus, this equation is a suitable vehicle for examining soliton behavior, energy transportation, as well as chaotic switching in plasmas [18]. The higher-order dispersion term is a central part of the model and is essential for modeling solitary and various other features of a wave, for instance, wave breaking, soliton fission, and chaos [19].
This equation describes all the main effects related to plasma waves, such as solitons [20] dispersion, nonlinear interactions between the waves or with the plasma, as well as interactions between the wave modes. Wave breaking, sudden transitions, and energy transfer are also simulated, and based on these physical rules, complex behaviors are mimicked. Nonlinear structures such as solitons, kink waves [21] and others are inherent in this equation, making it an ideal platform for analyzing energy conduction as well as stability in plasma-based systems. We also perform bifurcation analysis [22,23] to identify qualitative changes of waves depending on values of the parameters [24], for example, lying between stable and chaotic domains. The bifurcations enable investigation of the emergence of instability and chaos that prevail in most plasma applications in practice [25]. For instance, it may be observed that when a parameter is changed, the dynamics supported by the system change from a soliton-stabilized state to a turbulent or chaotic state [26]. The following steps outline our approach for identifying these transitions and, thus, potential approaches for controlling or inhibiting chaos to enhance the controllable nature of plasma systems and applications.
To illustrate and explain the dynamics of nonlinear wave formations, we use numerical simulations in addition to theoretical explanations. Performing these simulations helps us to see how solitons, kink waves, and other types of waves are produced [27], respond, and how they transform and evolve into chaos depending on certain conditions. For instance, we investigate the effect of small-scale perturbations on solitons and their behavior and dynamics when encountering other waves, which cause energy rearrangement and formation of non-trivial, stochastic configurations. In addition to verifying mathematical predictions, simulations also reveal complex processes occurring internally in plasma systems. Using elements of such a novel approach as fractional calculus, it is possible to improve the model [28].
In this case, through the use of the -method [29], and bifurcation analysis with numerical simulations, this work has sought to give details on the plasma wave dynamics [30]. In our work, we examine several aspects of solitons, non-linearities, and chaotic transitions with implications for plasma dynamics mechanisms. The presented results are relevant to plasma physics, energy systems, and nonlinear dynamics, hence enabling advancements in stability and efficiency of plasma-based technology [31].
1.1. Fractional Order Derivatives
Fractional derivatives increase the mathematical order of differentiation beyond integers to provide an advanced tool for analyzing memory-dependent physical systems in complex situations. Fractional derivatives find specialized application in describing anomalous diffusion as well as describing viscoelasticity and wave propagation phenomena in plasma and electromagnetic systems. Fractional differentiation offers many definitions, of which the Riemann–Liouville, Caputo, and Grunwald–Letnikov methods represent distinct implementations with different applications. Out of these, the Caputo one is commonly applied particularly when addressing the nonlinear evolution forms, such as the Lakshmanan–Porsezian–Daniel (LPD) model. The Caputo derivative is the first option in physical problems due to its preservation of traditional initial conditions and effective approximation of memory effects. In the LPD model, the Caputo fractional derivatives are used to characterize the wave propagation eventualities in an energy beam and a system of electromagnetism, where it provides an efficient mechanism to track down anomalous dispersion and nonlocal dispersion results. Fractional derivatives serve widely in diffusion-reaction systems to detect nonlocal transport phenomena, which produce better predictions regarding wave behavior and stability shifts.
1.2. Main Contributions
- This work develops the classical LPD model through Caputo fractional-order derivative integration, which enhances simulation accuracy for plasma wave propagation under conditions that include memory effects and extended interactions.
- This paper examines fractional-order terms that affect the stability and evolution of plasma waves while showing their effects on dispersion properties and nonlinear wave interactions.
- The mathematical solutions identify critical features consisting of bifurcations together with chaotic phase transitions that occur in plasma wave mechanics.
- This research evaluates how Caputo fractional-order LPD mathematics function in tracing actual wave propagation processes. The obtained results establish a base that allows for using fractional calculus in electromagnetic wave propagation, nonlinear optics, and plasma physics applications.
2. A Description of the Proposed Methodology
To create the traveling wave solutions for the LPD Equation (1), we first break down
Note that the transformation , leads to a stationary spatial profile modulated by a harmonic time dependence. This approach is more representative of standing wave or modal analysis, rather than a traveling wave with propagation. Hence, is interpreted as a temporal frequency, where represents the real-valued function, which is the stationary wave’s amplitude component. The temporal frequency of the solitons is represented by the coefficient . Equation (1) is converted into an ordinary differential equation by inserting Equation (2).
When the coefficients of the linearly independent elements in Equation (3) are equal to zero, certain limits are imposed on its integrability, guaranteeing the plasma wave dynamics’ consistency. Considering , along with and , the LPD Equation (3) is reformulated into the following simplified version based on the aforementioned limitations:
The reduction from Equation (1) to Equation (4) was carried out by setting , and , with the intent to isolate the fundamental nonlinear dynamical features such as bifurcation and chaos. This simplification enables the analysis of the core structure of the system under minimal assumptions, which is a standard approach in early-stage dynamical system investigations. However, we understand that such simplifications omit higher-order impacts, such as fourth-order dispersion and complex nonlinearities, which can also have significant effects on the behavior of such systems.
where N is the polynomial of and its derivative , and so on. We assume that Equation (5) has a solution in the manner shown below:
The solution for appears in Equation (6) as a combination of parameters and G derivative transformations. The model contains two parameters, including a constant baseline value together with a scaling factor . The derivative function divided by expresses a normalized relationship, suggesting that the solution utilizes known transformed functions to fulfill the nonlinear ordinary differential equation. Assessment methods apply special functions as solutions to solve problems in many analytical approaches, particularly when studying nonlinear dynamical systems through elliptic functions, as well as solitonic solutions and perturbative expansions. The framework serves as a standardized procedure to analyze both the stability and bifurcations, as well as the chaotic dynamics of intricate dynamic systems with nonlinear characteristics.
By substituting Equation (6) into Equation (4) and analyzing the coefficients of different powers of , we derive the following system of algebraic equations:
By using the Maple software to solve the above algebraic equations, the following nontrivial solutions are obtained.
- Set 1:
- Set 2:
- Set 3:
Different solution sets deriving from the nonlinear differential system appear in the figure because of Maple software operations. The system parameters along with higher-order roots together with complex factor determine , and n through Equations (7)–(9). The various solution sets imply multiple acceptable solutions because symmetry and complex transformations seem to be the cause. The mathematical functions can be expressed as trigonometric and hyperbolic expressions depending on whether or . This proves the alternative behavior between oscillatory and exponentially decaying responses. The Equation (12) demonstrates a polynomial structure for when . The collected results indicate further research into parameter-stable solution behavior because they suggest the system could exhibit oscillatory patterns, decreasing trajectories, or combinations of these responses in dynamic conditions.
2.1. Case 1
2.2. Case 2
2.3. Case 3
3. Physical Analysis
In this article, we use Mathematica to modify and graphs to illustrate the traveling wave solutions found using the method and highlight the features of different plasma wave solutions. Several methods for understanding and visualizing interconnected physical processes are shown in Figure 1, Figure 2, Figure 3 and Figure 4. For each result, we have refined multiple soliton profiles by adjusting the exact values of the predefined parameters. Here is the physical representation of Set 1 and Set 2. The graph shows the solution in both two and three dimensions.It is important to clarify that these visualizations are based on stationary spatial profiles , modulated by a harmonic time factor . The time dimension in the plots corresponds to selected values of t, used to demonstrate how the stationary profile behaves under harmonic modulation. These are not full time-evolution simulations governed by the original PDE but rather illustrate standing wave patterns with periodic features. Solitary waves are nonlinear waves with specific amplitudes that do not interfere with one another at specific velocities and appear in the same form. These are plasma waves that develop in nonlinear systems to further maintain their form during an interaction with other waves.
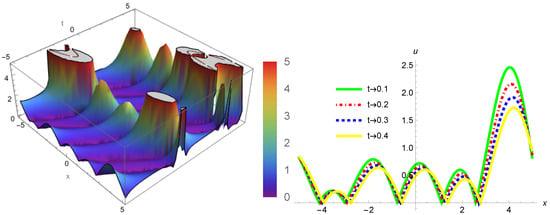
Figure 1.
The solution of describes the motion of a plasma wave propagating in two- and three-dimensional planes. Here, x represents the normalized distance through which the plasma wave has traveled, and t denotes the normalized time. Over time, the plasma wave’s behavior changes in various stages, such as .
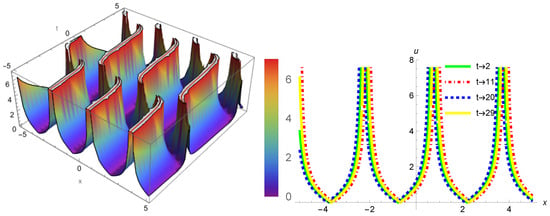
Figure 2.
The solution of describes the motion of a plasma wave propagating in two- and three-dimensional planes. Here, x represents the normalized distance through which the plasma wave has traveled, and t denotes the normalized time. Over time, the plasma wave’s behavior changes in various stages, such as .

Figure 3.
The solution of describes the motion of a plasma wave propagating in two- and three-dimensional planes. Here, x represents the normalized distance through which the plasma wave has traveled, and t denotes the normalized time. Over time, the plasma wave’s behavior changes in various stages, such as .
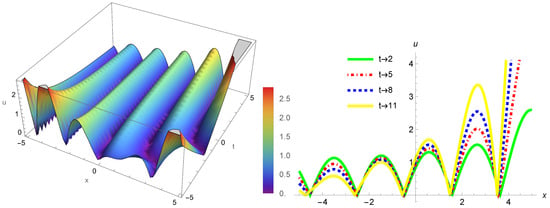
Figure 4.
The solution of describes the motion of a plasma wave propagating in two- and three-dimensional planes. Here, x represents the normalized distance through which the plasma wave has traveled, and t denotes the normalized time. Over time, the plasma wave’s behavior changes in various stages, such as .
Here, Figure 1 represents the variation of and concerning the spatial dimension x and the temporal dimension t, which can characterize plasma waves in a dynamic system. The structure of the graph corresponds to the solution, which has been deduced by solving Equation (13) of set 1 using parameters , , , , and . From a physical point of view, the spiky waves that can be observed in the graphical representation mean nonlinear oscillations of plasma waves, which suggests that there are areas in the waveform where the amplitude is high and areas where its level is low. The periodic structures along x indicate that these waves are dispersive, that is, wave components propagate through a medium with different velocities. This results in the peaks having varying characteristics over time, which is demonstrated along the t-axis. In conclusion, this graph reveals information concerning plasma wave propagation as well as its interaction in the context of a plasma system under the stated circumstances, focusing on their nonlinear as well as dispersive characteristics.
Figure 2 represent the solution of derived from Equation (16) of set 2 with specific parameters, , , , , and . The and structure of the graph emphasizes the dynamic behavior of plasma waves under these conditions. The peaked and periodic patterns appearing in the figure suggest nonlinear oscillations of the plasma waves, including areas of high and low amplitude. As time progresses along the t-axis, the dispersion leads to a change in the form of the wave peaks and their preservation of individuality with dynamic interconnections. The chosen graph allows for a clear display of both nonlinearity and dispersion within plasma systems.
In Figure 3, the and variations of are shown with the spatial dimension x and the temporal dimension t, which can be used to understand plasma waves in a dynamic system. By using the parameters, , , , , and , Equation (19) of set 3 was solved to obtain the structure of the graph. In the graph, regions of high and low amplitude are highlighted by the steep peaks and troughs that show the nonlinear oscillations of plasma waves. According to these oscillations, there is significant nonlinearity in the plasma system. It is suggested from the periodic structures along the x-axis that the waves are dispersive, meaning that the various components of the plasma wave propagate at different speeds. The dynamic evolution of these dispersive waves causes the formation and variation of sharp peaks throughout time, as shown along the t-axis. This graph does a good job of illustrating how nonlinearity and dispersion interact to produce the distinctive behavior of plasma waves.
Figure 4 illustrates the behavior of the solution, , which was obtained by solving Equation (19) from Set 3 with the following parameters, , , , , and . The surface plot displays plasma wave dynamics within a dynamic system by representing the u variation across spatial dimension x in addition to temporal dimension t. The dramatic shift in wave amplitude between high and low locations demonstrates nonlinearity among plasma waves through the regular peaks and troughs that appear across the x-axis. The plasma waves demonstrate dispersive properties through their smooth rhythm of fluctuations that unfold across the t-axis. Regarding acoustics, in this graph, the steepness of the oscillations is the expression of the nonlinear coupling between the plasma parameters, regulated by the values of , , , , , and . This analysis shows that plasma waves are both nonlinear and dispersive, depending on the conditions of the system and the governing equation.
4. Phase Portraits and the Behavior of Bifurcations
Bifurcation analysis is a very important factor when it comes to analyzing nonlinear fractional dynamical systems majorly in electromagnetic wave analysis in media. We thus apply bifurcation theory to determine the transition windows, with respect to wave motion, from stable to oscillatory waves or from periodic to chaotic motion. Therefore, by defining the equilibrium points in terms of the various parameters of the system, it is easy to identify regions of multiplicity and instability, which help in determining the nature of wave motion as described by fractional order nonlinear equations. This is closely associated with the numerical solution process of the fractional partial differential equations obtained based on GRMM and also with necessary input parameters like wave speed, dispersion coefficients or fractional orders, which slightly differ from the base values, influencing the waveform or the stability of the wave. It also improves the future behavior of the electromagnetic system behavior and sheds light on the sensitivity and memory-dependent behavior due to fractional derivatives as shown in the bifurcation diagrams. Also, the extension of bifurcation theory with fractional calculus adds more insights and realism into the model since it considers long-term memory and hereditary effects within the medium to describe the evolutions of electromagnetic waves in nonlinear dispersive mediums. In general, bifurcation analysis continues to be an important technique in this research and is useful for explaining chirped wave structures, determinations of multiple-stability domains, and theoretical developments of the current wave-based systems such as fiber optics and electromagnetic controls.
We analyze the behavior of the variable analytically, and phase portraits are effective tools for visualization of w in the dynamical system (22). These portraits allow us to determine how many fixed points there are and to gain insight into the dynamics of the system (plasma wave behavior). The fixed points can be identified by solving the dynamical system (22). These fixed points are , and with ; .
According to the theory of planar dynamical systems, a saddle point is an equilibrium point where the system’s trajectories approach but ultimately escape and move away from it, whereas a dynamic system oscillates around an equilibrium point called a center. We can investigate the existence of these equilibrium points in the following ways by solving the system (22): If , in the dynamical system (22), three fixed points are accepted , and ; with ; with ; ; .
However, the system only allows the fixed points , with when . The effective potential for different values of , , and is shown in Figure 5a,b. Figure 6a,b shows the same phase pictures for the identical values in Figure 5.
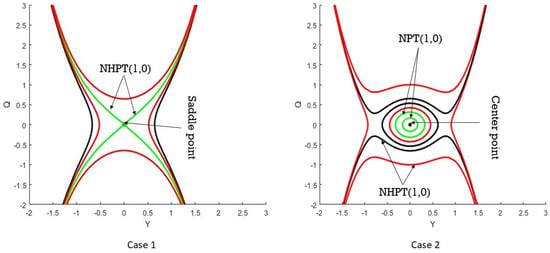
Figure 5.
Phase Portraits, Case 1 () and Case 2 ().
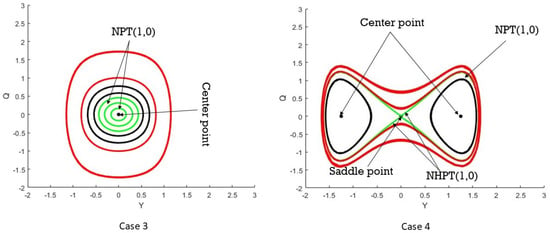
Figure 6.
Phase Portraits, Case 3 () and Case 4 ().
4.1. Case 1
- , , .
The dynamical structure of the system, Figure 5a, only shows saddle points for a phase portrait showing unstable equilibrium points where trajectories converge on the fixed point before diverging in different directions, corroborating the system’s saddle nature. Additional evidence of instability comes from the existence of intersecting separatrices. This structure, for example, is commonly realized in plasma wave dynamics, where perturbations of the system give rise to divergent trajectories that indicate regions of instability and energy transfer in the system.
4.2. Case 2
- , , .
The dynamical structure of the system (22) is given by a single fixed point.
- , and , with . The phase portrait, shown in Figure 5, shows a center equilibrium (green and black curves), by which closed orbits (periodic) indicate stable motion and boundedness. We find these trajectories to oscillate around the equilibrium point non divergently, demonstrating that the system remains conservative. In the case of the outermost trajectories, regions are demonstrated in the phase space where the motion is still contained but does not escape to infinity, confirming the stability of the central equilibrium.
4.3. Case 3
- , , .
The dynamical structure of the system, as depicted in Figure 6, can have a single fixed point , which represents a center. The phase portrait suggests the nature of oscillations as closed and cyclic, suggesting that the magnitude of displacement is finite, and it is not chaotic but stable around the equilibrium point. The existence of nested trajectories proved the fact of the system’s conservativeness since there is no energy loss. This is routine behavior in plasma wave systems in which wave–particle interactions result in oscillations about quasi-steady states, which can be attributed to trapping and recurrence characteristics of plasma systems.
4.4. Case 4
- , , .
The dynamical structure of the system (22) exhibits both saddle and center points, as shown in Figure 6. The saddle point at governs the unstable trajectories, where nearby orbits diverge away from the equilibrium along the separatrices. In contrast, for the center points at and , the system traces closed periodic orbits, which indicate equilibrium stability. Nonlinear stability results occur during plasma wave interactions due to energy exchange and lead to genuine orbits forming around centers, as unbounded motion is influenced by saddle points.
5. Chaos and Quasi-Periodic Behaviors
The characteristics of the dynamical systems’ chaotic and quasi-periodic motions will be covered in detail in this section. The term will be specifically added to system (22) to produce the following form:
where is the constant of the external periodic disturbance’s magnitude and w is the constant of the external disturbance’s frequency, respectively. To facilitate chaos analysis involving time-dependent forcing, we reinterpret the variable as a time-like variable t. This transition allows us to treat system (23) as a dynamical system evolving in time under external periodic excitation. The chaotic behavior of the system (23), as examined by [18], offers vital insights into the unpredictable dynamics present in nonlinear systems, including the behavior of plasma waves. Here, we use several numerical techniques to examine each type of quasi-periodic. The dynamical system consists of nine independent parameters: I, a, b, c, d, A, B, C, and D. Because there are so many systems, it is challenging to analyze them by varying each parameter. Therefore, we considered specific parameter values, such as , , , , , , , and , in order to simplify the study. The latter two parameters, w and , are crucial systems to perceive the chaotic and quasi-periodic features in the dynamical system (23).
5.1. Quasi Periodic Oscillations
Case 1: :
Figure 7a–c illustrates the quasi-periodic behavior of the dynamical system (23) at . These figures present the and phase portrait alongside the time series plot. The phase portrait shows typical trajectories through the overlay of multiple trajectories that mirror the phase portrait’s fundamental structures. Additionally, the presence of a plasma wave is evident in the phase portrait, highlighting the nonlinear energy distribution and reinforcing the quasi-periodic motions observed in the system. In the time series plot, both the period and systemic amplitude remain constant, whereas the subsequent period exhibits slight reductions. The system’s behavior confirms a quasi-periodic cycling pattern. A comparative analysis with the findings in [18] reveals significant similarities and differences between the studied systems. The system’s stable structure depends on the plasma wave’s primary role in controlling both instabilities and maintaining ordered dynamics.
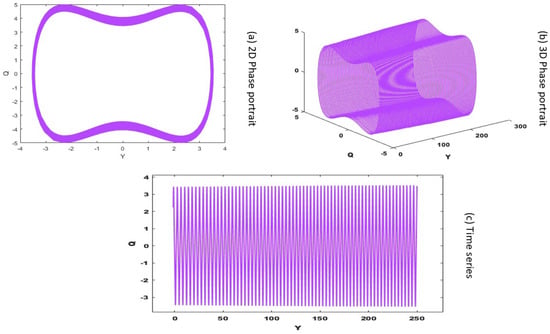
Figure 7.
Quasi-periodic behavior for .
Case 2: : the quasi-periodic behavior of the dynamical system (23) is examined by setting and . The results are displayed in Figure 8a–c, which show the time series and phase portrait, respectively, using the same parameters as in Figure 7. The phase portrait shows a regular trajectory superimposed on another but with a different shape compared to Figure 7. The time series generates packets with similar amplitudes within a clearly defined time interval. These graphs demonstrate the quasi-periodic behavior of the system.
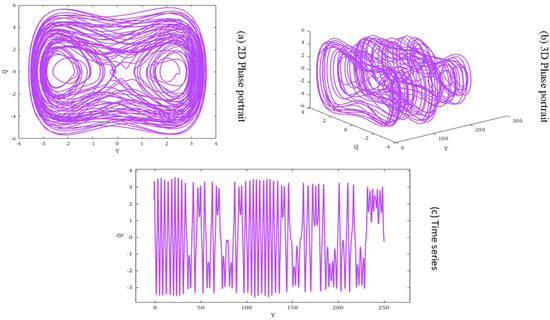
Figure 8.
Quasi-periodic behavior for and .
Additionally, the presence of a plasma wave in the system can be inferred from the dynamics in the phase portrait, as it influences the nonlinear energy distribution and affects the quasi-periodic motions. The plasma wave further reinforces the quasi-periodic cycling observed in the system. It is worth noting that although the parameters in Figure 7 and Figure 8 are the same, the different values of and w have caused variations in the shapes and patterns of the phase portrait and time series, highlighting the system’s sensitivity to changes in these parameters.
5.2. Chaotic Pattern
As for the properties of the dynamical system (23), we will proceed to analyze the chaotic behavior. First, we take a case where all parameters are fixed except for one parameter. When and , the response system (23) in its time series and phase portrait demonstrates quasi-periodicity, as is depicted in Figure 8. Subsequently, we investigate the effect of shifting by fixing while holding all other parameters constant, as depicted in Figure 8. These results are provided in Figure 9a–c, for time series, phase portrait, and plasma wave effects. When , the phase profile is rather ambiguous, the time series exhibits irregular oscillations of the amplitude, and the impact of the plasma wave can be observed. Such outcomes show that the system is vulnerable to variations in parameters and how it can transition to chaotic dynamics. The quasi-periodic signal can be described as a sum of periodic and random signals, with the result that, when this signal undergoes periodic external interference, productive chaos occurs. Chaotic signals can be employed in sc conversion, making the signals suitable for the transmission of secure information.
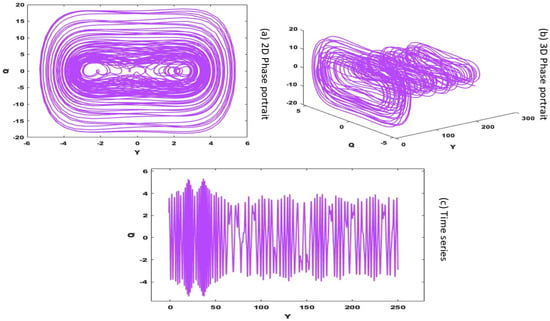
Figure 9.
Chaotic behavior for .
6. Comparison with Existing Models
- Classical integer-order models vs. fractional-order models: the traditional plasma wave models base their analysis on integer-order differential equations that use local interaction methods while having no memory features. The simplified wave behavioral representation offered by these models proves insufficient because they lack a full understanding of longer-scale correlations, together with complex wave movement patterns. The fractional-order approach includes memory-dependent terms because they enable more accurate simulations of wave propagation along with dispersion phenomena and system stability features.
- Existing chaotic wave models vs. lpd-based fractional model: most research on plasma chaos previously employed standard nonlinear Schrödinger equations as well as Ginzburg–Landau equations or Duffing-like oscillators. Periodic waveforms and solitary wave solutions match the performance of these models until they fail to capture chaotic wave behavior. Through the introduction of fractional diffusion-reaction components, the Caputo type LPD model expands previous research to enhance the characterization of plasma systems regarding their multi-stability features and periodic wave patterns and chaotic attractor dynamics.
- Comparison with perturbative and numerical methods: two main analytical tools, referred to as multiple-scale analysis and variational approaches, have traditionally been used to research wave stability patterns in plasma systems. These analysis techniques need to establish specific restrictions when studying wave phenomena. Bifurcation analysis, together with numerical simulations, allows a complete assessment of wave behavior as it depends on varying parameters, which reveals important information about stable and unstable domains.
- Phase portraits and bifurcation analysis: research on wave dynamics fails to provide organized phase analysis for visualizing how waves transform into different operating states. The systematic creation of phase diagrams through our research enables the identification of stable, periodic, and chaotic regions through system parameter assessment. The visual diagrams enhance understanding of plasma instabilities, together with nonlinear effects.
7. Conclusions
This research analyzed how fractional derivatives affect plasma wave dynamical patterns through the Lakshmanan–Porsezian–Daniel (LPD) model by studying phase portraits and nonlinear wave propagation. The research findings demonstrate how fractional-order diffusion–reaction mechanisms form complex patterns that determine the stability of waves and interactions between solitons and the onset of chaotic behavior. System parameters led to the appearance of multi-stability patterns and periodic waveforms and chaotic wave patterns through bifurcation analysis and numerical simulations. Fractional-order derivatives affect plasma wave solutions through memory effects that produce important modifications to their long-term behavior, which allows a better understanding of wave dispersion relations with external perturbations and dissipation effects. The main achievement of this research involves employing nonlinear dynamical systems analysis to identify factors that lead to plasma wave stability and chaotic shifts. Our analysis of phase portraits and bifurcation diagrams demonstrated the successful discovery of parameter domains that resulted in complex pattern emergence in wave structures, thus explaining the basic principles of plasma instability development. This study conducted an extensive performance review, which demonstrated how the proposed system successfully predicted wave changes while describing how fractional models outperform standard integer-order methods.
The promising research outcomes need to consider specific limitations in their evaluation. The current investigation concentrates on single-dimensional wave propagation analysis, although it lacks an extensive examination of multidimensional plasma dynamic behavior. Future research should develop the model to incorporate multi-dimensional structures to study additional nonlinear response patterns. Experimental testing is required to verify that the proposed model can accurately predict real-world plasma systems even after its numerical simulations provide useful information. Studies of fractional-order systems encounter difficulties due to the absence of analytical solutions because researchers must create advanced numerical methods for better performance. Research needs to probe fractional plasma wave reactions under external stimuli and boundary constraints because these mechanisms remain uncertain. The work builds essential knowledge for dimensional plasma wave analysis by creating direction for improved nonlinear wave modeling approaches in upcoming research. The research creates foundations for precise wave prediction and new electromagnetic applications by resolving identified drawbacks while expanding evaluation across additional domains of plasma and optical systems and electromagnetic systems.
Future Developments
Future research aims to improve fractional dynamical system applications for plasma physics, along with other fields, through theoretical advancements that achieve an advanced understanding of complex wave behavior.
- Research into multi-component plasma environments using higher-dimensional plasma wave systems needs further development of the fractional-order Lakshmanan–Porsezian–Daniel (LPD) model.
- Experiments should be conducted to test computational and theoretical findings through the simulation of plasma wave phenomena under fractional-order rules.
- By adopting machine learning approaches, scientists can enhance their capability to predict plasma wave bifurcation patterns and chaotic transitions, which would benefit nonlinear wave control and optimization strategies.
- These research methods demonstrate value for advancement in different fields, primarily including nonlinear optics and quantum mechanics, as well as geophysical fluid dynamics since fractional-order models excel at evaluating long-term relationships and accumulated past responses.
- New computational approaches should be developed to enhance both the speed and accuracy of plasma wave simulations and electromagnetic wave propagation forecasts for live applications.
Author Contributions
Conceptualization, A.G.K.; formal analysis, Z.U.R.; funding acquisition, S.S.; investigation, Z.U.R.; methodology, A.G.K.; project administration, M.Z.; software, M.M.; supervision, S.S.; validation, M.M.; writing—original draft, M.Z.; writing—review and editing, S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research is self funded.
Data Availability Statement
No data required for this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rehman, Z.U.; Zahid, M.; Bolla, D.P.; Shoaib, S.; Amin, Y.; Khattak, R.; Muddassar, M. Nonlinear wave dynamics and multistability in engineering electromagnetics: Numerical analysis of perturbed and un-perturbed systems within the Higgs field. Results Eng. 2025, 25, 104375. [Google Scholar] [CrossRef]
- Chatterjee, R. Fundamental Concepts and Discussion of Plasma Physics. TECHNO REVIEW J. Technol. Manag. 2022, 2, 1–14. [Google Scholar] [CrossRef]
- Ren, Y.; Yang, Z.Y.; Liu, C.; Yang, W.L. Different types of nonlinear localized and periodic waves in an erbium-doped fiber system. Phys. Lett. A 2015, 379, 2991–2994. [Google Scholar] [CrossRef]
- Demiray, S.T.; Bulut, H. Soliton solutions of some nonlinear evolution problems by GKM. Neural Comput. Appl. 2019, 31, 287–294. [Google Scholar] [CrossRef]
- Yang, L.; Gao, B. Solitons, kink-solitons and breather solutions of the two-coupled incoherent nonlinear Schrödinger equation. Nonlinear Dyn. 2024, 112, 5621–5633. [Google Scholar] [CrossRef]
- Ghandour, R.; Karar, A.S.; Al Barakeh, Z.; Barakat, J.; Rehman, Z. Non-Linear Plasma Wave Dynamics: Investigating Chaos in Dynamical Systems. Mathematics 2024, 12, 2958. [Google Scholar] [CrossRef]
- Shu, W.; Zhao, C.; Wen, S. Dispersion and nonlinearity in subwavelength-diameter optical fiber with high-index-contrast dielectric thin films. Proc. SPIE Int. Soc. Opt. Eng. 2010, 7846. [Google Scholar] [CrossRef]
- Singh, P.; Senthilnathan, K. Evolution of a solitary wave: Optical soliton, soliton molecule and soliton crystal. Discov. Appl. Sci. 2024, 6, 464. [Google Scholar] [CrossRef]
- Hussain, Z.; Rehman, Z.; Abbas, T.; Smida, K.; Le, Q.; Abdelmalek, Z.; Tlili, I. Analysis of bifurcation and chaos in the traveling wave solution in optical fibers using the Radhakrishnan–Kundu–Lakshmanan equation. Results Phys. 2023, 55, 107145. [Google Scholar] [CrossRef]
- Irimiciuc, S.; Saviuc, A.; Tudose-Sandu-Ville, F.; Toma, S.; Nedeff, F.; Rusu, C.; Agop, M. Non-Linear Behaviors of Transient Periodic Plasma Dynamics in a Multifractal Paradigm. Symmetry 2020, 12, 1356. [Google Scholar] [CrossRef]
- Breedt, I.; Fourie, A. The Ripple Effect: How Chaos Theory can Transform Education. Int. Conf. Educ. Res. 2024, 1, 29–35. [Google Scholar] [CrossRef]
- Ham, C.; Kirk, A.; Pamela, S.; Wilson, H. Filamentary plasma eruptions and their control on the route to fusion energy. Nat. Rev. Phys. 2020, 2, 159–167. [Google Scholar] [CrossRef]
- Ortigueira, M.; Tenreiro Machado, J. What is a fractional derivative? J. Comput. Phys. 2014, 293, 4–13. [Google Scholar] [CrossRef]
- Lazarević, M.; Rapaić, M.; Šekara, T. Introduction to Fractional Calculus with Brief Historical Background; WSEAS Press: Zografou, Greece, 2014; pp. 3–16. [Google Scholar]
- Grach, S.; Mishin, E.; Sergeev, E.; Shindin, A. Dynamic properties of ionospheric plasma turbulence driven by high-power high-frequency radiowaves. Physics-Uspekhi 2016, 59. [Google Scholar] [CrossRef]
- Tang, L.; Biswas, A.; Yildirim, Y.; Alshomrani, A. Bifurcations and optical soliton perturbation for the Lakshmanan–Porsezian–Daniel system with Kerr law of nonlinear refractive index. J. Opt. 2024. [Google Scholar] [CrossRef]
- Khelil, K.; Dekhane, A.; Benselhoub, A.; Bellucci, S. Higher order dispersions effect on high-order soliton interactions. Technol. Audit. Prod. Reserv. 2023, 2, 70. [Google Scholar] [CrossRef]
- Hamza, A.; Suhail, M.; Alsulami, A.; Mustafa, A.; Aldwoah, K.; Saber, H. Exploring Soliton Solutions and Chaotic Dynamics in the (3+1)-Dimensional Wazwaz–Benjamin–Bona–Mahony Equation: A Generalized Rational Exponential Function Approach. Fractal Fract. 2024, 8, 592. [Google Scholar] [CrossRef]
- Alraqad, T.; Suhail, M.; Saber, H.; Aldwoah, K.; Eljaneid, N.; Alsulami, A.; Muflh, B. Investigating the Dynamics of a Unidirectional Wave Model: Soliton Solutions, Bifurcation, and Chaos Analysis. Fractal Fract. 2024, 8, 672. [Google Scholar] [CrossRef]
- Zabolotnykh, A. Nonlinear Schrodinger equation for a two-dimensional plasma: The analysis of solitons, breathers, and plane wave stability. arXiv 2023, arXiv:2302.01057. [Google Scholar] [CrossRef]
- Seadawy, A.; Iqbal, M.; Lu, D. Propagation of kink and anti-kink wave solitons for the nonlinear damped modified Korteweg–de Vries equation arising in ion-acoustic wave in an unmagnetized collisional dusty plasma. Phys. A Stat. Mech. Its Appl. 2019, 544, 123560. [Google Scholar] [CrossRef]
- Bhowmike, N.; Rehman, Z.U.; Zahid, M.; Shoaib, S.; Mudassar, M. Bifurcation and multi-stability analysis of microwave engineering systems: Insights from the Burger–Fisher equation. Phys. Open 2024, 21, 100242. [Google Scholar] [CrossRef]
- Jhangeer, A.; Almusawa, H.; Hussain, Z. Bifurcation study and pattern formation analysis of a nonlinear dynamical system for chaotic behavior in traveling wave solution. Results Phys. 2022, 37, 105492. [Google Scholar] [CrossRef]
- El-Dessoky, M.; Elmandouh, A. Qualitative analysis and wave propagation for Konopelchenko-Dubrovsky equation. Alex. Eng. J. 2023, 67, 525–535. [Google Scholar] [CrossRef]
- Triki, H.; Biswas, A.; Milović, D.; Belić, M. Chirped femtosecond pulses in the higher-order nonlinear Schrödinger equation with non-Kerr nonlinear terms and cubic–quintic–septic nonlinearities. Opt. Commun. 2016, 366, 362–369. [Google Scholar] [CrossRef]
- Bohr, T.; Jensen, M.; Paladin, G.; Vulpiani, A. Dynamical Systems Approach to Turbulence; Cambridge University Press: Cambridge, UK, 2005; Volume 8. [Google Scholar] [CrossRef]
- Bibi, A.; Shakeel, M.; Khan, D.; Hussain, S.; Chou, D. Study of solitary and kink waves, stability analysis, and fractional effect in magnetized plasma. Results Phys. 2023, 44, 106166. [Google Scholar] [CrossRef]
- Kumar, M.; Mehta, U.; Cirrincione, G. A Novel Approach to Modeling Incommensurate Fractional Order Systems Using Fractional Neural Networks. Mathematics 2023, 12, 83. [Google Scholar] [CrossRef]
- Wang, M.; Li, X.; Zhang, J.L. The G′G2-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A 2007, 372, 417–423. [Google Scholar] [CrossRef]
- Salinger, A.; Phipps, E.; Dijkstra, H.; Wubs, F.; Cliffe, K.; Doedel, E.; Dragomirescu, I.; Eckhardt, B.; Gelfgat, A.; Hazel, A.; et al. Numerical Bifurcation Methods and their Application to Fluid Dynamics: Analysis beyond Simulation. Commun. Comput. Phys. 2014, 15, 1–45. [Google Scholar] [CrossRef]
- Bonizzoni, G.; Vassallo, E. Plasma physics and technology; Industrial applications. Vacuum 2002, 64, 327–336. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).